力矩分配法的基本概念

§8.1力矩分配法的基本概念力矩分配法是在位移法的基础上发展起来的一种渐近法，它主要应用于分析连续梁和无结点线位移的刚架。

杆端弯矩的正负号规定与位移法相同。

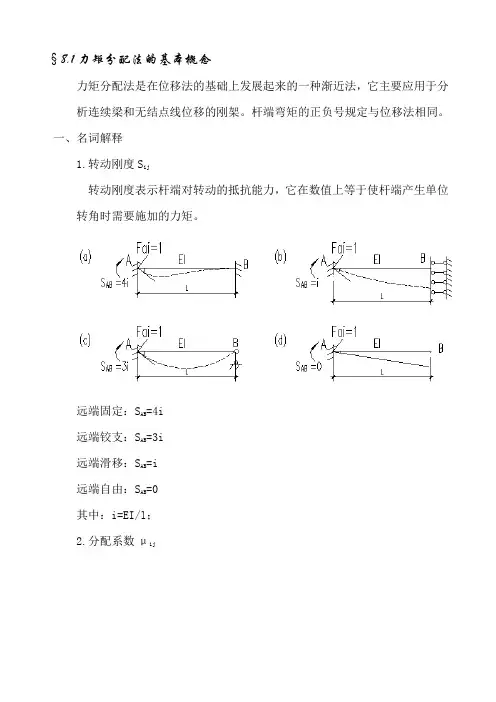
一、名词解释1.转动刚度S ij转动刚度表示杆端对转动的抵抗能力，它在数值上等于使杆端产生单位转角时需要施加的力矩。

远端固定：S AB=4i远端铰支：S AB=3i远端滑移：S AB=i远端自由：S AB=0其中：i=EI/l；2.分配系数μij由转动刚度的定义可知：M AB= S AB•θA=4i AB•θAM AC= S AC•θA=i AC•θAM AD= S AD•θA=3i AD•θA取结点A为隔离体，列ΣM=0，可得：M= S AB•θA+ S AC•θA+ S AD•θAM M∴θ= ──────── = ──S AB + S AC + S AD ΣSΣS表示各杆A端转动刚度之和，把θ反代入，可得：M AB=M• S AB/ΣS M AC=M• S AC/ΣS M AD=M• S AD/ΣS令μAj= S Aj/ΣS 则 M Aj=μAj•MμAj称为分配系数，等于某杆的转动刚度与交于结点的各杆的转动刚度之和的比值；同一结点各杆分配系数之间存在下列关系：ΣμAj=μAB +μAC +μAD = 13.传递系数C AjM AB =4i AB•θA，M BA =2i AB•θAM AC =i AC•θA， M CA = -i AC•θAM AD =3i AD•θA，M DA =0C AB= M BA / M AB =1/2∴远端固定：C=1/2远端滑动：C=-1远端铰支：C=0用下列公式表示传递系数的应用：M BA = C AB• M AB系数C AB称为由A端至B端的传递系数；二、力矩分配的基本概念如下图所示结构，用位移法计算时，此结构有一具未知量Z1，典型方程为：r11•Z1 + R1p = 0r11=3i12 + i13 + 4i14 = S12 + S13 + S14 =ΣSR1P =ΣM1j g =M12g +M13g =M1gR1P代表附加刚臂上反力矩，它等于汇交于结点1的各杆端的固端弯矩的代数和，用M1g表示。

第十七章力矩分配法一、力矩分配法的基本概念力矩分配法是在位移法基础上发展起来的一种数值解法，它不必计算节点位移，也无须求解联立方程，可以直接通过代数运算得到杆端弯矩。

力矩分配法的适用对象:是连续梁和无节点线位移刚架。

内力正负号的规定:同位移法的规定一致。

杆端弯矩使杆端顺时针转向为正，固端剪力使杆端顺时针转向为正。

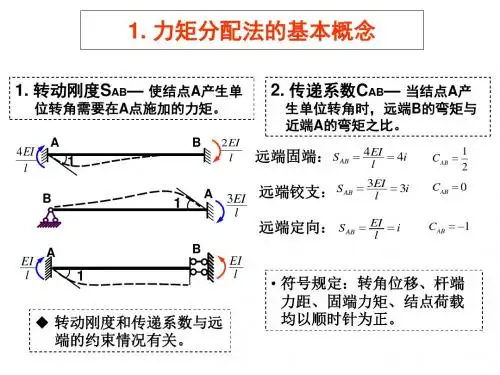
1、转动刚度(S)定义:杆件固定端转动单位角位移所引起的力矩称为该杆的转动刚度，(转动刚度也可定义为使杆件固定端转动单位角位移所需施加的力矩)。

转动刚度与远端约束及线刚度有关远端固定: S = 4 i远端铰支: S = 3i远端双滑动支座: S = i远端自由: S = 0 (i为线刚度)力矩分配法的基本思路,刚节点B将产生一个转角位移FM固端弯矩():是被约束隔离各杆件在荷载单独作用下引起的杆端弯矩。

FFFF MMMM,，，BBABCBDFM一般地不等于零，称为节点不平衡力矩现放松转动约束，即去掉刚臂，这个状态称为放松状态，节点B将产生角位移，并在各杆端(包括近端和远端)引起杆端弯矩，记作M’，则固端弯矩与位移弯矩的代数和就是最终杆端弯矩2、近端位移弯矩的计算及分配系数AB杆:远端为固定支座，转动刚度SBA = 4iBC杆:远端为铰支座，转动刚度SBC = 3iBD杆:远端为双滑动支座，转动刚度SBD = i 各杆近端(B端)的杆端弯矩表达式:FFF,MMMiMSM4,,,，,，,，BABABABABABAFFF,MMMiMSM3,,,，,，,，CCBBCBCBBCBCFFF,MMMiMSM,,,，,，,，BBDBDBBDBDDD式中:23FlqlFFFM,,M,0M,CBDBAB1612显然，杆的近端位移弯矩为:,,,MS,MS,,MS,,,BABABDBDBCBC由B节点的力矩平衡条件ΣM = 0得:FFFS,，M，S,，M，S,，M,0BABABCBCBDBDM，M，M,0 BABCBD解得未知量θ为:FFFF(,M,M,M)(,,M)BCBCBCB,,, S，S，S,SBABCBDB解得的未知量代回杆近端位移弯矩的表达式，得到将未知量代回杆近端分配弯矩的表达式，得到:SFBA,M,S,,(,,M)BABAB,SBSFBC,M,S,,(,,M)BCBCB,SBSFBD,M,S,,(,,M)BDBDB,SB上式中括号前的系数称为分配系数，记作μ，即:SSSBCBABD,,,,,,BABCBD,S,,SSBBB一个杆件的杆端分配系数等于自身杆端转动刚度除以杆端节点所连各杆的杆端转动刚度之和。

前面介绍的力法和位移法，是分析超静定结构的两种基本方法。

两种方法都要建立方程并解联立方程解联立方程直接解法渐近解法结构力学中的渐近法有两种应用方式。

•先从力学上建立方程组，然后从数学上对方程组采用渐近解法。

•不建立方程组，直接考虑结构的受力状态，从开始时的近似状态，逐步调整，最后收敛于真实状态。

力矩分配法属于位移法类型的渐近解法。

力矩分配法适用于连续梁和无结点线位移的刚架。

一、力矩分配法中使用的的几个名词(1) 转动刚度转动刚度表示杆端对转动的抵抗能力。

杆端的转动刚度以S表示，它在数值上等于使杆端产生单位转角时在转动端需要施加的力矩。

第一节力矩分配法的基本概念l EI A B 1l EI S AB /4=lEI S AB /3=A B 1A B 1lEI S AB /=A B 0=AB S (a)(b)(c)(d)远端固定，S ＝4i 远端简支，S ＝3i 远端滑动，S ＝i 远端自由，S ＝0(10-1)(10-2)(10-3)(10-4)图10-1给出了等截面杆件在A 端的转动刚度S AB 的数值。

1)在S AB 中，A 点是施力端，B 点称为远端。

当远端为不同支承地情况时，S AB 的数值也不同。

2)S AB 是指施力端A 在没有线位移的条件下的转动刚度。

在图10–1中，A 端画成铰支座，其目的是为了强调A 端只能转动、不能移动这个特点。

如果把A 端改成辊轴支座，则S AB 的数值不变。

也可以把A 端看作可转动(但不能移动)的刚结点。

这时S AB 就代表当刚结点产生单位转角时在杆端A 引起的杆端弯矩。

关于S AB 应当注意下列几点：3)式(10–1)到(10–3)可由位移法中的杆端弯矩公式导出。

式中lEI i(2) 分配系数图7–2a 所示为三杆AB 、AC 和AD 在刚结点A 连结在一起。

为了便于说明问题，设B 端为固定端，C 端为定向支座，D 端为铰支座。

设有力偶荷载M加于结点A ，使结点A产生转角 A ，然后达到平衡。

力矩分配法的基本概念力矩分配法是计算连续梁和无侧移刚架的一种实用计算方法，它不需要建立和求解基本方程，可直接得到杆端弯矩。

运算简单，计算方法有一定规律，便于掌握，适合手算。

理论基础：位移法；计算结果：杆端弯矩；适用范围：连续梁和无侧移刚架。

一、正负号规定在力矩分配法中，杆端转角、杆端弯矩、固端弯矩的正负号规定与位移法相同，即都假定对杆端顺时针转动为正。

作用在结点上的外力偶荷载，约束力矩，也假定顺时针转动为正，而杆端弯矩在结点上表示时逆时针转动为正。

二、转动刚度S转动刚度表示杆端对转动的抵抗能力。

在数值上等于使杆端发生单位转动时需在杆端施加的力矩。

AB杆A端的转动刚度S B与AB杆的线刚度i （材料的性质、横截面的形状和尺寸、杆长）及远端支承有关，而与近端支承无关。

当远端是不同支承时，等截面杆的转动刚度如下：三、传递系数C杆端转动时产生的远端弯矩与近端弯矩的比值。

即:远端弯矩可表达为：M BA C AB M AB等截面直杆的传递系数与远端的支撑情况有关:远端固定: C=1/2远端铰支: C=0远端滑动: C=-1四、多结点无侧移结构的计算注意:①多结点结构的力矩分配法得到的是渐近解。

②首先从结点不平衡力矩较大的结点开始，以加速收敛。

③不能同时放松相邻的结点（因为两相邻结点同时放松时，它们之间的杆的转动刚度和传递系数定不出来）；但是，可以同时放松所有不相邻的结点，这样可以加速收敛。

④每次要将结点不平衡力矩变号分配。

⑤结点i的不平衡力矩M i等于附加刚臂上的约束力矩，可由结点平衡求得。

例题；用力矩分配法画连续梁的M图，EI为常数。

2 S BA =4订人=4 X g = 1 »BA =0・43 3 S B C ==4t BC =4Xy = y P BC =O ・ 6S CB = 4/CB = 4X-|- = -|-卩CB = O ・ 6oScD = 3 2 CD = 3 X — = 1 o （2）计算固端弯矩腹=_城8 = _+ • p • Z=-jX10X8=-10kN •M D = -j - q - Z 2 = yX2X62 = -9k N ・m ・ （3）分配与传递p 解：（i ）计算分配系数（令EI=1） q“CD=0・ 4(4) 画弯矩图(kN • m)>12.39。