换元法在不定积分和定积分中的联系与区别

积分的定积分与不定积分积分是微积分中的重要概念之一，用于求解曲线下面积、函数的平均值、变化率等问题。

在积分中，我们常常会遇到定积分和不定积分两种形式。

本文将从定义、性质、计算方法等方面介绍定积分和不定积分的基本知识。

一、定积分的定义与性质定积分是对函数在给定区间上的积分，它的定义如下：设函数f(x)在区间[a, b]上有界，将[a, b]分成n个小区间，其中第i 个小区间为[x_(i-1), x_i]，对于任意一个小区间，取其左端点上的函数值f(x_(i-1))作为近似值，求所有小区间上的近似求和，然后令n趋向于无穷大，即可得到定积分的值。

定积分的性质如下：1. 定积分的值和积分的区间有关，即[a, b]上的积分与[b, a]上的积分相差一个负号，表示积分的方向。

2. 一个区间上的定积分可以分割成多个子区间的积分之和，即[a, b]上的积分等于[a, c]上的积分加上[c, b]上的积分。

3. 函数的常数倍不影响定积分的值，即k∫f(x)dx = ∫(k*f(x))dx。

4. 定积分有加法原理，即∫(f(x)+g(x))dx = ∫f(x)dx + ∫g(x)dx。

二、不定积分的定义与性质不定积分是求解函数的原函数的过程，它的定义如下：设函数f(x)在区间I上有原函数F(x)，则F(x)+C称为f(x)在I上的不定积分，其中C为任意常数。

不定积分的性质如下：1. 函数的不定积分是原函数的集合，因为对于任意一个原函数F(x)，都有F(x)+C是f(x)的不定积分，其中C为任意常数。

2. 不定积分具有线性性质，即∫(af(x)+bg(x))dx = a∫f(x)dx + b∫g(x)dx，其中a、b为常数。

3. 不定积分有积分微分的逆运算性质，即函数f(x)在[a, b]上可积的充分必要条件是它在[a, b]上有连续的原函数。

三、定积分与不定积分的关系在计算上，定积分和不定积分是相互联系的。

下面是一些常见的关系：1. 定积分可以通过不定积分来求解，即∫(a, b)f(x)dx = F(x)∣_(a, b) = F(b) - F(a)，其中F(x)为f(x)的一个原函数。

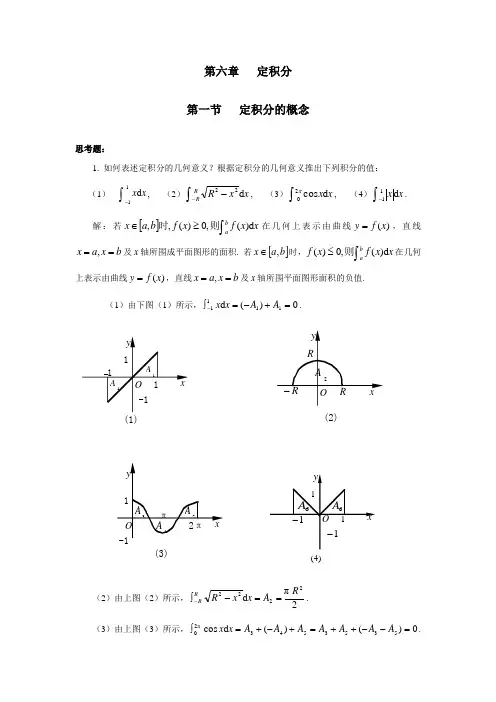
第六章 定积分第一节 定积分的概念思考题：1. 如何表述定积分的几何意义？根据定积分的几何意义推出下列积分的值： （1）⎰-x x d 11, （2）⎰--x x R R R d 22, （3）⎰x x d cos 02π, （4）⎰-x x d 11.解：若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时，⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围平面图形面积的负值.（1）由下图（1）所示，0)(d 1111=+-=⎰-A A x x .（2）由上图（2）所示，2πd 2222R A x x R R R==-⎰-.（3）由上图（3）所示，0)()(d cos 5353543π20=--++=+-+=⎰A A A AA A A x x .( 2)( 1 )( 3 )(4)（4）由上图（4）所示，1112122d 611=⋅⋅⋅==⎰-A x x . 2. 若当b x a ≤≤，有)()(x g x f ≤，下面两个式子是否均成立，为什么？（1）x x g x x f ba b a d )(d )(⎰≤⎰, （2）x x g x x f d )(d )(⎰≤⎰.答：由定积分的比较性质知（1）式成立，而不定积分的结果表示一族函数，x x f d )(⎰与x x g d )(⎰不能比较大小，故（2）式不成立.3. n 个数的算术平均值与连续函数在闭区间上的平均值有何区别与联系？答：二者均反映了多个数的平均值大小，后者是前者的推广，但n 个数的算术平均值是有限个数的平均值，而连续函数在闭区间上的平均值反映的是无限个数的平均值，前者计算公式是∑=ni i a n 11,后者计算公式是⎰-b a x x f a b d )(1.习作题：1. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解：任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =，小区间长度记为∆i=i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式：∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.2. 利用定积分的估值公式，估计定积分⎰-+-1134)524(x x x d 的值.解：先求524)(34+-=x x x f 在[]1,1-上的最值，由0616)(23=-='x x x f , 得0=x 或83=x . 比较 7)1(,102427)83(,5)0(,11)1(=-===-f f f f 的大小，知 11,102427max min =-=f f ，由定积分的估值公式，得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即 22d )524(512271134≤+-≤-⎰-x x x . 3. 求函数21)(x x f -=在闭[-1，1]上的平均值.解：平均值⎰-=⋅⋅=---=11224π21π21d 1)1(11x x μ.4. 利用定积分的定义证明⎰-=b aa b x d .证明：令1)(=x f ,则⎰⎰=b ab a x x f x d )(d ，任取分点10x x a <=…b x n =<,把[]b a ,分成n 个小区间[]i i x x ,1-，并记小区间长度为),2,1(1n i x x x i i i ⋅⋅⋅⋅=-=∆-，在每个小区间[]i i x x ,1-上任取一点i ξ，作乘积⋅)(i f ξi x ∆的和式a b x x f n i ni i i i -=∆=∆⋅∑∑==11)(ξ,记}{max 1i ni x ∆=≤≤λ, 则 a b a b x f x x ni i i ba -=-=∆⋅=→=→∑⎰)(lim )(lim d 01ξλ.第二节 微积分基本公式思考题：1. ='⎰)d sin (d d 1xt t t ?答：因为⎰x t t 1d sin 是以x 为自变量的函数，故⎰xt t t1d sin d d =0. 2. ?)d )((21='⎰x x f答：因为⎰21d )(x x f 是常数，故0)d )((21='⎰x x f .3.=⎰ba x x f xd )(d d ？ 答：因为⎰b ax x f d )(的结果中不含x ，故=⎰ba x x f xd )(d d 0. 4. =⎰xax t x d cos d d 2？ 答：由变上限定积分求导公式，知=⎰x ax t x d cos d d 22cos x .5.=⎰1d e d d 2xt t x ？ 答：=⎰1d e d d 2x t t x 22e )d e (d d 1x x t t x-=-⎰. 6. 若⎰=2d sin )(2x xt t x f ，则)(x f '=？答：)(x f '=242222sin sin 2sin )sin()(x x x x x x -=-'.7. 当)(x f 为积分区间],[b a 上的分段函数时，问如何计算定积分⎰b ax x f d )(？试举例说明.答：分段函数的定积分应采用定积分关于积分区间的分割性质，将⎰b ax x f d )(分解为部分区间上的定积分来计算.例如：若⎩⎨⎧<≤-≤≤=,01,,10,)(2x x x x x f 则x x f d )(11⎰-=x x d 01⎰-+x x f d )(11⎰-=1301232x x +-=61-.8. 对于定积分，凑微分法还能用吗？为什么？答：能用.因为定积分是通过被积函数的原函数来计算，而凑微分法所得原函数不须作变量置换.习作题：1. 计算下列定积分（1）⎰-20d |1|x x , （2）⎰-122d ||x x x , （3）⎰π20d |sin |x x .解：（1）⎰-20d |1|x x =⎰-1d )1(x x +⎰-21d )1(x x=212122)1(2)1(-+--x x =2121+=1.（2）⎰-122d ||x x x =⎰--023d )(x x +⎰103d x x=1402444x x +--=4+41741=. （3）⎰π20d |sin |x x =⎰π0d sin x x +⎰-π2πd )sin (x x=π2ππ0cos )cos (xx +-=2+2=4.2. 求极限x tt x x πcos 1d πsin lim11+⎰→.解：此极限是“0”型未定型，由洛必达法则，得x tt x x πcos 1d πsin lim11+⎰→=)πcos 1()d πsin (lim11'+'⎰→x t t xx =π1)π1(lim πsin ππsin lim11-=-=-→→x x x x3. 计算下列各题： （1）⎰10100d x x ， （2）⎰41d x x ， （3）⎰1d e x x , （4）x xd 10010⎰,（5）x x d sin 2π0⎰, （6）x x x d e 210⎰, （7）x x d )π2sin(2π0+⎰,（8）x x d )4π4cos(π+⎰, （9）x x x d 2ln e 1⎰, （10）⎰+102100d x x , （11）⎰4π02d cos tan x xx, （12）⎰10d sh x x , （13）⎰10d ch x x .解：（1）⎰10100d x x =101110110101=x .（2）⎰41d x x =314324123=x. （3）1e ed e 1010-==⎰xx x .（4）x xd 10010⎰=100ln 99100ln 10010=x .（5）1cos d sin 2π02π0=-=⎰x x x .（6）21e 2e )(d e 21d e 121010222-==⎰=⎰x x x x x x . （7）x x d )π2sin(2π0+⎰=)π2(d )π2sin(212π++⎰x x =2π0)π2cos(21+-x =1-. （8）x x d )4π4cos(π+⎰=)4π4d()4π4cos(4π0++⎰x x =π0)4π4sin(4+x =224-.(9)x x x d 2ln e 1⎰=)d(ln ln 21e 1x x ⎰=41ln 41e12=x .(10) ⎰+102100d x x=⎰+102)10(1d 1001x x =1010arctan 101x =101arctan 101.（11）⎰4π02d cos tan x x x =⎰4π0)tan d(tan x x =4π022)(tan x =21. （12）⎰⎰--=1010d 2e e d sh x x x x x =12e e xx -+=11ch 12e e 1-=-+-. （13）⎰10d ch x x =⎰-+10d 2e e x x x =12e e xx --=1sh 2e e 1=--.第三节 定积分的积分方法思考题：1. 下面的计算是否正确，请对所给积分写出正确结果：（1）x x x d cos cos 2π2π3⎰--=x x x d sin )(cos 2π2π21⎰-=)cos d()(cos 2π2π21x x ⎰--=0cos 322π2π23=--x .（2）⎰⎰---=-111122)sin d()(sin 1d 1t t x x=⎰-⋅11d cos cos t t t=⎰-112d )(cos t t =2⎰12d )(cos t t=22sin 211)2sin 21(d 22cos 11010+=+=+⎰t t t t . 答：（1）不正确，应该为：x x x x x x d sin )(cos 2d cos cos 212π2π2π3⎰⎰-=-=34cos 34)cos d()(cos 22π0232π021=-=-⎰x x x .（2）不正确，应该为：⎰⎰⎰---=-=-112π2π2π2π222d )(cos )sin d()(sin 1d 1t t t t x x=2=+=+=⎰⎰2π02π02π02)2sin 21(d 22cos 12d )(cos t t t t t t 2π.2. 定积分与不定积分的换元法有何区别与联系？答：定积分与不定积分的换元法的区别在于：不定积分换元积分后要作变量回代，定积分在换元时要同时变换积分限，而不用作变量回代. 联系在于：二者均要求置换的变元)(t x ϕ=单调可导，且选择变元)(t x ϕ=的规律相同.3. 利用定积分的几何意义，解释奇偶函数在对称区间上的积分所具有的规律. 答：如图, 设)(x f 在[]a ,0上满足)(x f ≥0，则⎰a x x f 0d )(表示由曲线)(x f y =，直线0=x ，a x =及x 轴所围图形的面积，不妨记为A ，则当)(x f 为偶函数时，⎰⎰==-aaa x x f A x x f 0d )(22d )((如下图(1)所示)，当)(x f 为奇函数时，0)(d )(=+-=⎰-A A x x f aa(如下图(2)所示).（1）习作题:1. 计算下列定积分:(1)x x d 16402⎰-, (2)⎰+12d 41x x .解：（1）令x =t sin 4, 则t t x t x d cos 4d ,cos 4162==-,当x = 0 时，t = 0 ; 当x = 4 时，2π=t ， 于是 x x d 16402⎰-=π4)2sin 48(d )2cos 1(8d cos 4cos 42π02π020=+=+=⋅⎰⎰t t t t t t t π.（2）⎰+102d 41x x =⎰+12)2d()2(1121x x =21arctan 212arctan 2110=x . 2. 计算下列定积分： （1）x x xd e )15(405⎰+, （2）x x d )12ln(e21⎰+,（3）x x xd πcos e10π⎰, （4）x x x x x d )e 3(1033⎰++.解：（1）x x xd e )15(405⎰+=5ed )15(540xx ⎰+=⎰+-+10515)15(d 5e )15(5e x x x x=5155e 5e 51e 6=--x.(2)x x d )12ln(e21⎰+=()())12ln d(12ln e21e21+-+⎰x x x xx x xd 1223ln )1e 4ln(e 2e21⎰+--+= --+=3ln )1e 4ln(e 2x x )d 1211(e 21⎰+---+=3ln )1e 4ln(e 2()e21)12ln 21(+-x x()1e 23ln 231e 4ln )21e 2(+--++=.(3) x x xd πcose 10π⎰=ππsin d e 10πx x ⎰x x x x πde ππsin πsin e π11010π⎰-= =0x x x d πsin e 10π⎰-=)ππcos d(e 10πx x--⎰ xx x x πde ππcos πcos e π11010π⎰-= =-+-)1e (π1πx x x d πcos e 10π⎰移项合并得x x x d πcos e 10π⎰)1e (π21π+-=. （4）x x x xxd )e 3(1033⎰++)e 313ln 34(d 3104xx x x ++=⎰ ⎰++-++=1034134d )e 313ln 34()e 313ln 34(x x x x xx x x=4514e 923ln 23ln 3)e 913ln 320(e 313ln 3413213253++-=++-++x x x .第四节 广义积分思考题:1. 下列解法是否正确？为什么？2ln 1ln 2ln ||ln d 12121=-==--⎰x x x .答：不正确.因为x1在[1-，2]上存在无穷间断点0=x ，⎰-21d 1x x 不能直接应用Leibniz Newton -公式计算，事实上，⎰-21d 1x x =⎰-01d 1x x +⎰20d 1x x =⎰--→+1110d 1lim εεx x +⎰+→2022d 1lim εεx x=[]1110)ln(lim εε--→-+x +[]222ln lim εεx +→=10ln lim 1εε+→+-2ln 202lim εε+→不存在,故⎰-21d 1x x 发散.2. 指出下面广义积分的计算错误:101)e 1(lim elim d e lim d e 0=-=-=-==-∞→-∞→-∞→∞⎰⎰b b bx b bxb xx x .答：本题计算错误在于0e lim =-∞→bb ，因为0e lim =-+∞→b b ，而-∞=--∞→b b e lim ，故bb -∞→elim 不存在，从而⎰∞0d e x x 发散.习作题：1. 研究广义积分⎰∞+02d 1x x 的敛散性. 解：⎰∞+02d 1x x =+∞=-=-+∞→→+∞+x x x x x 1lim 1lim )1(00,∴⎰∞+02d 1x x 发散. 2. 计算广义积分x x d )4(6032⎰--.解：x x d )4(6032⎰-- =x x d )4(6432⎰--+x x d )4(4032⎰--=)42(3430023)4(3)4(3333340316431+=--+-⋅=-+-x x .3. 计算广义积分x x d e 1100⎰∞+-.解：x xd e1100⎰∞+-=1001001100e 1001)100e (0100e --+∞-=--=-x .4. 计算广义积分⎰∞++02100d xx. 解： ⎰∞++02100d x x =20π10arctan 1010=+∞x .。

疑难问题解析问题1 下列两个命题是否正确（1） 如果在)(x f [a ，b]上有原函数，那么在)(x f [a ，b]上可积； （2） 如果在)(x f [a ，b]上有可积，那么在)(x f [a ，b]上有原函数。

答： 这两个命题都不正确（1） 在[a ，b]上有原函数存在的函数)(x f 未必是可积的。

例如 ⎪⎩⎪⎨⎧=≠=.0,0,0,1sin )(22x x xx x F 在[-1,1]上处处有导数，⎪⎩⎪⎨⎧=≠-=='.0,0,0,1cos 21sin 2)()(22x x xx x x x f x F 因此)(x f 在[-1,1]上有原函数)(x F ，但)(x f 在[-1,1]上无界，故)(x f 在[-1,1]上不可积。

（2） 在[a ，b]上可积的函数不一定存在的原函数例如符号函数 ⎪⎩⎪⎨⎧<-=>=0,10,00,1sgn x x x x在区间[-1,1]上可积，因为它只有一个第一类间断点0=x ，但在某区间上具有第一类间断点的函数不存在原函数，从而sgnx 在[-1,1]上不可积。

问题2 在什么条件下，牛顿-莱布尼兹公式()()()baf x dx F b F a =-⎰成立？答：如果函数[]()f x 在a,b 上连续，则牛顿-莱布尼兹公式()()()baf x dx F b F a =-⎰成立，此公式也成为微积分基本定理，它把函数[]()f x 在a,b 上的定积分的计算转化为求()f x 的原函数在区间[]a,b 上的增量，使定积分的计算十分方便。

当连续条件不满足时，慎用该公式，比如函数1()[11]f x x=-在区间，上不连续，就不能用该公式。

当然，牛顿-莱布尼兹公式成立的条件还可以适当放宽，常见的有以下两个结论： 定理 设[]()f x 在a,b 上可积，且原函数()F x 存在，则()()()baf x dx F b F a =-⎰。

(下转第49页)摘要不定积分是高等数学中的教学重点与难点，不定积分计算方法一般被分为换元积分法、直接积分法与分部积分法几种方式，其中，换元积分法又可以分为第一类换元法与第二类换元法两种，帮助学生掌握好第一类积分法与第二类积分法在归类上的联系与区别，能够有效提高学生应用积分法求解积分问题的能力，第一类积分法与第二类积分法最大的区别就是，第一类积分法不需要设置变量，可以通过凑微法和转化法进行计算，而在使用第二类积分法时，就必须要选择好变量进行替换。

关键词两类“换元积分法”联系区别On the Relationship and Distinction between Two Types of "Integration by Substitution"//Yang YanhuaAbstract Indefinite integral is a key and difficult point of higher mathematics,and the computing methods of indefinite integral are generally classified into integration by substitution,immediate integration and integration by parts,among which integration by substitution can be classified into the first type of substitution and the second type of substitution.To help students master the rela-tionship and distinction between the two types of substitution caneffectively improve students'ability of using integration methodsto solve integration problems.The biggest distinction between the two types of substitution is that variables are not needed in the former but improvising differentiation and conversion method can be used in the computing,while a certain variable must be se-lected to be substituted in the latter.Key words two types of "integration by substitution";relation-ship;distinction不定积分是高等数学中的教学重点与难点，此类知识也是学生学习重积分、定积分与微分方程等知识的学习技术。

毕业论文文献综述信息与计算科学换元法在数学解题中的应用一、前言部分有些数学问题，由于条件与结论中的变量关系在形式上的隐蔽，它们之间实质性的逻辑联系不易从表面形式上发现，即使看出它们之间的联系，也由于表面形式的复杂而不易直接求解。

但当我们进行适当的变量代换，把问题的条件和结论作形式上的转换，这样就容易揭示出它们之间的内在联系，把问题化难为易，化繁为简。

掌握了换元思想，不但可以比较顺利地解决一些较难的题目，还可以用多种方法解答同一个个问题，提高我们的思维。

数学中这样的例子有很多，无论是对一些具体问题的解决，还是在经典的数学方法中，都无不渗透着这一思想。

解题中常用到的换元法，其实也就是这一思想的具体体现。

解数学题时，把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化，这种方法叫做换元法。

换元法又称辅助元素法、变量代换法。

通过引进新的变量，可以把分散的条件联系起来，隐含的条件显露出来，或者把条件与结论联系起来。

或者变为熟悉的形式，把复杂的计算和推证简化。

它可以化高次为低次、化分式为整式、化无理式为有理式、化超越式为代数式，在研究方程、不等式、函数、数列、三角等问题中有广泛的应用。

尤其是在积分中应用很是广泛。

换元的实质是转化，关键是构造元和设元，理论依据是等量代换，目的是变换研究对象，将问题移至新对象的知识背景中去研究，从而使非标准型问题标准化、复杂问题简单化，变得容易处理。

为了使复杂繁琐的数学问题得到解决，利用换元法应进行有效替换。

在具体问题中，针对替换的有效性，人们做了很多的探讨。

有很多文章探讨了数学问题中的换元技巧，例如积分中的换元技巧、三角换元、无理递推式换元技巧等等。

每一类问题又由于其具体形式的不同，换元的形式也多种多样。

分析各种换元形式的共同规律，可以捡起归纳为以下几类：定积分换元法、不定积分换元法、三角换元、二重积分换元法、含无理递推式的换元法和换元法在其他方面的应用。

当遇到题中含有几个变量或次数较高问题时，我们可以考虑用换元法，能否消去某些变量或降低变量次数，起到减元降次的作用。