Origin软件研究聚丙烯热降解性能的数据处理及曲线拟合

origin数据拟合曲线
拟合曲线是指通过对给定的数据进行统计分析和数学处理，得到符合数据规律的一条曲线。

拟合曲线可以用来描述和预测数据之间的关系，常用于模型建立和预测分析。

在数据拟合中，拟合曲线的形状和方程式取决于拟合的方法和模型的选择。

常见的拟合方法包括线性回归、多项式拟合、指数拟合、对数拟合、非线性最小二乘拟合等。

对于给定的origin数据，可以根据具体问题的需要选择合适的拟合方法和模型，进行数据拟合，得到拟合曲线的方程式。

拟合曲线的方程式可以通过计算、回归分析等方法来确定，具体的过程和方法可以参考统计学、回归分析等相关领域的知识。

拟合曲线可以用来揭示数据之间的规律和趋势，进而进行预测和推断。

同时，拟合曲线也有其局限性，可能存在与实际数据不一致的情况，因此在应用拟合曲线结果时需要谨慎。

origin,指定数据拟合曲线解释说明1. 引言1.1 概述在科学研究和工程实践中，经常会遇到需要对一组数据进行拟合的情况。

数据拟合是根据已有的观测数据，利用数学模型寻求最佳的拟合函数与观测值之间的关系，从而得到一条曲线来描述这些数据的趋势和规律。

通过进行数据拟合，我们能够更好地理解现象背后的规律，并可以预测未知观测点的结果。

此外，数据拟合还可以用于优化设计、参数估计、信号处理、模式识别等领域。

本文将详细探讨数据拟合曲线的选择和评估指标，并通过实际应用案例进行分析。

同时，我们将介绍数据拟合的原理和方法，并讨论不同方法在实践中的适用性和局限性。

1.2 文章结构本文共分为五个部分：引言、正文、数据拟合曲线解释说明、结论和参考文献。

其中，引言部分将介绍本文内容概述以及文章结构安排；正文部分将详细讨论相关概念和方法；数据拟合曲线解释说明部分将进一步探讨数据拟合原理、拟合曲线选择以及评估指标；结论部分将总结文章的主要内容和研究成果；参考文献部分将列举本文所引用的相关文献。

1.3 目的本文的目的在于深入探讨数据拟合曲线的原理与方法，以及其在实际应用中的具体案例。

通过对数据拟合原理和方法进行阐述，并借助实例分析，我们旨在帮助读者更好地理解数据拟合问题，并能够正确选择适用于自己实际需求的拟合曲线和评估指标。

此外，我们还希望通过本文能够激发读者对数据拟合问题进一步探索和研究的兴趣。

2. 正文数据拟合曲线是一种数学模型，可以用于描述和预测实际数据中的趋势和关系。

在科学研究和工程应用中，我们经常遇到需要通过拟合曲线来分析和解释数据的情况。

本节将介绍一些常见的数据拟合方法，并探讨它们在不同场景下的应用。

首先，最简单也是最常见的数据拟合方法是线性回归。

在线性回归中，我们假设变量之间存在线性关系，并试图找到最佳拟合直线来表示这种关系。

通过最小二乘法等统计方法，可以确定直线的斜率和截距，从而得到一个近似解。

除了线性回归，还有很多其他的拟合曲线方法可供选择。

以英文版origin75为例：
首先是输入数据（以两个拟合曲线为例）：
一、在origin里面增加两列：点击鼠标右键，选择add new column，
二、选择C列，并将其设为X（点击鼠标右键选择）
三、从excel表格中选择需要的数据复制过来
然后是曲线拟合:
一、画散点图
全选数据后点击表格左下角的散点符号即可画出散点图
二、断开两组数据的关联
任选一点，双击，将dependent改为independent
三、第一条曲线拟合
单击最小梯度数据点，然后选择analysis→fit exponential decay→first order
这样第一条线就拟合出来了
四、第二条曲线拟合
拟合之前需要将第一条线的拟合方程剪切，因为直接拟合第二条会将第一条曲线方程覆盖
先选择需要拟合的数据，选择data→2g1 data1:C(X),D(Y)
然后依旧是analysis→fit exponential decay→first order，然后将剪切的方程粘贴上去，这样两个方程就出来了。

然后双击进行修改。

去掉方程的文本框：鼠标放在文本框上，右键→properties→选择none即可
增加图名，右键add text即可。

最后是输出图件
一、输出图片格式二、输出工程文件
file→export page
file→save project as
单曲线拟合在输入数据的时候不需要增加列数，直接输入，然后拟合即可。

带有异常值的数据在输入时就要再增加两列输入异常值，并将其中一列设置为X，然后和两条曲线一样进行拟合即可。

origin曲线拟合的主要步骤,曲线方程的确定方法origin曲线拟合的主要步骤如下：
1. 根据实验数据，确定可能的拟合函数。

2. 调整拟合函数的参数，并用特定的优化算法求出使绝对值最小的参数。

3. 根据最优参数计算出拟合曲线。

4. 输出拟合曲线图。

5. 根据拟合曲线的表现，获取有用的结论。

至于曲线方程的确定方法，有直接法和间接法两种。

直接法适用于动点满足的几何条件本身就是一些几何量的等量关系，或这些几何量间的等量关系简单明了且易于表达的情况。

而间接法则需要通过实验数据确定可能的拟合函数，然后调整参数进行优化，以获得最佳拟合曲线。

如需了解更多关于origin曲线拟合步骤的信息，建议阅读相关论文或咨询专业人士。

用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据在科学研究和实验中，数据处理是一个至关重要的环节。

通过对实验数据进行分析和拟合，可以得到对现象的更深入和准确的理解。

Origin软件是一种功能齐全且易于使用的数据分析软件，它提供了各种分析和拟合功能，包括线性拟合和非线性曲线拟合。

本文将探讨如何使用Origin软件的这两个功能来处理实验数据。

首先，我们需要明确线性拟合的概念。

线性拟合是通过一条直线来近似表示实验数据的趋势。

它通常用于分析变量之间的线性关系，并确定其相关性。

在Origin软件中，我们可以通过选择线性拟合的功能来进行这一分析。

以某个实验数据为例，我们首先打开Origin软件并加载实验数据。

然后，在图表中选择需要进行线性拟合的数据集，并点击工具栏上的“线性拟合”按钮。

Origin软件会自动计算最佳拟合直线，并在图表中显示出来。

此外，Origin软件还提供了拟合曲线的各种统计信息，如拟合趋势线的斜率、截距、相关系数和拟合误差等。

线性拟合的结果可以帮助我们推断实验数据中的相关性和趋势。

如果拟合直线的斜率为正值，并且有较高的相关系数，那么我们可以得出结论，实验数据之间存在正相关关系。

反之，如果斜率为负值，则表示实验数据之间存在负相关关系。

此外，线性拟合还可以用于预测未知数据的数值。

值得注意的是，线性拟合适用于处理线性关系较为明显的数据。

如果实验数据的分布较为复杂，并且存在非线性关系，就需要使用非线性曲线拟合功能来分析数据。

非线性曲线拟合是通过曲线来近似表示实验数据的趋势。

与线性拟合类似，非线性曲线拟合也能提供各种统计信息，如拟合曲线的拟合度、参数值、相关系数等。

使用Origin软件的非线性曲线拟合功能，可以进行多种拟合模型的选择和分析。

例如，常见的非线性模型有指数、对数、幂函数等。

我们可以根据实验数据的特点和分布选择合适的非线性模型，并进行参数估计和曲线拟合。

origin拟合的曲线
Origin软件是一款常用的科学数据处理和绘图软件，其拟合曲线主要基于以下两种方式：
1. 线性拟合（Linear Fit）：这种拟合方法通过输入的数据点进行线性拟合，可以拟合直线、二次项和三次项等线性关系。

具体步骤包括在软件中导入数据、选择拟合类型、设置拟合参数、进行拟合等。

2. 非线性拟合（Nonlinear Fit）：这种拟合方法适用于更复杂的非线性关系，如指数、对数、幂等。

在Origin中，可以通过选择合适的函数类型和参数进行非线性拟合。

以上是Origin软件中常见的两种拟合曲线方式，具体的操作步骤可能会因为软件的版本和功能而有所不同。

如有需要，可以参考软件的使用手册或在线教程。

Origin7.5计算数据、作图和拟合过程介绍注意：阅读过程中，看不清图可以把word放大到200%。

可参考教材第30-33页。

其中第31页图2-13的头顶一行中的“平方”应改为“均方根”，平方的表达为“Col(C)^2”。

一、整体介绍如图1所示图1二、数据计算处理的数据有8列，默认的只有2列，需要插入5列，方法见图2。

图2得到8列表格后（见图3），双击“A(X)”后弹出菜单，在左下的“Column label”输入标签文字，方便知道该列数据代表什么物理量，如励磁电流（Im/mA）。

还可以对8列表格的名称按A、B、C、D顺序重新排列，方法见图3的“Column Name”，得到图4的效果。

排序的过程中，若要将“D”列改为“B”列，但是已经存在“B”列了，你可以先将“B”列改为“M”列，然后在修改，其他情况也类似。

图3图4是输入数据后的图，列的名称重新进行了排列。

图4三、计算数据要计算的数据有电阻R，磁感应强度B的平方（并用单位T来表示），以及磁阻MR。

1、在C列上右键，选择“Set Column Values…”，见图5。

弹出图6的对话框。

将B列的磁场用单位T表示，因此公式为：Col(B)/1000。

图5图62、同样的方法计算F列的电阻R，公式为：Col(D)/Col(E)。

3、计算B2的数据公式为：Col(C)^2，单位用T表示；4、计算MR的公式为：(Col(F)-316.12648)/316.12648，316.12648即为R（0）的电阻值【请注意，Im=0时的电阻为R（0）】，计算结果见图7。

图7中第一MR数据应该为0，但是软件中存在保留位长度不一样，导致不为0，为10-9的一个很小值，手动改为0即可。

图7四、计算机作图作图必须有X轴和Y轴数据，X轴为磁场，Y轴为磁阻。

因此将B（Y）改为B（X），G（Y）改为G（X）。

修改的方法如图3一样，结果见图8。

而且X轴数据列必须在作图的Y轴数据列的前面。

origin数据拟合成曲线
Origin数据拟合成曲线的步骤如下：
1. 打开Origin软件，导入数据。

在菜单栏上选择“File”->“Import Data”->“From File”，然后选择数据文件导入。

2. 将数据添加到表格中。

在菜单栏上选择“File”->“New”->“Worksheet”，将数据添加到新的工作表中。

3. 选择数据列，然后在工具栏上选择“Plot”->“Line”，将数据绘制成散点图。

4. 在散点图上右键单击，选择“Add Trendline”->“Linear”，添加线性拟合线。

5. 在弹出的“Linear Fit”对话框中，设置拟合参数，如截距、斜率等，然后点击“OK”。

6. 拟合线将自动添加到散点图中，可以根据需要调整线条样式和颜色等属性。

需要注意的是，Origin提供了多种拟合函数和参数估计方法，可以根据实际需要选择适合的拟合函数和方法。

同时，在拟合过程中需要注意数据的异常值和缺失值等可能影响拟合结果的因素。

学术干货再来一波，如何利用Origin实现曲线拟合现实生活中，变量间未必都会有线性关系，比如疾病疗效与疗程长短的关系。

在材料科学的研究中，也会遇到一些非线性的数量关系，那么面对大量的离散点组或者数据，我们如何来透过零散的“外表”来发现它们“真实的内心”呢？今天小编就一步一步告诉大家。

曲线拟合（curve fitting）是指选择适当的曲线类型来拟合观测数据，并用拟合的曲线方程分析两个变量之间的关系。

通过对数据进行曲线拟合，我们不但能找到它的变化规律，还能对数据的变化进行一定程度的预测。

我们将以Origin 8.0为例，为大家详细的讲解利用Origin进行曲线拟合的方法。

本文共分为3个小节，分别是线性回归（直线拟合）、多项式拟合和非线性拟合。

一、线性回归（直线拟合）1.首先打开Origin 8，在A(X)和B(Y)列分别输入对应的横坐标和纵坐标数据，本节中的A(X)列为电流，B(Y)列为电压。

如图1-1所示。

研究的规律是当电阻不变时，电压随着电流增加的情况。

其中，Long Name:名称；Units:单位；Comments:注释。

图1-12.选中A(X)和B(Y)列的全部数据，然后依次Plot→Symbol→Scatter（或者点击左下角的作图，如图1-2所示）。

得到图1-3。

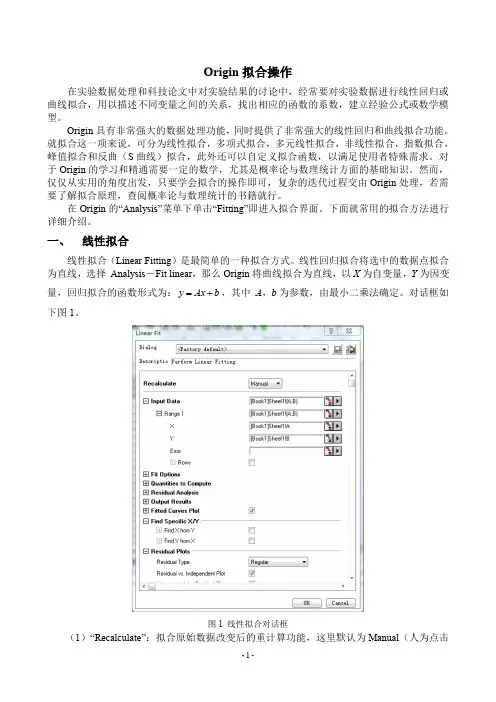
图1-33.根据图1-3可知，电流跟电压是线性关系，所以要进行线性拟合，接下来点击Analysis→Fitting→Fit Linear→Open Dialog...，如图1-4所示，得到图1-5。

图1-54.根据在图1-5的Linear Fit选项卡中单击OK按钮，得到图1-6。

在跳出来的Reminder Message选项卡中单击OK按钮，得到直线的拟合结果报告，如图1-7所示。

得到的电压与电流的函数关系为：y=3.02747x+0.01209，拟合度R2因子达0.99984。

图1-6图1-7二、多项式拟合打开Origin 8，在A(X)和B(Y)列分别输入对应的横坐标和纵坐标数据，如本节中A(X)列为电流，B(X)列为光强度。

基于Origin软件的聚丙烯流变性曲线拟合与数据处理
何小芳;王俊豪;曹新鑫;陈建宇;王雷;花星;李俊
【期刊名称】《上海塑料》
【年(卷),期】2010(000)001
【摘要】以Obtwald-de Waele法,Arrhenius法处理聚丙烯熔体流变性为例,讨论基于Origin软件进行流变曲线、非牛顿指数测定曲线等的拟合问题、数据处理方法以及论文插图的编辑.
【总页数】4页(P37-40)
【作者】何小芳;王俊豪;曹新鑫;陈建宇;王雷;花星;李俊
【作者单位】河南理工大学材料科学与工程学院,河南,焦作,454000;河南理工大学材料科学与工程学院,河南,焦作,454000;河南理工大学材料科学与工程学院,河南,焦作,454000;河南理工大学材料科学与工程学院,河南,焦作,454000;河南理工大学材料科学与工程学院,河南,焦作,454000;河南理工大学材料科学与工程学院,河南,焦作,454000;河南理工大学材料科学与工程学院,河南,焦作,454000
【正文语种】中文
【中图分类】TQ320.66+3
【相关文献】
1.基于Origin软件的低渗透油藏单相渗流曲线拟合 [J], 魏爱霞;张烈辉;赵玉龙
2.Origin软件研究聚丙烯热降解性能的数据处理及曲线拟合 [J], 何小芳;王俊豪;董帅;王宾宾;吴新玉;聂卫光
3.基于Zview和Origin软件的交流阻抗谱的实验数据处理 [J], 徐加焕;盖志强
4.基于Origin软件的多峰实验曲线拟合与数据处理 [J], 金哲;朱哲松
5.基于Origin软件的化工原理实验曲线拟合方法与应用 [J], 张习博
因版权原因，仅展示原文概要，查看原文内容请购买。