高2021届高2018级高三化学一轮复习步步高第五章本章易错题重练

专项提能特训1物质分离、提纯过程的综合分析1.(2020·西安交通大学附属中学高三检测)某硝酸钠固体中混有少量硫酸铵和碳酸氢钠杂质,现设计一实验方案,既除去杂质,又配成硝酸钠溶液。

实验方案：先将固体溶于蒸馏水配成溶液,选择合适的试剂和操作完成表格中各步实验。

下列试剂或操作不合理的是()A.试剂①为Ba(OH)2溶液B.操作②为结晶C.操作③为过滤D.试剂④为稀HNO3答案 B【本题解析】根据题意,可用Ba(OH)2溶液除去SO2－4、NH＋4和HCO－3,NH3·H2O通过加热除去,操作②为加热；过量的Ba2＋用Na2CO3溶液除去,过滤除去沉淀,滤液中过量的OH－和CO2－3用硝酸除去,则操作③为过滤,试剂④为稀HNO3。

2.(2016·上海,16)实验室提纯含少量氯化钠杂质的硝酸钾的过程如图所示。

下列分析正确的是()A.操作Ⅰ是过滤,将固体分离除去B.操作Ⅱ是加热浓缩、趁热过滤,除去杂质氯化钠C.操作Ⅲ是过滤、洗涤,将硝酸钾晶体从溶液中分离出来D.操作Ⅰ～Ⅲ总共需两次过滤答案 C【本题解析】KNO3中混有NaCl应提纯KNO3,将它们都溶于水,并降温结晶。

因为KNO3的溶解度随温度的升高而升高,NaCl的溶解度随温度的升高而基本无明显变化。

则有,操作Ⅰ是在烧杯中加水溶解,操作Ⅱ是蒸发浓缩,得到较高温度下的KNO3饱和溶液,操作Ⅲ为冷却结晶,利用溶解度差异使KNO3结晶析出,过滤,洗涤,干燥即得KNO3晶体。

故选C。

3.(2020·广东茂名五大联盟学校联考)某同学查阅教材得知,普通锌锰电池筒内的无机物主要为MnO2、NH4Cl、ZnCl2等。

他在探究废干电池内的黑色固体并回收利用时,进行如图所示实验。

下列有关实验的叙述不正确的是()A.操作①中玻璃棒能加快固体溶解B.操作②为过滤,得到的滤液显酸性C.操作③盛放滤渣的仪器是坩埚D.操作④的目的是除去滤渣中的杂质答案 D【本题解析】操作①中玻璃棒搅拌起到加速溶解的作用,A 项正确；操作②得到的滤液中含有NH 4Cl 、ZnCl 2,溶液呈酸性,B 项正确；操作③是在坩埚内灼烧滤渣,C 项正确；二氧化锰是黑色固体,能作过氧化氢分解的催化剂,灼烧后的滤渣能加快过氧化氢分解产生氧气的速率,证明黑色固体是二氧化锰,所以操作④的目的不是除去滤渣中的杂质,D 项错误。

高中有机化学步步高选修5高2021届高2018级化学课件配套学案章末检测试卷（三）章末检测试卷(三)(时间:90分钟满分:100分)一、选择题(本题包括15小题,每小题3分,共45分)1.(2018·大连市高二下学期期末)下列有机物中,不属于烃的衍生物的是( ) A.醋酸 B.邻二甲苯 C.四氯化碳 D.酒精答案 B解析邻二甲苯中只含有C 、H 元素,属于芳香烃,不属于烃的衍生物,B 正确。

2.(2018·吉安市高二下学期期末)下列各化合物的命名中正确的是( ) A.CH 2==CH —CH ==CH 2 1,3-二丁烯B. 3-丁醇C. 2-甲基苯酚D. 2-乙基丙烷答案 C解析含有碳碳双键在内的主碳链含碳原子数为4,双键在1、3位碳上,命名为1,3-丁二烯,A 错误；该物质为醇,主碳链含碳原子数为4,羟基在2位碳上,命名为2-丁醇,B 错误；该物质属于酚类,甲基在羟基的邻位,为2-甲基苯酚,C 正确；主碳链含碳原子数为4,甲基在2位碳上,命名为2-甲基丁烷,D 错误。

3.关于下列物质的用途的说法错误的是( ) A.酚类化合物有毒,不能用于杀菌消毒B.乙二醇可用于配制汽车防冻液C.部分卤代烃可用作灭火剂D.甲醛的水溶液(福尔马林)可用于防腐答案 A解析酚类化合物虽然有毒,但是可以用来杀菌消毒,如医院经常用来消毒的来苏水主要成分就是甲酚。

4.(2018·宝坻区高二下学期联考)下列有机反应类型判断不正确的是( )A.HOCH 2CH 2CH 2OH ――→浓硫酸△＋ H 2O 消去反应B.CH 3CH 2OH ＋CuO ――→△CH 3CHO ＋Cu ＋H 2O 氧化反应 C.H 2C ==CHCH ==CH 2＋Cl 2―→CH 2ClCH ==CHCH 2Cl 加成反应 D.ClCH 2CH 3＋CH 3NH 2―→CH 3NHCH 2CH 3＋HCl 取代反应答案 A5.中学化学中下列各物质间不能实现(“→”表示一步完成)转化的是( )答案 A解析 A 中的CH 3COOH 不能一步转化为CH 3CH 2OH ；B 中CH 2==CH 2――→＋HBr CH 3CH 2Br ――→＋NaOH△CH 3CH 2OH ――→浓硫酸△CH 2==CH 2；C 中Cl 2――→＋H 2OHClO ――→光或热HCl ――→＋MnO 2△Cl 2；D 中C ――→＋O 2CO ――→＋O 2CO 2――→＋MgC 。

大题冲关滚动练之一——氧化还原反应、离子反应综合题1．有一瓶澄清溶液，可能含有NH错误!、K＋、Na＋、Mg2＋、Ba2＋、Al3＋、Fe3＋、Cl－、I －、NO错误!、CO错误!、SO错误!中的一种或几种。

取该溶液进行以下实验：①用pH试纸检验，表明溶液呈强酸性。

②取出部分溶液，加入少量CCl4及数滴新制氯水，经振荡CCl4层呈紫红色。

③另取部分溶液，向其中逐滴加入NaOH溶液，使溶液从酸性变为碱性，在滴加过程中先生成白色沉淀后完全溶解；取部分碱性溶液加热，有气体放出，该气体能使润湿的红色石蕊试纸变蓝。

④另取部分③中的碱性溶液，向其中加入Na2CO3溶液，有白色沉淀生成。

根据以上实验事实回答下列问题：(1>该溶液中肯定存在的离子是_________________________________________，肯定不存在的离子是_________________________________________________。

(2>步骤③加入NaOH溶液过程中先生成白色沉淀后完全溶解的离子方程式为________________________________________________________________________；________________________________________________________________________。

答案 (1>Ba2＋、Al3＋、I－、NH错误!Mg2＋、Fe3＋、CO错误!、SO错误!、NO错误!(2>Al3＋＋3OH－===Al(OH>3↓Al(OH>3＋OH－===AlO错误!＋2H2O2．(1>往该溶液中逐滴加入NaOH溶液并适当加热，产生沉淀和气体的物质的量(n>与加入NaOH溶液的体积(V>的关系如下图所示。

则该溶液中确定含有的阳离子有________________________________________，不能确定是否含有的阳离子有__________________________________________，要确定其存在可补充做的实验是________________________________________，肯定不存在的阴离子有________________________________________________。

阶段检测五 铝、氮与其他元素的融合加试题1.(8分)在一定条件下可实现下图所示物质之间的变化：请填写下列空白：(1)孔雀石的主要成分是CuCO 3·Cu(OH)2(碱式碳酸铜)受热易分解。

上图中的F 是________。

(2)写出明矾与过量NaOH 溶液反应的离子方程式：________________________________________________________________________。

(3)图中所得G 和D 都是固体，混和后在高温下可以发生反应，写出该反应的化学方程式： ________________________________________________________________________。

(4)每生成1 mol D ，同时生成________mol E 。

答案 (1)CO 2(或二氧化碳)(2)Al 3＋＋4OH －===AlO －2＋2H 2O (3)3CuO ＋2Al=====高温Al 2O 3＋3Cu(4)34解析 A 是NaAlO 2，反应离子方程式Al 3＋＋4OH －===AlO －2＋2H 2O ；孔雀石受热分解的反应式为CuCO 3·Cu(OH)2=====△2CuO ＋CO 2＋H 2O ；F 是CO 2，G 是CuO 。

A 、F 发生的反应式是CO 2＋AlO －2＋2H 2O===Al(OH)3↓＋HCO －3，沉淀是Al(OH)3，受热分解后生成Al 2O 3(B)和水。

Al 和CuO 的反应，类似于铝热反应。

第四问可根据2Al 2O 3=====通电4Al ＋3O 2↑计算。

2.(10分)某校化学兴趣小组用如图所示过程除去AlCl 3中含有的Mg 2＋、K ＋杂质离子并尽可能减少AlCl 3的损失。

⎦⎥⎥⎤Al 3＋Mg 2＋K＋Cl －――→足量NaOH 溶液⎣⎢⎡ Mg (OH )2沉淀溶液a ――→盐酸⎣⎢⎡ 沉淀c ――→盐酸AlCl 3溶液溶液b请回答下列问题：(1)写出混合物中加入足量氢氧化钠溶液时，溶液中发生反应的离子方程式：________________________________________________________________________。

模块综合试卷(时间：90分钟满分：100分)一、选择题(本题包括16小题，每小题3分，共48分)1．化学与生产、生活密切相关，下列说法正确的是()A．合成纤维、人造纤维及碳纤维都属于有机高分子材料B．煤经过气化和液化等物理变化可转化为清洁燃料C．利用粮食酿酒经过了淀粉→葡萄糖→乙醇的化学变化过程D．偏二甲基肼[NH2N(CH3)2]是火箭动力液体燃料，它是一种氨基酸答案 C解析碳纤维是无机物，不属于有机高分子材料，A错误；煤的气化和液化有新物质生成，属于化学变化，B错误；粮食酿酒：粮食中的淀粉水解生成葡萄糖，葡萄糖在酒曲酶的作用下生成酒精，C正确；偏二甲基肼[NH2N(CH3)2]不含羧基，不属于氨基酸，D错误。

【考点】有机物的性质及用途【题点】有机物的性质及用途2．下列化学用语正确的是()A．聚丙烯的结构简式：CH2—CH2—CH2B．丙烷分子的比例模型：C．甲醛分子的电子式：D．2-乙基-1,3-丁二烯分子的键线式：【考点】常见化学用语【题点】有机物分子的表示方法答案 D解析聚丙烯的结构简式为是丙烷分子的球棍模型；甲醛分子的电子式为。

3．下列有机物的命名肯定错误的是()A．3-甲基-2-戊烯B．2-甲基-2-丁烯C．2,2-二甲基丙烷D．2-甲基-3-丁炔答案 D解析根据有机物的名称，写出其结构简式，然后再由系统命名法重新命名。

D选项结构简式为编号错误，应为3-甲基-1-丁炔。

【考点】有机物命名的一般规律【题点】有机物命名的综合考查4．下列物质既能发生消去反应生成相应的烯烃，又能氧化成相应的醛的是() A．CH3OH B．CH3CH2CH2OHC．(CH3)2COHCH3D．(CH3)2CHOH答案 B解析CH3OH不能发生消去反应，A错误；CH3CH2CH2OH发生消去反应生成丙烯，发生氧化反应生成丙醛，B正确；(CH3)2COHCH3不能氧化生成相应的醛，C错误；(CH3)2CHOH 不能氧化生成相应的醛，D错误。

排查落实练五钠、铝及其化合物一、重要方程式的书写1．钠及其重要化合物(1>知识网络构建(2>重要反应必练写出下列反应的离子方程式①Na和H2O的反应2Na＋2H2O===2Na＋＋2OH－＋H2↑②Na和CH3COOH的反应2Na＋2CH3COOH===2CH3COO－＋2Na＋＋H2↑③Na2O2和H2O的反应2Na2O2＋2H2O===4Na＋＋4OH－＋O2↑④Na H和水的反应NaH＋H2O===Na＋＋OH－＋H2↑⑤向NaOH溶液中通入过量CO2OH－＋CO2===HCO错误!⑥将Na2CO3溶液与石灰乳混合CO错误!＋Ca(OH>2===CaCO3↓＋2OH－⑦向Na2CO3溶液中通入过量CO2CO错误!＋CO2＋H2O===2HCO错误!⑧将Na2CO3和Ca(HCO3>2混合CO错误!＋Ca2＋===CaCO3↓⑨将NaHCO3溶液和NaOH溶液等物质的量混合HCO错误!＋OH－===CO错误!＋H2O⑩将NaHCO3溶液与澄清石灰水等物质的量混合HCO错误!＋Ca2＋＋OH－===CaCO3↓＋H2O⑪将NaHCO3溶液与少量澄清石灰水混合2HCO错误!＋Ca2＋＋2OH－===CaCO3↓＋CO错误!＋2H2Ob5E2RGbCAP⑫向饱和Na2CO3溶液中通入过量CO2气体2Na＋＋CO错误!＋CO2＋H2O===2NaHCO3↓2．铝及其重要化合物(1>知识网络构建(2>重要反应必练写出下列反应的离子方程式①Al和NaOH溶液的反应2Al＋2OH－＋2H2O===2AlO错误!＋3H2↑②Al(OH>3和NaOH溶液的反应Al(OH>3＋OH－===AlO错误!＋2H2O③Al(OH>3和盐酸的反应Al(OH>3＋3H＋===Al3＋＋3H2O④Al2O3和NaOH的反应Al2O3＋2OH－===2AlO错误!＋H2O⑤Al2O3和盐酸的反应Al2O3＋6H＋===2Al3＋＋3H2O⑥NaAlO2和过量盐酸的反应AlO错误!＋4H＋===Al3＋＋2H2O⑦向NaAlO2溶液中通入过量CO2气体AlO错误!＋CO2＋2H2O===Al(OH>3↓＋HCO错误!p1EanqFDPw⑧将NaAlO2与NaHCO3混合AlO错误!＋HCO错误!＋H2O===Al(OH>3↓＋CO错误! DXDiTa9E3d⑨将NaAlO2与AlCl3溶液混合3AlO错误!＋Al3＋＋6H2O===4Al(OH>3↓⑩向AlCl3溶液中加入过量NaOH溶液Al3＋＋4OH－===AlO错误!＋2H2O⑪向AlCl3溶液加入过量氨水Al3＋＋3NH3·H2O===Al(OH>3↓＋3NH错误!⑫将AlCl3溶液与NaHCO3溶液混合Al3＋＋3HCO错误!===Al(OH>3↓＋3CO2↑二、值得强化记忆的实验现象1．Na和水反应的实验现象答案Na浮在水面上，四处游动，发出“嘶嘶”的响声，并熔化成光亮的小球，最后小球完全消失，滴入酚酞试液，立即变红。

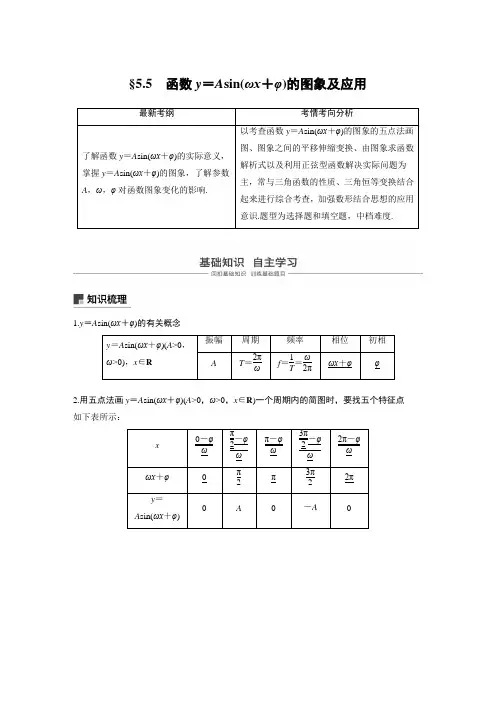
§5.5函数y＝A sin(ωx＋φ)的图象及应用1.y＝A sin(ωx＋φ)的有关概念2.用五点法画y＝A sin(ωx＋φ)(A>0，ω>0，x∈R)一个周期内的简图时，要找五个特征点如下表所示：3.函数y ＝sin x 的图象经变换得到y ＝A sin(ωx ＋φ)(A >0，ω>0)的图象的两种途径知识拓展1.函数y ＝A sin(ωx ＋φ)＋k 图象平移的规律：“左加右减，上加下减”.2.由y ＝sin ωx 到y ＝sin(ωx ＋φ)(ω>0，φ>0)的变换：向左平移φω个单位长度而非φ个单位长度.3.函数y ＝A sin(ωx ＋φ)的对称轴由ωx ＋φ＝k π＋π2，k ∈Z 确定；对称中心由ωx ＋φ＝k π，k ∈Z确定其横坐标.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)y ＝sin ⎝⎛⎭⎫x －π4的图象是由y ＝sin ⎝⎛⎭⎫x ＋π4的图象向右平移π2个单位长度得到的.( √ ) (2)将函数y ＝sin ωx 的图象向右平移φ(φ>0)个单位长度，得到函数y ＝sin(ωx －φ)的图象.( × )(3)函数y ＝A cos(ωx ＋φ)的最小正周期为T ，那么函数图象的两个相邻对称中心之间的距离为T2.( √ ) (4)由图象求函数解析式时，振幅A 的大小是由一个周期内图象中最高点的值与最低点的值确定的.( √ ) 题组二 教材改编2.[P55T2]为了得到函数y ＝2sin ⎝⎛⎭⎫2x －π3的图象，可以将函数y ＝2sin 2x 的图象( ) A.向右平移π6个单位长度B.向右平移π3个单位长度C.向左平移π6个单位长度D.向左平移π3个单位长度答案 A3.[P58A 组T3]函数y ＝2sin ⎝⎛⎭⎫12x －π3的振幅、频率和初相分别为( ) A.2,4π，π3B.2，14π，π3C.2，14π，－π3D.2,4π，－π3答案 C解析 由题意知A ＝2，f ＝1T ＝ω2π＝14π，初相为－π3.4.[P62例4]如图，某地一天从6至14时的温度变化曲线近似满足函数y ＝A sin(ωx ＋φ)＋b ，则这段曲线的函数解析式为__________________________.答案 y ＝10sin ⎝⎛⎭⎫π8x ＋3π4＋20，x ∈[6,14]解析 从图中可以看出，从6至14时的温度变化曲线是函数y ＝A sin(ωx ＋φ)＋b 图象的半个周期，所以A ＝12×(30－10)＝10，b ＝12×(30＋10)＝20， 又12×2πω＝14－6，所以ω＝π8. 又π8×10＋φ＝2π＋2k π，k ∈Z ，取φ＝3π4， 所以y ＝10sin ⎝⎛⎭⎫π8x ＋3π4＋20，x ∈[6,14]. 题组三 易错自纠5.(2018·嘉兴第一中学期中考试)为了得到函数y ＝sin ⎝⎛⎭⎫2x ＋π6的图象，可以将函数y ＝cos 2x 的图象( )A.向右平移π6个单位长度B.向右平移π3个单位长度C.向左平移π6个单位长度D.向左平移π3个单位长度答案 A解析 y ＝sin ⎝⎛⎭⎫2x ＋π6＝cos ⎝⎛⎭⎫π2－2x －π6 ＝cos ⎝⎛⎭⎫π3－2x ＝cos ⎝⎛⎭⎫2x －π3， 故把函数y ＝cos 2x 的图象向右平移π6个单位长度得到函数y ＝sin ⎝⎛⎭⎫2x ＋π6的图象. 6.将函数y ＝cos 2x ＋1的图象向右平移π4个单位长度，再向下平移1个单位长度后得到的函数图象对应的表达式为( ) A.y ＝sin 2x B.y ＝sin 2x ＋2 C.y ＝cos 2x D.y ＝cos ⎝⎛⎭⎫2x －π4 答案 A解析 将函数y ＝cos 2x ＋1的图象向右平移π4个单位长度得到y ＝cos 2⎝⎛⎭⎫x －π4＋1＝sin 2x ＋1，再向下平移1个单位长度得到y ＝sin 2x ，故选A.7.函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ为常数，A >0，ω>0，0<φ<π)的图象如图所示，则f ⎝⎛⎭⎫π3的值为________.答案 1解析 由三角函数图象可得A ＝2，34T ＝11π12－π6＝34π，所以周期T ＝π＝2πω，解得ω＝2.又函数图象过点⎝⎛⎭⎫π6，2，所以f ⎝⎛⎭⎫π6＝2sin ⎝⎛⎭⎫2×π6＋φ＝2,0<φ<π， 解得φ＝π6，所以f (x )＝2sin ⎝⎛⎭⎫2x ＋π6， 所以f ⎝⎛⎭⎫π3＝2sin ⎝⎛⎭⎫2π3＋π6＝1.题型一 函数y ＝A sin(ωx ＋φ)的图象及变换典例 已知函数y ＝2sin ⎝⎛⎭⎫2x ＋π3. (1)求它的振幅、周期、初相；(2)用“五点法”作出它在一个周期内的图象；(3)说明y ＝2sin ⎝⎛⎭⎫2x ＋π3的图象可由y ＝sin x 的图象经过怎样的变换而得到. 解 (1)y ＝2sin ⎝⎛⎭⎫2x ＋π3的振幅A ＝2， 周期T ＝2π2＝π，初相φ＝π3.(2)令X ＝2x ＋π3，则y ＝2sin ⎝⎛⎭⎫2x ＋π3＝2sin X . 列表如下：描点画出图象，如图所示：(3)方法一 把y ＝sin x 的图象上所有的点向左平移π3个单位长度，得到y ＝sin ⎝⎛⎭⎫x ＋π3的图象； 再把y ＝sin ⎝⎛⎭⎫x ＋π3的图象上所有点的横坐标缩短到原来的12倍(纵坐标不变)，得到y ＝sin ⎝⎛⎭⎫2x ＋π3的图象； 最后把y ＝sin ⎝⎛⎭⎫2x ＋π3上所有点的纵坐标伸长到原来的2倍(横坐标不变)，即可得到y ＝2sin ⎝⎛⎭⎫2x ＋π3的图象. 方法二 将y ＝sin x 的图象上所有点的横坐标缩短为原来的12倍(纵坐标不变)，得到y ＝sin 2x的图象；再将y ＝sin 2x 的图象向左平移π6个单位长度，得到y ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6＝sin ⎝⎛⎭⎫2x ＋π3的图象； 再将y ＝sin ⎝⎛⎭⎫2x ＋π3的图象上所有点的纵坐标伸长为原来的2倍(横坐标不变)，即得到y ＝2sin ⎝⎛⎭⎫2x ＋π3的图象. 思维升华 (1)y ＝A sin(ωx ＋φ)的图象可用“五点法”作简图得到，可通过变量代换z ＝ωx ＋φ计算五点坐标.(2)由函数y ＝sin x 的图象通过变换得到y ＝A sin(ωx ＋φ)图象有两条途径：“先平移后伸缩”与“先伸缩后平移”.跟踪训练 (1)将函数y ＝sin ⎝⎛⎭⎫2x ＋π3的图象向右平移m (m >0)个单位长度，所得函数图象关于y 轴对称，则m 的最小值为( ) A.5π12 B.π3 C.π12 D.7π12答案 A解析 平移后的函数解析式为y ＝sin ⎝⎛⎭⎫2x ＋π3－2m ，又图象关于y 轴对称， 则sin ⎝⎛⎭⎫π3－2m ＝±1， ∴π3－2m ＝k π＋π2，k ∈Z ， ∴m ＝－k π2－π12，k ∈Z ，又m >0，∴m 的最小值为5π12.(2)(2014·浙江)为了得到函数y ＝sin 3x ＋cos 3x 的图象，可以将函数y ＝2cos 3x 的图象( ) A.向右平移π4个单位长度B.向左平移π4个单位长度C.向右平移π12个单位长度D.向左平移π12个单位长度答案 C解析 因为y ＝sin 3x ＋cos 3x ＝2sin ⎝⎛⎭⎫3x ＋π4 ＝2sin ⎣⎡⎦⎤3⎝⎛⎭⎫x ＋π12， 又y ＝2cos 3x ＝2sin ⎝⎛⎭⎫3x ＋π2＝2sin ⎣⎡⎦⎤3⎝⎛⎭⎫x ＋π6， 所以应由y ＝2cos 3x 的图象向右平移π12个单位长度得到.题型二 由图象确定y ＝A sin(ωx ＋φ)的解析式1.(2018·杭州第二中学测试)已知函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫A >0，ω>0，|φ|<π2的部分图象如图所示，则函数f (x )的解析式为( )A.f (x )＝2sin ⎝⎛⎭⎫π8x ＋π4 B.f (x )＝2sin ⎝⎛⎭⎫π8x －π4 C.f (x )＝2sin ⎝⎛⎭⎫π8x ＋3π4 D.f (x )＝2sin ⎝⎛⎫π8x －3π4 答案 A解析 由题意知A ＝2，T ＝16，又T ＝2πω，∴ω＝π8，当x ＝－2时，f (x )＝0，即sin ⎣⎡⎦⎤π8×(－2)＋φ＝0， ∵|φ|＜π2，∴φ＝π4，函数f (x )的解析式为f (x )＝2sin ⎝⎛⎭⎫π8x ＋π4.2.已知函数f (x )＝A sin(ωx ＋φ)＋B ⎝⎛⎭⎫A >0，ω>0，|φ|<π2的部分图象如图所示，将函数f (x )的图象向左平移m (m >0)个单位长度后，得到函数g (x )的图象关于点⎝⎛⎭⎫π3，32对称，则m 的值可能为( )A.π6B.π2C.7π6D.7π12 答案 D解析 依题意得⎩⎨⎧A ＋B ＝332，－A ＋B ＝－32，解得⎩⎪⎨⎪⎧A ＝3，B ＝32， T 2＝πω＝2π3－π6＝π2， 故ω＝2，则f (x )＝3sin(2x ＋φ)＋32. 又f ⎝⎛⎭⎫π6＝3sin ⎝⎛⎭⎫π3＋φ＋32＝332， 故π3＋φ＝π2＋2k π(k ∈Z )，即φ＝π6＋2k π(k ∈Z ). 因为|φ|<π2，故φ＝π6，所以f (x )＝3sin ⎝⎛⎭⎫2x ＋π6＋32. 将函数f (x )的图象向左平移m 个单位长度后得到g (x )＝3sin ⎝⎛⎭⎫2x ＋π6＋2m ＋32的图象，又函数g (x )的图象关于点⎝⎛⎭⎫π3，32对称，即h (x )＝3sin ⎝⎛⎭⎫2x ＋π6＋2m 的图象关于点⎝⎛⎭⎫π3，0对称，故3sin ⎝⎛⎭⎫2π3＋π6＋2m ＝0，即5π6＋2m ＝k π(k ∈Z )，故m ＝k π2－5π12(k ∈Z ). 令k ＝2，则m ＝7π12.3.已知函数f (x )＝sin(ωx ＋φ) ⎝⎛⎭⎫ω>0，|φ|<π2的部分图象如图所示，则y ＝f ⎝⎛⎭⎫x ＋π6取得最小值时x 的集合为________. 答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k π－π3，k ∈Z 解析 根据所给图象，周期T ＝4×⎝⎛⎭⎫7π12－π3＝π，故π＝2πω，∴ω＝2，因此f (x )＝sin(2x ＋φ)，另外图象经过点⎝⎛⎭⎫7π12，0，代入有2×7π12＋φ＝π＋2k π(k ∈Z )，再由|φ|<π2，得φ＝－π6，∴f (x )＝sin ⎝⎛⎭⎫2x －π6，∴f ⎝⎛⎭⎫x ＋π6＝sin ⎝⎛⎭⎫2x ＋π6，当2x ＋π6＝－π2＋2k π(k ∈Z )，即x ＝－π3＋k π(k ∈Z )时，y ＝f ⎝⎛⎭⎫x ＋π6取得最小值. 4.已知函数f (x )＝A sin(ωx ＋φ)(A >0，|φ|<π2，ω>0)的图象的一部分如图所示，则f (x )图象的对称轴方程是______.答案 x ＝k π2＋π6(k ∈Z )解析 由图象知A ＝2，又1＝2sin(ω×0＋φ)，即sin φ＝12，又|φ|<π2，∴φ＝π6.又11π12×ω＋π6＝2π，∴ω＝2， ∴f (x )＝2sin ⎝⎛⎭⎫2x ＋π6，令2x ＋π6＝π2＋k π(k ∈Z )， 解得x ＝k π2＋π6(k ∈Z )，∴f (x )＝2sin ⎝⎛⎭⎫2x ＋π6的对称轴方程为 x ＝k π2＋π6(k ∈Z ).思维升华 y ＝A sin(ωx ＋φ)中φ的确定方法(1)代入法：把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入.(2)五点法：确定φ值时，往往以寻找“五点法”中的特殊点作为突破口.题型三 三角函数图象性质的应用命题点1 三角函数模型典例 如图，某港口一天6时到18时的水深变化曲线近似满足函数y ＝3sin ⎝⎛⎭⎫π6x ＋φ＋k ，据此函数可知，这段时间水深(单位：m)的最大值为( )A.5B.6C.8D.10 答案 C解析 由题干图易得y min ＝k －3＝2，则k ＝5. ∴y max ＝k ＋3＝8.命题点2 函数零点(方程根)问题典例 已知关于x 的方程2sin 2x －3sin 2x ＋m －1＝0在⎝⎛⎭⎫π2，π上有两个不同的实数根，则m 的取值范围是____________. 答案 (－2，－1)解析 方程2sin 2x －3sin 2x ＋m －1＝0可转化为 m ＝1－2sin 2x ＋3sin 2x ＝cos 2x ＋3sin 2x ＝2sin ⎝⎛⎭⎫2x ＋π6，x ∈⎝⎛⎭⎫π2，π. 设2x ＋π6＝t ，则t ∈⎝⎛⎭⎫76π，136π， ∴题目条件可转化为m2＝sin t ，t ∈⎝⎛⎭⎫76π，136π有两个不同的实数根. ∴y ＝m2和y ＝sin t ，t ∈⎝⎛⎭⎫76π，136π的图象有两个不同交点，如图：由图象观察知，m2的取值范围是⎝⎛⎭⎫－1，－12，故m 的取值范围是(－2，－1). 引申探究本例中，若将“有两个不同的实数根”改成“有实根”，则m 的取值范围是__________. 答案 [－2,1)解析 由上例题知，m2的取值范围是⎣⎡⎭⎫－1，12， ∴－2≤m <1，∴m 的取值范围是[－2,1).命题点3 三角函数图象性质的综合典例 已知函数f (x )＝3sin ⎝⎛⎭⎫2ωx ＋π3 (ω>0)的图象与x 轴相邻两个交点的距离为π2. (1)求函数f (x )的解析式；(2)若将f (x )的图象向左平移m (m >0)个单位长度得到函数g (x )的图象恰好经过点⎝⎛⎭⎫－π3，0，求当m 取得最小值时，g (x )在⎣⎡⎦⎤－π6，7π12上的单调递增区间. 解 函数f (x )的图象与x 轴相邻两个交点的距离为π2，得函数f (x )的最小正周期为T ＝2×π2＝2π2ω，得ω＝1， 故函数f (x )的解析式为f (x )＝3sin ⎝⎛⎭⎫2x ＋π3. (2)将f (x )的图象向左平移m (m >0)个单位长度得到函数g (x )＝3sin ⎣⎡⎦⎤2(x ＋m )＋π3＝3sin ⎝⎛⎭⎫2x ＋2m ＋π3的图象， 根据g (x )的图象恰好经过点⎝⎛⎭⎫－π3，0， 可得3sin ⎝⎛⎭⎫－2π3＋2m ＋π3＝0，即sin ⎝⎛⎭⎫2m －π3＝0， 所以2m －π3＝k π(k ∈Z )，m ＝k π2＋π6(k ∈Z )，因为m >0，所以当k ＝0时，m 取得最小值，且最小值为π6.此时，g (x )＝3sin ⎝⎛⎭⎫2x ＋2π3. 因为x ∈⎣⎡⎦⎤－π6，7π12， 所以2x ＋2π3∈⎣⎡⎦⎤π3，116π，当2x ＋2π3∈⎣⎡⎦⎤π3，π2， 即x ∈⎣⎡⎦⎤－π6，－π12时，g (x )单调递增； 当2x ＋2π3∈⎣⎡⎦⎤3π2，116π，即x ∈⎣⎡⎦⎤512π，712π时， g (x )单调递增，故g (x )在⎣⎡⎦⎤－π6，7π12上的单调递增区间为⎣⎡⎦⎤－π6，－π12和⎣⎡⎦⎤5π12，7π12. 思维升华 (1)三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，建立数学模型，再利用三角函数的有关知识解决问题. (2)方程根的个数可转化为两个函数图象的交点个数.(3)研究y ＝A sin(ωx ＋φ)的性质时可将ωx ＋φ视为一个整体，利用换元法和数形结合思想进行解题.跟踪训练 (1)已知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，－π2≤φ≤π2的图象上的两个相邻的最高点和最低点的距离为22，且过点⎝⎛⎭⎫2，－12，则函数f (x )的解析式为__________. 答案 f (x )＝sin ⎝⎛⎭⎫πx 2＋π6解析 据已知两个相邻最高点和最低点的距离为22， 可得⎝⎛⎭⎫T 22＋(1＋1)2＝22，解得T ＝4，故ω＝2πT ＝π2，即f (x )＝sin ⎝⎛⎭⎫πx 2＋φ. 又函数图象过点⎝⎛⎭⎫2，－12， 故f (2)＝sin ⎝⎛⎭⎫π2×2＋φ＝－sin φ＝－12， 又－π2≤φ≤π2，解得φ＝π6，故f (x )＝sin ⎝⎛⎭⎫πx 2＋π6. (2)若函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π6(ω>0)满足f (0)＝f ⎝⎛⎭⎫π3，且函数在⎣⎡⎦⎤0，π2上有且只有一个零点，则f (x )的最小正周期为________. 答案 π解析 x ＝π6是f (x )图象的一条对称轴，∴f ⎝⎛⎭⎫π6＝±1，∴π6×ω＋π6＝π2＋k π，k ∈Z ， ∴ω＝6k ＋2，k ∈Z ， ∴T ＝π3k ＋1(k ∈Z ).又f (x )在⎣⎡⎦⎤0，π2上有且只有一个零点， ∴π6≤T 4≤π2－π6， ∴2π3≤T ≤4π3， 即2π3≤π3k ＋1≤4π3(k ∈Z )， ∴－112≤k ≤16(k ∈Z )，∴k ＝0，∴T ＝π.三角函数图象与性质的综合问题典例 (14分)已知函数f (x )＝23sin ⎝⎛⎭⎫x 2＋π4·cos ⎝⎛⎭⎫x 2＋π4－sin(x ＋π). (1)求f (x )的最小正周期；(2)若将f (x )的图象向右平移π6个单位长度，得到函数g (x )的图象，求函数g (x )在区间[0，π]上的最大值和最小值.思维点拨 (1)先将f (x )化成y ＝A sin(ωx ＋φ)的形式再求周期； (2)将f (x )解析式中的x 换成x －π6，得g (x )，然后利用整体思想求最值.规范解答解 (1)f (x )＝23sin ⎝⎛⎭⎫x 2＋π4cos ⎝⎛⎭⎫x 2＋π4 －sin(x ＋π)＝3cos x ＋sin x [4分] ＝2sin ⎝⎛⎭⎫x ＋π3，于是T ＝2π1＝2π.[6分] (2)由已知得g (x )＝f ⎝⎛⎭⎫x －π6＝2sin ⎝⎛⎭⎫x ＋π6， [8分]∵x ∈[0，π]，∴x ＋π6∈⎣⎡⎦⎤π6，7π6， ∴sin ⎝⎛⎭⎫x ＋π6∈⎣⎡⎦⎤－12，1，[10分]∴g (x )＝2sin ⎝⎛⎭⎫x ＋π6∈[－1,2]. [12分] 故函数g (x )在区间[0，π]上的最大值为2，最小值为－1.[14分]解决三角函数图象与性质的综合问题的一般步骤： 第一步：(化简)将f (x )化为a sin x ＋b cos x 的形式； 第二步：(用辅助角公式)构造f (x )＝a 2＋b 2· ⎝⎛⎭⎪⎫sin x ·a a 2＋b 2＋cos x ·b a 2＋b 2； 第三步：(求性质)利用f (x )＝a 2＋b 2sin(x ＋φ)研究三角函数的性质； 第四步：(反思)反思回顾，查看关键点、易错点和答题规范.1.(2017·全国Ⅰ)已知曲线C 1：y ＝cos x ，C 2：y ＝sin ⎝⎛⎭⎫2x ＋2π3，则下面结论正确的是( ) A.把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B.把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C.把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D.把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2 答案 D解析 因为y ＝sin ⎝⎛⎭⎫2x ＋2π3＝cos ⎝⎛⎭⎫2x ＋2π3－π2＝ cos ⎝⎛⎭⎫2x ＋π6，所以曲线C 1：y ＝cos x 上各点的横坐标缩短到原来的12倍，纵坐标不变，得到曲线y ＝cos 2x ，再把得到的曲线y ＝cos 2x 向左平移π12个单位长度，得到曲线y ＝cos 2⎝⎛⎭⎫x ＋π12＝cos ⎝⎛⎭⎫2x ＋π6.故选D.2.若将函数f (x )＝sin 2x ＋cos 2x 的图象向右平移φ个单位长度，所得图象关于y 轴对称，则φ的最小正值是( ) A.π8 B.π4 C.3π8 D.5π4答案 C解析 f (x )＝sin 2x ＋cos 2x ＝2cos ⎝⎛⎭⎫2x －π4，将函数f (x )的图象向右平移φ个单位长度后所得图象对应的函数为y ＝2cos ⎝⎛⎭⎫2x －π4－2φ，且该函数为偶函数， 故2φ＋π4＝k π(k ∈Z )，所以φ的最小正值为3π8.3.(2017·丽水模拟)若函数y ＝sin(ωx －φ)⎝⎛⎭⎫ω>0，|φ|<π2在区间⎣⎡⎦⎤－π2，π上的图象如图所示，则ω，φ的值分别是( )A.ω＝2，φ＝π3B.ω＝2，φ＝－2π3C.ω＝12，φ＝π3D.ω＝12，φ＝－2π3答案 A解析 由图可知，T ＝2⎣⎡⎦⎤π6－⎝⎛⎭⎫－π3＝π， 所以ω＝2πT ＝2，又sin ⎝⎛⎭⎫2×π6－φ＝0， 所以π3－φ＝k π(k ∈Z )，即φ＝π3－k π(k ∈Z )，而|φ|<π2，所以φ＝π3，故选A.4.函数f (x )＝tan ωx (ω>0)的图象的相邻两支截直线y ＝2所得线段长为π2，则f ⎝⎛⎭⎫π6的值是( ) A.－ 3 B.33C.1D. 3答案 D解析 由已知得T ＝π2，∴ω＝2.∴f ⎝⎛⎭⎫π6＝tan π3＝ 3. 5.(2017·宁波江北区调研)将函数f (x )＝3sin x －cos x 的图象沿着x 轴向右平移a (a >0)个单位长度，所得函数图象关于y 轴对称，则a 的最小值是( ) A.π6 B.π3 C.π2 D.2π3 答案 B解析 依题意得f (x )＝2sin ⎝⎛⎭⎫x －π6， 因为函数f (x －a )＝2sin ⎝⎛⎭⎫x －a －π6的图象关于y 轴对称， 所以sin ⎝⎛⎭⎫－a －π6＝±1，a ＋π6＝k π＋π2，k ∈Z ， 即a ＝k π＋π3，k ∈Z ，因此正数a 的最小值是π3，故选B.6.函数f (x )＝sin(2x ＋φ)⎝⎛⎭⎫|φ|＜π2的图象向左平移π6个单位长度后所得图象对应的函数是奇函数，则函数f (x )在⎣⎡⎦⎤0，π2上的最小值为( ) A.－32 B.－12 C.12 D.32答案 A解析 由函数f (x )的图象向左平移π6个单位长度，得g (x )＝sin ⎝⎛⎭⎫2x ＋φ＋π3的图象， 因为是奇函数，所以φ＋π3＝k π，k ∈Z ，又因为|φ|＜π2，所以φ＝－π3，所以f (x )＝sin ⎝⎛⎭⎫2x －π3. 又x ∈⎣⎡⎦⎤0，π2，所以2x －π3∈⎣⎡⎦⎤－π3，2π3， 所以当x ＝0时，f (x )取得最小值为－32.7.(2018·镇海中学期中)函数f (x )＝sin 2x ＋sin x cos x ＋1的最小正周期是________，单调递增区间是________.答案 π ⎝⎛⎭⎫k π－π8，k π＋3π8(k ∈Z ) 解析 f (x )＝sin 2x ＋sin x cos x ＋1 ＝1－cos 2x 2＋sin 2x 2＋1 ＝22sin ⎝⎛⎭⎫2x －π4＋32， 最小正周期T ＝2π2＝π.令－π2＋2k π<2x －π4<π2＋2k π，k ∈Z ，解得－π8＋k π<x <3π8＋k π，k ∈Z .所以单调递增区间是⎝⎛⎭⎫k π－π8，k π＋3π8(k ∈Z ).8.函数f (x )＝2sin(ωx ＋φ)⎝⎛⎭⎫ω>0，0<φ<π2的部分图象如图所示，已知图象经过点A (0，1)，B ⎝⎛⎭⎫π3，－1，则f (x )＝________. 答案 2sin ⎝⎛⎭⎫3x ＋π6 解析 由已知得T 2＝π3，∴T ＝2π3，又T ＝2π，∴ω＝3.∵f (0)＝1，∴sin φ＝12，又∵0<φ<π2，∴φ＝π6，∴f (x )＝2sin ⎝⎛⎭⎫3x ＋π6(经检验满足题意). 9.已知函数f (x )＝3sin ⎝⎛⎭⎫ωx －π6(ω>0)和g (x )＝3cos(2x ＋φ)的图象完全相同，若x ∈⎣⎡⎦⎤0，π2，则f (x )的值域是____________. 答案 ⎣⎡⎦⎤－32，3 解析 f (x )＝3sin ⎝⎛⎭⎫ωx －π6 ＝3cos ⎣⎡⎦⎤π2－⎝⎛⎭⎫ωx －π6＝3cos ⎝⎛⎭⎫ωx －2π3， 易知ω＝2，则f (x )＝3sin ⎝⎛⎭⎫2x －π6， ∵x ∈⎣⎡⎦⎤0，π2，∴－π6≤2x －π6≤5π6， ∴－32≤f (x )≤3.10.已知函数f (x )＝sin ωx ＋cos ωx (ω＞0)，x ∈R .若函数f (x )在区间(－ω，ω)内单调递增，且函数y ＝f (x )的图象关于直线x ＝ω对称，则ω的值为________. 答案π2解析 f (x )＝sin ωx ＋cos ωx ＝2sin ⎝⎛⎭⎫ωx ＋π4， 因为f (x )在区间(－ω，ω)内单调递增，且函数图象关于直线x ＝ω对称，所以f (ω)必为一个周期上的最大值，所以有ω·ω＋π4＝2k π＋π2，k ∈Z ，所以ω2＝π4＋2k π，k ∈Z .又ω－(－ω)≤2πω2，即ω2≤π2，即ω2＝π4，所以ω＝π2. 11.已知函数y ＝A sin(ωx ＋φ)⎝⎛⎭⎫A >0，ω>0，|φ|<π2的图象过点P ⎝⎛⎭⎫π12，0，图象上与点P 最近的一个最高点是Q ⎝⎛⎭⎫π3，5. (1)求函数的解析式； (2)求函数f (x )的单调递增区间.解 (1)依题意得A ＝5，周期T ＝4⎝⎛⎭⎫π3－π12＝π， ∴ω＝2ππ＝2.故y ＝5sin(2x ＋φ)，又图象过点P ⎝⎛⎭⎫π12，0， ∴5sin ⎝⎛⎭⎫π6＋φ＝0，由已知可得π6＋φ＝k π，k ∈Z ， 又∵|φ|<π2，∴φ＝－π6，∴y ＝5sin ⎝⎛⎭⎫2x －π6.(2)由－π2＋2k π≤2x －π6≤π2＋2k π，k ∈Z ，得－π6＋k π≤x ≤π3＋k π，k ∈Z ，故函数f (x )的单调递增区间为⎣⎡⎦⎤k π－π6，k π＋π3(k ∈Z ). 12.已知函数f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π6＋a (ω>0)图象上最高点的纵坐标为2，且图象上相邻两个最高点的距离为π. (1)求a 和ω的值；(2)求函数f (x )在[0，π]上的单调递减区间. 解 (1)f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π6＋a ＝4cos ωx ·⎝⎛⎭⎫32sin ωx ＋12cos ωx ＋a ＝23sin ωx cos ωx ＋2cos 2ωx －1＋1＋a ＝3sin 2ωx ＋cos 2ωx ＋1＋a ＝2sin ⎝⎛⎭⎫2ωx ＋π6＋1＋a . 当sin ⎝⎛⎭⎫2ωx ＋π6＝1时， f (x )取得最大值2＋1＋a ＝3＋a .又f (x )最高点的纵坐标为2，∴3＋a ＝2，即a ＝－1. 又f (x )图象上相邻两个最高点的距离为π， ∴f (x )的最小正周期为T ＝π， ∴2ω＝2πT ＝2，ω＝1.(2)∵x ∈[0，π]， ∴2x ＋π6∈⎣⎡⎦⎤π6，136π， 当2x ＋π6∈⎣⎡⎦⎤π2，3π2，即x ∈⎣⎡⎦⎤π6，2π3时，f (x )单调递减， ∴函数f (x )在[0，π]上的单调递减区间为⎣⎡⎦⎤π6，2π3.13.将函数f (x )＝sin(2x ＋θ)⎝⎛⎭⎫－π2<θ<π2的图象向右平移φ(0<φ<π)个单位长度后，得到函数g (x )的图象，若f (x )，g (x )的图象都经过点P ⎝⎛⎭⎫0，32，则φ的值为________. 答案5π6解析 g (x )＝sin[2(x －φ)＋θ]＝sin(2x －2φ＋θ)，若f (x )，g (x )的图象都经过点P ⎝⎛⎭⎫0，32， 所以sin θ＝32，sin(－2φ＋θ)＝32， 又－π2<θ<π2，所以θ＝π3，sin ⎝⎛⎭⎫π3－2φ＝32. 又0<φ<π，所以－5π3<π3－2φ<π3，所以π3－2φ＝－4π3.即φ＝5π6.14.已知函数f (x )＝3sin ωx ＋cos ωx (ω>0)，x ∈R .在曲线y ＝f (x )与直线y ＝1的交点中，若相邻交点距离的最小值为π3，则f (x )的最小正周期为________.答案 π解析 f (x )＝3sin ωx ＋cos ωx ＝2sin ⎝⎛⎭⎫ωx ＋π6(ω>0). 由2sin ⎝⎛⎭⎫ωx ＋π6＝1，得sin ⎝⎛⎭⎫ωx ＋π6＝12， ∴ωx ＋π6＝2k π＋π6或ωx ＋π6＝2k π＋5π6(k ∈Z ).令k ＝0，得ωx 1＋π6＝π6，ωx 2＋π6＝5π6，∴x 1＝0，x 2＝2π3ω.由|x 1－x 2|＝π3，得2π3ω＝π3，∴ω＝2.故f (x )的最小正周期T ＝2π2＝π.15.设偶函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0,0<φ<π)的部分图象如图所示，△KLM 为等腰直角三角形，∠KML ＝90°，KL ＝1，则f ⎝⎛⎭⎫16的值为________.答案 34解析 由题意知，点M 到x 轴的距离是12，根据题意可设f (x )＝12cos ωx ， 又由题图知12·2πω＝1， 所以ω＝π，所以f (x )＝12cos πx ， 故f ＝12cos π6＝34. 16.(2017·山东)设函数f (x )＝sin ⎝⎛⎭⎫ωx －π6＋sin ⎝⎛⎭⎫ωx －π2，其中0＜ω＜3.已知f ⎝⎛⎭⎫π6＝0. (1)求ω；(2)将函数y ＝f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变)，再将得到的图象向左平移π4个单位长度，得到函数y ＝g (x )的图象，求g (x )在⎣⎡⎦⎤－π4，3π4上的最小值. 解 (1)因为f (x )＝sin ⎝⎛⎭⎫ωx －π6＋sin ⎝⎛⎭⎫ωx －π2， 所以f (x )＝32sin ωx －12cos ωx －cos ωx ＝32sin ωx －32cos ωx ＝3⎝⎛⎭⎫12sin ωx －32cos ωx ＝3sin ⎝⎛⎭⎫ωx －π3. 由题设知f ⎝⎛⎭⎫π6＝0，所以ωπ6－π3＝k π，k ∈Z ， 故ω＝6k ＋2，k ∈Z .又0＜ω＜3，所以ω＝2.(2)由(1)得f (x )＝3sin ⎝⎛⎭⎫2x －π3， 所以g (x )＝3sin ⎝⎛⎭⎫x ＋π4－π3＝3sin ⎝⎛⎭⎫x －π12. 因为x ∈⎣⎡⎦⎤－π4，3π4，所以x －π12∈⎣⎡⎦⎤－π3，2π3， 当x －π12＝－π3，即x ＝－π4时，g (x )取得最小值－32.。