下载文档原格式
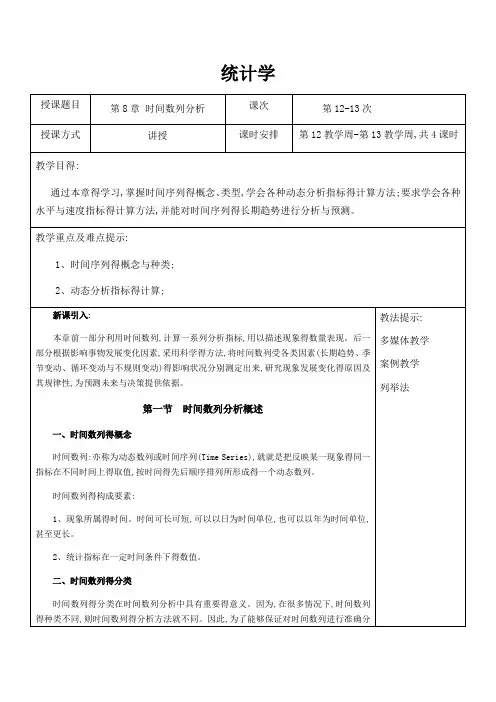
统计学时间数列分析课程统计学时间数列分析课程是一门重要的课程，它涵盖了统计学的基础理论和方法，并着重介绍了时间数列分析在实际应用中的各种技术和工具。
这门课程通常会从时间数列的概念和特性开始，详细讲解时间数列的基本统计性质，诸如均值、方差、自相关函数等。
随后，会介绍时间数列的平稳性和非平稳性，并讨论如何通过平稳性的检验来决定是否适合进行时间数列分析。
在时间数列的分析方法方面，该课程会讲解经典的时间数列模型，例如自回归移动平均模型（ARMA）、季节自回归模型（SARIMA）和傅里叶分析等。
还会介绍一些高级模型，如广义自回归条件异方差模型（GARCH）和协整模型等，用于更复杂的时间数列分析和预测。
此外，该课程还将提供实际案例和实验，通过使用统计软件进行数据处理和模型建立，培养学生运用时间数列分析进行实际问题解决的能力。
学生将有机会学习如何预测未来的时间数列趋势，并评估预测效果的方法。
在学习这门课程时，学生需要具备一定的概率论和数理统计的基础知识。
同时，他们还需要熟悉一些统计软件，如R或Python等，以便能够更好地进行数据处理和模型建立。
通过学习统计学时间数列分析课程，学生将能够掌握时间数列分析的基本理论和方法，并能够应用这些方法进行实际问题的解决。
这将有助于他们在未来的工作中，更好地理解和利用时间数列数据，为决策提供可靠的依据。
继续深入学习统计学时间数列分析课程，学生将进一步探索时间数列的高级理论和方法，并学习如何处理更复杂的时间数列数据。
在高级理论方面，学生将学习时间数列的非线性建模方法。
这包括非线性自回归移动平均模型（NARMA）、非线性协整模型等。
通过学习这些方法，学生可以更好地捕捉时间数列中的非线性特征，并提高预测的准确性。
此外，课程还会介绍一些时间数列分析中的实际应用领域，例如金融市场预测、经济指标预测、天气预测等。
学生将了解如何使用时间数列分析模型来预测股票价格、利率走势、GDP 增长等。
