20141019分数应用题综合练习
- 格式:doc
- 大小:31.00 KB
- 文档页数:2
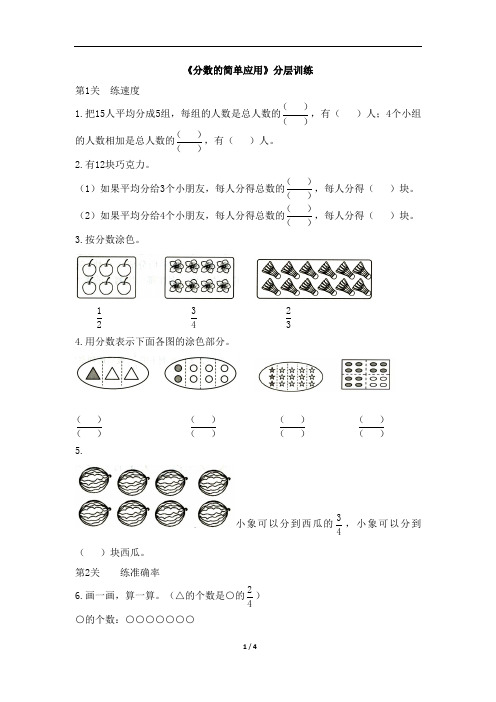
《分数的简单应用》分层训练第1关 练速度1.把15人平均分成5组,每组的人数是总人数的( )( ),有( )人;4个小组的人数相加是总人数的( )( ),有( )人。
2.有12块巧克力。
(1)如果平均分给3个小朋友,每人分得总数的( )( ),每人分得( )块。
(2)如果平均分给4个小朋友,每人分得总数的( )( ),每人分得( )块。
3.按分数涂色。
12 34 23 4.用分数表示下面各图的涂色部分。
( )( ) ( )( ) ( )( ) ( )( ) 5.小象可以分到西瓜的34,小象可以分到( )块西瓜。
第2关 练准确率6.画一画,算一算。
(△的个数是○的24) ○的个数:○○○○○○○△的个数:(画图表示)用算式表示:7.看图填空。
如图是一堆圆片,如果将其中的34涂成红色,那就需要涂红()个圆片;如果拿走4个圆片,将剩下的圆片的34涂成红色,那就需要涂红()个圆片。
8.下面的涂色部分可以用哪几个分数表示?▲▲△△▲▲△△9.三(2)班有48人,女生占38,男生有多少人?10.市民广场管理处用一批花美化广场环境,预计用36盆花,其中14是一串红,29是金盏菊,这两种类型的花哪种用的多?多多少盆?11.王军有36枚小印章,把其中的29给了李欢,把其中的16给了刘海,王军一共给出了多少枚印章?12.露出的三角形的个数占总数的35,请你画出纸片盖住的三角形。
△△△△△△13.明明带24元去买文具,买钢笔用去总钱数的14,买笔记本比买钢笔多用去总钱数的16,买钢笔和笔记车一共用去多少元?第3关练思维14.妈妈买了两块同样大的技萨,把其中一块平分成6小块,小明吃了一块,爸爸也吃了一块,把另一块平均分成3小块,爸爸吃了其中的一块。
现在哪一块剩下的多?15.一根长24米的电线,第一次用去它的14,第二次用去第一次剩下的16,最后还剩多少米?参考答案:1. 15345122.(1)134 (2)1433.涂色略4. 131415344812185.8÷4×3=6(个)6.画图略12÷4×2=6(个)7.24 218. 1224489.5183-=848÷8×5=30(人)10.一串红:36÷4×1=9(盆)金盏菊:36÷9×2=8(盆) 9>8一串红多,多9-8=1(盆)11.36÷9×2=8(枚)36÷6×1=6(枚) 8+6=14(枚)12. 提示:露在外面的是3份,那么每份是6÷3=2(个),一共5份,一共有2×5=10(个)。

分数的运算综合应用题分数是数学中一种特殊的数形式,它由一个分子和一个分母组成,可以表示部分或整体的大小关系。
在日常生活和学习中,我们经常会遇到与分数相关的运算问题。
本文将通过几个实际应用的例子,探讨分数的运算综合应用。
例题一:小明买了一张长方形的地毯,长是2 5/8米,宽是1 3/4米。
求这张地毯的面积。
解析:要求长方形地毯的面积,需要将长度和宽度相乘。
根据分数的乘法运算法则,我们可以将分数换算成带分数的形式,然后进行运算。
长方形地毯的面积 = 长度 ×宽度= (2 + 5/8) × (1 + 3/4)= 21/8 × 7/4= (21 × 7) / (8 × 4)= 147/32≈ 4 19/32 平方米答案:这张地毯的面积约为4 19/32平方米。
例题二:一台机器从早上8点40分工作到下午3点25分,共工作了多长时间?解析:要计算机器工作的时间,需要减去起始时间和终止时间。
首先,我们将时间转换成分数的形式,然后进行减法运算。
工作的时间 = 下午3点25分 - 早上8点40分= (15 + 25/60) - (8 + 40/60)= 15 + 25/60 - 8 - 40/60= 7 + 25/60 - 40/60= 7 + (25 - 40)/60= 7 - 15/60= 6 45/60 小时答案:这台机器共工作了6小时45分钟。
例题三:某家用品店举行“3折促销”活动,某商品原价60元,现在是打了3折后的价格是多少?解析:打折可以看作是减少原价格的一部分。
要计算打折后的价格,我们需要将原价乘以折扣率,然后进行减法运算。
打折后的价格 = 原价 ×折扣率= 60 × 3/10= 18元答案:打了3折后的价格为18元。
通过以上例题,我们可以看到分数的运算在日常生活中的实际应用。
无论是计算面积、时间还是打折,掌握好分数的运算规则和方法可以帮助我们更好地解决实际问题,提高数学运算能力。

分数应用题1.、12颗糖,平均分给3个人,每人分得几颗?2、12颗糖,平均分给3个人,每人分得这些糖的几分之几?3、 5个苹果平均分给8个人,每人分得几个?每人分得这些苹果的几分之几?4、五年级有男生23人,女生25人,女生占男生的几分之几?男、女生各占全班人数的几分之几?6、把3吨大米平均分成5份,每份是多少吨?每份是大米总数的几分之几?7、学校图书馆有连环画280本,文艺书140本,连环画的本数是文艺书的几倍?文艺书是连环画的几分之几?8、胜利小学五年级3班体育达标人数是24人,没达标人数是12人,达标人数占全班人数的几分之几?9.王师傅6小时加工零件34个,李师付7小时加工零件40个.谁的工作效率高?10.一本书185页,看了95页,看了的占这本书的几分之几?没看的页数占这本书的几分之几?11.动物园里有梅花鹿25头,长颈鹿5头,梅花鹿的数量是长颈鹿的多少倍?长颈鹿的数量是梅花鹿的几分之几?12、有一根木头,第一次截去2/5 米,第二次截去7/10 米,剩下4/15 米,这根木头有多长?12、果园里栽了一些果树,其中荔枝树占总数的12/27,龙眼树占总数的12/25 ,其余的是杨梅树,杨梅树占总数的几分之几?13、妈妈买回600 克油,第一天用了1/3 ,第二天用了1/4 ,剩下多少油?,14、庆丰粮店运进1800千克大米,卖出59 ,还剩多少千克?15、无线电厂五月份生产收录机1260台,比四月份增产18 ,四月份生产多少台?16、有一捆电线,第一次用去全长的13 ,第二次用去全长的59 ,两次共用去40米。
这捆电线共长多少米?17、开学后小明和哥哥共发了18本书,哥哥比小明多发了14 ,小明发了多少本书?18、一项工程,单独做,甲要20天完成,乙要15天完成,开始二人一起干,因工作需要乙中途调走,这时剩下的工程甲又用了3天才完成。
甲乙合干了几天?19、小红家原来有一袋大米,吃掉87后,又买来25千克大米,这样,现有的大米正好是原来一袋大米的43。


分数运算的综合练习在数学学习中,分数运算是一个非常重要的基础知识。
掌握好分数的四则运算不仅可以帮助我们更好地理解和解决实际问题,还能够为我们打下更深厚的数学基础。
本文将为大家提供一些分数运算的综合练习题,旨在帮助读者巩固和扩展自己的分数运算能力。
一、四则运算1. 将下列分数转化为相同的分母,并进行加(减)法运算:⅔ + ½ =⅝ - ¼ =2. 将下列分数转化为相同的分母,并进行乘法运算:⅓ × ¼ =½ × ⅔ =3. 计算下列各式的结果(结果保留最简形式):1/3 + 5/6 × 3/4 =4/5 ÷ 2/3 - 1/2 =二、混合数与假分数的互化1. 将下列混合数转化为假分数:1 2/5 =3 3/4 =2. 将下列假分数转化为混合数:8/3 =5/2 =三、分数的比较与排序1. 比较下列各组分数的大小(>、<、=):⅔ ¾7/8 5/65/6 2/32. 将下列分数从小到大进行排序:4/5, 1/2, 2/3, 3/4四、运算应用题1. 小明买了一条绳子,长2米6分米,他想把绳子分成相等的4段,每段多长?2. 甲乙二人合作完成一项任务,甲完成了任务的2/5,乙完成了任务的3/4,他们共完成了多少?3. 一桶果汁原有3升,小红喝了1/5,小明喝了2/3,还剩多少升果汁?通过以上练习题的练习,相信大家对于分数的四则运算有了更深入的了解。
在日常学习中,可以多进行类似的练习加深对分数运算的掌握。
只有不断地练习和巩固,才能在数学学习中取得更好的成绩。
希望本文对大家的数学学习有所帮助!。

分数乘法专项练习(2014.9.26) 姓名:
一、列式计算
(1)比24多它的
61的数是多少? (2)比56多0.8的数是多少?
(3)比5吨多
51吨是多少吨? (4)比10吨多51是多少吨?多了多少吨?
(6)比
109千克多31是多少千克?(7)比109千克少31是多少千克?(8)比109千克多3
1千克是多少千克?
(9从
43吨水泥中运走51,还剩多少吨? (10从43吨水泥中运走51吨,还剩多少吨?
(10)一袋大米25千克,已经吃了它的
52少53千克,吃了多少千克?还剩这袋大米的几分之几?
(11)一件西服原价320元,现在的价格比原来降低了
51。
降低了多少钱?原价是现价的几分之几?
(12)育才小学六年级有240人,五年级的人数是六年级的
87,四年级比五年级的人数的少51,四年级比五年级少了多少人?
(13)公交车上有36人,到青年路站后下去了
95,上来的人数是车上人数的43,下车的人多还剩上车的人多?
(14)甲数的41等于乙数的52,甲数是乙数的几分之几?乙数是两数和的几分之几?。
分数的综合运算练习题1. 小明去超市买了1/3千克的香蕉和2/5千克的苹果,他一共买了多少千克的水果?解答:要计算小明购买的水果的总重量,我们需要将香蕉和苹果的重量相加。
首先,我们可以将香蕉和苹果的分数转化为相同的分母,以便于计算。
香蕉的分母为3,苹果的分母为5。
我们可以找到两个数的最小公倍数,即15。
所以,香蕉的分子变为(1/3)*(15/3)=5/15,苹果的分子变为(2/5)*(15/5)=6/15。
现在,我们可以将香蕉和苹果的重量相加:5/15 + 6/15 = 11/15。
所以,小明一共买了11/15千克的水果。
2. 小华家庭共购买了1/2千克的鸡肉和3/4千克的牛肉,他们共购买了多少千克的肉?解答:要计算小华家庭购买的肉的总重量,我们需要将鸡肉和牛肉的重量相加。
首先,我们可以将鸡肉和牛肉的分数转化为相同的分母,以便于计算。
鸡肉的分母为2,牛肉的分母为4。
我们可以找到两个数的最小公倍数,即4。
所以,鸡肉的分子变为(1/2)*(2/2)=2/4,牛肉的分子变为(3/4)*(1/1)=3/4。
现在,我们可以将鸡肉和牛肉的重量相加:2/4 + 3/4 = 5/4。
所以,小华家庭共购买了5/4千克的肉。
3. 一个篮球队共有12名队员,其中5/6是男队员,剩下的队员都是女队员。
女队员的人数是男队员人数的几分之几?解答:首先,我们可以计算男队员的人数。
男队员的人数是总队员人数的5/6,即(5/6)*12 = 10。
剩下的队员就是女队员,女队员的人数是总队员人数减去男队员的人数,即12-10=2。
所以,女队员的人数是男队员人数的2/10,即2/10=1/5。
所以,女队员的人数是男队员人数的1/5。
4. 小王点了1/3千克的牛肉和3/8千克的鱼,他还想买2/5千克的鸡肉,他一共需要购买多少千克的肉?解答:要计算小王购买的肉的总重量,我们需要将牛肉、鱼和鸡肉的重量相加。
首先,我们可以将牛肉、鱼和鸡肉的分数转化为相同的分母,以便于计算。
1 分数应用题(二)姓名1、 一项工程,甲队单独做要20天完成,如果甲、乙两队合作12天可以完成。
如果由乙队单独做,多少天可以完成?2、 一份稿件,甲、乙两个打字员合打12小时可以完成。
现在两人合打,由于中途甲因故停工5小时,因此用了15小时才完成。
如果由甲单独打,多少小时完成?3、 一项工程,由甲、乙两队合做12天可以完成。
现在由甲队先做了8天,乙队接着做18天,恰好完成。
这项工程如果由乙队单独做,需要多少天完成?4、 一件工作,甲单独做要8天完成,乙单独做要10天完成。
现在两人合做,中途甲因事请假一天,完成这件工作共需用多少天?5、 一件工作,甲、乙合做10天可以完成,乙、丙合做12天可以完成,甲、丙合做15天可以完成。
现在三人合做,需要多少天才能完成?6、 客、货两车分别从甲、乙两地同时出发,相向而行,经过6小时两车相遇后,客车继续行驶4小时到达乙地。
货车还需再行驶几小时才能到达甲地?7、 一个游泳池装有一个进水管和一个排水管,单开进水管5小时可将空池注满。
由于管理员的疏忽,将两个水管同时打开,结果用了8小时才将空池注满。
如果单独打开排水管,多少小时才能将满池水放完?8、 一位登山爱好者攀登紫金山,上山时每小时行3千米,沿原路下山时,每小时行5千米。
求这位登山爱好者上、下山的平均速度。
9、 修一条水渠,单独修,甲队要10天,乙队要15天。
现在两队合修2天后,还剩下240米没有修。
这条水渠长多少米?10、 两列火车同时从甲、乙两地出发,相向而行,相遇时快车行了全程的95。
已知慢车每小时行72千米,快车行完全程要10小时。
甲、乙两地相距多少千米?。
分数应用题综合练习题1. 小明有3/5的苹果,他分给小红1/4,小芳1/3,小亮1/10,那么他还剩下多少苹果?解析:设小明有x个苹果,根据题意,小明剩下的苹果数量可以表示为x * (1 - 1/4 - 1/3 - 1/10)。
化简得:x * (6/12 - 3/12 - 4/12 - 1/12) = x * (6/12) = x/2。
所以小明还剩下2/5的苹果。
2. 一辆汽车一小时行驶150公里,问它行驶x小时能够行驶的距离是多少?解析:设行驶距离为y公里,根据题意,可以列出方程:150/1 =y/x。
解方程可以得到y = 150x。
所以它行驶x小时能够行驶的距离是150x公里。
3. 小明以每小时30公里的速度骑自行车到学校,蹬车用了1.5小时,那么他距离学校有多远?解析:设距离学校为d公里,根据题意,可以列出方程:30 * 1.5 = d。
解方程可以得到d = 45。
所以他距离学校有45公里远。
4. 一群小鸟从一座山上飞下来,每秒钟下降50米,如果它们从山顶起点下降4秒钟,那么它们下降的总距离是多少?解析:设小鸟下降的总距离为d米,根据题意,可以列出方程:d = 50 * 4。
解方程可以得到d = 200。
所以它们下降的总距离是200米。
5. 小明的体重是小亮的3/5,小亮的体重是小红的4/9,那么小明的体重是小红的几分之几?解析:设小红的体重为x千克,根据题意,小亮的体重可以表示为4/9 * x千克,小明的体重可以表示为3/5 * (4/9 * x千克)。
化简得:3/5 * 4/9 * x千克 = 12/45 * x千克 = 4/15 * x千克。
所以小明的体重是小红的4/15。
6. 飞机以600公里/小时的速度飞行,已经飞行4小时,还需要飞行多久才能到达目的地,目的地距离800公里?解析:设还需要飞行的时间为t小时,根据题意,可以列出方程:600 * 4 + 600t = 800。
解方程可以得到t = 1。
分数乘除法综合练习
教学目标:
1、通过综合练习,让学生掌握解决分数乘除法问题的一般方法,培养学生解决问题能力。
2、培养学生小组合作,研究问题的能力。
教学重难点:培养学生解决问题的能力及良好的习惯。
教学过程: 一、谈话导入。
进入六年级我们一直在和分数打交道,要顺利的解决分数问题,先要弄清两个概念:带单位的分数和不带单位的分数。
师:你能举出一两个带单位的分数和不带单位的分数,并说说它表示的意思吗?
学生说,师板书。
带单位的分数,如3/4吨,叫数量,与我们以前学过的“3吨”、“0.3吨”表示的意义一 样,都是表示一个物体的具体的数量。
只不过在这里用分数的形式表示出来而已。
不带单位的分数,如3/4,叫分率,它表示一个数的几分之几。
练习:
1、一根铁丝长5米,用去了2/5米,还剩下( )米。
一根铁丝长5米,用去了2/5,还剩下( )米。
2、一袋面粉,已经吃了3/4,还剩这袋面粉的( )。
是把( )看作单位“1”。
( )×( )=已经吃的重量;( )×( )=剩下的重量。
3、一台电脑现价比原价降低了2/9,是把( )看作单位“1”,现价是原价的( )。
原价×( )=降低了的价钱;原价×( )=现价。
4、学校五年级有150人,比四年级多1/4,四年级有多少人?是把( )看作单位“1”,五年级人数是四年级的( )。
四年级人数×( )=五年级人数。
5、一堆煤,运走2/5,还剩75吨,这堆煤有多少吨?是把( )看作单位“1”,还剩这堆煤的( ),一堆煤×( )=剩下的煤。
同学们真不错,能迅速的找到单位“1”,和等量式,这对我们解决有关分数问题很重要。
下面这里有 道题,请大家把题目通读两到三遍,看哪些题在解题思路上属于同一种类型,请你标上相同的记号。
二、练习题分析。
1、大约从一万年前开始,青藏高原平均每年上升约7/100M。
按照这个速度,50年它能长高多少米?
2、一台织布机53小时织布2
5 米。
照这样计算,这台织布机每小时可以织布多少米? 3、某种农药3/2KG加水稀释后可喷洒1公顷的菜地。
喷洒1/5公顷菜地需要多少千克的农药? 4、某饮料厂使用一种自动检测仪来检测饮料是否有缺陷,检测一个瓶子所用的时间为1/25秒。
1分
钟可以检测多少个瓶子?
5、小明看一本120页的书,已经看了全书的3/4,看了多少页?还剩多少页没看?
6、水果店运来140千克梨,正好是苹果的7/8,运进苹果多少千克?
7、某粮店上一周卖出面粉18吨,大米比面粉多 16
,粮店上周卖出大米多少千克? 8、某工厂十月份用水480吨,比原计划节约了1/9。
十月份原计划用水多少吨?
9、某校有男生300人,女生比男生少1/5,女生有多少人?
10、光明小学去年体检时发现有280名同学近视,今年比去年多
10
1。
今年全校近视的同学一共有多少人?
11、小明看一本书,第一天看了全书的1/3,第二天看了全书的1/5,两天一共看了72页,这本书有多少页? 12、一套运动服300元,裤子价钱是上衣的2/3,上衣和裤子的价钱分别是多少?
学生独立完成,差不多的请学生在小组交流自己的做法,给小组内同学说说你这样分的想法?
三、分析讨论
谁来说说你认为哪些题是一种类型?为什么?
生说师写。
1、3表示数量,表示几个几分之几相乘。
2、4 表示有几个几分之几
5、7、9已知单位“1”,
6、8、10、11、12求单位“1”。
请大家在每一种类型题中选择排在前面的一道题分析解决,要求写出分析思路及算式,不解答。
谁愿意说说第1题,为什么用乘法?
7/100×50
7/100M表示单位量,50表示数量,单位量×数量=总量
谁愿意说说第2题,为什么用除法? 25÷5
3 25表示工作总量,5
3表示工作时间 总量÷数量=单位量 谁愿意说说第5题,为什么用乘法?
120×3/4
表示120的3/4
谁愿意说说第6题,为什么用方程(除法)?
苹果的7/8=140千克,求单位“1”.
四、全课小结。
我们今天通过读题(找已知条件和问题),分析(表示数量时运用数量关系,表示关系时,找单位“1”,写出等量关系式,已知单位“1”,直接用分数乘法解决,求单位“1”用方程或除法解决),列出算式解答,一定记得验算,再作答。