下载文档原格式
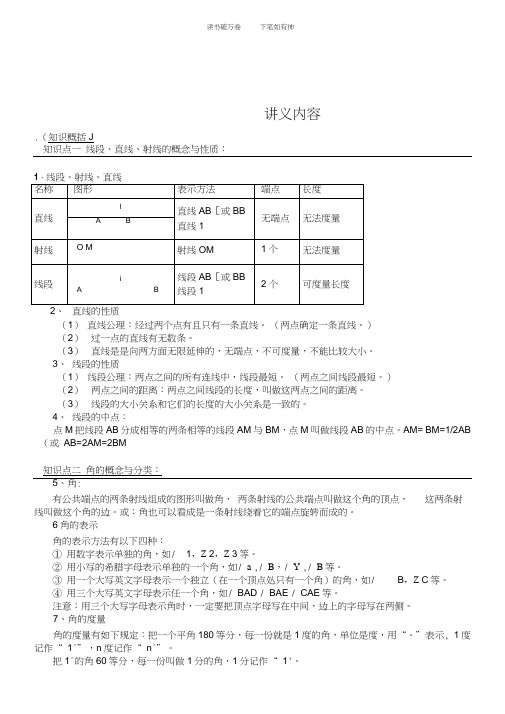
讲义内容.（知识概括J知识点一线段、直线、射线的概念与性质：1、2、直线的性质（1）直线公理：经过两个点有且只有一条直线。
（两点确定一条直线。
）（2）过一点的直线有无数条。
（3）直线是是向两方面无限延伸的，无端点，不可度量，不能比较大小。
3、线段的性质（1）线段公理：两点之间的所有连线中，线段最短。
（两点之间线段最短。
）（2）两点之间的距离：两点之间线段的长度，叫做这两点之间的距离。
（3）线段的大小关系和它们的长度的大小关系是一致的。
4、线段的中点：点M把线段AB分成相等的两条相等的线段AM与BM，点M叫做线段AB的中点。
AM= BM=1/2AB （或AB=2AM=2BM知识点二角的概念与分类：5、角:有公共端点的两条射线组成的图形叫做角，两条射线的公共端点叫做这个角的顶点，这两条射线叫做这个角的边。
或：角也可以看成是一条射线绕着它的端点旋转而成的。
6角的表示角的表示方法有以下四种：①用数字表示单独的角，如/ 1，Z 2，Z 3等。
②用小写的希腊字母表示单独的一个角，如/ a ,/ B，/ Y ,/ B等。
③用一个大写英文字母表示一个独立（在一个顶点处只有一个角）的角，如/ B，Z C等。
④用三个大写英文字母表示任一个角，如/ BAD / BAE / CAE等。
注意：用三个大写字母表示角时，一定要把顶点字母写在中间，边上的字母写在两侧。
7、角的度量角的度量有如下规定：把一个平角180等分，每一份就是1度的角，单位是度，用“。
”表示, 1度记作“ 1°”，n度记作“ n°”。
把1°的角60等分，每一份叫做1分的角，1分记作“ 1'。
把1'的角60等分，每一份叫做1秒的角，1秒记作“ T”。
O B1° =60' 1' =60”8、 角的平分线从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线。
9、 角的性质（1） 角的大小与边的长短无关，只与构成角的两条射线的幅度大小有关。
第四章 4.1.1立体图形与平面图形
知识点1
图形
侧面是曲面
有两个面是互相
立体图形的左面与右面之间的水平长度记为长
从上面看
立体图形是由平面或曲面或平面和曲面围成的,
按不同的方式展开得到的平面展开图可能是不一样的
对于同一个立体图形当我们按不同的方式展开时
11种
②一三二型,如图所示:
如图所示:
如图所示:
常见的其他立体图形的展开图如下表所示
立体图形平面展开图
①展开图全是长方形或正方形
考点1：展开图
【例1】骰子是一种特别的数字立方体(见图),它符合规则:相对两面的点数之和总是7,图中可以折成符合规则的骰子的是( )
A
B C D
答案:C
点拨：用排除法:A选项中,点数1与点数3相对,它们的和为4,不等于7.B选项和D选项中,点数1与点数5相对,它们的和不等于7,所以选C.排除法是解决此类问题常用的方法. 考点2:从不同方向看几何体
【例2】如图是一个由4个相同的正方体组成的立体图形,从正面、上面、左面看,所得图形为下面的( )
A
B C D
答案:B
点拨：注意本题中四个正方体组成的立体图形从左面看与从正面看得到的图形是一样的.
考点3:由从不同方向看几何体所得图形确定小正方体个数
【例3】如图所示是由几个相同的小正方体搭成的几何体从不同方向看所得的图形,则搭成这个几何体的小正方体的个数是( )
A.3
B.4
C.5
D.6
答案:C
点拨：这个几何体的底层应该有3+1=4(个)小正方体,第二层应该有1个小正方体,因此搭成这个几何体所用小正方体的个数是4+1=5.此题主要体现了对空间想象能力的考查.。
4 角的比较
知能演练提升
一、能力提升
1.如图,OB表示秋千静止时的位置,当秋千从OC荡到OA时,OB平分∠AOC,∠BOC=60°,则秋千从OC 到OA转动的角度是().
A.30°
B.60°
C.90°
D.120°
2.如图,已知射线OC平分∠AOB,射线OD,OE三等分∠AOB.又OF平分∠AOD,则图中等于∠BOE的角共有().
A.1个
B.2个
C.3个
D.4个
3.已知∠α和∠β的顶点和一边都重合,另一边都在公共边的同侧,且∠α>∠β,则∠α的另一边落在∠β的().
A.另一边上
B.内部
C.外部
D.以上结论都不对
4.(2017·山东德州夏津县一模)如图,将一副三角尺叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=().
A.90°
B.120°
C.160°
D.180°
5.如图,已知OM是∠AOB的平分线,射线OC在∠BOM内,ON是∠BOC的平分线,∠AOC=80°,则∠MON 的度数等于.
6.已知∠AOC=80°,∠BOC=50°,OD平分∠BOC,则∠AOD的度数是.
7.已知直线AB上有一点O,射线OD和射线OC在AB的同侧,∠AOD=42°,∠BOC=34°,则∠AOD与∠BOC的平分线的夹角的度数是.
8.如图,A,O,B三点在同一直线上,∠BOC=50°,∠AOD与∠DOC的度数比为10∶3,OE平分∠AOC,求∠DOE的度数.
二、创新应用
9.
(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)若(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)若(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中能看出什么规律?
知能演练·提升
一、能力提升
1.D
2.C
3.C
4.D
5.40°
6.105°
7.142°
8.解因为∠AOD+∠DOC+∠BOC=180°,∠BOC=50°,
所以∠AOD+∠DOC=130°.
又因为∠AOD与∠DOC的度数比为10∶3,
所以∠AOD=130°×=100°,
∠DOC=130°×=30°.
因为OE平分∠AOC,
所以∠EOC=∠AOC
=(∠AOD+∠DOC)=65°.
所以∠DOE=65°-30°=35°.
二、创新应用
9.解 (1)∠MON=(90°+30°)-×30°=60°-15°=45°.
(2)∠MON=(∠AOB+∠BOC)-∠BOC=(α+30°)-×30°=α.
(3)∠MON=(∠AOB+∠BOC)-∠BOC=×90°+β-β=45°.
(4)∠MON的度数始终等于∠AOB度数的一半.。
