广东省惠州市惠东县吉隆镇吉隆中学七年级数学下册5.1.3同位角、内错角、同旁内角课堂检测(无答案.pdf

精品“正版”资料系列，由本公司独创。

旨在将“人教版”、”苏教版“、”北师大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友。

本资源创作于2020年8月，是当前最新版本的教材资源。

包含本课对应内容，是您备课、上课、课后练习以及寒暑假预习的最佳选择。

同位角、内错角、同旁内角教学目标：1、理解同位角、内错角、同旁内角的概念；（并能正确判断两个角的位置关系）2、会识别同位角、内错角、同旁内角.（能说出两个同位角、内错角、同旁内角分别是由哪两条直线被那一条直线截得）重点：同位角、内错角、同旁内角的概念与识别； 难点：识别同位角、内错角、同旁内角。

在较为复杂的图形中能辨认同位角、内错角、同旁内角教学过程一、导入新课前面我们研究了一条直线与另一条直线相交的情形，接下来，我们进一步研究一条直线分别与两条直线相交的情形。

二、同位角、内错角、同旁内角如图，直线a 、b 与直线c 相交，或者说，两条直线a 、b 被第三条直线c 所截，得到八个角。

我们来研究那些没有公共顶点的两个角的关系。

∠1与∠2、∠4与∠8、∠5与∠6、∠3与∠7有什么位置关系？在截线的同旁，被截直线的同方向（同上或同下）.具有这种位置关系的两个角叫做同位角。

（同位角形如字母“F ”。

）∠3与∠2、∠4与∠6的位置有什么共同的特点？在截线的两旁，被截直线之间。

具有这种位置关系的两个角叫做内错角.（内错角形如字母“Z ”。

）∠3与∠6、∠4与∠2的位置有什么共同的特点？在截线的同旁，被截直线之间。

具有这种位置关系的两个角叫做同旁内角.（同旁内角形如字母“U ”。

）思考：这三类角有什么相同的地方？（1）都不相邻即不存在共公顶点；（2）有一边在同一条直线（截线）上。

三、例题cb a43215 6 87例如图，直线DE ，BC 被直线AB 所截，（1）∠1与∠2、∠1与∠3、∠1与∠4各是什么角？为什么？（2）如果∠1=∠4，那么∠1与∠2相等吗？∠1与∠3互补吗？为什么？解：（1）∠1与∠2是内错角，因为∠1与∠2在直线DE ，BC 之间，在截线AB 的两旁；∠1与∠3是同旁内角，因为∠1与∠3在直线DE ，BC 之间，在截线AB 的同旁；∠1与∠4是同位角，因为∠1与∠4在直线DE ，BC 的同方向，在截线AB 的同方向。

5.1.3、同位角、内错角、同旁内角学习目标：1. 理解并识别同位角、内错角、同旁内角的定义及基本图形2. 注意掌握冋位角、内错角、冋旁内角的基本特征学习重点：同位角、内错角、同旁内角的定义与识别。

学习难点：辨别“三线八角”。

教学内容:、问题感知，情景切入-----并识别同位角、内错角、同旁内角如®;直线AB、CD、EF相交（即两条直线AB、线EF所截）构成的八个角:⑴、/ 1与/ 5是同位角，那么图中的同位角还有:⑵、/ 3与/5是内错角，那么图中的内错角还有:⑶、/ 3与/5是同旁内角，那么图中的同旁内角还有总结同位角：O内错角：同旁内角:如图，直线DE 、BC 被直线AB 所截.⑴、/ 1与/2,/ 1与/ 3,2 1与/4各是什么角？⑵、如果/ 1 = 24,那么2 1与2 2相等吗？ 2 1与2 3 互补吗？为什么？1•如右图所示，指出下列各组角是哪条两条直线 被哪条直线所截 而得到的并指出它们的名称。

解：2 1的同位角:2 1的内错角： 21的同旁内角:⑴、 2 1与2 D 是直线 和 被 所截的 角 ⑵、 2 1与2A 是直线 和 被 所截的 角 ⑶、 2 A 与23是直线 和 被 所截的 角 ⑷、 2 2与2 3是直线 和 被 所截的 角 ⑸、2 C 与23是直线 和被所截的角2.在右图中的找出2 1的同位角、内错角、同旁内角课堂小测试：1、如图①所示，/ 1与/ 2是_______ 角，/ 2与/4是 _________ 角，/ 2与/3是________ 角。

2、如图②所示，/ 1与/ 2是角，是直线_和—被所截而形成的；/ 1与/ 3是______________________ 角，是直线和被所截的而形成的.3、如图③所示，下列说法错误的是（）A、/ B与/ A是同旁内角B、/ A与/ 3是内错角C、/ 1与/ 3是内错角D、/ C与/ 3是同位角4、如图④所示，按各组角的位置，判断错误的（）A、/3与/6是同旁内角B、/7与/C是内错角C、/ 1与/ 8是同位角D、/ 2与/6是同位角5、两条直线被第三条直线所截，角平分线互相垂直的是（）A、同位角B、内错角C、同旁内角D、对顶角6、如图⑤所示，能与/ B构成同位角的有（）A、1个B、2个C、3个D、4个7、如图⑥所示，/ 1与/ 2是同位角的个数（）① ② ③ ④A、1个B、2个C、3个D、4个8如图⑦所示，两条直线被第三条直线所截，若/ 1的同旁内角等于180°，求/ 1的内错角的度数。

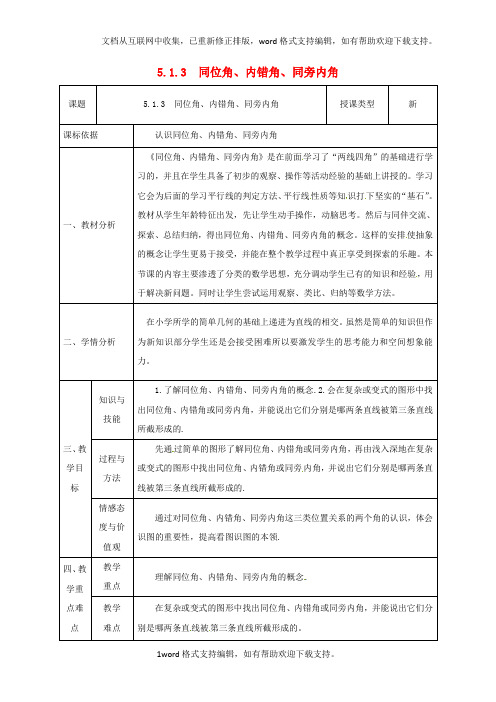
5.1.3 同位角、内错角、同旁内角课题 5.1.3 同位角、内错角、同旁内角授课类型新课标依据认识同位角、内错角、同旁内角一、教材分析《同位角、内错角、同旁内角》是在前面学习了“两线四角”的基础进行学习的，并且在学生具备了初步的观察、操作等活动经验的基础上讲授的。

学习它会为后面的学习平行线的判定方法、平行线性质等知识打下坚实的“基石”。

教材从学生年龄特征出发，先让学生动手操作，动脑思考。

然后与同伴交流、探索、总结归纳，得出同位角、内错角、同旁内角的概念。

这样的安排使抽象的概念让学生更易于接受，并能在整个教学过程中真正享受到探索的乐趣。

本节课的内容主要渗透了分类的数学思想，充分调动学生已有的知识和经验，用于解决新问题。

同时让学生尝试运用观察、类比、归纳等数学方法。

二、学情分析在小学所学的简单几何的基础上递进为直线的相交。

虽然是简单的知识但作为新知识部分学生还是会接受困难所以要激发学生的思考能力和空间想象能力。

三、教学目标知识与技能1.了解同位角、内错角、同旁内角的概念.2.会在复杂或变式的图形中找出同位角、内错角或同旁内角，并能说出它们分别是哪两条直线被第三条直线所截形成的.过程与方法先通过简单的图形了解同位角、内错角或同旁内角，再由浅入深地在复杂或变式的图形中找出同位角、内错角或同旁内角，并说出它们分别是哪两条直线被第三条直线所截形成的.情感态度与价值观通过对同位角、内错角、同旁内角这三类位置关系的两个角的认识，体会识图的重要性，提高看图识图的本领.四、教学重点难点教学重点理解同位角、内错角、同旁内角的概念.教学难点在复杂或变式的图形中找出同位角、内错角或同旁内角，并能说出它们分别是哪两条直线被第三条直线所截形成的。

五、教法学法观察、分析、类比、归纳、概括。

六、教师生活动设计意图学过程设计一、导入新课前面我们研究了一条直线与另一条直线相交的情形，接下来，我们进一步研究一条直线分别与两条直线相交的情形。

5.1.3 同位角、内错角、同旁内角【知识与技能】1.了解同位角、内错角、同旁内角的概念.2.会在复杂或变式的图形中找出同位角、内错角或同旁内角，并能说出它们分别是哪两条直线被第三条直线所截形成的.【过程与方法】先通过简单的图形了解同位角、内错角或同旁内角，再由浅入深地在复杂或变式的图形中找出同位角、内错角或同旁内角，并说出它们分别是哪两条直线被第三条直线所截形成的.【情感态度】通过对同位角、内错角、同旁内角这三类位置关系的两个角的认识，体会识图的重要性，提高看图识图的本领.【教学重点】理解同位角、内错角、同旁内角的概念.【教学难点】在复杂或变式的图形中找出同位角、内错角或同旁内角，并能说出它们分别是哪两条直线被第三条直线所截形成的.一、情境导入，初步认识问题如图，两条直线AB，CD被直线EF所截，形成了八个角：∠1，∠2，∠3，∠4，∠5，∠6，∠7，∠8.（1）观察∠1与∠5的位置关系，这种位置关系的角还有哪些？（2）观察∠3与∠5的位置关系，这种位置关系的角还有哪些？（3）观察∠3与∠6的位置关系，这种位置关系的角还有哪些？【教学说明】在本问题中，全班同学合作交流，完成上面的问题，教师可作如下指导：先看这两个角与两条直线AB、CD的位置关系，再看这两个角与第三条直线EF的位置关系.二、思考探究，获取新知思考已知同位角、内错角或同旁内角，怎样判断它们是哪两条直线被第三条直线所截形成的？【归纳结论】1.定义：同位角:两条直线被第三条直线所截，如果两个角在这两条直线的同一方，在第三条直线的同一侧，那么这两个角叫同位角.内错角:两条直线被第三条直线所截，如果两个角在这两条直线之内，并且分别在第三条直线的两侧，那么这两个角叫内错角.同旁内角:两条直线被第三条直线所截，如果两个角在这两条直线之内，在第三条直线同一旁，那么这两个角叫同旁内角.2.要判断同位角，内错角或同旁内角是由哪两条直线被第三条直线所截形成的，可先判断出第三条直线，第三条直线的显著特点是与两个角的边都有关.三、运用新知，深化理解如图，（1）∠B与哪个角是同位角，它们分别是哪两条直线被第三条直线所截形成的？（2）∠B与哪个角是同旁内角，它们分别是哪两条直线被第三条直线所截形成的？（3）∠C与哪个角是内错角，它们分别是哪两条直线被第三条直线所截形成的？（4）∠1与∠B是同位角吗？为什么？【教学说明】本环节易采用抢答的形式让同学们回答，激发学生学习的趣味性.【答案】略.四、师生互动，课堂小结同位角、内错角、同旁内角的概念.1.布置作业：从教材“习题5.1”中选取.2.完成练习册中本课时的练习.本节课学生对简单图形的同位角、内错角和同旁内角的判定较正确，但一些略复杂图形的同位角、内错角、同旁内角的判定就不够全面.针对课堂反馈的信息应及时对学生补差补缺，对角的理解的问题应及时纠正，让所有学生都有收获，激发他们的学习兴趣.。