第九章根树
- 格式:ppt
- 大小:382.50 KB
- 文档页数:35

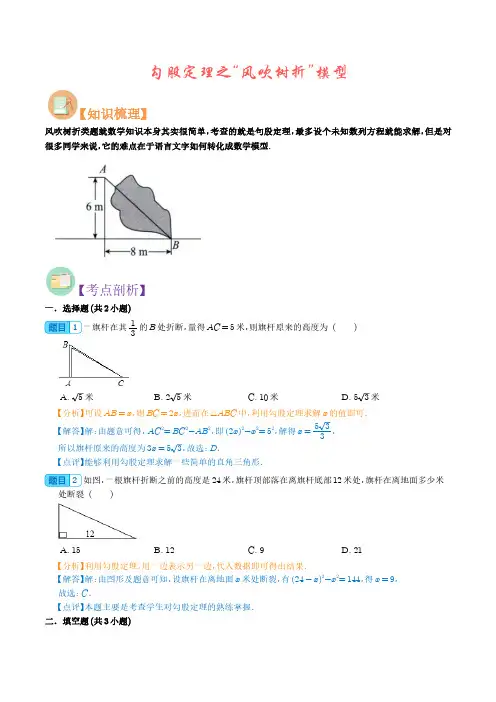
勾股定理之“风吹树折”模型【知识梳理】风吹树折类题就数学知识本身其实很简单,考查的就是句股定理,最多设个未知数列方程就能求解,但是对很多同学来说,它的难点在于语言文字如何转化成数学模型.【考点剖析】一.选择题(共2小题)1一旗杆在其13的B处折断,量得AC=5米,则旗杆原来的高度为()A.5米B.25米C.10米D.53米【分析】可设AB=x,则BC=2x,进而在△ABC中,利用勾股定理求解x的值即可.【解答】解:由题意可得,AC2=BC2-AB2,即(2x)2-x2=52,解得x=53 3,所以旗杆原来的高度为3x=53,故选:D.【点评】能够利用勾股定理求解一些简单的直角三角形.2如图,一根旗杆折断之前的高度是24米,旗杆顶部落在离旗杆底部12米处,旗杆在离地面多少米处断裂()A.15B.12C.9D.21【分析】利用勾股定理,用一边表示另一边,代入数据即可得出结果.【解答】解:由图形及题意可知,设旗杆在离地面x米处断裂,有(24-x)2-x2=144,得x=9,故选:C.【点评】本题主要是考查学生对勾股定理的熟练掌握.二.填空题(共3小题)3如图,一次“台风”过后,一根旗杆被台风从离地面9米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断前至少有24m高.【分析】根据旗杆未断部分与折断部分及地面正好组成直角三角形,利用勾股定理解答即可.【解答】解:由勾股定理得斜边为:92+122=15米,则原来的高度为9+15=24米.故答案为:24m.【点评】本题考查的是勾股定理在实际生活中的运用,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.4如图,今年第8号台风“桑美”是50多年以来登陆我国大陆地区最大的一次台风,一棵大树受“桑美”袭击于离地面5米处折断倒下,倒下部分的树梢到树的距离为7米,则这棵大树折断前有13.6米(保留到0.1米).【分析】首先根据勾股定理求得折断的树高是25+49=74,所以折断前树的高度是5+74≈13.6米.【解答】解:在Rt△ABC中,AC=52+72=74≈8.6米,5+8.6=13.6米.故答案为:13.6.【点评】考查了勾股定理的应用,比较简单.5有一棵9米高的大树,树下有一个1米高的小孩,如果大树在距地面4米处折断(未完全折断),则小孩至少离开大树4米之外才是安全的.【分析】根据题意构建直角三角形ABC,利用勾股定理解答.【解答】解:如图,BC即为大树折断处4m减去小孩的高1m,则BC=4-1=3m,AB=9-4=5m,在Rt△ABC中,AC=AB2-BC2=52-32=4.【点评】此题考查直角三角形的性质及勾股定理的应用,要根据题意画出图形即可解答.三.解答题(共6小题)6如图,受台风影响,一棵大树在高于地面5米处折断,大树顶部落在距离大树底部10米处的地面上,问这棵大树原来有多高?【分析】该大树折断后,折断部分与地面、原来的树干恰好构成一直角三角形,设大树高为x,则折断部分为x-5,由勾股定理可得出方程:52+102=(x-5)2,解该方程可得出大树原来的高.【解答】解:设大树断掉的部分长为x米,利用勾股定理:52+102=(x-5)2,解得x=5+55,答:大树原来的高为(5+55)米.【点评】利用勾股定理解应用题,关键在于把折断部分、大树原来部分和地面看作一个直角三角形,利用勾股定理列出方程求解.7某地遭台风袭击,马路边竖有一根高为7m的电线杆AC,被台风从离地面2m的B处吹断裂,倒下的电线杆顶部C′是否会落在距离它的底部4m的快车道上?说说你的道理.【分析】电线杆折断后构成一个直角三角形,利用勾股定理求出AC′的长,即可得出正确结论.【解答】解:根据题意,AB=2m,则BC=7-2=5m,于是AC′=52-22=21,又因为21>4,∴电线杆顶部C′会落在距它的底部4m的快车道上.【点评】此题是勾股定理在生活中应用的典型例子,只要善于观察,便可用数学知识解决生活中的诸多问题.8如图,一次“台风”过后,一根旗杆被台风从离地面9米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断前至少有多高?【分析】根据旗杆未断部分与折断部分及地面正好组成直角三角形,利用勾股定理解答即可.【解答】解:由勾股定理得斜边为92+122=15米,则原来的高度为9+15=24米.【点评】此题主要考查学生对勾股定理的运用,比较简单.9台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,求旗杆在什么位置断裂的?【分析】旗杆折断的部分,未折断的部分和旗杆顶部离旗杆底的部分构成了直角三角形,运用勾股定理可将折断的未知求出.【解答】解:设旗杆未折断部分长为x米,则折断部分的长为(16-x)m,根据勾股定理得:x2+82=(16-x)2,可得:x=6m,即距离地面6米处断裂.【点评】本题的关键是建立数学模型,将实际问题运用数学思想进行求解.10如图,一次“台风”过后,一根旗杆被台风从高地面5米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断裂前至少有多高?【分析】先根据勾股定理求出BC的长,再由旗杆高度=AB+BC解答即可.【解答】解:∵旗杆剩余部分、折断部分与地面正好构成直角三角形,∴BC=AB2+AC2=13m,∴旗杆的高=AB+BC=13+5=18m.答:这根旗杆被吹断裂前有18米高.【点评】本题考查的是勾股定理在实际生活中的应用,解答此题的关键是从题中抽象出勾股定理这一数学模型,再根据勾股定理进行解答.11学校的一棵大树被风吹断了,如图,距地面6m处折断,折断的树梢顶部落在距树干底部8m处,求此树原高是多少米?(图1)有两棵大树,一棵高8m,另一棵高2m,BC=6,一只小鸟从一棵树梢飞到另一棵树梢,至少飞多少米?(图2)一架长10m的梯子斜靠在墙上,梯子顶端距地面8m,现将梯子顶端沿墙面下滑2m,则梯子底端与墙面距离是否也增长2m?请说明理由(图3)【分析】解决本题的关键是找出合适的直角三角形,并且运用勾股定理求解.(1)△ABC为直角三角形,可以运用勾股定理;(2)将BC向上平移2m,可以得到直角三角形,在三角形中已知2边,求第3边.(3)在直角三角形ABC中求AB,在直角三角形中求BE.【解答】(1)在直角三角形ABC中,AC2=AB2+BC2,所以AC=62+82=10m;∴此树原高=10+6=16m.(2)两点之间,直线最短,所以最短距离为直接从D点飞到A点,所以最短距离为:AD=8-22+62=62m;(3)在直角三角形ABC中,AB=8m,AC=10m,则BC=102-82=6m,现将梯子顶端下移至D点,则BD=6m,DE=10m,所以在直角三角形BDE中,BE=102-8-22=8m,8m-6m=2m,因此梯子底端与墙面的距离增加了2m.【点评】本题考查的是在直角三角形中勾股定理的应用,找出题目中的隐藏信息是解决本题的关键.【过关检测】一.选择题(共2小题)1(2021秋•长沙期中)一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为()A.10米B.15米C.25米D.30米【分析】如图,在Rt△ABC中,∠ABC=30°,由此即可得到AB=2AC,而根据题意找到CA=5米,由此即可求出AB,也就求出了大树在折断前的高度.【解答】解:如图,在Rt△ABC中,∵∠ABC=30°,∴AB=2AC,∵CA=5米,∴AB=10米,∴AB+AC=15米.所以这棵大树在折断前的高度为15米.故选:B.【点评】本题主要利用定理--在直角三角形中30°的角所对的直角边等于斜边的一半,解题关键是善于观察题目的信息,利用信息解决问题.2(2021秋•常宁市期末)如图,一棵大树在离地面9米高的B处断裂,树顶A落在离树底BC的12米处,则大树断裂之前的高度为()A.9米B.15米C.21米D.24米【分析】根据大树折断部分、下部、地面恰好构成直角三角形,根据勾股定理解答即可.【解答】解:由题意得BC=9,在直角三角形ABC中,根据勾股定理得:AB=92+122=15米.所以大树的高度是15+9=24米.故选:D.【点评】本题考查了勾股定理.熟记9,12,15这组勾股数,计算的时候较快.二.填空题(共7小题)3(2021秋•郓城县校级月考)如图所示,一棵大树折断后倒在地上,请按图中所标的数据,计算大树没折断前的高度的结果是18米.【分析】该大树折断后,AB,BC,AC构成直角三角形,且AB,AC已知,则根据勾股定理可以求得BC,大树折断前的高度为AB+BC.【解答】解:大树折断后形成直角△ABC,且BC为斜边,∴AB2+AC2=BC2,∵AB=5米,AC=12米,∴BC=AB2+AC2=13米,大树折断前的高度为AB+BC=5米+13米=18米.故答案为:18米.【点评】本题考查了勾股定理在实际生活中的应用,本题中明白题目的意思求AB+BC,并根据勾股定理求BC是解题的关键.4(2022秋•东方期末)如图,一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前的高度是16m.【分析】图中为一个直角三角形,根据勾股定理两个直角边的平方和等于斜边的平方.此题要求斜边和直角边的长度,解直角三角形即可.【解答】解:旗杆折断后,落地点与旗杆底部的距离为8m,旗杆离地面6m折断,且旗杆与地面是垂直的,所以折断的旗杆与地面形成了一个直角三角形.根据勾股定理,折断的旗杆为62+82=10m,所以旗杆折断之前高度为10m+6m=16m.故此题答案为16m.【点评】本题考查的是勾股定理的正确应用,找出可以运用勾股定理的直角三角形是关键.5(2021春•鄯善县期末)如图,一棵大树在一次强台风中于离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为8m.【分析】根据大树末端部分、折断部分及地面正好构成直角三角形,利用勾股定理解答即可.【解答】解:由勾股定理得,断下的部分为32+42=5米,折断前为5+3=8米.【点评】此题主要考查学生运用勾股定理解决实际问题的能力,比较简单.6(2023春•云阳县期中)如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有24米.【分析】根据勾股定理,计算树的折断部分是15米,则折断前树的高度是15+9=24米.【解答】解:因为AB=9米,AC=12米,根据勾股定理得BC=92+122=15米,于是折断前树的高度是15+9=24米.故答案为:24.【点评】本题考查了勾股定理的应用,熟练运用勾股定理进行计算,是基础知识,比较简单.7(2021秋•靖江市校级期中)《九章算术》中有一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高一丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,则折断处离地面的高度为 4.55尺.【分析】设折断处离地面的高度为x尺,则折断的长度为(10-x)尺,根据勾股定理列方程解方程即可.【解答】解:设折断处离地面的高度为x尺,则折断的长度为(10-x)尺,由勾股定理得x2+32=(10-x)2,解得x=4.55,∴折断处离地面的高度为4.55尺,故答案为:4.55.【点评】本题主要考查勾股定理的应用,熟练利用勾股定理列出方程是解题的关键.8(2021秋•邓州市期末)我国古代的数学名著《九章算术》中有这样一个题目“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽,问绳索AC 的长为736尺.【分析】设绳索AC 的长为x 尺,则木柱AB 的长为(x -3)尺,在Rt △ABC 中,根据勾股定理即可列出方程解答即可.【解答】解:设绳索AC 的长为x 尺,则木柱AB 的长为(x -3)尺,在Rt △ABC 中,由勾股定理得,AC 2-AB 2=BC 2,x 2-(x -3)2=82,解得:x =736,答:绳索长为736尺.故答案为:736.【点评】本题考查了勾股定理的应用,找准等量关系,正确列出一元二次方程是解题的关键.9(2022•灞桥区校级模拟)折竹抵地(源自《九章算术》):“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意即:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子处3尺远.则原处还有 4.55尺竹子.(1丈=10尺)【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x 尺,则斜边为(10-x )尺.利用勾股定理解题即可.【解答】解:设竹子折断处离地面x 尺,则斜边为(10-x )尺,根据勾股定理得:x 2+32=(10-x )2.解得:x =4.55.答:原处还有4.55尺高的竹子.故答案为:4.55.【点评】此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.三.解答题(共1小题)10(2021秋•广南县期末)如图,一棵竖直生长的竹子高为8米,一阵强风将竹子从C处吹折,竹子的顶端A刚好触地,且与竹子底端的距离AB是4米.求竹子折断处与根部的距离CB.【分析】竹子折断后刚好构成一直角三角形,设竹子折断处与根部的距离CB是x米,则斜边为(8-x)米.利用勾股定理解题即可.【解答】解:由题意知BC+AC=8,∠CBA=90°,∴设BC长为x米,则AC长为(8-x)米,∴在Rt△CBA中,有BC2+AB2=AC2,即:x2+16=(8-x)2,解得x=3,∴竹子折断处C与根部的距离CB为3米.【点评】此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.。





《离散数学》考试大纲教学用书:《离散数学》左孝凌李为儖刘永才编著上海科学技术出版社一课程的性质、目的和任务离散数学课程是介绍离散数学各分支的基本概念、基本理论和基本研究方法、研究工具的基础课程,已成为计算机科学与技术的核心基础课程。
通过对离散数学课程的系统学习,学生应具备离散数学的基本概念和基本理论,掌握主要的研究方法和研究工具,训练学生的概括抽象能力、逻辑思维能力、归纳构造能力。
除此以外,还要培养学生严谨、完整、规范的科学态度。
二考核知识点与考核要求第一章命题逻辑1.命题概念掌握(1) 命题与真值的概念(2) 复合命题与联结词关系(3) 命题公式与联结词的简化2.命题公式化简掌握,会应用(重点)(1) 命题等价式与蕴涵式的定义(2) 构造真值表证明等价式(3) 不构造真值表证明蕴涵式与等价式3.命题公式的形式化描述掌握(1) 命题符号化与翻译4.范式与主范式掌握,会应用(重点)(1) 合取范式与析取范式概念(2) 主合取范式与主析取范式求法。
5.推理理论了解(1) P规则、T规则的推理证明(2) 应用CP规则等间接推理证第二章谓词逻辑1.谓词概念掌握(1) 客体与谓词(2) 谓词与命题函数(3) n元谓词2.量词以及合式公式掌握(1)个体域与全总个体域(2) 全称量词与存在量词(3) 谓词的合式公式(4) 量词的辖域(5) 约束变元与自由变元(6) 谓词公式的简单翻译3.谓词演算的等价式与蕴涵式了解(1) 谓词公式的赋值(2) 谓词演算的等价式与蕴涵式(3) 前束范式4.谓词演算的推理理论了解,不做要求(1) 谓词演算的US,UG,ES,EG规则第三章集合与关系和第四章函数1.集合概念与运算。
掌握,会应用(1) 集合概念与表示法(2) 集合运算的图示法(3) 集合运算的证明2.关系概念与性质掌握,会应用(重点)(1) 序偶与笛卡儿乘积(2) 关系的定义与表示法(3) 关系的性质及复合关系,逆关系3.关系的闭包求法掌握,会应用(1) 关系图表示法(2) 关系闭包运算4.关系分类掌握,会应用(重点)(1) 相容关系与覆盖(不做要求)(2) 等价关系与划分(3) 偏序关系与特殊元5.函数的定义与性质掌握(1) 函数的定义与图示(2) 复合函数与逆函数的定义与运算第五章代数系统和第六章格和布尔代数1.代数系统及运算掌握,会判断(重点)(1) 运算概念与性质(2) 代数系统的封闭性、幺元、零元,逆元2.半群与独异点掌握定义(1) 广群与半群定义(2) 独异点的定义与举例(3) 子半群与子独异点定义3.群与子群掌握,会应用(重点)(1) 群的定义(2) 群的性质(3) 子群的定义与判别(4) 循环群和ABEL群的定义及生成元。

第九章植物的生长生理1.名词解释发育: 是植物一生中形态,结构,机能的质变过程,从种子萌发开始,按着物种特有的规律,有顺序地营养生长向生殖生长的转变,直到死亡的全过程.生长 : 是指植物在体积和重量(干重)上的不可逆增加, 是由细胞分裂、细胞伸长以及原生质体、细胞壁的增长而引起。
分化 :指来自同一合子或遗传上同质的细胞转变为形态上,机能上,化学结构上异质的细胞过程.生命周期.一般将植物从种子萌发到形成新种子的整个过程.极性:是指植物体或植物体的一部分在形态学的两端具有不同形态结构和生理生化特性的现象。
光敏色素:吸收红光和远红光并发生可逆转换的光受体.隐花色素: 吸收蓝光(BL, 400~500nm)和近紫外线(UV-A, 320~400nm)的色素系统。
组织培养: 是指在无菌条件下, 将外植体(植物器官、组织、花药、花粉、体细胞甚至原生质体)接种到人工配制的培养基上培育成植株的技术。
生长大周期: 植物体或器官所经历的“慢-快-慢”的整个生长过程.温周期现象:植物的生长按温度的昼夜周期性发生有规律的变化.生物钟: 植物的一些生理活动具有近似昼夜周期的节奏自由运行的过程.向性运动:指植物器官受到外界环境中单方向的刺激而产生的运动.感性运动:指由没有一定方向性的外界刺激所引起的运动。
后熟作用: 指成熟种子离开母体后, 需要经过一系列的生理生化变化后才能完成生理成熟而具备发芽的能力的一个生理过程。
种子寿命:从种子成熟到失去发芽力的时间。
协调最适温度:把植物生长健壮的温度.光的形态建成作用:光控制植物生长、发育和分化的过程.根冠比(R/T):地下部分的重量与地上部分重量的比值。
顶端优势:植物顶端在生长上始终占优势并抑制侧枝或侧根生长的现象.2.问答题1.种子萌发必需的外界条件有哪些种子萌发时吸水可分为哪三个阶段第一、第三阶段细胞靠什么方式吸水水分,氧气,温度,光等等.第一阶段: 吸胀吸水,是一个物理过程,速度快;第二阶段:吸水缓慢, 又称为吸水的停滞(滞后)期;第三阶段: 胚根突破种皮后的快速吸水(渗透性吸水) 。

第九章植物的抗逆性试题一、判断题1.根的皮层细胞是柱状排列的比偏斜排列的空间大。
对(正确答案)错2.小麦的皮层细胞是柱状排列。
对错(正确答案)3.只要生长环境的温度在零度以上,植物就不会受到伤害。
对错(正确答案)4.由于土壤干旱造成的萎蔫为永久性萎蔫。
对(正确答案)错5.油菜比马铃薯和番茄耐涝。
对(正确答案)错6.果树中的柿子、梨抗涝性强,而桃、杏的抗涝性差。
对(正确答案)错7.增施磷、钾肥可以提高作物的抗旱性和抗寒性。
对(正确答案)错8夏季一般植物都不能忍受较低的温度,而冬季则能忍受更低的温度。
对(正确答案)错9.热害常与旱害相伴发生。
对(正确答案)错10.碳3植物的耐热性高于碳4植物。
对错(正确答案)11.习惯上将含有氯化钠、硫酸钠为主要成分的土壤叫做碱士对错(正确答案)12.湿冷比干冷对作物的危害大。
对(正确答案)错13.水生作物和阴生作物的热害界限为35度。
对(正确答案)错14.植物因大气干旱造成的萎蔫是永久萎蔫。
对错(正确答案)15.冷害是喜温作物经常遇到的危害。
对(正确答案)错16.冷害指0摄氏度以下低温对植物的伤害。
对错(正确答案)17.抗寒能力强的植物或经过抗寒锻炼的植物,容易发生细胞间隙结冰,不易发生细胞内结冰。
对(正确答案)错18.一般植物受冷害后会立即出现症状。
对错(正确答案)19.抗旱性强的植物根细胞的质量分数较小,水势大,容易从土壤中吸收水分。
对错(正确答案)20.盐碱地一般含氮量很低,通过增施氮肥,可以促进植物的生长。
对(正确答案)错21.抗旱性强的作物蒸腾系数较大。
对错(正确答案)22.土壤干旱会造成植物永久性萎蔫。
对(正确答案)错23.植物涝害的形成主要是因为根系吸水过多造成的。
对错(正确答案)24.当气温降低到0摄氏度以下时,细胞内的水首先结冰,体积增大。
对错(正确答案)25.在盐碱地中虽然含有各种盐类,但往往是以一种盐为主,使植物发生单盐危害。
对(正确答案)错26.一般旱田作物在土壤水分饱和的情况下就会发生涝害对(正确答案)错27.植物越抗旱,其蒸腾騰系数就越大。
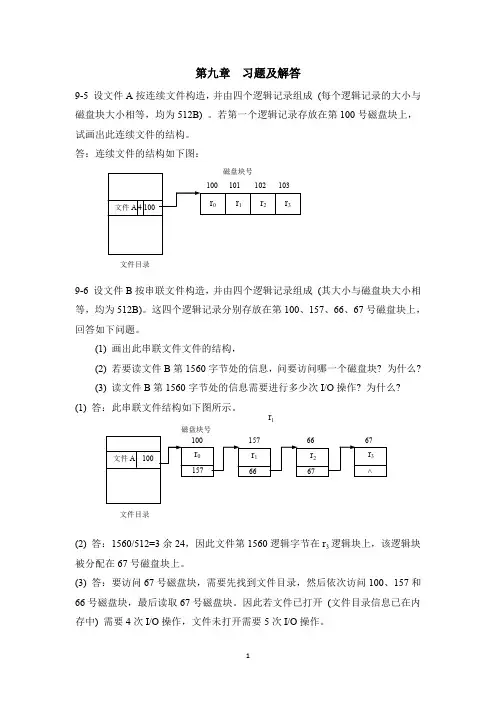
第九章 习题及解答9-5 设文件A 按连续文件构造,并由四个逻辑记录组成 (每个逻辑记录的大小与磁盘块大小相等,均为512B) 。
若第一个逻辑记录存放在第100号磁盘块上,试画出此连续文件的结构。
答:连续文件的结构如下图:9-6 设文件B 按串联文件构造,并由四个逻辑记录组成 (其大小与磁盘块大小相等,均为512B)。
这四个逻辑记录分别存放在第100、157、66、67号磁盘块上,回答如下问题。
(1) 画出此串联文件文件的结构,(2) 若要读文件B 第1560字节处的信息,问要访问哪一个磁盘块? 为什么? (3) 读文件B 第1560字节处的信息需要进行多少次I/O 操作? 为什么? (1) 答:此串联文件结构如下图所示。
(2) 答:1560/512=3余24,因此文件第1560逻辑字节在r 3逻辑块上,该逻辑块被分配在67号磁盘块上。
(3) 答:要访问67号磁盘块,需要先找到文件目录,然后依次访问100、157和66号磁盘块,最后读取67号磁盘块。
因此若文件已打开 (文件目录信息已在内存中) 需要4次I/O 操作,文件未打开需要5次I/O 操作。
文件目录文件目录 r 1磁盘块号9-16什么是“重名”问题? 二级文件目录结构如何解决这一问题?答:重名是指不同用户对不同文件起了相同的名字。
在二级文件目录结构中,每个用户建立用户文件目录,系统建立主目录,登记所有用户目录的信息,用目录名加文件名唯一标识每个文件解决重名问题。
9-18 假设两个用户共享一个文件系统,用户甲要用到文件a、b、c、e,用户乙要用到文件a、d、e、f。
已知:用户甲的文件a与用户乙的文件a实际上不是同一文件;用户甲的文件c与用户乙的文件f实际上是同一文件;甲、乙两用户的文件e是同一文件。
试拟定一个文件组织方案,使得甲、乙两用户能共享该文件系统而不致造成混乱。
答:如下图所示。
用户甲的主目录名为jia,有四个文件,文件名为a、b、c、e。
第九章营养器官的变态前面已分别论述了植物营养器官根、茎、叶的形态结构及生理功能,但这是指在一般情况下,绝大多数植物所表现的。
还有一些植物因其长期适应不同的环境,行使特殊的生理功能,使其营养器官无论是在形态上、构造上,还是生理功能上都发生了非常大的变化。
并且历经若干世代以后,一代代的遗传下来,成为这种植物的遗传性状,这种现象称为变态。
变态器官较正常营养器官,难以在外形上区分,常常要从其形态发生上来加以判断。
营养器官的变态,根、茎、叶都有,现分述如下:一、根的变态变态根从其功能上来看,可分为三大类:(一)贮藏根主要适应于贮藏大量的营养物质,一般分肉质直根和块根。
1. 肉质直根(fleshy tap root)如萝卜、胡萝卜、甜菜的根均属此类。
肉质直根并不完全是根。
其上部为下胚轴发育而成,顶部为节间很短的茎,上面着生许多叶。
肉质直根的下部为主根肥大发育而成,具有二纵列、四纵列侧根,这部分也是我们食用的主要部分。
在发达膨大的主根内,薄壁细胞极为发达,其内贮存大量养料,以供给植物过冬后,次年生长的需要。
第二年便会在肉质直根上抽出茎来,然后开花结实。
一般一株植物仅有一个肉质直根。
各种变态的肥大直根虽然在外表上相似,都由主根肥大而成,但不同的植物其肉质直根的内部结构却不一样的。
例1:萝卜其肉质直根大部分是次生木质部,其中的木薄壁组织非常发达,贮藏有大量的营养物质,且非木质化,为食用的主要部分。
木质部中没有木纤维,且导管也很少。
相反,次生韧皮部所占比例极小,与外部的周皮组成皮部。
例2:胡萝卜其肉质直根大部分是次生韧皮部,其中的韧皮薄壁组织非常发达,含糖量很高,并含有大量的胡萝卜类,为食用的主要部分,由于胡萝卜素在食用后可转变为维生素甲,因此胡萝卜根具有很高的营养价值。
例3:甜菜甜芽根较为特殊。
它除有正常的次生结构外,还具有发达的由副形成层(accessory cambium)产生的三生结构(tertiary structure)。
重难点:勾股定理之“风吹树折”模型【知识梳理】风吹树折类题就数学知识本身其实很简单,考查的就是句股定理,最多设个未知数列方程就能求解,但是对很多同学来说,它的难点在于语言文字如何转化成数学模型.【考点剖析】一.选择题(共2小题)1.一旗杆在其的B处折断,量得AC=5米,则旗杆原来的高度为()A.米B.2米C.10米D.米【分析】可设AB=x,则BC=2x,进而在△ABC中,利用勾股定理求解x的值即可.【解答】解:由题意可得,AC2=BC2﹣AB2,即(2x)2﹣x2=52,解得x=,所以旗杆原来的高度为3x=5,故选:D.【点评】能够利用勾股定理求解一些简单的直角三角形.2.如图,一根旗杆折断之前的高度是24米,旗杆顶部落在离旗杆底部12米处,旗杆在离地面多少米处断裂()A.15B.12C.9D.21【分析】利用勾股定理,用一边表示另一边,代入数据即可得出结果.【解答】解:由图形及题意可知,设旗杆在离地面x米处断裂,有(24﹣x)2﹣x2=144,得x=9,故选:C.【点评】本题主要是考查学生对勾股定理的熟练掌握.二.填空题(共3小题)3.如图,一次“台风”过后,一根旗杆被台风从离地面9米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断前至少有高.【分析】根据旗杆未断部分与折断部分及地面正好组成直角三角形,利用勾股定理解答即可.【解答】解:由勾股定理得斜边为:=15米,则原来的高度为9+15=24米.故答案为:24m.【点评】本题考查的是勾股定理在实际生活中的运用,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.4.如图,今年第8号台风“桑美”是50多年以来登陆我国大陆地区最大的一次台风,一棵大树受“桑美”袭击于离地面5米处折断倒下,倒下部分的树梢到树的距离为7米,则这棵大树折断前有米(保留到0.1米).【分析】首先根据勾股定理求得折断的树高是=,所以折断前树的高度是5+≈13.6米.【解答】解:在Rt△ABC中,AC==≈8.6米,5+8.6=13.6米.故答案为:13.6.【点评】考查了勾股定理的应用,比较简单.5.有一棵9米高的大树,树下有一个1米高的小孩,如果大树在距地面4米处折断(未完全折断),则小孩至少离开大树米之外才是安全的.【分析】根据题意构建直角三角形ABC,利用勾股定理解答.【解答】解:如图,BC即为大树折断处4m减去小孩的高1m,则BC=4﹣1=3m,AB=9﹣4=5m,在Rt△ABC中,AC===4.【点评】此题考查直角三角形的性质及勾股定理的应用,要根据题意画出图形即可解答.三.解答题(共6小题)6.如图,受台风影响,一棵大树在高于地面5米处折断,大树顶部落在距离大树底部10米处的地面上,问这棵大树原来有多高?【分析】该大树折断后,折断部分与地面、原来的树干恰好构成一直角三角形,设大树高为x,则折断部分为x﹣5,由勾股定理可得出方程:52+102=(x﹣5)2,解该方程可得出大树原来的高.【解答】解:设大树断掉的部分长为x米,利用勾股定理:52+102=(x﹣5)2,解得x=5+5,答:大树原来的高为(5+5)米.【点评】利用勾股定理解应用题,关键在于把折断部分、大树原来部分和地面看作一个直角三角形,利用勾股定理列出方程求解.7.某地遭台风袭击,马路边竖有一根高为7m的电线杆AC,被台风从离地面2m的B处吹断裂,倒下的电线杆顶部C′是否会落在距离它的底部4m的快车道上?说说你的道理.【分析】电线杆折断后构成一个直角三角形,利用勾股定理求出AC′的长,即可得出正确结论.【解答】解:根据题意,AB=2m,则BC=7﹣2=5m,于是AC′==,又因为>4,∴电线杆顶部C′会落在距它的底部4m的快车道上.【点评】此题是勾股定理在生活中应用的典型例子,只要善于观察,便可用数学知识解决生活中的诸多问题.8.如图,一次“台风”过后,一根旗杆被台风从离地面9米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断前至少有多高?【分析】根据旗杆未断部分与折断部分及地面正好组成直角三角形,利用勾股定理解答即可.【解答】解:由勾股定理得斜边为=15米,则原来的高度为9+15=24米.【点评】此题主要考查学生对勾股定理的运用,比较简单.9.台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,求旗杆在什么位置断裂的?【分析】旗杆折断的部分,未折断的部分和旗杆顶部离旗杆底的部分构成了直角三角形,运用勾股定理可将折断的未知求出.【解答】解:设旗杆未折断部分长为x米,则折断部分的长为(16﹣x)m,根据勾股定理得:x2+82=(16﹣x)2,可得:x=6m,即距离地面6米处断裂.【点评】本题的关键是建立数学模型,将实际问题运用数学思想进行求解.10.如图,一次“台风”过后,一根旗杆被台风从高地面5米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断裂前至少有多高?【分析】先根据勾股定理求出BC的长,再由旗杆高度=AB+BC解答即可.【解答】解:∵旗杆剩余部分、折断部分与地面正好构成直角三角形,∴BC==13m,∴旗杆的高=AB+BC=13+5=18m.答:这根旗杆被吹断裂前有18【点评】本题考查的是勾股定理在实际生活中的应用,解答此题的关键是从题中抽象出勾股定理这一数学模型,再根据勾股定理进行解答.11.学校的一棵大树被风吹断了,如图,距地面6m处折断,折断的树梢顶部落在距树干底部8m处,求此树原高是多少米?(图1)有两棵大树,一棵高8m,另一棵高2m,BC=6,一只小鸟从一棵树梢飞到另一棵树梢,至少飞多少米?(图2)一架长10m的梯子斜靠在墙上,梯子顶端距地面8m,现将梯子顶端沿墙面下滑2m,则梯子底端与墙面距离是否也增长2m?请说明理由(图3)【分析】解决本题的关键是找出合适的直角三角形,并且运用勾股定理求解.(1)△ABC为直角三角形,可以运用勾股定理;(2)将BC向上平移2m,可以得到直角三角形,在三角形中已知2边,求第3边.(3)在直角三角形ABC中求AB,在直角三角形中求BE.【解答】(1)在直角三角形ABC中,AC2=AB2+BC2,所以AC==10m;∴此树原高=10+6=16m.(2)两点之间,直线最短,所以最短距离为直接从D点飞到A点,所以最短距离为:AD==m;(3)在直角三角形ABC中,AB=8m,AC=10m,则BC==6m,现将梯子顶端下移至D点,则BD=6m,DE=10m,所以在直角三角形BDE中,BE==8m,8m=2m,因此梯子底端与墙面的距离增加了2m.【点评】本题考查的是在直角三角形中勾股定理的应用,找出题目中的隐藏信息是解决本题的关键.【过关检测】一.选择题(共2小题)1.(2021秋•长沙期中)一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为()A.10米B.15米C.25米D.30米【分析】如图,在Rt△ABC中,∠ABC=30°,由此即可得到AB=2AC,而根据题意找到CA=5米,由此即可求出AB,也就求出了大树在折断前的高度.【解答】解:如图,在Rt△ABC中,∵∠ABC=30°,∴AB=2AC,∵CA=5米,∴AB=10米,∴AB+AC=15米.所以这棵大树在折断前的高度为15米.故选:B.【点评】本题主要利用定理﹣﹣在直角三角形中30°的角所对的直角边等于斜边的一半,解题关键是善于观察题目的信息,利用信息解决问题.2.(2021秋•常宁市期末)如图,一棵大树在离地面9米高的B处断裂,树顶A落在离树底BC的12米处,则大树断裂之前的高度为()A.9米B.15米C.21米D.24米【分析】根据大树折断部分、下部、地面恰好构成直角三角形,根据勾股定理解答即可.【解答】解:由题意得BC=9,在直角三角形ABC中,根据勾股定理得:AB==15米.所以大树的高度是15+9=24米.故选:D.【点评】本题考查了勾股定理.熟记9,12,15这组勾股数,计算的时候较快.二.填空题(共7小题)3.(2021秋•郓城县校级月考)如图所示,一棵大树折断后倒在地上,请按图中所标的数据,计算大树没折断前的高度的结果是.【分析】该大树折断后,AB,BC,AC构成直角三角形,且AB,AC已知,则根据勾股定理可以求得BC,大树折断前的高度为AB+BC.【解答】解:大树折断后形成直角△ABC,且BC为斜边,∴AB2+AC2=BC2,∵AB=5米,AC=12米,∴BC==13米,大树折断前的高度为AB+BC=5米+13米=18米.故答案为:18米.【点评】本题考查了勾股定理在实际生活中的应用,本题中明白题目的意思求AB+BC,并根据勾股定理求BC 是解题的关键.4.(2022秋•东方期末)如图,一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前的高度是m.【分析】图中为一个直角三角形,根据勾股定理两个直角边的平方和等于斜边的平方.此题要求斜边和直角边的长度,解直角三角形即可.【解答】解:旗杆折断后,落地点与旗杆底部的距离为8m,旗杆离地面6m折断,且旗杆与地面是垂直的,所以折断的旗杆与地面形成了一个直角三角形.根据勾股定理,折断的旗杆为=10m,所以旗杆折断之前高度为10m+6m=16m.故此题答案为16m.【点评】本题考查的是勾股定理的正确应用,找出可以运用勾股定理的直角三角形是关键.5.(2021春•鄯善县期末)如图,一棵大树在一次强台风中于离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为m.【分析】根据大树末端部分、折断部分及地面正好构成直角三角形,利用勾股定理解答即可.【解答】解:由勾股定理得,断下的部分为=5米,折断前为5+3=8米.【点评】此题主要考查学生运用勾股定理解决实际问题的能力,比较简单.6.(2023春•云阳县期中)如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有米.【分析】根据勾股定理,计算树的折断部分是15米,则折断前树的高度是15+9=24米.【解答】解:因为AB=9米,AC=12米,根据勾股定理得BC==15米,于是折断前树的高度是15+9=24米.故答案为:24.【点评】本题考查了勾股定理的应用,熟练运用勾股定理进行计算,是基础知识,比较简单.7.(2021秋•靖江市校级期中)《九章算术》中有一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高一丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,则折断处离地面的高度为尺.【分析】设折断处离地面的高度为x尺,则折断的长度为(10﹣x)尺,根据勾股定理列方程解方程即可.【解答】解:设折断处离地面的高度为x尺,则折断的长度为(10﹣x)尺,由勾股定理得x2+32=(10﹣x)2,解得x=4.55,∴折断处离地面的高度为4.55尺,故答案为:4.55.【点评】本题主要考查勾股定理的应用,熟练利用勾股定理列出方程是解题的关键.8.(2021秋•邓州市期末)我国古代的数学名著《九章算术》中有这样一个题目“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽,问绳索AC的长为尺.【分析】设绳索AC的长为x尺,则木柱AB的长为(x﹣3)尺,在Rt△ABC中,根据勾股定理即可列出方程解答即可.【解答】解:设绳索AC的长为x尺,则木柱AB的长为(x﹣3)尺,在Rt△ABC中,由勾股定理得,AC2﹣AB2=BC2,x2﹣(x﹣3)2=82,解得:x=,答:绳索长为尺.故答案为:.【点评】本题考查了勾股定理的应用,找准等量关系,正确列出一元二次方程是解题的关键.9.(2022•灞桥区校级模拟)折竹抵地(源自《九章算术》):“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意即:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子处3尺远.则原处还有尺竹子.(1丈=10尺)【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(10﹣x)尺.利用勾股定理解题即可.【解答】解:设竹子折断处离地面x尺,则斜边为(10﹣x)尺,根据勾股定理得:x2+32=(10﹣x)2.解得:x=4.55.答:原处还有4.55尺高的竹子.故答案为:4.55.【点评】此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.三.解答题(共1小题)10.(2021秋•广南县期末)如图,一棵竖直生长的竹子高为8米,一阵强风将竹子从C处吹折,竹子的顶端A刚好触地,且与竹子底端的距离AB是4米.求竹子折断处与根部的距离CB.【分析】竹子折断后刚好构成一直角三角形,设竹子折断处与根部的距离CB是x米,则斜边为(8﹣x)米.利用勾股定理解题即可.【解答】解:由题意知BC+AC=8,∠CBA=90°,∴设BC长为x米,则AC长为(8﹣x)米,∴在Rt△CBA中,有BC2+AB2=AC2,即:x2+16=(8﹣x)2,解得x=3,∴竹子折断处C与根部的距离CB为3米.【点评】此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.。
勾股定理之“风吹树折”模型【知识梳理】风吹树折类题就数学知识本身其实很简单,考查的就是句股定理,最多设个未知数列方程就能求解,但是对很多同学来说,它的难点在于语言文字如何转化成数学模型.【考点剖析】一.选择题(共2小题)1一旗杆在其13的B处折断,量得AC=5米,则旗杆原来的高度为()A.5米B.25米C.10米D.53米2如图,一根旗杆折断之前的高度是24米,旗杆顶部落在离旗杆底部12米处,旗杆在离地面多少米处断裂()A.15B.12C.9D.21二.填空题(共3小题)3如图,一次“台风”过后,一根旗杆被台风从离地面9米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断前至少有高.4如图,今年第8号台风“桑美”是50多年以来登陆我国大陆地区最大的一次台风,一棵大树受“桑美”袭击于离地面5米处折断倒下,倒下部分的树梢到树的距离为7米,则这棵大树折断前有米(保留到0.1米).5有一棵9米高的大树,树下有一个1米高的小孩,如果大树在距地面4米处折断(未完全折断),则小孩至少离开大树米之外才是安全的.三.解答题(共6小题)6如图,受台风影响,一棵大树在高于地面5米处折断,大树顶部落在距离大树底部10米处的地面上,问这棵大树原来有多高?7某地遭台风袭击,马路边竖有一根高为7m的电线杆AC,被台风从离地面2m的B处吹断裂,倒下的电线杆顶部C′是否会落在距离它的底部4m的快车道上?说说你的道理.8如图,一次“台风”过后,一根旗杆被台风从离地面9米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断前至少有多高?9台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,求旗杆在什么位置断裂的?10如图,一次“台风”过后,一根旗杆被台风从高地面5米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断裂前至少有多高?11学校的一棵大树被风吹断了,如图,距地面6m处折断,折断的树梢顶部落在距树干底部8m处,求此树原高是多少米?(图1)有两棵大树,一棵高8m,另一棵高2m,BC=6,一只小鸟从一棵树梢飞到另一棵树梢,至少飞多少米?(图2)一架长10m的梯子斜靠在墙上,梯子顶端距地面8m,现将梯子顶端沿墙面下滑2m,则梯子底端与墙面距离是否也增长2m?请说明理由(图3)【过关检测】一.选择题(共2小题)1(2021秋•长沙期中)一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为()A.10米B.15米C.25米D.30米2(2021秋•常宁市期末)如图,一棵大树在离地面9米高的B处断裂,树顶A落在离树底BC的12米处,则大树断裂之前的高度为()A.9米B.15米C.21米D.24米二.填空题(共7小题)3(2021秋•郓城县校级月考)如图所示,一棵大树折断后倒在地上,请按图中所标的数据,计算大树没折断前的高度的结果是.4(2022秋•东方期末)如图,一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前的高度是m.5(2021春•鄯善县期末)如图,一棵大树在一次强台风中于离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为m.6(2023春•云阳县期中)如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有米.7(2021秋•靖江市校级期中)《九章算术》中有一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高一丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,则折断处离地面的高度为尺.8(2021秋•邓州市期末)我国古代的数学名著《九章算术》中有这样一个题目“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽,问绳索AC的长为尺.9(2022•灞桥区校级模拟)折竹抵地(源自《九章算术》):“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意即:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子处3尺远.则原处还有尺竹子.(1丈=10尺)三.解答题(共1小题)10(2021秋•广南县期末)如图,一棵竖直生长的竹子高为8米,一阵强风将竹子从C处吹折,竹子的顶端A刚好触地,且与竹子底端的距离AB是4米.求竹子折断处与根部的距离CB.。
2024年高一生物知识点的总结____年高一生物知识点总结第一章细胞的结构和功能1. 细胞的基本结构:质膜、细胞质、细胞器、细胞核。
2. 细胞的功能:营养摄取、分解代谢、合成代谢、运动、生长和繁殖。
3. 细胞的能量代谢:光合作用和呼吸作用。
4. 细胞膜的结构和功能:磷脂双分子层、选择性通透性、运输蛋白、细胞识别。
第二章细胞的遗传物质1. 核酸的结构和功能:DNA和RNA。
2. DNA的复制:半保留复制、DNA聚合酶、起始子、终止子。
3. RNA的合成:转录、基因的调控。
4. 遗传信息传递:从DNA到蛋白质的转录翻译过程。
第三章基因的细胞遗传规律1. 遗传性状:显性和隐性、纯合和杂合。
2. 孟德尔的遗传定律:自由组合定律、同质和异质、基因的分离和再组合。
3. 遗传的分子基础:等位基因、基因座、基因的互作。
第四章遗传的分子基础1. DNA的结构和特点:碱基对、双螺旋结构、组蛋白。
2. DNA的复制、转录和翻译:酶、启动子、终止子、密码子、反编码。
第五章生物体的性别和性染色体1. 性别的决定:异配子、同配子、环系、多性系。
2. 性染色体:X染色体和Y染色体、性-linked遗传、非经典性遗传。
第六章细胞的有丝分裂和无丝分裂1. 有丝分裂:染色体的形态变化、纺锤体的形成和消失、核分裂和细胞质分裂。
2. 无丝分裂:核的变化、核块的分裂、核膜的重组。
第七章遗传与进化1. 进化的证据:化石、地质年代的划分、同功酶、DNA的同源性。
2. 进化的驱动力:自然选择、突变、基因流、遗传漂变。
3. 人类的进化:人类的起源、进化树、人类的智力和语言。
第八章生物的分子基础1. 蛋白质的结构和功能:胺基酸、多肽链、蛋白质的三级结构。
2. 酶的结构和功能:酶的介体、酶的催化过程、酶的调控。
第九章生物体的调节和反应1. 神经调节:神经元、突触、神经递质。
2. 荷尔蒙调控:腺体、激素、反馈调节。
3. 对环境变化的反应:刺激、感受器、反射弧。