福建省重点中学2019届高三11月月考数学(文)试卷(带答案)

福建省三明市里心中学2019年高三数学文月考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 若i为虚数单位，图1中网格纸的小正方形的边长是1，复平面内点Z表示复数z，则复数的共轭复数是()A．－i B.i C．－i D．i参考答案：C略2. 已知函数（为常数）为奇函数，那么（）A. 0B.C.D. 1参考答案：A【分析】根据奇函数定义，代入即可求得的值．【详解】因为函数（为常数）为奇函数所以，代入所以选A【点睛】本题考查了奇函数的应用及三角函数的求值，属于基础题．3. 下列命题：①经过三点可以确定一个平面；②复数在复平面上对应的点在第四象限；③已知平面④若回归直线方程的斜率的估计值是样本的中心点为，则回归直线的方程是：以上命题中错误的命题个数是（）参考答案：D4. 已知椭圆的左、右焦点分别为，若椭圆上存在点P使，则该椭圆的离心率的取值范围为（）A.（0，B.（）C.（0，） D.（，1）参考答案：D略5. 已知函数的反函数. 若的图象过点，则等于（）A. B. C.D.参考答案：D略6. 已知集合A={（x，y）|y2＜x}，B={（x，y）|xy=﹣2，x∈Z，y∈Z}，则A∩B=（）A．? B．{（2，﹣1）}C．{（﹣1，2），（﹣2，1）} D．{（1，﹣2），（﹣1，2），（﹣2，1）}参考答案：B【考点】1E：交集及其运算．【分析】根据集合A、B在平面直角坐标系内表示的图形，结合交集的定义，即可求出结果．【解答】解：集合A={（x，y）|y2＜x}，在平面直角坐标系内表示平面区域阴影面积；B={（x，y）|xy=﹣2，x∈Z，y∈Z}，在平面直角坐标系内表示孤立的两组点；由，求得点P（，﹣）；如图所示，则x=2，y=﹣1时满足条件，∴A∩B={（2，﹣1）}．故选：B．7. （5分）已知点A（，﹣1）在抛物线C：x2=2py（p＞0）的准线l1上，过点A作一条斜率为2的直线l2，点P是抛物线上的动点，则点P到直线l1和到直线l2的距离之和的最小值是（）A． B． C． 2 D．参考答案：B【考点】：抛物线的简单性质．【专题】：计算题；圆锥曲线的定义、性质与方程．【分析】：点F作直线l2的垂线FH，垂足为H，则线段FH与抛物线C的交点为所求的点P．由抛物线的定义可得，|PF|为点P到直线的l1距离，又|PH|为点P到直线l2的距离，所以点P到直线l1和到直线l2的距离之和的最小值是F到直线l2的距离．解：由题意，抛物线的焦点为F（0，1），则直线l2的方程为2x﹣y﹣4=0，过点F作直线l2的垂线FH，垂足为H，则线段FH与抛物线C的交点为所求的点P．由抛物线的定义可得，|PF|为点P到直线的l1距离，又|PH|为点P到直线l2的距离，所以点P到直线l1和到直线l2的距离之和的最小值是F到直线l2的距离d==，所以点P到直线l1和到直线l2的距离之和的最小值是．故选：B．【点评】：此题考查学生灵活运用抛物线的简单性质解决实际问题，灵活运用点到直线的距离公式化简求值，是一道中档题．8. 将函数的图象上各点的纵坐标不变，横坐标伸长到原来的2倍，再向右平移个单位长度，所得到的图象解析式是---------------------------（）A. B. C. D.参考答案：A9. 若函数y=a x+b的图象如图，则函数y=+b+1的图象为（）A．B．C．D．参考答案：C【考点】指数函数的图象变换．【分析】由y=a x+b的图象知，0＜a＜1，﹣2＜b＜﹣1，然后利用y=的图象平移变换可得答案．【解答】解：由y=a x+b的图象知，0＜a＜1，﹣2＜b＜﹣1，y=+b+1的图象可看作由y=先向左平移a个单位，再向下平移﹣（b+1）个单位得到，故选C．10. 设i是虚数单位，复数为纯虚数，则实数a为（A）2 （B）-2 （C）-（D）参考答案：A本题主要考查复数的乘法运算和复数的概念，难度较小。

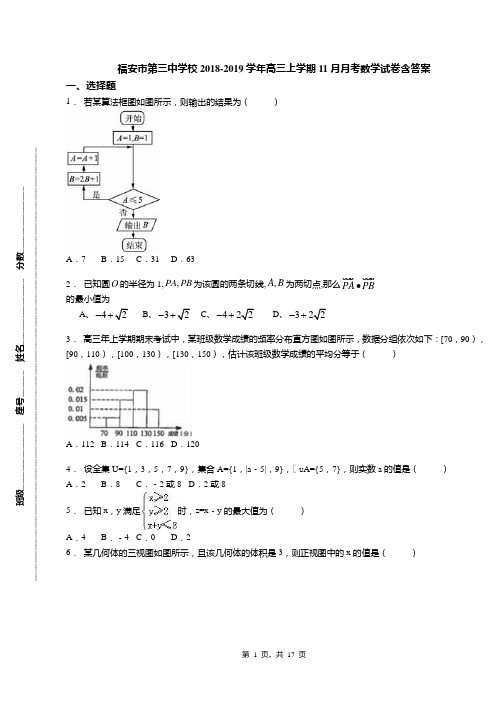
福安市第三中学校2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 若某算法框图如图所示，则输出的结果为（ ）A ．7B ．15C ．31D ．632． 已知圆O 的半径为1,,PA PB 为该圆的两条切线,,A B 为两切点,那么PA PB ∙ 的最小值为A、4- B、3-+ C、4-+ D、3-+3． 高三年上学期期末考试中，某班级数学成绩的频率分布直方图如图所示，数据分组依次如下：[70，90），[90，110），[100，130），[130，150），估计该班级数学成绩的平均分等于（ ）A ．112B ．114C ．116D ．1204． 设全集U={1，3，5，7，9}，集合A={1，|a ﹣5|，9}，∁U A={5，7}，则实数a 的值是（ ） A ．2B ．8C ．﹣2或8D ．2或85． 已知x ，y满足时，z=x ﹣y 的最大值为（ ） A ．4B ．﹣4C ．0D ．26． 某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x 的值是（ ）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A ．2B ．C ．D ．37． 已知抛物线24y x =的焦点为F ，(1,0)A -，点P 是抛物线上的动点，则当||||PF PA 的值最小时，PAF ∆的 面积为（ ）A.2B.2C.D. 4【命题意图】本题考查抛物线的概念与几何性质，考查学生逻辑推理能力和基本运算能力.8． 若函数f （x ）=2sin （ωx+φ）对任意x 都有f （+x ）=f （﹣x ），则f （）=（ ）A ．2或0B ．0C ．﹣2或0D ．﹣2或29． 已知双曲线的渐近线与圆x 2+（y ﹣2）2=1相交，则该双曲线的离心率的取值范围是（ ）A ．（，+∞） B ．（1，） C ．（2．+∞） D ．（1，2）10．若实数x ，y 满足，则（x ﹣3）2+y 2的最小值是（ ）A ．B ．8C ．20D ．211．某人以15万元买了一辆汽车，此汽车将以每年20%的速度折旧，如图是描述汽车价值变化的算法流程图，则当n=4吋，最后输出的S 的值为（ ）A．9.6 B．7.68 C．6.144 D．4.915212．某个几何体的三视图如图所示，该几何体的表面积为92＋14π，则该几何体的体积为（）A．80＋20πB．40＋20πC．60＋10πD．80＋10π二、填空题13．计算：×5﹣1=．14．若函数f（x），g（x）满足：∀x∈（0，+∞），均有f（x）＞x，g（x）＜x成立，则称“f（x）与g（x）关于y=x分离”．已知函数f（x）=a x与g（x）=log a x（a＞0，且a≠1）关于y=x分离，则a的取值范围是．15．二面角α﹣l﹣β内一点P到平面α，β和棱l的距离之比为1：：2，则这个二面角的平面角是度．16．运行如图所示的程序框图后，输出的结果是17．已知点F 是抛物线y 2=4x 的焦点，M ，N 是该抛物线上两点，|MF|+|NF|=6，M ，N ，F 三点不共线，则△MNF 的重心到准线距离为 ．18．如图，△ABC 是直角三角形，∠ACB=90°，PA ⊥平面ABC ，此图形中有 个直角三角形．三、解答题19．（本小题满分12分）已知1()2ln ()f x x a x a R x=--∈． （Ⅰ）当3a =时，求()f x 的单调区间；（Ⅱ）设()()2ln g x f x x a x =-+，且()g x 有两个极值点，其中1[0,1]x ∈，求12()()g x g x -的最小值． 【命题意图】本题考查导数的应用等基础知识，意在考查转化与化归思想和综合分析问题、解决问题的能力．20．【徐州市2018届高三上学期期中】已知函数（,是自然对数的底数）.（1）若函数在区间上是单调减函数,求实数的取值范围；（2）求函数的极值；（3）设函数图象上任意一点处的切线为，求在轴上的截距的取值范围．21．设函数f （x ）=lnx ﹣ax+﹣1． （Ⅰ）当a=1时，求曲线f （x ）在x=1处的切线方程；（Ⅱ）当a=时，求函数f （x ）的单调区间；（Ⅲ）在（Ⅱ）的条件下，设函数g （x ）=x 2﹣2bx ﹣，若对于∀x 1∈[1，2]，∃x 2∈[0，1]，使f （x 1）≥g （x 2）成立，求实数b 的取值范围．22．如图所示，两个全等的矩形ABCD 和ABEF 所在平面相交于AB ，M AC ∈，N FB ∈，且AM FN =，求证：//MN 平面BCE ．23．如图，四边形ABCD 与A ′ABB ′都是边长为a 的正方形，点E 是A ′A 的中点，AA ′⊥平面ABCD ． （1）求证：A ′C ∥平面BDE ；（2）求体积V A ′﹣ABCD 与V E ﹣ABD 的比值．24．在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且=2csinA （1）确定角C的大小；（2）若c=，且△ABC的面积为，求a+b的值．福安市第三中学校2018-2019学年高三上学期11月月考数学试卷含答案（参考答案） 一、选择题1． 【答案】 D【解析】解：模拟执行算法框图，可得 A=1，B=1满足条件A ≤5，B=3，A=2 满足条件A ≤5，B=7，A=3 满足条件A ≤5，B=15，A=4 满足条件A ≤5，B=31，A=5 满足条件A ≤5，B=63，A=6不满足条件A ≤5，退出循环，输出B 的值为63． 故选：D ．【点评】本题主要考查了程序框图和算法，正确得到每次循环A ，B 的值是解题的关键，属于基础题．2． 【答案】D.【解析】设PO t =，向量PA 与PB 的夹角为θ，PA PB ==，1sin2t θ=，222cos 12sin 12t θθ=-=-，∴222cos (1)(1)(1)PA PB PA PB t t t θ==-->，2223(1)PA PB t t t∴=+->，依不等式PA PB ∴的最小值为3.3． 【答案】B【解析】解：根据频率分布直方图，得； 该班级数学成绩的平均分是=80×0.005×20+100×0.015×20 +120×0.02×20+140×0.01×20 =114． 故选：B ．【点评】本题考查了根据频率分布直方图，求数据的平均数的应用问题，是基础题目．4． 【答案】D【解析】解：由题意可得3∈A ，|a ﹣5|=3， ∴a=2，或a=8， 故选 D ．5．【答案】A【解析】解：由约束条件作出可行域如图，联立，得A（6，2），化目标函数z=x﹣y为y=x﹣z，由图可知，当直线y=x﹣z过点A时，直线在y轴上的截距最小，z有最大值为4．故选：A．【点评】本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．6．【答案】D【解析】解：根据三视图判断几何体为四棱锥，其直观图是：V==3⇒x=3．故选D．【点评】由三视图正确恢复原几何体是解题的关键．7．【答案】B【解析】设2(,)4yP y，则21||||yPFPA+=.又设214yt+=，则244y t=-，1t…，所以||||PFPA==，当且仅当2t=，即2y=±时，等号成立，此时点(1,2)P±，PAF∆的面积为1||||22222AF y⋅=⨯⨯=，故选B.8．【答案】D【解析】解：由题意：函数f（x）=2sin（ωx+φ），∵f（+x）=f（﹣x），可知函数的对称轴为x==，根据三角函数的性质可知，当x=时，函数取得最大值或者最小值．∴f（）=2或﹣2故选D．9．【答案】C【解析】解：∵双曲线渐近线为bx±ay=0，与圆x2+（y﹣2）2=1相交∴圆心到渐近线的距离小于半径，即＜1∴3a2＜b2，∴c2=a2+b2＞4a2，∴e=＞2故选：C．【点评】本题主要考查了双曲线的简单性质，直线与圆的位置关系，点到直线的距离公式等．考查了学生数形结合的思想的运用．10．【答案】A【解析】解：画出满足条件的平面区域，如图示：，由图象得P（3，0）到平面区域的最短距离d min=，∴（x﹣3）2+y2的最小值是：．故选：A．【点评】本题考查了简单的线性规划问题，考查数形结合思想，是一道基础题．11．【答案】C【解析】解：由题意可知，设汽车x年后的价值为S，则S=15（1﹣20%）x，结合程序框图易得当n=4时，S=15（1﹣20%）4=6.144．故选：C．12．【答案】【解析】解析：选D.该几何体是在一个长方体的上面放置了半个圆柱．依题意得（2r×2r＋12）×2＋5×2r×2＋5×2r＋πr×5＝92＋14π，2πr即（8＋π）r2＋（30＋5π）r－（92＋14π）＝0，即（r－2）[（8＋π）r＋46＋7π]＝0，∴r＝2，∴该几何体的体积为（4×4＋12）×5＝80＋10π.2π×2二、填空题13．【答案】9．【解析】解：×5﹣1=×=×=（﹣5）×（﹣9）×=9，∴×5﹣1=9，故答案为：9．14．【答案】（，+∞）．【解析】解：由题意，a＞1．故问题等价于a x＞x（a＞1）在区间（0，+∞）上恒成立．构造函数f（x）=a x﹣x，则f′（x）=a x lna﹣1，由f′（x）=0，得x=log a（log a e），x＞log a（log a e）时，f′（x）＞0，f（x）递增；0＜x＜log a（log a e），f′（x）＜0，f（x）递减．则x=log a（log a e）时，函数f（x）取到最小值，故有﹣log a（log a e）＞0，解得a＞．故答案为：（，+∞）．【点评】本题考查恒成立问题关键是将问题等价转化，从而利用导数求函数的最值求出参数的范围．15．【答案】75度．【解析】解：点P可能在二面角α﹣l﹣β内部，也可能在外部，应区别处理．当点P在二面角α﹣l﹣β的内部时，如图，A、C、B、P四点共面，∠ACB为二面角的平面角，由题设条件，点P到α，β和棱l的距离之比为1：：2可求∠ACP=30°，∠BCP=45°，∴∠ACB=75°．故答案为：75．【点评】本题考查与二面角有关的立体几何综合题，考查分类讨论的数学思想，正确找出二面角的平面角是关键．16．【答案】0【解析】解：模拟执行程序框图，可得程序框图的功能是计算并输出S=sin+sin+…+sin的值，由于sin周期为8，所以S=sin+sin+…+sin=0．故答案为：0．【点评】本题主要考查了程序框图和算法，考查了正弦函数的周期性和特殊角的三角函数值的应用，属于基本知识的考查．17．【答案】 ．【解析】解：∵F 是抛物线y 2=4x 的焦点， ∴F （1，0），准线方程x=﹣1， 设M （x 1，y 1），N （x 2，y 2）， ∴|MF|+|NF|=x 1+1+x 2+1=6， 解得x 1+x 2=4，∴△MNF 的重心的横坐标为，∴△MNF 的重心到准线距离为．故答案为：．【点评】本题考查解决抛物线上的点到焦点的距离问题，利用抛物线的定义将到焦点的距离转化为到准线的距离．18．【答案】 4【解析】解：由PA ⊥平面ABC ，则△PAC ，△PAB 是直角三角形，又由已知△ABC 是直角三角形，∠ACB=90°所以BC ⊥AC ，从而易得BC ⊥平面PAC ，所以BC ⊥PC ，所以△PCB 也是直角三角形，所以图中共有四个直角三角形，即：△PAC ，△PAB ，△ABC ，△PCB ．故答案为：4【点评】本题考查空间几何体的结构特征，空间中点线面的位置关系，线面垂直的判定定理和性质定理的熟练应用是解答本题的关键．三、解答题19．【答案】【解析】（Ⅰ）)(x f 的定义域),0(+∞，当3a =时，1()23ln f x x x x =--，2'2213231()2x x f x x x x-+=+-= 令'()0f x >得，102x <<或1x >；令'()0f x <得，112x <<，故()f x 的递增区间是1(0,)2和(1,)+∞；()f x 的递减区间是1(,1)2．（Ⅱ）由已知得x a xx x g ln 1)(+-=，定义域为),0(+∞，222111)(xax x x a x x g ++=++='，令0)(='x g 得012=++ax x ，其两根为21,x x ，且212124010ax x ax x⎧->⎪+=->⎨⎪⋅=>⎩，20．【答案】（1）（2）见解析（3）【解析】试题分析：（1）由题意转化为在区间上恒成立，化简可得一次函数恒成立，根据一次函数性质得不等式，解不等式得实数的取值范围；（2）导函数有一个零点，再根据a的正负讨论导函数符号变化规律，确定极值取法（3）先根据导数得切线斜率再根据点斜式得切线方程，即得切线在x轴上的截距，最后根据a的正负以及基本不等式求截距的取值范围．试题解析：（1）函数的导函数，则在区间上恒成立，且等号不恒成立，又，所以在区间上恒成立，记，只需，即，解得．（2）由，得，①当时，有；，所以函数在单调递增，单调递减，所以函数在取得极大值，没有极小值．②当时，有；，所以函数在单调递减，单调递增，所以函数在取得极小值，没有极大值．综上可知: 当时，函数在取得极大值，没有极小值；当时，函数在取得极小值，没有极大值．（3）设切点为，则曲线在点处的切线方程为，当时，切线的方程为，其在轴上的截距不存在．当时，令，得切线在轴上的截距为，当时，，当且仅当，即或时取等号；当时，，当且仅当，即或时取等号.所以切线在轴上的截距范围是.点睛：函数极值问题的常见类型及解题策略（1）知图判断函数极值的情况.先找导数为0的点，再判断导数为0的点的左、右两侧的导数符号.（2）已知函数求极值.求→求方程的根→列表检验在的根的附近两侧的符号→下结论.（3）已知极值求参数.若函数在点处取得极值，则，且在该点左、右两侧的导数值符号相反.21．【答案】【解析】解：函数f（x）的定义域为（0，+∞），（2分）（Ⅰ）当a=1时，f（x）=lnx﹣x﹣1，∴f（1）=﹣2，，∴f′（1）=0，∴f（x）在x=1处的切线方程为y=﹣2（5分）（Ⅱ）=（6分）令f′（x）＜0，可得0＜x＜1，或x＞2；令f'（x）＞0，可得1＜x＜2故当时，函数f（x）的单调递增区间为（1，2）；单调递减区间为（0，1），（2，+∞）.（Ⅲ）当时，由（Ⅱ）可知函数f（x）在（1，2）上为增函数，∴函数f（x）在[1，2]上的最小值为f（1）=（9分）若对于∀x1∈[1，2]，∃x2∈[0，1]使f（x1）≥g（x2）成立，等价于g（x）在[0，1]上的最小值不大于f（x）在（0，e]上的最小值（*）（10分）又，x∈[0，1]①当b＜0时，g（x）在[0，1]上为增函数，与（*）矛盾②当0≤b≤1时，，由及0≤b≤1得，③当b＞1时，g（x）在[0，1]上为减函数，，此时b＞1（11分）综上，b的取值范围是（12分）【点评】本题考查导数知识的运用，考查导数的几何意义，考查函数的单调性，考查恒成立问题，解题的关键是将对于∀x1∈[1，2]，∃x2∈[0，1]使f（x1）≥g（x2）成立，转化为g（x）在[0，1]上的最小值不大于f（x）在（0，e]上的最小值．22．【答案】证明见解析．【解析】考点：直线与平面平行的判定与证明．23．【答案】【解析】（1）证明：设BD交AC于M，连接ME．∵ABCD为正方形，∴M为AC中点，又∵E为A′A的中点，∴ME为△A′AC的中位线，∴ME∥A′C．又∵ME⊂平面BDE，A′C⊄平面BDE，∴A′C∥平面BDE．（2）解：∵V E﹣ABD====V A′﹣ABCD．∴V A′﹣ABCD：V E﹣ABD=4：1．24．【答案】【解析】解：（1）∵=2csinA∴正弦定理得，∵A锐角，∴sinA＞0，∴，又∵C锐角，∴（2）三角形ABC中，由余弦定理得c2=a2+b2﹣2abcosC即7=a2+b2﹣ab，又由△ABC的面积得．即ab=6，∴（a+b）2=a2+b2+2ab=25由于a+b为正，所以a+b=5．【点评】本题主要考查了正弦定理和余弦定理的运用．考查了学生对三角函数基础知识的综合运用．。

福建省福州市福清侨中学2019年高三数学文月考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知三点A(2，1)，B(1，2)，C(，)，动点P(a，b)满足0≤≤2，且0≤≤2，则点P到点C的距离大于的概率为(A) 1 (B) (C) 1 (D)参考答案：A略2. 已知向量, ，如果向量与垂直，则的值为( )A．1 B． C.D．参考答案：无略3. 如果执行如图程序框图，那么输出的（）A．2450B．2500C．2550D．2652参考答案：C4. 已知二面角为600 ，动点P、Q分别在面内，P到的距离为，Q到的距离为，则P、Q两点之间距离的最小值为（A）（B）2 （C）（D）4参考答案：C5. 已知条件P：|x|>1，条件q:x< -2，则是的(A)充分而不必要条件（B)必要而不充分条件(C)充要条件 (D)既不充分也不必要条件参考答案：A6. 若展开式的常数项为60，则a的值为( ).A.4B. ±4C.2D. ±2参考答案：D因为展开式的通项为，令，则，所以常数项为，即，所以.故选D7. 《九章算术》是我国古代第一部数学专著，全书收集了246个问题及其解法，其中一个问题为“现有一根九节的竹子，自上而下各节的容积成等差数列，上面四节容积之和为3升，下面三节的容积之和为4升，求中间两节的容积各为多少？”该问题中第2节，第3节，第8节竹子的容积之和为（）A．升B．升C．升D．升参考答案：A【考点】等差数列的性质．【分析】自上而下依次设各节容积为：a1、a2、…、a9，由题意列出方程组，利用等差数列的性质化简后可得答案．【解答】解：自上而下依次设各节容积为：a1、a2、…、a9，由题意得，，即，得，所以a2+a3+a8=（升），故选：A．8. 已知向量，，（m＞0，n＞0），若m+n∈[1，2]，则的取值范围是（）A．B．C．D．参考答案：B【考点】简单线性规划；简单线性规划的应用；平面向量数量积的运算．【分析】根据题意，由向量的坐标运算公式可得=（3m+n，m﹣3n），再由向量模的计算公式可得=，可以令t=，将m+n∈[1，2]的关系在直角坐标系表示出来，分析可得t=表示区域中任意一点与原点（0，0）的距离，进而可得t的取值范围，又由=t，分析可得答案．【解答】解：根据题意，向量，，=（3m+n，m﹣3n），则==，令t=，则=t，而m+n∈[1，2]，即1≤m+n≤2，在直角坐标系表示如图，t=表示区域中任意一点与原点（0，0）的距离，分析可得：≤t＜2，又由=t，故≤＜2；故选：B．【点评】本题考查简单线性规划问题，涉及向量的模的计算，关键是求出的表达式．9. 函数y=的图象大致是（）A．B．C．D．参考答案：D【考点】利用导数研究函数的单调性；函数的图象．【分析】判断函数的奇偶性，排除选项，利用函数经过的特殊点，以及特殊函数的值，判断函数的单调性，然后判断函数的图象即可．【解答】解：函数y=是偶函数，所以选项B错误，第x=e时，y=e，所以选项A，错误；当x∈（0，1）时，y=xlnx，y′=lnx+1，x=时，y′=0，0＜x＜，y′＜0，函数是减函数，＜x＜1，y′＞0，函数是增函数．所以C错误．故选：D．【点评】本题考查函数的图象的判断，函数的奇偶性，单调性，特殊点，往往是判断函数的图象的方法，考查转化思想以及计算能力．10. 已知，若，则（A）（B）（C）（D）参考答案：B因为，所以，，==二、填空题:本大题共7小题,每小题4分,共28分11. 如图是斯特林数三角阵表，表中第行每一个数等于它左肩上的数加上右肩上的数的倍，则此表中：（Ⅰ）第6行的第二个数是______________；（Ⅱ）第行的第二个数是___________．（用表示）参考答案：274；12. 函数f（x）=e x?sinx在点（0，f（0））处的切线方程是．参考答案：y=x【考点】利用导数研究曲线上某点切线方程．【分析】先求出f′（x），欲求出切线方程，只须求出其斜率即可，故先利用导数求出在x=0处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．【解答】解：∵f（x）=e x?sinx，f′（x）=e x（sinx+cosx），（2分）f′（0）=1，f（0）=0，∴函数f（x）的图象在点A（0，0）处的切线方程为y﹣0=1×（x﹣0），即y=x（4分）．故答案为：y=x．【点评】本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识，考查运算求解能力．属于基础题．13. 执行右侧的程序框图,输出的结果S的值为。

2019年高三11月期中联考（数学文）本试卷共4页，分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题目）两部分，共150分，考试时间120分钟。

注意事项：1.答第Ⅰ卷前，考生务必将自己的姓名、准备考证号、考试科目用铅笔涂写在答题卡上。

2.每题选出答案后，用2B铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再改涂在其它答案标号。

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合}3=n∈-<NnmZmBA，则<},2{|1=3∈-<|{≤A.{0，1}B.{-1，0，1}C.{0，1，2}D.{-1，0，1，2}2.下列命题中的假命题是A. B.C. D.3.已知条件，条件，则是成立的A.充分不必要条件B.必要不充分条件C.充要条件D.既非充分也非必要条件4.将函数的图象向右平移个单位，再向上平移1个单位，所得函数图象对应的解析式为A. B.C. D.5.已知，那么等于A. B. C. D.6.设等比数列中，前n项和为,已知，则A. B. C. D.7.设3.0log ,9.0,5.054121===c b a ，则的大小关系是A. B. C. D.8.函数的图象大致是9.的三个内角A ，B ，C 所对的边分别为a A b B A a c b a 3cos sin sin ,,,2=+，则A. B. C. D.10.若函数⎪⎩⎪⎨⎧<->=0),(log 0,log )(212x x x x x f ，若,则实数的取值范围是 A. B.C. D.11.已知是的一个零点，，则A. B.C. D.12.已知，把数列的各项排列成如下的三角形状，记表示第行的第个数，则=A. B. C. D.第Ⅱ卷 （非选择题 共90分）二、填空题：本大题共4个小题，每小题4分，共16分。

13.若角满足，则的取值范围是 .14.若实数满足⎪⎩⎪⎨⎧≤≥+≥+-,0,0,01x y x y x ，则的值域是 .15.已知奇函数满足，且当时，，则的值为16.已知函数的定义域［-1，5］，部分对应值如表，的导函数的图象如图所示，x-1 0 2 4 5 F(x) 1 2 1.5 2 1下列关于函数的命题；①函数的值域为［1，2］；②函数在［0，2］上是减函数③如果当时，的最大值是2，那么t 的最大值为4；④当时，函数最多有4个零点.其中正确命题的序号是 .三、解答题：本大题共6小题，共74分。

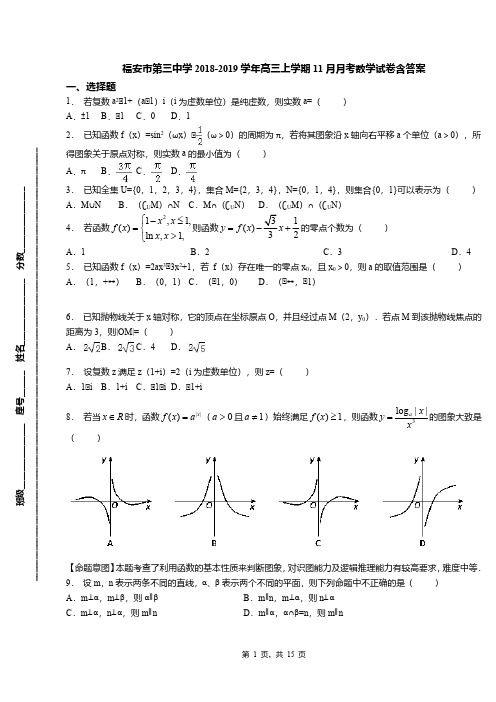
福安市第三中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 若复数a 2﹣1+（a ﹣1）i （i 为虚数单位）是纯虚数，则实数a=（ ）A ．±1B ．﹣1C ．0D ．12． 已知函数f （x ）=sin 2（ωx ）﹣（ω＞0）的周期为π，若将其图象沿x 轴向右平移a 个单位（a ＞0），所得图象关于原点对称，则实数a 的最小值为（ ）A ．πB ．C ．D ．3． 已知全集U={0，1，2，3，4}，集合M={2，3，4}，N={0，1，4}，则集合{0，1}可以表示为（ ）A ．M ∪NB ．（∁U M ）∩NC ．M ∩（∁U N ）D ．（∁U M ）∩（∁U N ）4． 若函数则函数的零点个数为（ ）21,1,()ln ,1,x x f x x x ⎧-≤=⎨>⎩1()2y f x x =+A ．1 B ．2C ．3D ．45． 已知函数f （x ）=2ax 3﹣3x 2+1，若 f （x ）存在唯一的零点x 0，且x 0＞0，则a 的取值范围是（）A ．（1，+∞）B ．（0，1）C ．（﹣1，0）D ．（﹣∞，﹣1）6． 已知抛物线关于x 轴对称，它的顶点在坐标原点O ，并且经过点M （2，y 0）．若点M 到该抛物线焦点的距离为3，则|OM|=（ ）A ．B ．C ．4D ．7． 设复数z 满足z （1+i ）=2（i 为虚数单位），则z=（ ）A ．1﹣iB ．1+iC ．﹣1﹣iD ．﹣1+i8． 若当时，函数（且）始终满足，则函数的图象大致是R x ∈||)(x a x f =0>a 1≠a 1)(≥x f 3||log x x y a =（）【命题意图】本题考查了利用函数的基本性质来判断图象，对识图能力及逻辑推理能力有较高要求，难度中等．9． 设m ，n 表示两条不同的直线，α、β表示两个不同的平面，则下列命题中不正确的是（ ）A ．m ⊥α，m ⊥β，则α∥βB ．m ∥n ，m ⊥α，则n ⊥αC ．m ⊥α，n ⊥α，则m ∥nD ．m ∥α，α∩β=n ，则m ∥n班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________10．已知某运动物体的位移随时间变化的函数关系为，设物体第n 秒内的位移为a n ，则数列{a n }是（）A ．公差为a 的等差数列B ．公差为﹣a 的等差数列C ．公比为a 的等比数列D ．公比为的等比数列11．已知在数轴上0和3之间任取一实数，则使“”的概率为（ ）2log 1x <A ．B ．C ．D ．14182311212．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若（acosB+bcosA ）=2csinC ，a+b=8，且△ABC 的面积的最大值为4，则此时△ABC 的形状为（ ）A ．等腰三角形B ．正三角形C ．直角三角形D ．钝角三角形二、填空题13．如图所示是y=f （x ）的导函数的图象，有下列四个命题：①f （x ）在（﹣3，1）上是增函数；②x=﹣1是f （x ）的极小值点；③f （x ）在（2，4）上是减函数，在（﹣1，2）上是增函数；④x=2是f （x ）的极小值点．其中真命题为 （填写所有真命题的序号）．14．一组数据2，x ，4，6，10的平均值是5，则此组数据的标准差是 ．　15．已知正整数的3次幂有如下分解规律：m ；；；；…113=5323+=119733++=1917151343+++=若的分解中最小的数为，则的值为.)(3+∈N m m 91m 【命题意图】本题考查了归纳、数列等知识，问题的给出比较新颖，对逻辑推理及化归能力有较高要求，难度中等.16．设函数f （x ）=，①若a=1，则f （x ）的最小值为 ；②若f （x ）恰有2个零点，则实数a 的取值范围是 ．　17．已知含有三个实数的集合既可表示成}1,,{aba ，又可表示成}0,,{2b a a +，则=+20042003b a .18．已知函数，且，则，的大小关系()f x 23(2)5x =-+12|2||2|x x ->-1()f x 2()f x 是．三、解答题19．已知函数f （x ）=（ax 2+x ﹣1）e x ，其中e 是自然对数的底数，a ∈R ．（Ⅰ）若a=0，求曲线f （x ）在点（1，f （1））处的切线方程；（Ⅱ）若，求f （x ）的单调区间；（Ⅲ）若a=﹣1，函数f （x ）的图象与函数的图象仅有1个公共点，求实数m 的取值范围．　20．（本题12分）正项数列{}n a 满足2(21)20n n a n a n ---=．（1）求数列{}n a 的通项公式n a ；（2）令1(1)n nb n a =+，求数列{}n b 的前项和为n T .21．设定义在（0，+∞）上的函数f （x ）=ax++b （a ＞0）（Ⅰ）求f （x ）的最小值；（Ⅱ）若曲线y=f （x ）在点（1，f （1））处的切线方程为y=，求a ，b 的值．22．已知y=f （x ）是R 上的偶函数，x ≥0时，f （x ）=x 2﹣2x （1）当x ＜0时，求f （x ）的解析式．（2）作出函数f （x ）的图象，并指出其单调区间．23．一台还可以用的机器由于使用的时间较长，它按不同的转速生产出来的某机械零件有一些会有缺陷，每小时生产有缺陷零件的多少随机器运转的速率而变化，下表为抽样试验结果：转速x （转/秒）1614128每小时生产有缺陷的零件数y （件）11985（1）画出散点图； （2）如果y 与x 有线性相关的关系，求回归直线方程；（3）若实际生产中，允许每小时的产品中有缺陷的零件最多为10个，那么机器的转运速度应控制在什么范围内？参考公式：线性回归方程系数公式开始=， =﹣x ．24．【2017-2018学年度第一学期如皋市高三年级第一次联考】设函数．()1ln 1f x a x x=+-（1）当时，求函数在点处的切线方程；2a =()f x ()()11f ，（2）讨论函数的单调性；()f x （3）当时，求证：对任意，都有．102a <<1+2x ⎛⎫∈∞ ⎪⎝⎭，1e x aa x +⎛⎫+< ⎪⎝⎭福安市第三中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题1．【答案】B【解析】解：因为复数a2﹣1+（a﹣1）i（i为虚数单位）是纯虚数，所以a2﹣1=0且a﹣1≠0，解得a=﹣1．故选B．【点评】本题考查复数的基本概念的应用，实部为0并且虚部不为0，是解题的关键．2．【答案】D【解析】解：由函数f（x）=sin2（ωx）﹣=﹣cos2ωx （ω＞0）的周期为=π，可得ω=1，故f（x）=﹣cos2x．若将其图象沿x轴向右平移a个单位（a＞0），可得y=﹣cos2（x﹣a）=﹣cos（2x﹣2a）的图象；再根据所得图象关于原点对称，可得2a=kπ+，a=+，k∈Z．则实数a的最小值为．故选：D【点评】本题主要考查三角恒等变换，余弦函数的周期性，函数y=Acos（ωx+φ）的图象变换规律，正弦函数、余弦函数的奇偶性，属于基础题．3．【答案】B【解析】解：全集U={0，1，2，3，4}，集合M={2，3，4}，N={0，1，4}，∴∁U M={0，1}，∴N∩（∁U M）={0，1}，故选：B．【点评】本题主要考查集合的子交并补运算，属于基础题．4．【答案】D【解析】考点：函数的零点．【易错点睛】函数零点个数的判断方法：（1）直接求零点：令，如果能求出解，则有几个解就有几0)(=x f 个零点．（2）零点存在性定理法：要求函数在上是连续的曲线，且.还必须结合函数的图],[b a 0)()(<b f a f 象和性质（如单调性）才能确定函数有多少个零点．（3）图象法：先把所求函数分解为两个简单函数，再画两个函数图象，看其交点的个数有几个，其中交点的横坐标有几个不同的值，就有几个不同的零点.5． 【答案】D【解析】解：若a=0，则函数f （x ）=﹣3x 2+1，有两个零点，不满足条件．若a ≠0，函数的f （x ）的导数f ′（x ）=6ax 2﹣6x=6ax （x ﹣），若 f （x ）存在唯一的零点x 0，且x 0＞0，若a ＞0，由f ′（x ）＞0得x ＞或x ＜0，此时函数单调递增，由f ′（x ）＜0得0＜x ＜，此时函数单调递减，故函数在x=0处取得极大值f （0）=1＞0，在x=处取得极小值f （），若x 0＞0，此时还存在一个小于0的零点，此时函数有两个零点，不满足条件．若a ＜0，由f ′（x ）＞0得＜x ＜0，此时函数递增，由f ′（x ）＜0得x ＜或x ＞0，此时函数单调递减，即函数在x=0处取得极大值f （0）=1＞0，在x=处取得极小值f （），若存在唯一的零点x 0，且x 0＞0，则f （）＞0，即2a （）3﹣3（）2+1＞0，（）2＜1，即﹣1＜＜0，解得a ＜﹣1，故选：D【点评】本题主要考查函数零点的应用，求函数的导数，利用导数和极值之间的关系是解决本题的关键．注意分类讨论．　6． 【答案】B【解析】解：由题意，抛物线关于x 轴对称，开口向右，设方程为y 2=2px （p ＞0）∵点M （2，y 0）到该抛物线焦点的距离为3，∴2+=3∴p=2∴抛物线方程为y 2=4x ∵M （2，y 0）∴∴|OM|=故选B ．【点评】本题考查抛物线的性质，考查抛物线的定义，解题的关键是利用抛物线的定义求出抛物线方程．　7． 【答案】A【解析】解：∵z （1+i ）=2，∴z===1﹣i ．故选：A ．【点评】本题考查了复数的运算法则、共轭复数的定义，属于基础题．　8． 【答案】C【解析】由始终满足可知．由函数是奇函数，排除；当时，||)(x a x f =1)(≥x f 1>a 3||log xx y a =B )1,0(∈x ，此时，排除；当时，，排除，因此选．0||log <x a 0||log 3<=x x y a A +∞→x 0→y D C 9． 【答案】D【解析】解：A 选项中命题是真命题，m ⊥α，m ⊥β，可以推出α∥β；B 选项中命题是真命题，m ∥n ，m ⊥α可得出n ⊥α；C 选项中命题是真命题，m ⊥α，n ⊥α，利用线面垂直的性质得到n ∥m ；D 选项中命题是假命题，因为无法用线面平行的性质定理判断两直线平行．故选D ．【点评】本题考查了空间线面平行和线面垂直的性质定理和判定定理的运用，关键是熟练有关的定理．　10．【答案】A 【解析】解：∵，∴a n =S （n ）﹣s （n ﹣1）==∴a n ﹣a n ﹣1==a∴数列{a n }是以a 为公差的等差数列故选A【点评】本题主要考察了数列的递推公式求解数列的通项公式，等差数列的定义的应用，属于数列知识的简单应用　11．【答案】C 【解析】试题分析：由得,由几何概型可得所求概率为.故本题答案选C.2log 1x <02x <<202303-=-考点：几何概型．12．【答案】A 【解析】解：∵（acosB+bcosA ）=2csinC ，∴（sinAcosB+sinBcosA ）=2sin 2C ，∴sinC=2sin 2C ，且sinC ＞0，∴sinC=，∵a+b=8，可得：8≥2，解得：ab ≤16，（当且仅当a=b=4成立）∵△ABC 的面积的最大值S △ABC =absinC ≤=4，∴a=b=4，则此时△ABC 的形状为等腰三角形．故选：A ．　二、填空题13．【答案】　①　【解析】解：由图象得：f （x ）在（1，3）上递减，在（﹣3，1），（3，+∞）递增，∴①f （x ）在（﹣3，1）上是增函数，正确，x=3是f （x ）的极小值点，②④不正确；③f （x ）在（2，4）上是减函数，在（﹣1，2）上是增函数，不正确，故答案为：①．　14．【答案】　2　．【解析】解：∵一组数据2，x ，4，6，10的平均值是5，∴2+x+4+6+10=5×5，解得x=3，∴此组数据的方差 [（2﹣5）2+（3﹣5）2+（4﹣5）2+（6﹣5）2+（10﹣5）2]=8，∴此组数据的标准差S==2．故答案为：2．【点评】本题考查一组数据的标准差的求法，解题时要认真审题，注意数据的平均数和方差公式的求法．　15．【答案】10【解析】的分解规律恰好为数列1，3，5，7，9，…中若干连续项之和，为连续两项和，为接下来三3m 3233项和，故的首个数为.3m 12+-m m ∵的分解中最小的数为91，∴，解得.)(3+∈N m m 9112=+-m m 10=m 16．【答案】　≤a ＜1或a ≥2　．【解析】解：①当a=1时，f （x ）=，当x ＜1时，f （x ）=2x ﹣1为增函数，f （x ）＞﹣1，当x ＞1时，f （x ）=4（x ﹣1）（x ﹣2）=4（x 2﹣3x+2）=4（x ﹣）2﹣1，当1＜x ＜时，函数单调递减，当x ＞时，函数单调递增，故当x=时，f （x ）min =f （）=﹣1，②设h （x ）=2x ﹣a ，g （x ）=4（x ﹣a ）（x ﹣2a ）若在x ＜1时，h （x ）=与x 轴有一个交点，所以a ＞0，并且当x=1时，h （1）=2﹣a ＞0，所以0＜a ＜2，而函数g （x ）=4（x ﹣a ）（x ﹣2a ）有一个交点，所以2a ≥1，且a ＜1，所以≤a ＜1，若函数h （x ）=2x ﹣a 在x ＜1时，与x 轴没有交点，则函数g （x ）=4（x ﹣a ）（x ﹣2a ）有两个交点，当a ≤0时，h （x ）与x 轴无交点，g （x ）无交点，所以不满足题意（舍去），当h （1）=2﹣a ≤0时，即a ≥2时，g （x ）的两个交点满足x 1=a ，x 2=2a ，都是满足题意的，综上所述a 的取值范围是≤a ＜1，或a ≥2．　17．【答案】-1【解析】试题分析：由于，所以只能，，所以。

福安市第一中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 已知m ，n 为不同的直线，α，β为不同的平面，则下列说法正确的是（ ）A ．m ⊂α，n ∥m ⇒n ∥αB ．m ⊂α，n ⊥m ⇒n ⊥αC ．m ⊂α，n ⊂β，m ∥n ⇒α∥βD ．n ⊂β，n ⊥α⇒α⊥β2． 某几何体的三视图如下（其中三视图中两条虚线互相垂直）则该几何体的体积为（）A. B ．483C.D ．1632033． 若某几何体的三视图 （单位：cm ） 如图所示，则此几何体的体积是（ ）cm3A ．πB ．2πC ．3πD ．4π4． 已知圆方程为，过点与圆相切的直线方程为（ ）C 222x y +=(1,1)P -C A ． B ．C ．D ．20x y -+=10x y +-=10x y -+=20x y ++=5． 阅读如下所示的程序框图，若运行相应的程序，则输出的的值是（）S A ．39B ．21C ．81D ．102班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________6． 在ABC ∆中，若60A ∠=o，45B ∠=o，BC =，则AC =（）A ．B ． C.D 7． 已知函数f （x ）=x 2﹣6x+7，x ∈（2，5]的值域是（ ）A ．（﹣1，2]B ．（﹣2，2]C ．[﹣2，2]D ．[﹣2，﹣1）8． 已知为的三个角所对的边，若，则,,a b c ABC ∆,,A B C 3cos (13cos )b C c B =-sin :sin C A =（）A ．2︰3B ．4︰3C ．3︰1D ．3︰2【命题意图】本题考查正弦定理、余弦定理，意在考查转化能力、运算求解能力．9． 学校将5个参加知识竞赛的名额全部分配给高一年级的4个班级，其中甲班级至少分配2个名额，其它班级可以不分配或分配多个名额，则不同的分配方案共有（ ）A ．20种B ．24种C ．26种D ．30种10．数列{a n }满足a 1=3，a n ﹣a n •a n+1=1，A n 表示{a n }前n 项之积，则A 2016的值为（ ）A ．﹣B ．C ．﹣1D ．111．连续抛掷两次骰子得到的点数分别为m 和n ，记向量=（m ，n ），向量=（1，﹣2），则⊥的概率是（ ）A ．B ．C ．D ．12．已知函数f （x ）=2x ，则f ′（x ）=（ ）A ．2xB ．2x ln2C ．2x +ln2D ．二、填空题13．已知i是虚数单位，复数的模为 ．14．已知函数f（x）的定义域为[﹣1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图示．x﹣1045f（x）1221下列关于f（x）的命题：①函数f（x）的极大值点为0，4；②函数f（x）在[0，2]上是减函数；③如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；④当1＜a＜2时，函数y=f（x）﹣a有4个零点；⑤函数y=f（x）﹣a的零点个数可能为0、1、2、3、4个．其中正确命题的序号是 ．15．若正方形P1P2P3P4的边长为1，集合M={x|x=且i，j∈{1，2，3，4}}，则对于下列命题：①当i=1，j=3时，x=2；②当i=3，j=1时，x=0；③当x=1时，（i，j）有4种不同取值；④当x=﹣1时，（i，j）有2种不同取值；⑤M中的元素之和为0．其中正确的结论序号为 ．（填上所有正确结论的序号）16．（﹣）0+[（﹣2）3]= ．17．已知直线l：ax﹣by﹣1=0（a＞0，b＞0）过点（1，﹣1），则ab的最大值是 ．18．在（1+2x）10的展开式中，x2项的系数为 （结果用数值表示）．三、解答题19．某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]（Ⅰ）求图中x的值，并估计该班期中考试数学成绩的众数；（Ⅱ）从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人，求这2人成绩均不低于90分的概率．20．如图所示，已知+=1（a＞＞0）点A（1，）是离心率为的椭圆C：上的一点，斜率为的直线BD交椭圆C于B、D两点，且A、B、D三点不重合．（Ⅰ）求椭圆C的方程；（Ⅱ）求△ABD面积的最大值；（Ⅲ）设直线AB、AD的斜率分别为k1，k2，试问：是否存在实数λ，使得k1+λk2=0成立？若存在，求出λ的值；否则说明理由．21．请你设计一个包装盒，如图所示，ABCD 是边长为60cm 的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A ，B ，C ，D 四个点重合于图中的点P ，正好形成一个正四棱柱形状的包装盒，E 、F 在AB 上，是被切去的等腰直角三角形斜边的两个端点，设AE=FB=x （cm ）．（1）若广告商要求包装盒侧面积S （cm 2）最大，试问x 应取何值？（2）若广告商要求包装盒容积V （cm 3）最大，试问x 应取何值？并求出此时包装盒的高与底面边长的比值．22．已知、、是三个平面，且，，，且．求证：、αβc αβ=I a βγ=I b αγ=I a b O =I 、三线共点．23．在极坐标系中，圆C 的极坐标方程为：ρ2=4ρ（cos θ+sin θ）﹣6．若以极点O 为原点，极轴所在直线为x 轴建立平面直角坐标系．（Ⅰ）求圆C 的参数方程；（Ⅱ）在直角坐标系中，点P （x ，y ）是圆C 上动点，试求x+y 的最大值，并求出此时点P 的直角坐标．24．如图，在长方体ABCD﹣A1B1C1D1中，AB=2，AD=1，A1A=1，（1）求证：直线BC1∥平面D1AC；（2）求直线BC1到平面D1AC的距离．福安市第一中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题1． 【答案】D【解析】解：在A 选项中，可能有n ⊂α，故A 错误；在B 选项中，可能有n ⊂α，故B 错误；在C 选项中，两平面有可能相交，故C 错误；在D 选项中，由平面与平面垂直的判定定理得D 正确．故选：D ．【点评】本题考查命题真假的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．　2． 【答案】【解析】选D.根据三视图可知，该几何体是一个棱长为2的正方体挖去一个以正方体的中心为顶点，上底面为底面的正四棱锥后剩下的几何体如图，其体积V ＝23－×2×2×1＝，故选D.132033． 【答案】B【解析】解：由三视图可知：此几何体为圆锥的一半，∴此几何体的体积==2π．故选：B ．　4． 【答案】A 【解析】试题分析：圆心，由(0,0),C r =1(1),10y k x kx y k -=+∴-++=，所以切线方程为，故选A.,1d r k =∴=20x y -+=考点：直线与圆的位置关系．5． 【答案】]【解析】试题分析：第一次循环：；第二次循环：；第三次循环：．结束循环，2,3==n S 3,21==n S 4,102==n S 输出．故选D. 1102=S考点：算法初步．6． 【答案】B 【解析】考点：正弦定理的应用.7． 【答案】C【解析】解：由f （x ）=x 2﹣6x+7=（x ﹣3）2﹣2，x ∈（2，5]．∴当x=3时，f （x ）min =﹣2．当x=5时，．∴函数f （x ）=x 2﹣6x+7，x ∈（2，5]的值域是[﹣2，2]．故选：C ．　8． 【答案】C【解析】由已知等式，得，由正弦定理，得，则3cos 3cos c b C c B =+sin 3(sin cos sin cos )C B C C B =+，所以，故选C ．sin 3sin()3sin C B C A =+=sin :sin 3:1C A =9． 【答案】A【解析】解：甲班级分配2个名额，其它班级可以不分配名额或分配多个名额，有1+6+3=10种不同的分配方案；甲班级分配3个名额，其它班级可以不分配名额或分配多个名额，有3+3=6种不同的分配方案；甲班级分配4个名额，其它班级可以不分配名额或分配多个名额，有3种不同的分配方案；甲班级分配5个名额，有1种不同的分配方案．故共有10+6+3+1=20种不同的分配方案，故选：A ．【点评】本题考查分类计数原理，注意分类时做到不重不漏，是一个中档题，解题时容易出错，本题应用分类讨论思想．　10．【答案】D【解析】解：∵a 1=3，a n ﹣a n •a n+1=1，∴，得，，a 4=3，…∴数列{a n }是以3为周期的周期数列，且a 1a 2a 3=﹣1，∵2016=3×672，∴A 2016 =（﹣1）672=1．故选：D ．　11．【答案】A【解析】解：因为抛掷一枚骰子有6种结果，设所有连续抛掷两次骰子得到的点数为（m ，n ），有36种可能，而使⊥的m ，n 满足m=2n ，这样的点数有（2，1），（4，2），（6，3）共有3种可能；由古典概型公式可得⊥的概率是：；故选：A．【点评】本题考查古典概型，考查用列举法得到满足条件的事件数，是一个基础题．12．【答案】B【解析】解：f（x）=2x，则f'（x）=2x ln2，故选：B．【点评】本题考查了导数运算法则，属于基础题．二、填空题13．【答案】 ．【解析】解：∵复数==i﹣1的模为=．故答案为：．【点评】本题考查了复数的运算法则、模的计算公式，属于基础题．14．【答案】　①②⑤　．【解析】解：由导数图象可知，当﹣1＜x＜0或2＜x＜4时，f'（x）＞0，函数单调递增，当0＜x＜2或4＜x＜5，f'（x）＜0，函数单调递减，当x=0和x=4，函数取得极大值f（0）=2，f（4）=2，当x=2时，函数取得极小值f（2），所以①正确；②正确；因为在当x=0和x=4，函数取得极大值f（0）=2，f（4）=2，要使当x∈[﹣1，t]函数f（x）的最大值是4，当2≤t≤5，所以t的最大值为5，所以③不正确；由f（x）=a知，因为极小值f（2）未知，所以无法判断函数y=f（x）﹣a有几个零点，所以④不正确，根据函数的单调性和极值，做出函数的图象如图，（线段只代表单调性），根据题意函数的极小值不确定，分f（2）＜1或1≤f（2）＜2两种情况，由图象知，函数y=f（x）和y=a的交点个数有0，1，2，3，4等不同情形，所以⑤正确，综上正确的命题序号为①②⑤．故答案为：①②⑤．【点评】本题考查导数知识的运用，考查导函数与原函数图象之间的关系，正确运用导函数图象是关键．15．【答案】　①③⑤　【解析】解：建立直角坐标系如图：则P1（0，1），P2（0，0），P3（1，0），P4（1，1）．∵集合M={x|x=且i，j∈{1，2，3，4}}，对于①，当i=1，j=3时，x==（1，﹣1）•（1，﹣1）=1+1=2，故①正确；对于②，当i=3，j=1时，x==（1，﹣1）•（﹣1，1）=﹣2，故②错误；对于③，∵集合M={x|x=且i，j∈{1，2，3，4}}，∴=（1，﹣1），==（0，﹣1），==（1，0），∴•=1；•=1；•=1；•=1；∴当x=1时，（i，j）有4种不同取值，故③正确；④同理可得，当x=﹣1时，（i，j）有4种不同取值，故④错误；⑤由以上分析，可知，当x=1时，（i，j）有4种不同取值；当x=﹣1时，（i，j）有4种不同取值，当i=1，j=3时，x=2时，当i=3，j=1时，x=﹣2；当i=2，j=4，或i=4，j=2时，x=0，∴M中的元素之和为0，故⑤正确．综上所述，正确的序号为：①③⑤，故答案为：①③⑤．【点评】本题考查命题的真假判断与应用，着重考查平面向量的坐标运算，建立直角坐标系，求得=（1，﹣1），==（0，﹣1），==（1，0）是关键，考查分析、化归与运算求解能力，属于难题．16．【答案】 ．【解析】解：（﹣）0+[（﹣2）3]=1+（﹣2）﹣2=1+=．故答案为：．17．【答案】 ．【解析】解：∵直线l：ax﹣by﹣1=0（a＞0，b＞0）过点（1，﹣1），∴a+b﹣1=0，即a+b=1，∴ab≤=当且仅当a=b=时取等号，故ab的最大值是故答案为：【点评】本题考查基本不等式求最值，属基础题．18．【答案】　180　【解析】解：由二项式定理的通项公式T r+1=C n r a n﹣r b r可设含x2项的项是T r+1=C7r（2x）r可知r=2，所以系数为C102×4=180，故答案为：180．【点评】本题主要考查二项式定理中通项公式的应用，属于基础题型，难度系数0.9．一般地通项公式主要应用有求常数项，有理项，求系数，二项式系数等．三、解答题19．【答案】【解析】解：（Ⅰ）由（0.006×3+0.01+0.054+x）×10=1，解得x=0.018，前三组的人数分别为：（0.006×2+0.01+0.018）×10×50=20，第四组为0.054×10×50=27人，故数学成绩的众数落在第四组，故众数为75分．（Ⅱ）分数在[40，50）、[90，100]的人数分别是3人，共6人，∴这2人成绩均不低于90分的概率P==．【点评】本题考查频率分布直方图及古典概型的问题，前者要熟练掌握直方图的基本性质和如何利用直方图求众数；后者往往和计数原理结合起来考查．20．【答案】【解析】解：（Ⅰ）∵，∴a=c，∴b2=c2∴椭圆方程为+=1又点A（1，）在椭圆上，∴=1，∴c2=2∴a=2，b=，∴椭圆方程为=1 …（Ⅱ）设直线BD方程为y=x+b，D（x1，y1），B（x2，y2），与椭圆方程联立，可得4x2+2bx+b2﹣4=0△=﹣8b2+64＞0，∴﹣2＜b＜2x1+x2=﹣b，x1x2=∴|BD|==，设d为点A到直线y=x+b的距离，∴d=∴△ABD面积S=≤=当且仅当b=±2时，△ABD的面积最大，最大值为…（Ⅲ）当直线BD过椭圆左顶点（﹣，0）时，k1==2﹣，k2==﹣2此时k1+k2=0，猜想λ=1时成立．证明如下：k1+k2=+=2+m=2﹣2=0当λ=1，k1+k2=0，故当且仅当λ=1时满足条件…【点评】本题考查直线与椭圆方程的综合应用，考查存在性问题的处理方法，椭圆方程的求法，韦达定理的应用，考查分析问题解决问题的能力．21．【答案】【解析】解：设包装盒的高为h（cm），底面边长为a（cm），则a=x，h=（30﹣x），0＜x＜30．（1）S=4ah=8x（30﹣x）=﹣8（x﹣15）2+1800，∴当x=15时，S取最大值．（2）V=a2h=2（﹣x3+30x2），V′=6x（20﹣x），由V′=0得x=20，当x∈（0，20）时，V′＞0；当x∈（20，30）时，V′＜0；∴当x=20时，包装盒容积V（cm3）最大，此时，．即此时包装盒的高与底面边长的比值是．22．【答案】证明见解析．【解析】考点：平面的基本性质与推论．23．【答案】【解析】（本小题满分10分）选修4﹣4：坐标系与参数方程解：（Ⅰ）因为ρ2=4ρ（cosθ+sinθ）﹣6，所以x2+y2=4x+4y﹣6，所以x2+y2﹣4x﹣4y+6=0，即（x﹣2）2+（y﹣2）2=2为圆C的普通方程．…所以所求的圆C的参数方程为（θ为参数）．…（Ⅱ）由（Ⅰ）可得，…当时，即点P的直角坐标为（3，3）时，…x+y取到最大值为6．…24．【答案】【解析】解：（1）因为ABCD﹣A1B1C1D1为长方体，故AB∥C1D1，AB=C1D1，故ABC1D1为平行四边形，故BC1∥AD1，显然B不在平面D1AC上，故直线BC1平行于平面DA1C；（2）直线BC1到平面D1AC的距离即为点B到平面D1AC的距离（设为h）以△ABC为底面的三棱锥D1﹣ABC的体积V，可得而△AD1C中，，故所以以△AD1C为底面的三棱锥B﹣﹣AD1C的体积，即直线BC1到平面D1AC的距离为．【点评】本题考查了线面平行的判定定理，考查线面的距离以及数形结合思想，是一道中档题．　。

大同中学2019-2019学年高三上学期第二次月考数学（文科）一、选择题（本题共12小题，每小题5分，共60分）（2019-2019年大同中学高三（文）上11月1）已知集合{}02|2>-=x x x A ，{}55|<<-=x x B ，则（ ）A.o B A /=⋂B.R B A =⋃C.A B ⊆D.B A ⊆ （2019-2019年大同中学高三（文）上11月2）下列说法正确的是（ ） A.命题“若b a lg lg >，则b a >”的逆否命题是假命题 B.命题“R x ∈∀，02>x”的否定是“R x ∈∃︒，02≤︒x” C.若命题p 为真命题，命题q 为假命题，则命题“q p ∧”为真命题 D.“21sin =α”是“6πα=”的充分不必要条件 （2019-2019年大同中学高三（文）上11月3）函数()9ln 3-+=x x x f 的零点所在的区间为（ ）A.()1,0B.()2,1C.()3,2D.()4,3（2019-2019年大同中学高三（文）上11月4）在ABC ∆中，a AB=，b AC =，若点D满足=BD 21DC ，则=AD （ ） A.b a 3132+ B.b a 3235- C.b a 3231+- D.b a 3231+（2019-2019年大同中学高三（文）上11月5）函数()⎪⎭⎫⎝⎛-=3sin πωx x f ()0,>∈ωR x 的最小正周期为π，为了得到()x f 的图象，只需将函数x y ωsin =的图象（ ）A.向左平移3π个单位 B.向右平移3π个单位 C.向左平移6π个单位 D.向右平移6π个单位（2019-2019年大同中学高三（文）上11月6）已知βα，为锐角，53c os=α，()31tan -=-βα，则βtan 的值为（ ）A.31 B.3 C.139 D.913 （2019-2019年大同中学高三（文）上11月7）函数x x y ln 212-=的单调递减区间为（ ）A.(]1,1-B.(]1,0C.()∞+，1 D.()∞+，0 （2019-2019年大同中学高三（文）上11月8）已知2.12=a ，8.021-⎪⎭⎫ ⎝⎛=b ，2log 25=c ，则c b a ,,的大小关系为（ ）A.a b c <<B.b a c <<C.c a b <<D.a c b <<（2019-2019年大同中学高三（文）上11月9）在ABC ∆中，角C B A ,,所对的边分别为c b a ,,，且bc a c b +=+222，若A C B 2sin sin sin =∙，则ABC ∆的形状是（ ）A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形（2019-2019年大同中学高三（文）上11月10）函数()x kx x f ln -=在区间()∞+，1上单调递增，则k 的取值范围是（ ）A.(]2--，∞ B.(]1--，∞ C.[)∞+，2 D.[)∞+，1 （2019-2019年大同中学高三（文）上11月11）已知函数()2cos sin cos sin xx x x x f -++=，则下列结论正确的是（ ）A.()x f 是奇函数B.()x f 在⎥⎦⎤⎢⎣⎡20π，上递增C.()x f 是周期函数D.()x f 的值域为[]11-， （2019-2019年大同中学高三（文）上11月12）若函数()x f e x（⋅⋅⋅=71828.2e 是自然对数的底数）在()x f 的定义域上单调递增，则称函数()x f 具有M 性质，下列函数中具有M 性质的是（ ）A.()xx f -=2 B.()2x x f = C.()xx f -=3 D.()x x f cos =二、填空题（本题共4题，共20分）（2019-2019年大同中学高三（文）上11月13）已知向量()3-,2=a，()1-,x b = ，若()b a a-⊥，则=x .（2019-2019年大同中学高三（文）上11月14）已知4=a ，8=b ，a 与b的夹角是︒120，则b 在a方向上的投影为 .（2019-2019年大同中学高三（文）上11月15）已知函数()13++=x ax x f 的图像在点()()1,1f 处的切线过点()7,2，则=a .（2019-2019年大同中学高三（文）上11月16）关于函数()xx x x f 2cos 2cos sin 21-+=有下列命题:①函数()x f y =的最小正周期为π; ②直线4π=x 是()x f y =的一条对称轴;③点⎪⎭⎫⎝⎛08，π是()x f y =的图象的一个对称中心; ④将()x f y =的图象向左平移4π个单位,可得到x y 2sin 2=的图象. 其中真命题的序号是 .(把你认为真命题的序号都写上)三、解答题（本题共6小题，共70分）（2019-2019年大同中学高三（文）上11月17）已知c b a ,,分别为内角C B A ,,的对边，C A B sin sin 2sin =。

福建省厦门市大同中学高三第一学期第二次月考（11月）数学（文）试卷数学（文科）一、选择题（本题共12小题，每小题5分，共60分）（2019-2019年大同中学高三（文）上11月1）已知集合{}02|2>-=x x x A ，{}55|<<-=x x B ，则（ ） A.o B A /=⋂ B.R B A =⋃ C.A B ⊆D.B A ⊆（2019-2019年大同中学高三（文）上11月2）下列说法正确的是（ ）A.命题“若b a lg lg >，则b a >”的逆否命题是假命题B.命题“R x ∈∀，02>x ”的否定是“R x ∈∃︒，02≤︒x ” C.若命题p 为真命题，命题q 为假命题，则命题“q p ∧”为真命题D.“21sin =α”是“6πα=”的充分不必要条件 （2019-2019年大同中学高三（文）上11月3）函数()9ln 3-+=x x x f 的零点所在的区间为（ ）A.()1,0B.()2,1C.()3,2D.()4,3 （2019-2019年大同中学高三（文）上11月4）在ABC ∆中，a ρ=，b ρ=，若点D 满足=21，则=（ ） A.b a ρρ3132+ B.b a ρρ3235- C.b a ρρ3231+- D.b a ρρ3231+ （2019-2019年大同中学高三（文）上11月5）函数()⎪⎭⎫ ⎝⎛-=3sin πωx x f ()0,>∈ωR x 的最小正周期为π，为了得到()x f 的图象，只需将函数x y ωsin =的图象（ ）A.向左平移3π个单位B.向右平移3π个单位C.向左平移6π个单位D.向右平移6π个单位 （2019-2019年大同中学高三（文）上11月6）已知βα，为锐角，53cos =α，()31tan -=-βα，则βtan 的值为（ ） A.31 B.3 C.139 D.913 （2019-2019年大同中学高三（文）上11月7）函数x x y ln 212-=的单调递减区间为（ ）A.(]1,1-B.(]1,0C.()∞+，1D.()∞+，0 （2019-2019年大同中学高三（文）上11月8）已知2.12=a ，8.021-⎪⎭⎫ ⎝⎛=b ，2log 25=c ， 则c b a ,,的大小关系为（ ）A.a b c <<B.b a c <<C.c a b <<D.a c b <<（2019-2019年大同中学高三（文）上11月9）在ABC ∆中，角C B A ,,所对的边分别为c b a ,,，且bc a c b +=+222，若A C B 2sin sin sin =•，则ABC ∆的形状是（ ）A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形（2019-2019年大同中学高三（文）上11月10）函数()x kx x f ln -=在区间()∞+，1上单调递增，则k 的取值范围是（ ） A.(]2--，∞ B.(]1--，∞ C.[)∞+，2 D.[)∞+，1 （2019-2019年大同中学高三（文）上11月11）已知函数()2cos sin cos sin xx x x x f -++=，则下列结论正确的是（ ）A.()x f 是奇函数B.()x f 在⎥⎦⎤⎢⎣⎡20π，上递增 C.()x f 是周期函数 D.()x f 的值域为[]11-，（2019-2019年大同中学高三（文）上11月12）若函数()x f e x （⋅⋅⋅=71828.2e 是自然对数的底数）在()x f 的定义域上单调递增，则称函数()x f 具有M 性质，下列函数中具有M 性质的是（ ）A.()x x f -=2B.()2x x f =C.()x x f -=3D.()x x f cos =二、填空题（本题共4题，共20分）（2019-2019年大同中学高三（文）上11月13）已知向量()3-,2=a ρ，()1-,x b =ρ，若()b a a ρρρ-⊥，则=x . （2019-2019年大同中学高三（文）上11月14）已知4=a ρ，8=b ρ，a ρ与b ρ的夹角是︒120，则b ρ在a ρ方向上的投影为 .（2019-2019年大同中学高三（文）上11月15）已知函数()13++=x ax x f 的图像在点()()1,1f 处的切线过点()7,2，则=a .（2019-2019年大同中学高三（文）上11月16）关于函数()x x x x f 2cos 2cos sin 21-+=有下列命题:①函数()x f y =的最小正周期为π; ②直线4π=x 是()x f y =的一条对称轴; ③点⎪⎭⎫ ⎝⎛08，π是()x f y =的图象的一个对称中心; ④将()x f y =的图象向左平移4π个单位,可得到x y 2sin 2=的图象. 其中真命题的序号是 .(把你认为真命题的序号都写上)三、解答题（本题共6小题，共70分）（2019-2019年大同中学高三（文）上11月17）已知c b a ,,分别为内角C B A ,,的对边，C A B sin sin 2sin =。

福州市一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 已知全集I={1，2，3，4，5，6}，A={1，2，3，4}，B={3，4，5，6}，那么∁I （A ∩B ）等于（ ）A ．{3，4}B ．{1，2，5，6}C ．{1，2，3，4，5，6}D ．∅2． “”是“圆关于直线成轴对称图形”的（ ）3<-b a 056222=++-+a y x y x b x y 2+=A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件 D ．既不充分也不必要条件【命题意图】本题考查圆的一般方程、圆的几何性质、常用逻辑等知识，有一定的综合性，突出化归能力的考查，属于中等难度．3． ∃x ∈R ，x 2﹣2x+3＞0的否定是（ ）A ．不存在x ∈R ，使∃x 2﹣2x+3≥0B ．∃x ∈R ，x 2﹣2x+3≤0C ．∀x ∈R ，x 2﹣2x+3≤0D ．∀x ∈R ，x 2﹣2x+3＞04． 复数（为虚数单位），则的共轭复数为（ ）2(2)i z i-=i z A ． B ． C ． D ．43i -+43i +34i +34i-【命题意图】本题考查复数的运算和复数的概念等基础知识，意在考查基本运算能力．5． 定义在（0，+∞）上的函数f （x ）满足：＜0，且f （2）=4，则不等式f （x ）﹣＞0的解集为（ ）A ．（2，+∞）B ．（0，2）C ．（0，4）D ．（4，+∞）6． 直径为6的球的表面积和体积分别是（ ）A ．B ．C ．D ．144,144ππ144,36ππ36,144ππ36,36ππ7． 设函数f （x ）在R 上的导函数为f ′（x ），且2f （x ）+xf ′（x ）＞x 2，下面的不等式在R 内恒成立的是（）A ．f （x ）＞0B ．f （x ）＜0C ．f （x ）＞xD ．f （x ）＜x8． 若集合A={x|﹣2＜x ＜1}，B={x|0＜x ＜2}，则集合A ∩B=（）A ．{x|﹣1＜x ＜1}B ．{x|﹣2＜x ＜1}C ．{x|﹣2＜x ＜2}D ．{x|0＜x ＜1}9． 已知命题且是单调增函数；命题，.:()(0xp f x a a =>1)a ≠5:(,)44q x ππ∀∈sin cos x x >则下列命题为真命题的是（ ）A ．B ． C. D ．p q ∧p q ∨⌝p q ⌝∧⌝p q⌝∧10．矩形ABCD 中，AD=mAB ，E 为BC 的中点，若，则m=（）A ．B ．C ．2D ．311．将n 2个正整数1、2、3、…、n 2（n ≥2）任意排成n 行n 列的数表．对于某一个数表，计算某行或某列中的任意两个数a 、b （a ＞b ）的比值，称这些比值中的最小值为这个数表的“特征值”．当n=2时，数表的所有可能的“特征值”的最大值为（）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A ．B ．C ．2D ．312．已知函数f （x ）=lnx+2x ﹣6，则它的零点所在的区间为（ ）A ．（0，1）B ．（1，2）C ．（2，3）D ．（3，4）二、填空题13．在矩形ABCD 中，=（1，﹣3），，则实数k= ．14．已知A （1，0），P ，Q 是单位圆上的两动点且满足，则+的最大值为 ．15．已知球与棱长均为3的三棱锥各条棱都相切，则该球的表面积为 ．　16．函数()x f x xe =在点()()1,1f 处的切线的斜率是.17．△ABC 中，，BC=3，，则∠C=　　．18．下列命题：①函数y=sinx 和y=tanx 在第一象限都是增函数；②若函数f （x ）在[a ，b]上满足f （a ）f （b ）＜0，函数f （x ）在（a ，b ）上至少有一个零点；③数列{a n }为等差数列，设数列{a n }的前n 项和为S n ，S 10＞0，S 11＜0，S n 最大值为S 5；④在△ABC 中，A ＞B 的充要条件是cos2A ＜cos2B ；⑤在线性回归分析中，线性相关系数越大，说明两个量线性相关性就越强．其中正确命题的序号是 （把所有正确命题的序号都写上）． 三、解答题19．一块边长为10cm 的正方形铁片按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器，试建立容器的容积V 与x 的函数关系式，并求出函数的定义域．20．定义在R 上的增函数y=f （x ）对任意x ，y ∈R 都有f （x+y ）=f （x ）+f （y ），则（1）求f （0）；（2）证明：f （x ）为奇函数；（3）若f （k •3x ）+f （3x ﹣9x ﹣2）＜0对任意x ∈R 恒成立，求实数k 的取值范围．　21．（本小题满分12分）已知向量，，(cos sin ,sin )m x m x x w w w =-a (cos sin ,2cos )x x n x w w w =--b 设函数的图象关于点对称，且．()()2n f x x R =×+Îa b (,1)12p(1,2)w Î（I ）若，求函数的最小值；1m =)(x f （II ）若对一切实数恒成立，求的单调递增区间．()()4f x f p£)(x f y 【命题意图】本题考查三角恒等变形、三角形函数的图象和性质等基础知识，意在考查数形结合思想和基本运算能力．22．(本小题满分10分）选修4­4：坐标系与参数方程．在直角坐标系中，曲线C 1：（α为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐{x ＝1＋3cos αy ＝2＋3sin α)标系，C 2的极坐标方程为ρ＝.2sin （θ＋π4）（1）求C 1，C 2的普通方程；（2）若直线C 3的极坐标方程为θ＝（ρ∈R ），设C 3与C 1交于点M ，N ，P 是C 2上一点，求△PMN 的面3π4积．23．2016年1月1日起全国统一实施全面两孩政策．为了解适龄民众对放开生育二胎政策的态度，某市选取70后和80后作为调查对象，随机调查了100位，得到数据如表：生二胎不生二胎合计70后30154580后451055合计7525100（Ⅰ）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若从该市70后公民中随机抽取3位，记其中生二胎的人数为X ，求随机变量X 的分布列和数学期望；（Ⅱ）根据调查数据，是否有90%以上的把握认为“生二胎与年龄有关”，并说明理由．参考数据：P （K 2＞k ）0.150.100.050.0250.0100.005k 2.0722.7063.8415.0246.6357.879（参考公式：，其中n=a+b+c+d ）24．已知定义在的一次函数为单调增函数，且值域为．[]3,2-()f x []2,7（1）求的解析式；()f x （2）求函数的解析式并确定其定义域．[()]f f x福州市一中2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案B CABDADDA题号1112答案BC 二、填空题13．　4　．14． ．15．　3π　． 16．2e 17．　18．　②③④⑤　三、解答题19． 20． 21．22．23．24．（1），；（2），.()5f x x =+[]3,2x ∈-[]()10f f x x =+{}3x ∈-。