一个屈曲分析实例
- 格式:pdf
- 大小:551.15 KB
- 文档页数:10

实用标准文档整个计算过程包括 2 个分析步,第 1 步做屈曲分析,第 1 步:屈曲分析载荷步定义如下:Step 1-InitialStep 2- Buckle2 步做极限强度分析0奪莖UWICWHIK . 叽I J I*' *iirl |U*ii:* ri«-2- c.仲[U**t Wfl| «R =・|0T* |«|M4 11 屮W Ml 町扌垮・3 4M4; *E>|轴亠白*wr»44* «*M *A*S MMM-in 4414-* Ita1! I >H*d *■.■ Lrfi|i-t*b*i UWi^ *4」>jU***^ ::切2冲<a:K-.L口sMwSniLpc^l Efl «o 誓光n-3 wa HF HB・・n c:^ > q士* f *B£ -A <MI '■■*W■uTp*』«MLrii4 *M;■pofit ■直j.i t…叫町■ ' H.,机...i . r |fl»-L , | |-£I -t fr E叶*盅1并在Model-Edit Keywords 的图中位置加入下面的文字,输出屈曲模态*nodefile, global=yesU,Create job 名称为“ Buckling点击continue ,完成第 1 步的计算第 2 步:极限强度分析将“ buckle ”分析步替换为“ riks ”分析步在Basic 选项卡中,Nlgeom:选择打开在Instrumentation 选项卡中,定义如下参数,然后点击OK Array定义一个新计算工作,输入名称,点击continue在Parallelization 选项卡,选择 2 个CPU,如下所示,点击OK。
在此编辑Model-edit keywords ,删除“第 1 步”加入的文字“ *nodefile, global=yesU,”,并在下图位置加入下段文字:*imperfection, file=buckling, step=1 1, 2.5点击OK,再保存文件最后提交计算。


![5.2.3 基于初始缺陷的非线性屈曲分析实例[共4页]](https://img.taocdn.com/s1/m/25904328f705cc175427091d.png)
第5章 非线性静力学分析
– 352 –
图5-2-15 屈曲载荷因子
5.2.3 基于初始缺陷的非线性屈曲分析实例
非线性屈曲不仅包括材料非线性、几何非线性和状态非线性,而且还包括初始缺陷和微小扰动,能够比线性特征值屈曲得到更精确的屈曲载荷。
上例蜂窝结构经过线性特征值屈曲发现载荷因子密集分布,这表示该模型对缺陷非常敏感,后续必须进行带缺陷的非线性屈曲分析。
利用上例屈曲模态得出初始缺陷,观察前6阶模态,仅有第5阶模态为结构整体屈曲变形,其余均为局部变形,如图5-2-16所示,所以选择第5阶屈曲模态形状作为初始缺陷的依据。
初始缺陷与屈曲模态形状之比一般根据模型厚度与第一阶屈曲模态振幅比和加工公差决定。
例如,本蜂窝结构中第1阶模态振幅约为0.29mm ,厚度为0.05mm ,两者之比为0.05/0.29≈0.17;另六边形的每个边长尺寸公差为0.5mm ,0.5/8.7(六边形边长)≈0.0575;综合初始缺陷与屈曲模态形状之比取0.05。
1.建立分析流程
如图5-2-17所示,建立非线性屈曲分析流程。
在前面线性屈曲分析之后再依次建立Mechanical APDL 模块、Finite Element Modeler 模块和Static Structural 模块,其中将Linear Buckling 中的Solution 与Mechanical APDL 中的Analysis 建立关联,Mechanical APDL 中的。
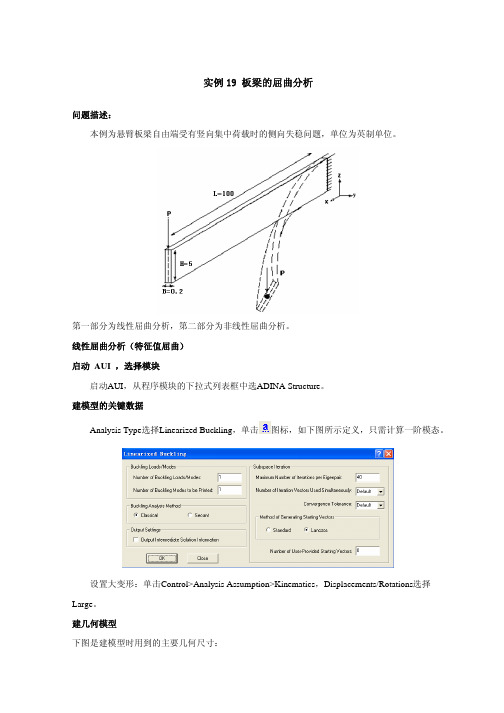
实例19 板梁的屈曲分析问题描述:本例为悬臂板梁自由端受有竖向集中荷载时的侧向失稳问题,单位为英制单位。
第一部分为线性屈曲分析,第二部分为非线性屈曲分析。
线性屈曲分析(特征值屈曲)启动 AUI ,选择模块启动AUI,从程序模块的下拉式列表框中选ADINA Structure。
建模型的关键数据Analysis Type选择Linearized Buckling,单击图标,如下图所示定义,只需计算一阶模态。
设置大变形:单击Control>Analysis Assumption>Kinematics,Displacements/Rotations选择Large。
建几何模型下图是建模型时用到的主要几何尺寸:定义点:单击Define Points图标,并把以下信息输入到表中,然后单击OK。
Point # X1 X2 X3 System...1 0.0 0.0 -2.5 02 100.0 0.0 -2.53 100.0 0.0 2.5 04 0.0 0.0 2.5 0定义面:单击Define Surfaces图标,定义以下面后,单击OK。
定义并施加约束单击Apply Fixity 图标,把Apply Fixity 对话框中的“Apply to”域设置成Lines。
在表的第一行输入2,单击OK。
定义并施加荷载Model>Loading>Apply on Nodes/Elements,把Load Type设置成Force/Moment。
如下图所示定义,施加在Node12上,荷载类型为Z-Force,Weight=-0.001,负号荷载方向表示为Z轴负向,单击OK关闭对话框。
注意:所施加的荷载值要小于临界荷载,所以根据经验,这个值一般取得非常小。
定义材料单击OK关闭对话框。
再单击Close关闭Manage Material Definitions对话框。
定义单元单元组:用壳单元模拟板梁,单击Define Element Groups图标,增加group number 1, 把Type设置为shell,厚度设为0.2,单击OK。

整个计算过程包括2个分析步,第1步做屈曲分析,第2步做极限强度分析。
第1步:屈曲分析载荷步定义如下:Step 1-InitialStep 2- Buckle并在Model-Edit Keywords的图中位置加入下面的文字,输出屈曲模态*nodefile, global=yesU,Create job 名称为“Buckling”点击continue,完成第1步的计算。
第2步:极限强度分析将“buckle”分析步替换为“riks”分析步在Basic选项卡中,Nlgeom:选择打开在Instrumentation选项卡中,定义如下参数,然后点击OK定义一个新计算工作,输入名称,点击continue在Parallelization选项卡,选择2个CPU,如下所示,点击OK。
在此编辑Model-edit keywords,删除“第1步”加入的文字“*nodefile, global=yesU,”,并在下图位置加入下段文字:*imperfection, file=buckling, step=11, 2.5点击OK,再保存文件。
最后提交计算。
提取计算结果进入visualization Module点击 Create XY data选择 ODB filed output,点击continuePosition选择 Unique Nodal, CF:point loads选择 CF2,再点击elements/nodes选项卡,选择跨中载荷加载点,最后点击save。
重复上一步操作,Position选择 Unique Nodal, U:spatial displacement 选择 U3,再点击elements/nodes选项卡,选择板格中心点,最后点击save。
点击Create XY data, 选择operate on XY data,点击continue选择Combine(X,X)命令,横坐标选择保存的displacement曲线,纵坐标选择保存的Point load曲线,点击最后一行Create XY Data与Save as。
第21例非线性屈曲分析实例—悬臂梁本例通过计算悬臂梁的临界载荷,介绍了利用ANSYS进行非线性屈曲分析的方法、步骤和过程。
21.1非线性屈曲分析过程1.建立模型非线性屈曲分析的建模过程与其他分析相似,包括选择单元类型、定义单元实常数、定义材料特性、定义横截面、建立几何模型和划分网格等。
2.求解(1)进入求解器。
(2)指定分析类型。
非线性屈曲分析属于非线性静力学分析。
(3)定义分析选项。
激活大变形效应。
(4)施加初始几何缺陷或初始扰动。
可以先进行线性屈曲分析,将分析所得到的屈曲模态形状乘以一个较小的系数后作为初始扰动施加到结构上,本例即采用该方法。
(5)施加载荷。
所施加的载荷应比预测值高10%一21%。
(6)定义载荷步选项。
(7)设置弧长法。
(8)求解。
3.查看结果在POST26时间历程后处理器中,建立载荷和位移关系曲线,从而确定结构的临界载荷。
21.2问题描述及解析解图21-1 (a)所示为一悬臂梁,图21-1 (b)为梁的横横截面形状,分析其在集中力P作用下的临界载荷。
已知截面各尺寸分别为H=50mm、h=43mm、B=35mm、b=32mm,梁的长度L=1m。
钢的弹性模量E=2xl011N/m2,泊松比p=0.3。
图21-1工子悬臂梁21.3分析步骤21.3.1改变任务名拾取菜单Utility Menu→Jobname,弹出如图21-2所示的对话框,在“[/FJLNAM]”文本框中输入EXAMPLE21,单击“OK”按钮。
21.3.2选择单元类型拾取菜单Main Menu→Preprocessor→Element Type→Add/Edit/Delete,弹出如图21-3所示的对话框,单击“Add.”按钮,弹出如图21-4所示的对话框,在左侧列表中选“Structural Beam”,在右侧列表中选“3 node 189”,单击“OK”按钮,返回到如图21-3所示的对话框,单击“Close”按钮。
整个计算过程包括2个分析步,第1步做屈曲分析,第2步做极限强度分析。
第1步:屈曲分析载荷步定义如下:Step 1-InitialStep 2- Buckle并在Model-Edit Keywords的图中位置加入下面的文字,输出屈曲模态*nodefile, global=yesU,Create job 名称为“Buckling”点击continue,完成第1步的计算。
第2步:极限强度分析将“buckle”分析步替换为“riks”分析步在Basic选项卡中,Nlgeom:选择打开在Instrumentation选项卡中,定义如下参数,然后点击OK定义一个新计算工作,输入名称,点击continue在Parallelization选项卡,选择2个CPU,如下所示,点击OK。
在此编辑Model-edit keywords,删除“第1步”加入的文字“*nodefile, global=yesU,”,并在下图位置加入下段文字:*imperfection, file=buckling, step=11,点击OK,再保存文件。
最后提交计算。
提取计算结果进入visualization Module 点击 Create XY data选择 ODB filed output,点击continuePosition选择 Unique Nodal, CF:point loads选择 CF2,再点击elements/nodes选项卡,选择跨中载荷加载点,最后点击save。
重复上一步操作,Position选择 Unique Nodal, U:spatial displacement 选择 U3,再点击elements/nodes选项卡,选择板格中心点,最后点击save。
点击Create XY data, 选择operate on XY data,点击continue选择Combine(X,X)命令,横坐标选择保存的displacement曲线,纵坐标选择保存的Point load曲线,点击最后一行Create XY Data与Save as。
板的屈曲分析为证明ansys 程序计算的有效性,特分析了两个个有代表性的算例。
算例1四边简支的矩形板,边长a =600mm ,b =600mm ,t =10mm ,E =206000 N/m m 2 ν=0.3,两对边受到均匀分布的压力。
图1.1 薄板有限元模型约束图根据简支模型和及均布压力屈曲模式建立板模型,下面是对模型的说明。
(1) 单元:采用三维壳体单元shell63。
(2) 单元划分情况:沿长度a 方向为100份,沿宽度b 方向为100份。
(3) 约束情况:四边为简支。
(4) 加载情况:两对边受单位均布压力XY Z图1.2加载图最终利用ansys 计算出的临界屈曲应力为196.67Mpa 。
根据板的稳定理论可知:在a/b ≤ 2的情况下F =π2D b 2 b a +a b2D =Et 312 1−ν2根据计算得到σ =206.66Mpa Ansys 计算结果的相对误差为4.8%图1.3 应力云图算例2XYZSEP 3 2012MNMXXY ZSEP 4 2012三边简支的矩形板,边长a =600mm ,b =600mm ,t =10mm ,E =206000 N/m m 2 ν=0.25,两对边受到单位均匀分布的压力。
图1.4单元剖分与约束图根据简支模型和及均布压力屈曲模式建立板模型,下面是对模型的说明。
(1) 单元:采用三维壳体单元shell63。
(2) 单元划分情况:沿长度a 方向为100份,沿宽度b 方向为100份。
(3) 约束情况:三边为简支。
(4) 加载情况:两对边受单位均布压力图1.5加载图XYZXYZSEP 3 2012最终利用ansys 计算出的临界屈曲应力为72.42Mpa 。
根据板的稳定理论可知:F =k π2D b 2D =Et 312 1−ν2当a/b =1时,k=1.44 根据计算得到σ = 74.4 Mpa Ansys 计算结果的相对误差为3.9%图1.6 应力云图加筋板算例1四边简支的矩形板,边长a =3000mm ,b =1500mm ,t =10mm ,E =206000 N/m m 2ν=0.3,两对边受到均匀分布的压力,中间加一道纵向扁钢。
一个屈曲分析实例
一、问题和条件:
钢闸门断面为工字钢,具体尺寸如下,试作屈曲分析:
弹性模量E=200GPa
泊松比μ=0.3
集中力F=1N(单位力)
二、进入ANSYS界面
单击开始→程序→ansys10.0→configure ANSYS product
然后在File Management中定义Working Directory(工作路径)如:class 定义Job Name(工作文件名)。
如:file。
如图所示。
然后,点击run。
三、定义单元及材料
1新建单元类型
运行主菜单Preprocessor→Element Type→Add/Edit/Delete(新建/编辑/删除单元类型)命令,接着在对话框中单击“Add”按钮新建单元类型。
2定义单元类型
因为beam188单元适合于分析柔性梁结构,支持弹性,蠕变和塑性模型的计算。
先选择单元为beam,接着选择3D2node188,然后单击“OK”按钮确定,完成单元类型的选择。
3关闭单元类型对话框
回到单元类型对话框,已经新建了beam单元,单击对话框中“Close”按钮关闭对话框。
4定义截面形状及参数
运行主菜单Preprocessor→Sections→Beam→Common sections命令,接着在对话框中sub-type中选择“工”字钢断面,在下面的尺寸中分别填入:W1=0.2,W2=0.2,W3=0.4,t1=0.01,t2=0.01,t3=0.01,点击OK结束。
5设置材料属性
运行主菜单Preprocessor→Material props→Material Models(材料属性)命令。
选择材料属性命令后,系统会显示材料属性设置对话框。
6设置杨氏弹性模量与泊松比
在材料属性设置对话框右侧依次选择Structural→Linear→Elastic
→Isotropic。
完成选择命令后,接着在对话框中EX杨氏弹性模量输入2e11,PPXY泊松
比输入0.3。
在输入数值后,单击“OK”按钮完成。
7关闭材料属性对话框
完成材料属性的设置后,可在对话框右上方单击,关闭材料属性设置。
四、建立框架几何图形
改变坐标系为球坐标系,在应用菜单中选择WorkPlane→Change active CS to→global spherical(球坐标系),此时状态栏中的csys的值由0变为2。
1生成关键点
运行主菜单Preprocessor→Modeling→Create→keypoints→In Active CS生成节点于目前坐标系统命令。
接着在keypoint number输入1,接着依照顺序输入第一点XYZ的坐标值为0,0,0,完成输入后单击“Apply”按钮生成第一点。
如上同理依次输入
210,90,100单击“Apply”按钮继续生成第二点。
310,90,116单击OK,在右侧工具栏中点击right view按钮,观看右视图。
2生成线
运行主菜单Preprocessor→Modeling→Create→Lines→Lines→Straight line,在图中分别拾取1、2两点和1、3两点,单击OK。
生成线L1和L2。
3剖分线
运行主菜单Preprocessor→Meshing→Size Cntrls→ManualSize→Lines→All Lines,弹出element sizes on all selected lines对话框,在NDIV框中输入5,点击ok,即将线L1和L2都分成5份。
运行主菜单Preprocessor→Meshing→MeshTool,在弹出的对话框中点击Mesh,拾取L1和L2,再单击OK即可。
4生成单元
在应用菜单中选择plot→nodes,画出结点;再给节点编号,在应用菜单中选择PlotCtrls→Numbering,在弹出的对话框中点击NODE后面的复选框为on,单击OK。
直接通过节点生成单元,Preprocessor→Modeling→Create→Elements →Auto Numbered→Thru Nodes,拾取6、7号节点,单击Apply,继续分别拾取6、11;5、11;5、10;4、10;4、9;3、8单击OK。
在应用菜单中选择Plot→Elements,画出单元。
为了看清楚单元的截面特性,可以在应用菜单中选择PlotCtrls→Style→Size and Shape,在弹出的对话框中点击[/ESHAPE]后面的复选框为on;再将其点击为off,
就不在显示梁单元的截面了。
五、施加荷载
1约束设置
运行主菜单Solution→Define Loads→Apply→Structural→Displacement→On Nodes施加位移在节点上命令。
接着选择节点1,完成选择后按单击对话框中的“OK”按钮。
然后选择All DOF(全部自由度)。
在Displacement value输入数值0,完成输入后选择“OK”按钮。
完成定义约束后,系统会显示定义后的图形。
2施加单位集中力
由于支臂上的力是沿支臂轴向的,因此需要分别在加力的两点建立局部坐标系,这样避免了将荷载分解的复杂性从而便于加载。
应用菜单中选择Workplane→Local Coordinate Systems→Create Local CS →By3nodes;拾取2、6、7号节点,单击对话框的OK。
激活局部坐标系,应用菜单中选择Workplane→Change Active CS to→Specified Coord sys,弹出的对话框中coordinate system number为11,单击OK。
运行主菜单Preprocessor→Modeling→Move/Modify→Rotate Node CS→to Active CS,拾取2号节点,将节点坐标系转到当前激活的局部坐标系上。
运行主菜单Solution→Define Loads→Apply→Structural→Force/Moment→On Nodes施加力在节点上命令。
接着选择节点2,完成选择后按单击对话框中的“OK”按钮。
然后选择Fx方向的集中力。
在Force/Moment value输入数值1,完成输入后选择“OK”按钮。
完成施加集中力后,系统会显示施加后的图形。
同理,应用菜单中选择Workplane→Local Coordinate Systems→Create Local CS→By3nodes;拾取7、11、6号节点,单击对话框的OK,剩下的操作同上。
六、求解分析
先进行静力分析,运行主菜单Solution→Analysis Type→New Analysis,在对话框中选择Static,单击OK。
运行主菜单Solution→Solve→Current LS分析目前的荷载步骤命令。
接着单击“OK”按钮开始运行分析,分析完毕后,在信息窗口中提示计算完成。
单击“Close”按钮将其关闭,统计窗口可单击上方按钮将其关闭。
在静力分析的基础上进行屈曲分析,运行主菜单Solution→Analysis Type →New Analysis,在对话框中选择Eigen Buckling,单击OK。
运行主菜单Solution →Analysis Type→Analysis Options,在弹出的对话框中Method后的单选框选择Block Lanczos作为模态提取方法,在Nmode中输入1,设置提取1阶模态。
再次运行主菜单Solution→Solve→Current LS进行求解,单击“Close”按钮将其关闭。
七、结果
1显示变形图
改变坐标系为笛卡儿坐标系,在Workplane→Change Active CS to→Global Cartesian,此时状态栏中的csys的值由11变为0。
读结果,运行主菜单General Postproc→Read Results→Last set。
运行主菜单General Postproc→Plot Result→Deformed Shape变形图命令。
弹出Plot Deformed Shape对话框,选择显示Def+undeformed变形与未变形图,然后单击“OK”按钮。
完成后,系统会显示闸门未受集中力与受集中力后的变形显示图形。
运行主菜单General Postproc→Plot Result→Nodal Solution;选择DOF Solution/Translation UX。
可以看出支臂发生了屈曲,最大变形处为2号节点处。
2提取屈曲特征值
运行主菜单General Postproc →Results Summary;在弹出的文本文件中,TIME/FREQ 下面的数字即为屈曲特征值,本例中屈曲特征值为67508N。