数字信号处理-时域离散随机信号处理(丁玉美)第二章习题答案

2－1 试求如下序列的傅里叶变换： （1）)()(01n n n x -=δ （2）)1(21)()1(21)(2--++=n n n n x δδδ （3）),2()(3+=n u a n x n10<<a（4）)4()3()(4--+=n u n u n x（5）∑∞=-⎪⎭⎫⎝⎛=05)3(41)(k nk n n x δ（6）()6cos ,14()0,n n x n π⎧-≤≤=⎨⎩其他解： （1） 010()()j n j j nn X e n n ee ωωωδ∞--=-∞=-=∑（2） 2211()()122j j nj j n X e x n e e e ωωωω∞--=-∞==+-∑ωsin 1j +=（3） 2232()(2)1j j nj nn j nj n n a e X e a u n ea eaeωωωωω-∞∞---=-∞=-=+==-∑∑， 10<<a（4） []4()(3)(4)j j nn X e u n u n eωω∞-=-∞=+--∑∑-=-=33n nj e ω∑∑==-+=313n n j n nj e eωω（等比数列求解）ωωωωωj j j j j e e e e e --+--=--111134=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=----ωωωωω21sin 27sin 1137j j j e ee ((1-e^a)提出e^(0.5a))（5） 3350011()(3)44nkj jn j k n k k X e n k e e ωωωδ∞∞+∞--=-∞==⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∞+=--⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛=033411141k j kj e e ωω（6） 44336441()cos 32j j j jn jn n n X e nee e e ππωωωπ---=-=-⎛⎫==+ ⎪⎝⎭∑∑994()()4()()3333001122j j n j j n n n e e e e ππππωωωω--++===+∑∑ ()9()9334()4()33()()3311112211j j j j j j e e e e e e ππωωππωωππωω-+-+-+⎡⎤⎡⎤--⎢⎥⎢⎥=+⎢⎥⎢⎥++⎢⎥⎢⎥⎣⎦⎣⎦2－2 设信号}1,2,3,2,1{)(---=n x ，它的傅里叶变换为)(ωj e X ，试计算(1)0()j X e （２）()j X ed πωπω-⎰（３）2()j X e d πωπω-⎰。

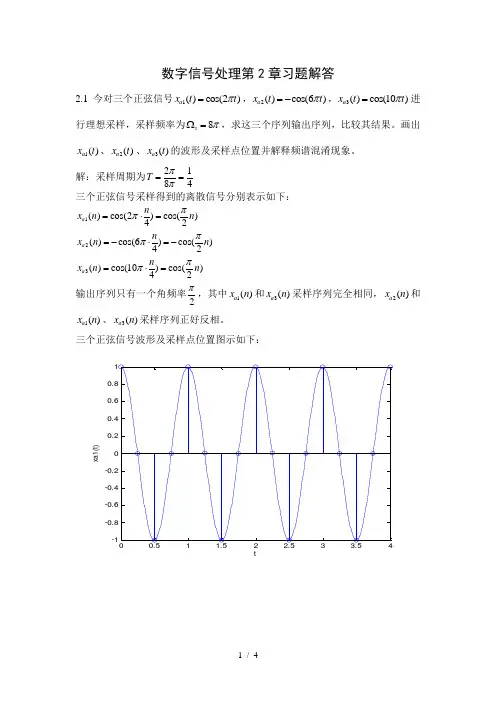
数字信号处理第2章习题解答2.1 今对三个正弦信号1()cos(2)a x t t π=，2()cos(6)a x t t π=-，3()cos(10)a x t t π=进行理想采样，采样频率为8s πΩ=，求这三个序列输出序列，比较其结果。

画出1()a x t 、2()a x t 、3()a x t 的波形及采样点位置并解释频谱混淆现象。

解：采样周期为2184T ππ== 三个正弦信号采样得到的离散信号分别表示如下：1()cos(2)cos()42a n x n n ππ=⋅=2()cos(6)cos()42a n x n n ππ=-⋅=-3()cos(10)cos()42a n x n n ππ=⋅=输出序列只有一个角频率2π，其中1()a x n 和3()a x n 采样序列完全相同，2()a x n 和1()a x n 、3()a x n 采样序列正好反相。

三个正弦信号波形及采样点位置图示如下：tx a 1(t )tx a 2(t )tx a 3(t )三个正弦信号的频率分别为1Hz 、3Hz 和5Hz ，而采样频率为4Hz ，采样频率大于第一个正弦信号频率的两倍，但是小于后两个正弦信号频率的两倍，因而由第一个信号的采样能够正确恢复模拟信号，而后两个信号的采样不能准确原始的模拟信号，产生频谱混叠现象。

2.3 给定一连续带限信号()a x t 其频谱当f B >时，()a X f 。

求以下信号的最低采样频率。

（1）2()a x t （2）(2)a x t （3）()cos(7)a x t Bt π 解：设()a x t 的傅里叶变换为()a X j Ω（1）2()a x t 的傅里叶变换为22()[()]Ba a BX j X j d ππωωω-⋅Ω-⎰因为22,22B B B B πωππωπ-≤≤-≤Ω-≤ 所以44B B ππ-≤Ω≤即2()a x t 带限于2B ，最低采样频率为4B 。

第一章习题解答2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值； （2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解： （1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（5）2()()y n x n =； （6）y (n )=x (n 2)解：（5） 2()()y n x n = 令：输入为0()x n n -，输出为'20()()y n x n n =-，因为2'00()()()y n n x n n y n -=-=故系统是时不变系统。

又因为21212122212[()()](()()) [()][()] ()()T ax n bx n ax n bx n aT x n bT x n ax n bx n +=+≠+=+因此系统是非线性系统。

（6） y (n )=x (n 2) 令输入为x (n －n 0) 输出为y ′(n )=x ((n －n 0)2)y (n －n 0)=x ((n －n 0)2)=y ′(n)故系统是非时变系统。