数字信号处理习题与解答

数字信号处理习题及答案数字信号处理作业(1)1、画出离散信号的波形（1）)2(3)3(2)(1++-=n n n x δδ（2）)2()(2+-=n u n x（3）)5()()(3--=n u n u n x（4）)()()(214n u n x n ?= （5）)()25.0sin(3)(5n u n n x ??=π2、设x (n )、y (n )分别为系统的输⼊、输出变量，根据定义确定系统是否为：（1）线性，（2）稳定，（2）因果① )()]([ )(2n ax n x T n y == ② b n x n x T n y +==)()]([ )( ③ )0( )()]([ )(00>-==n n n x n x T n y④ ∑+-=>=0)0( )( )(0n n n n m n m x n y3、已知:描述系统的差分⽅程为)()1(5- )(n x n y n y =-且初始条件为： 0)1(=-y 求：系统的单位冲激响应h (n )4、已知：线性时不变系统的单位脉冲响应为10 , )( )(<求：该系统的单位阶跃响应。

数字信号处理作业(1)解答1、画出离散信号的波形（1）)2(3)3(2)(1++-=n n n x δδ（2）)2()(2+-=n u n x（3）)5()()(3--=n u n u n x（4）)()()(214n u n x n ?= （5）)()25.0sin(3)(5n u n n x ??=π2、设x (n )、y (n )分别为系统的输⼊、输出变量，根据定义确定系统是否为：（1）线性，（2）稳定，（3）因果因果：输出只取决于当前和之前的输⼊。

线性移不变系统的因果的充要条件：h (n )＝0 ， n < 0稳定系统：有界输⼊产⽣有界输出。

线性移不变系统稳定的充要条件：∞<=∑∞-∞=n n n x n x T n y （线性，稳定，因果）④ )0( )( )(0>=∑+-=n m x n y n n n n m （线性，稳定，⾮因果）注意：⾮线性系统的稳定、因果只能按定义判断，不能按线性、移不变系统的h (n )特点判断。

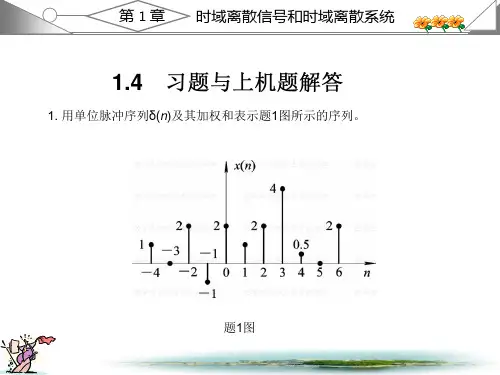
目录习题一 (3)习题二 (26)习题三 (40)习题四 (61)习题五 (83)习题一1.1序列)(n x 如图T1.1所示，用延迟的单位采样序列加权和表示出这个序列。

图 T1.1 习题1.1图【解答】 任一数字序列都可表达为)()()(k n k x n x k -=∑∞-∞=δ所以图T1-1信号可表达为)3(2)1(3)()3(2)(-+-+-+-=n n n n n x δδδδ1.2 分别绘出以下各序列的图形： （1）)(2)(1n u n x n =（2）)(21)(2n u n x n⎪⎭⎫⎝⎛=（3）()3()2()nx n u n =-（4）)(21)(4n u n x n⎪⎭⎫⎝⎛-=【解答】 用MATLAB 得到的各序列图形如图T1.2所示。

图T1.2习题1.2解答1.3 判断下列每个序列是否是周期性的；若是周期性的，试确定其周期。

（1）⎪⎭⎫ ⎝⎛-=873cos )(ππn A n x（2）⎪⎭⎫⎝⎛=n A n x 313sin )(π（3）⎪⎭⎫⎝⎛-=n j e n x 6)(π（4）{}{}/12/18()Re Im jn jn x n e e ππ=+（5）16()cos(/17)jnx n e n ππ=【解答】（1）因为730πω=，而31473220==ππωπ，这是一有理数。

所以)(n x 是周期的，周期为14。

（2）因为3130πω=，而136313220==ππωπ，也为有理数。

所以)(n x 是周期的，周期为6。

（3）注意此序列的10=ω，πωπ220=，是无理数，所以)(n x 是非周期的。

（4）实际上()cos(/12)sin(/18)x n n n ππ=+因此)(n x 有两个频率分量，即1201πω=，1802πω=，而 24122201==ππωπ；02223618πππω==都是有理数，所以)(n x 是两个周期信号之和，第一个周期信号的周期241=N ，第二个周期信号的周期362=N ，因此)(n x 的周期是这两个周期的最小公倍数，即72123624)36,24gcd(3624),gcd(2121=⋅=⋅=⋅=N N N N N（5）()x n 是两个周期序列的乘积，其中132N =，234N =，所以该序列的周期是121232343234544gcd(,)gcd(32,34)2N N N N N ⋅⋅⋅====1.4 已知序列)]6()()[6()(---=n u n u n n x ，画出下面序列的示意图。

==============================绪论==============================1。

A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1。

①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用（n ） 表示y （n )=｛2，7,19，28,29，15｝2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的； 若是周期的， 确定其周期。

（1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2）)81(j e )(π-=n n x 解: （1） 因为ω=73π， 所以314π2=ω， 这是有理数， 因此是周期序列， 周期T =14。

（2） 因为ω=81, 所以ωπ2=16π， 这是无理数, 因此是非周期序列。

③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。

3.加法 乘法序列｛2，3，2，1}与序列｛2，3，5，2，1}相加为__｛4，6，7,3，1}__，相乘为___｛4，9，10，2｝ 。

移位翻转：①已知x(n)波形，画出x(—n ）的波形图。

②尺度变换:已知x(n)波形，画出x （2n ）及x(n/2）波形图.卷积和:①h(n)*求x(n)，其他2n 0n 3，h(n)其他3n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=}23,4,7,4，23{0,h(n)*答案：x(n)=②已知x (n )=｛1,2，4,3},h （n ）={2，3，5}， 求y （n ）=x （n ）＊h （n ）x (m ）={1，2，4,3},h （m ）=｛2,3,5｝，则h (—m ）={5，3,2｝(Step1：翻转)解得y （n )=｛2，7，19,28,29，15}③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案：x(n)=4. 如果输入信号为,求下述系统的输出信号。

数字信号处理试题及答案一、选择题1. 数字信号处理中的离散傅里叶变换（DFT）是傅里叶变换的______。

A. 连续形式B. 离散形式C. 快速算法D. 近似计算答案：B2. 在数字信号处理中，若信号是周期的，则其傅里叶变换是______。

A. 周期的B. 非周期的C. 连续的D. 离散的答案：A二、填空题1. 数字信号处理中，______是将模拟信号转换为数字信号的过程。

答案：采样2. 快速傅里叶变换（FFT）是一种高效的______算法。

答案：DFT三、简答题1. 简述数字滤波器的基本原理。

答案：数字滤波器的基本原理是根据信号的频率特性，通过数学运算对信号进行滤波处理。

它通常包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器等类型，用于选择性地保留或抑制信号中的某些频率成分。

2. 解释什么是窗函数，并说明其在信号处理中的作用。

答案：窗函数是一种数学函数，用于对信号进行加权，以减少信号在离散化过程中的不连续性带来的影响。

在信号处理中，窗函数用于平滑信号的开始和结束部分，减少频谱泄露效应，提高频谱分析的准确性。

四、计算题1. 给定一个信号 x[n] = {1, 2, 3, 4}，计算其 DFT X[k]。

答案：首先，根据 DFT 的定义，计算 X[k] 的每个分量：X[0] = 1 + 2 + 3 + 4 = 10X[1] = 1 - 2 + 3 - 4 = -2X[2] = 1 + 2 - 3 - 4 = -4X[3] = 1 - 2 - 3 + 4 = 0因此，X[k] = {10, -2, -4, 0}。

2. 已知一个低通滤波器的截止频率为0.3π rad/sample，设计一个简单的理想低通滤波器。

答案：理想低通滤波器的频率响应为：H(ω) = { 1, |ω| ≤ 0.3π{ 0, |ω| > 0.3π }五、论述题1. 论述数字信号处理在现代通信系统中的应用及其重要性。

答案：数字信号处理在现代通信系统中扮演着至关重要的角色。

《数字信号处理》考试试卷（附答案）一、填空（每空 2 分 共20分）1．连续时间信号与数字信号的区别是：连续时间信号时间上是连续的，除了在若干个不连续点外，在任何时刻都有定义，数字信号的自变量不能连续取值，仅在一些离散时刻有定义，并且幅值也离散化㈠。

2．因果系统的单位冲激响应h (n )应满足的条件是：h(n)=0,当n<0时㈡。

3．线性移不变系统的输出与该系统的单位冲激响应以及该系统的输入之间存在关系式为：()()*()()()m y n x n h n x m h n m ∞=-∞==-∑，其中x(n)为系统的输入，y(n)为系统的输出，h(n)w 为系统的单位冲激响应。

㈢。

4．若离散信号x (n )和h (n )的长度分别为L 、M ，那么用圆周卷积)()()(n h n x n y N O=代替线性卷积)()(n x n y l =*h (n)的条件是：1N L M ≥+-㈣。

5．如果用采样频率f s = 1000 Hz 对模拟信号x a (t ) 进行采样，那么相应的折叠频率应为 500 Hz ㈤，奈奎斯特率（Nyquist ）为1000Hz ㈥。

6．N 点FFT 所需乘法（复数乘法）次数为2N ㈦。

7．最小相位延迟系统的逆系统一定是最小相位延迟系统㈧。

8．一般来说，傅立叶变换具有4形式㈨。

9．FIR 线性相位滤波器有4 种类型㈩。

二、叙述题（每小题 10 分 共30分） 1．简述FIR 滤波器的窗函数设计步骤。

答：（1）根据实际问题所提出的要求来确定频率响应函数()j d H e ω;（2.5分）（2）利用公式1()()2j j d d h n H e e d πωωπωπ-=⎰来求取()d h n ； （2.5分）（3）根据过渡带宽及阻带最小衰减的要求，查表选定窗的形状及N 的大小；（2.5分）（4）计算()()(),0,1,...1d h n h n w n n N ==-，便得到所要设计的FRI 滤波器。

数字信号处理试卷及答案1一、填空题（每空1分, 共10分）1．序列()sin(3/5)x n n π=的周期为 。

2．线性时不变系统的性质有 律、 律、 律。

3．对4()()x n R n =的Z 变换为 ，其收敛域为 。

4．抽样序列的Z 变换与离散傅里叶变换DFT 的关系为 。

5．序列x(n)=(1，-2，0，3；n=0，1，2，3), 圆周左移2位得到的序列为 。

6．设LTI 系统输入为x(n) ，系统单位序列响应为h(n)，则系统零状态输出y(n)= 。

7．因果序列x(n)，在Z →∞时，X(Z)= 。

二、单项选择题（每题2分, 共20分）1．δ(n)的Z 变换是 （ ）A.1 B.δ(ω) C.2πδ(ω) D.2π 2．序列x 1（n ）的长度为4，序列x 2（n ）的长度为3，则它们线性卷积的长度是 （ ）A. 3 B. 4 C. 6 D. 73．LTI 系统，输入x （n ）时，输出y （n ）；输入为3x （n-2），输出为 （ ） A. y （n-2） B.3y （n-2） C.3y （n ） D.y （n ）4．下面描述中最适合离散傅立叶变换DFT 的是 （ ）A.时域为离散序列，频域为连续信号B.时域为离散周期序列，频域也为离散周期序列C.时域为离散无限长序列，频域为连续周期信号D.时域为离散有限长序列，频域也为离散有限长序列5．若一模拟信号为带限，且对其抽样满足奈奎斯特条件，理想条件下将抽样信号通过 即可完全不失真恢复原信号 A.理想低通滤波器 B.理想高通滤波器 C.理想带通滤波器 D.理想带阻滤波器6．下列哪一个系统是因果系统 （ ）A.y(n)=x (n+2) B. y(n)= cos(n+1)x (n) C. y(n)=x (2n) D.y(n)=x (- n)7．一个线性时不变离散系统稳定的充要条件是其系统函数的收敛域包括 （ ）A. 实轴B.原点C.单位圆D.虚轴8．已知序列Z 变换的收敛域为｜z ｜>2，则该序列为A.有限长序列B.无限长序列C.反因果序列D.因果序列 9．若序列的长度为M ，要能够由频域抽样信号X(k)恢复原序列，而不发生时域混叠现象，则频域抽样点数N 需满足的条件是 A.N≥M B.N≤M C.N≤2M D.N≥2M 10．设因果稳定的LTI 系统的单位抽样响应h(n)，在n<0时，h(n)= ( )A.0 B .∞ C. -∞ D.1 三、判断题（每题1分, 共10分）1．序列的傅立叶变换是频率ω的周期函数，周期是2π。

数字信号处理试题及答案1. 试题1.1 选择题1. 设x(n)为长度为N的实序列，其中0≤n≤N-1。

要将其进行离散傅立叶变换（DFT），DFT的结果为X(k)，其中0≤k≤N-1。

以下哪个式子为正确的傅立叶变换公式？A. X(k) = ∑[x(n) * exp(-j2πkn/N)]，0≤k≤N-1B. X(k) = ∑[x(n) * exp(-j2πnk/N)]，0≤k≤N-1C. X(k) = ∑[x(n) * exp(-jπkn/N)]，0≤k≤N-1D. X(k) = ∑[x(n) * exp(-jπnk/N)]，0≤k≤N-12. 在基于FFT算法的离散傅立叶变换中，当序列长度N为2的整数幂时，计算复杂度为：A. O(N^2)B. O(NlogN)C. O(logN)D. O(N)3. 对于一个由N个采样值组成的序列，它的z变换被定义为下式：X(z) = ∑[x(n) * z^(-n)]，其中n取0至N-1以下哪个选项正确表示该序列的z变换？A. X(z) = X(z)e^(-i2π/N)B. X(z) = X(z)e^(-iπ/N)C. X(z) = X(z^-1)e^(-i2π/N)D. X(z) = X(z^-1)e^(-iπ/N)1.2 简答题1. 请简要说明数字信号处理（DSP）的基本概念和应用领域。

2. 解释频率抽样定理（Nyquist定理）。

3. 在数字滤波器设计中，有两种常见的滤波器类型：FIR和IIR滤波器。

请解释它们的区别，并举例说明各自应用的情况。

2. 答案1.1 选择题答案1. B2. B3. D1.2 简答题答案1. 数字信号处理（DSP）是一种利用数字计算机或数字信号处理器对信号进行采样、量化、处理和重建的技术。

它可以应用于音频处理、图像处理、通信系统、雷达系统等领域。

DSP可以实现信号的滤波、变换、编码、解码、增强等功能。

2. 频率抽样定理（Nyquist定理）指出，为了正确地恢复一个连续时间信号，我们需要对其进行采样，并且采样频率要大于信号中最高频率的两倍。

数字信号处理复习题一、选择题1、某系统 y(n) g( n) x(n), g( n) 有界，则该系统（A ）。

A. 因果稳定B.非因果稳定C.因果不稳定D. 非因果不稳定2、一个离散系统（D）。

A. 若因果必稳定B. 若稳定必因果C.因果与稳定有关D. 因果与稳定无关3、某系统 y(n) nx(n), 则该系统（A ）。

A. 线性时变B. 线性非时变C. 非线性非时变D. 非线性时变 4.因果稳定系统的系统函数 H ( z) 的收敛域是（ D）。

A. z 0.9B. z 1.1C. z1.1D.z 0.95. x 1 (n) 3sin(0.5 n) 的周期（ A）。

A.4B.3C.2D.16.某系统的单位脉冲响应h(n) ( 1) nu(n), 则该系统（C ）。

2A. 因果不稳定B.非因果稳定C.因果稳定D. 非因果不稳定7.某系统 y(n) x(n) 5 ，则该系统（B ）。

A. 因果稳定B.非因果稳定C.因果不稳定D. 非因果不稳定8.序列 x(n) a n u( n 1), 在 X ( z) 的收敛域为（ A）。

A. z aB. zaC.z a D. z a9.序列 x(n)(1) nu(n) ( 1)n u( n 1), 则 X (z) 的收敛域为（ D ）。

1 3 12 1 1 1B. zC. z zA. z3 2 D. 223 10.关于序列 x( n) 的 DTFT X (ej) ，下列说法正确的是（C ）。

A. 非周期连续函数B.非周期离散函数C.周期连续函数，周期为 2D.周期离散函数，周期为211.以下序列中（ D ）的周期为 5。

A. x( n)cos( 3n)B. x(n)sin( 3 n)5 588C. x( n) e j ( 2n)x(n)j (2n) 58D. e 5812. x(n)ej (n)3 6，该序列是（ A ）。

A. 非周期序列B.周期 N6C.周期 N6D.周期N 213. ((4)) 4 ________ 。

1设序列x(n)={4，3，2，1} ， 另一序列h(n) ={1，1，1，1}，n=0,1,2,3 （1）试求线性卷积 y(n)=x(n)*h(n) （2）试求6点圆周卷积。

（3）试求8点圆周卷积。

解：1．y(n)=x(n)*h(n)={4,7,9,10,6,3,1}2．6点圆周卷积={5,7,9,10,6,3}3．8点圆周卷积={4,7,9,10,6,3,1,0}2二．数字序列 x(n)如图所示. 画出下列每个序列时域序列： (1) x(n-2); (2)x(3-n);(3)x[((n-1))6],(0≤n ≤5);(4)x[((-n-1))6],(0≤n ≤5);n12340.5x(3-n)x[((n-1))]n43210.5n12340.5x[((-n-1))6]3．已知一稳定的LTI 系统的H(z)为)21)(5.01()1(2)(111------=z z z z H试确定该系统H(z)的收敛域和脉冲响应h[n]。

解:0.52ReIm系统有两个极点，其收敛域可能有三种形式，|z|<0.5, 0.5<|z|<2, |z|>2 因为稳定，收敛域应包含单位圆，则系统收敛域为：0.5<|z|<211111213/25.013/4)21)(5.01()1(2)(--------=---=z z z z z z H)1(232)()5.0(34)(--+=n u n u n h n n4．设x(n)是一个10点的有限序列x （n ）={ 2,3,1,4,-3,-1,1,1,0,6}，不计算DFT ，试确定下列表达式的值。

(1) X(0), (2) X(5), (3)∑=9)(k k X ,（4）∑=-95/2)(k k j k X eπ解：（1） （2）（3）（4）5． x(n)和h(n)是如下给定的有限序列 x(n)={5, 2, 4, -1, 2}， h(n)={-3, 2, -1 }(1) 计算x(n)和h(n)的线性卷积y(n)= x(n)* h(n)； (2) 计算x(n)和h(n)的6 点循环卷积y 1(n)= x(n)⑥h (n)； (3) 计算x(n)和h(n)的8 点循环卷积y 2(n)= x(n)⑧h (n)； 比较以上结果，有何结论？ 解：（1）14][]0[190===∑=n Nn x X W 12][][]5[119180510-=-===⎩⎨⎧-=∑∑====奇偶奇数偶数n n n n n n x n x X n n W20]0[*10][][101]0[99===∑∑==x k X k X x k k 0]8[*10][][101]))210[((][]))[((2)10/2(92)10/2(9010)/2(===-⇔--=-=-∑∑x k X ek X ex k X e m n x k j k k j k m N k j N πππ5 2 4 -1 2-3 2 15 2 4 -1 210 4 8 -2 4-15 -6 -12 3 -6-15 4 -3 13 -4 3 2y(n)= x(n)* h(n)={-15,4,-3,13,-4,3,2}(2)5 2 4 -1 2-3 2 15 2 4 -1 210 4 8 -2 4-15 -6 -12 3 -6-15 4 -3 13 -4 3 22-13 4 -3 13 -4 3 2y1(n)= x(n)⑥h(n)= {-13,4,-3,13,-4,3}(3)因为8>(5+3-1),所以y3(n)= x(n)⑧h(n)＝{-15,4,-3,13,-4,3,2，0}y3(n)与y(n)非零部分相同。

《数字信号处理(第四版)》部分课后习题解答一、简答题1. 什么是数字信号处理？数字信号处理（DSP）是指对数字信号进行处理和分析的一种技术。

它使用数学和算法处理模拟信号，从而实现信号的采样、量化、编码、存储和重构等过程。

DSP广泛应用于通信、音频处理、图像处理和控制系统中。

2. 数字信号处理的主要特点有哪些？•数字信号处理能够处理和分析具有广泛频谱范围的信号。

•数字信号处理能够实现高精度的信号处理和复杂的算法运算。

•数字信号处理能够实现信号的存储、传输和复原等功能。

•数字信号处理可以利用计算机等处理硬件进行实时处理和系统集成。

3. 数字信号处理的基本原理是什么？数字信号处理的基本原理是将连续时间的模拟信号转换成离散时间的数字信号，然后通过一系列的算法对数字信号进行处理和分析。

该过程主要涉及信号的采样、量化和编码等环节。

4. 什么是离散时间信号？离散时间信号是指信号的取样点在时间上呈现离散的情况。

在离散时间信号中，只能在离散时间点上获取信号的取样值，而无法观测到连续时间上的信号变化。

5. 描述离散时间信号的功率和能量的计算方法。

对于离散时间信号，其功率和能量的计算方法如下：•功率：对于离散时间信号x(n)，其功率可以通过求平方和的平均值来计算，即功率P = lim(T->∞) [1/T *∑|x(n)|^2]，其中T表示信号x(n)的观测时间。

•能量：对于离散时间信号x(n)，其能量可以通过求平方和来计算，即能量E = ∑|x(n)|^2。

二、计算题1. 设有一个离散时间周期序列x(n) = [2, 3, -1, 4, 0, -2]，求其周期N。

由于x(n)是一个周期序列，我们可以通过观察序列来确定其周期。

根据观察x(n)的取值，我们可以发现序列在n=1和n=5两个位置上取得了相同的数值。

因此，序列x(n)的周期为N = 5 - 1 = 4。

2. 设有一个信号x(t) = 2sin(3t + π/4)，请将其离散化为离散时间信号x(n)。

. WORD 格式整理. .习题及答案4一、填空题（每空1分, 共10分）1．序列()sin(3/5)x n n π=的周期为 。

2．线性时不变系统的性质有 律、 律、 律。

3．对4()()x n R n =的Z 变换为 ，其收敛域为 。

4．抽样序列的Z 变换与离散傅里叶变换DFT 的关系为 。

5．序列x(n)=(1，-2，0，3；n=0，1，2，3), 圆周左移2位得到的序列为 。

6．设LTI 系统输入为x(n) ，系统单位序列响应为h(n)，则系统零状态输出y(n)= 。

7．因果序列x(n)，在Z →∞时，X(Z)= 。

二、单项选择题（每题2分, 共20分）1．δ(n)的Z 变换是 （ ）A.1 B.δ(ω) C.2πδ(ω) D.2π2．序列x 1（n ）的长度为4，序列x 2（n ）的长度为3，则它们线性卷积的长度是 （ ）A. 3 B. 4 C. 6 D. 73．LTI 系统，输入x （n ）时，输出y （n ）；输入为3x （n-2），输出为 （ ） A. y （n-2） B.3y （n-2） C.3y （n ） D.y （n ）4．下面描述中最适合离散傅立叶变换DFT 的是 （ ）A.时域为离散序列，频域为连续信号B.时域为离散周期序列，频域也为离散周期序列C.时域为离散无限长序列，频域为连续周期信号D.时域为离散有限长序列，频域也为离散有限长序列5．若一模拟信号为带限，且对其抽样满足奈奎斯特条件，理想条件下将抽样信号通过 即可完全不失真恢复原信号 （ ）A.理想低通滤波器 B.理想高通滤波器 C.理想带通滤波器 D.理想带阻滤波器 6．下列哪一个系统是因果系统 （ ）A.y(n)=x (n+2) B. y(n)= cos(n+1)x (n) C. y(n)=x (2n) D.y(n)=x (- n)7．一个线性时不变离散系统稳定的充要条件是其系统函数的收敛域包括 （ ） A. 实轴 B.原点 C.单位圆 D.虚轴8．已知序列Z 变换的收敛域为｜z ｜>2，则该序列为 （ ）A.有限长序列 B.无限长序列 C.反因果序列 D.因果序列9．若序列的长度为M，要能够由频域抽样信号X(k)恢复原序列，而不发生时域混叠现象，则频域抽样点数N需满足的条件是 ( ) A.N≥M B.N≤M C.N≤2M D.N≥2M10．设因果稳定的LTI系统的单位抽样响应h(n)，在n<0时，h(n)= ( ) A.0 B.∞ C. -∞ D.1三、判断题（每题1分, 共10分）1．序列的傅立叶变换是频率ω的周期函数，周期是2π。

第一章数字信号处理概述简答题：1．在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器，它们分别起什么作用？答：在A/D变化之前为了限制信号的最高频率，使其满足当采样频率一定时，采样频率应大于等于信号最高频率2倍的条件。

此滤波器亦称为“抗混叠”滤波器。

在D/A变换之后为了滤除高频延拓谱，以便把抽样保持的阶梯形输出波平滑化，故又称之为“平滑”滤波器。

判断说明题：2．模拟信号也可以与数字信号一样在计算机上进行数字信号处理，自己要增加一道采样的工序就可以了。

（）答：错。

需要增加采样和量化两道工序。

3．一个模拟信号处理系统总可以转换成功能相同的数字系统，然后基于数字信号处理理论，对信号进行等效的数字处理。

（）答：受采样频率、有限字长效应的约束，与模拟信号处理系统完全等效的数字系统未必一定能找到。

因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析，再考虑幅度量化及实现过程中有限字长所造成的影响。

故离散时间信号和系统理论是数字信号处理的理论基础。

第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理计算题：1．过滤限带的模拟数据时，常采用数字滤波器，如图所示，图中T 表示采样周期（假设T 足够小，足以防止混叠效应），把从)()(t y t x 到的整个系统等效为一个模拟滤波器。

（a ） 如果kHz rad n h 101,8)(=π截止于，求整个系统的截止频率。

（b ） 对于kHz T 201=，重复（a ）的计算。

解 （a ）因为当0)(8=≥ωπωj e H rad 时，在数 — 模变换中)(1)(1)(Tj X Tj X Te Y a a j ωω=Ω=所以)(n h 得截止频率8πω=c 对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ，因此对T8π没有影响，故整个系统的截止频率由)(ωj e H 决定，是625Hz 。

数字信号处理习题及答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】==============================绪论============================== 1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统================== 1.①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用(n) 表示y (n )={2,7,19,28,29,15} 2. ①求下列周期②判断下面的序列是否是周期的; 若是周期的， 确定其周期。

（1）A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= （2）)81(j e )(π-=n n x 解： （1） 因为ω=73π, 所以314π2=ω, 这是有理数， 因此是周期序列， 周期T =14。

（2） 因为ω=81, 所以ωπ2=16π, 这是无理数， 因此是非周期序列。

③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。

3.加法乘法序列{2，3，2，1}与序列{2，3，5，2，1}相加为__{4，6，7，3，1}__，相乘为___{4，9，10，2} 。

移位翻转：①已知x(n)波形，画出x(-n)的波形图。

②尺度变换：已知x(n)波形，画出x(2n)及x(n/2)波形图。

卷积和：①h(n)*求x(n)，其他2n 0n 3，h(n)其他3n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5}，则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15} ③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=4. 如果输入信号为，求下述系统的输出信号。