本章复习与测试 教案5 北师大七年上
- 格式:doc
- 大小:59.00 KB
- 文档页数:10


北师大版初一上册第五章一元一次方程复习教案教学目标:【知识与技能】把握本章重要知识,能灵活运用有关知识解决具体问题.【过程与方法】通过梳理本章知识,回忆解决问题中所涉及转化思想和数学建模思想,加深对本章知识的明白得.【情感态度】在运用本章知识解决具体问题过程中,进一步体会数学与生活的紧密联系,增强数学应用意识,感受数学的应用价值,激发学生爱好.教学重难点:【教学重点】回忆本章知识,构建知识体系.【教学难点】利用相关知识解决具体问题.教学过程:一、知识框图,整体把握【教学说明】引导学生回忆本章知识点,展现本章知识结构框图,使学生系统地了解本章知识及它们之间的关系.教学时,边回忆边建立结构框图.二、释疑解惑,加深明白得1.一元一次方程和方程的解在一个方程中,只含有一个未知数,且未知数的指数差不多上1,如此的方程叫做一元一次方程.使方程左、右两边的值相等的未知数的值,叫做方程的解.2.等式的差不多性质等式两边同时加上(或减去)同一个代数式,所得结果仍是等式.等式两边同时乘以同一个数(或除以同一个不为0的数)所得结果仍是等式.3.解一元一次方程的一样步骤(1)去分母.(2)去括号.(3)移项.(4)合并同类项.(5)未知数的系数化为1.4.列方程解应用题的一样步骤(1)设未知数.(2)找等量关系式.(3)列方程.(4)解方程.(5)检验.(6)写出答案.三、典例精析,复习新知例1 已知下列方程:①x+3=1/x;②7x=3;③4x-3=3x+2;④x=2;⑤x+y=5;⑥x2+3x=1.其中是一元一次方程的有()A.2个B.3个C.4个D.5个【分析】①中分母中含有未知数,⑤中含有两个未知数,⑥中未知数的最高次数是2,因此是一元一次方程的是②,③,④,故选B.例2 下列等式变形正确的是()A.假如1/2x=6,那么x=3B.假如x-3=y-3,那么x-y=0C.假如mx=my,那么x=yD.假如S=1/2ab,那么b=S/(2a)【分析】C两边同时除以m,m可能为0,A、D变形都显现了错误,故选B.例3 解方程.解:(1)去分母,得:5(3x-2)+20=2(x+1).去括号,得:15x-10+20=2x+2.移项,合并同类项,得:13x=-8.系数化为1,得:x=-8/13.(2)去分母,得:6x-3(x-1)=12-2(x+2).去括号,得:6x-3x+3=12-2x-4.移项,合并同类项,得:5x=5.系数化为1,得:x=1.例4 若关于x的一元一次方程的解是x=-1,则k的值是()A.2/7B.1C.-3/11D.0【分析】本题从“关于x的方程的解关于x的方程关于k的方程关于k的方程的解”的思维路线,考查学生对“方程的解”和“解方程”的知识的把握情形,故选B.例5 商场将某种品牌的冰箱先按进价提高50%作为标价,然后打出“八折酬宾,外送100元运装费”的广告,结果每台冰箱仍获利300元,求每台冰箱的进价是多少元.解:设每台冰箱的进价为x元,则标价为x(1+50%)元,实际售价为x (1+50%)×80%元,由题意得:x(1+50%)×80%-100-x=300.解得x=2021.答:每台冰箱的进价是2021元.例6 甲、乙两站相距480km,一列慢车从甲站开出,每小时行90km,一列快车从乙站开出,每小时行140km.(1)慢车先开出1h,快车再开,两车相向而行,快车开出多少小时后两车相遇?(2)两车同时开出,相背而行多少小时后两车相距600km?(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600km?【分析】此题关键是要明白得清晰相向、相背、同向等的含义,弄清晰行驶过程,故可结合图形分析.(1)相遇问题,画图表示为:等量关系是:慢车走的路程+快车走的路程=480公里.解:设快车开出xh后两车相遇,由题意得140x+90(x+1)=480,解之得x=16.123答:快车开出16h后两车相遇.123(2)相背而行,画图表示为:等量关系是:两车所走的路程+480km=600km.解:设xh后两车相距600km.由题意,得(140+90)x+480=600.解之得x=12.23h后,两车相距600km.答:相背而行1623(3)等量关系为:快车所走路程-慢车所走路程+480km=600km.解:设x小时后两车相距600km,由题意,得(140-90)x+480=600.解之得x=12/5.答:12/5h后两车相距600km.四、复习训练,巩固提高1.运用等式性质进行的变形,正确的是()A.假如a=b,那么a+c=b-cB.假如ac=bc,a=bC.假如a=b,那么ac=bcD.假如a2=3a,那么a=32.若x=2是关于x的方程2x+3m-1=0的解.则m的值等于______.3.当m=______时,(m-1)/4的值比(2-m)/3的值大2.4.若(m-1)x|m|+5=0是关于x的一元一次方程.(1)求m的值;(2)请写出那个方程;(3)判定x=1,x=2.5,x=3是否是方程的解.5.解方程.6.小明在做家庭作业时练习册上一道解方程的题目被墨水污染了:,“”是被污染的内容,他专门着急,翻开书后面的答案,这道题的解是x=2,你能关心他补上“”的内容吗?说出你的方法.7.某童车厂生产由一个车身和三个车轮组成的童车,工厂有88名工人,每名工人每个星期可生产5个车身或9个车轮,问如何安排这些工人,使得他们每个星期生产的车身和车轮配套?8.某商场因换季预备处理一些羊绒衫,若每件羊绒衫按标价的六折出售将亏110元,若按标价的八折出售,每件将赚70元.每件羊绒衫的标价是多少元?进价是多少元?9.已知A 、B 两地相距100千米,甲每小时走11千米,乙每小时走9千米,甲、乙两人分别从A 、B 两地同时动身.(1)相向而行,通过多少小时两人相遇?(2)同向而行,通过多少小时甲追上乙?(3)反向而行,通过多少小时相距160千米?【教学说明】 这部分安排了几个较典型的重点题型,加深对本章知识的明白得,进一步提高学生综合运用所学知识的能力.前5题可由学生自主完成,后4题可由师生共同探讨得出结论.【答案】1.B 2.-1 3.54.(1)m=-1(2)-2x+5=0(3)x=2.5是原方程的解;x=1,x=3不是原方程的解.5.(1)x=-3 (2)x=17/256.解:设空格内的数为a ,把x=2代入方程得3101232a --=-,解得a=4. 7.解:设安排x 人一辈子产车身,则生产车轮有(88-x )人,依照题意得:5x=(88-x)×9÷3.解得x=33.故安排生产车轮有88-33=55(人).因此安排33名工人一辈子产车身,55名工人一辈子产车轮.8.解:设每件羊毛衫的标价为x 元,由题意得:0.6x+110=0.8x-70.解得x=900,进价为900×0.6+110=650元.因此每件羊毛衫的标价是900元,进价为650元.9.解:(1)设相向而行,通过x小时两人相遇,则有11x+9x=100,解得x=5,因此相向而行,通过5小时两人相遇.(2)设同向而行,通过y小时甲追上乙,则有100+9y=11y,解得y=50.因此同向而行,通过50小时甲追上乙.(3)设反向而行,通过z小时两人相距160千米,则有11z+100+9z= 160,解得z=3.因此,反向而行通过3小时两人相距160千米.五、师生互动,课堂小结本堂课你能完整地回忆本章所学的有关知识吗?你学会了哪些与本章有关的数学思想方法?你还有哪些困惑与疑问?【教学说明】学生回忆本章知识,积极与同伴交流,关于学生的困惑与疑问,教师应及时指导.课后作业:1.布置作业:从教材“复习题5”中选取.2.完成练习册中本章复习课的练习.教学反思:本节课通过复习归纳本章重点知识,加深对本章知识的明白得,通过例题的讲解与复习训练,进一步提高学生综合运用所学知识的能力.。

第五章 一元一次方程小结与复习一、等式的概念和性质1.等式的概念,用等号“=”表示相等关系的式子,叫做等式. 在等式中,等号左、右两边的式子,分别叫做这个等式的左边、右边.等式可以是数字算式,可以是公式、方程,也可以是用式子表示的运算律、运算法则. 2.等式的类型楷体五号(1)恒等式:无论用什么数值代替等式中的字母,等式总能成立.如:数字算式123+=. (2)条件等式:只能用某些数值代替等式中的字母,等式才能成立.方程56x +=需要1x =才成立.(3)矛盾等式:无论用什么数值代替等式中的字母,等式都不能成立.如125+=,11x x +=-.注意:等式由代数式构成,但不是代数式.代数式没有等号.体五号3.等式的性质五号等式的性质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式.若a b =,则a m b m ±=±;等式的性质2:等式两边都乘以(或除以)同一个数(除数不能是0)或同一个整式,所得结果仍是等式.若a b =,则am bm =,a b mm=(0)m ≠.注意:(1)在对等式变形过程中,等式两边必须同时进行.即:同时加或同时减,同时乘以或同时除以,不能漏掉某一边. (2)等式变形过程中,两边同加或同减,同乘或同除以的数或整式必须相同.(3)在等式变形中,以下两个性质也经常用到:①等式具有对称性,即:如果a b =,那么b a =.②等式具有传递性,即:如果a b =,b c =,那么a c =.黑体小四 二、方程的相关概念黑体小四1.方程,含有未知数的等式叫作方程.注意:定义中含有两层含义,即:方程必定是等式,即是用等号连接而成的式子;方程中必定有一个待确定的数即未知的字母.二者缺一不可.楷体五号2.方程的次和元方程中未知数的最高次数称为方程的次,方程中不同未知数的个数称为元.楷体五号3.方程的已知数和未知数楷体五号已知数:一般是具体的数值,如50x+=中(x的系数是1,是已知数.但可以不说).5和0是已知数,如果方程中的已知数需要用字母表示的话,习惯上有a、b、c、m、n等表示.未知数:是指要求的数,未知数通常用x、y、z等字母表示.如:关于x、y的方程2ax by c-=中,a、2b-、c是已知数,x、y是未知数.4.方程的解使方程左、右两边相等的未知数的值,叫做方程的解.楷体五号5.解方程求得方程的解的过程.注意:解方程与方程的解是两个不同的概念,后者是求得的结果,前者是求出这个结果的过程.6.方程解的检验楷体要验证某个数是不是一个方程的解,只需将这个数分别代入方程的左边和右边,如果左、右两边数值相等,那么这个数就是方程的解,否则就不是.黑体小四三、一元一次方程的定义体小四1.一元一次方程的概念只含有一个未知数,并且未知数的最高次数是1,系数不等于0的方程叫做一元一次方程,这里的“元”是指未知数,“次”是指含未知数的项的最高次数.楷体五号2.一元一次方程的形式楷体五号标准形式:0ax b+=(其中0a≠,a,b是已知数)的形式叫一元一次方程的标准形式.最简形式:方程ax b =(0a ≠,a ,b 为已知数)叫一元一次方程的最简形式.注意:(1)任何一元一次方程都可以转化为最简形式或标准形式,所以判断一个方程是不是一元一次方程,可以通过变形为最简形式或标准形式验证.如方程22216x x x ++=-是一元一次方程.如果不变形,直接判断就出会现错误.(2)方程ax b =与方程(0)ax b a =≠是不同的,方程ax b =的解需要分类讨论完成.黑体小四四、一元一次方程的解法1.解一元一次方程的一般步骤五号(1)去分母:在方程的两边都乘以各分母的最小公倍数. 注意:不要漏乘不含分母的项,分子是个整体,含有多项式时应加上括号.(2)去括号:一般地,先去小括号,再去中括号,最后去大括号. 注意:不要漏乘括号里的项,不要弄错符号.(3)移项:把含有未知数的项都移到方程的一边,不含未知数的项移到方程的另一边. 注意:①移项要变号;②不要丢项.(4)合并同类项:把方程化成ax b =的形式. 注意:字母和其指数不变. (5)系数化为1:在方程的两边都除以未知数的系数a (0a ≠),得到方程的解b x a=. 注意:不要把分子、分母搞颠倒.体五号2.解一元一次方程常用的方法技巧 解一元一次方程常用的方法技巧有:整体思想、换元法、裂项、拆添项以及运用分式的恒等变形等.3.关于的方程 a b 解的情况 ⑴当a 0时, ⑵当a ,b 0时,方程有无数多个解 ⑶当a 0,b 0时,方程无解练习1、等式的概念和性质 1下列说法不正确的是( )A .等式两边都加上一个数或一个等式,所得结果仍是等式.B .等式两边都乘以一个数,所得结果仍是等式. .等式两边都除以一个数,所得结果仍是等式.D .一个等式的左、右两边与另一个等式的左、右两边分别相加,所得结果仍是等式. 2根据等式的性质填空.(1)4a b =-,则 a b =+; (2)359x -=,则39x =+ ; (3)683x y =+,则x = ;(4)122x y =+,则x = .练习2、方程的相关概念1列各式中,哪些是等式?哪些是代数式,哪些是方程?①34a +;②28x y +=;③532-=;④1x y ->;⑤61x x --;⑥83x-=; ⑦230y y +=;⑧2223a a -;⑨32a a <-. 2判断题.(1)所有的方程一定是等式. ( ) (2)所有的等式一定是方程. ( )(3)241x x -+是方程.( )(4)51x -不是方程.( )(5)78x x =不是等式,因为7x 与8x 不是相等关系.( )(6)55=是等式,也是方程.( )(7)“某数的3倍与6的差”的含义是36x -,它是一个代数式,而不是方程.( )练习3、一元一次方程的定义1在下列方程中哪些是一元一次方程?哪些不是?说明理由:(1)3+5=12; (2)31+x +2x =5; (3)2+y=3; (4)y 2+5y -6=0; (5)x3-x =22已知2(1)(1)30k x k x -+-+=是关于x 的一元一次方程,求k 的值.3已知方程()7421=+--m x m 是关于的一元一次方程,则=_________4已知方程1(2)40a a x --+=是一元一次方程,则a = ;x = . 练习4、一元一次方程的解与解法1)一元一次方程的解 一)、根据方程解的具体数值确定 1若关于的方程a xx -=+332的解是2x =-,则代数式21aa -的值是_________。

第五章 一元一次方程小结与复习一、等式的概念和性质1.等式的概念,用等号“=”来表示相等关系的式子,叫做等式. 在等式中,等号左、右两边的式子,分别叫做这个等式的左边、右边.等式可以是数字算式,可以是公式、方程,也可以是用式子表示的运算律、运算法则.2.等式的类型楷体五号(1)恒等式:无论用什么数值代替等式中的字母,等式总能成立.如:数字算式123+=.(2)条件等式:只能用某些数值代替等式中的字母,等式才能成立.方程56x +=需要1x =才成立.(3)矛盾等式:无论用什么数值代替等式中的字母,等式都不能成立.如125+=,11x x +=-. 注意:等式由代数式构成,但不是代数式.代数式没有等号.体五号3.等式的性质五号等式的性质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式.若a b =,则a m b m ±=±;等式的性质2:等式两边都乘以(或除以)同一个数(除数不能是0)或同一个整式,所得结果仍是等式.若a b =,则am bm =,a b m m=(0)m ≠.注意:(1)在对等式变形过程中,等式两边必须同时进行.即:同时加或同时减,同时乘以或同时除以,不能漏掉某一边.(2)等式变形过程中,两边同加或同减,同乘或同除以的数或整式必须相同.(3)在等式变形中,以下两个性质也经常用到:①等式具有对称性,即:如果a b =,那么b a =.②等式具有传递性,即:如果a b =,b c =,那么a c =.黑体小四二、方程的相关概念黑体小四1.方程,含有未知数的等式叫作方程. 注意:定义中含有两层含义,即:方程必定是等式,即是用等号连接而成的式子;方程中必定有一个待确定的数即未知的字母.二者缺一不可.楷体五号2.方程的次和元 方程中未知数的最高次数称为方程的次,方程中不同未知数的个数称为元.楷体五号3.方程的已知数和未知数楷体五号已知数:一般是具体的数值,如50x +=中(x 的系数是1,是已知数.但可以不说).5和0是已知数,如果方程中的已知数需要用字母表示的话,习惯上有a 、b 、c 、m 、n 等表示. 未知数:是指要求的数,未知数通常用x 、y 、z 等字母表示.如:关于x 、y 的方程2ax by c -=中,a 、2b -、c 是已知数,x 、y 是未知数.4.方程的解 使方程左、右两边相等的未知数的值,叫做方程的解.楷体五号5.解方程 求得方程的解的过程.注意:解方程与方程的解是两个不同的概念,后者是求得的结果,前者是求出这个结果的过程.6.方程解的检验楷体要验证某个数是不是一个方程的解,只需将这个数分别代入方程的左边和右边,如果左、右两边数值相等,那么这个数就是方程的解,否则就不是.黑体小四三、一元一次方程的定义体小四1.一元一次方程的概念 只含有一个未知数,并且未知数的最高次数是1,系数不等于0的方程叫做一元一次方程,这里的“元”是指未知数,“次”是指含未知数的项的最高次数.楷体五号2.一元一次方程的形式楷体五号标准形式:0ax b +=(其中0a ≠,a ,b 是已知数)的形式叫一元一次方程的标准形式. 最简形式:方程ax b =(0a ≠,a ,b 为已知数)叫一元一次方程的最简形式.注意:(1)任何一元一次方程都可以转化为最简形式或标准形式,所以判断一个方程是不是一元一次方程,可以通过变形为最简形式或标准形式来验证.如方程22216x x x ++=-是一元一次方程.如果不变形,直接判断就出会现错误.(2)方程ax b =与方程(0)ax b a =≠是不同的,方程ax b =的解需要分类讨论完成.黑体小四四、一元一次方程的解法1.解一元一次方程的一般步骤五号(1)去分母:在方程的两边都乘以各分母的最小公倍数. 注意:不要漏乘不含分母的项,分子是个整体,含有多项式时应加上括号.(2)去括号:一般地,先去小括号,再去中括号,最后去大括号. 注意:不要漏乘括号里的项,不要弄错符号.(3)移项:把含有未知数的项都移到方程的一边,不含未知数的项移到方程的另一边. 注意:①移项要变号;②不要丢项.(4)合并同类项:把方程化成ax b =的形式. 注意:字母和其指数不变.(5)系数化为1:在方程的两边都除以未知数的系数a (0a ≠),得到方程的解b x a=. 注意:不要把分子、分母搞颠倒.体五号2.解一元一次方程常用的方法技巧 解一元一次方程常用的方法技巧有:整体思想、换元法、裂项、拆添项以及运用分式的恒等变形等.3.关于x 的方程 ax b 解的情况 ⑴当a 0时,x⑵当a ,b 0时,方程有无数多个解 ⑶当a 0,b 0时,方程无解练习1、等式的概念和性质1.下列说法不正确的是( )A .等式两边都加上一个数或一个等式,所得结果仍是等式.B .等式两边都乘以一个数,所得结果仍是等式.C .等式两边都除以一个数,所得结果仍是等式.D .一个等式的左、右两边与另一个等式的左、右两边分别相加,所得结果仍是等式.2.根据等式的性质填空.(1)4a b =-,则 a b =+; (2)359x -=,则39x =+ ;(3)683x y =+,则x = ; (4)122x y =+,则x = . 练习2、方程的相关概念1.列各式中,哪些是等式?哪些是代数式,哪些是方程?①34a +;②28x y +=;③532-=;④1x y ->;⑤61x x --;⑥83x-=; ⑦230y y +=;⑧2223a a -;⑨32a a <-.2.判断题.(1)所有的方程一定是等式. ( )(2)所有的等式一定是方程. ( )(3)241x x -+是方程. ( )(4)51x -不是方程. ( )(5)78x x =不是等式,因为7x 与8x 不是相等关系. ( )(6)55=是等式,也是方程. ( )(7)“某数的3倍与6的差”的含义是36x -,它是一个代数式,而不是方程. ( ) 练习3、一元一次方程的定义 1.在下列方程中哪些是一元一次方程?哪些不是?说明理由:(1)3x+5=12; (2)31+x +2x =5; (3)2x+y=3; (4)y 2+5y -6=0; (5)x 3-x =2.2.已知2(1)(1)30k x k x -+-+=是关于x 的一元一次方程,求k 的值.3.已知方程()7421=+--m x m 是关于x 的一元一次方程,则m=_________4.已知方程1(2)40a a x --+=是一元一次方程,则a = ;x = .练习4、一元一次方程的解与解法1)一元一次方程的解 一)、根据方程解的具体数值来确定1.若关于x 的方程a x x -=+332的解是2x =-,则代数式21aa -的值是_________。
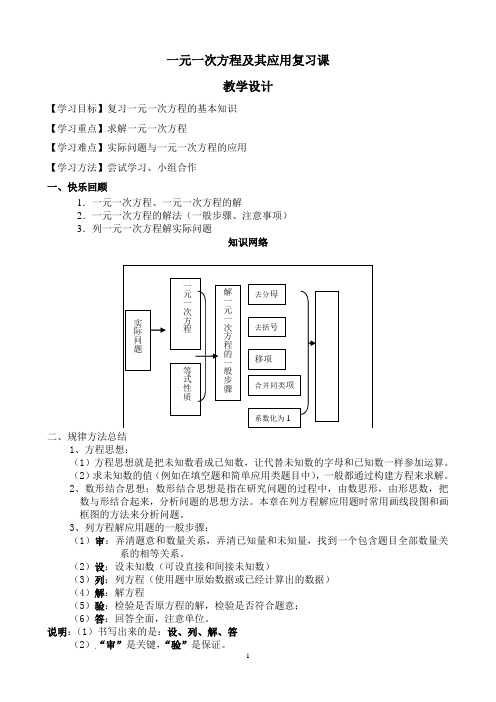
一元一次方程及其应用复习课教学设计【学习目标】复习一元一次方程的基本知识【学习重点】求解一元一次方程【学习难点】实际问题与一元一次方程的应用【学习方法】尝试学习、小组合作一、快乐回顾1.一元一次方程、一元一次方程的解2.一元一次方程的解法(一般步骤、注意事项)3.列一元一次方程解实际问题知识网络二、规律方法总结1、方程思想:(1)方程思想就是把未知数看成已知数,让代替未知数的字母和已知数一样参加运算。
(2)求未知数的值(例如在填空题和简单应用类题目中),一般都通过构建方程来求解。
2、数形结合思想:数形结合思想是指在研究问题的过程中,由数思形,由形思数,把数与形结合起来,分析问题的思想方法。
本章在列方程解应用题时常用画线段图和画框图的方法来分析问题。
3、列方程解应用题的一般步骤:(1)审:弄清题意和数量关系,弄清已知量和未知量,找到一个包含题目全部数量关系的相等关系。
(2)设:设未知数(可设直接和间接未知数)(3)列:列方程(使用题中原始数据或已经计算出的数据)(4)解:解方程(5)验:检验是否原方程的解,检验是否符合题意;(6)答:回答全面,注意单位。
说明:(1)书写出来的是:设、列、解、答(2)“审”是关键,“验”是保证。
解一元一次方程的一般步骤 去分母 一元一次方程 等式性质实际问题 系数化为1 去括号移项 合并同类项二、合作探究例1、A 、B 两地相距230千米,甲队从A 地出发两小时后,乙队从B 地出发与甲相向而行,乙队出发20小时后相遇,已知乙的速度比甲的速度每小时快1千米,求甲、乙的速度各是多少?分析:设:甲速为x 千米/时,则乙速为(x+1)千米/时画出示意图(图略)相等关系:甲走总路程+乙走路程=230指导学生列式三、巩固练习根据题意列方程:1、甲、乙骑自行车同时从相距 65千米的两地相向而行,2小 时相遇.甲比乙每小时多骑2.5千米,求乙的时速.2.某商店把原价为每台2640元的名牌彩电以九折优惠出售,仍可获利20%,则每台彩电的进价为多少元。

第5单元一元一次方程复习教案复习目标:1、进一步熟练掌握一元一次方程的解法,并会应用一元一次方程解决实际问题。
2、经历本章知识系统梳理过程,体会解方程中蕴含的转化思想和用方程解决问题过程中蕴含的方程模型思想3、提高知识的迁移能力,加强合作交流能力,体会数学的应用价值复习重点:熟练掌握一元一次方程的解法并应用一元一次方程解决实际问题。
复习难点:体会解方程中蕴含的转化思想,灵活应用一元一次方程解决实际问题并体会方程模型思想。
教学方法:自主复习,合作交流学情分析:学生对一元一次方程已经有初步的认识,并能够利用一元一次方程解决简单的实际问题,但这些零散的知识缺乏系统化、条理化,对应用题的分析能力不强。
教学准备:多媒体课件教学过程:一、导入同学们,方程是刻画现实生活中数量关系的重要模型。
今天我们复习第五章:一元一次方程。
通过陈省身的名言(数学是自己思考的产物;用自己的意见和别人交换会有很好的效果)鼓励大家多表达自己的思考,多把自己的想法跟别人交流,让我们在这个过程中复习《一元一次方程》。
二、梳理知识,温故知新活动设计(以学生列举一个一元一次方程为线索贯穿4个教学环节,以课堂资源的生成复习相关概念并深化理解):1、请你列举一个一元一次方程的例子,结合举例谈谈一元一次方程具有什么特征?(只含有一个未知数,未知数的次数是1,方程是等式,等式两边是整式),学生自主完成练习1。
练习1:如果5x IaI-1=0是关于x的一元一次方程,那么a的值为()。
A.1B.-1C. ±1D.02、请说出你的方程的解,请你谈谈什么是方程的解?完成练习2,并告诉学生练习2是常州市2015年的中招试题,体验成就感。
练习2:(常州2015)已知x=2是关于x的方程a(x+1)=12a+x的解,则a的值是。
3、刚才解方程的过程中,我们解一元一次方程的依据是什么?根据你的经验,在哪些地方容易出错?(等式的基本性质)展示小明错题本上收集的错例,鼓励学生自主练习,互动纠错,让不同观点的同学都有机会展示自己的想法,最好引发同学之间的辩论,引导学生说出习题背后所隐含的知识点。
第五章 一元一次方程小结与复习一、等式的概念和性质1.等式的概念,用等号“=”来表示相等关系的式子,叫做等式. 在等式中,等号左、右两边的式子,分别叫做这个等式的左边、右边.等式可以是数字算式,可以是公式、方程,也可以是用式子表示的运算律、运算法则.2.等式的类型(1)恒等式:无论用什么数值代替等式中的字母,等式总能成立.如:数字算式123+=.(2)条件等式:只能用某些数值代替等式中的字母,等式才能成立.方程56x +=需要1x =才成立.(3)矛盾等式:无论用什么数值代替等式中的字母,等式都不能成立.如125+=,11x x +=-. 注意:等式由代数式构成,但不是代数式.代数式没有等号.3.等式的性质等式的性质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式.若a b =,则a m b m ±=±;等式的性质2:等式两边都乘以(或除以)同一个数(除数不能是0)或同一个整式,所得结果仍是等式.若a b =,则am bm =,a b m m=(0)m ≠.注意:(1)在对等式变形过程中,等式两边必须同时进行.即:同时加或同时减,同时乘以或同时除以,不能漏掉某一边.(2)等式变形过程中,两边同加或同减,同乘或同除以的数或整式必须相同.(3)在等式变形中,以下两个性质也经常用到:①等式具有对称性,即:如果a b =,那么b a =.②等式具有传递性,即:如果a b =,b c =,那么a c =.二、方程的相关概念1.方程,含有未知数的等式叫作方程. 注意:定义中含有两层含义,即:方程必定是等式,即是用等号连接而成的式子;方程中必定有一个待确定的数即未知的字母.二者缺一不可.2.方程的次和元 方程中未知数的最高次数称为方程的次,方程中不同未知数的个数称为元.3.方程的已知数和未知数已知数:一般是具体的数值,如50x +=中(x 的系数是1,是已知数.但可以不说).5和0是已知数,如果方程中的已知数需要用字母表示的话,习惯上有a 、b 、c 、m 、n 等表示. 未知数:是指要求的数,未知数通常用x 、y 、z 等字母表示.如:关于x 、y 的方程2ax by c -=中,a 、2b -、c 是已知数,x 、y 是未知数.4.方程的解 使方程左、右两边相等的未知数的值,叫做方程的解.5.解方程 求得方程的解的过程.注意:解方程与方程的解是两个不同的概念,后者是求得的结果,前者是求出这个结果的过程.6.方程解的检验要验证某个数是不是一个方程的解,只需将这个数分别代入方程的左边和右边,如果左、右两边数值相等,那么这个数就是方程的解,否则就不是.三、一元一次方程的定义1.一元一次方程的概念 只含有一个未知数,并且未知数的最高次数是1,系数不等于0的方程叫做一元一次方程,这里的“元”是指未知数,“次”是指含未知数的项的最高次数.2.一元一次方程的形式标准形式:0ax b +=(其中0a ≠,a ,b 是已知数)的形式叫一元一次方程的标准形式. 最简形式:方程ax b =(0a ≠,a ,b 为已知数)叫一元一次方程的最简形式.注意:(1)任何一元一次方程都可以转化为最简形式或标准形式,所以判断一个方程是不是一元一次方程,可以通过变形为最简形式或标准形式来验证.如方程22216x x x ++=-是一元一次方程.如果不变形,直接判断就出会现错误.(2)方程ax b =与方程(0)ax b a =≠是不同的,方程ax b =的解需要分类讨论完成.四、一元一次方程的解法1.解一元一次方程的一般步骤(1)去分母:在方程的两边都乘以各分母的最小公倍数. 注意:不要漏乘不含分母的项,分子是个整体,含有多项式时应加上括号.(2)去括号:一般地,先去小括号,再去中括号,最后去大括号. 注意:不要漏乘括号里的项,不要弄错符号.(3)移项:把含有未知数的项都移到方程的一边,不含未知数的项移到方程的另一边. 注意:①移项要变号;②不要丢项.(4)合并同类项:把方程化成ax b =的形式. 注意:字母和其指数不变.(5)系数化为1:在方程的两边都除以未知数的系数a (0a ≠),得到方程的解b x a=. 注意:不要把分子、分母搞颠倒.2.解一元一次方程常用的方法技巧 解一元一次方程常用的方法技巧有:整体思想、换元法、裂项、拆添项以及运用分式的恒等变形等.3.关于x 的方程 ax b 解的情况 ⑴当a 0时,x⑵当a ,b 0时,方程有无数多个解 ⑶当a 0,b 0时,方程无解练习1、等式的概念和性质1.下列说法不正确的是( )A .等式两边都加上一个数或一个等式,所得结果仍是等式.B .等式两边都乘以一个数,所得结果仍是等式.C .等式两边都除以一个数,所得结果仍是等式.D .一个等式的左、右两边与另一个等式的左、右两边分别相加,所得结果仍是等式.2.根据等式的性质填空.(1)4a b =-,则 a b =+; (2)359x -=,则39x =+ ;(3)683x y =+,则x = ; (4)122x y =+,则x = . 练习2、方程的相关概念1.列各式中,哪些是等式?哪些是代数式,哪些是方程?①34a +;②28x y +=;③532-=;④1x y ->;⑤61x x --;⑥83x-=; ⑦230y y +=;⑧2223a a -;⑨32a a <-.2.判断题.(1)所有的方程一定是等式. ( )(2)所有的等式一定是方程. ( )(3)241x x -+是方程. ( )(4)51x -不是方程. ( )(5)78x x =不是等式,因为7x 与8x 不是相等关系. ( )(6)55=是等式,也是方程. ( )(7)“某数的3倍与6的差”的含义是36x -,它是一个代数式,而不是方程. ( ) 练习3、一元一次方程的定义1.在下列方程中哪些是一元一次方程?哪些不是?说明理由:(1)3x+5=12; (2)31+x +2x =5; (3)2x+y=3; (4)y 2+5y -6=0; (5)x 3-x =2.2.已知2(1)(1)30k x k x -+-+=是关于x 的一元一次方程,求k 的值.3.已知方程()7421=+--m x m 是关于x 的一元一次方程,则m=_________4.已知方程1(2)40a a x --+=是一元一次方程,则a = ;x = .练习4、一元一次方程的解与解法1)一元一次方程的解 一)、根据方程解的具体数值来确定1.若关于x 的方程a x x -=+332的解是2x =-,则代数式21a a -的值是_________。
北师版初中数学七年级上册复习教案第五章 一元一次方程小结与复习一、等式的概念和性质 1.等式的概念,用等号“=”来表示相等关系的式子,叫做等式. 在等式中,等号左、右两边的式子,分别叫做这个等式的左边、右边.等式可以是数字算式,可以是公式、方程,也可以是用式子表示的运算律、运算法则. 2.等式的类型楷体五号(1)恒等式:无论用什么数值代替等式中的字母,等式总能成立.如:数字算式123+=. (2)条件等式:只能用某些数值代替等式中的字母,等式才能成立.方程56x +=需要1x =才成立. (3)矛盾等式:无论用什么数值代替等式中的字母,等式都不能成立.如125+=,11x x +=-.注意:等式由代数式构成,但不是代数式.代数式没有等号.体五号 3.等式的性质五号等式的性质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式.若a b =,则a m b m ±=±;等式的性质2:等式两边都乘以(或除以)同一个数(除数不能是0)或同一个整式,所得结果仍是等式.若a b =,则am bm =,a b mm=(0)m ≠.注意:(1)在对等式变形过程中,等式两边必须同时进行.即:同时加或同时减,同时乘以或同时除以,不能漏掉某一边.(2)等式变形过程中,两边同加或同减,同乘或同除以的数或整式必须相同.(3)在等式变形中,以下两个性质也经常用到:①等式具有对称性,即:如果a b =,那么b a =.②等式具有传递性,即:如果a b =,b c =,那么a c =.黑体小四二、方程的相关概念黑体小四1.方程,含有未知数的等式叫作方程. 注意:定义中含有两层含义,即:方程必定是等式,即是用等号连接而成的式子;方程中必定有一个待确定的数即未知的字母.二者缺一不可.楷体五号2.方程的次和元 方程中未知数的最高次数称为方程的次,方程中不同未知数的个数称为元.楷体五号3.方程的已知数和未知数楷体五号已知数:一般是具体的数值,如50x +=中(x 的系数是1,是已知数.但可以不说).5和0是已知数,如果方程中的已知数需要用字母表示的话,习惯上有a 、b 、c 、m 、n 等表示.未知数:是指要求的数,未知数通常用x 、y 、z 等字母表示.如:关于x 、y 的方程2ax by c -=中,a 、2b -、c 是已知数,x 、y 是未知数.4.方程的解 使方程左、右两边相等的未知数的值,叫做方程的解.楷体五号 5.解方程 求得方程的解的过程.注意:解方程与方程的解是两个不同的概念,后者是求得的结果,前者是求出这个结果的过程.6.方程解的检验楷体要验证某个数是不是一个方程的解,只需将这个数分别代入方程的左边和右边,如果左、右两边数值相等,那么这个数就是方程的解,否则就不是.黑体小四三、一元一次方程的定义体小四1.一元一次方程的概念 只含有一个未知数,并且未知数的最高次数是1,系数不等于0的方程叫做一元一次方程,这里的“元”是指未知数,“次”是指含未知数的项的最高次数.楷体五号 2.一元一次方程的形式楷体五号标准形式:0ax b +=(其中0a ≠,a ,b 是已知数)的形式叫一元一次方程的标准形式.最简形式:方程ax b =(0a ≠,a ,b 为已知数)叫一元一次方程的最简形式. 注意:(1)任何一元一次方程都可以转化为最简形式或标准形式,所以判断一个方程是不是一元一次方程,可以通过变形为最简形式或标准形式来验证.如方程22216x x x ++=-是一元一次方程.如果不变形,直接判断就出会现错误.(2)方程ax b =与方程(0)ax b a =≠是不同的,方程ax b =的解需要分类讨论完成.黑体小四四、一元一次方程的解法1.解一元一次方程的一般步骤五号(1)去分母:在方程的两边都乘以各分母的最小公倍数. 注意:不要漏乘不含分母的项,分子是个整体,含有多项式时应加上括号.(2)去括号:一般地,先去小括号,再去中括号,最后去大括号. 注意:不要漏乘括号里的项,不要弄错符号.(3)移项:把含有未知数的项都移到方程的一边,不含未知数的项移到方程的另一边. 注意:①移项要变号;②不要丢项.(4)合并同类项:把方程化成ax b =的形式. 注意:字母和其指数不变. (5)系数化为1:在方程的两边都除以未知数的系数a (0a ≠),得到方程的解bx a=. 注意:不要把分子、分母搞颠倒.体五号2.解一元一次方程常用的方法技巧 解一元一次方程常用的方法技巧有:整体思想、换元法、裂项、拆添项以及运用分式的恒等变形等. 3.关于x 的方程 ax b 解的情况 ⑴当a 0时,x⑵当a,b 0时,方程有无数多个解 ⑶当a 0,b 0时,方程无解练习1、等式的概念和性质1.下列说法不正确的是( )A .等式两边都加上一个数或一个等式,所得结果仍是等式.B .等式两边都乘以一个数,所得结果仍是等式.C .等式两边都除以一个数,所得结果仍是等式.D .一个等式的左、右两边与另一个等式的左、右两边分别相加,所得结果仍是等式.2.根据等式的性质填空.(1)4a b =-,则 a b =+; (2)359x -=,则39x =+ ;(3)683x y =+,则x = ; (4)122x y =+,则x = .练习2、方程的相关概念1.列各式中,哪些是等式?哪些是代数式,哪些是方程?①34a +;②28x y +=;③532-=;④1x y ->;⑤61x x --;⑥83x-=;⑦230y y +=;⑧2223a a -;⑨32a a <-. 2.判断题.(1)所有的方程一定是等式. ( )(2)所有的等式一定是方程. ( )(3)241x x -+是方程. ( ) (4)51x -不是方程. ( )(5)78x x =不是等式,因为7x 与8x 不是相等关系. ( ) (6)55=是等式,也是方程. ( )(7)“某数的3倍与6的差”的含义是36x -,它是一个代数式,而不是方程. ( )练习3、一元一次方程的定义1.在下列方程中哪些是一元一次方程?哪些不是?说明理由:(1)3x+5=12; (2)31+x +2x =5; (3)2x+y=3; (4)y 2+5y -6=0; (5)x3-x =2.2.已知2(1)(1)30k x k x -+-+=是关于x 的一元一次方程,求k 的值.3.已知方程()7421=+--m x m 是关于x 的一元一次方程,则m=_________4.已知方程1(2)40a a x --+=是一元一次方程,则a = ;x = .练习4、一元一次方程的解与解法1)一元一次方程的解 一)、根据方程解的具体数值来确定1.若关于x 的方程a xx -=+332的解是2x =-,则代数式21aa -的值是_________。
第五章一元一次方程小结与复习教学目的:1.复习本章的知识要点及其联系;2.巩固并熟练掌握一元一次方程的解法;3.较熟练地列出一元一次方程解应用题教学重点:一元一次方程的解法及应用教学难点:依据相等关系准确地列出一元一次方程教学过程:一、复习提问:1.你学完本章后有何收获?(学习一元一次方程的解法及应用)2.本章主要学习了哪些知识?(一元一次方程的意义、解法、应用)3.什么叫一元一次方程?什么叫一元一次方程的解?强调:一个未知数,最高次数一次。
1x+2=0 不是一元一次方程。
自觉养成检验的习惯4.叙述一元一次方程的解法步骤及每一个解题步骤应注意什么?去分母:不漏乘加括号去括号:注意分配;括号前是负号时要变号移项:注意要变号5.列方程解应用题的步骤有哪些?关键是什么?审题:分析题意,找出题中的数量关系及其关系;设元:选择一个适当的未知数用字母表示(例如x);列方程:根据相等关系列出方程;解方程:求出未知数的值;检验:检验求得的值是否正确和符合实际情形,并写出答案.关键:正确审清题意,找准“等量关系”二、习题讲解:1.有关定义运用的习题(填空题)2.有关方程解的判断及运用(解与解法的结合)(填空选择题)3.解下列各方程:P195/复习题/知识技能第一题(1~8)4.列方程解应用题(只要求写出假设步骤并列出一元一次方程)P195/问题解决/第1~11题。
三、作业一、选择题(每小题3分,共30分)1.下列方程中,是一元一次方程的是()A.243x x -=B.0x =C.23x y +=D.11x x -= 2.(2013•福建晋江中考)已知关于x 的方程2x a --5=0的解是2x =-,则a 的值为( ) A .1 B .-1 C .9 D .-93.已知方程235x +=,则610x +等于( )A.15B.16C.17D.344.甲、乙两人练习赛跑,甲每秒跑7 m ,乙每秒跑6.5 m ,甲让乙先跑5 m ,设x s 后甲可追上乙,则下列四个方程中不正确的是( )A.7 6.55x x =+B.75 6.5x x +=C.(7 6.5)5x -=D.6.575x x =-5.如果三个正整数的比是1∶2∶4,它们的和是84,那么这三个数中最大的数是( )A.56B.48C.36D.126.某商人在一次买卖中均以120元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )A.赚16元B.赔16元C.不赚不赔D.无法确定7.已知21(35)m --有最大值,则关于x 的方程5432m x -=+的解是x =( )A.79B.97C.79-D.97- 8. 已知等式523+=b a ,则下列等式中不.成立的是( ) A.b a 253=- B.6213+=+b aC.f bf ac 523+=D.3532+=b a 9.若关于x 的方程042=-+a x 的解是2-=x ,则a 等于( )A.-8B.0C.2D.810.小明在做解方程作业时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是:11222y y -=,怎么办呢?小明想了一想,便翻看书后答案,此方程的解是53y =-,于是很快就补好了这个常数,你能补出这个常数吗?它应是( )A.1B.2C.3D.4二、填空题(每小题3分,共24分)11. 若与互为相反数,则的值是 .12.如果关于x 的方程340x +=与方程3418x k +=是同解方程,则k = . 13.已知方程23252x x -+=-的解也是方程32x b -=的解,则b =_________. 14.已知方程233m x x -=+的解满足10x -=,则m ________.15.若52x +与29x -+互为相反数,则2x -的值为 .16.(2013•四川凉山中考)购买一本书,打八折比打九折少花2元钱,那么这本书的原价是 元.17.(四川自贡中考)某公路一侧原有路灯106盏,相邻两盏灯的距离为36 m ,为节约用电,现计划全部更换为新型节能灯,且相邻两盏灯的距离变为54 m ,则需更换新型节能灯 盏.18.当日历中同一行中相邻三个数的和为63,则这三个数分别为 .三、解答题(共46分)19.(12分)解下列方程:(1)10(1)5x -=;(2)7151322324x x x -++-=-; (3)2(2)3(41)9(1)y y y +--=-;(4)0.89 1.33511.20.20.3x x x --+-=. 20.(5分)m 为何值时,关于x 的方程4231x m x -=-的解是关于x 的方程23x x m =-的解的2倍?21.(5分)将一批工业最新动态信息输入管理储存网络,甲单独做需要6 h ,乙单独做需要4 h ,甲先做30 min ,然后甲、乙一起做,则甲、乙一起做还需要多长时间才能完成工作?22.(6分)有一列火车要以每分钟600 m 的速度过完第一、第二两座铁桥,过第二座铁桥比过第一座铁桥多5 s 时间,又知第二座铁桥的长度比第一座铁桥长度的2倍短50 m ,试求两座铁桥的长分别为多少?23.(6分)某生态食品加工厂收购了一批质量为10 000 kg 的某种山货,根据市场需求对其进行粗加工和精加工处理,已知精加工的该种山货质量比粗加工的质量3倍还多2 000 kg ,求粗加工的该种山货质量.24.(6分)植树节期间,两所学校共植树834棵,其中海石中学植树的数量比励东中学的2倍少3棵,求两校各植树多少棵.25.(6分) 为了鼓励居民节约用水,某市自来水公司对每户月用水量进行计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费标准相同,以下是小明家15月份用水量和交费情况:月份 1 2 3 4 5 用水量(吨)810 11 15 18费用(元)16 2023 35 44根据表格中提供的信息,回答以下问题:(1)求出规定吨数和两种收费标准.(2)若小明家6月份用水20吨,则应缴多少元?(3)若小明家7月份缴水费29元,则7月份用水多少吨?参考答案一、选择题1.B 解析:243x x -=中,未知数的次数是2,所以不是一元一次方程;23x y +=中,有两个未知数,所以不是一元一次方程;11x x -=不是整式方程.故选B.2.D 解析:将2x =-代入方程,得450a ---=,解得9a =-.故选D.3.B 解析:解方程235x +=,可得1x =.将1x =代入610x +,可得61061016x +=+=.4.B 解析:x s 后甲可追上乙,是指x s 时,甲跑的路程等于乙跑的路程,所以可列方程7 6.55x x =+,所以A 正确;将7 6.55x x =+移项、合并同类项,可得(7 6.5)5x -=,所以C 正确;将7 6.55x x =+移项,可得6.575x x =-,所以D 正确.故选B.5.B 解析:设这三个正整数分别为,2,4x x x .根据题意,得2484x x x ++=.解得12x =.所以这三个数中最大的数是448x =,故选B.6.B 解析:设此商人赚钱的那件衣服的进价为x 元,则x (1+25%)=120.解得96x =.设此商人赔钱的那件衣服进价为y 元,则y (1-25%)=120.解得160y =.所以他一件衣服赚了120-96=24(元),一件衣服赔了160-120=40(元),所以卖这两件衣服,总共赔了40-24=16(元).故选B.7.A 解析:由21(35)m --有最大值,可得350m -=,则53m =,554323x ⨯-=+,解得79x =.故选A. 8.C 解析:A 项可由移项得到;B 项可由方程两边都加上1得到;D 项可由方程两边同除以3得到,只有C 项是不一定成立的. 9. D 解析:将2-=x 代入方程得044=-+-a ,解得8=a .10.C 解析:设所缺的部分为,则x y y -=-21212, 把53y =-代入,可求得,故选C .二、填空题11. 5 解析:∵与互为相反数,∴ ,解得,则. 12.112解析:由340x +=可得43x =-.又因为340x +=与3418x k +=是同解方程,所以43x =-也是3418x k +=的解代入可求得112k =. 13.137 解析:由23252x x -+=-,得2420(515)x x -=-+.解得97x =. 所以9133277b =⨯-=. 14.-6或-12 解析:由10x -=,得1x =±.当1x =时,由233m x x -=+,得2313m -=+,解得6m =-; 当1x =-时,由233m x x -=+,得2313m --=-,解得12m =-. 综上可知,6m =-或12m =-.15.173- 解析:由题意可列方程52(29)x x +=--+,解得11.3x =- 所以11172233x -=--=-. 16.20 解析:设这本书的原价为x 元,由题意得0.9x -0.8x =2,解得x =20. 17.71 解析:设需更换的新型节能灯有x 盏,则54(x -1)=36×(106-1),54x =3 834,x =71,故需更换的新型节能灯有71盏.18.20,21,22 解析:设中间一个数为x ,则与它相邻的两个数分别为1,1x x -+.根据题意,得1163x x x -+++=.解得21x =.所以这三个数分别为20,21,22.三、解答题19.解:(1)10(1)5x -=.去括号,得10105x -=.移项,得1015x =.系数化为1,得32x =. (2)7151322324x x x -++-=-. 去分母,得4(71)6(51)243(32)x x x --+=-+.去括号,得2843062496x x x ---=--.移项,得2830924664x x x -+=-++.合并同类项,得728x =.系数化为1,得4x =.(3)2(2)3(41)9(1)y y y +--=-.去括号,得2412399y y y +-+=-.移项,得2129934y y y -+=--.合并同类项,得2y -=.系数化为1,得2y =-.(4)0.89 1.33511.20.20.3x x x --+-=. 去分母,得(0.89)6(1.33)451)x x x ---=+(.去括号,得0.897.818204x x x --+=+.移项,得9182047.80.8x x x -+-=+-.合并同类项,得1111x -=.系数化为1,得1x =-.20.解:关于x 的方程4231x m x -=-的解为21x m =-.关于x 的方程23x x m =-的解为3x m =.因为关于x 的方程4231x m x -=-的解是关于x 的方程23x x m =-的解的2倍,所以2123m m -=⨯,所以14m =-. 21.解:设甲、乙一起做还需要x h 才能完成工作. 根据题意,得111116264x ⎛⎫⨯++= ⎪⎝⎭.解得115x =. 115h=2 h 12 min. 答:甲、乙一起做还需要2 h 12 min 才能完成工作.22.解:设第一座铁桥的长为x m ,则第二座铁桥的长为(250)x -m ,过完第一座铁桥所需要的时间为600x min ,过完第二座铁桥所需要的时间为250600x -min . 依题意,可列出方程600x +560=250600x -.解得100x =. 所以250210050150x -=⨯-=.答:第一座铁桥长100 m ,第二座铁桥长150 m .23.解:设粗加工的该种山货质量为x kg.根据题意,得(32000)10000 x x ++=.解得2000 x =.答:粗加工的该种山货质量为2 000 kg .24.解:设励东中学植树x 棵.根据题意,得(23)834x x +-=,解得279x =.2322793555x -=⨯-=.答:励东中学植树279棵,海石中学植树555棵.25. 分析:(1)根据1、2月份可知,当每月用水量不超过10吨时,每吨收费2元.根据3月份的条件,用水11吨,其中10吨应交20元,超过的1吨收费3元,则超出10吨的部分每吨收费3元.(2)根据求出的收费标准,则用水20吨应缴水费就可以算出.(3)中存在的相等关系是:10吨的费用20元+超过部分的费用=29元.解:(1)从表格中可以看出规定吨数为不超过10吨(包括10吨),每吨2元,超过10吨的部分每吨3元.(2)小明家6月份的水费是:(元). (3)设小明家7月份用水吨,因为,所以. 由题意得,解得:. 故小明家7月份用水13吨.学习名言:1、学习必须与实干相结合。
第7章绿色植物与生物圈第1节绿色植物在生物圈中的作用整理要点:开始课前自主学习了,先试试你的身手吧!1:生物圈中生活着多种多样的生物,其中,是生物圈中最基本和最重要的生物成分,它对生物圈的存在和发展起着决定性的作用。
2:绿色植物能够通过作用吸收光能,并将其转化为化学能,储存在有机物中。
3:绿色植物的光合作用起到维持大气中二氧化碳和氧的作用。
从而为人类和一切需氧生物的生存创造了必要条件。
4:植物通过根吸收水分,再通过作用散失水分,从而促进了生物圈的水循环。
自主研练:重点,难点,常考点,当堂学习,当堂巩固,高效率!判断下列说法是否正确,正确的画“V”,错误的画“X”。
植物的蒸腾作用会散失大量的水分,这是一种浪费。
()植物的气孔很小,因此,通过气孔散失的水分很少。
()在植物体内,水住高处流,这主要是蒸腾作用拉动的。
()1.(1)×;(2)×;(3)√。
3、将绿色水草放在金鱼缸里的作用,主要是为了()A、增加养料B、增加氧气C、保持水清洁4.下列何种生态结构较为稳定 [ ]A.生物种类少 B.食物链构成的食物的网络复杂C.食物链较长 D.食物链中消费者多7.在生态系统的碳循环过程中,CO2进入生物群落是通过 [ ]A.呼吸作用 B.光合作用C.蒸腾作用 D.自由扩散12.生活在高山上的人,血液中红细胞数量比普通人多,和这一现象有关的生态因素是 [ ] A.阳光B.温度 C.水分 D.大气3.C 4.B 7.B 12.D16.下面是生态系统的碳循环示意图,请回答:(1)生态系统中碳循环首先依赖于_________________。
(2)图中分解者通过________和________两种分解方式将生物组织内的碳放回大气中。
(3)图中A里的碳,除碳酸盐外,通过________回到大气中。
(4)在生态系统中,碳元素主要以________状态进行循环,碳循环始终与________结合在一起进行。
16.(1)绿色植物的光合作用;(2)有氧呼吸、无氧呼吸(发酵)(3)燃烧(4)CO2(气体)能量流动1:春季植树时,移栽的树苗常被剪去了大量的枝叶,这是为什么?2:有的草原比较干旱,为改变这种状况,有人主张多种树,因为树林能够保持水土,树林的蒸腾作用强烈,会消耗大量的地下水,导致地下水位下降,进而加重旱情。
你对此持什么看法?3:根据你的理解,谈一谈“治水先治山”的道理。
答案:2.因为叶片会通过蒸腾作用散失大量的水分,导致树苗因缺水而死亡,所以要剪去大量的枝叶。
3.这是一道开放性的讨论题,不要求得出一致的结论。
以下提示仅供参考。
提示:在草原适度种树,可以保持水土;但是如果种树过多,叶片的蒸腾作用会带走大量的地下水。
4.山水相依,唇亡齿寒。
治水必须先治山,植树造林,绿化荒山,能够防治水土流失,保持土壤中的水分含量。
同时,植物的蒸腾作用还能促进降水,改善小气候。
这对防止或减少洪、涝、旱灾的发生有很重要的意义。
人与自然:走出教材,进入大自然,里面的世界真精彩哟!植物相亲相克行为将两种植物种在一起,常常出现这样一些有趣的现象。
有些表现“相亲相爱”,相互助长;有些则冤家对头,“八字相克”,搞得不是一方受害,就是两败俱伤。
这种现象就是植物间的相亲相克行为。
如果把蓖麻和芥菜种在一起,虽然前者要比后者粗壮许多,但前者下部的叶子会大量枯黄而逐渐死去。
如果让番茄和黄瓜生活在同一个“房子”里,它们就会彼此天天赌气,不好好地生长,因而导致减产。
如果甘蓝和芹菜间种,两者生长都不会好,甚至死亡。
在葡萄园种甘蓝,葡萄的生长就会受到抑制。
在森林里,如果栎树和榆树碰到一起,那么你会发现栎树的枝条会背向榆树弯曲生长,力求远避这个“坏邻居”。
上述这些现象是怎么一回事呢?原来很多植物会从体内分泌出某种气体或汁液,影响或者抑制了其它植物的生长。
但也有些植物的分泌物对某些病毒、细菌和害虫有很强的杀伤力,因而,它能同其它植物相处甚密,相得益彰。
因此它们能互惠互利,长期共存。
如果韭菜和甘蓝间行种植,就能使甘蓝的根腐病减轻。
这是由于韭菜能产生一种浓烈的特殊的怪味,能驱虫杀菌。
因此,韭菜常常是许多其它植物的好朋友。
大蒜和棉花、大白菜等间行种植,大蒜所挥发出来的大蒜素,既能杀菌,又能赶走害虫。
所以,大蒜和棉花、大白菜等植物能“相亲相爱”过一生。
各种植物间的这种相亲相克的关系是极其复杂的,研究它们的关系及其奥秘,对于发展农业生产,提高农作物的产量,从而获得丰收是很有意义的。
探究性学习:学习探究,迁移发展,你的能耐不是真的有长进了么?“君不见黄河之水天上来,奔流到海不复回。
”这是唐朝大诗人李白的著名诗句。
根据所学的知识,分析这句话有没有科学依据?并到图书馆查阅相关的资料,和周围的同学讨论交流各自的意见。
(可参考网站)/tyweb/Article_Show.asp?ArticleID=406第2节我国的植物资源整理要点:开始课前自主学习了,先试试你的身手吧!1:覆盖地表而有规律地生活在一起的一群植物叫做。
2:常绿阔叶林又叫,是温带地区在湿润的海洋性气候条件下生长的植被类型之一。
我国落叶阔叶林主要分布在和的大部分地区。
针叶林在我国主要分布在和。
我国的草原主要分布在平原、高原和高原等地。
3:我国的植物资源十分丰富,名列世界第位。
4:被誉为植物界的“大熊猫”的是。
5:被称为“鸽子树”的是。
自主研练:重点,难点,常考点,当堂学习,当堂巩固,高效率!根据所学的知识填表。
(1)你已经知道我国有哪些珍稀的动植物?(2)怎样保护珍稀动植物?(3)讨论:假如你遇到了一只受伤的黑颈鹤,应该怎么办?调查:当地有哪些珍稀的动植物?有没有自然保护区?人与自然:走出教材,进入大自然,里面的世界真精彩哟!热带雨林——地球的“肺”世界上的热带雨林主要分布在赤道附近。
那里土地肥沃,雨量充沛,生活着种类繁多,形态各异的植物、动物和其它生物。
热带雨林不仅为生物提供了理想的生存环境,更为重要的是,它通过光合作用吸收了大量的二氧化碳,转化为有机物,储藏在植物体内;同时,释放出大量氧气,维持了生物圈中的碳——氧平衡,因而被称为地球的“肺”。
不仅如此,热带雨林还通过蒸腾作用调节气候,通过扎根大地保持水土。
热带雨林是人类和其他生物生存和发展不可缺少的宝贵的自然遗产。
从20世纪60年代开始,人类在经济利益的驱动下,对热带雨林实话了毁灭性的野蛮开发,随着推土机、斧头、锯子的推进,热带雨林大片大片地倒下。
热带雨林被毁,失去的难道仅仅是树木吗?虽然人们已经意识到热带雨林对于生物圈的重要价值,但是有人仍然为了眼前利益,不惜以牺牲子孙后代的幸福为代价,继续砍伐热带雨林。
如果再不采取保护措施,用不了50年,热带雨林就会全部消失。
想想那是多么可怕和悲惨的前景。
保护热带雨林,人类责无旁贷。
探究性学习:学习探究,迁移发展,你的能耐不是真的有长进了么?1998年6月到8月。
我国长江、嫩江和松花江都发生了特大洪涝灾害。
2000年春天,我国北方地区出现了罕见的沙尘暴。
根据所学的知识,并到图书馆查阅相关的资料,为什么会发生这样的自然灾难?和周围的同学交流各自的意见。
(可查阅网站/newscenter/2002-03/22/content_327092.htm)第3节我国的绿色生态工程整理要点:开始课前自主学习了,先试试你的身手吧!1:我国的全国“植树节”是每年的月日。
2:“三北”防护林工程是我国十大生态建设工程的第一个巨大植树造林工程。
所谓“三北”,指的是我国、和地区。
3:1989年,邓小平同志为“三北”防护林工程题名“”。
4:1987年,“三北”工程被联合国环境规划署授予“”称号。
自主研练:重点,难点,常考点,当堂学习,当堂巩固,高效率!1.许多树木对大气粉尘污染起到阻滞、过滤作用,其原因是 [ ]①森林枝叶茂盛,能减小风速②叶面有茸毛,能分泌油质和粘性物质③能分泌强大抗生素④能吸收各种有毒气体⑤蒙尘的植物经雨水的冲洗后,又能迅速恢复以阻拦尘埃。
A.①④B.③④ C.①②⑤ D.②③⑤2.经过十多年努力,我国西北防护林带已经初步建成,建立了新的生态平衡,其重要意义是 [ ]A.解决了环境污染问题 B.使生态系统朝着更有益于人类的方向发展C.建立了畜牧业的生产基地 D.建立了自然保护区3.我国为了保护丹顶鹤,在南方和北方分别设立了自然保护区,这是由于丹顶鹤的生活习性受下列何种因素的影响 [ ]A.水分 B.温度 C.阳光 D.食物4.自然保护区具有的功能是 [ ]A.保护自然和自然资源 B.保护代表不同自然地带的自然环境C.保护生态系统 D.上述三项的总和5.国际上公认的评价一个国家环境质量的主要指标之一是 [ ]A.有无环境保护法规 B.工厂三废的处理水平C.人均占有绿地面积 D.自然保护区的总面积与国土面积之比6.在长白山建立自然保护区的目的,是为了保护 [ ]A.稀有动物东北虎 B.稀有植物金钱松C.稀有鸟类丹顶鹤 D.代表不同地带的自然生态系统7.下列生物属于我国特有的珍贵爬行动物是 [ ]A.大鲵 B.中华鲟 C.扬子鳄 D.白鳍豚8.衡量某地区的生态环境是否优越,主要看该地区的森林覆盖率是否达到 [ ] A.20%以上 B.30%以上C.12.7%以上 D.10%以上9.在城市的闹市区,人口稠密,空气中细菌的密度相对比较高。
在绿化市区时,下列4组树木品种,比较适宜的一组是 [ ]A.法国梧桐、圆柏、黑核桃 B.柳杉、月季、洋槐C.泡桐、樟树、柳树 D.银杏、白杨、雪松10.林木在低浓度范围内能吸收有毒气体,使空气得到净化。
这个现象说明 [ ] A.生态系统具有自动调节的能力 B.植物具有应激性C.生物具有适应性 D.生物具有遗传性11.为了保护野生动物,我国已经决定禁止使用两种动物中药材,它们是 [ ] A.斑马肉和犀牛角 B.熊猫肉和虎肉C.犀牛角和虎骨 D.眼镜蛇胆和大鲵肉12.我国特有的珍贵的哺乳动物,俗称“四不像”的是 [ ]A.猫熊 B.金丝猴C.麋鹿 D.大鲵13.为保护稀世珍宝大熊猫,我国建立的自然保护区是 [ ]A.西双版纳自然保护区 B.鼎湖山自然保护区C.武夷山自然保护区 D.卧龙、王朗自然保护区14.我国的虎已经处在灭绝的边缘,造成这种现象的原因是 [ ]A.虎适应自然环境的能力下降 B.虎处的营养级较高,食物不足C.环境污染造成虎的出生率下降D.虎被乱捕乱杀且栖息的森林减少15.保护草原生态系统的生态平衡,使人与自然和谐发展的有效措施是 [ ]A.开垦草原,改牧场为农田 B.禁止狩猎,引入食草动物C.保护植被,实行适度放牧 D.提倡狩猎,扩大放牧数量16.城市绿化常用圆柏、法国梧桐等树种,它们对环境最突出的作用是 [ ]A.保持水土 B.调节气候C.杀灭细菌 D.净化空气17.引起环境污染的因素不包括 [ ]A.大量使用化肥和有机农药 B.森林吸收CO2放出O2C.生活垃圾、汽车排放尾气 D.工业排放的“三废”18.哪一措施最可能是与可持续发展的原则不相符合 [ ]A.森林的采伐量小于生长量B.人工鱼塘生产者的能量少于消费者的能量C.农田从收获中输出的氮素多于补充的氮素 D.农田施用无机氮肥多于生物固定的氮肥1:造成环境污染和破坏的重要原因是_______不合理,______________不合理。