《数学模型》(第四版)第二章初等模型(2.3 划艇比赛的成绩 2.7 核军备竞赛)

佛山科学技术学院上 机 报 告课程名称 数学建模 上机项目 划艇比赛的成绩专业班级 姓 名 学 号一、问题提出数学建模：划艇比赛的成绩赛艇是一种靠桨手划桨前进的小船，分单人艇、双人艇、四人艇和八人艇四种。

各种艇虽大小不同，但形状类似。

现T.A.McMahon 对四种赛艇 (单人、双人、四人、八人) 4次国际大赛冠军的成绩进行比较（见教材P29数据），认为比赛成绩与桨手数之间存在某种关系。

试根据比赛数据（见教材P29数据），揭示：这种关系，建立并求解数学模型，画出图形进行检验。

问题分析：赛艇前进时收到的阻力主要是艇浸没部分与水之间的摩擦力。

艇靠桨手的力量克服阻力保持一定的速度前进。

桨手越多划艇前进的动力越大。

但是艇与桨手总质量的增加会使艇浸没面积加大，于是阻力加大，增加的阻力将抵消一部分增加的动力。

建模目的时寻求桨手数量与比赛成绩（航行一定距离所需时间）之间的数量规律。

如果假设艇速在整个赛程中保持不变，那么只需构造一个静态模型，使问题简化为建立桨手数量与艇速之间的关系。

注意到在实际比赛中桨手在极短的时间内使艇加速到最大速度,然后把这个速度保持到终点,那么上述假设也是合理的。

为了分析所受阻力的情况，调差了各种艇的几何尺寸和重量，给出了上表的数据。

可以看出，桨手数n 增加时，艇的尺寸l,b 及艇重0w 都随之增加，但比值l b 和0w n 变化不大。

若假定lb是常数，即各种艇的形状一样，则可得到艇浸没面积与排水体积之间的关系。

若假定0wn是常数，则可得到艇和桨手的总重量与桨手数之间的关系。

此外还需要对桨手体重、划桨功率、阻力与艇速的关系等方面作出简化且合理的假定，才能运用合适的物理定律建立需要的模型。

模型假设：1. 各种艇的几何形状相同，lb为常数；艇重0w 与桨手数n 成正比。

这是艇的静态特性。

2. 艇速v 是常数，前进时受的阻力f 与2sv 成正比（s 是艇浸没部分面积）。

这是艇的动态特性。

3. 所有桨手的体重都相同，记住w;在比赛中每个桨手功率p 保持不变，且p 与w 成正比。

第一部分初等模型1. 划艇比赛赛艇是一种靠桨手划桨前进的小船，分单人、双人、四人、八人四种，八人艇还分重量级（平均体重86公斤）和轻量级（平均体重73公斤）。

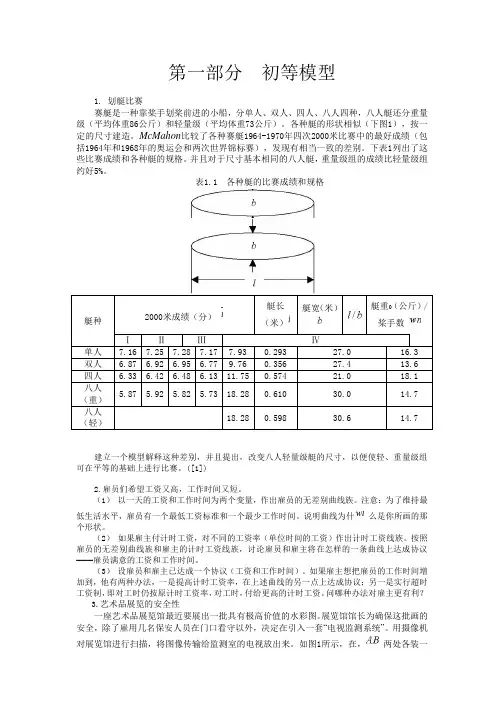
各种艇的形状相似（下图1），按一定的尺寸建造。

McMahon比较了各种赛艇1964-1970年四次2000米比赛中的最好成绩（包括1964年和1968年的奥运会和两次世界锦标赛），发现有相当一致的差别。

下表1列出了这些比赛成绩和各种艇的规格。

并且对于尺寸基本相同的八人艇，重量级组的成绩比轻量级组约好5%。

表1.1 各种艇的比赛成绩和规格Ⅳ建立一个模型解释这种差别，并且提出，改变八人轻量级艇的尺寸，以便使轻、重量级组可在平等的基础上进行比赛。

([1])2.雇员们希望工资又高，工作时间又短。

（1）以一天的工资和工作时间为两个变量，作出雇员的无差别曲线族。

注意：为了维持最低生活水平，雇员有一个最低工资标准和一个最少工作时间。

说明曲线为什么是你所画的那个形状。

（2）如果雇主付计时工资，对不同的工资率（单位时间的工资）作出计时工资线族。

按照雇员的无差别曲线族和雇主的计时工资线族，讨论雇员和雇主将在怎样的一条曲线上达成协议——雇员满意的工资和工作时间。

（3）设雇员和雇主已达成一个协议（工资和工作时间）。

如果雇主想把雇员的工作时间增加到，他有两种办法，一是提高计时工资率，在上述曲线的另一点上达成协议；另一是实行超时工资制，即对工时仍按原计时工资率，对工时，付给更高的计时工资。

问哪种办法对雇主更有利？3.艺术品展览的安全性一座艺术品展览馆最近要展出一批具有极高价值的水彩图。

展览馆馆长为确保这批画的安全，除了雇用几名保安人员在门口看守以外，决定在引入一套“电视监测系统”。

用摄像机对展览馆进行扫描，将图像传输给监测室的电视放出来。

如图1所示，在，两处各装一台摄像机。

在展览馆的展墙上，每隔挂一幅画。

两个摄像机镜头的视角为，完成一次来回扫描。

但是，在监测室的工作人员只有的时间在观察电视画面。

第二章 初等模型如果研究对象的机理比较简单，一般用静态、线性、确定性模型描述就能达到建模的目的时，我们基本上可以用初等数学的方法来构造和求解模型。

通过下面的几个实例我们能够看到，用很简单的数学方法就可以解决一些有趣的实际问题。

需要强调的是，衡量一个模型的优劣完全在于它的应用效果，而不是它看它采用了多么高深的数学方法。

进一步说，对于某个实际问题我们如果能够用初等方法和所谓的高等方法建立了两个模型，而它们的应用效果相差无几的话，那么受人们欢迎并采用的，一定是前者而非后者。

§2.1公平的席位分配设有A 、B 两个单位，各有人数1p 、2p 个，现在要求按人数选出q 个代表召开一次代表会议。

那么怎样分配这q 个席位呢？一般的方法是令：q p p p q 211*1+= q p p p q 212*2+= （2.1）若*1q ，*2q 恰好是两个整数，就以*1q ，*2q 分别作为A ，B 两个单位的席位数，即可以获得一个完全合理的分配方案。

当*1q ，*2q 不是两个整数时，那么怎样分配才合理呢？下面我们就来讨论这个问题。

首先给出一种自然的想法，也就是通常所执行的方法。

即由（2.1）式计算出的*1q ，*2q ，用][*i i q q =表示*i q 的整数部分。

当*1q －1q ＞*2q －2q 时，则用1q ＋1与2q 分别作为A ，B 两个单位的席位数；当*2q －2q ＞*1q －1q 时，则用1q 与2q ＋1分别作为A ，B 两个单位的席位数；而当*2q －2q ＝*1q －1q 时，就只能由A ，B 两个单位协商来确定那多余的一个席位了。

这个方法的优点是简单、方便，并被很多人所接受，同时也容易推广到m （m ＞2）个单位的席位分配问题。

但是这个分配方案是存在弊病的，它有明显的不合理性。

例1 某学校有3个系共200名学生，其中甲系100名，乙系60名，丙系40名。

若学生代表会议设20个席位，公平而又简单的席位分配办法是按学生人数的比例分配，显然甲乙丙三系分别应占有10、6、4个席位。

数学建模实验⼆初等模型实验集美⼤学计算机⼯程学院实验报告课程名称：数学模型班级：计算12 实验成绩：指导教师：付永钢姓名：实验项⽬名称：初等模型试验学号：上机实践⽇期：实验项⽬编号：实验⼆上机实践时间：2014.11⼀、实验⽬的掌握初等模型的建⽴的基本思路和⽅法，并了解其求解过程。

对给定的初等模型问题能够借助Matlab ⼯具进⾏求解。

⼆、实验内容实验 1 ⽤Matlab 验证划艇⽐赛成绩模型的结果，通过数值结果来检验你所得到的模型正确性。

(⾸先要阅读本⽬录中的Matlab 数据拟合和matlab 数据处理的相关材料)实验2 求解汽车刹车距离的模型，⽤Matlab 给出你的求解结果。

验证应该遵循的t 秒准则的标准。

实验3 从教材P56中的第7，13，14题，任选⼀题，建⽴相应的初等模型，并借助matlab 进⾏求解，并给出合理的模型解释。

三、实验使⽤环境WindowsXP 、Matlab6.1四、实验步骤1、划艇⽐赛成绩的模型检验根据推导出的模型公式和数据，对参数βα,进⾏求解βαn t =。

⾸先转换成对数形式：,log 'log n t βα+=其中ααlog '=然后对给定数据进⾏拟合。

代码：n=[1 2 4 8]t=[7.21 6.88 6.32 5.84]lgn=log(n);lgt=log(t);p=polyfit(lgn,lgt,1);alpha=exp(p(2));belta=p(1);x=1:20;y=alpha*x.^belta ;plot(x,y,’c*-‘) ;xlabel(‘Number of Athlete ’);ylabel(‘Time Cost ’);Matlab 拟合函数图像：结果分析：划艇⽐赛模型的结果为t∞n-（1/9）.。

在matlab中检验得belta =-0.1035与-（1/9）接近。

因此，模型正确。

2、汽车刹车距离验证代码：function E=fun1(a,x,y)Y=a(1)*x.*x+0.75*x;E=y-Y;%M⽂件结束%⽤lsqnonlin调⽤解决:x=[29.3 44 58.7 73.3 88 102.7 117.3];y=[44 78 124 186 268 372 506];a0=[0.5];options=optimset('lsqnonlin');a=lsqnonlin(@fun1,a0,[],[],options,x,y)%绘图plot(x,y,'o');hold on;x=[0:200];y=a(1)*x.*x+0.75*x;plot(x,y,'-');hold off结果分析：汽车刹车距离求解结果在Matlab的模型如上所⽰。

数学模型姜启源第四版答案【篇一：姜启源数学模型课后答案(3版)】t>第二章(1)（2008年9月16日）1．学校共1000名学生，235人住在a宿舍，333人住在b宿舍，432人住在c宿舍.学生们要组织一个10人的委员会，试用下列办法分配各宿舍的委员数：（1）. 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者; （2）. 1中的q值方法；（3）.d’hondt方法：将a、b、c各宿舍的人数用正整数n=1,2,3,??相除，其商数如下表：将所得商数从大到小取前10个（10为席位数），在数字下标以横线，表中a、b、c行有横线的数分别为2，3，5，这就是3个宿舍分配的席位.你能解释这种方法的道理吗？如果委员会从10个人增至15人，用以上3种方法再分配名额，将3种方法两次分配的结果列表比较.解：先考虑n=10的分配方案，3p1?235,p2?333,p3?432, ?pi?1000.i?1方法一（按比例分配）q1?p1n3?2.35,q2?p2n3?3.33, q3?p3n3?4.32?i?1pi?i?1pii?1pi分配结果为： n1?3, n2?3, n3?4 方法二（q值方法）9个席位的分配结果（可用按比例分配）为：n1?2,n2?3, n3?4第10个席位：计算q值为 q1?23522?3?9204.17, q2?33323?4?9240.75, q3?43224?5?9331.2q3最大，第10个席位应给c.分配结果为 n1?2,n2?3,n3?5方法三（d’hondt方法）此方法的分配结果为：n1?2,n2?3,n3?5此方法的道理是：记pi和ni为各宿舍的人数和席位（i=1,2,3代表a、b、c宿舍）.pinipinipini是每席位代表的人数，取ni?1,2,?,从而得到的近.中选较大者，可使对所有的i,尽量接再考虑n?15的分配方案，类似地可得名额分配结果.现将3种方法两次分配的结果列表如下：2．试用微积分方法，建立录像带记数器读数n与转过时间的数学模型. 解：设录像带记数器读数为n时，录像带转过时间为t.其模型的假设见课本.考虑t到t??t时间内录像带缠绕在右轮盘上的长度，可得vdt?(r?wkn)2?kdn,两边积分，得 ?vdt?2?k?(r?wkn)dntn22) ?t?2?rkvn??wkv2n.2第二章(2)（2008年10月9日）15．速度为v的风吹在迎风面积为s的风车上，空气密度是? ，用量纲分析方法确定风车获得的功率p与v、s、?的关系.解: 设p、v、s、?的关系为f(p,v,s,?)?0，其量纲表达式为: [p]=ml2t?3, [v]=lt量纲矩阵为：?2?1????3(p)10?1(v)200(s)?3?(l)?1(m)? ?0?(t)(??1,[s]=l2,[?]=ml?3,这里l,m,t是基本量纲.a=齐次线性方程组为：?2y1?y2?2y3?3y4?0??0 ?y1?y4??3y?y?012?它的基本解为y?(?1,3,1,1)由量纲pi定理得 ??p?1v3s1?1，?p??v3s1?1 ，其中?是无量纲常数. 16．雨滴的速度v与空气密度?、粘滞系数?和重力加速度g 有关，其中粘滞系数的定义是：运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比，比例系数为粘滞系数，用量纲分析方法给出速度v的表达式.解：设v,?,?,g 的关系为f(v,?,?,g)=0.其量纲表达式为[v]=lm0t-1，[?]=l-3mt0，[?]=mlt-2（lt-1l-1）-1l-2=mll-2t-2t=l-1mt-1，[g]=lm0t-2,其中l，m，t是基本量纲.量纲矩阵为?1?0?a=???1(v)?310(?)?11?1(?)1?(l)?0(m)? ?2?(t)?(g)齐次线性方程组ay=0 ，即? y1-3y2-y3?y4?0??0 ?y2?y3?-y-y-2y?034?1的基本解为y=(-3 ,-1 ,1 ,1) 由量纲pi定理得 ??v?*?3?1?g. ?v???g?，其中?是无量纲常数.16．雨滴的速度v与空气密度?、粘滞系数?、特征尺寸?和重力加速度g有关，其中粘滞系数的定义是：运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比，比例系数为粘滞系数，用量纲分析方法给出速度v的表达式.解：设v,?,?,?，g 的关系为f(v,?,?,?,g)?0.其量纲表达式为[v]=lmt，[?]=lmt，[?]=mlt（ltl）l=mlltt=lmt，[?]=lmt ，[g]=lmt 其中l，m，t是基本量纲. 量纲矩阵为?1?0a=????1(v)100(?)?310(?)?11?1(?)1?(l)?0(m)? ?2?(t)?(g)-1-3-2-1-1-1-2-2-2-1-1000-2齐次线性方程组ay=0 即 ?y1?y2?3y3?y4?y5?0?y3?y4?0 ???y1?y4?2y5?0?的基本解为??y1?(1,???y2?(0,??)2 1,?1,1,?)22231,0,0,?1得到两个相互独立的无量纲量 ??1?v??1/2g?1/2??3/2?1?1/2??g??2??即 v??g?1,?3/2?g1/2??1??2. 由?(?1,?2)?0 , 得 ?1??(?2)3/2?1?1? ??g?(??g1/2??1) , 其中?是未定函数.20.考察阻尼摆的周期，即在单摆运动中考虑阻力，并设阻力与摆的速度成正比.给出周期的表达式，然后讨论物理模拟的比例模型，即怎样由模型摆的周期计算原型摆的周期. 解：设阻尼摆周期t,摆长l, 质量m,重力加速度g，阻力系数k的关系为f(t,l,m,g,k)?0其量纲表达式为：[t]?lmt,[l]?lmt,[m]?lmt,[g]?lmt?2,[k]?[f][v]?1?mlt?2(lt?1)?1?lmt0?1，其中l，m，t是基本量纲.量纲矩阵为?0?0a=???110001010?20?(l)?1(m)? ??1?(t)(t)(l)(m)(g)(k)齐次线性方程组y2?y4?0??y3?y5?0 ??y?2y?y?045?1的基本解为11?y?(1,?,0,,0)?122 ?11?y2?(0,,?1,?,1)22?得到两个相互独立的无量纲量?tl?1/2g1/2??1?1/2?1?1/2k??2?lmg∴t?lg?1, ?1??(?2), ?2?klmg1/21/2klmg1/21/2∴t?lg() ，其中?是未定函数 .考虑物理模拟的比例模型，设g和k不变，记模型和原型摆的周期、摆长、质量分别为l?gkl?1/21/2t,t；l,l;m,m. 又t??(m?g)当无量纲量?l?l时，就有t?t?l?g?gl?l?l.《数学模型》作业解答第三章1（2008年10月14日）1. 在3.1节存贮模型的总费用中增加购买货物本身的费用,重新确定最优订货周期和订货批量．证明在不允许缺货模型中结果与原来的一样，而在允许缺货模型中最优订货周期和订货批量都比原来结果减少．【篇二：数学建模陈东彦版课后答案】t>2.9-3.7 3.6-5.144.1-7.14.4-7.35.9-11.1 5.1-9.1 6.5-4.7 6.10-4.14第1章建立数学模型1.1 在稳定的椅子问题中，如设椅子的四脚连线呈长方形，结论如何？（稳定的椅子问题见姜启源《数学模型》第6页）1.2 在商人们安全过河问题中，若商人和随从各四人，怎样才能安全过河呢？一般地，有n名商人带n名随从过河，船每次能渡k人过河，试讨论商人们能安全过河时，n与k应满足什么关系。

第三章 初等数学模型所谓初等数学模型主要是指建立模型所用的数学知识和方法主要是初等的，而不是高等的。

在解决实际问题的过程中，往往主要是是看解决问题的效果和应用的结果如何，而不在于用了初等的方法还是高等的方法，对于数学建模也是这样。

本章介绍了量纲分析法、比例与函数建模法，并给出了相应的一些模型。

第一节 量纲分析法量纲分析提出于20世纪初，是物理学中常用的一种定性分析方法，也是在物理领域中建立数学模型的一个有力工具。

它是在经验和实验的基础上, 利用物理定律的量纲齐次原则，确定各物理量之间的关系。

1.1 量纲齐次原则许多物理量是有量纲的，有些物理量的量纲是基本的，另一些物理量的量纲则可以由基本量纲根据其定义或某些物理定律推导出来。

例如在动力学中，把长度l ， 质量m 和时间t 的量纲作为基本量纲，记为[][][]T t M m L l ===,,；而速度f v ，力的量纲可表示为[][]21,--==MLT f LT v .在国际单位制中，有7个基本量：长度、质量、时间、电流、温度、光强度和物质的量，它们的量纲分别为L 、M 、T 、I 、Θ、J 、和N ，称为基本量纲。

任一个物理量q 的量纲都可以表成基本量纲的幂次之积，[]ηξεδγβαJ N I T M L q Θ=量纲齐次性原则 用数学公式表示一个物理定律时，等式两端必须保持量纲一致。

量纲分析就是在保证量纲一致的原则下，分析和探求物理量之间关系。

先看一个具体的例子，再给出。

1.2量纲分析的一般方法例1 （单摆运动）质量为m 的小球系在长度为l 的线的一端，线的另一端固定，小球偏离平衡位置后，在重力mg 作用下做往复摆动，忽略阻力，求摆动周期t 的表达式。

解：在这个问题中有关的物理量有g l m t ,,,设它们之间有关系式3211αααλg l m t =---------------（1.1）其中32,,ααα为待定常数，入为无量纲的比例系数，取（1.1）式的量纲表达式有[][][][]321αααg l m t = 整理得：33212αααα-+=T L MT --------------（1.2）由量纲齐次原则应有⎪⎩⎪⎨⎧=-=+=12003321αααα ---------------（1.3）解得：,21,21,0321-===ααα 代入（3．1）得 glt λ= -------（1.4）（1.4）式与单摆的周期公式是一致的1.3 Buckingham Pi 定理下面我们给出用于量纲分析建模的 Buckingham Pi 定理，定理（Buckingham Pi 定理） 设n 个物理量n x x x ,,,21 之间存在一个函数关系 ()0,,,21=n x x x f --------------（1.5）[][]m x x 1为基本量纲，n m ≤。