均匀传输线的分布参数计算
- 格式:doc
- 大小:388.50 KB
- 文档页数:7








传输线理论均匀传输线的传播常数γ:γ=()()C G L R j j 0000ωω++=α+j β式中α称为衰减常数,β称为相移常数,R 0 、 G 0 、 L 0 和 C 0分别为分布在传输线上的每米的电阻、电导、电感、电容。
均匀传输线的特性阻抗: Z c =C G L Rj j 0000ωω++ 传输线终端的反射系数:p=Z Z Z ZC L C L+- (Z L 为终端负载阻抗)当Z L =Z C 时,p=0,称为无反射匹配。
此时传输线的输入阻抗以及沿传输线任一点向终端看去的阻抗,都等于传输线的特性阻抗。
特性阻抗为Z C ,负载阻抗为Z L ,长度为ι的传输线的输入阻抗Z i :Z i =Z e e cl l p p γγ2211---+ 或用双曲线函数的形式表示为:Z i =Z Z Z Z Z C L C C Ll sh l ch l sh l ch γγγγ++由以上两式可以看出,对于同一负载Z L ,通过不同参数和不同长度的传输线接信号源,其输入阻抗是不同的。
因此,传输线可以作负载的阻抗变换器。
无损耗传输线R 0 =0 ,G 0=0的传输线称为无损耗传输线。
无损耗传输线的特性阻抗与传播常数: Z c =C L 0(是与频率无关的纯电阻) γ=j C L 00ω(α=0,β=C L 00ω)无损耗传输线上的驻波与驻波比设无损耗传输线终端负载阻抗为 Z L =R L +jX L ,则终端的反射系数为:p=Z Z Z ZC L C L+-=X Z R X Z R LC L L C L j j +++-))((=︳p ︱e j ϕ p 一般为复数。
除开Z L =∞(终端开路),Z L =0(终端短路)及R L =O (负载为纯电抗)外,都有︳p ︱<1,即在传输线终端及沿线各点,反射波的幅度都小于入射波的幅度。
反射波与入射波叠加,电压幅度沿线成为驻定的波浪式分布,这一现象称为线上存在驻波。

传输线基本公式1、电报方程对于一段均匀传输线,在有关书上可查到,等效电路如下图所示。
Z i V1V2Z2等效电路根据线的微分参数可列出经典的电报方程,解出的结果为:V1=21(V2+I2Z0)eγχ+21(V2-I2Z0)e-γχI1=Z21(V2+I2Z0)eγχ-Z21(V2-I2Z0) e-γχ式中,x是传输线上距离的坐标,它由负载端起算,即负载端的x为0。
γ为传输线的传输系统,γ=α+jβ,α为衰减常数,β为相移常数。
无耗时γ=jβ。
一般情况下常用无耗线来进行分析,这样公式简单一些,也明确一些,或者说理想化一些。
而这样做实际上是可行的,真要计算衰减时,再把衰减常数加上。
Z0为传输线的特性阻抗。
Z i为源的输出阻抗(或源内阻),通常假定亦为Z0;若不是Z0,其数值仅影响线上电压的幅度大小,并不影响其分布曲线形状。
上述两式中,前一项x 越大值越大,相位也越领先,即为入射波。
后一项x 越大值越小,相位也越落后,即为反射波。
由于一般只对线上的电压、电流的空间分布感兴趣,因此上式中没有写时间因子e j ωt (下同)。
2、无耗线上的电压电流分布上面式(1.1)和式(1.2)中,下标2为负载端,下标1为源端,而x 可为任意值,那么V 1、I 1可以泛指线上任意一点的电压与电流,因此下面将V 1、I 1的下标1字省掉。
V=21(V 2+I 2Z 0)e j βχ +21(V 2-I 2Z 0) e -j βχ =21(V 2+I 2Z 0)e j βχ{1+Γe -j (2βχ-ψ)} I=21{ (V 2+I 2Z 0)/ Z 0}e j βχ{1-Γe -j (2βχ-ψ)} 式中,发射系数Γ=Γ∠ψ=022022Z I V Z I V +-=0202Z Z Z Z +- Γ≤1,要想反射为零,只要Z 2 =Z 0即成。
上式中,首项不是x 的函数,而e jβχ为相位因子,不影响幅度。
只是末项影响幅度分布。
本节要点传输线分类均匀传输线等效及传输线方程传输线方程的解传输线方程解的分析传输线的工作特性参数本节要点尺寸小平行双线同轴线带状线微带线介质波导镜像线单根表面波传输线5短线λlu inu out ≈u in集总参数电路表示集总参数lu out ≠u inu in长线分布参数电路表示z zt z i t z i t z z i z z t z u t z u t z z u Δ∂∂=−Δ+Δ∂∂=−Δ+),(),(),(),(),(),(3. 传输线方程的解第一章 均匀传输线理论之•均匀传输线方程及其解U ( z ) = A1e γz + A2 e − γz = U + +U − 电压和电流解为: I ( z ) = A1e γz − A2 e −γz Z 0 = I + + I −()eγz 表示向-z方向传播的波,即自源到负载方向的入射 波,用U+或I +表示;U + = A1e γz I + = A1e γz Z 0 U − = A2 e − γz I − = − A2 e −γz Z 0e −γz 表示向+z方向传播的波,即自负载到源方向的反射波, 用U-或I -表示。
《微波技术与天线》第一章 均匀传输线理论之•均匀传输线方程及其解始端 传输线的边界条件通常有以下三种 已知始端电压和始端电流Ui、Ii 已知终端电压和终端电流Ul、Il已知信号源电动势Eg和内阻Zg以及负载阻抗Zl终端《微波技术与天线》第一章 均匀传输线理论之•均匀传输线方程及其解U ( z ) = A1e γz + A2 e − γz边界条件: V (0) = VL , I (0) = I LI ( z ) = A1e γz − A2 e −γz Z 0()U L + Z0 I L ; A1 = 2U L − Z0 I L A2 = 2jZ 0 sin βz ⎤ ⎥ ⎡U l ⎤ cos βz ⎥ ⎢ I l ⎥ ⎣ ⎦ ⎦⎡ cos βz ⎡U ( z )⎤ ⎢ ⎢ I ( z ) ⎥ = ⎢ j 1 sin βz ⎦ ⎣ ⎣ Z0《微波技术与天线》第一章 均匀传输线理论之•均匀传输线方程及其解4.传输线方程解的分析u ( z , t ) = Re[U ( z )e jωt ] = A1 e +αz cos(ωt + β z ) + A2 e −αz cos(ωt − β z ) i ( z , t ) = Re[ I ( z )e jωt ] = 1 A1 e +αz cos(ωt + βz ) − A2 e −αz cos(ωt − β z ) Z0[]结论传输线上任意点处电压或电流均由沿-z方向传播的入射波和沿+z方向 传播的反射波叠加而成。
均匀传输线的分布参数计算0 引言传输线作为一种输送能量和传递信号的装置,由于其应用十分广泛而成为了很有意义的研究对象。
在长距离输电线路、远距离通信线路、高频测量线路、计算机信号传输以及高速数控系统中均应该考虑线路参数的分布性。
[1]均匀传输线模型是电路、电磁场理论中重要而又简单的简化模型。
典型的均匀传输线是由在均匀媒质中放置的两根平行直导线构成的。
常见的有平行双板、同轴线、和平行双线等。
当然,实际中并不存在真实的均匀线,架空线的支架、导线自身的重力都会使传输线不均匀。
为了简化问题,需要忽略这些次要因素。
以平行双线为例。
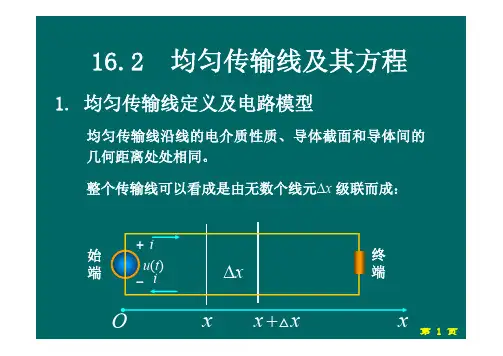
假设传输线是均匀的,即两导体间的距离、截面形状以及介质的电磁特性沿着整个长线保持不变,单位长度的线路电阻和电感分别为0R 和0L ,单位长度的线间电容和电导分别为0C 和0G ,如图1所示。
传输线最左端为起点,即0x =,选取距平行双线起点为x 的一小段x ∆进行研究。
虽然传输线本质上是一个分布参数系统,但可以采用一个长度为x ∆的集中参数模型来描述。
显然,x ∆越小就越接近传输线的实际情况 当0x ∆→时,该模型就逼近真实的分布参数系统。
[2]根据基尔霍夫定律,可以得到电报方程,它是均匀传输线上关于电压、电流的偏微分方程组。
0000i R i L t ux i G u xuC t ∂⎧-=⎪⎪∂⎨∂⎪-=⎪∂∂∂+∂⎩∂+ 方程表明,电流在传输线上连续分布的电阻中引起电压降,并在导线周围产生磁场,即沿线有电感的存在,变化的电流沿线产生电感电压降,所以,导线间的电压连续变化;又由于导线间存在电容,导线间存在电容电流,导线间的非理想电介质存在漏电导,所以还有电导电流,所以沿线的电流也连续变化。
图1 有损均匀传输线及其等效模型均匀传输线方程是一组常系数线性偏微分方程,在给定的初始条件和边界条件下,可以唯一地确定(),u x t 和(),i x t 。
从方程可以知道,给定初始条件和边界条件时,影响电学量的因素就是分布参数0R 、0L 、0G 、0C 。
均匀传输线的分布参数计算0 引言传输线作为一种输送能量和传递信号的装置,由于其应用十分广泛而成为了很有意义的研究对象。
在长距离输电线路、远距离通信线路、高频测量线路、计算机信号传输以及高速数控系统中均应该考虑线路参数的分布性。
[1]均匀传输线模型是电路、电磁场理论中重要而又简单的简化模型。
典型的均匀传输线是由在均匀媒质中放置的两根平行直导线构成的。
常见的有平行双板、同轴线、和平行双线等。
当然,实际中并不存在真实的均匀线,架空线的支架、导线自身的重力都会使传输线不均匀。
为了简化问题,需要忽略这些次要因素。
以平行双线为例。
假设传输线是均匀的,即两导体间的距离、截面形状以及介质的电磁特性沿着整个长线保持不变,单位长度的线路电阻和电感分别为0R 和0L ,单位长度的线间电容和电导分别为0C 和0G ,如图1所示。
传输线最左端为起点,即0x =,选取距平行双线起点为x 的一小段x ∆进行研究。
虽然传输线本质上是一个分布参数系统,但可以采用一个长度为x ∆的集中参数模型来描述。
显然,x ∆越小就越接近传输线的实际情况 当0x ∆→时,该模型就逼近真实的分布参数系统。
[2]根据基尔霍夫定律,可以得到电报方程,它是均匀传输线上关于电压、电流的偏微分方程组。
0000i R i L t ux i G u xuC t ∂⎧-=⎪⎪∂⎨∂⎪-=⎪∂∂∂+∂⎩∂+ 方程表明,电流在传输线上连续分布的电阻中引起电压降,并在导线周围产生磁场,即沿线有电感的存在,变化的电流沿线产生电感电压降,所以,导线间的电压连续变化;又由于导线间存在电容,导线间存在电容电流,导线间的非理想电介质存在漏电导,所以还有电导电流,所以沿线的电流也连续变化。
图1 有损均匀传输线及其等效模型均匀传输线方程是一组常系数线性偏微分方程,在给定的初始条件和边界条件下,可以唯一地确定(),u x t 和(),i x t 。
从方程可以知道,给定初始条件和边界条件时,影响电学量的因素就是分布参数0R 、0L 、0G 、0C 。
利用电磁场理论,我们可以根据传输线的位置、尺寸、形状、材料等参数求出这几个分布参数。
下面以圆柱平行双线为例,说明计算分布参数的方法。
其他常见的几种传输线,比如平行双板、同轴线的计算类似。
1 模型说明仅考虑低频时参数的计算。
(1) 导体媒质的电导率很高。
传输线常用的材料是铝合金,铝的电导率是3.82×107(S/m ),远大于磁导率和介电常数。
跟据欧姆定律J E γ=r r (γ是电导率),电流在百安及千安级别时,导线中的电场强度极小,可以忽略。
(2) 两导线间距远小于电磁波波长,即d λ=。
工频供电时,电磁波波长为6000km ,一般的输电线路都满足这个要求。
在这种情形下,可以忽略推迟效应。
(3) 导线的材料、导线周围介质均为线性、均匀、各向同性的物质。
平行双线的结构如图2所示。
由于导线中只有轴向电流,可知磁矢位A r只有轴向分量,由B A =∇⨯r r,可得0z B =;由于忽略了导线内部电场,根据电场强度在切线方向连续,可知0z E =。
所以,传输线周围的电磁波只有横向分量,导线所导引的电磁波近似为TEM 波(横电磁波)。
导线及周围介质中的场分布可以视为平行平面场。
同时,由于可以忽略导线内部的电场,可以将导线视为等电位体,导线表面是等位面。
接下来,首先计算电容、电导和电感,这三者的计算有一定共性,因为它们三个参数主要依赖于导体外介质的电磁性质,可以借由静态场的分析来处理。
而分布电阻由于涉及到场和导体媒质的相互作用,计算相对复杂一些。
z O 1O 2R =a x O Y d 图2 平行双线示意图2 分布电容的计算根据前文的叙述,可以知道,传输线间电容的计算可以按照静电场的方式进行。
在静电场中,由于两平行长直导线之间存在静电感应,导致导体表面的电荷分布不均匀,所以不能直接计算导线之间的电位差,必须利用镜像法。
如图3,导体外介质的介电常数为ε,对导体外部的电场,可以设想将两圆柱导体撤去,其表面电荷效应代之以两根长的带电细线,图中相距2b 的两根电荷线密度分别为 +p 和-p 。
文献[3]中给出了镜像带电细线位置的计算过程。
两镜像带电细线的位置满足()222/2b a d +=,所以两导线之间的电位差为0(/2)2ln2(/2)p b d a U b d a πε+-=--g ,则两导线间单位长度的电容为00/2arccos ()ln 2/2p C d b a d U h a b a d πεπε===-+⎛⎫ ⎪+-⎝⎭(2.1)其中,arccos ()ln(h x x =这是两平行圆柱导线间单位长度电容的准确解。
在实际中,导线的半径往往远小于导线间距,即a d =,于是/1d a ?,arccos ()ln(ln()22d d dh a a a =≈0ln()C d aπε=(2.2) 式(2.2)是常用的计算公式,但当不能忽略导线间的相互作用时,应当利用(2.1)式计算。
3 分布电导和电感的计算P(x,y)图3 镜像法计算导线电位差示意图在恒定场中,根据电导和电容的定义式:S S ll D dS E dS Q C U E dl E dl ε⋅⋅===⋅⋅⎰⎰⎰⎰r rr r r r r rS S llJ dS E dS I G U E dl E dlγ⋅⋅===⋅⋅⎰⎰⎰⎰r r r r r r r r可得公式G C γε=,需要注意的是这里的ε和γ都是指导体外介质的电磁特性,故只能用来计算漏电导,不能计算电阻。
在计算电容时,考虑到传输线线所导引的电磁波近似为TEM 波,导线及周围介质中的场分布为平行平面场,所以利用静电场的方式计算电容。
同理,电导的计算也可以按照恒定电场的方式进行。
于是,由G C γε=,可知00arccos ()2G C d h aγπγε==, 类似的,在a d =时,由于/21d a ?,有0ln()G daπγ=。
下面讨论电感的计算。
在多数文献里,计算二线传输线的分布电感(自感)时,都采用定义式S SN B dS L J dS⋅ψ==I ⋅⎰⎰rr r r其中Ψ是磁链,I 是和磁链交链的电流,在考虑导线半径时,需要区分内自感和外自感。
例如文献[3]中,当图2所示的平行双线通有恒定电流时,得到的电感值为01(ln )ln 4d a dL a aμμππ-=+≈(a d =)。
事实上,这种方法没有考虑两导线的相互作用,所以在计算时按照电流均匀分布进行的,当然,在a d =时,所得到的结果是足够准确地。
如果考虑两导线间的相互作用,那么还需要利用对电流的镜像法,这比较复杂,通过对传输线电磁场分布的分析,可以得到下面一个简单的方法,在一些文献,例如[4]、[5]中有介绍。
根据麦克斯韦方程组,可以推导出无源区导电媒质内的平面波。
根据前文对传输线的描述,电磁波的传播方向为+z 。
在谐变场的条件下,可得到场量满足的波动方程22222200y y x x d H k H dz d E k E dz⎧-=⎪⎪⎨⎪-=⎪⎩&&&&其中,k j j αβ==+ (3.1) k 称为传播常数。
注意到正弦激励下传输线方程(电报方程)的形式22222200d U k U dx d I k I dx⎧-=⎪⎪⎨⎪-=⎪⎩&&&&其中,k j αβ==+,称为传播常数。
可以发现传输线方程和平面电磁波方程形式相同,而相同的方程对应的解的形式也必然相同,显然,两个传播系数所代表的物理意义也是统一的。
按照前文的叙述,由于导线电导率很大,同时忽略了导体内部电场,所以这里的分布电阻0R 和传播常数相比可以忽略。
于是,传输线的传播系数可化为k j == (3.2) 对比(3.1)、(3.2)两式,由于00G C γε=,可知 00L C με=。
根据前文电容的计算值,可以得到分布电感的值为0arccos ()2d L h aμπ=于是,在a d =时,由于/21d a ?,有0ln()d L aμπ=,这和直接利用电感定义式所计算的近似结果是一致的,可以互相印证。
可以注意到电容、电导和电感在形式上有一致性,这是三者都依赖于导线外空间的电磁性质,以及无源区电场和磁场的对称性所决定的。
在低频情况下,可认为这三者和电学量没有关系。
文献[5]中,利用静态时电场和磁场的相互关系,推导了平行平面场情形下电容和电感满足关系00L C με=。
这两种分析方法有所不同,利用电磁波的传播系数对比的方法,更能显示传输线作为导波系统,对电磁波的引导作用,但是,所必须的是忽略分布电阻对空间电磁场的影响。
而利用静态场引出等式00L C με=,但是其物理意义不如前者明显。
当然,这两种方法都做了不同的近似。
4 分布电阻的计算电阻的存在使得电源必须向其提供电压,以使得电流能够维持持续的流动。
而电阻本身会产生热损耗,以焦耳定律表示。
于是电阻有两种计算方式,一是根据l lSSE dl E dl U R I J dS E dSγ⋅⋅===⋅⋅⎰⎰⎰⎰r rr r r r r r ,其中γ是导线电导率;二是根据焦耳定律,2PR I =来计算。
先考虑直流稳态时的情形。
对于直流电路,有熟知的公式lR Sρ=,其中ρ是电阻率。
对直流稳态而言,如果忽略两导线间的相互影响,则均匀传输线只是延长了线路,而不影响电学量的分布,故在直流稳态时分布电阻仍应按照此公式进行 ,即021R aρπ=。
对于交流电路,电阻的计算十分复杂。
首先,导体媒质内电磁波的传播规律不同于理想介质,电磁波的波速和波长较介质会减小许多,甚至可能出现波长与导线半径同一数量级的情况。
而且,磁场和电场会产生相位差,对应于电路理论就是复数电阻,电阻部分会产生损耗,而电抗部分对应无功分量。
同时,由于存在趋肤效应,场量是矢径r r的函数。
为了简化问题,下面仅考虑一种情况。
对于正弦稳态电路,场量按正弦规律变化。
假设电流仅在导线表面一薄层内均匀流动,薄层的厚度取趋肤效应的透入深度dd =这个值是通过解良导体(c γωε?)中的波动方程,并认为数值减少至最大值的1e -得到的。
直接利用波动方程的解析解求交流电阻的方法,文献[6]有所介绍。
根据上面的假设,交流电路使得电流所分布的截面面积减少而增大电阻,所以,有01122c R ad γπ=⨯==乘2是由于考虑到平行双线,下标c 是为了说明是导体的电导率和磁导率。
5 结论根据前文的计算,可将平行双线的四个分布参数列于下表1。
这些是一般文献中可以查到的公式。
表1 分布参数的表达式参考文献[1] 孙韬.传输线方程解析解的研究,2005.[2] 王小艳.一般有损均匀传输线中电流电压的瞬态过程分析[J].2008.[3] 冯慈璋,马西奎.工程电磁场导论.北京:高等教育出版社[M].2000.[4] David K.Cheng.电磁场与电磁波.北京:清华大学出版社[M].2007.[5] 冯慈璋.电磁场. 北京:高等教育出版社[M].1983.[6] 张小林,徐精华.信号传输线趋肤效应的分析[J].大学物理,2009(7):10-12.。