深圳市南山区2014年7月八年级下数学期末测试卷及参考答案全国通用

初二下册数学期末考试试卷答案2014
一、积累与运用 (20分)
1、1、A、徙 B、源 C、悴 D、滥(共2分，每字0.5分)
2、①xun ②zhōu ③di ④chu(共2分，注音正确一字0.5分)
3、B (2分)
4、② 将“提升自我“与“增长知识”位置对调。

(找到病句，1分;正确修改，1分。

共2分)
5、④②⑦⑥①③⑤ (2分)
6、凡尔纳;在科学的基础上进行既大胆又合理的想象。

(2分)
7、①独怆然而涕下②山河破碎风飘絮③以中有足乐者，不知口体之奉不若人也。

④折戟沉沙铁未销;宫阙万间都做了土;到乡翻似烂柯人;天涯若比邻。

(共6分。

每错、多、漏一字均扣1分，扣完为止。

)
二、口语交际与综合性学习 (10分)
8、示例：师傅您好，眼看就要上课了，可我的车被扎了，请您帮帮忙，能先给我修修吗?(2分，符合要求即可)
9、(1)示例：探幽寻胜增阅历.(2分) (2)示例：依次：
稀客、递烟、泡茶、慢走(每空0.5分，共2分，答案只要合理即可) (3)无统一答案，符合要求即可。

(写出对联1.5分，写出有关的名胜古迹0.5分，共2分)) (4)示例：红色旅游让我们不忘过去，更加珍惜今天的幸福，为祖国创造美好的未来而努力。

(2分)
只要这样踏踏实实完成每天的计划和小目标，就可以自如地应对新学习，达到长远目标。

由为您提供的初二下册数学期末考试试卷答案2014，祝您学习愉快!。

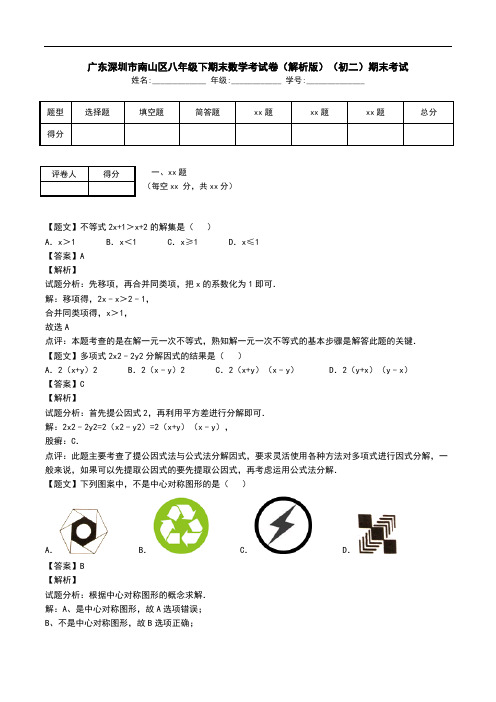
广东深圳市南山区八年级下期末数学考试卷（解析版）（初二）期末考试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx 题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）【题文】不等式2x+1＞x+2的解集是（）A．x＞1 B．x＜1 C．x≥1 D．x≤1【答案】A【解析】试题分析：先移项，再合并同类项，把x的系数化为1即可．解：移项得，2x﹣x＞2﹣1，合并同类项得，x＞1，故选A点评：本题考查的是在解一元一次不等式，熟知解一元一次不等式的基本步骤是解答此题的关键．【题文】多项式2x2﹣2y2分解因式的结果是（）A．2（x+y）2 B．2（x﹣y）2 C．2（x+y）（x﹣y） D．2（y+x）（y﹣x）【答案】C【解析】试题分析：首先提公因式2，再利用平方差进行分解即可．解：2x2﹣2y2=2（x2﹣y2）=2（x+y）（x﹣y），股癣：C．点评：此题主要考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．【题文】下列图案中，不是中心对称图形的是（）A． B． C． D．【答案】B【解析】试题分析：根据中心对称图形的概念求解．解：A、是中心对称图形，故A选项错误；B、不是中心对称图形，故B选项正确；C、是中心对称图形，故C选项错误；D、是中心对称图形，故D选项错误；故选：B．点评：本题考查了中心对称图形的知识，解题的关键是掌握中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180°后重合．【题文】如图，△ABC中，AB的垂直平分线交AC于D，如果AC=5cm，BC=4cm，那么△DBC的周长是（）A．6cm B．7cm C．8cm D．9cm【答案】D【解析】试题分析：由于AB的垂直平分线交AC于D，所以AD=BD，而△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC，而AC=5cm，BC=4cm，由此即可求出△DBC的周长．解：∵DE是AB的垂直平分线，∴AD=BD，∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC，而AC=5cm，BC=4cm，∴△DBC的周长是9cm．故选：D．点评：此题主要考查了线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等．结合图形，进行线段的等量代换是正确解答本题的关键．【题文】要使分式有意义，那么x的取值范围是（）A．x≠3 B．x≠3且x≠﹣3 C．x≠0且x≠﹣3 D．x≠﹣3【答案】D【解析】试题分析：根据分式有意义的条件列出关于x的不等式，求解即可．解：∵x2+6x+9≠0，∴（x+3）2≠0，∴x+3≠0，∴x≠﹣3，∴分式有意义，x的取值范围x≠﹣3，故选D．点评：本题考查了分式有意义的条件：分母不为0，掌握不等式的解法是解题的关键．【题文】如果关于x的不等式（a+1）x＞a+1的解集为x＜1，那么a的取值范围是（）A．a＜﹣1 B．a＜0 C．a＞﹣1 D．a＞0a＜﹣1【答案】A【解析】试题分析：根据不等式的性质，两边同时除以a+1，a+1是正数还是负数不确定，所以要分两种情况，再根据解集为x＜1，发现不等号的符号发生了变化，所以确定a+1＜0，从而得到答案．解：（a+1）x＞a+1，当a+1＞0时，x＞1，当a+1＜0时，x＜1，∵解集为x＜1，∴a+1＜0，a＜﹣1．故选：A．点评：此题主要考查了解不等式，当不等式两边除以同一个数时，这个数的正负性直接影响不等号．【题文】如图，在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则AB的长为（）A．4 B．3 C． D．2【答案】B【解析】试题分析：根据平行四边形性质得出AB=DC，AD∥BC，推出∠DEC=∠BCE，求出∠DEC=∠DCE，推出DE=DC=AB ，得出AD=2DE即可．解：∵四边形ABCD是平行四边形，∴AB=DC，AD∥BC，∴∠DEC=∠BCE，∵CE平分∠DCB，∴∠DCE=∠BCE，∴∠DEC=∠DCE，∴DE=DC=AB，∵AD=2AB=2CD，CD=DE，∴AD=2DE，∴AE=DE=3，∴DC=AB=DE=3，故选：B．点评：本题考查了平行四边形性质，平行线性质，角平分线定义，等腰三角形的性质和判定的应用，关键是求出DE=AE=DC．【题文】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图，则三角板的最大边的长为（）A．3cm B．6cm C．cm D．cm【答案】D【解析】试题分析：过另一个顶点C作垂线CD如图，可得直角三角形，根据直角三角形中30°角所对的边等于斜边的一半，可求出有45°角的三角板的直角边，再由等腰直角三角形求出最大边．解：过点C作CD⊥AD，∴CD=3，在直角三角形ADC中，∵∠CAD=30°，∴AC=2CD=2×3=6，又∵三角板是有45°角的三角板，∴AB=AC=6，∴BC2=AB2+AC2=62+62=72，∴BC=6，故选：D．点评：此题考查的知识点是含30°角的直角三角形及等腰直角三角形问题，关键是先求得直角边，再由勾股定理求出最大边．【题文】如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，若AE=4，AF=6，平行四边形ABCD的周长为40．则平行四边形ABCD的面积为（）A．24 B．36 C．40 D．48【答案】D【解析】试题分析：已知平行四边形的高AE、AF，设BC=xcm，则CD=（20﹣x）cm，根据“等面积法”列方程，求BC，从而求出平行四边形的面积．解：设BC=xcm，则CD=（20﹣x）cm，根据“等面积法”得4x=6（20﹣x），解得x=12，∴平行四边形ABCD的面积=4x=4×12=48．故选D．点评：本题应用的知识点为：平行四边形一组邻边之和为平行四边形周长的一半，平行四边形的面积=底×高，可用两种方法表示．【题文】如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＜ax+4的解集为（）A．x＜ B．x＜3 C．x＞ D．x＞3【答案】A【解析】试题分析：先根据函数y=2x和y=ax+4的图象相交于点A（m，3），求出m的值，从而得出点A的坐标，再根据函数的图象即可得出不等式2x＜ax+4的解集．解：∵函数y=2x和y=ax+4的图象相交于点A（m，3），∴3=2m，m=，∴点A的坐标是（，3），∴不等式2x＜ax+4的解集为x＜；故选A．点评：此题考查的是用图象法来解不等式，充分理解一次函数与不等式的联系是解决问题的关键．【题文】已知a2+b2=6ab，则的值为（）A． B． C．2 D．±2【答案】B【解析】试题分析：首先由a2+b2=6ab，即可求得：（a+b）2=8ab，（a﹣b）2=4ab，然后代入即可求得答案．解：∵a2+b2=6ab，∴a2+b2+2ab=8ab，a2+b2﹣2ab=4ab，即：（a+b）2=8ab，（a﹣b）2=4ab，a+b=±2，a﹣b=±2，∴当a+b=2，a﹣b=2时，=；当a+b=2，a﹣b=﹣2时，=﹣；当a+b=﹣2，a﹣b=2时，=﹣；当a+b=﹣2，a﹣b=﹣2时，=．故选：B．点评：本题主要考查完全平方公式．注意熟记公式的几个变形公式，还要注意整体思想的应用．【题文】△ABC为等腰直角三角形，∠ACB=90°，AC=BC=2，P为线段AB上一动点，D为BC上中点，则PC+PD 的最小值为（）A． B．3 C． D．【答案】C【解析】试题分析：作D关于AB的对称点F，连接CF交AB于P，连接PD，BF，则AB垂直平分DF，于是可得PF=PD ，BD=BF，即可求得∠CBF=90°，根据勾股定理即可得到结论．解：作D关于AB的对称点F，连接CF交AB于P，则CF的长度=PC+PD的最小值，连接PD，BF，则AB垂直平分DF，∴PF=PD，BD=BF=BC=1，∠FBP=∠DBP，∵△ABC为等腰直角三角形，AC=BC，∴∠ACB=45°，∴∠CBF=90°，∴CF2=BC2+BF2=5，∴CF=，∴PC+PD的最小值是．故选C．点评：此题考查了线路最短的问题，确定动点P何位置时，使PC+PD的值最小是关键．【题文】分解因式：2x2﹣4x+2=．【答案】2（x﹣1）2．【解析】试题分析：先提取公因数2，再利用完全平方公式进行二次分解．完全平方公式：（a±b）2=a2±2ab+b2．解：2x2﹣4x+2，=2（x2﹣2x+1），=2（x﹣1）2．点评：本题主要考查提公因式法分解因式和利用完全平方公式分解因式，难点在于需要进行二次分解因式．【题文】一个多边形的内角和与外角和的比是4：1，则它的边数是．【答案】10．【解析】试题分析：多边形的外角和是360度，内角和与外角和的比是4：1，则内角和是1440度．n边形的内角和是（n﹣2）•180°，如果已知多边形的内角和，就可以得到一个关于边数的方程，解方程就可以求出多边形的边数．解：根据题意，得（n﹣2）•180=1440，解得：n=10．则此多边形的边数是10．故答案为：10．点评：本题考查了多边形内角和定理和外角和定理：多边形内角和为（n﹣2）•180°，外角和为360°．【题文】如图，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD的长为．【答案】2【解析】试题分析：过P作PE垂直与OB，由∠AOP=∠BOP，PD垂直于OA，利用角平分线定理得到PE=PD，由PC与OA平行，根据两直线平行得到一对内错角相等，又OP为角平分线得到一对角相等，等量代换可得∠COP=∠CPO，又∠ECP为三角形COP的外角，利用三角形外角的性质求出∠ECP=30°，在直角三角形ECP中，由30°角所对的直角边等于斜边的一半，由斜边PC的长求出PE的长，即为PD的长．解：过P作PE⊥OB，交OB与点E，∵∠AOP=∠BOP，PD⊥OA，PE⊥OB，∴PD=PE，∵PC∥OA，∴∠CPO=∠POD，又∠AOP=∠BOP=15°，∴∠CPO=∠BOP=15°，又∠ECP为△OCP的外角，∴∠ECP=∠COP+∠CPO=30°，在直角三角形CEP中，∠ECP=30°，PC=4，∴PE=PC=2，则PD=PE=2．故答案为：2．点评：此题考查了含30°角直角三角形的性质，角平分线定理，平行线的性质，以及三角形的外角性质，熟练掌握性质及定理是解本题的关键．同时注意辅助线的作法．【题文】如图，在Rt△ABC中，∠ABC=90°，AB=BC=，将△ABC绕点A逆时针旋转60°，得到△ADE，连接BE，则BE的长是．【答案】2+2【解析】试题分析：首先考虑到BE所在的三角形并不是特殊三角形，所以猜想到要求BE，可能需要构造直角三角形．由旋转的性质可知，AC=AE，∠CAE=l∴AC=CE=AE=4在△ABE与△CBE中，∴△ABE≌△CBE（SSS）∴∠ABE=∠CBE=45°，∠CEB=∠AEB=30°∴在△ABF中，∠BFA=180°﹣45°﹣45°=90°∴∠AFB=∠AFE=90°在Rt△ABF中，由勾股定理得，BF=AF==2又在Rt△AFE中，∠AEF=30，°∠AFE=90°FE=AF=2∴BE=BF+FE=2+2故，本题的答案是：2+2点评：此题是旋转性质题，解决此题，关键是思路要明确：“构造”直角三角形．在熟练掌握旋转的性质的基础上，还要应用全等的判定及性质，直角三角形的判定及勾股定理的应用【题文】解方程：．【答案】无解【解析】试题分析：找出分式方程的最简公分母为（x+2）（x﹣2），去分母后转化为整式方程，求出方程的解得到x的值，代入最简公分母中检验即可得到原分式方程的解．解：最简公分母为（x+2）（x﹣2），去分母得：（x﹣2）2﹣（x+2）（x﹣2）=16，整理得：﹣4x+8=16，解得：x=﹣2，经检验x=﹣2是增根，故原分式方程无解．点评：此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．【题文】解不等式组：．【答案】x＜2【解析】试题分析：分别解两个不等式得到x＞﹣2和x≤2，然后根据同小取小确定不等式组的解集．解：，解①得x≤4，解②得x＜2，所以不等式的解集为x＜2．点评：本题考查了解一元一次不等式组：求解出两个不等式的解集，然后按照“同大取大，同小取小，大于小的小于大的取中间，小于小的大于大的无解”确定不等式组的解集．【题文】先化简，再求值：，其中a满足方程a2+4a+1=0．【答案】原式=【解析】试题分析：把原式括号里的第二项提取﹣1，然后把原式的各项分子分母都分解因式，找出括号里两项分母的最简公分母，利用分式的基本性质对括号里两项进行通分，然后利用同分母分式的减法运算法则：分母不变，只把分子相减，计算出结果，然后利用分式的除法法则：除以一个数等于乘以这个数的倒数，变形为乘法运算，约分后即可把原式化为最简分式，把a满足的方程变形后，代入原式化简后的式子中即可求出值．解：原式=====，（6分）∵a2+4a+1=0，∴a2+4a=﹣1，∴原式=．（10分）点评：此题考查了分式的混合运算，以及多项式的运算．分式的化简求值题，应先对原式的分子分母分解因式，在分式的化简运算中，要通观全局，弄清有哪些运算，然后观察能否用法则，定律，分解因式及公式来简化运算，同时注意运算的结果要化到最简，然后再代值计算．【题文】如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上，将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1，然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2．（1）在网格中画出△A1B1C1和△A1B2C2；（2）计算线段AC在变换到A1C2的过程中扫过区域的面积（重叠部分不重复计算）【答案】见解析【解析】试题分析：（1）根据图形平移及旋转的性质画出△A1B1C1及△A1B2C2即可；（2）根据图形平移及旋转的性质可知，将△ABC向下平移4个单位AC所扫过的面积是以4为底，以2为高的平行四边形的面积；再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积；当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时，A1C1所扫过的面积是以A1为圆心以以2为半径，圆心角为90°的扇形的面积，再减去重叠部分的面积，根据平行四边形的面积及扇形面积公式进行解答即可．解：（1）如图所示：（2）∵图中是边长为1个单位长度的小正方形组成的网格，∴AC==2，∵将△ABC向下平移4个单位AC所扫过的面积是以4为底，以2为高的平行四边形的面积；再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积；当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时，A1C1所扫过的面积是以A1为圆心以2为半径，圆心角为90°的扇形的面积，重叠部分是以A1为圆心，以2为半径，圆心角为45°的扇形的面积，∴线段AC在变换到A1C2的过程中扫过区域的面积=4×2+3×2+﹣=14+π．点评：本题考查的是旋转变换及平移变换，扇形的面积公式，熟知图形旋转、平移不变性的特点是解答此题的关键．【题文】如图，在△ABC中，D、E分别是AB、AC的中点，F是DE延长线上的点，且EF=DE（1）图中的平行四边形有哪几个？请选择其中一个说明理由；（2）若△AEF的面积是3，求四边形BCFD的面积．【答案】（1）平行四边形ADCF，平行四边形BDFC，（2）12．【解析】试题分析：（1）由E为AC的中点，可得AE=CE，再由条件EF=DE 可得四边形ADCF是平行四边形；（2）根据等底等高的三角形面积相等可得平行四边形对角线分成的四个小三角形面积相等可得△CEF的面积和△CED的面积都等于△AEF的面积为3，从而可得四边形BCFD的面积为12．（1）图中的平行四边形有：平行四边形ADCF，平行四边形BDFC，理由是：∵E为AC的中点，∴AE=CE，∵DE=EF，∴四边形ADCF是平行四边形，∴AD∥CF，AD=CF，∵D为AB的中点，∴AD=BD，∴BD=CF，BD∥CF，∴四边形BDFC是平行四边形．（2）由（1）知四边形ADCF是平行四边形，四边形BDFC是平行四边形，∴S△CEF=S△CED=S△AEF=3，∴平行四边形BCFD的面积是12．点评：此题主要考查了平行四边形的判定和性质，关键是掌握平行四边形的判定定理，掌握平行四边形对角线分成的四个小三角形面积相等．【题文】我县某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降，今年5月份A 款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元．（1）今年5月份A款汽车每辆售价多少万元？（2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？（3）如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，返还顾客现金a万元，要使（2）中所有的方案获利相同，a值应是多少？此时，哪种方案对公司更有利？【答案】见解析【解析】试题分析：（1）求单价，总价明显，应根据数量来列等量关系．等量关系为：今年的销售数量=去年的销售数量．（2）关系式为：99≤A款汽车总价+B款汽车总价≤105．（3）方案获利相同，说明与所设的未知数无关，让未知数x的系数为0即可；多进B款汽车对公司更有利，因为A款汽车每辆进价为7.5万元，B款汽车每辆进价为6万元，所以要多进B款．解：（1）设今年5月份A款汽车每辆售价x万元．根据题意得：=，解得：x=9，经检验知，x=9是原方程的解．所以今年5月份A款汽车每辆售价9万元．（2）设A款汽车购进y辆．则B款汽车每辆购进（15﹣y）辆．根据题意得：解得：6≤y≤10，所以有5种方案：方案一：A款汽车购进6辆；B款汽车购进9辆；方案二：A款汽车购进7辆；B款汽车购进8辆；方案三：A款汽车购进8辆；B款汽车购进7辆；方案四：A款汽车购进9辆；B款汽车购进6辆；方案五：A款汽车购进10辆；B款汽车购进5辆．（3）设利润为W则：W=（8﹣6）×（15﹣y）﹣a（15﹣y）+（9﹣7.5）y=30﹣2y﹣a（15﹣y）+1.5y=30﹣a（15﹣y）﹣0.5y方案一：W=30﹣a（15﹣6）﹣0.5×6=30﹣9a﹣3=27﹣9a方案二：W=30﹣a（15﹣7）﹣0.5×7=30﹣8a﹣3.5=26.5﹣8a方案三：W=30﹣a（15﹣8）﹣0.5×8=30﹣7a﹣4=26﹣7a方案四：W=30﹣a（15﹣9）﹣0.5×9=30﹣6a﹣4.5=25.5﹣6a方案五：W=30﹣a（15﹣10）﹣0.5×10=30﹣5a﹣5=25﹣5a由27﹣9a=26.5﹣8a 得a=0.5方案一对公司更有利．点评：本题考查分式方程和一元一次不等式组的综合应用，找到合适的等量关系及不等关系是解决问题的关键．【题文】已知两个共一个顶点的等腰直角△ABC和等腰直角△CEF，∠ABC=∠CEF=90°，连接AF，M是AF的中点，连接MB、ME．（1）如图1，当CB与CE在同一直线上时，求证：MB∥CF；（2）如图1，若CB=a，CE=2a，求BM，ME的长；（3）如图2，当∠BCE=45°时，求证：BM=ME．【答案】（1）见解析（2）BM=ME==a（3）见解析【解析】试题分析：（1）如答图1a所示，延长AB交CF于点D，证明BM为△ADF的中位线即可；（2）如答图2a所示，作辅助线，推出BM、ME是两条中位线；（3）如答图3a所示，作辅助线，推出BM、ME是两条中位线：BM=DF，ME=AG；然后证明△ACG≌△DCF，得到DF=AG，从而证明BM=ME．（1）证明：如答图1a，延长AB交CF于点D，则易知△ABC与△BCD均为等腰直角三角形，∴AB=BC=BD，∴点B为线段AD的中点，又∵点M为线段AF的中点，∴BM为△ADF的中位线，∴BM∥CF；（2）如答图2a所示，延长AB交CF于点D，则易知△BCD与△ABC为等腰直角三角形，∴AB=BC=BD=a，AC=CD=a，∴点B为AD中点，又点M为AF中点，∴BM=DF．分别延长FE与CA交于点G，则易知△CEF与△CEG均为等腰直角三角形，∴CE=EF=GE=2a，CG=CF=2a，∴点E为FG中点，又点M为AF中点，∴ME=AG．∵CG=CF=2a，CA=CD=a，∴AG=DF=a，∴BM=ME=×a=a．（3）如答图3a，延长AB交CE于点D，连接DF，则易知△ABC与△BCD均为等腰直角三角形，∴AB=BC=BD，AC=CD，∴点B为AD中点，又点M为AF中点，∴BM=DF，延长FE与CB交于点G，连接AG，则易知△CEF与△CEG均为等腰直角三角形，∴CE=EF=EG，CF=CG，∴点E为FG中点，又点M为AF中点，∴ME=AG，在△ACG与△DCF中，，∴△ACG≌△DCF（SAS），∴DF=AG，∴BM=ME．点评：本题考查了三角形中位线定理、全等三角形的判定与性质，等腰直角三角形的性质，作辅助线构造出中位线、全等三角形和等腰直角三角形是解题的关键，也是本题的难点．。

2013-2014学年广东省深圳市南山区八年级（下）期末数学试卷一、选择题：本题有12小题，每题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的 B x 23．（3分）（2014秋•茌平县期末）如图，△ABC 中，AB=AC ，D 是BC 中点，下列结论中不正确的是（ ）4．（3分）（2014•衡阳）不等式组的解集在数轴上表示为（ ）B5．（3分）（2014春•深圳期末）如图，▱ABCD 中，对角线AC 、BD 交于点O ，点E 是BC 的中点．若OE=3cm ，则AB 的长为（ ）7．（3分）（2013•攀枝花）如图，在△ABC中，∠CAB=70°．在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=（）8．（3分）（2014春•深圳期末）若解分式方程=产生増根．则m等于（）20132014210．（3分）（2014春•深圳期末）如图，△ABC中，AB边的垂直平分线交AB于点E，交BC于点D，已知AC=5cm，△ADC的周长为17cm，则BC的长为（）11．（3分）（2014春•深圳期末）关于x的不等式组的整数解共有6个，则a的12．（3分）（2014•江阴市校级模拟）如图1，在平面直角坐标系中，将▱ABCD放置在第一象限，且AB∥x轴．直线y=﹣x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2，那么ABCD面积为（）二、填空题：本题共4小题，每小题3分，共12分，把答案填在答题卡上13．（3分）（2014春•深圳期末）分解因式：ax2﹣16ay2=．14．（3分）（2014•淮阴区校级模拟）如图，已知函数y=3x+b和y=ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式3x+b＞ax﹣3的解集是．15．（3分）（2014春•深圳期末）已知4x2+mxy+y2是完全平方式，则m的值是．16．（3分）（2013•菏泽）如图，▱ABCD中，对角线AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内，若点B的落点记为B′，则DB′的长为．三、解答题（本大题有七题，其中第17题9分、第18题6分、第19题6分、第20题6分、第21题9分、第22题7分、第23题9分，共52分）解答应写出文字说明或演算步骤.17．（9分）（2014春•深圳期末）（1）解不等式：+1＞x﹣3；（2）解方程：=3﹣．18．（6分）（2014春•深圳期末）先化简（﹣）÷，然后从﹣1≤x≤1的范围内选取一个合适的整数作为x的值代入求值．19．（6分）（2014春•深圳期末）△ABC在平面直角坐标系xOy中的位置如图所示．（1）作△ABC关于点C成中心对称的△A1B1C1，并直接写出A1、B1、C1各点的坐标；（2）将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2．20．（6分）（2011•禅城区模拟）已知：如图，点D是△ABC的BC边上的中点，DE⊥AC 于E，DF⊥AB于F，且DE=DF．求证：△ABC是等腰三角形．21．（9分）（2012•淮安模拟）由于受金融危机的影响，某店经销的甲型号手机今年的售价比去年每台降价500元．如果卖出相同数量的手机，那么去年销售额为8万元，今年销售额只有6万元．（1）今年甲型号手机每台售价为多少元？（2）为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每台进价为1000元，乙型号手机每台进价为800元，预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台，请问有几种进货方案？22．（7分）（2014春•深圳期末）如图，在▱ABCD中，AE、AF是高，∠BAE=30°，BE=2，CF=1，DE交AF于点G．（1）求▱ABCD的面积；（2）求证：△AEG是等边三角形．23．（9分）（2014春•深圳期末）如图，在梯形ABCD中，AD∥BC，∠B=90°，AD=8cm，AB=6cm，BC=10cm，点Q从点A出发以1cm/s的速度向点D运动，点P从点B出发以2cm/s 的速度在线段BC间往返运动，P、Q两点同时出发，当点Q到达点D时，两点同时停止运动．（1）当t=s时，四边形PCDQ的面积为36cm2；（2）若以P、Q、C、D为顶点的四边形是平行四边形，求t的值；（3）当0＜t＜5时，若DQ≠DP，当t为何值时，△DPQ是等腰三角形？2013-2014学年广东省深圳市南山区八年级（下）期末数学试卷参考答案与试题解析一、选择题：本题有12小题，每题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的Bx2分母中不含有字母，因此它们是整式，而不是分式，故分母中不含有字母，因此它们是整式，而不是分式，故分母中含有字母，因此是分式，故、不是字母，是常数，所以3．（3分）（2014秋•茌平县期末）如图，△ABC中，AB=AC，D是BC中点，下列结论中不正确的是（）4．（3分）（2014•衡阳）不等式组的解集在数轴上表示为（）B在数轴上可表示为：5．（3分）（2014春•深圳期末）如图，▱ABCD中，对角线AC、BD交于点O，点E是BC 的中点．若OE=3cm，则AB的长为（）7．（3分）（2013•攀枝花）如图，在△ABC中，∠CAB=70°．在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=（）8．（3分）（2014春•深圳期末）若解分式方程=产生増根．则m等于（）==产生増根，20132014210．（3分）（2014春•深圳期末）如图，△ABC中，AB边的垂直平分线交AB于点E，交BC于点D，已知AC=5cm，△ADC的周长为17cm，则BC的长为（）11．（3分）（2014春•深圳期末）关于x的不等式组的整数解共有6个，则a的，得12．（3分）（2014•江阴市校级模拟）如图1，在平面直角坐标系中，将▱ABCD放置在第一象限，且AB∥x轴．直线y=﹣x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2，那么ABCD面积为（）DN=2DN=2×二、填空题：本题共4小题，每小题3分，共12分，把答案填在答题卡上13．（3分）（2014春•深圳期末）分解因式：ax2﹣16ay2=a（x+4y）（x﹣4y）．14．（3分）（2014•淮阴区校级模拟）如图，已知函数y=3x+b和y=ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式3x+b＞ax﹣3的解集是x＞﹣2．15．（3分）（2014春•深圳期末）已知4x2+mxy+y2是完全平方式，则m的值是±4．16．（3分）（2013•菏泽）如图，▱ABCD中，对角线AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内，若点B的落点记为B′，则DB′的长为．BE=BD=1=BE=．．故答案为：三、解答题（本大题有七题，其中第17题9分、第18题6分、第19题6分、第20题6分、第21题9分、第22题7分、第23题9分，共52分）解答应写出文字说明或演算步骤.17．（9分）（2014春•深圳期末）（1）解不等式：+1＞x﹣3；（2）解方程：=3﹣．18．（6分）（2014春•深圳期末）先化简（﹣）÷，然后从﹣1≤x≤1的范围内选取一个合适的整数作为x的值代入求值．=[﹣=•=19．（6分）（2014春•深圳期末）△ABC在平面直角坐标系xOy中的位置如图所示．（1）作△ABC关于点C成中心对称的△A1B1C1，并直接写出A1、B1、C1各点的坐标；（2）将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2．20．（6分）（2011•禅城区模拟）已知：如图，点D是△ABC的BC边上的中点，DE⊥AC 于E，DF⊥AB于F，且DE=DF．求证：△ABC是等腰三角形．21．（9分）（2012•淮安模拟）由于受金融危机的影响，某店经销的甲型号手机今年的售价比去年每台降价500元．如果卖出相同数量的手机，那么去年销售额为8万元，今年销售额只有6万元．（1）今年甲型号手机每台售价为多少元？（2）为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每台进价为1000元，乙型号手机每台进价为800元，预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台，请问有几种进货方案？=22．（7分）（2014春•深圳期末）如图，在▱ABCD中，AE、AF是高，∠BAE=30°，BE=2，CF=1，DE交AF于点G．（1）求▱ABCD的面积；（2）求证：△AEG是等边三角形．=23==22；（23．（9分）（2014春•深圳期末）如图，在梯形ABCD中，AD∥BC，∠B=90°，AD=8cm，AB=6cm，BC=10cm，点Q从点A出发以1cm/s的速度向点D运动，点P从点B出发以2cm/s的速度在线段BC间往返运动，P、Q两点同时出发，当点Q到达点D时，两点同时停止运动．（1）当t=2s时，四边形PCDQ的面积为36cm2；（2）若以P、Q、C、D为顶点的四边形是平行四边形，求t的值；（3）当0＜t＜5时，若DQ≠DP，当t为何值时，△DPQ是等腰三角形？==QD=（（（t=；t=，t=或时，。

新人教版2013—2014学年八年级第二学期期末检测数学试题（满分：120分；考试时间：120分钟）一、选择题。

(本题共10小题，每小题3分，共30分)1．若式子2在实数范围内有意义，则x的取值范围是（）．A．x>1 B．x<1 C．x≥1 D．x≤12．一组数据：0，1，2，3，3，5，5，10的中位数是（）．A．2.5 B．3 C．3.5 D．53．在平面中，下列命题为真命题的是（）A、四个角相等的四边形是矩形。

B、只有对角线互相平分且垂直的四边形是菱形。

C、对角线互相平分且相等的四边形是矩形。

D、四边相等的四边形是菱形。

4．在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到AB的距离是（）A. 365 B.1225 C.94D.5．某特警队为了选拔”神枪手”，举行了1 000米射击比赛，最后由甲、乙两名战士进入决赛，两人各射靶10次，经过统计计算，甲、乙两名战士的总成绩都是99.68环，甲的方差是0.28，乙的方差是0.21．则下列说法中，正确的是（）A．甲的成绩比乙的成绩稳定B．乙的成绩比甲的成绩稳定[中国教育&%出版C．甲、乙两人成绩的稳定性相同D．无法确定谁的成绩更稳定6．如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于（）．A．50° B．60° C．70° D．80°7．在“大家跳起来”的乡村学校舞蹈比赛中，某校10名学生参赛成绩统计如图所示，对于这10名学生的参赛成绩，下列说法中错误的是（）A．众数是90 B．中位数是90C．平均数是90 D．极差是158．甲、乙两人在一次百米赛跑中，路程s（米）与赛跑时间t（秒）的关系如图所示，则下列说法正确的是（）A 、甲、乙两人的速度相同B 、甲先到达终点C 、乙用的时间短D 、乙比甲跑的路程多9．童童从家出发前往奥体中心观看某演出，先匀速步行至轻轨车站，等了一会儿，童童搭乘轻轨至奥体中心观看演出，演出结束后，童童搭乘邻居刘叔叔的车顺利到家．其中x 表示童童从家出发后所用时间，y 表示童童离家的距离．下图能反映y 与x 的函数关系式的大致图象是（ ）10．如图，在正方形ABCD 中，边长为2的等边三角形AEF 的顶点E 、F 分别在BC 和CD 上，下列结论：①CE ＝CF ②∠AEB ＝750③BE+DF ＝EF ④S 正方形ABCD ＝2+3，其中正确的序号是 。

2014-2015学年广东省深圳市南山区期末试卷八年级（下）数学一、选择题：本题有12小题，每题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的选项用铅笔涂在答题卡上.1．（3分）下列各式从左到右的变形为分解因式的是（）A．m﹣m﹣6=（m+2）（m﹣3）B．（m+2）（m﹣3）=m﹣m﹣6C．x+8x﹣9=（x+3）（m﹣3）+8x D．18x y=3x y•62．（3分）在下列交通标志中，是中心对称图形的是（）A．B．C．D．3．（3分）若代数式有意义，则x应满足（）A．x=0 B．x≠1 C．x≥﹣5 D．x≥﹣5且x≠14．（3分）一个多边形的每个内角均为108°，则这个多边形是（A．4 B．5 C．6 D．7）边形．5．（3分）如图，直线l经过第二、三、四象限，l的解析式是y=（m﹣2）x+n，则m的取值范围在数轴上表示为（）第5题图第6题图A．B．C．D．6．（3分）如图，△ABC中，AB=AC，∠A=40°，延长AC到D，使CD=BC，点P是∠ABD 和∠ADB的平分线的交点，则∠BPD的度数是（）A．105°B．110°C．130°D．145°222 3 2 3 27．（3分）如图，三条公路两两相交，现计划修建一个油库，要求油库到这三条公路的距离相等，那么选择油库的位置有（）处．A．1 B．2 C．3 D．48．（3分）下列命题中是真命题的有（①相等的角是对顶角；）个．②两直线被第三条直线所截，内错角相等；③若m=n，则m=n；④平行四边形的对角线互相平分；⑤一组对边平行，一组对边相等的四边形是平行四边形．A．0 B．1 C．2 D．39．（3分）如图，平行四边形ABCD中，∠ABC=60°，E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，EF=，则AB的长是（）A．0.5 B．1 C．1.5 D．210．（3分）如图，Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC 的延长线于点E，则CE的长为（）A．第10图第11图B．C．D．11．（3分）直线l1：y=k1x+b与直线l2：y=k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k2x＞k1x+b的解集为（）A．x＞3 B．x＜3 C．x＞﹣1 D．x＜﹣12212．（3分）如图，平行四边形ABCD的面积为acm ，对角线交于点 O ；以AB 、AO 为邻 依此类推，则平行四边形AO n ﹣1C n B的面积为（ ）cm ．A ． aB ． aC ． aD ． a二、填空题：（本题共 4小题，每小题 3 分，共 12分）把答案填在答题卡上 13．（3分）如图，将 Rt △ABC 绕直角顶点顺时针旋转 90°，得到△A′B′C ，连结AA′，若∠AA′B′=20°，则∠B的度数为 °．14．（3 分）如果不等式组的解集是 x ＞3，那么 m 的取值范围是．15．（3分）在平行四边形ABCD中，BC边上的高为4，AB=5，AC=2ABCD 的周长等于 ． ，则平行四边形16．（3分）已知分式方程的的解x是正数，则m 的取值范围是．三、解答题（本大题有七题，其中第17题9分、第 18题6分、第19题6分、第20题 7 分、第 21 题 7 分、第22题 8分、第 23 题 9 分，共52分）17．（9分）（1）分解因式：3x ﹣12x y +12xy ．（2）先化简，再求值：÷（﹣x ﹣2），其中x=﹣2．2边作平行四边形AOC B ，连接AC 交BD 于O ，以AB 、AO 为邻边作平行四边形AO C B ；…；232 218．（6分）解不等式组，并把解集在数轴上表示出来．19．（6分）如图，E，F是平行四边形ABCD的对角线AC上的点，CE=AF．请你猜想：BE与DF有怎样的位置关系和数量关系？并对你的猜想加以证明：猜想：；证明：．20．（7分）华联商场预测某品牌衬衫能畅销市场，先用了8万元购入这种衬衫，面市后果然供不应求，于是商场又用了17.6万元购入第二批这种衬衫，所购数量是第一批购入量的2倍，但单价贵了4元．商场销售这种衬衫时每件定价都是58元，最后剩下的150件按定价的八折销售，很快售完．试求：（1）第一次购买这种衬衫的单价是多少？（2）在这两笔生意中，华联商场共赢利多少元？21．（7分）在△ABC中，AB=AC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．（1）在图1中请你通过观察猜想BF与CG满足的数量关系，并证明你的结论．（2）当三角尺沿AC方向平移到图2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、猜想DE、DF与CG满足的数量关系，并证明你的猜想．22．（8分）某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个，摆放在迎宾大道两侧．已知搭配一个A种造型需甲种花卉8盆，乙种花卉4盆；搭配一个B种造型需甲种花卉5盆，乙种花卉9盆．（l）某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来；（2）若搭配一个A种造型的成本是200元，搭配一个B种造型的成本是360元，试说明（1）中哪种方案成本最低，最低成本是多少元？23．（9分）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣3，0），（0，6）．动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从B出发，沿射线BO方向以每秒2个单位的速度运动，以CP，CO为邻边构造平行四边形PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．（1）直接写出当点C运动到线段OB的中点时，求t的值及点E的坐标．（2）当点C在线段OB上运动时，四边形ADEC的面积为S．①求证：四边形ADEC为平行四边形．②写出s与t的函数关系式，并求出t的取值范围．（3）是否存在某一时刻，使OC是PC的一半？若存在，求出t的值，若不存在，请说明理由．。

2015-2016学年广东省深圳市南山区八年级（下）期末数学试卷12小题，每小题3分，共36分.在每小题给出的四个选项中，只有 一项是符合题目要求的） 不等式2x+1 >x+2的解集是x - 35 .要使分式 /+6行9有意义,那么x 的取值范围是（ ）A. xw3B. xw3 且xw — 3C. xw0 且 xw —3D. xw—36 .如果关于x 的不等式（a+1） x>a+1的解集为xv1,那么a 的取值范围是（）A. av-1 B, a<0 C. a>- 1 D. a>0a< - 17 .如图，在平行四边形 ABCD^, AD=2AB CE 平分/ BCD^ AD 边 于点E,且AE=3贝U AB 的长为( )、选择题（本题有 A. x> 1B. xv 1C. x>1D. x< 12.多项式2x 2-2y 2分解因式的结果是（ A. 2 (x+y) 2B. 2 (x - y) 2C. 2 (x+y) ( x — y)D. 2 (y+x) (y —x)3. 卜列图案中，不是中心对称图形的是（A.C.4. 如图，△ ABC 中，AB 的垂直平分线交 AC 于D,如果 AC=5cm BC=4cm 那么△ DBC 的周长B. 7cmC. 8cmD. 9cmB.是（）CA. 6cmA- cc 5c cA. 4B. 3C. ,D. 28 .将一个有45。

角的三角板的直角顶点放在一张宽为3cm 的纸带边沿上.另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30。

角，如图，则三角板9 .如图，在平行四边形 ABCD^, A 已BC 于E, AF± CD 于F,若AE=4, AF=6,平行四边形 ABCD 勺周长为40.则平行四边形ABCM 面积为（）A D10 .如图，函数 y=2x 和y=ax+4的图象相交于点 A （ m, 3）,则不等式2xvax+4的解集为点，则PC+P 曲最小值为（二、填空题：（本题有 4小题，每小题3分，共12分）13.分解因式：2x2- 4x+2=.C.' cm D. ' cmA. 24B. 36C. 40D. 48. 3A. x vB. x<3C.3 x >ED. x>311.已知 a 2+b 2=6ab, a+b则二毛的值为（B. 一一C. D. ± 212. △ ABC 为等腰直角三角形，/ ACB=90 ,AC=BC=2 P 为线段 AB 上一动点，D 为BC 上中 A.B. 3C .7弃 E C15.如图，/ AOPN BOP=15 , PC// OA PD)± OA 若 PC=4 贝U PD 的长为三、解答题(本大题有七道题，其中 17题6分，18题7分，19题7分，20题7分，21题7分，22题9分，23题9分，共52分；)L 2 _ 1 二1617 .解方程：x+2 ¥2- 4 -- 642 (x+3)18 .解不等式组：｛或_]<3—显.[4 4r a+2 土 8、. a 2-419 .先化简，再求值： ^2 _ 2a 4- a 2 ；* 日，其中a 满足方程a2+4a+1=0.20 .如图，在边长为1个单位长度的小正方形组成的网格中，△ ABC 的顶点A 、B C 在小正 方形的顶点上，将△ABC0下平移4个单位、再向右平移3个单位得到△ A 1B 1C 1,然后将△ A 1BQ 绕点A 顺时针旋转90°得到△ AE 2C 2.(1)在网格中画出△ A 1B 1G 和△ A 1B 2c 2；(2)计算线段AC 在变换到A 1C 2的过程中扫过区域的面积(重叠部分不重复计算)14. 一个多边形的内角和与外角和的比是 4: 1,则它的边数是16.如图，在 Rt^ABC 中，/ABC=90 ,AB=BC=&,将△ AB 微点A 逆时针旋转60° ,得到△ ADE 连接 BE 则BE 的长是21.如图，在^ ABC中，D E分别是AB AC的中点，F是DE延长线上的点，且EF=DE(1)图中的平行四边形有哪几个？请选择其中一个说明理由；(2)若△ AEF的面积是3,求四边形BCFD勺面积.22.我县某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降，今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元.(1)今年5月份A款汽车每辆售价多少万元？(2)为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？(3)如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，返还顾客现金a万元，要使(2)中所有的方案获利相同，a值应是多少？此时，哪种方案对公司更有利？23.已知两个共一个顶点的等腰直角△ABC和等腰直角△ CEF /ABC=Z CEF=90 ,连接AF,M是AF的中点，连接MB ME图1 图2(1)如图1,当CB与CE在同一直线上日求证：MB CF;(2)如图1,若CB=a CE=2a 求BM ME的长；(3)如图2,当/ BCE=45 时，求证：BM=ME2015-2016学年广东省深圳市南山区八年级(下)期末数学试卷参考答案与试题解析一、选择题(本题有12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.不等式2x+1>x+2的解集是( )A. x>1B. x< 1C. x>1D. x<1【考点】解一元一次不等式.【分析】先移项，再合并同类项，把x的系数化为1即可.【解答】解：移项得，2x-x>2- 1,合并同类项得，x>1,故选A【点评】本题考查的是在解一元一次不等式，熟知解一元一次不等式的基本步骤是解答此题的关键.2.多项式2x2-2y2分解因式的结果是( )A. 2 (x+y) 2B. 2 (x-y) 2C. 2 (x+y) (x-y)D. 2 (y+x) (y-x) 【考点】提公因式法与公式法的综合运用.【分析】首先提公因式2,再利用平方差进行分解即可.【解答】解：2x2 - 2y2=2 ( x2 - y2) =2 (x+y) (x-y),股癣：C.【点评】此题主要考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解.3.下列图案中，不是中心对称图形的是(9 B.【考点】中心对称图形.【分析】根据中心对称图形的概念求解.【解答】解：A、是中心对称图形，故A选项错误;日不是中心对称图形，故B选项正确；C是中心对称图形，故C选项错误；D是中心对称图形，故D选项错误；故选：B.【点评】本题考查了中心对称图形的知识，解题的关键是掌握中心对称图形的概念. 中心对称图形是要寻找对称中心，旋转180。

八年级数学第1 页共6 页2013-2014学年度（下）八年级期末质量检测数学(满分：150分；考试时间：120分钟) 注意：本试卷分为“试题”和“答题卡”两部分，答题时请按答题卡中的“注意事项”要求认真作答，答案写在答题卡上的相应位置．一、精心选一选：本大题共8小题，每小题4分，共32分．1、下列计算正确的是（）A ．234265+=B ．842=C ．2733¸=D ．2(3)3-=-2、顺次连接对角线相等的四边形的各边中点，所得图形一定是（）A ．矩形B ．直角梯形C ．菱形D ．正方形3、甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差分别为0.56s =2甲，0.60s =2乙，20.50s =丙，20.45s =丁，则成绩最稳定的是（）A ．甲B ．乙C ．丙D ．丁4、一组数据4，5，6，7，7，8的中位数和众数分别是（）A ．7，7 B ．7，6.5 C ．5.5，7 D ．6.5，7 5、若直线y=kx+b 经过第一、二、四象限，则k,b 的取值范围是（）(A) k>0, b>0 (B) k>0,b<0 (C) k<0,b>0 (D) k<0,b<0 6、如图，把直线L 沿x 轴正方向向右平移2个单位得到直线L ′，则直线L /的解析式为（）A.12+=x yB. 42-=x yC. 22y x =- D. 22+-=x y 7、如图是一张直角三角形的纸片，两直角边AC ＝6 cm 、BC ＝8 cm ，现将△ABC 折叠，使点B 与点A 重合，折痕为DE ，则BE 的长为（）（A ）4 cm （B ）5 cm （C ）6 cm （D ）10 cm A第7题BCDEEDCBA（第8题A B C D E F 8、如图，ABC D 和DCE D 都是边长为4的等边三角形，的等边三角形，点点B 、C 、E 在同一条直线上，连接BD ，则BD 的长为（的长为（ ）（A ）3（B ）23（C ）33（D ）43二、细心填一填：本大题共8小题，每小题4分，共32分．分． 9、计算123-的结果是的结果是 ． 10、实数p 在数轴上的位置如图所示，化简22(1)(2)_______p p -+-=。

广东省深圳市2014年八年级下学期考试数学试题3.下列图案中是中心对称图形但不是轴对称图形的是A.B. C. D.4.不等式组的解集在数轴上表示正确的是( )5. 等腰三角形的一个角是80deg;，则它顶角的度数是( )A.80deg;B.80deg;或20deg;C.80deg;或50deg;D.20deg;6. 如图，已知AE=CF，ang;AFD=ang;CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是( )A.ang;A=ang;CB.AD=CBC.BE=DFD.AD∥BC(第6题图) (第8题图) (第12题图)7.若是一个完全平方式，则的值为( )A.6B.6C.12D.128.如图，在△ABC中，ang;ABC和ang;ACB的平分线交于点O，过O点作EF∥BC，交AB于E，交AC于F，若BE=3，CF=2，则线段EF的长为( ).A.5B.6C.7D.89.不等式的非负整数解的个数是( )A.1B.2C.3D.无数个10.下列命题是真命题的是( ).A.有两条边、一个角相等的两个三角形全等。

B.等腰三角形的对称轴是底边上的中线。

C.全等三角形对应边上的中线相等。

D.有一个角是60deg;的三角形是等边三角形。

11.不等式组的解集是，那么的取值范围是( )A. B. C. D.12. 如图，在△ABC中，ang;C=90deg;，ang;B=30deg;，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是( )①AD是ang;BAC的平分线;②ang;ADC=60deg;;③点D 在AB的中垂线上;④S△DAC：S△ABC=1：3.A.1个B.2个C.3个D.4个第二部分非选择题二、填空题(本题共4小题，每小题3分，共12分)13.分解因式 =答案请填在答题表内。

初二下册数学期末试卷答案20141、(1)在□ABCD中，ang;A=44，则ang;B= ，ang;C= 。

(2)若□ABCD的周长为40cm， AB:BC=2:3，则CD= ，AD= 。

2、若一个正方体棱长扩大2倍，则体积扩大倍。

要使一个球的体积扩大27倍，则半径扩大倍。

3、对角线长为2的正方形边长为 ;它的面积是。

4、化简：(1) (2) , (3) = ______。

5、估算：(1) asymp;_____(误差小于1)，(2) asymp;_____(精确到0.1)。

6、5的平方根是，的平方根是，-8的立方根是。

7、如图1,64、400分别为所在正方形的面积，则图中字母所代表的正方形面积是。

8、如图2，直角三角形中未知边的长度 = 。

9、已知 ,则由此为三边的三角形是三角形。

10、钟表上的分针绕其轴心旋转,分针经过15分后,分针转过的角度是。

11、如图3，一直角梯形,ang;B=90deg;,AD‖BC,AB=BC=8,CD=10,则梯形的面积是。

12、如图4，已知 ABCD中AC=AD，ang;B=72deg;，则ang;CAD=_________。

13、图5中，甲图怎样变成乙图：__ _____________________________ _。

14、用两个一样三角尺(含30deg;角的那个)，能拼出______种平行四边形。

二、选择题(15～25题每题2分，共22分)15、下列运动是属于旋转的是( )A.滚动过程中的篮球B.钟表的钟摆的摆动C.气球升空的运动D.一个图形沿某直线对折过程16、如图6，是我校的长方形水泥操场，如果一学生要从A角走到C角，至少走( )A.140米B.120米C.100米D.90米17、下列说法正确的是( )A. 有理数只是有限小数B. 无理数是无限小数C. 无限小数是无理数D. 是分数18、下列条件中，不能判定四边形ABCD为平行四边形的条件是( )A. AB‖CD，AB=CDB. AB‖CD，AD‖BCC. AB=AD, BC=CDD. AB=CD AD=BC19、下列数组中，不是勾股数的是( )A 3、4、5B 9、12、15C 7、24、25D 1.5、2、2.520、和数轴上的点成一一对应关系的数是( )A.自然数B.有理数C.无理数D. 实数21、小丰的妈妈买了一部29英寸(74cm)的电视机,下列对29英寸的说法中正确的是( )A. 小丰认为指的是屏幕的长度; B 小丰的妈妈认为指的是屏幕的宽度;C. 小丰的爸爸认为指的是屏幕的周长;D. 售货员认为指的是屏幕对角线的长度.22、小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )A. 2m;B. 2.5m;C. 2.25m;D. 3m.23、对角线互相垂直且相等的四边形一定是( )A、正方形B、矩形C、菱形D、无法确定其形状24、下列说法不正确的是( )A. 1的平方根是1B. ndash;1的立方根是-1C. 是2的平方根D. ndash;3是的平方根25、平行四边形的两条对角线和一边的长可依次取( )A. 6，6，6B. 6，4，3C. 6，4，6D. 3，4，5三、解答题(26～33题共50分)26、(4分)把下列各数填入相应的集合中(只填序号)(1)3.14(2)- (3)- (4) (5)0 (6)1.212212221 (7) (8)0.15无理数集合{ };有理数集合{ }。

深圳市2014-2015学年第二学期期末质量检测八年级数学试卷说明：1、试卷共4页，答题卡共4页（2面）。

考试时间90分钟，满分100分。

2、请在答题卡上填涂学校、班级、姓名、考生号，不得在其它地方作任何标记。

3、答案必须写在答题卡指定位置上，否则不给分。

一、选择题（每题3分，共36分）每小题有四个选项，其中只有一个是正确的，请把选出的答案按要求填涂到答题卡相应位置上。

1．如图，所给图形中是中心对称图形但不是轴对称图形的是（ ）2．若x ＞y ，则下列式子错误的是（ ）A.x ﹣3＞y ﹣3B.﹣3x ＞﹣3yC.x+3＞y+3D.x y>333．不等式1＋x ＜0的解集在数轴上表示正确的是（ ）A ．B ．C ．D ．4．等腰三角形一个角等于50°，则此等腰三角形的顶角为（ ） A ．︒50 B ．︒80 C ．︒︒6550或 D ．︒︒8050或5．不等式组⎩⎨⎧≤>+103x x 的解集在数轴上表示正确的是（ ）A B C D6. 深圳市某天最高气温是33℃，最低气温是24℃，则这天气温t （℃）的变化范围是（ ） A.t ＞33 B.t≤24 C.24＜t ＜33 D.24≤t≤337．若点P （2k-1，1-k ）在第四象限，则ｋ的取值范围为（ ） A. k ＞１ B. k ＜21 C. k ＞21 D. 21＜k ＜１ 8. 下列命题是真命题的是（ ）B ．两边和一角对应相等的两个三角形全等 C. 三角形的一个外角等于它的两个内角之和 D ． 直角三角形两锐角互余9. 如图，△ABC 中，AB 边的垂直平分线交AB 于点E ，交BC 于点D ， 已知AC=5cm ，△ADC 的周长为17cm ，则BC 的长为（ ） A.7cm B.10cm C.12cm D. 22cm10. 如图，△ABC 中，AB=6cm ，AC=5cm ，∠ABC 与∠ACB 的平分线相交于 点O ，过点O 作DE ∥BC 交AB 于点D ，交AC 于点E ，则△ADE 的周长 等于（ ）cm 。

新八年级（下）数学期末考试试题(含答案)一、选择题（本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是正确的，请将正确答案前的字母填入题后的括号内，每小题选对得3分，选错、不选或多选均得零分）1．若＝2﹣a，则a的取值范围是（）A．a＝2B．a＞2C．a≥2D．a≤22．若一个直角三角形的两直角边长分别为3和4，则下列说法不正确的是（）A．这个直角三角形的斜边长为5B．这个直角三角形的周长为12C．这个直角三角形的斜边上的高为D．这个直角三角形的面积为123．如图，在平行四边形ABCD中，DE平分∠ADC交BC于E，AF⊥DE，垂足为F，已知∠DAF＝50°，则∠B＝（）A．50°B．40°C．80°D．100°4．用一长一短的两根木棒，在它们的中心处固定一个小螺钉，做成一个可转动的叉形架，四个顶点用橡皮筋连成一个四边形，转动木条，这个四边形变成菱形时，两根木棒所成角的度数是（）A．90°B．60°C．45°D．30°5．一组数据：2，3，4，x中，若中位数与平均数相等，则数x不可能是（）A．1B．2C．3D．56．若样本数据3，4，2，6，x的平均数为5，则这个样本的方差是（）A．3B．5C．8D．27．若直线l与直线y＝2x﹣3关于y轴对称，则直线l的解析式是（）A．y＝﹣2x+3B．y＝﹣2x﹣3C．y＝2x+3D．y＝2x﹣38．正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，则一次函数y＝kx+k的图象大致是（）A．B．C．D．二、填空题（本大题共6小题，每小题3分，共18分）9．根式+1的相反数是．10．在△ABC中，AC＝BC＝，AB＝2，则△ABC中的最小角是．11．若一组数据1，2，3，x，0，3，2的众数是3，则这组数据的中位数是．12．若直线y＝kx+b与直线y＝2x平行，且与y轴相交于点（0，﹣3），则直线的函数表达式是．13．如图，矩形纸片ABCD中，AB＝2cm，点E在BC上，且AE＝CE．若将纸片沿AE折叠，点B恰好与AC上的点B1重合，则BC＝．14．菱形ABCD中，∠B＝60°，AB＝4，点E在BC上，CE＝2，若点P是菱形上异于点E的另一点，CE＝CP，则EP的长为．三、解答题（本大题共4小题，每小题6分，共24分）15．（6分）（1）计算：2•（﹣3）•（2）化简++x÷16．（6分）如果一组数据﹣1，0，2，3，x的极差为6（1）求x的值；（2）求这组数据的平均数．17．（6分）在图1，图2中，点E是矩形ABCD边AD上的中点，请用无刻度的直尺按下列要求画图（保留画图痕迹，不写画法）（1）在图1中，以BC为一边画△PBC，使△PBC的面积等于矩形ABCD的面积．（2）在图2中，以BE、ED为邻边画▱BEDK．18．（6分）如图，直线y＝x+与x轴相交于点B，与y轴相交于点A．（1）求∠ABO的度数；（2）过点A的直线l交x轴的正半轴于点C，且AB＝AC，求直线的函数解析式．四、解答题（本大题共3小题，每小题8分，共24分）19．（8分）如图，在矩形ABCD中，点E在AD上，EC平分∠BED（1）判断△BEC的形状，并加以证明；（2）若∠ABE＝45°，AB＝2时，求BC的长．20．（8分）甲、乙两班各推选10名同学进行投篮比赛，按照比赛规则，每人各投了10个球，两个班选手的进球数统计如表，请根据表中数据解答下列问题（1）分别写出甲、乙两班选手进球数的平均数、中位数与众数；（2）如果要从这两个班中选出一个班级参加学校的投篮比赛，争取夺得总进球团体的第一名，你认为应该选择哪个班？如果要争取个人进球数进入学校前三名，你认为应该选择哪个班？21．（8分）小明家今年种植的“红灯”樱桃喜获丰收，采摘上市20天全部销售完，小明对销售情况进行跟踪记录，并将记录情况绘成图象，日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图1所示，樱桃价格z（单位：元/千克）与上市时间x（单位：天）的函数关系式如图2所示．（1）观察图象，直接写出日销售量的最大值；（2）求小明家樱桃的日销售量y与上市时间x的函数解析式；（3）试比较第10天与第12天的销售金额哪天多？五、探究题（本大题共1小题，共10分）22．（10分）如图，在正方形ABCD中，点E、F是正方形内两点，BE∥DF，EF⊥BE，为探索研究这个图形的特殊性质，某数学学习小组经历了如下过程：（1）在图1中，连接BD，且BE＝DF①求证：EF与BD互相平分②求证：（BE+DF）2+EF2＝2AB2（2）在图2中，当BE≠DF，其它条件不变时，（BE+DF）2+EF2＝2AB2是否成立？若成立，请你加以证明：若不成立，请你说明理由．（3）在图3中，当AB＝4，∠DPB＝135°，BP+2PD＝4时，求PD的长．参考答案与试题解析一、选择题（本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是正确的，请将正确答案前的字母填入题后的括号内，每小题选对得3分，选错、不选或多选均得零分）1．解：∵＝|a﹣2|＝2﹣a，∴a﹣2≤0，故选：D．2．解：根据勾股定理可知，直角三角形两直角边长分别为3和4，则它的斜边长是＝5，周长是3+4+5＝12，斜边长上的高为＝，面积是3×4÷2＝6．故说法不正确的是D选项．故选：D．3．解：在Rt△ADF中，∵∠DAF＝50°，∴∠ADE＝40°，又∵DE平分∠ADC，∴∠ADC＝80°，∴∠B＝∠ADC＝80°．故选：C．4．解：如图，∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形，∴当AC⊥BD时，四边形ABCD是菱形，故选：A．5．解：（1）将这组数据从小到大的顺序排列为2，3，x，4，处于中间位置的数是3，x，那么由中位数的定义可知，这组数据的中位数是（3+x）÷2，平均数为（2+3+4+x）÷4，∴（3+x）÷2＝（2+3+4+x）÷4，解得x＝3，大小位置与3对调，不影响结果，符合题意；（2）将这组数据从小到大的顺序排列后2，3，4，x，中位数是（3+4）÷2＝3.5，此时平均数是（2+3+4+x）÷4＝3.5，解得x＝5，符合排列顺序；（3）将这组数据从小到大的顺序排列后x，2，3，4，中位数是（2+3）÷2＝2.5，平均数（2+3+4+x）÷4＝2.5，解得x＝1，符合排列顺序．∴x的值为1、3或5．故选：B．6．解：∵数据3，4，2，6，x的平均数为5，∴＝5，解得：x＝10，则方差为×[（3﹣5）2+（4﹣5）2+（2﹣5）2+（6﹣5）2+（10﹣5）2]＝8，故选：C．7．解：与直线y＝2x﹣3关于y轴对称的点的坐标为横坐标互为相反数，纵坐标不变，则y＝2（﹣x）﹣3，即y＝﹣2x﹣3．所以直线l的解析式为：y＝﹣2x﹣3．故选：B．8．解：∵正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，∴k＜0，∴一次函数y＝kx+k的图象经过二、三、四象限．故选：D．二、填空题（本大题共6小题，每小题3分，共18分）9．解：+1的相反数是﹣﹣1，故答案为：﹣﹣1．10．解：∵AC＝BC＝，AB＝2，∴AC2+BC2＝2+2＝4＝22＝AB2，∴△ABC是等腰直角三角形，∴△ABC中的最小角是45°；故答案为：45°．11．解：∵1，2，3，x，0，3，2的众数是3，∴x＝3，先对这组数据按从小到大的顺序重新排序0，1，2，2，3，3，3，位于最中间的数是2，∴这组数的中位数是2．故答案为：2；12．解：∵直线y＝kx+b与直线y＝2x平行，∴k＝2，把点（0，﹣3）代入y＝2x+b得b＝﹣3，∴所求直线解析式为y＝2x﹣3．故答案为：y＝2x﹣3．13．解：∵AB＝2cm，AB＝AB1∴AB1＝2cm，∵四边形ABCD是矩形，AE＝CE，∴∠ABE＝∠AB1E＝90°∵AE＝CE，∴AB1＝B1C，∴AC＝4cm．在Rt△ABC中，BC＝＝＝2．故答案为：2cm．14．解：如图所示：连接EP交AC于点H．∵菱形ABCD中，∠B＝60°，∴∠BCD＝120°，∠ECH＝∠PCH＝60°．在△ECH和△PCH中，∴△ECH≌△PCH．∴∠EHC＝∠PHC＝90°，EH＝PH．∴EP＝2EH＝2sin60°•EC＝2××2＝6．如图2所示：△ECP为等腰直角三角形，则EP＝EC＝2．过点P′作P′F⊥BC．∵P′C＝2，BC＝4，∠B＝60°，∴P′C⊥AB．∴∠BCP′＝30°．∴FC＝×2＝3，P′F＝，EF＝2﹣3．∴EP′＝＝3﹣．故答案为：6或2或3﹣．三、解答题（本大题共4小题，每小题6分，共24分）15．解：（1）原式＝2×（﹣3）××＝﹣9；（2）原式＝3++x•＝3++＝5．16．解：（1）∵3+1＝4＜6，∴x为最大值或最小值．当x为最大值时，有x+1＝6，解得x＝5．当x为最小值时，3﹣x＝6，解得x＝﹣3；（2）当x为5时，平均数为．当x为﹣3时，平均数为．17．解：（1）图1中△PBC为所画；（2）图2中▱BEDK为所画．18．解：（1）对于直线y＝x+，令x＝0，则y＝，令y＝0，则x＝﹣1，故点A的坐标为（0，），点B的坐标为（﹣1，0），则AO＝，BO＝1，在Rt△ABO中，∵tan∠ABO＝，∴∠ABO＝60°；（2）在△ABC中，∵AB＝AC，AO⊥BC，∴AO为BC的中垂线，即BO＝CO，则C点的坐标为（1，0），设直线l的解析式为：y＝kx+b（k，b为常数），则，解得：，即函数解析式为：y＝﹣x+．四、解答题（本大题共3小题，每小题8分，共24分）19．解：（1）△BEC是等腰三角形，∵在矩形ABCD中，AD∥BC，∴∠DEC＝∠BCE，∵EC平分∠BED，∴∠BEC＝∠DEC，∴∠BEC＝∠BCE，∴BE＝BC，∴△BEC是等腰三角形（2）在矩形ABCD中，∠A＝90°，且∠ABE＝45°，∴△ABE是等腰直角三角形，∴AE＝AB＝2，∴BE＝＝2，由（1）知BC＝BE，∴BC＝220．解：（1）甲班选手进球数的平均数为7，中位为7，众数为7；乙班选手进球数的平均数为7，中位为7，众数为7；（2）甲班S12＝[（10﹣7）2+（9﹣7）2+（8﹣7）2+4×（7﹣7）2+0×（6﹣7）2+3×（5﹣7）2]＝2.6，乙班S22＝[0×（10﹣7）2+（9﹣7）2+2×（8﹣7）2+5×（7﹣7）2+（6﹣7）2+2×（5﹣7）2]＝1.4．∵甲方差＞乙方差，∴要争取夺取总进球团体第一名，应选乙班．∵甲班有一位百发百中的出色选手，∴要进入学校个人前3名，应选甲班．21．解：（1）由图象得：120千克，（2）当0≤x≤12时，设日销售量与上市的时间的函数解析式为y＝k1x，∵直线y＝k1x过点（12，120），∴k1＝10，∴函数解析式为y＝10x，当12＜x≤20，设日销售量与上市时间的函数解析式为y＝k2x+b，∵点（12，120），（20，0）在y＝k2x+b的图象上，∴，解得：∴函数解析式为y＝﹣15x+300，∴小明家樱桃的日销售量y与上市时间x的函数解析式为：y＝；（3）∵第10天和第12天在第5天和第15天之间，∴当5＜x≤15时，设樱桃价格与上市时间的函数解析式为z＝mx+n，∵点（5，32），（15，12）在z＝mx+n的图象上，∴，解得：，∴函数解析式为z＝﹣2x+42，当x＝10时，y＝10×10＝100，z＝﹣2×10+42＝22，销售金额为：100×22＝2200（元），当x＝12时，y＝120，z＝﹣2×12+42＝18，销售金额为：120×18＝2160（元），∵2200＞2160，∴第10天的销售金额多．五、探究题（本大题共1小题，共10分）22．（1）证明：①连接ED、BF，∵BE∥DF，BE＝DF，∴四边形BEDF是平行四边形，∴BD、EF互相平分；②设BD交EF于点O，则OB＝OD＝BD，OE＝OF＝EF．∵EF⊥BE，∴∠BEF＝90°．在Rt△BEO中，BE2+OE2＝OB2．∴（BE+DF）2+EF2＝（2BE）2+（2OE）2＝4（BE2+OE2）＝4OB2＝（2OB）2＝BD2．在正方形ABCD中，AB＝AD，BD2＝AB2+AD2＝2AB2．∴（BE+DF）2+EF2＝2AB2；（2）解：当BE≠DF时，（BE+DF）2+EF2＝2AB2仍然成立，理由如下：如图2，过D作DM⊥BE交BE的延长线于M，连接BD．∵BE∥DF，EF⊥BE，∴EF⊥DF，∴四边形EFDM是矩形，∴EM＝DF，DM＝EF，∠BMD＝90°，在Rt△BDM中，BM2+DM2＝BD2，∴（BE+EM）2+DM2＝BD2．即（BE+DF）2+EF2＝2AB2；（3）解：过P作PE⊥PD，过B作BE⊥PE于E，则由上述结论知，（BE+PD）2+PE2＝2AB2．∵∠DPB＝135°，∴∠BPE＝45°，∴∠PBE ＝45°，∴BE ＝PE ．∴△PBE 是等腰直角三角形，∴BP ＝BE ， ∵BP +2PD ＝4，∴2BE +2PD ＝4，即BE +PD ＝2， ∵AB ＝4，∴（2）2+PE 2＝2×42，解得，PE ＝2， ∴BE ＝2， ∴PD ＝2﹣2．新八年级下册数学期末考试试题(答案)一.选择题（每小题3分，共30分）1x 应满足的条件是（ ）A ．x ≠2的实数B ．x ＜2的实数C ．x ＞2的实数D ．x ＞0且x ≠2的实数2．一组数据：﹣3，1，2，6，6，8，16，99，这组数据的中位数和众数分别是（ ）A ．6和6B ．8和6C ．6和8D ．8和163、中，最简二次根式的个数有（ ）A ．4B ．3C ．2D ．14．一次函数y ＝﹣x+6的图象上有两点A （﹣1，y1）、B （2，y2），则y1与y2的大小关系是（ ）A ．y1＞y2B ．y1＝y2C ．y1＜y2D ．y1≥y25．如果点P （2，b ）和点Q （a ，﹣3）关于x 轴对称，则a+b 的值是（ ）A ．﹣1B ．1C ．﹣5D ．56．矩形各内角的平分线能围成一个（ ）A ．矩形B ．菱形C ．等腰梯形D ．正方形7）A ．14B ．﹣14C ．12D ．±128．直角梯形的一个内角为120°，较长的腰为6cm ，有一底边长为5cm ，则这个梯形的面积为（ ）ABC ．cm2 Dcm2cm29．不能判定四边形ABCD 为平行四边形的题设是（ ）A ．AB ＝CD ，AB ∥CD B ．∠A ＝∠C ，∠B ＝∠DC ．AB ＝AD ，BC ＝CD D ．AB ＝CD ，AD ＝BC10．某人出去散步，从家里出发，走了20min ，到达一个离家900m 的阅报亭，看了10min 报纸后，用了15min 返回家里，下面图象中正确表示此人离家的距离y （m ）与时间x （min ）之家关系的是（ ）A ．B ．C ．D ．二.填空题（每小题4分，共32分）11．菱形的两条对角线分别为18cm 与24cm ，则此菱形的周长为 ．1213．计算：200220025)5)＝ ．14．在实数范围内分解因式：3x2﹣6＝ ．15．如图，已知一次函数y ＝ax+b 和y ＝kx 的图象相交于点P ，则根据图中信息可得二元一次方程组0y ax b kx y =+⎧⎨-=⎩的解是 ．16、已知一次函数y＝kx+3k+5的图象与y轴的交点在y轴的正半轴上，且函数值y随x的增大而减小，则k所有可能取得的整数值为17．如图，已知在Rt△ABC中，∠ACB＝90°，AB＝4，分别以AC、BC为直径作半圆，面积分别记为S1、S2，则S1+S2等于．18．甲、乙两人各进行10次射击比赛，平均成绩均为9环，方差分别是：S甲2＝2，S乙2＝4，则射击成绩较稳定的是（选填“甲”或“乙”）．三、解答题一（共38分）19．计算：计算：（1）(32+（2）20．如图，已知BE∥DF，∠ADF＝∠CBE，AF＝CE，求证：四边形DEBF是平行四边形．21．若x＝3＋，y＝3－22．如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画三角形和平行四边形．（1）使三角形三边长为3；（2）使平行四边形有一锐角为45°，且面积为4．23．如图，AD∥BC，AC⊥AB，AB＝3，AC＝CD＝2．（1）求BC的长；（2）求BD的长．四、解答题二（共50分）24．已知：如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交于BE的延长线于点F，且AF＝DC，连接CF．（1）求证：D是BC的中点；（2）如果AB＝AC，试判断四边形ADCF的形状，并证明你的结论．25．如图，一个正比例函数与一个一次函数的图象交于点A（3，4），其中一次函数与y轴交于B点，且OA＝OB．（1）求这两个函数的表达式；（2）求△AOB的面积S．26．如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．（1）求证：△BEC≌△DFA；（2）求证：四边形AECF是平行四边形．27．某公司为了了解员工每人所创年利润情况，公司从各部抽取部分员工对每年所创年利润情况进行统计，并绘制如图1，图2统计图．（1）求抽取员工总人数，并将图补充完整；（2）每人所创年利润的众数是，每人所创年利润的中位数是，平均数是；（3）若每人创造年利润10万元及（含10万元）以上为优秀员工，在公司1200员工中有多少可以评为优秀员工？28．在体育局的策划下，市体育馆将组织明星篮球赛，为此体育局推出两种购票方案（设购票张数为x，购票总价为y）：方案一：提供8000元赞助后，每张票的票价为50元；方案二：票价按图中的折线OAB所表示的函数关系确定．（1）若购买120张票时，按方案一和方案二分别应付的购票款是多少？（2）求方案二中y与x的函数关系式；（3）至少买多少张票时选择方案一比较合算？参考答案与试题解析1. 【分析】根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0，列不等式组求解．【解答】解：根据题意得：10 220xx-≥--≠⎧⎪⎨⎪⎩，∴2-x＜0，∴x＞2．故选C．（a≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．当二次根式在分母上时还要考虑分母不等于零，此时被开方数大于0．2. 【分析】中位数是一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；众数是一组数据中出现次数最多的数据．【解答】解：在这一组数据中6是出现次数最多的，故众数是6；将这组数据已从小到大的顺序排列，处于中间位置的两个数是6、6，那么由中位数的定义可知，这组数据的中位数是6；故选：A．【点评】本题为统计题，考查众数与中位数的意义．将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）叫做这组数据的中位数；如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．3. 【分析】最简二次根式就是被开方数不含分母，并且不含有开方开的尽的因数或因式的二次根式，根据以上条件即可判断．综上可得最简二次根式的个数有2个．故选C．【点评】本题考查最简二次根式的定义，一定要掌握最简二次根式必须满足两个条件，被开方数不含分母且被开方数不含能开得尽方的因数或因式．4. 【分析】k=-1＜0，y将随x的增大而减小，根据-1＜2即可得出答案．【解答】解：∵k=-1＜0，y将随x的增大而减小，又∵-1＜2，∴y1＞y2．故选：A．【点评】本题考查一次函数的图象性质的应用，注意：一次函数y=kx+b（k、b为常数，k≠0），当k＞0，y随x增大而增大；当k＜0时，y将随x的增大而减小．5. 【分析】直接利用关于x轴对称点的性质得出a，b的值，进而得出答案．【解答】解：∵点P（2，b）和点Q（a，-3）关于x轴对称，∴a=2，b=3，则a+b的值是：5．故选：D．【点评】此题主要考查了关于x轴对称点的性质，正确记忆横纵坐标的关系是解题关键．6. 【分析】根据矩形的性质及角平分线的性质进行分析即可．【解答】解：矩形的四个角平分线将矩形的四个角分成8个45°的角，因此形成的四边形每个角是90°又知两条角平分线与矩形的一边构成等腰直角三角形，所以这个四边形邻边相等，根据有一组邻边相等的矩形是正方形，得到该四边形是正方形．故选：D．【点评】此题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：①先说明它是矩形，再说明有一组邻边相等；②先说明它是菱形，再说明它有一个角为直角7. 【分析】直接利用算术平方根的定义得出答案．14的算术平方根是：1 2．故选：C．【点评】此题主要考查了算术平方根，正确把握定义是解题关键．8. 【分析】根据“直角梯形的一个内角为120°，较长的腰为6cm”可求得直角梯形的高为6×sin60°，由于一底边长为5cm不能确定是上底还是下底，故要分两种情况讨论梯形的面积，根据梯形的面积公式=12（上底+下底）×高，分别计算即可．【解答】解：根据题意可作出下图，BE为高线，BE⊥CD，即∠A=∠C=90°，∠ABD=120°，BD=6cm，∵AB∥CD，∠ABD=120°，∴∠D=60°，∴BE=6×sin60°；ED=6×cos60°=3cm；当AB=5cm时，CD=5+3=8cm，梯形的面积=12×（5+8）；当CD=5cm时，AB=5-3=2cm，梯形的面积=12×（2+5）=；cm2，选D．【点评】本题考查了直角梯形的性质及面积公式，涉及到特殊角的三角函数计算，注意当题意所给数据不明确时，要注意分类讨论思想．9. 【分析】根据平行四边形的判定定理（一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；两组对边分别相等的四边形是平行四边形）求解即可求得答案．【解答】解：A、∵AB=CD，AB∥CD，∴四边形ABCD为平行四边形（一组对边平行且相等的四边形是平行四边形）；故本选项能判定四边形ABCD为平行四边形；B、∵∠A=∠C，∠B=∠D，∴四边形ABCD为平行四边形（两组对角分别相等的四边形是平行四边形）；故本选项能判定四边形ABCD为平行四边形；C、由AB=AD，BC=CD，不能判定四边形ABCD为平行四边形；D、∵AB=CD，AD=BC，∴四边形ABCD为平行四边形（两组对边分别相等的四边形是平行四边形）；故本选项能判定四边形ABCD为平行四边形．故选：C．【点评】此题考查了平行四边形的判定．此题难度不大，注意熟记定理是解此题的关键．10. 【分析】由于某人出去散步，从家走了20分钟，到一个离家900米的阅报亭，并且看报纸10分钟，这是时间在加长，而离家的距离不变，再按原路返回用时15分钟，离家的距离越来越短，由此即可确定表示张大伯离家时间与距离之间的关系的函数图象．【解答】解：依题意，0～20min散步，离家路程从0增加到900m，20～30min看报，离家路程不变，30～45min返回家，离家从900m路程减少为0m，且去时的速度小于返回的速度，故选：D．【点评】此题主要考查了函数图象，利用图象信息隐含的数量关系确定所需要的函数图象是解答此题的关键．11. 【分析】根据菱形的性质对角线互相垂直平分，利用勾股定理求出菱形的边长即可解决问题．【解答】解：如图，四边形ABCD是菱形，AC=24，BD=18，∵四边形ABCD是菱形，∴AC⊥BD，AO=OC=12，OD=OB=9，AB=BC=CD=AD，∴．∴菱形的周长为60cm．故答案为60cm【点评】本题考查菱形的性质、勾股定理等知识，解题的关键是熟练掌握菱形的性质，属于中考常考题型．12. 分析】的倒数值，判断即可．2==，2==，+2，故答案为＜．【点评】本题考查了实数大小比较法则，任意两个实数都可以比较大小．根据两正数比较倒数大的反而小得出是解题关键．13. 【分析】直接利用积的乘方运算法则将原式变形进而得出答案．【解答】解：原式=[（−5）（+5）]2002=1．故答案为：1．【点评】此题主要考查了二次根式的混合运算，正确运用乘法公式是解题关键．14. 【分析】先提取公因式3，然后把2，再利用平方差公式继续分解因式即可．【解答】解：3x2-6，=3（x2-2），=3（2），=3（）（）．故答案为：3（）（）．【点评】本题考查了实数范围内分解因式，注意把22的形式继续进行因式分解．15. 【分析】直接利用已知图形结合一次函数与二元一次方程组的关系得出答案．【解答】解：如图所示：根据图中信息可得二元一次方程组0y ax b kx y +-⎧⎨⎩＝＝的解是：42x y -⎩-⎧⎨＝＝． 故答案为：42x y -⎩-⎧⎨＝＝． 【点评】此题主要考查了一次函数与二元一次方程组的关系，正确利用图形获取正确信息是解题关键．16. 【分析】由一次函数图象与系数的关系可得出关于k 的一元一次不等式组，解不等式组即可得出结论．【解答】解：由已知得：2300k k ⎨⎩+⎧＞＜，解得：-32＜k ＜0．∵k 为整数，∴k=-1．故答案为：-1．【点评】本题考查了一次函数图象与系数的关系，解题的关键是得出关于k 的一元一次不等式组．本题属于基础题，难度不大，解决该题型题目时，根据一次函数图象与系数的关系找出关于系数的不等式（或不等式组）是关键．17. 【分析】根据半圆面积公式结合勾股定理，知S1+S2等于以斜边为直径的半圆面积．【解答】解：S1=12π（2AC ）2=18πAC2，S2=18πBC2，所以S1+S2=18π（AC2+BC2）=18πAB2=2π．故答案为：2π．【点评】此题根据半圆的面积公式以及勾股定理证明：以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的半圆面积，重在验证勾股定理．18. 【分析】根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．【解答】解：因为甲的方差最小，所以射击成绩较稳定的是甲；故答案为：甲【点评】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．19. 【分析】（1）直接利用二次根式的混合运算法则化简得出答案；（2）直接利用二次根式的性质化简，进而计算得出答案．【解答】解：（1）原式=（2）原式=-1--1）==0．【点评】此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．20. 【分析】首先根据平行线的性质可得∠BEC=∠DFA ，再加上条件∠ADF=∠CBE ，AF=CE ，可证明△ADF ≌△CBE ，再根据全等三角形的性质可得BE=DF ，根据一组对边平行且相等的四边形是平行四边形进行判定即可．【解答】证明：∵BE ∥DF ，∴∠BEC=∠DFA ，在△ADF 和△CBE 中ADF CBE AFD CEBAF CE ∠∠∠∠⎧⎪⎨⎪⎩＝＝＝，∴△ADF ≌△CBE （AAS ），∴BE=DF ，又∵BE ∥DF ，∴四边形DEBF 是平行四边形．【点评】此题主要考查了平行四边形的判定，关键是掌握一组对边平行且相等的四边形是平行四边形．21. 【分析】先运用平方差及完全平方公式进行因式分解，再约分，将分式化到最简即可．【解答】解：====0．故当x＝，y＝时，原式=0．【点评】本题考查了二次根式的化简求值．运用公式将分子因式分解可使运算简便．由于所求代数式化简之后是一个常数0，与字母取值无关．因而无论x、y取何值，原式都等于0．22. 【分析】（1新八年级下册数学期末考试试题(答案)一.选择题（每小题3分，共30分）1x应满足的条件是（）A．x≠2的实数B．x＜2的实数C．x＞2的实数D．x＞0且x≠2的实数2．一组数据：﹣3，1，2，6，6，8，16，99，这组数据的中位数和众数分别是（）A．6和6B．8和6C．6和8D．8和163、中，最简二次根式的个数有（）A．4B．3C．2D．14．一次函数y＝﹣x+6的图象上有两点A（﹣1，y1）、B（2，y2），则y1与y2的大小关系是（）A．y1＞y2B．y1＝y2C．y1＜y2D．y1≥y25．如果点P（2，b）和点Q（a，﹣3）关于x轴对称，则a+b的值是（）A．﹣1B．1C．﹣5D．56．矩形各内角的平分线能围成一个（）A．矩形B．菱形C．等腰梯形D．正方形7）A．14B．﹣14C．12D．±128．直角梯形的一个内角为120°，较长的腰为6cm，有一底边长为5cm，则这个梯形的面积为（）ABC．cm2Dcm2cm29．不能判定四边形ABCD为平行四边形的题设是（）A．AB＝CD，AB∥CD B．∠A＝∠C，∠B＝∠DC ．AB ＝AD ，BC ＝CD D ．AB ＝CD ，AD ＝BC10．某人出去散步，从家里出发，走了20min ，到达一个离家900m 的阅报亭，看了10min 报纸后，用了15min 返回家里，下面图象中正确表示此人离家的距离y （m ）与时间x （min ）之家关系的是（ ）A ．B ．C ．D ．二.填空题（每小题4分，共32分）11．菱形的两条对角线分别为18cm 与24cm ，则此菱形的周长为 ．1213．计算：200220025)5)＝ ．14．在实数范围内分解因式：3x2﹣6＝ ．15．如图，已知一次函数y ＝ax+b 和y ＝kx 的图象相交于点P ，则根据图中信息可得二元一次方程组0y ax b kx y =+⎧⎨-=⎩的解是 ．16、已知一次函数y ＝kx+3k+5的图象与y 轴的交点在y 轴的正半轴上，且函数值y 随x 的增大而减小，则k 所有可能取得的整数值为17．如图，已知在Rt △ABC 中，∠ACB ＝90°，AB ＝4，分别以AC 、BC 为直径作半圆，面积分别记为S1、S2，则S1+S2等于 ．18．甲、乙两人各进行10次射击比赛，平均成绩均为9环，方差分别是：S 甲2＝2，S 乙2＝4，则射击成绩较稳定的是 （选填“甲”或“乙”）．三、解答题一（共38分）19．计算：计算：（1）(32+（2）20．如图，已知BE ∥DF ，∠ADF ＝∠CBE ，AF ＝CE ，求证：四边形DEBF 是平行四边形．21．若x ＝3＋，y ＝3－22．如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画三角形和平行四边形．（1）使三角形三边长为3；（2）使平行四边形有一锐角为45°，且面积为4．23．如图，AD ∥BC ，AC ⊥AB ，AB ＝3，AC ＝CD ＝2．（1）求BC 的长；（2）求BD 的长．四、解答题二（共50分）24．已知：如图，在△ABC 中，D 是BC 边上的一点，E 是AD 的中点，过点A 作BC 的平行线交于BE 的延长线于点F ，且AF ＝DC ，连接CF ．（1）求证：D是BC的中点；（2）如果AB＝AC，试判断四边形ADCF的形状，并证明你的结论．25．如图，一个正比例函数与一个一次函数的图象交于点A（3，4），其中一次函数与y轴交于B点，且OA＝OB．（1）求这两个函数的表达式；（2）求△AOB的面积S．26．如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．（1）求证：△BEC≌△DFA；（2）求证：四边形AECF是平行四边形．27．某公司为了了解员工每人所创年利润情况，公司从各部抽取部分员工对每年所创年利润情况进行统计，并绘制如图1，图2统计图．（1）求抽取员工总人数，并将图补充完整；（2）每人所创年利润的众数是，每人所创年利润的中位数是，平均数是；（3）若每人创造年利润10万元及（含10万元）以上为优秀员工，在公司1200员工中有多少可以评为优秀员工？28．在体育局的策划下，市体育馆将组织明星篮球赛，为此体育局推出两种购票方案（设购票张数为x ，购票总价为y ）：方案一：提供8000元赞助后，每张票的票价为50元；方案二：票价按图中的折线OAB 所表示的函数关系确定．（1）若购买120张票时，按方案一和方案二分别应付的购票款是多少？（2）求方案二中y 与x 的函数关系式；（3）至少买多少张票时选择方案一比较合算？参考答案与试题解析1. 【分析】根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0，列不等式组求解． 【解答】解：根据题意得：10220x x -≥--≠⎧⎪⎨⎪⎩，∴2-x ＜0，∴x ＞2．故选C ．（a≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．当二次根式在分母上时还要考虑分母不等于零，此时被开方数大于0．2. 【分析】中位数是一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；众数是一组数据中出现次数最多的数据．【解答】解：在这一组数据中6是出现次数最多的，故众数是6；将这组数据已从小到大的顺序排列，处于中间位置的两个数是6、6，那么由中位数的定义可知，这组数据的中位数是6；故选：A ．。

新人教版数学八年级下册期末考试试题（答案）、选择题（本大题共10个小题，每小题3分，共30分，每小题均有四个选 项，其中只有一项符合题目要求，答案涂在答题卡上）1.下列四个图形分别是四届国际数学家大会的会标，其中属于中心对称图形的有（3.多项式m2-4与多项式m2-4m +4的公因式是6 .用正三角形和正方形镶嵌一个平面，在同一个顶点处，正三角形和正方形的个数之比为（ ）A. 1:1 B, 1: 2 C. 2: 3 D. 3: 27 .如图，将等边△ ABCB 直线BC 平移到△ DEF 使点E 与点C 重合，连接BD 若AB= 2,A. 2 :B. . ；C. 3D. 2 K8 .如图，在4ABC 中，AB= AC 直线I1//I2,且分别与^ ABC 勺两条边相交， 若/ 1 = 40 72=23 ,则/ C 的度数为（D. 4个2.若 a>b,则下列式子正确的是（ A. a +2V b +2B. - 2a>- 2bC. a-2>b- 2A. m- 2B. m +2C. m +4D. m — 44 .已知分式F-9"2的值等于零，则x 的值为（ A. - 2B. - 3C.D. ± 35 .将一次函数 y= - 2x 的图象向下平移6个单位, 得到新的图象的函数解析式为（A. y= - 8xB. y=4xC. y = — 2x — 6D. y = - 2x+6B. 2个3个 C .D . 则BD 的长为（）A. 40°B. 50°C. 63°D. 67°9.如图，在^ ABC中，点E, F分别是边BC上两点，ED垂直平分AB FG垂直平分AC连A. 45°B, 50°C, 60°D, 65°10.如图，直线y i = kx和直线y2= ax+b相交于点（1, 2）.则不等式组ax+b>kx>0的解集为（）A. xv0B. 0<x< 1C. xv 1D. x< 0 或x> 1二、填空题（本大题共4个小题，每小题4分，共16分，答案写在答题卡上）2 211.因式分解：x - 9y =.12.若关于x的分式方程号■=竺?产生增*则m= _________________ .工+2 工+213.如图，两张等宽的纸条交叉叠放在一起，在重叠部分构成的四边形ABCDK若AB= 10,AC= 12,则BD的长为.14 .如图，在7ABCDK 按以下步骤作图：①以C 为圆心，以适当长为半径画弧， 分别交BC, CD 于MN 两点；②分别以 M N 为圆心，以大于 L M N 勺长为半径画弧，两弧在/ BCD 勺内部交于点 P;⑨连接CP 并延长交AD 于E.若AE= 2, CE= 6, Z B= 60° ,则ABCD 勺周三、解答题(本大题共 6个小题，共54分，解答过程写在答题卡上)22315 . (1)分斛因式：ab-4ab +4b.3-2 tit-1) < 2s+ 9®-117 .化简求值：(二不一 1)一且二生等，其中a =2-|V2. a-1a-118 .如图，方格纸中每个小正方形的边长都是1个单位长度，Rt^ABC 勺三个顶点分别为 A(0, 4), B (-4, 2), C (0, 2).(1)画△ABG,使它与△ AB 暖于点C 成中心对称；(2)平移△ ABC 使点A 的对应点A 2坐标为(-2, 4),画出平移后对应的△ A 2B 2C 2; (3)若将△ A 1B 1C 绕点P 旋转可彳#到4 A2BG,请直接写出旋转中心 P 的坐标.16.解不等式组,并在数轴上表示出它的解集.(2)解方程(1)求证：四边形ADFO平行四边形；(2)若/ BDO90° ,求证：C叶分/ ACB(3)在(2)的条件下，若BD= DC= 6,求AB的长.20.如图1, E为正方形ABCD勺边BC±一点，F为边BA延长线上一点，且CE= AF.(1)求证：DEL DF;(2)如图2,若点G为边AB上一点，且/ BGE= 2/BFE △ BGEE勺周长为16,求四边形DEBFF勺面积；(3)如图3,在(2)的条件下，DG与EF交于点H,连接CH且CHh 5\回，求AG的长.B 卷（共50分）一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）21 .已知 a +b=0 目 awo,则2020b=2019a------22 .如图，在 RtA ABC^, / ACB= 90。