《高等代数》：学习笔记.doc

《高等代数》知识点梳理高等代数是一门重要的数学学科，它是线性代数的延伸和深化，主要研究向量空间和线性变换的性质和应用。

以下是《高等代数》常见的知识点梳理：1.矩阵和线性方程组：-矩阵：矩阵的定义和运算、矩阵的行列式、逆矩阵等。

-线性方程组：线性方程组的定义和解的分类、线性方程组的矩阵表示、线性方程组的消元法、高斯-约当法等。

2.向量空间：-向量空间的定义：向量空间的基本性质和运算规则。

-子空间和张成空间：子空间和子空间的运算、线性组合和线性相关、张成空间的定义和性质。

-基和维数：线性无关和极大线性无关组、基和维数的相关定义和性质。

3.线性变换：-线性变换的定义和性质：线性变换的基本性质和运算。

-线性变换的矩阵表示：矩阵的表示和判断、线性变换的示例和应用。

-矩阵相似和对角化：矩阵相似的定义和性质、对角化的定义和条件、对角化的意义和应用。

4.特征值和特征向量：-特征值和特征向量的定义：特征值和特征向量的基本概念和性质。

-特征多项式和特征方程：特征多项式和特征方程的定义和性质、求解特征多项式和特征方程的方法。

-对角化和相似对角化：对角化和相似对角化的概念和条件、对角化和相似对角化的关系和应用。

5.矩阵的特征值和特征向量的应用：-线性微分方程组：线性微分方程组的特征方程和特解、线性微分方程组的解的表示和求解方法。

-线性差分方程组：线性差分方程组的特征方程和特解、线性差分方程组的解的表示和求解方法。

- Markov过程：Markov过程的概念和性质、Markov过程的平稳分布和转移概率矩阵。

6.内积空间和正交变换：-内积和内积空间的定义：内积的基本性质和运算规则、内积空间的定义和性质。

-正交向量和正交子空间：正交向量和正交子空间的定义和性质。

-正交变换和正交矩阵：正交变换和正交矩阵的概念、正交变换的性质和应用。

7.对偶空间和广义逆：-对偶空间的定义和性质：对偶空间的定义和对偶基的求解方法、对偶空间的性质和应用。

第9章欧几里得空间9.1复习笔记一、定义与基本性质1．欧几里得空间定义设V是实数域R上一线性空间，在V上定义了一个二元实函数，称为内积，记作（α，β），它具有以下性质：（1）（α，β）＝（β，α）；（2）（kα，β）＝k（α，β）；（3）（α＋β，γ）＝（α，γ）＋（β，γ）；（4）（α，α）≥0，当且仅当α＝0时（α，α）＝0.这里α，β，r是V中任意的向量，k是任意实数，这样的线性空间V称为欧几里得空间．2．长度（1）定义非负实数称为向量α的长度，记为|α|．（2）关于长度的性质①零向量的长度是零，②|kα|＝|k||α|，③长度为1的向量称为单位向量.如果α≠0，向量1αα就是一个单位向量，通常称此为把α单位化．3．向量的夹角（1）柯西-布涅柯夫斯基不等式，即对于任意的向量α，β有|（α，β）|≤|α||β|当且仅当α，β线性相关时，等号才成立．（2）非零向量α，β的夹角＜α，β＞规定为（3）如果向量α，β的内积为零，即（α，β）＝0，那么α，β称为正交或互相垂直，记为α⊥β．零向量才与自己正交．（4）勾股定理，即当α，β正交时，|α＋β|2＝|α|2＋|β|2．4．有限维空间的讨论（1）度量矩阵设V是一个n维欧几里得空间，在V中取一组基ε1，ε2，…，εn，对V中任意两个向量α＝x1ε1＋x2ε2＋…＋x nεn，β＝y1ε1＋y2ε2＋…＋y nεn，由内积的性质得a ij＝（εi，εj）（i，j＝1，2，…，n），显然a ij＝a ji，于是利用矩阵，（α，β）还可以写成（α，β）＝X'AY，其中分别是α，β的坐标，而矩阵A＝（a ij）nn称为基ε1，ε2，…，εn的度量矩阵．（2）性质①设η1，η2，…，ηn是空间V的另外一组基，而由ε1，ε2，…，εn到η1，η2，…，ηn的过渡矩阵为C，即（η1，η2，…，ηn）＝（ε1，ε2，…，εn）C，于是基η1，η2，…，ηn的度量矩阵B＝（b ij）＝（ηi，ηj）＝C'AC；表明不同基的度量矩阵是合同的．②对于非零向量α，即有（α，α）＝X'AX＞0．因此，度量矩阵是正定的．二、标准正交基1．正交向量组欧式空间V中一组非零的向量，如果它们两两正交，就称为一正交向量组．按定义，由单个非零向量所成的向量组也是正交向量组．2．标准正交基（1）定义在n维欧氏空间中，由n个向量组成的正交向量组称为正交基；由单位向量组成的正交基称为标准正交基．说明：①对一组正交基进行单位化就得到一组标准正交基．②一组基为标准正交基的充分必要条件是：它的度量矩阵为单位矩阵．（2）标准正交基的求法①定理1n维欧氏空间中任一个正交向量组都能扩充成一组正交基．②定理2对于n维欧氏空间中任意一组基ε1，ε2，…，εn，都可以找到一组标准正交基η1，η2，…，ηn，使L（ε1，ε2，…，εi）＝L（η1，η2，…，ηi），i＝1，2，…，n．定理2中把一组线性无关的向量变成一单位正交向量组的方法称做施密特正交化过程．例：把α1＝（1，1，0，0），α3＝（－1，0，0，1），α2＝（1，0，1，0），α4＝（1，－1，－1，1）变成单位正交的向量组．解：①先把它们正交化，得β1＝α1＝（1，1，0，0），②再单位化，得3．基变换公式设ε1，ε2，…，εn与η1，η2，…，ηn是欧氏空间V中的两组标准正交基，它们之间的过渡矩阵是A＝（a ij），即因为η1，η2，…，ηn是标准正交基，所以矩阵A的各列就是η1，η2，…，ηn在标准正交基ε1，ε2，…，εn下的坐标．4．正交矩阵n级实数矩阵A称为正交矩阵，如果A'A＝E．由标准正交基到标准正交基的过渡矩阵是正交矩阵；反过来，如果第一组基是标准正交基，同时过渡矩阵是正交矩阵，那么第二组基一定也是标准正交基．三、同构1．同构定义实数域R上欧式空间V与V'称为同构的，如果由V到V'有一个双射σ，满足（1）σ（α＋β）＝σ（α）＋σ（β），（2）σ（kα）＝kσ（α），（3）（σ（α），σ（β））＝（α，β），这里α，β∈V，k∈R，这样的映射σ称为V到V'的同构映射．同构的欧氏空间必有相同的维数．每个n维的欧氏空间都与R n同构．2．同构的性质同构作为欧氏空间之间的关系具有（1）反身性；（2）对称性；（3）传递性；（4）两个有限维欧氏空间同构的充分必要条件是它们的维数相同．.四、正交变换1．定义欧氏空间V的线性变换A称为正交变换，如果它保持向量的内积不变，即对于任意的α，β∈V，都有（Aα，Aβ）＝（α，β）．2．性质。

第10章双线性函数与辛空间10.1复习笔记一、线性函数1．定义设V是数域P上的一个线性空间，f是V到P的一个映射，如果f满足（1）f（α＋β）＝f（α）＋f（β），（2）f（kα）＝kf（α），式中α、β是V中任意元素，k是P中任意数，则称f为V上的一个线性函数．2．性质（1）设f是V上的线性函数，则f（0）＝0，f（－α）＝－f（α）．（2）如果β是α1，α2，…，αs的线性组合：β＝k1α1＋k2α2＋…＋k sαs．那么f（β）＝k1f（α1）＋k2f（α2）＋…＋k s f（αs）．3．矩阵的迹A是数域P上一个n级矩阵．设则A的迹Tr（A）＝a11＋a22＋…＋a nn是P上全体n级矩阵构成的线性空间P n×n上的一个线性函数．4．定理设V是P上一个n维线性空间，ε1，ε2，…，εn是V的一组基，a1，a2，…，a n是P中任意n个数，存在唯一的V上线性函数f使f（εi）＝a i，i＝1，2，…，n．二、对偶空间1．L（V，P）的加法和数量乘法（1）设f，g是V的两个线性函数定义函数f＋g如下：（f＋g）（α）＝f（α）＋g（α），α∈V，f＋g也是线性函数：f＋g称为f与g的和．（2）设f是V上线性函数．对P中任意数k，定义函数kf如下：（kf）（α）＝k（f（α）），α∈V，kf称为k与f的数量乘积，易证kf也是线性函数．2．L（V，P）的性质（1）对V中任意向量α，有而对L（V，P）中任意向量f，有（2）L（V，P）的维数等于V的维数，而且f1，f2，…，f n是L（V，P）的一组基．3．对偶空间（1）定义L（P，V）称为V的对偶空间．由决定的L（V，P）的基，称为ε1，ε2，…，εn的对偶基．V的对偶空间记作V*．（2）对偶基的性质（1）设ε1，ε2，…，εn及η1，η2，…，ηn是线性空间V的两组基，它们的对偶基分别为f1，f2，…，f n及g1，g2，…，g n．如果由ε1，ε2，…，εn到η1，η2，…，ηn的过渡矩阵为A，那么由f1，f2，…，f n到g1，g2，…，g n的过渡矩阵为（A'）－1．（2）设V是P上一个线性空间，V*是其对偶空间．取定V中一个向量x，定义V*的一个函数x**如下：x**（f）＝f（x），f∈V*．则x**是V*上的一个线性函数，因此是V*的对偶空间（V*）*＝V**中的一个元素．（3）V是一个线性空间，V**是V的对偶空间的对偶空间．V到V**的映射x→x**是一个同构映射．结论：任一线性空间都可看成某个线性空间的线性函数所成的空间．三、双线性函数1．定义V是数域P上一个线性空间，f（α，β）是V上一个二元函数，即对V中任意两个向量α，β，根据f都唯一地对应于P中一个数f（α，β）．如果f（α，β）有下列性质：（1）f（α，k1β1＋k2β2）＝k1f（α，β1）＋k2f（α，β2）；（2）f（k1α1＋k2α2，β）＝k1f（α1，β）＋k2f（α2，β）．其中α，α1，α2，β，β1，β2是V中任意向量，k1，k2是P中任意数，则称f（α，β）为V 上的一个双线性函数．2．常用结论（1）欧氏空间V的内积是V上双线性函数；（2）设f1（α），f2（α）都是线性空间V上的线性函数，则f（α，β）＝f1（α）f2（β），α，β∈V是V上的一个双线性函数．（3）设P n是数域P上n维列向量构成的线性空间X，Y∈P n，再设A是P上一个n 级方阵．令f（X，Y）＝X'AY，则f（X，Y）是P n上的一个双线性函数．3．度量矩阵（1）定义设f（α，β）是数域P上n维线性空间V上的一个双线性函数．ε1，ε2，…，εn是V的一组基，则矩阵称为f（α，β）在ε1，ε2，…，εn下的度量矩阵．（2）性质①度量矩阵被双线性函数及基唯一确定．②不同的双线性函数在同一组基下的度量矩阵一定是不同的．③在不同的基下，同一个双线性函数的度量矩阵一般是不同的，但是在不同基下的度量矩阵是合同的．4．非退化设f（α，β）是线性空间V上一个双线性函数，如果f（α，β）＝0，对任意β∈V，可推出α＝0，f就称为非退化的．双线性函数f（α，β）是非退化的充要条件为其度量矩阵A为非退化矩阵．5．对称双线性函数（1）定义f（α，β）是线性空间V上的一个双线性函数，如果对V中任意两个向量α，β都有f （α，β）＝f（β，α），则称f（α，β）为对称双线性函数．如果对V中任意两个向量α，β都有f（α，β）＝－f（β，α），则称f（α，β）为反对称双线性函数．这就是说，双线性函数是对称的，当且仅当它在任一组基下的度量矩阵是对称矩阵．同样地，双线性函数是反对称的当且仅当它在任一组基下的度量矩阵是反对称矩阵．（2）性质（1）设V是数域P上n维线性空间，f（α，β）是V上对称双线性函数，则存在V的一组基ε1，ε2，…，εn，使f（α，β）在这组基下的度量矩阵为对角矩阵．（2）设V是复数域上n维线性空间，f（α，β）是V上对称双线性函数，则存在V的一组基ε1，ε2，…，εn，对V中任意向量，有（3）设V是实数域上n维线性空间．f（α，β）是V上对称双线性函数．则存在V的一组基ε1，ε2，…，εn，对V中任意向量，有（4）V上的对称双线性函数f（α，β）如果是非退化的．则有V的一组基ε1，ε2，…，εn满足前面的不等式是非退化条件保证的，这样的基称为V的对于f（α，β）的正交基．6．二次齐次函数对称双线性函数与二次齐次函数是1－1对应的．设V是数域P上线性空间，f（α，β）是V上双线性函数．当α＝β时，V上函数f（α，β）称为与f（α，β）对应的二次齐次函数．7．反对称双线性函数性质（1）设f（α，β）是n维线性空间V上的反对称线性函数，则存在V的一组基ε1，ε。

高等代数知识点梳理第四章 矩阵一、矩阵及其运算 1、矩阵的概念（1）定义：由n s ×个数ij a （s i ,2,1=；n j ,2,1=）排成s 行n 列的数表sn s n a aa a 1111，称为s 行n 列矩阵，简记为n s ij a A ×=)(。

（2）矩阵的相等：设n m ij a A ×=)(，k l ij a B ×=)(，如果l m =，k n =，且ij ijb a =，对m i ,2,1=；n j ,2,1=都成立，则称A 与B 相等，记B A =。

（3）各种特殊矩阵：行矩阵，列矩阵，零矩阵，方阵，（上）下三角矩阵，对角矩阵，数量矩阵，单位矩阵。

2、矩阵的运算（1）矩阵的加法：++++= +sn sn s s n n sn s n sn s n b a b a b a b a b b b b a a a a 1111111111111111。

运算规律：①A B B A +=+②)()(C B A C B A ++=++③A O A =+ ④O A A =−+)(（2）数与矩阵的乘法：= sn s n sn s n ka ka ka ka a a a a k 11111111运算规律：①lA kA A l k +=+)( ②kB kA B A k +=+)(③A kl lA k )()(= ④O A A =−+)(（3）矩阵的乘法：= sm s m nm n m sn s n c c c c b b b b a a a a 111111111111其中nj in i i i i ij b a b a b a c +++= 2211，s i ,2,1=；m j ,2,1=。

运算规律：①)()(BC A C AB = ②AC AB C B A +=+)( ③CA BA A C B +=+)( ④B kA kB A AB k )()()(==一般情况，①BA AB ≠②AC AB =，0≠A ，⇒C B =③0=AB ⇒0=A 或0=A（4）矩阵的转置： =sn s n a a a a A 1111，A 的转置就是指矩阵=ns n s a a a a A 1111'运算规律：①A A =)''( ②'')'(B A B A +=+③'')'(A B AB = ④')'(kA kA =（5）方阵的行列式：设方阵1111n n nn a a A a a= ，则A 的行列式为1111||n n nn a a A a a = 。

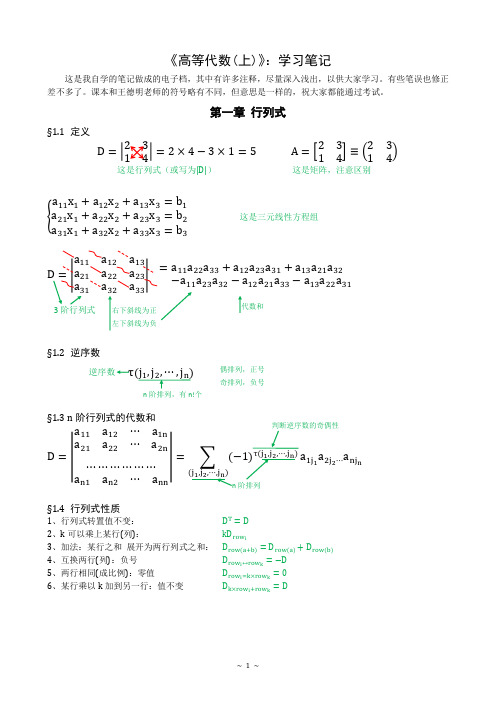
《高等代数(上)》：学习笔记这是我自学的笔记做成的电子档，其中有许多注释，尽量深入浅出，以供大家学习。

有些笔误也修正差不多了。

课本和王德明老师的符号略有不同，但意思是一样的，祝大家都能通过考试。

第一章 行列式§1.1 定义D =|2314|=2×4−3×1=5 A =[2314]≡(2314) 这是行列式（或写为|D|）这是矩阵，注意区别{a 11x 1+a 12x 2+a 13x 3=b 1a 21x 1+a 22x 2+a 23x 3=b 2a 31x 1+a 32x 2+a 33x 3=b 3这是三元线性方程组=|11a 12a 13a 22a 23a 3233|=a 11a 22a 33+a 12a 23a 31+a 13a 21a 32−a 11a 23a 32−a 12a 21a 33−a 13a 22a 31§1.2 逆序数τ§1.3 n 阶行列式的代数和D =|a 11a 12⋯a 1n a 21a 22⋯a 2n⋯⋯⋯⋯⋯⋯a n1a n2⋯a nn|=∑(a 1j 1a 2j 2⋯a nj n§1.4 行列式性质1、行列式转置值不变： D T =D2、k 可以乘上某行(列)： kD row i3、加法：某行之和 展开为两行列式之和： D row(a+b)=D row(a)+D row(b)4、互换两行(列)：负号 D row i ↔row k =−D5、两行相同(成比例)：零值 D row i =k×row k =06、某行乘以k 加到另一行：值不变D k×row i +row k =D右下斜线为正 左下斜线为负代数和n 阶排列，有n!个逆序数 偶排列，正号 奇排列，负号阶排列§1.5 代数余子式=ij|D|=a k1A k1+a k2A k2+⋯+a kn A kn (k =1,2,⋯,n )即展开第k 行(列)§1.6 范德蒙行列式|D|=|111⋯1a 1a 2a 3⋯a n a 12a 22a 32⋯a n2⋯⋯⋯a 1n−1a 2n−1a 3n−1⋯a nn−1|=∏(a i −a j )第二章 线性方程组§2.1 克莱姆法则D 1=|b 1a 12a 13b 2a 22a 23b 3a 32a 33| D 2、D 3 类似左边 解集：x i =D i D(D ≠0) 当D ≠0时，方程组有唯一解：x 1=D 1D,x 2=D 2D,x 3=D 3D.(D ≠0)§2.2 消元法初等变换：反复对方程进行row 变换，最后剩下一个上三角矩阵。

高等代数笔记与做题思路总结一、行列式相关（5题）1. 计算三阶行列式begin{vmatrix}1 2 3 4 5 6 7 8 9end{vmatrix}解析：- 按第一行展开，begin{vmatrix}1 2 3 4 5 6 7 8 9end{vmatrix}=1×begin{vmatrix}5 6 8 9end{vmatrix}-2×begin{vmatrix}4 6 7 9end{vmatrix}+3×begin{vmatrix}4 5 78end{vmatrix}- 计算二阶行列式begin{vmatrix}ab cdend{vmatrix}=ad - bc- begin{vmatrix}5 6 8 9end{vmatrix}=5×9-6×8 = 45 - 48=- 3- begin{vmatrix}4 6 7 9end{vmatrix}=4×9 - 6×7=36 - 42=-6- begin{vmatrix}4 5 7 8end{vmatrix}=4×8 - 5×7=32 - 35=-3- 所以原行列式=1×(-3)-2×(- 6)+3×(-3)=-3 + 12-9 = 02. 已知n阶行列式D = λ^n+a_1λ^n - 1+·s+a_n-1λ + a_n，求D的第一行元素的代数余子式之和。

解析：- 根据行列式按行展开定理D=a_i1A_i1+a_i2A_i2+·s+a_inA_in（i为行标）- 令λ = 1，构造一个新的行列式D_1，它的第一行元素全为1，其余元素与D 相同。

- 那么D_1按第一行展开D_1=A_11+A_12+·s+A_1n- 又因为D_1也是n阶行列式，且D_1 = 1^n+a_1×1^n - 1+·s+a_n-1×1+a_n- 所以第一行元素的代数余子式之和为1 + a_1+·s+a_n3. 证明：若一个n阶行列式D中零元素的个数多于n^2-n个，则D = 0。

高等代数课本笔记及其例题详解第一章 多项式1.1 数域定义1.1（数域）：设P 是由一些复数组成的集合，其中包括0与1. 如果P 中任意两个数（这两个数也可以相同）的和、差、积、商（除数不为零）仍然是P 中的数，那么P 就称为一个数域.即：设{}C x x P ∈=，P b a ∈∀,，其中0≠a 且P ∈0,1都有P abab b a b a ∈-+,,,，称P为一个数域. （注：Z 表示全体整数；R 表示全体实数；C 表示全体复数；Q 表示全体有理数；N 表示全体自然数；）例题1. 设(){}Q b a b a Q ∈+=,22证明：()2Q 是一个数域. 证明：1）()22000,2011Q ∈+=+=（其中：Q ∈1,0）2）Q d c b a ∈∀,,,有()()()2222Q d b c a d c b a ∈+++=+++（其中： Q d b c a ∈++,）；()()()2222Q d b c a d c b a ∈-+-=+-+（其中：Q d b c a ∈--,）； ()()()()()22222Q bc ad bd ac d c b a ∈+++=++（其中：Q bc ad bd ac ∈++,2）； 若02≠+b a ，有()22222222222Q b a bcad b a bd ac b a d c ∈--+--=++（其中：Q b a bc ad b a bd ac ∈----22222,22，且0222≠-b a ）. 2Q ∴是一个数域.例题2. 证明：()()⎭⎬⎫⎩⎨⎧==∈∈++++++=+m j n i Z b a N n m b b b a a a P j i mm n n ,,0;,,0,,,1010 πππππ是一个数域.证明：1) ()πππππP m n ∈++++++=0010011 , ()πππππP mn∈++++++=0000000 2) 显然该集合的和、差、积封闭；若商不封闭，得()πππππππππP d d d c c c b b b a a a tt ss m m n n ∈++++++≠+++++ 101101010,0,得 ()πππππππππππππππππP a a a b b b d d d c c c b b b a a a d d d c c c n n mm t t s s m n n t t s s ∉++++++⋅++++++=++++++++++++ 1010101010101010,这与该集合的积封闭的结论矛盾，故()πP是一个数域.注：最小的数域为有理数域，任何数域都包含有理数域.1.2 一元多项式定义 1.2.1（一元多项式） 设n 是一非负整数. 形式表达式011a x a x a n n n n +++-- ,其中∈n a a a ,,,10 数域P ,称为系数在数域P 中的一元多项式，或者简称为数域P 上的一元多项式. （注：i i x a 称为i 次项; i a 称为i 次项的系数. ）定义1.2.2 （多项式相等）如果在多项式()x f 与()x g 中，除去系数为零的项外，同次项的系数全相等，那么()x f 与()x g 就称为相等，记为()()x g x f =. 系数全为零的多项式称为零多项式，记为0. （注：若0≠n a ，则n n x a 称为多项式的首项；n a 称为首项系数; n 称为多项式的次数，记为()()x f ∂; 零多项式是唯一不定义次数的多项式. ） 性质1.2.1 ()()()()()()()()x g x f x g x f ∂∂≤±∂,max .性质1.2.2 ()()()()()()()x g x f x g x f ∂+∂=⋅∂（其中()0≠x f 且()0≠x g ）. 运算规律：1. 加法交换律：()()()()x f x g x g x f +=+.2. 加法结合律：()()()()()()()()x h x g x f x h x g x f ++=++.3. 乘法交换律：()()()()x f x g x g x f =.4. 乘法结合律：()()()()()()()()x h x g x f x h x g x f =.5. 乘法对加法的分配律：()()()()()()()()x h x f x g x f x h x g x f +=+.6. 乘法消去律：如果()()()()x h x f x g x f =且()0≠x f ，那么()()x h x g =.定义1.2.3 （一元多项式环）所有系数在数域P 中的一元多项式的全体，称为数域P 上的一元多项式环，记为[]x P ，P 称为[]x P 的系数域.1.3 整除的概念性质1.3.1 （带余除法）对于[]x P 中任意两个多项式()x f 与()x g ，其中()0≠x g ，一定有[]x P 中的多项式()()x r x q ,存在，使()()()()x r x g x q x f +=成立，其中()()()()x g x r ∂<∂或者()0=x r ，并且这样的()()x r x q ,是唯一决定的. （注：()x q 通常称为()x g 除()x f 的商；()x r 称为()x g 除()x f 的余式）定义1.3.1（整除）数域P 上的多项式()x g 称为整除()x f ，如果有数域P 上的多项式()x h 使等式()()()x h x g x f =成立. 我们用“()()x f x g ”表示()x g 整除()x f ，用“()x g ()x f ”表示()x g 不能整除()x f .（注：当()()x f x g 时，()x g 就称为()x f 的因式；()x f 称为()x g 的倍式.）定理1.3.1 对于数域P 上的任意两个多项式()()x g x f ,，其中()0≠x g ，()()x f x g 的充分必要条件是()x g 除()x f 的余式为零. 整除性的常用的性质：1. 如果()()x g x f ，()()x f x g ，那么()()x cg x f =，其中0≠c .2. 如果()()x g x f ，()()x h x g ，那么()()x h x f （整除的传递性）.3. 如果()()x g x f i ，r i ,,2,1 =，那么()()()()()()()x g x u x g x u x g x u x f r r +++ 2211其中()x u i 是数域P 上的任意的多项式.（注：()()()()()()x g x u x g x u x g x u r r +++ 2211称为多项式()()()x g x g x g r ,,,21 的一个组合.） 注：两个多项式之间的整除关系不因为系数域的扩大而改变.1.4 最大公因式定义 1.4.1（最大公因式）设()()x g x f ,是[]x P 中两个多项式. []x P 中多项式()x d 称为()()x g x f ,的一个最大公因式，如果它满足下面两个条件：1）()x d 是()()x g x f ,的公因式；2）()()x g x f ,的公因式全是()x d 的因式.（注：两个零多项式的最大公因式就是0） 引理1.4.1 如果有等式()()()()x r x g x q x f +=成立，那么()()x g x f ,和()()x r x g ,有相同的公因式.定理 1.4.1 对于[]x P 中任意两个多项式()()x g x f ,，在[]x P 中存在一个最大公因式()x d ，且()x d 可以表成()()x g x f ,的一个组合，即有[]x P 中多项式()()x v x u ,使()()()()()x g x v x f x u x d +=.（注：两个多项式的最大公因式在可以相差一个非零常数倍的意义下是唯一确定的；()()()x g x f ,表示首项系数为1的公因式.） 辗转相除法：例题3. 设()343234---+=x x x x x f ，()3210323-++=x x x x g 求()()()x g x f ,，并求()()x v x u ,使()()()()()()()x g x v x f x u x g x f +=,. 解：即：()()()()()()131092595913112x r x q x g x x x x g x f +=⎪⎪⎭⎫⎝⎛++-⎪⎭⎫ ⎝⎛-=310925952---x x即：()()()()()()22793109259595272212x r x q x r x x x x x g +=++⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛+-=. ()()()327981108153109259521 +⎪⎭⎫⎝⎛--=---=x x x x x r()()()3,+=∴x x g x f .将（1）代入（2）式可得：()()35251532+=⎪⎪⎭⎫ ⎝⎛+-+⎪⎭⎫⎝⎛-x x g x x x f x ()()525,1532x x x v x x u +-=-=∴就有()()()()()()()x g x f x g x v x f x u ,=+.定义1.4.2（互素）[]x P 中两个多项式()()x g x f ,称为互素（也称互质）的，如果()()()1,=x g x f .定理 1.4.2 []x P 中两个多项式()()x g x f ,称为互素的充要条件是有[]x P 中的多项式()()x v x u ,使()()()()1=+x g x v x f x u .定理1.4.3 如果()()()1,=x g x f ，且()()()x h x g x f ，那么()()x h x f .推论1.4.3.1 如果()()x g x f 1，()()x g x f 2，且()()()1,21=x f x f ，那么()()()x g x f x f 21.推广：定义1.4.3 ()x d 称为()()()()2,,,21≥s x f x f x f s 的一个最大公因式，如果()x d 具有下面的性质：2) ()()s i x f x d i ,,2,1, =；3) 如果()()s i x f x i ,,2,1, =ϕ，那么()()x d x ϕ.（注：符号()()()()x f x f x f s ,,,21 表示首项系数为1的最大公因式.）性质1.4.1()()()()()()()()()()x f x f x f x f x f x f x f s s s ,,,,,,,21121 =-性质1.4.2 ()()()()()()()()()()x f x f x f x f x u x f x u x f x u s s s ,,,212211 =+++，其中 ()()()[]x P x u x u x u s ∈,,,21 .性质1.4.3 ()()()()()()()[],,,,1,,,2121x P x u x u x u x f x f x f s s ∈∃⇔=()()()()()()1:2211=+++x f x u x f x u x f x u st s s .1.5 因式分解定理定义1.5.1（不可约多项式） 数域P 上次数的多项式()x p 称为域上的不可约多项式，如果它不能表示成数域P 上的两个次数比()x p 的次数低的多项式的乘积（注：一个多项式是否是不可约是依赖于系数域的）.性质1.5.1 ()x p 在数域[]x P 是不可约多项式，()[]x P x f ∈∀，()()x p x f 当且仅当()0≠=c x f 或()()x cp x f =.即：对于()[]x P x f ∈∀，有()()x f x p 或者()()()1,=x f x p . 定理1.5.1 如果()x p 是不可约多项式，那么对于任意的两个多项式()()x g x f ,，由()()()x g x f x p 一定推出()()x f x p 或者()()x g x p .定理1.5.2（定理1.5.1的推广） 如果()x p 是不可约多项式，若()()()(),21x f x f x f x p s 则()()()(){}x f x f x f x f s i ,,,21 ∈∃使得()()x f x p i .定理1.5.3（因式分解及唯一性定理）数域P 上每一个次数1≥的多项式()x f 都可以唯一地分解成数域P 上一些不可约多项式的乘积.所谓唯一性是说，如果有两个分解式()()()()()()()x q x q x q x p x p x p x f s s 2121==，那么必有t s =，并且适当排列因式的次序后有()()s i x q c x p i i i ,,2,1, ==，其中()s i c i ,,2,1 =是一些非零常数.（注：()()()()x p x p x cp x f s r s r r 2121=的分解称为标准分解式；已知两个多项式()()x g x f ,的标准分解式，那么()x f 与()x g 的最大公因式()x d 就是那些同时在与的标准式中出现的不可约多项式方幂的乘积，所带的方幂的指数等于它在()x f 与()x g 中所带的方幂中的较小的一个.）1.6 重因式定义1.6.1（k 重因式）不可约多项式()x p 称为多项式()x f 的k 重因式，如果()()x f x p k ，而()x p k 1+ ()x f .（注：0=k 时，()x p 不是()x f 的因式；1=k 时，()x p 是()x f 的单因式；1≥k 时，()x p 是()x f 的重因式.）定义1.6.2（微商）设有多项式()0111a x a x a x a x f n n n n ++++=-- .我们规定它的微商（也称导数）是()()1211'1a x n a nx a x f n n n n ++-+=--- . 性质1.6.1 ：1）()()()()()x g x f x g x f '''+=+2）()()()x cf x cf ''=，3）()()()()()()()x g x f x g x f x g x f '''+=，4）()()()()()x f x f m x f m m '1'-=.定义1.6.3（高阶微商）微商()x f '称为()x f 的一阶微商；()x f '的微商()x f ''称为的二阶()x f 微商；等等.()x f 的k 阶微商记为()()x f k .（注：()()n x f =∂ο，则()()c x f n =，()()01=+x f n .）定理1.6.1 如果不可约多项式()x p 是()x f 的k 重因式()1≥k ，那么它是微商()x f '的1-k 重因式.推论1.6.1.1 如果不可约多项式()x p 是()x f 的k 重因式()1≥k ，那么()x p 是()()()()x f x f x f k 1''',,,- 的因式，但不是()()x f k 的因式.推论1.6.1.2 不可约多项式()x p 是()x f 的重因式的充分必要条件为()x p 是()x f 与()x f ' 的公因式.推论 1.6.1.3 多项式()x f 没有重因式的充分必要条件是()x f 与()x f '互素.（注：辗转相除法可用于求解重因式；()()()()x f x f x f ',是一个没有重因式的多项式与()x f 有完全相同的不可约因式.）1.7 多项式函数定义1.7.1（多项式函数）设()()10111 a x a x a x a x f n n n n ++++=--是[]x P 中的多项式，α是P 中的数，在()1中用α代x 所得的数0111a a a a n n n n ++++--ααα 称为()x f 当α=x 时的值，记为()αf .这样一来，多项式就定义了一个数域上的函数.定理1.7.1（余数定理）用一次多项式α-x 去除多项式()x f ，所得的余式是一个常数，这个常数等于函数值()αf .（注：其中()0=αf 时，α=x 是()x f 的一个根或者零点.） 推论1.7.1.1 α是()x f 的根的充分必要条件是()()x f x α-.定义1.7.2（重根）α称为()x f 的重根，如果()α-x 是()x f 的k 重因式.当1=k 时，α称为单根；当1>k 时，α称为重根.定理1.7.2 []x P 中n 次多项式()0≥n 在数域P 中的根不可能多于n 个，重根按重数计算. 定理1.7.3 如果多项式()()x g x f ,的次数都不超过n ，而它们对1+n 个不同的数121,,,+n ααα 有相同的值，即()()1,,2,1,+==n i g f i i αα，那么()()x g x f =.1.8 复系数与实系数多项式的因式分解定理1.8.1（代数基本定理）每个次数1≥的复系数多项式在复数域中有一根（即：复数域上所有次数大于1的多项式全是可约的.）.定理1.8.2（复系数多项式的分解定理）每个次数1≥的复系数多项式在复数域上都可以唯一地分解成一次因式的乘积.（复系数多项式的标准分解式：()()()()s ls lln x x x a x f ααα---= 2121，其中C s ∈≠≠≠ααα 21，+∈Z l l l s ,,,21 ）定理1.8.3 如果α是实系数多项式()x f 的复根，那么α的共轭数α也是()x f 的根. 定理1.8.4（实系数多项式因式分解定理）每个次数1≥的实系数多项式在实数域上都可以唯一地分解成一次因式与二次不可约因式的乘积（即是说：实数域上只含有一次不可约多项式和含二次共轭复根不可约多项式）.1.9 有理系数多项式定理 1.9.1 每个次数1≥的有理系数多项式都能唯一地分解成不可约的有理系数多项式的乘积.定义1.9.1（本原多项式）如果一个非零的整系数多项式()011b x b x b x g n n n n +++=-- 的系数01,,,b b b n n -没有异于的公因子，也就是说，它们是互素的，它就称为一个本原多项式.（任意一个非零的有理系数多项式()x f 都可以表示成一个有理数r 与一个本原多项式()x g 的乘积：()()x rg x f =）定理1.9.2（高斯（Gauss ）引理）两个本原多项式的乘积还是本原多项式.定理1.9.3 如果一非零的整系数多项式能够分解成两个次数较低的有理系数多项式的乘积，那么它一定能分解成两个次数较低的整系数多项式的乘积.推论1.9.3.1 设()()x g x f ,是整系数多项式，且()x g 是本原的. 如果()()()x h x g x f =，其中()x h 是有理系数多项式，那么()x h 一定是整系数的.定理1.9.4 设()011a x a x a x f n n n n +++=-- 是一个整系数多项式，而sr 是它的一个有理根，其中s r ,互素，那么必有n a s ，0a r .特别地，如果()x f 的首项系数1=n a ，那么()x f 的有理根都是整根，而且是0a 的因子. 例题4. 求方程032234=-+-x x x 的有理根. 解：令()32234-+-=x x x x f 得：24=a 的因子为：2,1±±30=a 的因子为：1±，3± ()x f ∴的有理根可能为：21±，23±，1±，2±.判别根的方法一：0321≠-=⎪⎭⎫⎝⎛-f （不为()x f 的根，舍弃）；0221≠-=⎪⎭⎫⎝⎛f （不为()x f 的根，舍弃）； ()021≠-=-f （不为()x f 的根，舍弃）； ()01=f （为()x f 的根）； 021523≠=⎪⎭⎫ ⎝⎛-f （不为()x f 的根，舍弃）； 042723≠=⎪⎭⎫ ⎝⎛f （不为()x f 的根，舍弃）；()0332≠=-f （不为()x f 的根，舍弃）； ()0252≠=f （不为()x f 的根，舍弃）； 1∴为032234=-+-x x x 方程的有理根.方法二：即2-=x 不是方程032234=-+-x x x 的根.…………经带余除法计算可得：1=x 为032234=-+-x x x 方程的有理根.方法三：21 22002-即21=x 不是方程032234=-+-x x x 的根. …………经综合除法计算可得：1=x 为032234=-+-x x x 方程的有理根.定理1.9.5（艾森斯坦（Eisenstein ）判别法）设()011a x a x a x f n n n n +++=-- 是一个整系数多项式.如果有一个素数p ，使得1. p n a ；2. 021,,,a a a p n n --；3. 2p 0a .那么()x f 在有理数域上不可约的.例题5.证明()153+-=x x x f 在有理数域上不可约. 证明：依题意可得()x f 的有理根可能为：1±.又()31-=f ,()51-=-f 都不为零1±=∴x 都不是()x f 的有理根，即()x f 在有理数域上不可约的.1.10 多元多项式定义1.10.1（n 元多项式）设P 是一个数域，n x x x ,,,21 是n 个文字. 形式为n k nk k x x ax 2121的式子，其中P a ∈，n k k k ,,,21 是非负整数，称为一个单项式. 由以上一些单项式的和∑nnn k k k k nk k k k k x x x a,,,21212121 就称为n 元多项式，或者简称多项式.（注：若两个单项式中相同文字的幂全一样，那么它们就称为同类项.）定义1.10.2（元多项式环）所有系数在数域P 中的n 元多项式的全体，称为数域P 上的n元多项式环，记为[]n x x x P ,,21.（注：n k k k +++ 21称为单项式n k nk k x x ax 2121的次数；系数不为零的单项式的最高次数就称为这个多项式的次数.多元多项式的排列顺序方法：字典排列法；）定理1.10.1 当()0,,,21≠n x x x f ，()0,,,21≠n x x x g 时，乘积()()n n x x x g x x x f ,,,,,,2121 的首项等于()n x x x f ,,,21 的首项与()n x x x g ,,,21 的首项的乘积.推论1.10.1.1 如果,,,2,1,0m i f i =≠那么m f f f 21的首项等于每个i f 的首项的乘积. 推论1.10.1.2 如果()()0,,,,0,,,2121≠≠n n x x x g x x x f ，那么()()0,,,,,,2121≠n n x x x g x x x f .（两个齐次多项式的乘积是齐次多项式，乘积的次数等于因子的次数的和.）1.11 对称多项式定理1.11.1（一元多项式根与系数的关系）设()n n n a x a x x f +++=- 11是[]x P 中的一个多项式.如果()x f 在数域P 中有个根n ααα,,,21 ，那么就可以分解成()()()()n x x x x f ααα---= 21.将其展开即得根与系数的关系如下：()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-=-+++=+++=-∑-n n n k k k k i in n n a i a a a j i αααααααααααααααα 211312122111121，的乘积之和个不同的所有可能的. 定义1.11.1（对称多项式）n 元多项式()n x x x f ,,,21 ，如果对于任意的n j i j i ≤≤≤1,,，都有()()n i j n j i x x x x f x x x x f ,,,,,,,,,,,,11 =，那么这个多项式称为对称多项式. 定理1.11.2 对于任意一个n 元对称多项式都有一个n 元多项式()n y y y ,,,21 ϕ，使得()()n n x x x f σσσϕ,,,,,,2121 =.（其中⎪⎪⎪⎩⎪⎪⎪⎨⎧=+++=+++=+++=----n n nn n n n n n n x x x xx x x x x x x x x x x x x x x x x x 21322211211131212211σσσσ称为n 元初等对称多项式.）例题6. 把三元对称多项式333231x x x ++表为321,,σσσ的多项式. 解：令()333231321,,x x x x x x f ++=得首项为：31x 对应的有序数对()0,0,3，()()332133323131333231321,,x x x x x x x x x x x x f ++-++=-++=∴σ()132123223132222132122163g x x x x x x x x x x x x x x x =-+++++-=得首项：2213x x 对应的有序数对()0,1,2.()()32123223132222132122132123223132222132122121133633x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x g +++++++-+++++-=+σσ23213g x x x =-=对应数对()1,1,1又0332=+σg ()3213132133,,σσσσ+-=∴x x x f .课后习题1. 用()x g 除()x f ，求商()x q 与余式()x r ：1）()1323---=x x x x f ，()1232+-=x x x g ； 解：()9113-=∴x x q ，()99+-=x r . 2）()524+-=x x x f ，()22+-=x x x g解：()12-+=∴x x x q ，()75+-=x x r . 3）()1434--=x x x f ，()132--=x x x g 解：()1032++=∴x x x q ，()929+=x x r . 4）()13235-+-=x x x x f ，()233+-=x x x g . 解：()x g233+-x x22+x()22+=∴x x q ，()562-+=x x x r . 5）()x x x x f 85235--=，()3+=x x g 解：带余除法：()109391362234+-+-=∴x x x x x q ，()()3327-=-=f x r . 6）()x x x x f --=23，()i x x g 21+-=. 解：综合除法：i 21-1 i 2- i 25-- i 89+-()i x r 89+-=∴，()i ix x x q 2522---=. 2. m ，p ，q 适合什么条件时，有 1）q px x mx x ++-+321 解：方法一：带余除法：12-+mx xm x -即：()()m q x p m x r ++++=12，又q px x mx x ++-+321()0=∴x r 可得⎩⎨⎧-==++q m p m 012. 2）q px x mx x ++++2421. 解：方法二：待定系数法：设商为：()c bx x x q ++=2，又由q px x mx x ++++2421可得：()()q px x x q mx x ++=++2421即⎪⎪⎩⎪⎪⎨⎧==+=++=+q c b m c p m b c b m 010.()⎩⎨⎧=-=+-∴0112q m p m q . 3. 把()x f 表成0x x -的方幂和，即表成()() +-+-+22010x x c x x c c 的形式：1）()5x x f =，10=x ；解：辗转相除法：即：()()()111234+++++-=x x x x x x f .即：()()()()[]()()()1154321154321123223+-++++-=+++++--=x x x x x x x x x x x f()()()()[]()()()()()11511063111510631122322+-+-+++-=+-++++--=∴x x x x x x x x x x x f()()()()[])()()()()115110110411151101041123423+-+-+-++-=+-+-+++--=x x x x x x x x x x x f ()()()()()1151101101512345+-+-+-+-+-=x x x x x ()()()()()()1151101101512345+-+-+-+-+-=∴x x x x x x f .2）()3224+-=x x x f ，20-=x 解：综合除法：2-2-2- 2-14a = 38a =-()()()()()11124122181234+---+---=∴x x x x x f . 3）()()i xx i ix x x f ++-+-+=7312234，i x -=0. 解：综合除法：i - i - i - i -即：()()()()()()i i x i x i i x i i x x f 57512234+++-++-+-+=. 4. 求()x f 与()x g 的最大公因式：1）()143234---+=x x x x x f ，()123--+=x x x x g 解：带余除法：即：1322即：()()()1434121322+-⎪⎭⎫ ⎝⎛+----=x x x x x g又：()()1121322++-=---x x x x()()()1,+=∴x x g xf .2）()1434+-=x x x f ，()1323+-=x x x g . 解：带余除法：即：()()()2312+--=x x x g x f .即：()()13213232-+⎪⎭⎫ ⎝⎛+-+-=xx x x g .即：41942729132232-⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=+-x x x .()()()1,=∴x g x f .3）()11024+-=x x x f ，()124624234+++-=x x x x x g . 解：即：()()x x f x g 242423-=即：()()12232124241624223++-⎪⎭⎫ ⎝⎛--++-=x x x x x x x f .即：()93292889323241223241624223++⎪⎪⎭⎫ ⎝⎛-++-=++-x x x x x x x .即：12192426328827932928812232+⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+=++-x x x x . ()()()1,=∴x g x f .5. 求()x u ，()x v 使()()()()()()():,x g x f x g x v x f x u =+1）()242234---+=x x x x x f ，()22234---+=x x x x x g . 解：()13即：()()()221223 -++-=x x x x x g()()32223 x x x x -=- ()()()2,2-=∴x x g x f将（1）代入（2）得：()()()()2212-=+++-x x g x x f x即：取()1--=x x u ，()2+=x x v 可得：()()()()()()()x g x f x g x v x f x u ,=+.2）()951624234++--=x x x x x f ,()45223+--=x x x x g 解：即：()()622--=x x x g x f 即：()()()213139362 +-⎪⎭⎫⎝⎛+-+--=x x x x x g()()()39619362 ++-=+--x x x x()()()1,-=∴x x g x f ，将（1）式代（2）式得：()()()()1322311312-=--+--x x g x x x f x .即：取()()131--=x x u ，()()322312--=x x x v 就有：()()()()()()()x g x f x g x v x f x u ,=+. 3）()144234++--=x x x x x f ，()12--=x x x g 解：即：1232 -+-=x x x g x f()()()()2312 ++-=x x x g()()()1,=∴x g x f将（1）式代入（2）式得：()()13233123=--+++-x g x x x x f x 即取()()131+-=x x u ，()()233123--+=x x x x v 就有：()()()()()()()x g x f x g x v x f x u ,=+. 6. 设()()u x x t x x f 22123++++=，()u tx x x g ++=3的最大公因式是一个二次多项式，t ，u 的值. 解：又()()u x x t x x f 22123++++=，()u tx x x g ++=3的最大公因式是一个二次多项式()()u tx x u x t x t +++-++∴3221.即()()()()[]()c x u x t x t u tx x t ++-++=+++21123即：()()()()⎪⎩⎪⎨⎧+=+=-+=++-u t cu t t t c u t c t 112012解得：⎩⎨⎧=-=04u t ，或⎪⎩⎪⎨⎧=+=02321u i t ，或⎪⎩⎪⎨⎧=-=0231u i t ，或⎪⎩⎪⎨⎧--=+-=i u i t 11721121，或⎪⎩⎪⎨⎧+-=--=i u i t 1172111. 7. 证明：如果()()x f x d ，()()x g x d ，且()x d 为()x f 与()x g 的一个组合，那么()x d 是()x f 与()x g 的一个最大公因式.证明：()x d 为()x f 与()x g 的一个组合即：()()()()()x d x g x v x f x u =+.又()()x f x d ，()()x g x d ，即()x d 是()x f 与()x g 的一个公因式.()()x f x h ∀，且()()x g x h 则()()x d x h ()x d ∴是()x f 与()x g 的一个最大公因式.8. 证明：()()()()()()()()()x h x g x f x h x g x h x f ,,=，（()x h 的首项系数为1）. 证明：()()()()x f x g x f , ，()()()()x g x g x f ,()()()()()()x h x f x h x g x f ,∴，()()()()()()x h x g x h x g x f ,. 即：()()()()x h x g x f ,是()()x h x f 与()()x h x g 的一个公因式. 又()()()()()()()()()x g x f x g x v x f x u st x v x u ,:,=+∃. 则()()()()()()()()()()x h x g x f x h x g x v x h x f x u ,=+()()()x h x f x c ∀，()()()x h x g x c 有()()()()()x h x g x f x c ,. 即()()()()x h x g x f ,是()()x h x f 与()()x h x g 的一个最大公因式. 又()x h 的首项系数为1.()()()()()()()()()x h x g x f x h x g x h x f ,,=∴.9. 如果()x f ，()x g 不全为零，证明：()()()()()()()()1,,,=⎪⎪⎭⎫ ⎝⎛x g x f x g x g x f x f .证明：()()()()x f x g x f , ,()()()()x g x g x f ,且()x f ，()x g 不全为零.()()()0,≠∴x g x f ，又()x u ∃，()x v ()()()()()()()x g x f x g x v x f x u st ,:=+()()()()()()()()()()1,,=+∴x g x f x g x v x g x f x f x u .即：()()()()()()()()1,,,=⎪⎪⎭⎫⎝⎛x g x f x g x g x f x f 成立. 10.证明：如果()x f ，()x g 不全为零，且()()()()()()()x g x f x g x v x f x u ,=+，那么()()()1,=x v x u .证明：()()()()x f x g x f , ,()()()()x g x g x f ,且()x f ，()x g 不全为零.且()()()()()()()x g x f x g x v x f x u ,=+()()()0,≠∴x g x f ()()()()()()()()()()1,,=+∴x g x f x g x v x g x f x f x u ()()()1,=x v x u .11.证明：如果()()()1,=x g x f ，()()()1,=x h x f ，那么()()()()1,=x h x g x f . 证明：()()()1,=x g x f ，()()()1,=x h x f .()x u 1∃∴，()x v 1，()x u 2，()x v 2使得：()()()()()1111 =+x g x v x f x u ()()()()()2122 =+x h x v x f x u . 由（1）式与（2）式相乘可得：()()()()()()()()()()()()()()()121212121=+++x h x g x v x v x f x g x u x v x h x v x u x f x u x u即()()()()1,=x h x g x f .12. 设()x f 1， ，()x f m ，()x g 1， ，()x g n 都是多项式，而且()()()1,=x g x f ji()n j m i ,,1;,,1 ==.求证：()()()()()1,11=x g x g x f x f nm.证明：由11题可得：()()()1,=x g x f ，()()()1,=x h x f ()()()()1,=⇒x h x g x f 又()()()1,=x g x f j i （其中m i ,,1 =；n j ,,1 =）可得，对于i 取m ,,2,1 中的任何一个固定值有：()()()()1,1=x g x g x f n i . 再将()()x g x g n 1看作一个整体可得：()()()()()1,11=x g x g x f x f n m . 13. 证明：如果()()()1,=x g x f ，那么()()()()()1,=+x g x f x g x f . 证明：()()()1,=x g x f 故有：()()()()1=+x g x v x f x u .即：()()()()()()()()()()()()()()()()1=++-=+-+x g x f x v x f x v x u x g x v x f x v x f x v x f x u()()()()1,=+∴x f x g x f ；同理可得：()()()()1,=+x g x f x g()()()()()1,=+∴x g x f x g x f .14. 求下列多项式的公共根：()12223+++=x x x x f ，()12234++++=x x x x x g . 解：()()()212+-=∴x x x f x g 即：()()()112+++=x x x x f()()()1,2++=∴x x x g x f 令：012=++x x 解得：2311i x +-=；2312ix --=. 即：()x f 与()x g 的公共根为：2311i x +-=和2312ix --=.（提示：公共根出现在多项式的公因式中.）15. 判别下列多项式有无重因式： 1）()842752345-+-+-=x x x x x x f解：()()()x x x x x x x x f 1524421205'2234+-=+-+-=又()()()1284275232345++-=-+-+-=x x x x x x x x x f即：()()()()22',-=x x f x f ()x f ∴有三重因式：2-x2）()34424--+=x x x x f解：()124484'33-+=x x x f即：()()()1',=x f x f ()x f ∴没有重因式. 16.求t 值使()1323-+-=tx x x x f 有重根.解：依题意可得：待定系数法：当有()x f 重根时，可得重根为有理根时，此时只能取重根为：1±=α.当重根为：1=α 1可得：3=t .当3=t 时，()()3231133-=-+-=x x x x x f 此时1=x 是()x f 的三重根；当重根为：1-=α1-解得：5-=t ，当5-=t 时，()()()141153223--+=---=x x x x x x x f 与1-=x 为重根矛盾，舍去.设重根为二重时得()⎪⎭⎫⎝⎛+-=+-=323163'22t x x t x x x f()()()()()()()()()12,''131,'',+=⎪⎭⎫ ⎝⎛--=x x f x f x x f x f x f x f 即得：021'=⎪⎭⎫⎝⎛-f .解得：415-=t . 17.求多项式q px x ++3有重根的条件.解：()()()()()()()()132,'3','3,',23≠⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛-=+++=q px x f x f x f x f p x q px x x f x f 得： ()x f q px'32+即得：027423=+q p . 18.如果()11242++-Bx Ax x ，求A ，B .解：依题意可由综合除法可得：1 1A A 2B A +3 B A 24+由()11242++-Bx Ax x 可得：⎩⎨⎧=+=++02401B A B A 解得：⎩⎨⎧-==21B A .19.证明：!!212n x x x n++++ 不能有重根.证明：令()!!212n x x x x f n ++++= 得：()()!1!21'12-++++=-n x x x x f n反证法：设()x f 的重根为α得：()()⎩⎨⎧==0'0ααf f 即：()()0'=-ααf f 0!=∴n nα得：0=α 又()010≠=f 矛盾.∴!!212n x x x n++++ 不能有重根.20.如果a 是()x f '''的一个k 重根，证明a 是()()()[]()()a f x f a f x f ax x g +-+-=''2的一个3+k 重根.证明：依题意可得：()()()[]()()0''2=+-+-=a f a f a f a f aa a g ()()()[]()()0'''22'''=--++=a f a f aa a f a f a g()()()()()a f a f aa a f a f a g '''''22''2''''--++=又()0'''=a f ()0''=∴a g()()()()02'''21'''4=-+-=a f a a a f a g又a 是()x f '''的一个k 重根a ∴是()x g '''的一个k 重根. 又()()()()0''''''====a g a g a g a g∴a 是()()()[]()()a f x f a f x f ax x g +-+-=''2的一个3+k 重根. 21.证明：0x 是()x f 的k 重根的充分必要条件是()()()()0'0100====-x f x f x f k ，而()()00≠x f k证明： 0x 是()x f 的k 重根()()x f x x k0-∴即()x g ∃，使得：()()()x g x x x f k0-=，其中0x x -不整除()x g()()()()()x g x x x g x x k x f kk ''010-+-=∴-可得：()()x f x x k '10--()0'0=∴x f同理由此类推可得到：()()()()0'0100====-x f x f x f k 若()()00=x f k 得：()()()x f x x k 0-()()x f x x s k s10+--⇒其中k s ≤，即()()x f x x k 10+-这与0x 是()x f 的k 重根矛盾.()()00≠∴x f k反之显然成立.∴0x 是()x f 的k 重根的充分必要条件是()()()()0'0100====-x f x f x f k ，而()()00≠x f k .22.举例说明断语“如果a 是()x f '的m 重根，那么a 是()x f 的1+m 重根”是不对的. 解：例如：()()111111+-=+m a x x f 则()()()ma x m x f -+=1'a 是()x f '的m 重根，但a 不是()x f 的1+m 重根.23. 证明：如果()()n x f x 1-，那么()()n n x f x 1-. 证明：令：n x y =得：()()y f x 1-即()()011==f f n ∴()()y f y 1-即()()n n x f x 1-.24. 证明：如果()()()323121x xf x f x x +++，那么()()x f x 11-，()()x f x 21-证明：.令：012=++x x 解得：2311i x +-=，2312ix --= 又()()()323121x xf x f x x +++即：()()()32311x f x f x x +-，()()()32312x f x f x x +-()()()()⎩⎨⎧=+=+∴0032223213121311x f x x f x f x x f 即：()()()()⎪⎪⎩⎪⎪⎨⎧=--+=+-+0123110123112121f i f f i f 又0323112311≠-=--+-i i i即该方程程组只有唯一零解：()()⎩⎨⎧==010121f f∴()()x f x 11-，()()x f x 21-.25. 求多项式1-n x 在复数域范围内和在实数范围内的因式分解. 解：在复数域上分解：()()()111----=-n n x x x x εε 其中ni n ππε2sin 2cos +=. 在实数范围内因式分解：当n 为奇数：()()[]()[]⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+-++-++--=-+---111112222222212x x x x x x x x n n n n nεεεεεε 其中：n i i n i πεε2cos2=+-为一个实数，21,,2,1-=n i . 当n 为偶数时：()()()[]()[]⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+-++-++--+=-+---1111112222222212x x x x x x x x x n n n n nεεεεεε 26. 求下列多项式的有理根： 1）1415623-+-x x x解：令()1415623-+-=x x x x f 则()x f 的有理根可能为：1±，2±，7±，14±.由综合除法计算得：1即：()41-=f同理：()361-=-f ，()762-=-f ，()02=f ，()7567-=-f ，()1407=f ，()414414-=-f()176414=f∴1415623-+-x x x 多项式的有理根为：2.2）157424---x x x解：令()157424---=x x x x f 则的有理根可能为：41±，21±，1± 将根挨个代入原式得：641114154174144124-=--⨯-⎪⎭⎫⎝⎛-⨯-⎪⎭⎫ ⎝⎛-⨯=⎪⎭⎫ ⎝⎛-f同理：6417141-=⎪⎭⎫ ⎝⎛f ，021=⎪⎭⎫ ⎝⎛-f ，521-=⎪⎭⎫⎝⎛f ，()11=-f ，()91-=f∴157424---x x x 多项式的有理根为：21-.3）3111462345----+x x x x x解：令()3111462345----+=x x x x x x f 则()x f 的有理根可能为：1±，3±由带余除法计算得：即：()01=-f 同理：()321-=f ，()963-=-f ，()03=f .∴3111462345----+x x x x x 多项式的有理根为：1-，3. 27. 下列多项式在有理数域上是否可约？ 1）12+x解：不可约；理由如下：依题意可得令()12+=x x f 则()x f 的有理根可能为：1± 又()()0211≠=-=f f 即1±不为()x f 的有理根∴多项式12+x 在有理数域上是不可约的.（二次有理多项式在有理数域上可约的话必有有理根）2）2128234++-x x x解：不可约；理由如下： 取素数2=p 得： （1）p 41a =.（2）38a p =-，212a p =，10a p =，02a p = （3）42=p 02a =由艾森斯坦判别法可得：多项式2128234++-x x x 是不可约的. 3）136++x x解：不可约；理由如下：令()136++=x x x f ，1+=y x 得：原多项式39182115623456++++++=y y y y y y 这时只要取3=p 可由艾森斯坦判别法得出：39182115623456++++++y y y y y y 不可约；∴136++x x 不可约.4）1++px x p ，p 为奇素数；解：令1+=y x 作转化，再由艾森斯坦判别法判别不可约； 5）144++kx x ，k 为整数. 解：同4），不可约：。

第4章矩阵4.1复习笔记一、矩阵的运算1．加法（１）定义设是两个s×n矩阵．则矩阵称为A和B的和．记为C＝A＋B 注意：相加的矩阵必须要有相同的行数和列数．（2）基本性质（1）A＋（B＋C）＝（A＋B）＋C；（结合律）（2）A＋B＝B＋A；（交换律）（3）A＋0＝A（4）A＋（－A）＝0（5）A－B＝A＋（－B）（6）秩（A＋B）≤秩（A）＋秩（B）．2．乘法（1）定义设A＝（a ik）sn，B＝（b kj）nm，那么矩阵C＝（c ij）sm，其中称为A与B的乘积，记为C＝AB．（2）性质①在乘积的定义中，要求第二个矩阵的行数与第一个矩阵的列数相等；②矩阵的乘法适合结合律；即（AB）C＝A（BC）；③矩阵的乘法不适合交换律，即AB BA；④分配律：A（B＋C）＝AB＋AC，（B＋C）＝BA＋CA．（3）单位矩阵主对角线上的元素全是1，其余元素全是0的n×n矩阵称为n级单位矩阵，记为E n，或者在不致引起含混的时候简单写为E．3．数量乘法（1）定义矩阵称为矩阵A＝（a ij）sn与数k的数量乘积，记为k A．换句话说，用数k乘矩阵就是把矩阵的每个元素都乘上k．（2）性质：①（k＋l）A＝k A＋l A；②k（A＋B）＝k A＋k B；③k（l A）＝（kl）A；④1A＝A；⑥k（AB）＝（k A）B＝A（k B）；⑦k A＝（k E）A＝A（k E），k E＋l E＝（k＋l）E，（k E）（l E）＝（kl）E，其中k E是数量矩阵．4．转置（1）定义设A的转置就是指矩阵显然，s×n矩阵的转置是n×s矩阵．（2）性质：①（A'）'＝A，②（A＋B）'＝A'＋B'，③（AB）'＝B'A'，④（k B）'＝k B'二、矩阵乘积的行列式与秩1．矩阵乘积的行列式（1）计算公式设A，B是数域P上的两个n×n矩阵，那么｜AB｜＝｜A｜｜B｜，即矩阵乘积的行列式等于它的因子的行列式的乘积．推论设A1，A2，…，A m是数域P上的n×n矩阵，于是｜A1A2…A m｜＝｜A1｜A2｜…｜A m｜．（2）退化的定义数域P上的n×n矩阵A称为非退化的，如果｜A｜≠0；否则称为退化的．一n×n矩阵是非退化的充分必要条件是它的秩等于n．推论设A，B是数域P上n×n矩阵，矩阵AB为退化的充分必要条件是A，B中至少有一个是退化的．2．矩阵的秩设A是数域P上n×m矩阵，B是数域P上m×s矩阵，于是秩（AB）≤min[秩（A），秩（B）]，即乘积的秩不超过各因子的秩．三、矩阵的逆1．逆矩阵n级方阵A称为可逆的，如果有n级方阵B，使得AB＝BA＝E．这里E是n级单位矩阵，那么B就称为A的逆矩阵，记为A-1．2．伴随矩阵设A i j是矩阵中元素a ij的代数余子式，矩阵称为A的伴随矩阵．3．性质（1）矩阵A是可逆的充分必要条件是A非退化，而（2）如果矩阵A，B可逆，那么A'与AB也可逆，且（3）A是一个s×n矩阵，如果P是s×s可逆矩阵，Q是n×n可逆矩阵，那么秩（A）＝秩（PA）＝秩（AQ）四、矩阵的分块1．定义。

1. 多项式除法（1）)(x f ＝1323---x x x )(x g ＝1232+-x x 普通带余除法 )(x f ＝（31x -97）)(x g -926x -92（2）)(x f ＝522+-x x )(x g ＝22+-x x∴)(x f ＝（12-+x x ）)(x g 75+-x2.（3）综合除法)(x f ＝x x x --23 )(x g ＝1-x +2i…………………∴)(x q ＝i ix x 2522--- )(x r ＝i 89+-3.整除（1）若12++x x 1f )(3x +x 2f )(3x 则)1(-x 1f )(x )1(-x 2f )(x 证：设12++x x 的两个复根为αβ 即α＝231i +- β＝231i-- 由于 3x -1＝)1(-x （12++x x ） 所以 3α＝ 1 3β＝ 1 因为12++x x ＝)(α-x )(β-x 且))((βα--x x 1f )(3x +x 2f )(3x故有⎩⎨⎧=+=+0)()(0)()(32313231βββαααf f f f 即⎩⎨⎧=+=+0)1()1(0)1()1(2121f f f f βα 解得 )1(1f ＝0 )1(2f ＝0 所以 )1(-x 1f )(x )1(-x 2f )(x （2）如果 )1(-x )(n x f 那么)1(-n x )(nx f证明：Θ )1(-x )(n x f 所以 1是)(nx f 的根，于是)1(nf ＝)1(f ＝0即)1(-x )(x f 故存在多项式)(x g 使得)(x f ＝)1(-x )(x g 从而 有)(n x f ＝)1(-n x )(n x g 此即)1(-n x )(n x f（3）1-nx 复域 实域 因式分解 解①令：k ε＝n k π2cos+i nk π2sin （k ＝0 1……1-n ）1-n x 复域内恰有n 个根k ε （k ＝0 1……1-n ） 1-n x ＝)1(-x )(1ε-x )(2ε-x ……)(1--n x ε②实域：-k ε＝k n -εk ε+k n -ε＝k ε+-k ε＝2nk π2cos2)(k n k -+εε-4＝2nk π2cos-4π0 （k ＝ 1……1-n ） 故 2x -（k ε+k n -ε）x +1 是实数域上的不可约多项式 当n 为奇数时，有1-n x ＝)1(-x [2x -)(11-+n εεx +1]……..[ 2x -)(2221--+n n εεx +1]当n 为偶数时，有1-n x ＝)1(-x )1(+x [2x -)(11-+n εεx +1]……..[ 2x - )(2222+-+n n εεx +1]＝)1(-x )1(+x ∏-=221n k [2x -2x nk π2cos+1] 4.有理根)(x f =n a n x +1-n a 1-n x +……+0a 是一个整系数多项式 而sr是一个有理根则s n a r 0a例：)(x f =157424---x x x若)(x f 有有理分肥，遇有理分化为既约分数后其分母为首项系数度4因数，而分子必为常数项-1的因数，所有可能 的有理根为1，-1，21，-2141，-41验证有)1(f ＝-9)1(-f ＝1)21(f ＝-5)21(-f ＝0)41(f ＝-64171)41(-f ＝-6411故-21是)(x f 的有理根，又综合除法…….∴-21是)(x f 的2重根5.最大公因式：（1）若（)(x f ，)(x g ）＝1，证明：对任意正整数n （)(x f ，)(x g n）＝1 （2）（)(x f ，)(x g ）＝1，（)(x f ，)(x h ）＝1，证明（)(x f ，)(x g )(x h ）＝1 证明：法2.反证 若设（)(x f ，)(x g )(x h ）＝)(x d ∂（)(x d ）φ0且)(x p 是)(x d的一个不可约多项式，则)(x p )(x f ，)(x p )(x g )(x h ，但因（)(x f ，)(x g ）＝1，所以)(x p 不整除)(x g ，∴)(x p )(x h 这与（)(x f ，)(x h ）＝1矛盾，∴（)(x f ，)(x g )(x h ）＝1（3）若（)(x f ，)(x g ）＝1，那么（)(x f )(x g ，)(x f +)(x g ）＝1 证明：由于（)(x f ，)(x g ）＝1，∴存在多项式)(x u )(x v 使得)(x u )(x f +)(x v )(x g ＝1∴)(x u )(x f -)(x v )(x f +)(x v )(x f +)(x v )(x g ＝（)(x u -)(x v ）)(x f +)(x v （)(x f +)(x g ）＝1 同理)(x u )(x f +)(x v )(x g -)(x u )(x g +)(x u )(x g ＝ （)(x v -)(x u ）)(x g +)(x u （)(x f +)(x g ）＝1 由互素的充要条件知()(x f ,)(x f +)(x g )=1 ()(x g ,)(x f +)(x g )=1若（)(x f )(x g ，)(x f +)(x g ）＝)(x d ，∂（)(x d ）φ0且)(x p 是)(x d 的一个不可约多项式，则)(x p )(x f )(x g 且)(x p [)(x f +)(x g ] 又()(x f ,)(x f +)(x g )=1， ∴ )(x p )(x g 这与()(x g ,)(x f +)(x g )=1 矛盾，∴（)(x f )(x g ，)(x f +)(x g ）＝1（4）若（)(x f i ，)(x g j ）＝1 （i ＝1，2…. m ，j ＝1，2…..n ）则 （)(1x f …..)(x f m ，)(1x g ……)(x g n ）＝1证明 由于（)(1x f ，)(x g j ）＝1 （j ＝1，2…..n ）首先证明若（)(1x f ，)(x g j ）＝1，（)(1x f ，)(x g i ）＝1 （i ，j ＝1，2…n ） 则（)(1x f ，)(x g i )(x g j ）＝1，若不然，设（)(1x f ，)(x g i )(x g j ）＝)(x d∂（)(x d ）φ0且)(x p 是)(x d 的一个不可约多项式，则)(x p )(1x f 且)(x p )(x g i )(x g j又（)(1x f ，)(x g j ）＝1， 则)(x p )(x g i 这与（)(1x f ，)(x g i ）＝1矛盾，∴（)(1x f ，)(x g i )(x g j ）＝1 重复此过程，得到（)(1x f ，)(1x g ……)(x g n ）＝1同理可证（)(x f i ，)(1x g ……)(x g n ）＝1 （i ＝2…. m ）再次反复应用上述证明过程，便可得到（)(1x f …..)(x f m ，)(1x g ……)(x g n ）＝1 二，行列式6.（1）44332211a b a b b a b a ＝＝＝＝＝4411a b b a 3322a b b a（2）12+n a ba bc b aba＝c n a ba b b a ba 2＝cab b a 22-n a bab b a b a＝c （2a +2b ）'22-n D7.nD =nnn a a a a a a a a ---------11111111133221⇒nn a a -+10＝1-n D +n )1(-n a ......1an D =1-n D +n )1(-n a ......1a ＝…….＝1-1a +1a 2a +………..+ n )1(-1a …n a8. n D =xz y x zyx zy x ++++1111＝（x +1）1-n D -y z 2-n D又 y z ＝x ∴n D =（x +1）1-n D -x 2-n D整理得 n D -1-n D ＝………＝nx8.基础解系⎪⎪⎩⎪⎪⎨⎧=-+++=+++=-+++=++++033450622032305432154325432154321x x x x x x x x x x x x x x x x x x x解：其系数矩阵A ＝⎪⎪⎪⎪⎪⎭⎫⎝⎛--133456*********11111对其只作行的初等变换A →⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------62210622106221011111→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----00000000006221011111 原方程与⎩⎨⎧=+++=++++06220543254321x x x x x x x x x 同解令3x ＝1，4x ＝5x ＝0 得 1η＝（1，-2，1，0，0） 令3x ＝5x ＝0，4x ＝1 得 2η＝（1，-2，0，1，0） 令3x ＝4x ＝0，5x ＝1 得 3η＝（5，-6，0，0，1） 则1η2η3η是方程组的一个基础解系，全部解为x ＝1c 1η+2c 2η+3c 3η （1c ，2c ，3c 为任意常数）（2）⎪⎪⎩⎪⎪⎨⎧=-+-+=-++-=-+-=--+0742420436240203543215432143215421x x x x x x x x x x x x x x x x x x解：其系数矩阵A ＝⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------74242436240121113011→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----5102200156601222013011→ ⎪⎪⎪⎪⎪⎭⎫⎝⎛---0000390001222013011∴原方程与⎪⎩⎪⎨⎧=-=+-+-=--+039022035454325421x x x x x x x x x x 同解，令2x ＝1， 5x ＝0 得 1η＝（-1，1，1，0，0） 令2x ＝0， 5x ＝1得 2η＝（2，0，-65，31，1） 则1η2η是方程组的一个基础解系，全部解为x ＝1c 1η+2c 2η （1c ，2c 为任意常数）9.证明：1α2α3α无关的充要条件1α+2α，2α+3α，3α+1α线性无关 （1）证明：设有线性关系式1k （1α+2α）+2k （2α+3α）+3k （3α+1α）＝0即（1k +2k ）2α+（1k +3k ）1α+（2k +3k ）3α＝0 由题设1α2α3α线性无关∴⎪⎩⎪⎨⎧=+=+=+000322131k k k k k k 解得1k ＝2k ＝3k ＝0 ∴1α+2α，2α+3α，3α+1α线性无关当奇数个线性无关向量1α…. 12+n α，则1α+2α，2α+3α，……. n 2α+12+n α，12+n α+1α也线性无关证明:设有线性关系式1k （1α+2α）+2k （2α+3α）+……+12+n k （12+n α+1α）＝0 即 （1k +12+n k ）1α+（1k +2k ）2α+….+ （n k 2+12+n k ）12+n α＝0 又由1α…. 12+n α线性无关，则有⎪⎪⎩⎪⎪⎨⎧=+=+=+++0 012221121n n n k k k k k k 其系数矩阵A ＝⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛11 (00)01.....000...............00 (1110) (01)其行列式A ＝2≠0 其方程组只有零解1k ＝……＝12+n k ＝0 ∴1α+2α，2α+3α，……. n 2α+12+n α，12+n α+1α线性无关（3）若有偶数个线性相关向量1α…. n 2α⇒1α+2α，2α+3α，……. n 2α+1α相关， 若有偶数个线性无关向量1α…. n 2α⇒1α+2α，2α+3α，……. n 2α+1α也相关， 证明：设有线性关系式1k （1α+2α）+2k （2α+3α）+……+n k 2（n 2α+1α）＝0 （1） 即（1k +n k 2）1α+（1k +2k ）2α+….+ （n k 2+12-n k ）n 2α＝0 （2） 又①若1α…. n 2α线性相关，即（2）式中存在不为零的系数，不妨设为1k +2k 不为零，则1k ，2k 至少一个不为零即1k ，2k ……n k 2不全为零 ，∴1α+2α，2α+3α，……. n 2α+1α相关 ②若1α…. n 2α线性无关，则有⎪⎪⎩⎪⎪⎨⎧=+=+=+-0 002122121n n nk k k k k k 其系数矩阵A ＝⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛11 (00)01 (00)0...............00 (1110) (01)则 A ＝11 001 (00)0...............00 (110).....1+12)1(+-n 11 01.....001...............00 (100).....11＝0∴方程组存在非零解 即1k ，2k ……n k 2不全为零 ∴1α+2α，2α+3α，……. n 2α+1α相关10.设1β＝1α，2β＝1α+2α，……，r β＝1α+…..+ r α 且1α…. r α线性无关，证明1β，…..，r β线性无关证明： （1β，…..，r β）＝（1α，…. ，r α）⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛11......001.....0011...........11 (10)11 (1)1设上述矩阵为A ，A 为上三角阵，显然A ≠0，∴A 可逆 即（1α，…. ，r α）＝（1β，…..，r β）1-A设1-A ＝⎪⎪⎪⎪⎪⎭⎫ ⎝⎛nn n n n a a a a a a 1221111............ 则1-A A ＝E 解得1-A ＝⎪⎪⎪⎪⎪⎭⎫⎝⎛---11......1...11 ∴（1α，…. ，r α）＝（1β，…..，r β）⎪⎪⎪⎪⎪⎭⎫⎝⎛---11......1 (11)∴1α，…. ，r α也可以被1β，…..，r β线性表出即1α，…. ，r α与1β，…..，r β等价，它们秩相等，又1α…. r α线性无关，∴1β，…..，r β线性无关11. 设秩（1α，…. ，r α）＝r πn ，且i α≠0，i ＝1，2，….，n 证明：存在 j α（2≤j ≤n ）使得 i α可由1α…1-j α，1+j α…n α线性表示（2）设1α，…. ，s α的秩为r ，证明：1α，…. ，s α中任意r 个线性无关向量都构成它的一个极大线性无关组证明：1i α….. r i α是1α，…. ，s α的一个线性无关组又向量组1i α….. ri αj α（j ＝1，2，….，s ）是线性相关的，否则，原向量组秩超过了r1i α….. ri αj α线性相关，则存在不全为零 的一组数1k ，2k ……1+r k 使得1k 1i α+…r k r i α+1+r k j α＝0 若1+r k ＝0 则由1k ，2k ……r k 不全为零 知1i α….. ri α相关与1i α….. ri α的选取矛盾，∴1+r k ≠0即j α＝-11+r k （1k 1i α+…r k r i α）∴1i α….. r i α是1α，…. ，s α的一个极大线性无关组，又由1i α….. r i α任意性知，命题成立。