第十章 时间序列截面数据模型
- 格式:doc
- 大小:1.13 MB
- 文档页数:50


横截面数据、时间序列数据、面板数据横截面数据:(时间固定)横截面数据是在同一时间,不同统计单位相同统计指标组成的数据列。
横截面数据是按照统计单位排列的。
因此,横截面数据不要求统计对象及其范围相同,但要求统计的时间相同。
也就是说必须是同一时间截面上的数据。
如:时间序列数据:(横坐标为t,纵坐标为y)在不同时间点上收集到的数据,这类数据反映某一事物、现象等随时间的变化状态或程度。
如:面板数据:(横坐标为t,斜坐标为y,纵坐标为z)是截面数据与时间序列数据综合起来的一种数据类型。
其有时间序列和截面两个维度,当这类数据按两个维度排列时,是排在一个平面上,与只有一个维度的数据排在一条线上有着明显的不同,整个表格像是一个面板,所以把panel data译作“面板数据”。
举例:如:城市名:北京、上海、重庆、天津的GDP分别为10、11、9、8(单位亿元)。
这就是截面数据,在一个时间点处切开,看各个城市的不同就是截面数据。
如:2000、2001、2002、2003、2004各年的北京市GDP分别为8、9、10、11、12(单位亿元)。
这就是时间序列,选一个城市,看各个样本时间点的不同就是时间序列。
如:2000、2001、2002、2003、2004各年中国所有直辖市的GDP分别为:北京市分别为8、9、10、11、12;上海市分别为9、10、11、12、13;天津市分别为5、6、7、8、9;重庆市分别为7、8、9、10、11(单位亿元)。
这就是面板数据。
关于面板数据的统计分析在写论文时经常碰见一些即是时间序列又是截面的数据,比如分析1999-2010的公司盈余管理影响因素,而影响盈余管理的因素有6个,那么会形成如下图的数据如上图所示的数据即为面板数据。
显然面板数据是三维的,而时间序列数据和截面数据都是二维的,把面板数据当成时间序列数据或者截面数据来处理都是不合适的。
处理面板数据的软件较多,一般使用Eviews6.0、Stata等。

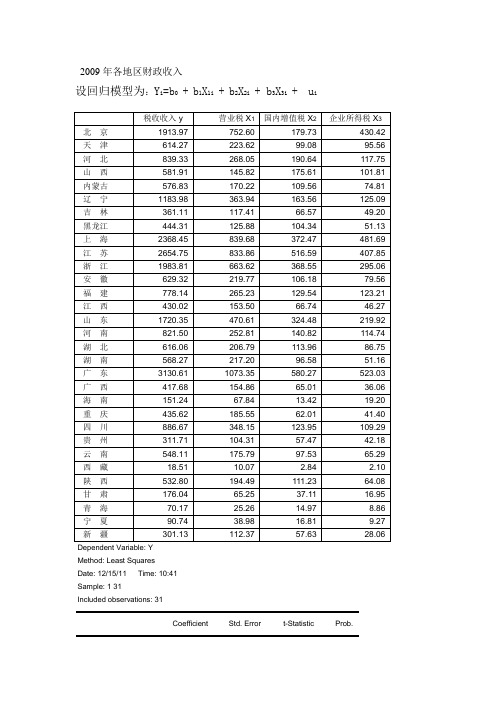
2009年各地区财政收入设回归模型为:Y i=b0+b1X1i+b2X2i+ b3X3i+ u i税收收入y 营业税X1国内增值税X2企业所得税X3北京1913.97 752.60 179.73 430.42 天津614.27 223.62 99.08 95.56 河北839.33 268.05 190.64 117.75 山西581.91 145.82 175.61 101.81 内蒙古576.83 170.22 109.56 74.81 辽宁1183.98 363.94 163.56 125.09 吉林361.11 117.41 66.57 49.20 黑龙江444.31 125.88 104.34 51.13 上海2368.45 839.68 372.47 481.69 江苏2654.75 833.86 516.59 407.85 浙江1983.81 663.62 368.55 295.06 安徽629.32 219.77 106.18 79.56 福建778.14 265.23 129.54 123.21 江西430.02 153.50 66.74 46.27 山东1720.35 470.61 324.48 219.92 河南821.50 252.81 140.82 114.74 湖北616.06 206.79 113.96 86.75 湖南568.27 217.20 96.58 51.16 广东3130.61 1073.35 580.27 523.03 广西417.68 154.86 65.01 36.06 海南151.24 67.84 13.42 19.20 重庆435.62 185.55 62.01 41.40 四川886.67 348.15 123.95 109.29 贵州311.71 104.31 57.47 42.18 云南548.11 175.79 97.53 65.29 西藏18.51 10.07 2.84 2.10 陕西532.80 194.49 111.23 64.08 甘肃176.04 65.25 37.11 16.95 青海70.17 25.26 14.97 8.86 宁夏90.74 38.98 16.81 9.27 新疆301.13 112.37 57.63 28.06 Dependent Variable: YMethod: Least SquaresDate: 12/15/11 Time: 10:41Sample: 1 31Included observations: 31Coefficient Std. Error t-Statistic Prob.C -1.361323 18.21374 -0.074742 0.9410X1 1.943192 0.254672 7.630183 0.0000X2 1.814357 0.202777 8.947566 0.0000X3 0.185165 0.406593 0.455407 0.6525R-squared 0.995288 Mean dependent var 843.7874Adjusted R-squared 0.994764 S.D. dependent var 795.4357S.E. of regression 57.55598 Akaike info criterion 11.06331Sum squared resid 89442.65 Schwarz criterion 11.24834Log likelihood -167.4813 Hannan-Quinn criter. 11.12362F-statistic 1900.982 Durbin-Watson stat 1.429213Prob(F-statistic) 0.000000= -1.361323 + 1.943192X1 + 1.814357X2 + 0.185165X3(-0.074742)(7.630183)(8.947566)(0.455407)R2=0.995288 d=1.429213 F=1900.982对给定显著水平a=0.05,查自由度分别为3和27的F分布得临界值F0.05=2.96,F>F0.05,说明回归方程是显著的。


1第十章 时间序列/截面数据模型在进行经济分析时经常会遇到时间序列和横截面两者相结合的数据,例如,在企业投资需求分析中,我们会遇到多个企业的若干系列的月度或年度经济指标;在城镇居民消费分析中,我们会遇到不同省市的反映居民消费和居民收入的年度经济指标等。
我们将这种含有双向信息(横向——时间、纵向——截面)的数据称为时间序列/截面数据,有的书中也称为平行数据或面板数据(Panel data )。
经典线性计量经济学模型在分析时只利用了时间序列/截面数据中的某一单向信息。
然而,在实际经济分析中,这种仅利用单向信息的模型在很多时候往往不能满足人们分析问题的需要。
例如,在生产函数分析中,只有利用时间序列/截面数据才能实现规模经济和技术革新的分离分析。
横截面数据提供了关于规模经济的信息,时间序列数据(在规模收益不变假设下)提供了技术革新的信息,利用时间序列/截面数据可以同时分析企业的规模经济(选择同一时期的不同规模的企业数据作为样本观测值)和技术革新(选择同一企业的不同时期的数据作为样本观测值)。
时间序列/截面数据含有时间和截面双向信息,利用时间序列/截面数据模型可以构造和检验比以往单独使用横截面数据或时间序列数据更现实的行为方程,进行更加深入的分析。
正是基于实际分析的需要,作为非经典计量经济学问题,时间序列/截面数据模型已经成为近20年来计量经济学理论方法的重要发展之一。
在本章中主要介绍三种常用的时间序列/截面数据模型——变截距模型、动态变截距模型、变系数模型。
10.1 时间序列/截面数据模型简介时间序列/截面数据模型的基本形式为:it it itit it x y μβα+'+= , i =1 , 2 , …, n ; t =1 , 2 ,…, T (10.1.1) 其中y it 是因变量,x it 是K ⨯ 1维解释变量向量,n 为截面成员个数,T 为每个截面成员的观测时期总数。
参数αit 表示模型的常数项,βit 为对应于回归向量x it 的系数向量。
统计学中的时间序列分析和模型时间序列分析是指对一组按时间排序的数据进行分析,以了解数据的趋势、季节性和周期性等特征,并进一步预测未来的发展趋势。
时间序列分析在统计学中扮演着重要的角色,广泛应用于经济学、金融学、气象学等领域。
本文将介绍时间序列分析的基本概念、常用方法和模型。
一、时间序列分析的基本概念时间序列是指按时间顺序排列的数据集合。
在进行时间序列分析时,我们通常关注以下几个方面的特征:1. 趋势(Trend):指数据在长期内的稳定增长或减少的趋势。
趋势可以是线性的、非线性的,也有可能是周期性的。
2. 季节性(Seasonality):指数据在周期性时间内的反复变化。
例如,零售业的销售额会在每年的圣诞节季节性地增长。
3. 周期性(Cyclical):指数据在相对较长的周期内的起伏波动。
周期性通常持续数年,而季节性则在一年内重复发生。
4. 随机性(Random):指时间序列数据中不规则的波动或噪声。
随机性往往难以预测和解释,但可以通过模型进行剔除。
二、时间序列分析的常用方法时间序列分析涉及到多种方法和技术,其中最常见的包括以下几种:1. 描述统计分析:通过计算统计量(如均值、标准差、相关系数等)来描述时间序列的基本特征。
2. 绘制图表:如折线图、散点图等,可以直观地展示时间序列的趋势、季节性等特征。
3. 移动平均法:通过计算一段时间内的平均值,平滑数据中的随机波动,以揭示趋势。
4. 自回归模型:常用于分析具有自相关性(即当前值受过去值的影响)的时间序列。
其中最著名的模型为ARIMA模型。
5. 季节性调整:将数据进行季节性调整,以剔除季节性的影响,突出数据的趋势和周期性。
三、常用的时间序列模型时间序列模型是用来描述时间序列数据之间关系的数学模型。
在时间序列分析中,常用的模型包括:1. ARIMA模型(差分自回归移动平均模型):是一种广泛应用于时间序列预测和分析的模型。
ARIMA模型考虑了时间序列的自相关性和季节性。
时间序列初步模型时间序列模型是用来描述一系列时间上连续的数据的数学模型。
它使用过去的观测值来预测未来的值,主要用于预测与时间相关的现象。
时间序列模型是研究经济、金融、气象等领域的重要工具,可以帮助我们理解和预测这些领域的变化趋势。
时间序列模型可以分为线性模型和非线性模型。
线性模型假设时间序列之间的关系是线性的,而非线性模型则允许时间序列之间的关系是非线性的。
线性模型包括传统的AR、MA、ARMA和ARIMA模型,非线性模型有ARCH、GARCH和非线性ARIMA模型等。
AR(自回归)模型是最简单的时间序列模型之一,它假设时间序列的当前值依赖于过去几个时期的值。
AR模型的数学表达式为:Yt = μ + Σφi * Yt-i + εt其中,Yt表示时间t的值,μ表示常数项,φi表示Y的滞后项,εt表示误差项。
AR模型的阶数p表示过去p个时期的值对当前值的影响程度。
通过估计参数φi和误差项的方差,可以预测未来时间的值。
MA(移动平均)模型也是一种常见的时间序列模型,它假设时间序列的当前值依赖于过去几个时期的误差项。
MA模型的数学表达式为:Yt = μ + Σθi* εt-i + εt其中,Yt表示时间t的值,θi表示Y的滞后的误差项,εt表示当前时期的误差项。
MA模型的阶数q表示过去q个误差项对当前值的影响程度。
通过估计参数θi和误差项的方差,可以预测未来时间的值。
ARMA(自回归滑动平均)模型是AR和MA模型的结合,它考虑了时间序列的滞后项和误差项对当前值的影响。
ARMA模型的数学表达式为:Yt = μ + Σφi * Yt-i + Σθi * εt-i + εt其中,Yt表示时间t的值,μ表示常数项,φi表示Y的滞后项,θi表示Y的滞后的误差项,εt表示当前时期的误差项。
ARMA模型的阶数p和q分别表示滞后项和误差项的个数。
通过估计参数φi、θi和误差项的方差,可以预测未来时间的值。
ARIMA(差分自回归滑动平均)模型是ARMA模型的延伸,它考虑了时间序列的差分项,用于处理非平稳时间序列。
1第十章 时间序列/截面数据模型在进行经济分析时经常会遇到时间序列和横截面两者相结合的数据,例如,在企业投资需求分析中,我们会遇到多个企业的若干系列的月度或年度经济指标;在城镇居民消费分析中,我们会遇到不同省市的反映居民消费和居民收入的年度经济指标等。
我们将这种含有双向信息(横向——时间、纵向——截面)的数据称为时间序列/截面数据,有的书中也称为平行数据或面板数据(Panel data )。
经典线性计量经济学模型在分析时只利用了时间序列/截面数据中的某一单向信息。
然而,在实际经济分析中,这种仅利用单向信息的模型在很多时候往往不能满足人们分析问题的需要。
例如,在生产函数分析中,只有利用时间序列/截面数据才能实现规模经济和技术革新的分离分析。
横截面数据提供了关于规模经济的信息,时间序列数据(在规模收益不变假设下)提供了技术革新的信息,利用时间序列/截面数据可以同时分析企业的规模经济(选择同一时期的不同规模的企业数据作为样本观测值)和技术革新(选择同一企业的不同时期的数据作为样本观测值)。
时间序列/截面数据含有时间和截面双向信息,利用时间序列/截面数据模型可以构造和检验比以往单独使用横截面数据或时间序列数据更现实的行为方程,进行更加深入的分析。
正是基于实际分析的需要,作为非经典计量经济学问题,时间序列/截面数据模型已经成为近20年来计量经济学理论方法的重要发展之一。
在本章中主要介绍三种常用的时间序列/截面数据模型——变截距模型、动态变截距模型、变系数模型。
10.1 时间序列/截面数据模型简介时间序列/截面数据模型的基本形式为:it it itit it x y μβα+'+= , i =1 , 2 , …, n ; t =1 , 2 ,…, T (10.1.1) 其中y it 是因变量,x it 是K ⨯ 1维解释变量向量,n 为截面成员个数,T 为每个截面成员的观测时期总数。
参数αit 表示模型的常数项,βit 为对应于回归向量x it 的系数向量。
随机误差项μit 相互独立,且满足零均值、等方差的假设。
在成员截面上,该模型共含有n 个截面成员方程,在时间截面上,该模型共含有T 个时间截面方程。
在(10.1.1)式描述的模型中,自由度(nT )远远小于参数个数(nT (K+1)+描述μit 分布的参数个数),这使得模型无法估计。
为了实现模型的估计,我们假定参数满足时间一致性,即参数值不随时间的不同而变化。
因此,模型简化为如下形式:it i iti it x y μβα+'+= (10.1.2) 其中,参数αi 和βi 都是个体时期恒量,其取值只受截面单元不同的影响。
根据截距项αi 以及系数向量βi 的不同限制要求,我们又可以将(10.1.2)式所描述的时间序列/截面数据模型划分为三种类型:无个体影响的不变系数模型、含有个体影响的不变系数模型即变截距模型和含有个体影响的2变系数模型即变系数模型。
无个体影响的不变系数模型的单方程回归形式可以写成:it itit x y μβα+'+= (10.1.3) 在该模型当中,假设在横截面上既无个体影响也没有结构变化,即在各截面方程中,系数向量相同且不含有个体影响δi 项。
对于该模型,将各截面成员的时间序列数据堆积在一起作为样本数据,利用普通最小二乘法便可给出参数α 和β 的一致有效估计。
因此,该模型也被称为联合回归模型(pooled regression model )。
变截距模型的单方程回归形式可以写成:it iti it x y μβα+'+= (10.1.4) 在该模型当中,我们假设在横截面上存在个体影响而无结构变化,并且个体影响可以用截距项αi 的差别来说明,即在该模型中各截面方程的截距项αi 不同,而系数向量β 相同。
我们称该模型为变截距模型。
从估计方法角度,有时也称该模型为个体均值修正回归模型(individual-mean corrected regression model )。
变系数模型的单方程回归形式可以写成:it i iti it x y μβα+'+= (10.1.5) 在该模型中,假设在横截面上既存在个体影响,又存在结构变化,即在允许个体影响由跨截面变化的截距项α i 来说明的同时还允许系数向量跨截面变化,用以说明横截面上的结构变化。
我们称该模型为变系数模型或无约束模型(unrestricted model )。
10.2 模型形式的设定在对时间序列/截面数据模型进行估计时,使用的样本数据包含了时间序列和横截面这两个方向上的信息,如果模型形式设定的不正确,估计结果将与所要模拟的经济现实偏离甚远。
因此,建立时间序列/截面数据模型的第一步便是检验刻画被解释变量y 的参数α i 和βi 是否在所有横截面样本点和时间上都是常数,即检验样本数据究竟符合上面哪种时间序列/截面数据模型形式,从而避免模型设定的偏差,改进参数估计的有效性。
经常使用的检验是协方差分析检验,主要检验如下两个假设:H 1: n βββ=== 21 H 2: n ααα=== 21n βββ=== 21可见如果接受假设H 2则可以认为样本数据符合模型(10.1.3),无需进行进一步的检验。
如果拒绝假设H 2,则需检验假设H 1。
如果拒绝假设H 1,则认为样本数据符合模型(10.1.5),反之,则认为样本数据符合模型(10.1.4)。
对应假设H 1和H 2,在检验的过程中构造的检验统计量分别为:)]1(,)1[(~))1((])1/[()(1121---+---=K T n K n F K n nT S K n S S F (10.2.1)3)]1(),1)(1[(~))1(()]1)(1/[()(1132--+-+-+--=K T n K n F K n nT S K n S S F (10.2.2)其中,S1、S2、S3分别为模型(10.1.5)、(10.1.4)和(10.1.3)的残差平方和。
如果记∑∑==-'-=-'-=Tt i it i it i xy Tt i it i it i xx y y x x W x x x x W 1,1,)()()()(21,)(∑=-=Tt i it i yy y y W其中T y y T x x Tt it i Tt it i ∑∑====11,则∑=-'-=ni ixy j xx i xy i yy W W W W S 1,1,,,1 (10.2.3)记1,1,1,∑∑∑======ni i yy yy n i i xy xy ni ixx xx W W W W W W则xy xx xy yy W W W W S 12-'-= (10.2.4)记∑∑∑∑====-'-=-'-=n i Tt it it xy n i Tt it it xx y y x x T x x x x T 1111)()()()(∑∑==-=n i Tt it yy y y T 121)(其中 nT y y nT xx n i Tt it n i Tt it∑∑∑∑======1111,则xy xx xy yy T T T T S 13-'-= (10.2.5)由于1、S 1/σμ2 ~ χ2[n (T -K -1)];2、 在H 2下,S 3 /σμ2 ~ χ2[nT -(K +1)]和(S 3 - S 1) /σμ2 ~ χ2[(n -1)(K +1)];3、 (S 3 - S 1) /σμ2与S 1/σμ2独立。
4所以,在假设H 2下检验统计量F 2服从相应自由度下的F 分布,即)]1(),1)(1[(~2--+-K T n K n F F (10.2.13)若计算所得到的统计量F 2的值不小于给定置信度下的相应临近值,则拒绝假设H 2,继续检验假设H 1。
反之,则认为样本数据符合模型(10.1.3)。
类似地,由于1、 在H 1下,S 2 /σμ2 ~ χ2[n (T -1)- K ]和(S 2 - S 1) /σμ2 ~ χ2[(n -1)K ];2、 (S 2- S 1) /σμ2与S 1/σμ2独立。
所以,在假设H 1下检验统计量F 1也服从相应自由度下的F 分布,即)]1(,)1[(~1---K T n K n F F (10.2.14)若计算所得到的统计量F 1的值不小于给定置信度下的相应临近值,则拒绝假设H 1,用模型(10.1.5)拟合样本,反之,则用模型(10.1.4)拟合。
10.3 变截距模型变截距模型是时间序列/截面数据模型中最常见的一种形式。
该模型允许横截面上存在个体影响,并用截距项的差别来说明。
模型的基本形式由如下:it iti it x y μβα+'+=, i =1 , 2 , …, n ; t =1 , 2 ,…, T (10.3.1) 其中,各截面方程间不同的截距项αi 为个体时期恒量,用来说明个体影响,即反映模型中忽略的反映个体差异的变量的影响;随机误差项μit 反映模型中忽略的随横截面和时间变化的因素的影响。
个体影响分为固定影响和随机影响两种情形,根据个体影响的不同形式,变截距模型又分为固定影响变截距模型和随机影响变截距模型两种。
固定影响变截距模型1. 模型形式及参数估计固定影响变截距模型假定各截面单位的个体影响可以由常数项的不同来说明,即在(10.3.1)式所表示的模型中,各截面方程中的截距项αi 为跨截面变化的常数。
模型对应的向量形式如下:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=n n n n u u X X X e e e y y Y 121211000000βααα (10.3.2)其中121⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=T iT i i i y y y y , K T KiT iTiT Ki i i Ki i i i x x x x x x x x x X ⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=212222111211 ()1,,1,11 ='⨯Te , ()iT i Ti u μμ,,11 ='⨯5并且,)(0,,02j i u Eu I u Eu Eu j i T u i i i ≠='='=σ,其中I T 为T ⨯T 维单位矩阵。
利用普通最小二乘法可以得到参数αi 和β 的最优线性无偏估计(BLUE )为:⎥⎦⎤⎢⎣⎡-'-⎥⎦⎤⎢⎣⎡-'-=∑∑∑∑==-==n i T t i it i it n i T t i it i it CVy y x x x x x x 11111)()()()(ˆβ iCV i i x y βαˆˆ-= (10.3.3) 在模型(10.3.2)中,我们把参数αi 写为可观测的虚拟变量的系数的形式,因此,(10.3.3)式所表示的OLS 估计也称为最小二乘虚拟变量(LSDV )估计。