平行线分线段成比例经典例题与变式练习(精选题目)92487

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图，如果1l ∥2l ∥3l ，则BC EF AC DF =，AB DE AC DF =，AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论：如图，在三角形中，如果DE BC ∥，则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理：如上图，如果有BCDEAC AE AB AD ==，那么DE ∥ BC 。

专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图，DE BC ∥，且DB AE =,若510AB AC ==，，求AE 的长。

EDCBA【例2】 如图，已知////AB EF CD ，若AB a =，CD b =，EF c =，求证：111c a b=+.FE DCBA【巩固】如图，AB BD ⊥，CD BD ⊥，垂足分别为B 、D ，AC 和BD 相交于点E ，EF BD ⊥，垂足为F .证明：111AB CD EF+=. FEDCBA【巩固】如图，找出ABD S ∆、BED S ∆、BCD S ∆之间的关系，并证明你的结论.FE DCBA【例3】 如图，在梯形ABCD 中，AB CD ∥， 129AB CD ==，，过对角线交点O 作EF CD ∥交AD BC ，于E F ，，求EF 的长。

OFED CBA【巩固】（上海市数学竞赛题）如图，在梯形ABCD 中，AD BC ∥，AD a BC b E F ==，，，分别是AD BC ，的中点，AF 交BE 于P ，CE 交DF 于Q ，求PQ 的长。

QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 （2007年北师大附中期末试题）（1）如图（1），在ABC ∆中，M 是AC 的中点，E 是AB 上一点，且14AE AB =， 连接EM 并延长，交BC 的延长线于D ，则BCCD=_______. （2）如图（2），已知ABC ∆中，:1:3AE EB =，:2:1BD DC =，AD 与CE 相交于F ，则EF AFFC FD+ 的值为（ ）A.52 B.1 C.32D.2(1)MEDC BA(2)F ED CA【例5】 （2001年河北省中考试题）如图，在ABC ∆中，D 为BC 边的中点，E 为 AC 边上的任意一点，BE 交AD 于点O . （1）当1A 2AE C =时，求AOAD的值；E AO（2）当11A 34AE C =、时，求AOAD的值； （3）试猜想1A 1AE C n =+时AOAD的值，并证明你的猜想.【例6】 （2003年湖北恩施中考题）如图，AD 是ABC ∆的中线，点E 在AD 上，F 是BE 延长线与AC 的交点.（1）如果E 是AD 的中点，求证：12AF FC =； （2）由（1）知，当E 是AD 中点时，12AF AEFC ED=⋅成立，若E 是AD 上任意一点（E 与A 、D 不重合），上述结论是否仍然成立，若成立请写出证明，若不成立，请说明理由.F E DCBA【巩固】（天津市竞赛题）如图，已知ABC ∆中，AD 是BC 边上的中线，E 是AD 上的一点，且BE AC =，延长BE 交AC 于F 。

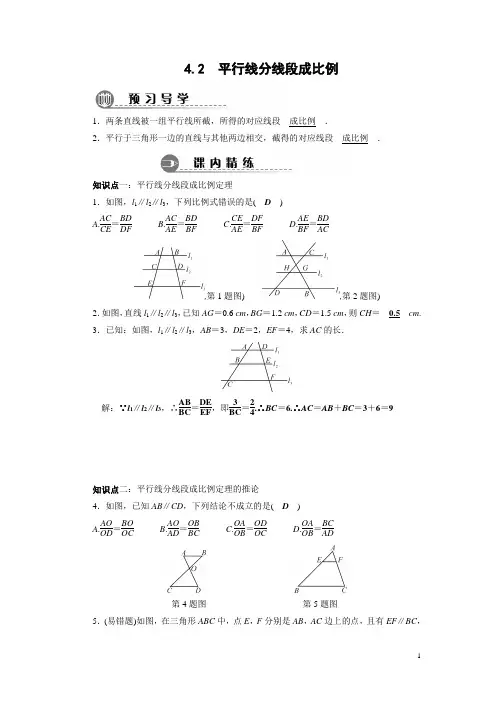
4.2 平行线分线段成比例1．两条直线被一组平行线所截，所得的对应线段__成比例__．2．平行于三角形一边的直线与其他两边相交，截得的对应线段__成比例__．知识点一：平行线分线段成比例定理1．如图，l 1∥l 2∥l 3，下列比例式错误的是( D )A .AC CE ＝BD DFB .AC AE ＝BD BF C .CE AE ＝DF BF D .AE BF ＝BD AC,第1题图) ,第2题图)2．如图，直线l 1∥l 2∥l 3，已知AG ＝0.6 cm ，BG ＝1.2 cm ，CD ＝1.5 cm ，则CH ＝__0.5__cm . 3．已知：如图，l 1∥l 2∥l 3，AB ＝3，DE ＝2，EF ＝4，求AC 的长．解：∵l 1∥l 2∥l 3，∴AB BC ＝DE EF ，即3BC ＝24.∴BC ＝6.∴AC ＝AB ＋BC ＝3＋6＝9知识点二：平行线分线段成比例定理的推论4．如图，已知AB ∥CD ，下列结论不成立的是( D ) A .AO OD ＝BO OC B .AO AD ＝OB BC C .OA OB ＝OD OC D .OA OB ＝BCAD第4题图 第5题图5．(易错题)如图，在三角形ABC 中，点E ，F 分别是AB ，AC 边上的点，且有EF ∥BC ，如果EB AB ＝45，则ACFC＝( C )A .94B .59C .54D .956．已知线段a ，b ，c ，求作线段x 使ax ＝bc ，下列每个图中的两条虚线都是平行线，则作法正确的是( A )7．如图，AD 是△ABC 的中线，AE ＝EF ＝FC ，BE 交AD 于点G ，则AG AD ＝__12__．8．已知，如图，EG ∥BC ，GF ∥DC ，AE ＝3，EB ＝2，AF ＝6，求AD 的值．解：∵EG ∥BC ，∴AE EB ＝AG GC ，又∵GF ∥DC ，∴AG GC ＝AF FD .∴AE EB ＝AF FD ，即32＝6FD .∴FD＝4，∴AD ＝109．如图，已知在△ABC 中，点D ，E ，F 分别是边AB ，AC ，BC 上的点，DE ∥BC ，EF ∥AB ，且AD ∶DB ＝3∶5，那么CF ∶CB 等于( A )A ．5∶8B ．3∶8C ．3∶5D ．2∶5第9题图 第10题图10．如图，已知直线l 1∥l 2∥l 3，直线AC 和DF 分别与l 1，l 2，l 3相交于点A ，B ，C 和点D ，E ，F ，如果AB ＝1，EF ＝3，那么下列各式中，正确的是( C )A ．BC ∶DE ＝3B ．BC ∶DE ＝1∶3 C ．BC ·DE ＝3D ．BC ·DE ＝1311．如图，l 1∥l 2∥l 3，AB BC ＝23，DF ＝15，则DE ＝__6__，EF ＝__9__．第11题图 第12题图12．如图，△ABC 中有菱形AMPN ，如果AM BM ＝12，那么BP BC ＝__23__．13．如图，已知AD ∥BE ∥CF ，它们依次交直线l 1，l 2于点A ，B ，C 和点D ，E ，F ，如果AB ＝6，BC ＝8，DF ＝21，求DE 的长．解：设DE 为x ，则EF ＝21－x ，∵AD ∥BE ∥CF ，∴AB BC ＝DE EF ，即68＝x21－x .解得x＝9，经检验，x ＝9是原分式方程的解，∴DE ＝914．如图，在Rt △ABC 中，∠C ＝90°，DE ⊥BC 于点E .AD ＝5，DB ＝10，CE ＝4.求DE ，AC 的长度．解：∵∠C ＝90°，DE ⊥BC ，∴DE ∥AC .∴BD AD ＝BE EC ，即105＝BE4.∴BE ＝8.由勾股定理可得DE ＝6.BC ＝BE ＋CE ＝8＋4＝12，AB ＝BD ＋AD ＝10＋5＝15，由勾股定理可得AC ＝915．如图，点E 是▱ABCD 的边AB 延长线上的一点，DE 交BC 于点F ，BE AB ＝13，EF ＝2，BF ＝1.5.求DF ，BC 的长．解：∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴BE AB ＝EF DF ，∴13＝2DF，∴DF ＝6，又∵CD ∥BE ，∴BF CF ＝EF DF ，∴1.5FC ＝26，∴CF ＝4.5，∴BC ＝FC ＋BF ＝616．如图，在△ABC 中，已知MN ∥BC ，DN ∥MC .小红同学由此得出了以下四个结论：①AN CN ＝AM AB ；②AD DM ＝AM MB ；③AM MB ＝AN NC ；④AD AM ＝ANAC.其中正确结论的个数为( C )A ．1个B ．2个C ．3个D ．4个17．如图，点E 为AC 的中点，点F 在AB 上，且AF ∶AB ＝2∶5，FE 与BC 的延长线交于点D ，求EF ∶ED 的值．解：作EG ∥BC 交AB 于点G ，∵点E 为AC 的中点，EG ∥BC ，∴AG ＝BG ，又∵AF ∶AB ＝2∶5，即AF ∶FB ＝2∶3，∴FG ∶BG ＝0.5∶2.5＝1∶5，又∵EG ∥BC ，∴FGBGEF＝ED，即EF∶ED＝1∶5。

平行线分线段成比例精选题40道一．选择题（共14小题）1．如图，在直角梯形ABCD 中，DC ∥AB ，∠DAB ＝90°，AC ⊥BC ，AC ＝BC ，∠ABC 的平分线分别交AD 、AC 于点E ，F ，则BF EF的值是（ ）A ．√2−1B ．2+√2C ．√2+1D ．√22．如图，在△ABC 中，DE ∥BC ，AD ＝6，DB ＝3，AE ＝4，则EC 的长为（ ）A ．1B ．2C ．3D ．43．如图，直线l 1∥l 2∥l 3，一等腰直角三角形ABC 的三个顶点A ，B ，C 分别在l 1，l 2，l 3上，∠ACB ＝90°，AC 交l 2于点D ，已知l 1与l 2的距离为1，l 2与l 3的距离为3，则AB BD的值为（ ）A ．4√25B ．√345C ．5√28D ．20√2234．如图所示，△ABC 中若DE ∥BC ，EF ∥AB ，则下列比例式正确的是（ ）A ．AD DB=DE BCB ．BF BC=EF ADC ．AE EC=BF FCD ．EFAB=DE BC5．如图，l 1∥l 2∥l 3，两条直线与这三条平行线分别交于点A 、B 、C 和D 、E 、F ．已知AB BC=32，则DE DF的值为（ ）A ．32B ．23C ．25D ．356．如图，在△ABC 中，D 在AC 边上，AD ：DC ＝1：2，O 是BD 的中点，连接AO 并延长交BC 于E ，则BE ：EC ＝（ ）A ．1：2B ．1：3C ．1：4D ．2：37．如图，直线l 1∥l 2∥l 3，直线AC 分别交l 1，l 2，l 3于点A ，B ，C ，直线DF 分别交l 1，l 2，l 3于点D ，E ，F ，AC 与DF 相交于点G ，且AG ＝2，GB ＝1，BC ＝5，则DE EF的值为（ ）A ．12B ．2C ．25D ．358．如图，直线l 1∥l 2∥l 3，直线AC 分别交l 1，l 2，l 3于点A ，B ，C ；直线DF 分别交l 1，l 2，l 3于点D ，E ，F ．AC 与DF 相交于点H ，且AH ＝2，HB ＝1，BC ＝5，则DE EF的值为（ ）A ．12B ．2C ．25D ．359．如图，已知直线a ∥b ∥c ，直线m 交直线a ，b ，c 于点A ，B ，C ，直线n 交直线a ，b ，c 于点D ，E ，F ，若AB BC=12，则DE EF=（ ）A ．13B ．12C ．23D ．110．如图，AD ∥BE ∥CF ，直线l 1、l 2与这三条平行线分别交于点A 、B 、C 和点D 、E 、F ．已知AB ＝1，BC ＝3，DE ＝2，则EF 的长为（ ）A ．4B ．5C ．6D ．811．如图，l 1∥l 2∥l 3，直线a ，b 与l 1、l 2、l 3分别相交于A 、B 、C 和点D 、E 、F ．若AB BC=23，DE ＝4，则EF 的长是（ ）A ．83B ．203C ．6D ．1012．如图，在平行四边形ABCD 中，AC 与BD 相交于点O ，E 是OD 的中点，连接AE 并延长交DC 于点F ，则DF ：FC ＝（ ）A ．1：4B ．1：3C ．1：2D ．1：113．如图，已知在△ABC 中，点D 、E 、F 分别是边AB 、AC 、BC 上的点，DE ∥BC ，EF ∥AB ，且AD ：DB ＝3：5，那么CF ：CB 等于（ ）A ．5：8B ．3：8C ．3：5D ．2：514．如图，点G 、F 分别是△BCD 的边BC 、CD 上的点，BD 的延长线与GF 的延长线相交于点A ，DE ∥BC 交GA 于点E ，则下列结论错误的是（ ）A ．AD BD=AE EGB ．DE CG=DF CFC ．AE AG=DE BCD ．AD AB=DE BG二．填空题（共17小题）15．如图，AB ∥CD ∥EF ，AF 与BE 相交于点G ，且AG ＝2，GD ＝1，DF ＝5，那么BC CE的值等于 ．16．如图，△ABC 的两条中线AD 和BE 相交于点G ，过点E 作EF ∥BC 交AD 于点F ，那么FG AG= ．17．将边长分别为2、3、5的三个正方形按图所示的方式排列，则图中阴影部分的面积为．18．如图，AD是△ABC的中线，E是AD上的一点，且AE=13AD，CE交AB于点F．若AF＝1.2cm，则AB＝cm．19．如图，等腰三角形ABC中，AB＝AC，P点在BC边上的高AD上，且APPD =12，BP的延长线交AC于E，若S△ABC＝10，则S△ABE＝；S△DEC＝．20．如图，AB∥CD，AD与BC交于点O，已知AB＝4，CD＝3，OD＝2，那么线段OA的长为．21．已知：△ABC 中，D 为BC 的中点，E 为AB 上一点，且BE =14AB ，F 为AC 上一点，且CF =25AC ，EF 交AD 于P ，则EP ：PF ＝ ．22．如图，已知：l 1∥l 2∥l 3，AB ＝6，DE ＝5，EF ＝7.5，则AC ＝ ．23．已知如图：CD ＝3BD ，AF ＝FD ，则AE ：AC ＝ ．24．如图，F 在BD 上，BC 、AD 相交于点E ，且AB ∥CD ∥EF ，若AB ＝2，CD ＝3，则EF ＝ ．25．如图，AB ∥CD ∥EF ．若AC CE=12，BD ＝5，则DF ＝ ．26．如图，△ABC 中，DE ∥BC ，G 为BC 上一点，连接AG 交DE 于F ，已知AD ＝3、AB ＝8、FG ＝4，则AG ＝ ．27．如图，直线l 1∥l 2∥l 3，直线AC 分别交l 1，l 2，l 3于点A ，B ，C ；直线DF 分别交l 1，l 2，l 3于点D ，E ，F ．AC 与DF 相交于点H ，且AH ＝2，HB ＝1，BC ＝5，则DE EF的值为 ．28．如图，体育兴趣小组选一名身高1.6m 的同学直立于旗杆影子的顶端处，其他人分为两部分，一部分同学测得该同学的影长为1.2m ，另一部分同学测得同一时刻旗杆影长为9m ，那么旗杆的高度是 m ．29．如图，a ∥b ∥c ，BC ＝1，DE ＝4.5，EF ＝1.5，则AC ＝ ．30．如图，AD 与BC 相交于点O ，如果AO DO=13，那么当BO CO的值是 时，AB ∥CD ．31．如图l 1∥l 2∥l 3，若AB BC=32，DF ＝10，则DE ＝ ．三．解答题（共9小题）32．如图，DE ∥BC ，EF ∥CG ，AD ：AB ＝1：3，AE ＝3． （1）求EC 的值；（2）求证：AD •AG ＝AF •AB ．33．阅读与计算，请阅读以下材料，并完成相应的问题．角平分线分线段成比例定理，如图1，在△ABC 中，AD 平分∠BAC ，则AB AC=BD CD．下面是这个定理的部分证明过程．证明：如图2，过C 作CE ∥DA ．交BA 的延长线于E ．… 任务：（1）请按照上面的证明思路，写出该证明的剩余部分；（2）填空：如图3，已知Rt △ABC 中，AB ＝3，BC ＝4，∠ABC ＝90°，AD 平分∠BAC ，则△ABD 的周长是 ．34．如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F．（1）如果AB＝6，BC＝8，DF＝21，求DE的长；（2）如果DE：DF＝2：5，AD＝9，CF＝14，求BE的长．35．如图，AD是△ABC的中线，E是AD上一点，AE：AD＝1：4，BE的延长线交AC于F，求AF：CF的值．36．如图，△ABC中∠A的平分线为AD，M为BC的中点，过点M作ME∥AD交BA的延长线于E，交AC于F．（1）求证：BE＝CF．（2）若∠BAC＝90°，BC＝10．AB＝6，求BE的长．37．如图，△ABC 中，DE ∥BC ，如果AD ＝2，DB ＝3，AE ＝4，求AC 的长．38．如图，D 是△ABC 的边AB 的中点，DE ∥BC ，CE ∥AB ，AC 与DE 相交于F ，求证：F 是DE 的中点．39．如图，在△ABC 中，点D 为BC 上一点，点P 在AD 上，过点P 作PM ∥AC 交AB 于点M ，作PN ∥AB 交AC 于点N ．（1）若点D 是BC 的中点，且AP ：PD ＝2：1，求AM ：AB 的值； （2）若点D 是BC 的中点，试证明AM AB=AN AC；（3）若点D 是BC 上任意一点，试证明AM AB+AN AC=AP AD．40．如图，已知：l 1∥l 2∥l 3，AB ＝2，BC ＝4，DF ＝12．求DE 的长．第11页（共11页）。

优秀学习资料 欢迎下载平行线分线段成比例专题练习题1．如图，若 DE//BC ，则下列式子不成立的是（）A.AD AE AD EC C.AD AE DE BD ECBDECB.ACABAC BCD.ACABAB2．如图，在△ ABC 中， DE ∥BC ， DE 分别与 AB 、AC 相交于点 D 、 E ，若 AD=4，DB=2，则 AE ︰ EC 的值为A. 0.5B. 2C.2 D. 3323．如图， l 1∥ l 2∥ l 3，根据“平行线分线段成比例定理” ，下列比例式中正确的是（ ）A.AD CE AD BC AB CD AD DFBCB.BEAFC.EFD.CEDFCDBCAD EBC4．如图所示，△ ABC 中若 DE ∥ BC ， EF ∥ AB ，则下列比例式正确的是（ ）A ．B ．C ．D ．5．如图，已知 AB//CD// EF ，AD: AF 3:5，BE 12 ， 那么 CE 的长等于（）．A．36B． 24C．15D．9 55226．如图，直线 l //l// l，直线 AC分别交 l， l， l3于点 A， B， C；直线 DF分别交 l， l， l3于点1231212 D， E， F ．AC与 DF相较于点H，且 AH=2， HB=1， BC=5，则的值为（）（A）1（B）2（C）2（D）257．如图， AD∥ BE∥ CF，直线 l 1、l 2这与三条平行线分别交于点A、B、C 和点 D、E、F．已知 AB=l ，BC=3，DE =2，则 EF' 的长为（）A．4B．5C．6D．88．如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点AB3DE A、B、C 和 D、E、F．已知2，则BC DF的值为（）A．3B ．2C ．2D ．3 23559．如图所示，△ ABC中， DE∥ BC，若AD1，则下列结论中正确的是（）DB 2A ．AE1 B． DE1 EC2BC2△ ADE 的周长1 △ ADE 的面积1 C ．=D ．=△ ABC 的周长 3△ ABC 的面积310．如图， 直线 l 1∥ l 2∥ l 3，直线 AC 分别交 l 1，l 2，l 3 于点 A ，B ，C ；直线 DF 分别交 l 1，l 2，l 3 于点 D ，E ，F ． AC 与 DF 相交于点 H ，且 AH=2， HB=1， BC=5，则DE的值为EF11．如图，已知：△ ABC 中， DE ∥ BC ， AD=3， DB=6， AE=2，则 EC=_______.12．如图，在△ ABC 中， DE ∥ BC ，分别交 AB ，AC 于点 D 、E ．若 AD=3，DB=2，BC=6，则 DE 的长为 ．13．如图，在△ABC中， DE∥BC，分别交A B， AC于点 D，E．若 AD =3， DB =2， BC =6，则 DE的长为．14．在平行四边形ABCD中， E 为 BC边上的一点．连结AE．A DBE C（1）若 AB=AE，求证：∠ DAE=∠ D；（2）若点 E 为 BC的中点，连接 BD，交 AE于 F，求 EF︰ FA的值．15．（本小题满分10 分）如图，已知B、C、E 三点在同一条直线上，△ABC与△ DCE都是等边三角形 . 其中线段 BD交 AC于点 G，线段 AE交 CD于点 F.求证：（ 1）△ ACE≌△ BCD；（2）AG AF. GC FE16．如图，在△ABC中，已知DE∥ BC， AD=4， DB=8， DE=3．（ 1）求的值；（ 2）求 BC的长．17．如图， a∥ b∥ c，（1）若 AC=6cm， EC=4cm， BD=8cm，则线段 DF 的长度是多少厘米？（2）若 AE： EC=5：2， DB=5cm，则线段 DF的长度是多少厘米？18．请阅读下面材料，并回答所提出的问题．三角形内角平分线定理：三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例．已知：如图，△ABC中， AD 是角平分线．求证：AB BD．AC DC证明：过C作 CE∥ DA，交 BA的延长线于E．∴D1= DE,D2 = D3．①AD 是角平分线，∴D1= D 2．3 E ．AC AE．②又 AD//CE，AB BD ．③AE DCAB BD ．AC DC（1）上述证明过程中，步骤①②③处的理由是什么？（写出两条即可）（2）用三角形内角平分线定理解答：已知，△ABC中， AD是角平分线， AB=7cm，AC=4cm，BC=6cm，求 BD的长；ACDB（ 3）我们知道如果两个三角形的高相等，那么它们面积的比就等于底的比．请你通过研究△ABD和△ ACD 面积的比来证明三角形内角平分线定理．19．如图，梯形ABCD中， DC//EF//AB ， AC交 EF于 G．若 AE=2ED，CF=2cm，那么 CB的长是多少？20．如图，在△ ABC中， D， E，F 分别是边A B，AC，BC上的点，且DE∥ BC，EF∥ AB，AD：DB=3：2，BC=20㎝，求 FC的长．优秀学习资料欢迎下载。

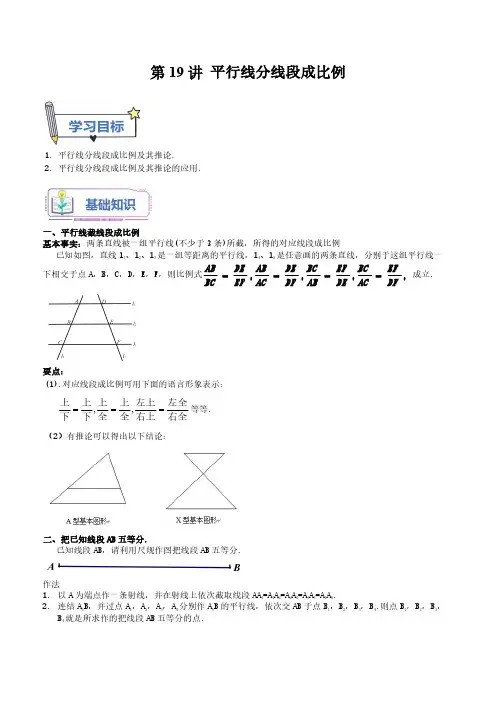
第19讲平行线分线段成比例1.平行线分线段成比例及其推论.2.平行线分线段成比例及其推论的应用.一、平行线截线段成比例基本事实：两条直线被一组平行线(不少于3条)所截，所得的对应线段成比例已知如图，直线l 1、l 2、l 3是一组等距离的平行线，l 4、l 5是任意画的两条直线，分别于这组平行线一下相交于点A，B，C，D，E，F，则比例式,,,,AB DE AB DE BC EF BC EFBC EF AC DF AB DE AC DF====成立.要点：(1).对应线段成比例可用下面的语言形象表示：右全左全右上左上全上全上下上下上===,,等等.（2）有推论可以得出以下结论：二、把已知线段AB 五等分.已知线段AB，请利用尺规作图把线段AB 五等分.作法1.以A 为端点作一条射线，并在射线上依次截取线段AA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5.2.连结A 5B，并过点A 1，A 2，A 3，A 4分别作A 5B 的平行线，依次交AB 于点B 1，B 2，B 3，B 4.则点B 1，B 2，B 3，B 4就是所求作的把线段AB 五等分的点.依据：实际上，过点A 作l∥A 5B，根据平行线分线段成比例的基本事实，就可以得到如下关系式11223344112233445.AB B B B B B B B BAA A A A A A A A A ====∵AA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5，∴AB 1=B 1B 2=B 2B 3=B 3B 4=B 4B,∴点B 1，B 2，B 3，B 4把线段AB 五等分.要点：在射线上截取等长的线段时使用的作图工具是圆规,不能使用直尺进行量取,尺规作图中的直尺是没有刻度的,它的用途是画线或者连线.考点1：A 字三角形例1．如图，在△ABC 中，DE ∥BC ，AE ＝4，EC ＝6，AB ＝5，则BD 的长为（）A ．1B ．2C ．3D ．4【答案】C【分析】根据平行线分线段成比例定理列出比例式，把已知数据代入计算即可．【解析】解：D E B C ∥，∴AD AEDB EC=，即546BD BD -=，解得：3BD =，故选：C ．【点睛】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．例2．如图，在ABC 中，点D 、E 分别在AB 、AC 上，连接DE ，432DE BC AE AD CE ===∥，，，，A．1.5B【答案】A【分析】根据平行线分线段成比例得出∥【解析】解：∵DE BC例A．1B．2例A．3【答案】B【分析】利用平行线分线段成比例定理得到【解析】解：∵∴AD AEDB EC=，即∴4AE=．故选：B．【点睛】本题考查了平行线分线段成比例定理．掌握平行线分线段成比例定理是解答本题的关键．例5．如图，在【答案】12【分析】利用平行线分线段成比例定理进行求解即可．例【答案】8例例【答案】10【分析】根据平行线分线段成比例可得【解析】解：∵DE∥例例A．3【答案】B【分析】由平行线分线段成比例定理，得到解决问题．【解析】解：∵AB∴BO AO CO DO=；∵AO=2，CO=6，∴362DO =，解得：DO=4，故选B.【点睛】本题考查平行线分线段成比例，解题的关键是读懂题意，掌握平行线分线段成比例例OD=A．4【答案】B【分析】根据平行线分线段成比例定理即可求解．例AD=5例【答案】8【分析】根据平行线分线段成比例定理得【解析】解：∵AB CD ∥，∴AO OBOD OC=，∵496AO BC OC ===，，，例正确的是（例错误的是A．AE AF=B．AE=例AM；②A．1个【答案】C【解析】①∵MN∥再由（1）得AD：例OD OC例1例中正确的是（A ．AC CD AE EF =B ．CD 【答案】C【分析】根据平行线分线段成比例逐项判断即可．【解析】∵123l l l ∥∥，∴AC BD AE BF=，AC BD CE DF =，所以A ，D ，不正确；C 正确．B 中的线段不是对应线段，所以不正确例A．AC CE BD DF⋅=⋅C．AC DF CE BD⋅=⋅【答案】C【分析】根据平行线分线段成比例定理得到断．【解析】解：∵AB//CD//∴AC BDCE DF=，AC BDAE BF=∴AC•DF=BD•CE；AC•BF故选：C．【点睛】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．考点6：X型平行线分线段成比例例1DG例DF=15A．3【答案】B【分析】根据平行线分线段成比例定理列出比例式，计算即可．【解析】解：∵a∥b∥2AB DE例作法是（．．．．例．．．D．【答案】C【分析】根据平行线分线段成比例定理进行求解即可【解析】解：bcxa=，即ax bc=MN PQ∥，，即ac bx=，故此选项不符合题意；MN PQ∥，，故此选项不符合题意；例错误的是（A．AF AEBF ED=B．【答案】D【分析】根据平行线分线段成比例定理一一判断即可．【解析】解：对A、B选项．∵∴EF AC∥，∴AF AEBF ED=，BF BEAF EC=，故C．∵AE AFAD AB=，BE BFBC AB=∴AE BE AF BF AD BC AB AB+=+=D．∵AF CEBF EB=，而DE≠∴AF CEBF ED≠，故D错误，不符合题意．故选：D．【点睛】本题主要考查平行线分线段成比例定理，解题的关键是熟练掌握平行线分线段成比例定理，属于例说法不正确的是（例列结论错误的是（A ．AB DE AF EA =B ．AE AD 【答案】D【分析】根据平行四边形的性质得出例定理逐项进行判断即可．【解析】解：A ．∵四边形ABCD ∴CD AB ∥，AD BC ∥，AD ∵CD AB ∥，∴CD DE AF EA=，∵AB CD =，∴AB DE AF EA =，故A 正确，不符合题意；B ．∵AE BC ∥，∴AE AF BC FB=，∵AD BC =，例平行线交A ．AD AE AB AC =【答案】C【分析】利用平行线分线段成比例，逐一进行判断即可；【解析】A 、∵DE ∥B 、∵DE BC ∥，∴C 、∵EF AB ∥，∴D 、∵DE BC ∥，∴∵EF AB ∥，∴BF BC ∴BF AD BC AB=；选项正确，不符合题意；故选C ．【点睛】本题考查平行线分线段成比例．熟练掌握平行线分线段对应成比例，是解题的关键．例29．如图， 交BC 于H ，则下列结论错误的是（A ．BH AG BC AD =B ．EG AG CD AD =【答案】D【分析】根据平行线分线段成比例定理、中点定义及相似三角形对应边成比例逐项判断即可得到答案．【解析】解：A 、 EF BC ∥，∴由平行线分线段成比例定理可得AE AB EF BC ∥，AEF B ∠∠∴=，BAC BAC ∠=∠Q ，AEF ABC ∴△∽△，∴EF AE BC AB =，即EF AE BC AB=， EF BC ∥，FH AB ∥，∴由平行四边形的判定定理得到四边形∴BH AG BC AD=，故该选项正确，不符合题意；B 、 EF BC ∥，AEF B ∠∠∴=，BAC BAC ∠=∠Q ，∽△△AGF ADC ∴，∴GF AG DC AD=， G 为EF 的中点，EG GF ∴=，一、单选题A ．25B ．12【答案】A【分析】利用平行线分线段成比例定理的推论得出【解析】解：∵ABC 中，DE ∴AE AD AC AB =，∵23AD BD ==，∴22235AE AD AC AD BD ===++，故选：A ．【点睛】本题考查平行线分线段成比例定理的推论，解题关键是牢记（或两边的延长线）所得对应线段成比例3．（2021·四川甘孜·统考中考真题）如图，直线和点D 、E 、F ，若:AB BCA．2B．3C【答案】D【分析】根据平行线分线段成比例定理得出比例式，代入已知线段得长度求解即可．二、填空题7．（2021·江苏扬州·统考中考真题）如图，在Rt ABC 中，90ACB ∠=︒，点D 是AB 的中点，过点D 作DE BC ⊥，【答案】3【分析】根据直角三角形的性质得到即可求出DE ．【解析】解：∵∠ACB =90°，点∴AB =2CD =10，∵BC =8，∴AC =22AB BC -=6，∵DE ⊥BC ，AC ⊥BC ，∴DE ∥AC ，∴12DE BD AC AB ==，即162DE BD AB ==三、解答题∴MN＝NR＝NF′+RF′＝NF′+MI′，∴△MNG′的周长＝MN+MG′+NG′＝MG′+MI′+NG′+F′R＝2I′G′＝4．【点睛】本题考查的是四边形综合题，涉及了矩形的性质、正方形的性质、平行线等分线段定理、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用旋转法添加辅助线，构造全等三角形解决问题，属于中考压轴题．A．1 3【答案】C【解析】解：∵∴2 AE AD EC DB==故选C．【点睛】考点：平行线分线段成比例．2．ABC中，直线A．AD CE DB AE=【答案】C【分析】作出图像证明△【点睛】本题考查了相似三角形的判定和性质键.3．如图，已知：AB 、CD 相交于点A ．23AO OB =，DO OCA．1 3【答案】A【分析】先由AB BC=【解析】解：∵AB BC∴13 ABAC=，∵a∥b∥c，∴13 DE ABDF AC==．故选：A．3AE AD BD BF 25二、填空题【答案】2 5【答案】CD FD AE【答案】12【分析】根据平行线分线段成比例定理列出比例式，分别求出【解析】∵DE ∥FG ∥BC ，∴AE ：EG ：GC=AD ：DF ：FB=2∵EG=4，816,33AE GC ∴==，12AC AE EG GC ∴=++=．故答案为：12．【点睛】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．14．如图，在ABC 中，AD 是中线，则AF =____________．1三、解答题19．如图，在△ABC中，DE∥BC，分别与AB、AC交于点D、E，若AE：EC=2：3，DB-AD=3，求AD 和DB的长．【答案】AD和DB【分析】首先由在(1)AB ACDB EC=(2)AD AEAB AC=．【答案】(1)见解析(2)见解析【分析】（1）根据成比例线段的性质求解即可；（2）根据成比例线段的性质求解即可．【解析】（1）证明：∵∴AD DB AE EC DB EC++=∵34AD AE DB CE ==，∴DE BC ∥；（2）6CE AC AE =-=∴DE BC ∥；【答案】3 5【分析】根据平行线分线段成比例定理列比例式，代入计算即可．【解析】解：∵1l∥【答案】见解析【分析】取AC 的中点M 12AC AB =，即可解答．【解析】解：证明：取AC E ，M ，分别是BC ，EM ∴是ABC 的中位线，12EM AB ∴=，又14AF =【点睛】本题考查了三角形中位线的性质，平行线分线段成比例，比较简单，解题的关键是根据中点判断出中位线，三角形中位线平行且等于第三边的一半．25．如图，ABCD Y 中，过【答案】见解析【分析】根据平行四边形的性质可得【解析】解：∵四边形∴AD CG ，CD AB ∥∴DE AE EG CE =，EF AE DE CE =∴DE EF EG DE=，即2DE =【点睛】本题主要考查了平行四边形的性质，平行线分线段成比例，解题的关键是掌握平行线分线段成比例定理指的是两条直线被一组平行线26．如图，P 为ABCD Y【答案】见解析【分析】根据平行四边形的性质得到PI PD PS PR PB PQ==，由此即可证明【解析】证明： 四边形ABCD AB CD AD BC ∴∥，∥，RB DI SD BQ ∴∥，∥，∴PI PD PD PSPR PB PB PQ ==，∴PI PD PS PR PB PQ==，PQ PI PR PS ∴⋅=⋅．【点睛】本题主要考查了平行线分线段成比例定理，平行四边形的性质，熟知平行线分线段成比例定理是解题的关键．27．如图，已知菱形ABCD 中，AC 交EF 于点M ，点N 在AC (1)求证：BCE FCM ∠=∠(2)若3BC =，1BE =，求【答案】(1)见详解(2)13【分析】（1）根据菱形的性质及等边三角形的判定先证明即可得证；（2）连接FN ，由（1）知ABC 是等边三角形，先证明CBE CAF ≌，即有BE AF =，根据菱形的性质得到AD BC ∥，根据平行线的性质得到==60FAN BCA ∠∠︒，利用SAS 易证SAS ABN ACF ≌（），根据全等三角形的性质得到=EF BN ，推出四边形BNFE 是平行四边形，根据平行线四边形的性质得出EF BN ∥，即可得出答案．【解析】（1）∵四边形ABCD 是菱形，∴BA BC =，∵=60ABC ∠︒，∴ABC 是等边三角形，∴=60ACB ∠︒，=AC BC ，∵ECF △是等边三角形，∴=EC CF ，==60ECF ACB ∠∠︒，∴=BCE ACF ∠∠，∴=BCE FCM ∠∠；（2）连接FN ，由（1）知ABC 是等边三角形，即=60BAC ∠︒，===3AB BC AC ，在CBE △和CAF V 中，BC AC BCE ACF EC CF =⎧⎪∠=∠⎨⎪=⎩，∴()SAS CBE CAF ≌，∴BE AF =，∵四边形ABCD 是菱形，∴AD BC ∥，∴==60FAN BCA ∠∠︒，即有=60CAD ∠︒，∵=AN BE ，(1)如图1，若点E与点C重合，且5AF=，求AD的长；(2)如图2，连接FH，求证：AFB HFB∠=∠；。

4.2平行线分线段成比例【十大题型】【北师大版】【题型1 由平行线分线段成比例判断比例式正误】 (1)【题型2 平行线分线段成比例之“A”字型求值】 (4)【题型3 平行线分线段成比例之“X”字型求值】..................................................................................................7【题型4 平行线分线段成比例之“8”字型求值】...................................................................................................9【题型5 平行线分线段成比例之“#”字型求值】. (13)【题型6 平行线分线段成比例与三角形的中位线的综合】 (15)【题型7 多次利用平行线分线段成比例求值】 (21)【题型8 平行线分线段成比例与三角形的重心的综合】 (25)【题型9 平行线分线段成比例的常用辅助线之作平行线】 (28)【题型10 平行线分线段成比例的常用辅助线之作垂线】 (33)【知识点 平行线分线段成比例定理】两条直线被三条平行线所截，所得的对应线段成比例，简称为平行线分线段成比例定理．如图：如果123////l l l ，则AB DE BC EF =，AB DE AC DF =，BC EF AC DF=．A D B E C F 1l 2l 3l 1l 2l 3l 【小结】若将所截出的小线段位置靠上的（如AB ）称为上，位置靠下的称为下，两条线段合成的线段称为全，则可以形象的表示为，，．【题型1 由平行线分线段成比例判断比例式正误】【例1】（2023春·广西梧州·九年级校考期中）如图，在△ABC 中，点D ，E ，F 分别在AB ，AC ，BC 边上，DE ∥BC ，EF ∥AB ，则下列结论正确的是（ ）A ．AD DB =AE AC B ．AD DB =BF FC C ．AD DB =FC BF D ．AD DB =FCBC =上上下下=上上全全=下下全全【答案】B【分析】根据平行线分线段成比例定理，在两组平行线里面，通过AD DB =AE EC ，AE EC =BF FC ，逐项判断，得出结论．【详解】∵DE//BC ，∴AD DB =AE EC .∵EF//AB ，∴AE EC =BF FC ，∴AD DB =AE EC =BF FC ，∴AD DB =BF FC .故选：B ．【点睛】本题主要考查了平行线分线段成比例定理及其应用问题，解题的关键是找准对应线段，准确列出比例式，推理论证．【变式1-1】（2023春·湖南娄底·九年级统考期中）如图，已知AB∥CD∥EF ，那么下列结论正确的是（ ）．A ．AB EF = AD DFB ．DF AD = BC CE C ．AD AF = BE BC D ．AD DF = BC CE 【答案】D 【分析】根据平行线分线段成比例定理判断即可．【详解】解：∵AB∥CD∥EF ，∴AD DF = BC CE ，故选：D ．【点睛】本题考查平行线分线段成比例定理，解题的关键是掌握平行线分线段成比例定理，属于中考常考题型．【变式1-2】（2023春·湖南娄底·九年级校联考期末）如图，已知AB∥CD∥EF，AC:AE=3:5，那么下列结论正确的是（）A．BD:DF=2:3B．AB:CD=2:3C．CD:EF=3:5D．DF:BF=2:5【答案】D【分析】根据平行线分线段成比例定理判断即可．【详解】解：∵AC:AE=3:5，∵AC:EC=3:2,CE:EA=2:5∵AB∥CD∥EF，，∴BD:DF=AC:EC=3:2，故A错误；DF:BF=CE:EA=2:5，故D正确；根据平行线分线段成比例定理无法判定B，C，故选：D．【点睛】本题考查了平行线分线段成比例定理，正确理解平行线分线段成比例定理是解本题的关键．【变式1-3】（2023春·山西晋城·九年级统考期末）如图，在△ABC中，点D在AB边上，点E在BC边上，过点D作DG//BC，交AC于点G，过点E作EH//AB，交AC于点H，DG的延长线与EH的延长线交于点F，则下列式子一定正确的是（）A．ADDB =DGBCB．GFEC=HCGHC．FHAD=GHAGD．HEAB=ECBE【答案】C【分析】根据平行线分线段成比例的性质进行逐一判断即可．【详解】解：∵DG//BC，∴AD AB =DGBC，故A选项错误；∵DG//BC，∴GF EC =GHHC，故B选项错误；∵EH//AB，∴FH AD =GHAG，故C选项正确；∵EH//AB，∴HE AB =ECBC，故D选项错误．故选：C．【点睛】此题主要考查线段的比，解题的关键是熟知平行线分线段成比例的性质．【题型2平行线分线段成比例之“A”字型求值】【例2】（2023春·河北保定·九年级统考期末）如图，点A，B在格点上，若BC=23，则AC的长为（）A．1B．43C．2D．3【答案】B【分析】根据平行线分线段成比例可得ACBC =AEDE=2，然后代入数据计算即可．【详解】解：如图，由题意，知CE∥BD，AEAD=2，∴AC BC =AEDE=2，又BC=23，∴AC=43．故选：B．【点睛】本题考查了平行线分线段成比例定理，求出ACBC=2，利用数形结合的思想解答是解题的关键．【变式2-1】（2023春·广西百色·九年级统考期末）如图，在△ABC中，点D、E分别在AB、AC上，DE∥BC．若AD=6，DB=3，则AEAC的值为（）A．23B．32C．34D．2【答案】A【分析】先求出AB，由平行线分线段成比例定理得出比例式，即可得出结果．【详解】∵AD=6，DB=3，∴AB=AD+DB=9，∵DE∥BC，∴AE AC =ADAB=69=23；故选：A．【点睛】本题考查了平行线分线段成比例定理；熟记平行线分线段成比例定理是解决问题的关键．【变式2-2】（2023春·四川成都·九年级四川省成都市七中育才学校校考期中）已知线段a、b、c，若求作线段x，使a∶b＝c∶x，则以下作图正确的是（）A．B．C．D．【答案】D【分析】根据平行线分线段成比例，逐项分析即可【详解】A.根据平行线分线段成比例，可得a:b=x:c，故该选项不符合题意；B.根据平行线分线段成比例，可得a:x=b:c，故该选项不符合题意；C.根据平行线分线段成比例，可得a:c=x:b，故该选项不符合题意；D.根据平行线分线段成比例，可得a:c=b:x，即a:b=c:x，故该选项符合题意；故选D【点睛】本题考查了平行线分线段成比例，掌握平行线分线段成比例是解题的关键．【变式2-3】（2023春·九年级课时练习）如图，在△ABC中，EF∥CD，DE∥BC．（1）求证：AF：FD＝AD：DB；（2）若AB＝30，AD：BD＝2：1，请直接写出DF的长．【答案】（1）见详解；（2）203．【分析】（1）利用平行线分线段成比例定理，由EF∥CD得到AF：FD=AE：EC，由DE∥BC得到AE：EC=AD：DB，再进行等量代换即可求解；（2）根据比例的性质得到AD=20，根据（1）结论得到AF：FD=2:1，即可求出DF．【详解】解：（1）证明：∵EF∥CD，∴AF：FD=AE：EC，∵DE∥BC，∴AE：EC=AD：DB，∴AF：FD＝AD：DB；（2）∵AB＝30，AD：BD＝2：1，∴AD=AB×23=30×23=20，∵AF：FD＝AD：DB，∴AF：FD=2:1，∴DF=AD×13=20×13=203【点睛】本题考查了平行线分线段成比例定理，熟知平行线分线段成比例定理“两直线被一组平行线所截，所得的对应线段成比例”是解题关键．【题型3 平行线分线段成比例之“X”字型求值】【例3】（2023春·吉林长春·九年级统考期末）如图 ，AB ∥CD ∥EF ，AF 与BE 相交于点G ，且AG ＝4，GD ＝2，DF ＝8，那么BC CE 的值等于 ．【答案】34【分析】根据平行线分线段成比例定理列出比例式，把已知数据代入计算即可．【详解】解：∵AB//CD//EF ，∴BC CE =AD DF =AG +GD DF ,∵AG =4,GD =2,DF =8,∴BC CE =AD DF =AG +GD DF =4+28=34,故答案为：34.【点睛】本题主要考查了平行线分线段成比例定理，灵活运用定理，找准对应关系是解此题的关键．【变式3-1】（2023春·浙江金华·九年级校联考阶段练习）如图：AB ∥CD ∥EF ，AD:DF =3:1，BE =16，那么CE 的长为（ ）A ．4B ．12C ．163D ．6【答案】A【分析】利用平行线分线段成比例定理求解即可．【详解】解：∵AB ∥CD ∥EF ，∴BC CE =ADDF=31，∴CE=14BC=4．故选：A．【点睛】本题考查平行线分线段成比例定理，解题的关键是掌握平行线分线段成比例定理．【变式3-2】（2023春·安徽六安·九年级校考期末）如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F，若ABBC =43，则DEDF的值为（）A．47B．37C．74D．43【答案】A【分析】根据平行线分线段成比例定理得到ABBC =DEEF=43，根据合比性质即得．【详解】∵l1∥l2∥l3，∴ABBC =DEEF=43，∴DEDF =47．故选：A．【点睛】本题主要考查了平行线分线段，解决问题的关键是熟练掌握平行线分线段成比例定理，合比性质．【变式3-3】（2023春·贵州铜仁·九年级统考期中）已知三条互相平行的直线l1，l2，l3分别截直线l4于点A，B，C，截直线l5于点D，E，F，直线l4与l5相交于点O，且AB=BC=EF=8，EO=2．(1)求DE的长；(2)求OB的长．【答案】(1)245【分析】（1）由l1∥l2∥l3，推出DEEF =ABCB，即可求解；（2）由BE∥AD，推出OBAB =OEDE，即可求解．【详解】（1）解：∵l1∥l2∥l3，∴DE EF =ABCB，∴DE8=∴DE=245；（2）解：∵BE∥AD，∴OB AB =OEDE，=2245，∴OB【点睛】本题考查平行线分线段成比例定理，解题的关键是掌握平行线分线段成比例定理，属于中考常考题型．【题型4平行线分线段成比例之“8”字型求值】【例4】（2023春·陕西西安·九年级高新一中校考阶段练习）如图，在平行四边形ABCD中，∠ABC的平分线BF分别与AC、AD交于点E、F，AB=3，FD=2，则EFFB的值为（）A．25B．38C．37D．35【答案】B【分析】根据平行四边形的性质证得AD∥BC，AD=BC，再根据角平分线的定义和平行线的性质以及等角对等边证得AF=AB=3，BC=5，再根据平行线分线段成比例和比例性质求解即可．【详解】解：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠AFB=∠CBF，∵BF平分∠ABC，∴∠ABF=∠CBF，∴∠ABF=∠AFB，∴AF=AB=3，又FD=2，∴BC=AD=AF+FD=5，∵AD∥BC，∴EF BE =AFBC=35，∴EF FB =38，故选：B．【点睛】本题考查平行四边形的性质、平行线的性质、角平分线的定义、等腰三角形的判定、平行线分线段成比例定理、比例性质等知识，熟练掌握相关知识的联系与运用是解答的关键．【变式4-1】（2023春·上海静安·九年级校考期中）已知ax=bc，求作x，那么下列作图正确的是（）A．B．C．D．【答案】C【分析】根据平行线分线段成比例结合题意，依次对各选项进行判断即可．【详解】∵ax=bc，∴a b =cx或ac=bx．A．作出的为ab=B．该情况无法作图，故不符合题意；C．作出的为ab =cx，故符合题意；D．作出的为ax =cb，故不符合题意；故选C．【点睛】本题考查平行线分线段成比例定理，第四比例线段的作法．熟练掌握定理是解题的关键．【变式4-2】（2023春·全国·九年级专题练习）如图，l1∥l2，AF：BF＝2：5，BC：CD＝4：1，则AE：EC 的值为（）A．5：2B．1：4C．2：1D．3：2【答案】C【分析】根据l1∥l2，可得△AFG∽△BFD，进而得出AGBD ＝AFBF＝25，AEEC＝AGCD，求出AG＝25BD，CD＝15BD，再求出AGCD即可．【详解】解：∵l1∥l2，∴△AFG∽△BFD∴AG BD ＝AF BF ，∵AF ：BF ＝2：5，∴AG BD ＝25，即AG ＝25BD ，∵BC ：CD ＝4：1，BC +CD ＝BD ，∴CD ＝15BD ，∴AG CD ＝25BD 15BD ＝21，∵l 1∥l 2，∴△AGE ∽△CDE ，∴AE EC ＝AG CD ＝21，故选：C ．【点睛】本题考查了相似三角形的性质与判定，掌握相似三角形的性质与判定是解题的关键．【变式4-3】（2023春·山东淄博·九年级统考期末）如图，AB ，CD 相交于点E ，且AC ∥EF ∥DB ，点C ，F ，B 在同一条直线上，已知AC ＝p ，EF ＝r ，DB ＝q ，则p ，q ，r 之间满足的数量关系式是（ ）A ．1r +1q =1pB ．1p +1q =2rC ．1p +1q =1rD ．1q +1r =2p 【答案】C 【分析】根据平行线分线段成比例，可证得EF AC =BF BC ，EF BD =CF BC ，两式相加即可得出结论．【详解】解：∵AC//EF ，∴ EF AC =BF BC ，∵EF//DB ，∴ EF BD =CF BC ，∴EFAC +EFBD=BFBC+CFBC=BF CFBC=BCBC=1，即rp+rq=1，∴1p +1q=1r．故选：C．【点睛】本题主要考查了平行线分线段成比例定理的运用，通过平行线分线段成比例定理得出线段的比是解题的关键．【题型5平行线分线段成比例之“#”字型求值】【例5】（2023春·全国·九年级期末）如图，直线a∥b∥c，点A，B在直线a上，点C，D在直线c上，线段AC，BD分别交直线b于点E，F，则下列线段的比与AEAC一定相等的是（）A．CEAC B．BFBDC．BFFDD．ABCD【答案】B【分析】根据平行线分线段成比例，即可得到BFBD =AEAC.【详解】解：∵a∥b∥c，∴BF FD =AEEC，∴BF BD =AEAC；故选择：B.【点睛】本题考查了平行线分线段成比例定理，掌握三条平行线截两条直线，所得的对应线段成比例是解题的关键．【变式5-1】（2023春·河北保定·九年级校考期末）如图，已知直线a∥b∥c，直线m，n与直线a，b，c分别交于点A，C，E，B，D，F，若AC＝4，CE＝6，BF＝152，则BD的值是．【答案】3【分析】根据平行线分线段成比例定理列出比例式，把已知数据代入计算即可．【详解】解：∵a∥b∥c，∴AC AE =BDBF，即446=BD152，解得：BD=3，故答案为：3．【点睛】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．【变式5-2】（2023春·上海青浦·九年级校考阶段练习）如图，梯形ABCD中，AD∥BC∥EF，AB:EB=3:1，DF=8，则FC=．【答案】4【分析】根据平行线分线段成比例定理列出比例式，再根据比例的基本性质进行计算．【详解】解：∵AB:EB=3:1∴AE:EB=2:1∵AD∥BC∥EF，AE:EB=2:1，DF=8，∴DFFC =AEBE=2，∴FC=4,故答案为：4．【点睛】此题考查了平行线分线段成比例定理和比例的基本性质．【变式5-3】（2023春·山西长治·九年级统考期末）如图，直线a，b，c分别与直线m，n交于点A，D，B，E，C，F．已知直线a∥b∥c，AB=2，BC=3，则DEDF的值为（）A ．23B ．32C ．25D ．35【答案】C【分析】根据平行线分线段成比例，即可进行解答．【详解】解：∵a∥b∥c ，∴AB AC =DE DF ，∵AB =2，BC =3，∴AC =AB +BC =5，∴DE DF =25，故选：C ．【点睛】本题主要考查了平行线分线段成比例，解题的关键是掌握：两条直线被第一组平行线所截的线段成比例．【题型6 平行线分线段成比例与三角形的中位线的综合】【例6】（2023·四川南充·校联考三模）如图， DE 是△ABC 的中位线， F 是CE 的中点，射线DF 与BE 交于点O ，与BC 的延长线交于点G ．下列结论：①OB =2OE ；②OD =OF ； ③DE BG =CF AF ；④S △ADE =12S 四边形OBCF ，正确的有 ．(填序号．)【答案】②③【分析】由题意可知，DE =12BC,DE//BC,DE =GC ，根据平行截线求相关线段的长或比值可判断①；由题意得出OG =3OD 与FD =FG 联立可得2OF =2OD ，由此可判断②；由平行截线求相关线段的长或比值及等量代换可判断③；连接BF ．设S △ODE =1，根据面积可判断④．【详解】解：∵DE是△ABC的中位线，∴DE//BC,DE=12 BC∴∠EDF=∠CGF∵F是CE的中点，∴EF=CF又∵∠EFD=∠CFG ∴△DEF≅△GCF ∴DE=CG,DF=FG ①∵DE//BC∴OEOB =DEGB=13，∴OB=3OE．∴①错误②∵DE//BG∴OD OG=13∴OG=3OD又∵FD=FG，∴由两式相减，得OF=2OD−OF ∴2OF=2OD．∴OF=OD．∴②正确③∵DE//BG,DE=12BC,DE=CG∴DEBG =13∵AE=CE,CF=EF∴CFAF=13∴DE BG =CFAF∴③正确④连接BF．设S△ODE=1，可得其他三角形面积如图∴S△ADE=47S四边形OBCF，∴④错误故答案为：②③．【点睛】本题考查了平行截线求相关线段的长或比值、全等三角形的判定及性质、三角形中位线的性质，熟练掌握性质定理是解题的关键．【变式6-1】（2023春·河北石家庄·九年级石家庄市第四十一中学校考期末）如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于点N，则NM：MC等于（ ）A．1：2B．1：3C．1：4D．1：5【答案】B【详解】∵DE是△ABC的中位线，∴DE∥BC，DE=12BC，∵M是DE的中∴DM=ME=14BC，∴MN NC =DMBC=14，∴MN MC =13【变式6-2】（2023春·浙江宁波·九年级统考期中）如图，DE、NM分别是△ABC、△ADE的中位线，NM的延长线交BC于点F，则S△DMN：S四边形MFCE等于（）A ．1：5B ．1：4C ．2：5D ．2：7【答案】B 【分析】过N 作NH ⊥DE 于H ，过A 作AP ⊥BC 于P 交DE 于G ，得到NM ∥AG ，根据三角形中位线定理得到DE ∥BC ，得到AG ＝PG ，求得NM ＝12AG ＝12PG ，根据三角形和平行四边形的面积即可得到结论．【详解】解：过N 作NH ⊥DE 于H ，过A 作AP ⊥BC 于P 交DE 于G ，∴NM ∥AG ，∵DE 是△ABC 的中位线，∴DE ∥BC ，∴AG ＝PG ，∵M 是DE 的中点，∴DM ＝ME ＝12DE ，∵NM ∥AG ，AN ＝DN ，∴NM AG ＝DN AD ＝12，∴NM ＝12AG ＝12PG ，∵DM ＝ME ，∴S △DMN ：S 四边形MFCE ＝12DM⋅NH EM⋅PG ＝12DM⋅NH 2DM⋅NM ＝1：4．故选：B ．【点睛】本题考查了三角形中位线定理及平行线分线段成比例定理．本题关键是找准比例关系求解．【变式6-3】（2023·山西运城·统考二模）请阅读下列材料，非完成相应的任务．利用辅助平行线求线段的比三角形的中位线定理是三角形的中位线平行于第三边，且等于第三边的一半．平行线分线段成比例定理是两条平行线被两条直线所截，截得的线段对应成比例．有些几何题，若题中出现了平行线，我们可以直接利用这两个定理求出两线段的比值，而有些几何题，题中没有平行线这样的条件，那么我们可以通过作辅助平行线，然后再利用这两个定理加以解决．举例：如图1，AD是△ABC的中线，AE:AD=1:5，BE的延长线交AC于点F．求AFCF的值．下面是该题的部分解题过程：解：如图2，过点D作DH∥BF交AC于点H．∵AD是△ABC的中线，∴BD=DC．∵DH∥BF，∴FH CH =BDCD，∴CH=FH．∵EF∥DH，…任务：(1)请补充材料中剩余部分的解答过程．(2)上述解题过程主要用的数学思想是______．（单选）A．方程思想B．转化思想C．分类思想D．整体思想(3)请你换一种思路求AFCF的值，直接写出辅助线的作法即可．【答案】(1)见解析(2)B(3)见解析【分析】（1）通过过点D作DH∥BF交AC于点H．根据△ABC的中线的定义即可得到BD=DC，根据平行线分线段成比例即可得到FHCH =BDCD与AEAD=AFAH，根据AE:AD=1:5即可得到AF:FH=1:4，进一步即可求出答案；Ｄ（2）由上述解题过程即可得到求AFCF 的值转化为了求AFFH与FHCH的值，通过转化即可求出答案，即可判断出答案；（3）通过过点D作DM∥AC交BE于点M，根据△ABC的中线的定义即可得到BD=DC，进一步得到BDBC =12，根据平行线分线段成比例即可得到DMCM =BDBC与AEED=AFDM，根据AEAD=15，即可得到AEED=14，进一步即可求出答案．【详解】（1）∴AEAD =AFAH，∵AE:AD=1:5，∴AF:AH=1:5，∴AF:FH=1:4，∵FH=CH，∴AF CF =18（2）上述解题过程主要用的数学思想是转化思想故选B（3）解：如图，过点D作DM∥AC交BF于点M．∵AD是△ABC的中线，∴BD=DC=12BC，∴BDBC =12，∵DM∥AC，∴DM CF =BDBC=12，∵AF∥DM，∴AE DE =AFDM，∵AE AD =15，∴AE ED =14，∴AF DM =14，∴AF CF =18【点睛】本题考查利用辅助平行线求线段的比，作出辅助线，利用平行线分线段成比例进行转化是解题关键．【题型7多次利用平行线分线段成比例求值】【例7】（2023春·陕西咸阳·九年级统考期中）如图，AB=AC，AD⊥BC于点D，M是AD的中点，CM交AB 于点P，DN∥CP．若AB=6cm，求PN的长．【答案】PN=2cm【分析】证明BD=DC，结合DN∥CM，可得BN=NP，AP=PN，从而可得答案．【详解】解：∵AB=AC，AD⊥BC，∴BD=DC，又∵DN∥CM，∴BN PN =BD DC =1，∴BN =NP ，∵点M 是线段AD 的中点，DN∥CM ，∴AP PN =AM MD =1，∴AP =PN ，∴PN =13AB ，∵AB =6cm ，∴PN =13AB =13×6=2(cm)．【点睛】本题考查的是三角形的中位线的性质，等腰三角形的性质，平行线分线段成比例的应用，熟记平行线分线段成比例并灵活运用是解本题的关键．【变式7-1】（2023春·陕西咸阳·九年级统考期中）如图，在△ABC 和△ACG 中，D 、E 、F 分别在线段AB 、AC 、AG 上，连接DE 、EF ，DE ∥BC ，EF ∥CG ，AD AB =13,AF =3，求AG 的长．【答案】9【分析】由DE ∥BC,EF ∥CG 可得AD AB =AE AC ,AF AG =AE AC ,从而可得AD AB =AE AC ,再由AD AB =13,AF =3可得结果．【详解】解:∵DE ∥BC,EF ∥CG ,∴AD AB =AE AC ,AF AG =AE AC ,∴AD AB =AF AG ,∵AD AB =13,AF =3∴AG =9【点睛】本题考查了平行线分线段成比例定理，解决本题的关键是熟练掌握平行线分线段成比例定理．【变式7-2】（2023春·陕西商洛·九年级校考期中）如图，在平行四边形ABCD 中，点F 是AD 上的点，AF=2FD，直线BF交AC于点E，交CD的延长线于点G，若BE=4则EG的值为（）A．8B．7C．6D．5【答案】C【分析】由AF=2DF可以假设DF=k，得到AF=2k，AD=3k（k是正整数），根据平行四边形的性质得到AD∥BC，AB∥CD，AD=BC=3k，然后根据平行线分线段成比例来求解．【详解】解：∵AF=2DF，∴设DF=k，则AF=2k，AD=3k（k是正整数）．∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AD=BC=3k，∴AEEC =AFBC=2k3k=23，∴BEEG =AEEC=23．∵BE=4，∴4EG =23，∴EG=6．故选：C．【点睛】本题考查了平行四边形的性质，平行线分线段成比例．理解相关知识是解答关键．【变式7-3】（2023春·安徽滁州·九年级校考期中）如图，点D是△ABC边BC上一点，连接AD，过AD上点E作EF∥BD，交AB于点F，过点F作FG∥AC交BC于点G，已知AEED =32，BG=4．(1)求CG 的长；(2)若CD =2，在上述条件和结论下，求EF 的长．【答案】(1)6(2)245【分析】（1）由EF ∥BD ，推出AF FB =AE ED =32，由FG //AC ，推出BG CG =BF AF =23，可得结论．（2）由EF ∥BD ，推出EF BD =AF AB ，可得结论．【详解】（1）∵EF ∥BD ，∴AF FB =AE ED =32，∵FG ∥AC ，∴BG CG =BF AF =23，∵BG =4，∴CG =32BG =32×4=6．（2）∵CD =2，CG =6，∴DG =CG−CD =4，∵BG =4，∴BD =BG +DG =8，∵AF BF =32，∴AF AB =35，∵EF ∥BD ，∴EF BD =AF AB ，∴EF 8=35，∴EF =245．【点睛】本题考查了平行线分线段成比例定理，掌握这个定理是关键．【题型8 平行线分线段成比例与三角形的重心的综合】【例8】（2023春·浙江宁波·九年级统考期中）已知点G 是△ABC 的重心，连结BG ，过点G 作GD ∥AB 交BC 于点D ，若△BDG 的面积为1，则△ABC 的面积为（ ）A ．6B ．8C ．9D ．12【答案】C 【分析】连接CG 并延长交AB 于E ，如图，利用三角形重心性质得到CG ＝2EG ，则利用平行线分线段成比例得到CD BD =CG EG =2，再根据三角形面积公式得到S △GDC ＝2S △BDG ＝2，则S △BCG ＝3，接着求出S △BEG ＝32，从而得到S △BCE ＝92，然后利用CE 为中线得到S △ABC ．【详解】解：连接CG 并延长交AB 于E ，如图，∵点G 是△ABC 的重心，∴CG ＝2EG ，∵DG ∥AB ，∴CD BD =CG EG =2，∴S △GDC ＝2S △BDG ＝2，∴S △BCG ＝1+2＝3，而EG ＝12CG ，∴S △BEG ＝12S △BCG ＝32，∴S △BCE ＝32+3＝92，∵CE 为中线，∴S△ABC＝2S△BCE＝2×92＝9．故选：C．【点睛】本题考查了三角形的重心：三角形的重心是三角形三边中线的交点；重心到顶点的距离与重心到对边中点的距离之比为2：1．也考查了平行线分线段成比例定理和三角形面积公式．【变式8-1】（2023·上海浦东新·九年级统考期中）如图，在△ABC中，AD是中线，G是重心，过点G作EF//BC，分别交AB、AC于点E、F，若AC=18，则AF=．【答案】12【分析】如图，运用平行线分线段成比例定理列出比例式：AFAC =AGAD=2DG3DG=23，根据AC=18，求出AF即可解决问题．【详解】解：∵G是△ABC的重心，∴AG=2DG，AD=3DG；∵EF∥BC，∴AF AC =AGAD=2DG3DG=23，∵AC=18，∴AF=12．故答案为12．【点睛】该题主要考查了三角形重心的性质、平行线分线段成比例定理等几何知识点及其应用问题；牢固掌握平行线分线段成比例定理是解题的关键．【变式8-2】（2023春·上海徐汇·九年级上海市田林第三中学校考期中）如图，△ABC的中线AD、CE交于点G，点F在边AC上，GF∥BC，那么GFBC的值是．【答案】13【分析】根据三角形的重心和相似三角形的判定和性质解答即可．【详解】解：∵△ABC的中线AD、CE交于点G，∴G是△ABC的重心，∴AG GD =21，∵GF∥BC，∴GF DC =AGAD＝23，∵DC＝12BC，∴GF BC =13，故答案为：13【点睛】此题考查三角形重心问题，关键是根据三角形的重心得出比例关系．【变式8-3】（2023春·浙江宁波·九年级校联考期中）如图，G是△ABC的重心，延长BG交AC于点D，延长CG 交AB于点E，P，Q分别是△BCE和△BCD的重心，BC长为12，则PQ的长为（）A．2B．2．5C．3D．4【答案】A【分析】连接EP、DQ，并延长，分别交BC于一点F，连接ED、PQ，由题意易得ED∥BC，ED=12BC，PQ∥ED，PQ=13ED，进而可求解．【详解】解：连接EP 、DQ ，并延长，分别交BC 于一点F ，连接ED 、PQ ，如图所示：∵G 是△ABC 的重心，延长BG 交AC 于点D ，延长CG 交AB 于点E ，∴AE =BE ，AD =DC ，∴ED∥BC ，ED =12BC ，又∵P,Q 分别是△BCE 和△BCD 的重心，∴EP PF =DQ QF =2，∴PQ∥ED ，PQ =13ED ，∴PQ =13×12BC =16BC ，∵BC =12∴PQ =2故选：A ．【点睛】本题主要考查三角形的重心及平行线所截线段成比例，熟练掌握三角形的重心及平行线所截线段成比例是解题的关键．【题型9 平行线分线段成比例的常用辅助线之作平行线】【例9】（2023春·河南郑州·九年级统考期中）如图，正方形ABCD 中，E ，F 分别在边AD ，CD 上，AF ，BE 相交于点G ，若AE =3ED ，DF =CF ，则AG ∶GF 的值是 ．【答案】6:5【分析】作FN ∥AD ，交AB 与N ，设DE =a ，则AE =3a ，利用平行线分线段成比例定理解决问题即可．【详解】解：如图所示，作FN∥AD，交AB与N，∵四边形ABCD是正方形，∴AB∥CD，∵FN∥AD，∴四边形ANFD是平行四边形，∵∠D=90°，∴四边形ANFD是矩形，设DE=a，则AE=3a，AD=AB=CD=FN=4a，AN=DF=2a，∵AN=BN，MN∥AE，∴BM=ME，∴MN=32a，∴FM=52a，∵AE∥FM，∴AGGF =AEFM=3a52a=65，故答案为：6:5．【点睛】本题考查了正方形的性质、平行线分线段成比例定理、三角形中位线等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题．【变式9-1】（2023春·九年级课时练习）对于平行线，我们有这样的结论：如图1，AB//CD，AD,BC交于点O，则AODO =BOCO．请利用该结论解答下面的问题：如图2，在△ABC中，点D在线段BC上，∠BAD=75°，∠CAD=30°，AD=2,BD=2DC，求AC的长．【答案】3【分析】过点C作CE∥AB交AD的延长线于E，根据平行线分线段成比例定理得到BDDC ＝ADDE，由已知代入求出DE的长，证明△ACE为等腰三角形即可．【详解】解：过点C作CE∥AB交AD的延长线于E，则BDDC ＝ADDE，又BD＝2DC，∴ADDE=2∵AD＝2，∴DE＝1，∵CE∥AB，∴∠E＝∠BAD＝75°，又∠CAD＝30°，∴∠ACE＝∠E＝75°，∴AC＝AE＝AD + DE =3．【点睛】本题考查的是平行线分线段成比例定理，恰当作辅助线，正确运用定理找准对应关系，列出比例式求值是解题的关键．【变式9-2】（2023春·陕西西安·九年级校考期末）如图，AG：GD=4∶1，BD ：DC=2∶3，则AE∶EC的值为．【答案】8:5【分析】过点D作DF∥CA交BE于F，如图，利用平行线分线段成比例定理，由DF∥CE得到DFCE =BDBC=25，则CE=52DF ，由DF ∥AE 得到DF AE =DG AG =DF AE =14，则AE=4DF ，然后计算AE EC 的值．【详解】过点D 作DF ∥CA 交BE 于F ，如图，∵DF ∥CE ，∴DF CE =BD BC ，而BD ：DC=2：3，∴DF CE =25，则CE=52DF ，∵DF ∥AE ，∴DF AE =DG AG ，∵AG ：GD=4：1，∴DF AE =14，则AE=4DF ，∴AE EC =4DF 52DF =85．故答案为85．【点睛】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．平行于三角形一边的直线截其他两边（或两边的延长线），所截得的三角形的三边与原三角形的三边对应成比例.【变式9-3】（2023春·广东深圳·九年级深圳市南山外国语学校校联考期中）如图，在等腰△ABC 中，AB =AC ，点P 在BA 的延长线上，PA =14AB ，点D 在BC 边上，PD =PC ，则CD BC 的值是 ．【答案】34【分析】过点P 作PE //AC 交DC 延长线于点E ，根据等腰三角形判定与性质，平行线的性质可证PB =PE ，再证△PCE≌△PDB ，可得BD =CE ，再利用平行线分线段成比例得PA AB =CE BC ，结合线段的等量关系及比例的性质即可得到结论．【详解】如图：过点P 作PE //AC 交DC 延长线于点E ，∵AB =AC ∴∠B =∠ACB∵AC //PE ∴∠ACB =∠E ∴∠B =∠E ∴PB =PE ∵PC =PD ∴∠PDC =∠PCD ∴∠BPD =∠EPC∴在△PCE 和△PDB 中PC =PD ∠EPC =∠BPD PE =PB∴△PCE≌△PDB∴BD =CE∵AC //PE ∴PA AB =CE BC∵PA =14AB ∴CE BC =14∴BD BC =14∴CD BC =34故答案为：34．【点睛】本题考查了等腰三角形的判定与性质，平行线分线段成比例，以及全等三角形的判定，解题关键是正确作出辅助线，列出比例式．【题型10 平行线分线段成比例的常用辅助线之作垂线】【例10】（2023春·四川达州·九年级校考期末）如图，在直角梯形ABCD 中，DC ∥AB ，∠DAB =90°，AC ⊥BC ，AC =BC ，∠ABC 的平分线分别交AD 、AC 于点E ，F ，则BF EF 的值是（ ）A B ．2+C +1D 【答案】C 【详解】解：作FG ⊥AB 于点G ，由AE ∥FG ，得BF EF =BG GA ，∵AC ⊥BC ，∴∠ACB =90°，又∵BE 是∠ACB 的平分线，∴FG =CF ，在Rt △BGF 和Rt △BCF 中，BF =BF FG =CF∴Rt △BGF ≌Rt △BCF ，∴CB =GB ，∵AC =BC ，∴∠CBA =45°，∴AB ，∴BFEF =BG GA =．故选：C ．【点睛】考点：1、平行线分线段成比例，2、全等三角形及角平分线【变式10-1】（2023春·广西钦州·九年级校考阶段练习）如图，在△ABC中，AB=AC,∠BAC=α，M为BC 的中点，点D在MC上，以点A为中心，将线段AD逆时针旋转α得到线段AE，连接BE,DE．(1)比较∠BAE与∠CAD的大小；用等式表示线段BE,BM,MD之间的数量关系，并证明；(2)过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明．【答案】(1)∠BAE=∠CAD，BE+MD=BM，理由见解析(2)NE=ND，理由见解析【分析】（1）证明△AEB≌△ADC，得到CD=BE，即可得到结论BE+MD=BM；（2）过点E作EH⊥AB，交BC于点H，可证BE=BH，再证MN∥EH，得到DNNE =DMMH=1，即可得到NE=ND．【详解】（1）解：由旋转得，AD=AE,∠DAE=∠BAC=α，∴∠DAC=∠BAE=α−∠DAB，又∵AB=AC，∴△AEB≌△ADC，∴CD=BE，∵CD+MD=BM，∴BE+MD=BM；（2）NE=ND，理由如下：过点E作EH⊥AB，交BC于点H，∵AC=AB，∴∠C=∠ABC，∵△AEB≌△ADC，∴∠C=∠ABE，∴∠ABE=∠ABC，∵EH⊥AB，∴∠BEH=∠BHE，∴BE=BH，∴CD=BH，∴MD=MH，∵MN⊥AB，EH⊥AB，∴MN∥EH，∴DN NE =DMMH=1，∴NE=ND．【点睛】此题考查了等腰三角形的性质，全等三角形的判定和性质，作EH⊥AB证明三角形全等是解题的关键．【变式10-2】（2023春·山西太原·九年级统考期中）已知△ABC中，∠ACB=90°,CD⊥AB于点D，AE平分∠BAC，交CD于点F．请从A，B两题中任选一题作答．我选择题．A．如图1，若AC=BC=1，则CF的长为．B．如图2，若AC=4,BC=3，则DF的长为．。

3.2平行线分线段成比例01 基础丿知识点1平行线分线段成比例1.（杭州中考）如图，已知a//b//c,直线刃分别交直线a, b, c于点仏B,AD 1 DFC、直线刀分别交直线＜3, b,（丁点0 E, F.若—=-,则—=（B）D C Z Er1A-32C-3直线厶〃厶〃厶若AB=2, BC=3, DE=\、则厅的长为（B2A-3C. 6己gAB〃CD〃EF、那么下列结论中，正确的是（0 CDA 一EF AEAC CE c一=一•BD DF1B-2D. 12.如图,3B-23.如图,ACD.AC DFAC BDB- AE=DFAB ADB 一=一'AC AE AB ADAC AEC 一=一D 一=一BC DE BC DE 10•如图，在△宓中，点2巧分别在初，边上，DE//BC,若AD : AB= 3 : 4,血'=6,则M 等于&11. 如图，若AB5F,则下列结论中，与环相等的是⑵AB CDBO BCA —— R —— C —— D ——EF EF OE BE12. 如图，四边形肋G?是平行四边形，点厅在 胡的延长线上，点尸在兀 的延长线上，连接亦分别交血?，CD 于点G, H,则下列结论错误的是AB_AD A 'BC -AE 02 中档EG AGB 一=一•GH GDFH CFD ，EH =AD（0EA_EGA,BE_EFAB BC r——=——AE CF13.如图，己知曲〃09〃矿，AC： CE=2 : 3,矿=15,那么BD=§.14.（扬州中考）如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点A. B. C都在横格线上，若线段AB=\ cm,则线段BC=VZcm.15.己知，如图，厶〃厶〃厶，肋=3, BC=5,莎=16,求防和疔的长.解：•・•厶〃厶〃厶，DE AB AB• ____ ______ee DF=AC Z=AB+BC，DE16一3 + 5:・DE=,：• EF= DF- DE=止一6 = Z •16•如图，在△遊中，点〃是初上的一点，过点〃作DE//BC交边M于点E,过点F作厅〃兀交肋于点尸己知血=2托cm, AB=8 cm.求:B「E 1 1H AC"~2~ 「1+1、，1 1H AC""3" 「1+2、，1 1'AC"■4" "1 + 3*A0 2 2 ....力胚丁注如HAF ⑴签的值;AF⑵誰的值.AF AD解:ZDE//BC, ：•=屁•・•仙=2衣,佃=8,・ AE_2&_&••AC_ 8 _ 4 '/、AF AE J6解得力尸=3.AF 3AB=8* 03 综合题17•在△宓中，〃为氏边的中点，尸为边上任意一点，BE交AD于点、0,李瑞同学在研究这一问题时，发现了如下的事实:时,时, ⑵时, ⑶*A0 2 2 ., ... 仃胚=厂2+2（如图刃；52 + 3（如图弘*A0 2 2有XBAF i在图4中，当需==时，参照上述研究结论，请你猜想用加刀是正整数） AC 1 十nAO 表示X5的一般结论，并证明. 证明：作DF//BE 交胚于尸CF CD•:DF 〃BE, A™=^=1. :.EF=CF.Er DU• AO 2*AD =J?+2- 解：猜想:A0 2 二P?•：OE 〃DF, •晋 AEEF• •AE 1 • AE_1e AC ==1Z H ，ee EC =n-。

平行线分线段成比例定理练习题一、选择题1、如图，已知直线a ∥b ∥c ，直线m 交直线a ，b ，c 于点A ，B ，C ，直线n 交直线a ，b ，c 于点D ，E ，F ，若BC AB =21，则EFDE =（ ）A ．31B ．21C ．32 D ．1 答案：B2、如图，在△ABC 中，点D 、E 分别为边AB 、AC 上的点，且DE ∥BC ，若AD=5，BD=10，AE=3，则CE 的长为（ ）A ．3B ．6C ．9D ．12答案：B 解析：由平行线分线段成比例定理，BD AD =2=CEAE ，AE=3，所以CE= 6。

3、如图，三角形ABC 中，D 、E 、F 分别是AB 、AC 、BC 上的点，且DE ∥BC ，EF ∥AB ，AD ：DB=1：2，BC=30cm ，则FC 的长为（ ）A ．10cmB ．20cmC ．5cmD ．6cm答案：B 解析：DE ∥BC ，所以BD AD =CE AE ，又EF ∥AB ，所以CE AE =CF BF ，于是有CF BF =BD AD =21，而BC=30cm ，所以CF=20cm 。

4、如图，点G 、F 分别是△BCD 的边BC 、CD 上的点，BD 的延长线与GF 的延长线相交于点A ，DE ∥BC 交GA 于点E ，则下列结论错误的是（ ）A ．BD AD =EG AEB ．CG DE =CF DFC ．AG AE =BC DED ．AB AD =BGDE 答案：C解析：DE ∥BC ，所以BD AD =EG AE ，CG DE =CF DF ，AB AD =BGDE ，选项A 、B 、D 正确。

选项C 不正确，应当是AG AE =BG DE 。

5、AD 是△ABC 的中线，E 是AD 上一点，AE ：ED =1：3，BE 的延长线交AC 于F ，AF ：FC=（ ）A ．1：3B ．1：4C ．1：5D ．1：6答案：D解析：作DH ∥BF 交AC 于H ，∵AD 是△ABC 的中线，∴FH=HC ，∵DH ∥BF ，∴FH AF =ED AE =31∴AF ：FC = 1：6。

4.2平行线分线段成比例【十大题型】【浙教版】【题型1 由平行线分线段成比例判断比例式正误】............................................................................................1【题型2 平行线分线段成比例之“A”字型求值】................................................................................................2【题型3 平行线分线段成比例之“X”字型求值】..................................................................................................3【题型4 平行线分线段成比例之“8”字型求值】...................................................................................................5【题型5 平行线分线段成比例之“#”字型求值】...................................................................................................6【题型6 平行线分线段成比例与三角形的中位线的综合】................................................................................7【题型7 多次利用平行线分线段成比例求值】....................................................................................................9【题型8 平行线分线段成比例与三角形的重心的综合】..................................................................................10【题型9 平行线分线段成比例的常用辅助线之作平行线】..............................................................................11【题型10 平行线分线段成比例的常用辅助线之作垂线】. (12)【知识点 平行线分线段成比例定理】两条直线被三条平行线所截，所得的对应线段成比例，简称为平行线分线段成比例定理．如图：如果123////l l l ，则AB DE BC EF =，AB DE AC DF =，BC EFAC DF=．AD BE CF1l2l 3l1l 2l 3l 【小结】若将所截出的小线段位置靠上的（如AB ）称为上，位置靠下的称为下，两条线段合成的线段称为全，则可以形象的表示为，，．【题型1 由平行线分线段成比例判断比例式正误】【例1】（2023春·广西梧州·九年级校考期中）如图，在△ABC 中，点D ，E ，F 分别在AB ，AC ，BC 边上，DE ∥BC ，EF ∥AB ，则下列结论正确的是（ ）A ．AD DB =AEACB ．AD DB =BFFCC ．AD DB =FCBFD ．AD DB =FCBC=上上下下=上上全全=下下全全【变式1-1】（2023春·湖南娄底·九年级统考期中）如图，已知AB∥CD∥EF ，那么下列结论正确的是（ ）．A ．AB EF = ADDFB ．DF AD = BCCEC ．AD AF = BEBCD ．AD DF = BCCE【变式1-2】（2023春·湖南娄底·九年级校联考期末）如图，已知AB ∥ CD ∥ EF ，AC:AE =3:5，那么下列结论正确的是（ ）A ．BD:DF =2:3B ．AB:CD =2:3C ．CD:EF =3:5D ．DF:BF =2:5【变式1-3】（2023春·山西晋城·九年级统考期末）如图，在△ABC 中，点D 在AB 边上，点E 在BC 边上，过点D 作DG //BC ，交AC 于点G ，过点E 作EH //AB ，交AC 于点H ，DG 的延长线与EH 的延长线交于点F ，则下列式子一定正确的是（ ）A ．AD DB =DGBCB ．GF EC =HCGHC ．FH AD =GHAGD ．HE AB =ECBE【题型2 平行线分线段成比例之“A”字型求值】【例2】（2023春·河北保定·九年级统考期末）如图，点A ，B 在格点上，若BC =23，则AC 的长为（ ）A．1B．43C．2D．3【变式2-1】（2023春·广西百色·九年级统考期末）如图，在△ABC中，点D、E分别在AB、AC上，DE∥BC．若AD=6，DB=3，则AEAC的值为（）A．23B．32C．34D．2【变式2-2】（2023春·四川成都·九年级四川省成都市七中育才学校校考期中）已知线段a、b、c，若求作线段x，使a∶b＝c∶x，则以下作图正确的是（）A．B．C．D．【变式2-3】（2023春·九年级课时练习）如图，在△ABC中，EF∥CD，DE∥BC．（1）求证：AF：FD＝AD：DB；（2）若AB＝30，AD：BD＝2：1，请直接写出DF的长．【题型3平行线分线段成比例之“X”字型求值】【例3】（2023春·吉林长春·九年级统考期末）如图，AB∥CD∥EF，AF与BE相交于点G，且AG＝4，GD＝2，DF＝8，那么BCCE的值等于．【变式3-1】（2023春·浙江金华·九年级校联考阶段练习）如图：AB ∥CD ∥EF ，AD:DF =3:1，BE =16，那么CE 的长为（ ）A ．4B ．12C ．163D ．6【变式3-2】（2023春·安徽六安·九年级校考期末）如图，l 1∥l 2∥l 3，两条直线与这三条平行线分别交于点A 、B 、C 和D 、E 、F ，若ABBC =43，则DEDF 的值为（ ）A ．47B ．37C ．74D ．43【变式3-3】（2023春·贵州铜仁·九年级统考期中）已知三条互相平行的直线l 1，l 2，l 3分别截直线l 4于点A ，B，C ，截直线l 5于点D ，E ，F ，直线l 4与l 5相交于点O ，且AB =BC =EF =8，EO =2．(1)求DE 的长；(2)求OB 的长．【题型4平行线分线段成比例之“8”字型求值】【例4】（2023春·陕西西安·九年级高新一中校考阶段练习）如图，在平行四边形ABCD中，∠ABC的平分线BF分别与AC、AD交于点E、F，AB=3，FD=2，则EFFB的值为（）A．25B．38C．37D．35【变式4-1】（2023春·上海静安·九年级校考期中）已知ax=bc，求作x，那么下列作图正确的是（）A．B．C．D．【变式4-2】（2023春·全国·九年级专题练习）如图，l1∥l2，AF：BF＝2：5，BC：CD＝4：1，则AE：EC 的值为（）A．5：2B．1：4C．2：1D．3：2【变式4-3】（2023春·山东淄博·九年级统考期末）如图，AB，CD相交于点E，且AC∥EF∥DB，点C，F，B在同一条直线上，已知AC ＝p ，EF ＝r ，DB ＝q ，则p ，q ，r 之间满足的数量关系式是（ ）A ．1r +1q =1pB ．1p +1q =2rC ．1p +1q =1rD ．1q +1r =2p【题型5 平行线分线段成比例之“#”字型求值】【例5】（2023春·全国·九年级期末）如图，直线a ∥b ∥c ，点A ，B 在直线a 上，点C ，D 在直线c 上，线段AC ，BD 分别交直线b 于点E ，F ，则下列线段的比与AEAC 一定相等的是（ ）A ．CEACB ．BFBDC ．BFFDD ．ABCD【变式5-1】（2023春·河北保定·九年级校考期末）如图，已知直线a ∥b ∥c ，直线m ，n 与直线a ，b ，c 分别交于点A ，C ，E ，B ，D ，F ，若AC ＝4，CE ＝6，BF ＝152，则BD 的值是 ．【变式5-2】（2023春·上海青浦·九年级校考阶段练习）如图，梯形ABCD 中，AD ∥BC ∥EF ，AB:EB =3:1，DF =8，则FC =．【变式5-3】（2023春·山西长治·九年级统考期末）如图，直线a ，b ，c 分别与直线m ，n 交于点A ，D ，B ，E ，C ，F ．已知直线a∥b∥c ，AB =2，BC =3，则DEDF 的值为（ ）A ．23B ．32C ．25D ．35【题型6 平行线分线段成比例与三角形的中位线的综合】【例6】（2023·四川南充·校联考三模）如图， DE 是△ABC 的中位线， F 是CE 的中点，射线DF 与BE 交于点O ，与BC 的延长线交于点G ．下列结论：①OB =2OE ；②OD =OF ； ③DEBG =CFAF ；④S △ADE =12S 四边形OBCF ，正确的有．(填序号．)【变式6-1】（2023春·河北石家庄·九年级石家庄市第四十一中学校考期末）如图，DE 是△ABC 的中位线，M 是DE 的中点，CM 的延长线交AB 于点N ，则NM ：MC 等于（ ）A ．1：2B ．1：3C ．1：4D ．1：5【变式6-2】（2023春·浙江宁波·九年级统考期中）如图，DE 、NM 分别是△ABC 、△ADE 的中位线，NM 的延长线交BC 于点F ，则S △DMN ：S 四边形MFCE 等于（ ）A．1：5B．1：4C．2：5D．2：7【变式6-3】（2023·山西运城·统考二模）请阅读下列材料，非完成相应的任务．利用辅助平行线求线段的比三角形的中位线定理是三角形的中位线平行于第三边，且等于第三边的一半．平行线分线段成比例定理是两条平行线被两条直线所截，截得的线段对应成比例．有些几何题，若题中出现了平行线，我们可以直接利用这两个定理求出两线段的比值，而有些几何题，题中没有平行线这样的条件，那么我们可以通过作辅助平行线，然后再利用这两个定理加以解决．举例：如图1，AD是△ABC的中线，AE:AD=1:5，BE的延长线交AC于点F．求AFCF的值．下面是该题的部分解题过程：解：如图2，过点D作DH∥BF交AC于点H．∵AD是△ABC的中线，∴BD=DC．∵DH∥BF，∴FH CH =BDCD，∴CH=FH．∵EF∥DH，…任务：(1)请补充材料中剩余部分的解答过程．(2)上述解题过程主要用的数学思想是______．（单选）A ．方程思想 B ．转化思想 C ．分类思想 D ．整体思想(3)请你换一种思路求AFCF 的值，直接写出辅助线的作法即可．【题型7 多次利用平行线分线段成比例求值】【例7】（2023春·陕西咸阳·九年级统考期中）如图，AB =AC ，AD ⊥BC 于点D ，M 是AD 的中点，CM 交AB 于点P ，DN∥CP ．若AB =6cm ，求PN 的长．【变式7-1】（2023春·陕西咸阳·九年级统考期中）如图，在△ABC 和△ACG 中，D 、E 、F 分别在线段AB 、AC 、AG 上，连接DE 、EF ，DE ∥BC ，EF ∥CG ，ADAB =13,AF =3，求AG 的长．【变式7-2】（2023春·陕西商洛·九年级校考期中）如图，在平行四边形ABCD 中，点F 是AD 上的点，AF=2FD，直线BF交AC于点E，交CD的延长线于点G，若BE=4则EG的值为（）A．8B．7C．6D．5【变式7-3】（2023春·安徽滁州·九年级校考期中）如图，点D是△ABC边BC上一点，连接AD，过AD上点E作EF∥BD，交AB于点F，过点F作FG∥AC交BC于点G，已知AEED =32，BG=4．(1)求CG的长；(2)若CD=2，在上述条件和结论下，求EF的长．【题型8平行线分线段成比例与三角形的重心的综合】【例8】（2023春·浙江宁波·九年级统考期中）已知点G是△ABC的重心，连结BG，过点G作GD∥AB 交BC于点D，若△BDG的面积为1，则△ABC的面积为（ ）A．6B．8C．9D．12【变式8-1】（2023·上海浦东新·九年级统考期中）如图，在△ABC中，AD是中线，G是重心，过点G作EF//BC，分别交AB、AC于点E、F，若AC=18，则AF=．【变式8-2】（2023春·上海徐汇·九年级上海市田林第三中学校考期中）如图，△ABC 的中线AD 、CE 交于点G ，点F 在边AC 上，GF ∥BC ，那么GF BC 的值是 ．【变式8-3】（2023春·浙江宁波·九年级校联考期中）如图，G 是△ABC 的重心，延长BG 交AC 于点D ，延长CG 交AB 于点E ，P ，Q 分别是△BCE 和△BCD 的重心，BC 长为12，则PQ 的长为（ ）A ．2B ．2．5C ．3D ．4【题型9 平行线分线段成比例的常用辅助线之作平行线】【例9】（2023春·河南郑州·九年级统考期中）如图，正方形ABCD 中，E ，F 分别在边AD ，CD 上，AF ，BE 相交于点G ，若AE =3ED ，DF =CF ，则AG ∶GF 的值是 ．【变式9-1】（2023春·九年级课时练习）对于平行线，我们有这样的结论：如图1，AB//CD ，AD,BC 交于点O ，则AO DO =BO CO ．请利用该结论解答下面的问题：如图2，在△ABC 中，点D 在线段BC 上，∠BAD =75°，∠CAD =30°，AD =2,BD =2DC ，求AC 的长．【变式9-2】（2023春·陕西西安·九年级校考期末）如图，AG ：GD =4∶1， BD ：DC =2∶3，则 AE ∶EC 的值为 ．【变式9-3】（2023春·广东深圳·九年级深圳市南山外国语学校校联考期中）如图，在等腰△ABC 中，AB =AC ，点P 在BA 的延长线上，PA =14AB ，点D 在BC 边上，PD =PC ，则CD BC 的值是 ．【题型10 平行线分线段成比例的常用辅助线之作垂线】【例10】（2023春·四川达州·九年级校考期末）如图，在直角梯形ABCD 中，DC ∥AB ，∠DAB =90°，AC ⊥BC ，AC =BC ，∠ABC 的平分线分别交AD 、AC 于点E ，F ，则BF EF 的值是（ ）A B ．2+C +1D 【变式10-1】（2023春·广西钦州·九年级校考阶段练习）如图，在△ABC 中，AB =AC,∠BAC =α，M 为BC的中点，点D在MC上，以点A为中心，将线段AD逆时针旋转α得到线段AE，连接BE,DE．(1)比较∠BAE与∠CAD的大小；用等式表示线段BE,BM,MD之间的数量关系，并证明；(2)过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明．【变式10-2】（2023春·山西太原·九年级统考期中）已知△ABC中，∠ACB=90°,CD⊥AB于点D，AE平分∠BAC，交CD于点F．请从A，B两题中任选一题作答．我选择题．A．如图1，若AC=BC=1，则CF的长为．B．如图2，若AC=4,BC=3，则DF的长为．,AB=BC，【变式10-3】（2023春·上海·九年级校考期中）如图，梯形ABCD中，AD//BC,∠B=90∘,tan C=43点E在边CD上，把△BCE绕点B逆时针旋转90°，点E的对应点是点F，点C的对应点是点M，如果EF//BC，那么DE:CE的值是．。

平行线分线段成比例知识点4：平行线分线段成比例定理（1）平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.已知l 1∥l 2∥l 3,可得EFBCDE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB =====或或或或等. 拓展：试用三角形的面积公式证明平行线分线段成比例定理 推广：过一点的一线束被平行线截得的对应线段成比例（2）推论1:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.推论2:平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例。

思考：平行线分线段成比例定理可以逆用吗？ 由DE ∥BC 可得：ACAEAB AD EA EC AD BD EC AE DB AD ===或或.A D l 1B E l 2C F l 3例1：（2012•嘉定区一模）如图，直线l 1、l 2、l 3分别交直线l 4于点A 、B 、C ，交直线l 5于点D 、E 、F ，专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图，DE BC ∥，且DB AE =,若510AB AC ==，，求AE 的长。

EDCBA【例2】 如图，已知////AB EF CD ，若AB a =，CD b =，EF c =，求证：111cab=+.FE DCBAABCD EEDC B A【巩固】如图，AB BD ⊥，CD BD ⊥，垂足分别为B 、D ，AC 和BD 相交于点E ，EF BD ⊥，垂足为F .证明：111AB CD EF+=. FEDCBA【例3】 如图，在梯形ABCD 中，AB CD ∥， 129AB CD ==，，过对角线交点O 作EF CD ∥交AD BC ，于E F ，，求EF 的长。

OFED CBA【巩固】（上海市数学竞赛题）如图，在梯形ABCD 中，AD BC ∥，AD a BC b E F ==，，，分别是AD BC ，的中点，AF 交BE 于P ，CE 交DF 于Q ，求PQ 的长。