材料力学(柴国钟、梁利华)第2章
- 格式:doc
- 大小:560.00 KB
- 文档页数:7
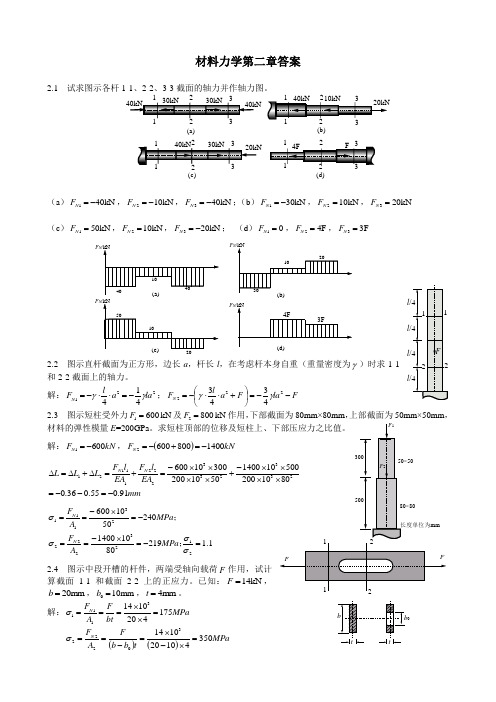
材料力学第二章答案2.1 试求图示各杆1122331123340kN 10kN 20kN40kN30kN 30kN11223340kN 30kN F 4F1233(a )kN 401-=N F ,kN 102-=N F ,kN 403-=N F ;(b )kN 301-=N F ,kN 102=N F ,kN 203=N F (c )kN 501=N F ,kN 102=N F ,kN 203-=N F ; (d )01=N F ,4F 2=N F ,3F 3=N FF N F N F N F N2.2 图示直杆截面为正方形,边长a ,杆长l ,在考虑杆本身自重(重量密度为γ)时求1-1和2-2截面上的轴力。
解:221414la a l F N γγ-=⋅⋅-=;F la F a l F N --=⎪⎭⎫⎝⎛+⋅⋅-=2224343γγ2.3 图示短柱受外力6001=F kN 及8002=F kN材料的弹性模量E =200GPa 解:kN F N 6001-=,()F N 14008006002-=+-=mmEA l F EA l F L L L N N 91.055.036.050102003001060023322211121-=--=+⨯⨯⨯⨯-=+=∆+∆=∆ 1.1219801014002405010600212322223111=-=⨯-==-=⨯-==σσσσ;;MPa A F MPa A F N N2.4 图示中段开槽的杆件,两端受轴向载荷F 算截面1-1和截面2-2上的正应力。
已知:F mm 20=b ,mm 100=b ,mm 4=t 。
解:MPa bt F A F N 17542010143111=⨯⨯===σ ()()MPa t b b F A F N 35041020101430222=⨯-⨯=-==σ2.5 正方形结构受力如图,各杆横截面积2mm 2000=A ,求各杆的正应力。

第二章杆件的内力.截面法一、基本要求1.了解轴向拉伸与压缩、扭转、弯曲的概念;2.掌握用截面法计算基本变形杆件截面上的内力;3.熟练掌握基本变形杆件内力图的绘制方法。
表示轴力沿杆件轴线变化规律的图线。
该图一般以平行于杆件轴线的横坐标x轴表示横截面位置,纵轴表示对应横截面上轴力的大小。
正的轴力画在x轴上方,负的轴力画在x轴下方。
当功率P单位为马力(PS),转速为n(r/min)时,外力偶矩为的变形,则该力或力偶在截面上产生正的弯矩,反之为负的弯矩(上挑为正,下压为负)。
4)剪力方程和弯矩方程一般情况下,梁横截面上的剪力和弯矩随截面位置不同而变化。
若以坐标x 表示横截面在梁轴线上的位置,则横截面上的剪力和弯矩可以表示为x 的函数,即)()(S S x M M x F F ==上述函数表达式称为梁的剪力方程和弯矩方程。
5)剪力图和弯矩图为了直观地表达剪力F S 和弯矩M 沿梁轴线的变化规律,以平行于梁轴线的横坐标x 表示横截面的位置,以纵坐标按适当的比例表示响应横截面上的剪力和弯矩,所绘出的图形分别称为剪力图和弯矩图。
剪力图和弯矩图的绘制方法有以下两种:(1)剪力、弯矩方程法:即根据剪力方程和弯矩方程作图。
其步骤为:第一,求支座反力。
第二,根据截荷情况分段列出F S (x )和M (x )。
在集中力(包括支座反力)、集中力偶和分布载荷的起止点处,剪力方程和弯矩方程可能发生变化,所以这些点均为剪力方程和弯矩方程的分段点。
第三,求控制截面内力,作F S 、M 图。
一般每段的两个端点截面为控制截面。
在有均布载荷的段内,F S =0的截面处弯矩为极值,也作为控制截面求出其弯矩值。
将控制截面的内力值标在的相应位置处。
分段点之间的图形可根据剪力方程和弯矩方程绘出。
并注明ma xma xMF S、的数值。
(2)微分关系法:即利用载荷集度、剪力与弯矩之间的关系绘制剪力图和弯矩图。
载荷集度q (x )、剪力F S (x )与弯矩M (x )之间的关系为:)()(S x q dxx dF = )()(S x F dxx dM = )()()(S 22x q dx x dF dxx M d == 根据上述微分关系,由梁上载荷的变化即可推知剪力图和弯矩图的形状。



2—1试求图示各杆1—1和2—2横截面上的轴力,并作轴力图.(a)解:;;(b)解:;;(c)解:;。
(d)解:。
2—2 试求图示等直杆横截面1—1,2—2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:返回2-3试求图示阶梯状直杆横截面1—1,2—2和3—3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:返回2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11。
5 cm2(拉)(拉)2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向.解:2-6(2—8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形.解:(压)(压)返回2—7(2—9)一根直径、长的圆截面杆,承受轴向拉力,其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解:2—8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E,,试求C与D两点间的距离改变量。
解:横截面上的线应变相同因此返回2—9(2—12) 图示结构中,AB为水平放置的刚性杆,杆1,2,3材料相同,其弹性模量E=210GPa,已知,,,。
试求C点的水平位移和铅垂位移。
解:(1)受力图(a),.(2)变形协调图(b)因,故=(向下)(向下)为保证,点A移至,由图中几何关系知;2—10(2-15)图示圆锥形杆受轴向拉力作用,试求杆的伸长。
材料力学第二章答案2.1 试求图示各杆1122331123340kN 10kN 20kN40kN30kN 30kN11223340kN 30kN F 4F1233(a )kN 401-=N F ,kN 102-=N F ,kN 403-=N F ;(b )kN 301-=N F ,kN 102=N F ,kN 203=N F (c )kN 501=N F ,kN 102=N F ,kN 203-=N F ; (d )01=N F ,4F 2=N F ,3F 3=N FF N F N F N F N2.2 图示直杆截面为正方形,边长a ,杆长l ,在考虑杆本身自重(重量密度为γ)时求1-1和2-2截面上的轴力。
解:221414la a l F N γγ-=⋅⋅-=;F la F a l F N --=⎪⎭⎫⎝⎛+⋅⋅-=2224343γγ2.3 图示短柱受外力6001=F kN 及8002=F kN材料的弹性模量E =200GPa 解:kN F N 6001-=,()F N 14008006002-=+-=mmEA l F EA l F L L L N N 91.055.036.050102003001060023322211121-=--=+⨯⨯⨯⨯-=+=∆+∆=∆ 1.1219801014002405010600212322223111=-=⨯-==-=⨯-==σσσσ;;MPa A F MPa A F N N2.4 图示中段开槽的杆件,两端受轴向载荷F 算截面1-1和截面2-2上的正应力。
已知:F mm 20=b ,mm 100=b ,mm 4=t 。
解:MPa bt F A F N 17542010143111=⨯⨯===σ ()()MPa t b b F A F N 35041020101430222=⨯-⨯=-==σ2.5 正方形结构受力如图,各杆横截面积2mm 2000=A ,求各杆的正应力。
解:F F F F F F F N N N N N =-====5432122; MPaA F MPaA F 0.25200010507.172000105022223534321=⨯==-=⨯⋅-=-====σσσσσ 2.6 等截面杆的横截面面积为A =5cm 2,受轴向拉力F 作用。
如图示杆沿斜截面被截开,若该截面上正应力ασ=120MPa ,切应力ατ=40MPa ,求F 力的大小和斜截面的角度。
解:()⎪⎪⎩⎪⎪⎨⎧==⨯===⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⇒⎪⎪⎭⎪⎪⎬⎫====--kN N A F A FAF 7.667.6666644.18cos 500120cos 44.1831tan tan cos sin 2sin 21cos cos 221122οοασσταααασταασσααααα2.7 如图刹车装置,试计算活塞杆的压应力。
解:N F N 247550275450-=⨯-=MPa A F N 5.874/624752=⨯==πσ2.8 图示钢杆,F =20kN 。
设GPa 200=E ,试求杆的伸长量。
解:mml A A E Fl EA l F EA l F L L L N N 92.0283.0637.030420410200200010201122332122211121=+=⎪⎭⎫⎝⎛⨯+⨯⨯⨯⨯=⎪⎪⎭⎫⎝⎛+=+=∆+∆=∆ππ2.9 等直杆截面积为A ,弹性模量为E 。
试绘制轴力图,并求D 端的位移。
解:EAFlEA Fl EA Fl EA Fl l l l l DC BC ABD A D 3333=+-=∆+∆+∆=∆=∆2.10 图示简单杆系中,圆截面杆AB 与AC 的直径分别为1d =215mm d =,F =35kN ,GPa 210=E 。
求A 点的垂直位移。
解:⎪⎩⎪⎨⎧=-+==+-=∑∑030cos 45cos 0030sin 45sin 02121F F F F F F F N N yN N x οοοο,, f 6mmf 202000f 30A B C D①②③④⑤αBC D A 2F 2F F N AB F45°30°1m 0.8m31262221+=+=FF F F N N , 两杆的功:()()()()22222112222222121222221121324322431244622422d E l F d E l F d El F d El F EA l F EA l F V N N ππππε+++=+++=+=外力做的功:A Fv W 21=由功能互等定理, ()()()()()()mmdE Fl d E Fl v vF W dE lF d E l F V A A 37.1809.0558.015102103216001035812102103210002103543283242132432223323322221122222112=+=⨯⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯=+++=⇒⨯==+++=ππππππε2.11 图示简单杆系中,圆截面杆AB 与AC 的直径分别为d 1=20mm 、d 2=24mm ,kN 5=F ,200GPa E =。
求A 点的垂直位移。
解:⎪⎩⎪⎨⎧=--==--=∑∑030sin 45sin 0030cos 45cos 02121F F F F F F F N N y N N x οοοο,, F F F F N N 31231621+-=+=, 两杆的功:()()()⎥⎥⎦⎤⎢⎢⎣⎡++=+⨯++⨯=+=2122222212222211213423313312243122622A A E aF EA a F EA a F EA l F EA l F V N N ε外力做的功:A Fv W 21=由功能互等定理,()W Fv A A E aF V A ==⎥⎥⎦⎤⎢⎢⎣⎡++=213423312122ε ()()mm A A E Fav A 25.03241620212311020020005000234233122223212=⎥⎥⎦⎤⎢⎢⎣⎡⨯⨯+⨯+⨯⨯⨯=⎥⎥⎦⎤⎢⎢⎣⎡++=ππ2.12 一直径为mm 15,标距为mm 200的圆截面钢杆,在比例极限内进行拉伸试验,当轴向荷载从零开始缓慢地增加到kN 4.58时,杆伸长了mm 9.0,直径缩小了mm 022.0,试确定材料的弹性模量E 、泊松比μ。
45°30°2mABCFAF解:GPa MPa l A Fl l l A F E 4.732.734399.015200584004//2==⨯⨯⨯⨯=∆=∆==πεσ 33.09.015200022.0//=⨯⨯=∆∆=∆∆='=l d dl l l d d εεμ2.13 某拉伸试验机的结构示意图如图所示。
设试验机的CD 杆与试样AB 材料同为低碳钢,其MPa 200=p σ,MPa 240=S σ,MPa 400=b σ。
试验机最大拉力为kN 100。
(1) 用这一试验机作拉断试验时,试样直径最大可达多大?(2) 若设计时取试验机的安全因数2=n ,则CD 杆的横截面面积为多少?(3) 若试样直径mm 10=d ,今欲测弹性模量E ,则所加载荷最大不能超过多少? 解:(1)利用材料拉断条件,材料被拉断的最小 应力b d Fσπσ≥=24mm Fd b8.1740010100443=⨯⨯⨯=≤ππσ故,作拉断试验时,试样直径最大可达17.8mm 。
(2)利用正常安全工作条件,[]22333.833.833240101002cm mm F n A n A F S S ==⨯⨯=≥⇒=≤=σσσσ(3)利用线弹性变形范围条件,试件的最大应力不应超过弹性极限,即kN N d F d F A F p p 7.151********10200410442222==⨯⨯=⨯⨯=≤⇒≤==ππσπσπσ2.14 图示简单支架,AB 和BC 两杆材料相同,材料的拉伸许用应力和压缩许用应力相等,均为[]σ。
为使支架使用的材料最省,求夹角α。
解:⎪⎩⎪⎨⎧=-==+-=∑∑0sin 00cos 0121W F F F F F N yN N x αα,,⎪⎪⎩⎪⎪⎨⎧==⇒ααtan sin 21W F W F N N [][][][]⎪⎪⎩⎪⎪⎨⎧≥≥⇒⎪⎪⎭⎪⎪⎬⎫≤==≤==ασασσασσασtan sin tan sin 2122221111W A W A A W A F A W A F N N [][]ασαασtan cos sin 2211WLWL l A l A V +=+= ()[][]()[]ο74.542tan 0cos sin sin cos 2sin cos sin sin cos 222222222=⇒=⇒=--=-+-=αααασααασαασαααWL WL WL d dV2.15 刚性梁AB 用两根钢杆AC 和BD 悬挂,受铅直力kN 100=F 作用。
已知钢杆AC 和BD 的直径分别为mm 251=d 和mm 182=d ,钢的许用应力[]MPa 170=σ,弹性模量GPa 210=E 。
(1)试校核钢杆的强度,并计算A 、B 两点的铅直位移A ∆、B ∆。
解:321F F N =,32FF N =[]σππσ≤=⨯⨯⨯⨯===MPa d F A F N 8.135253101008382321111 AB CA 12CαBLA BC[]σππσ≤=⨯⨯⨯⨯===MPa d F A F N 0.131183101004342322222 mm d E Fl EA Fl EA l F l N Ac A 62.1251021032500101008383223321111=⨯⨯⨯⨯⨯⨯⨯====∆=∆ππ mm d E Fl EA Fl EA l F l N BD B 56.118102103250010100434323322122=⨯⨯⨯⨯⨯⨯⨯====∆=∆ππ2.16 一拱由刚性块AB 、BC 和拉杆AC 组成,受均布载荷q =90kN/m 。
若m 12=R ,拉杆的许用应力[]MPa 150=σ,试设计拉杆的直径d 。
解:由对称性,qR F YC =∑=0B M ,R F R F qR YC N =+221kN 54012902121=⨯⨯==⇒qR F N[][][]mmF F d d F A F NNN N 7.6715054000044442=⨯⨯==≥⇒≤==πσπσπσπσ取整,[]mm d 68=2.17 图示结构中,钢索BC 由一组直径d =2mm 的钢丝组成。