下载文档原格式
第二单元第二章 杆件的轴向拉压应力与材料的力学性能§2-1 引言工程实例: 连杆、螺栓、桁架、房屋立柱、桥墩……等等。
力学特征: 构件：直杆外力：合力沿杆轴作用(偏离轴线、怎样处理?)内力：在轴向载荷作用下，杆件横截面上的唯一内力分量为轴力N ，它们在该截面的两部分的大小相等、方向相反。
规定拉力为正，压力为负。
变形：轴向伸缩§2-2 拉压杆的应力一、拉压杆横截面上的应力(可演示，杆件受拉，上面所划的横线和纵线仍保持直线，仅距离改变，表明横截面仍保持为平面)平面假设→应变均匀→应力均匀AN=σ或A P =σ(拉为正，压为负)二、Saint-Venant 原理(1797-1886，原理于1855年提出)问题：杆端作用均布力，横截面应力均布。
杆端作用集中力，横截面应力均布吗? 如图, 随距离增大迅速趋于均匀。
局部力系的等效代换只影响局部。
它已由大量试验和计算证实，但一百多年以来，无数数学力学家试图严格证明它，至今仍未成功。
这是固体力学中一颗难以采撷的明珠。
三、拉压杆斜截面上的应力(低碳钢拉伸，沿45°出现滑移线，为什么?)0cos =-P Ap αα ασ=α=αcos cos AP p ασ=α=σαα2cos cos pασ=α=ταα22sin sin p ()0=ασ=σm ax ()452=ασ=τmax方位角α：逆时针方向为正剪应力τ：使研究对象有顺时针转动趋势为正。
例1和例2，看书p17,18§2-3 材料拉伸时的力学性能(构件的强度、刚度和稳定性，不仅与构件的形状、尺寸和所受外力有关，而且与材料的力学性能有关。
拉伸试验是最基本、最常用的试验。
)一、拉伸试验P18： 试样 拉伸图绘图系统放大变形传感器力传感器--→→→→二、低碳钢拉伸时的力学性能材料分类：脆性材料（玻璃、陶瓷和铸铁）、塑性材料(低碳钢：典型塑性材料)四个阶段：线性阶段（应力应变成正比，符合胡克定律，正比阶段的结束点称为比例极限）、屈服阶段(滑移线)（可听见响声，屈服极限s σ）、强化阶段（b σ强度极限）、局部变形(颈缩)阶段（名义应力↓，实际应力↑） 三(四个)特征点：比例极限、（接近弹性极限）、屈服极限、强度极限(超过强度极限、名义应力下降、实际应力仍上升)。
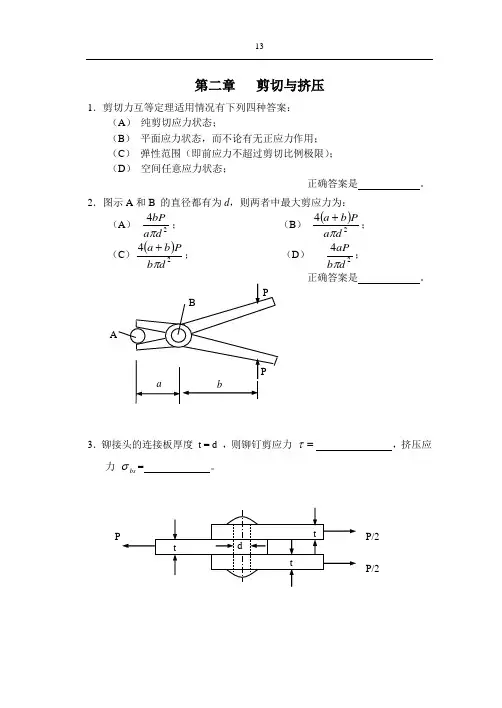
第二章 剪切与挤压1．剪切力互等定理适用情况有下列四种答案：（A ） 纯剪切应力状态；（B ） 平面应力状态，而不论有无正应力作用；（C ） 弹性范围（即前应力不超过剪切比例极限）；（D ） 空间任意应力状态；正确答案是 。
2．图示A 和B 的直径都有为d ，则两者中最大剪应力为：（A ） 24d a bP π； （B ） ()24d a P b a π+； （C ）()24d b P b a π+； （D ） 24db aP π；正确答案是 。
3．铆接头的连接板厚度 t = d ，则铆钉剪应力 =τ ，挤压应力 bs σ= 。
P/2P/24．图示在拉力P 的作用下的螺栓，已知材料的剪切许用应力 []τ 是拉伸许用应力][σ的0.6倍。
螺栓直径 d 和螺栓头高度h 的合理比值是 。
5．拉杆头部尺寸如图所示，已知 []τ =100MPa ，许用挤压应力[]MPa bs 200=σ 。
校核拉杆头部的强度。
6．在铆接头中，已知钢板的 MPa 170][=σ ，铆钉的 MPa 140][=τ ，许用挤压应力 MPa bs 320][=σ 。
拭校核强度。
7．在金属板上冲圆孔时，把板放在有圆孔的砧上，用圆柱形的冲头向下冲，如图所示（砧孔和冲头的直径应与要冲的孔直径相配合）。
设有厚度t = 6 mm 的金属板，要冲出直径d = 20 mm 的圆孔。
已知板的剪切强度极限 MPa b 330=τ 。
试求冲头应加于板上的压力 b Pb=100 t=10 t=108．把三块尺寸相同的木块胶合起来，如图所示。
若P=10KN时，该胶合联接被剪开，试计算胶合处的平均抗剪强度。
9．图示木榫接头，F=50KN，试求接头的剪切与挤压应力。
材料力学-第二章
————————————————————————————————作者：————————————————————————————————日期：
2005年注册岩土工程师考前辅导精讲班
材料力学
第四讲截面的几何性质
【内容提要】
本节主要了解静矩和形心、极惯性矩和惯性积的概念，熟悉简单图形静矩、形心、惯性矩和惯性积的计算，掌握其计算公式。
掌握惯性矩和惯性积平行移轴公式的应用，熟练掌握有一对称轴的组合截面惯性矩的计算方法。
准确理解形心主轴和形心主惯性矩的概念，熟悉常见组合截面形心主惯性矩的计算步骤。
【重点、难点】
重点掌握平行移轴公式的应用，形心主轴概念的理解和有一对称轴的组合截面惯性矩的计算步骤和方法
一、静矩与形心
(一)定义
设任意截面如图4-1所示，其面积为A，为截面所在平面内的任意直角坐标系。
c 为截面形心，其坐标为，。
则
截面对z轴的静矩
截面对轴的静矩
截面形心的位置
(二)特征
1．静矩是对一定的轴而言的，同一截面对不同轴的静矩值不同。
静矩可能为
正，可能为负，也可能为零。
2．静矩的量纲为长度的三次方．即。
单位为或。
3．通过截面形心的坐标称为形心轴。
截面对任一形心轴的静矩为零；反之，若截面对某轴的静矩为零，则该轴必通过截面之形心。
4．若截面有对称轴，则截面对于对称轴的静矩必为零，截面的形心一定在该对称轴上。
5．组合截面(由若干简单截面或标准型材截面所组成)对某一轴的静矩，等于其组成部分对同一轴的静矩之代数和(图4-2)，即
合截面的形心坐标为：
二、惯性矩惯性积
(一)定义
设任意截面如图4-3所示，其面积为A，为截面所在平面内任意直角坐标系。
则
图4-3
截面对轴的惯性矩
截面对y 轴的惯性矩
截面对0点的极惯性矩
截面对轴的惯性积
(二)特征
1．惯性矩是对某一坐标轴而言的．惯性积是对某一对坐标轴而言的，同一截面对不同的坐标轴，其数值不同。
极惯性矩是对点(称为极点)而言的，同一截面对不同的点，其值也不相同。
惯性矩。
极惯性矩恒为正值，而惯性积可能为正，可能为负，也可能为零。
2．惯性矩、惯性积、极惯性矩的量纲均为长度的四次方，即。
，单位为m4或mm4 3．对某一点的极惯性矩恒等于以该点为原点的任一对直角坐标轴的惯性矩之和。
即
4．惯性积是对某一对直角坐标的．若该对坐标中有一轴为截面的对称轴，则截面对这一
对坐标轴的惯性积必为零；但截面对某一对坐标轴的惯性积为零，则这对坐标中不一定有截面的对称轴。
5．组合截面对某一轴的惯性矩等于其组成部分对同一轴的惯性矩之和。
即
组合截面对某一对坐标轴的惯性积，等于其组成部分对同一对坐标轴的惯性积之和，即组合截面对某一点的极惯性矩，等于其组成部分对同一点极惯性矩之和，即
三、惯性半径
(一)定义设任意截面，其面积为A，则
截面对z轴的惯件半径
截面对y轴的惯性半径
(二)特征
1．惯性半径是对某一定坐标轴而言的。
2．惯性半径恒为正值。
3．惯性半径的量纲为长度一次方，即L，单位为m 或mm
四、惯性矩和惯性积的平行移轴公式
任意截面，面积为A，形心为C，如图4-3所示。
设z轴与形心轴平行，相距为；y轴与形心轴平行，相距为，截面对z、y轴的惯性矩、惯性积分别为、；截面对形心轴、。
的惯性矩，惯性积分别为，有如下结论
惯性矩的平行移轴公式
惯性积的平行移轴公式
分述如下：
截面对于任一轴的惯性矩．等于对其平行形心轴的惯性矩加上截面面积与两轴间距离平方之乘积。
截面对于任一直角坐标轴的惯性积．等于该截面对于平行形心坐标惯性积加上截面面积与其形心的坐标之乘积。
常用截面几何性质如表下表所示
五、形心主惯性轴与形心主惯性矩
(一)定义通过截面形心C点的一对特殊坐标轴()，其惯积( )为零，则该对坐标轴( )称为形心主惯性轴(简称形心主轴)。
截面对该一对形心主轴的惯性矩称为形心主惯性矩(简称形心主惯矩)。
(二)特征
1．通过截面形心C，至少具有一对形心主轴
2．若截面只有一根对称轴，则该轴即为形心主轴之一，另一形心主轴为通过形心，并与上述对称轴垂直的轴。
3．若截面有两根对称轴，则该两根轴即为形心主轴。
4．若截面有三根(或以上)对称轴时，则通过形心的任一根轴(所有轴)均为形心主轴，且形心主惯矩均相等。
5．若截面没有对称轴，则可由定性判定法，即根据绕形心转动轴，转至截面积最靠近分布某一轴时，截面对该轴的惯性矩最小()，此轴即为形心主轴之一，另一根通过形心与之垂直的轴为另一根惯性矩最大()的形心主轴。
6．形心主惯性矩是截面对通过同一形心C点，所有轴的惯性矩中的最大值()和最小值()。
截面对于通过同一形心C点的任意一对直角坐标轴的两个惯性矩之和恒为常数，即
7．若截面对通过形心C点的两主惯性矩相等，则通过形心c点的所有轴均为形心主轴，且所有形心主惯性矩均相等。
