点电荷的电场电势
- 格式:doc
- 大小:49.50 KB
- 文档页数:6

点电荷的电势强度公式
点电荷的电势强度公式可以表示为:
\[ V = \frac{k \cdot q}{r} \]
其中,V表示电势强度,k是库仑常数,q是电荷的大小,r是距离电荷的距离。
这个公式告诉我们,电势强度与电荷大小成正比,与距离成反比。
这意味着,电荷越大,电势强度越大;而距离越远,电势强度越小。
这个公式也可以帮助我们计算电荷在空间中的电势分布。
通过测量电荷的大小和距离,我们可以计算出任意点的电势强度,从而了解电场的分布情况。
除了理论上的意义,点电荷的电势强度公式在工程和科学领域也有着广泛的应用。
例如,在电路设计中,我们可以利用这个公式来计算电荷在电路中的电势分布,从而设计出更加稳定和高效的电路。
总之,点电荷的电势强度公式是物理学中非常重要的公式之一,它帮助我们理解电荷在空间中产生的电势场,并在工程和科学领域
中有着广泛的应用。

电场力与电势能的计算电场力与电势能是电学中重要的概念,它们用于描述电荷间的相互作用和能量转化。
本文将介绍如何计算电场力和电势能,并给出相关的公式及计算实例。
一、电场力的计算电场力描述了电荷在电场中受到的作用力。
根据库仑定律,电场力的大小与电荷的大小及其在电场中所受电场的强度有关。
1.1 单个点电荷的电场力计算公式对于一个点电荷Q1在电场中受到的电场力F1,其计算公式如下:F1 = k * Q1 * E,其中k为库仑常量,E为电场强度。
1.2 多个电荷的电场力计算公式若有多个电荷作用在同一个电荷上,那么电场力需要进行矢量相加。
对于在某点上的电荷Q所受到的总电场力F,则有:F = F1 + F2 + ··· + Fn,其中F1、F2、...、Fn分别为不同电荷在该点上的电场力。
二、电势能的计算电势能是描述电荷由于所处位置的不同而具有的能量差异,是电势的一种表现形式。
电势能的计算涉及到电势差和电荷的大小。
2.1 单个点电荷的电势能计算公式对于一个点电荷Q1在电场中的电势能Ep,其计算公式如下:Ep = k * Q1 / r,其中k为库仑常量,r为该点与电荷间的距离。
2.2 电场中的电势能计算公式若有多个点电荷在电场中产生的电势能,则有:Ep = Ep1 + Ep2 + ··· + Epn,其中Ep1、Ep2、...、Epn分别为不同电荷产生的电势能。
三、计算实例下面通过一个简单的计算实例来说明电场力和电势能的计算方法。
假设有两个等量的正电荷Q1=Q2=2C,它们相距为2m。
求它们之间的电场力和电势能。
首先,计算电场力。
根据库仑定律,电场力的计算公式为:F = k * Q1 * Q2 / r^2,其中k为库仑常量,Q1、Q2为电荷的大小,r为两电荷的距离。
代入已知数值,得到:F = 9 * 10^9 * 2C * 2C / (2m)^2 = 9 * 10^9 N。

两等量点电荷连线及中垂线上的场强、电势和电势能的情况分析1.等量同种电荷(1)两点电荷的连线上分析:在其连线上的中点,由于Q 相等,r相等,即E 大小相等,而两点电荷在的场强方向相反,故合场强为零,由||||212212r Q k r Q k E E E -=-=知,从中点往两边合场强增大,且关于中点对称。
(2)两点电荷的中垂线上分析:中垂线上的某点的场强由两点电荷分别在该点的场强叠加而成。
由于中垂线上的点到线两端的距离相等,由2rQ k E =知|E 1|=|E 2|,即大小相等,方向如图2所示:把E 1、E 2进行合成,故合场强E 如图所示。
所以从中垂线上中点往两边场强先是由零增大,但由2r Q k E =可知。
r 越大,E 减小,所以合场强又开始减小。
2.等量异种电荷(1)两点电荷的连线上分析:可根据电场线的疏密直接知中点最稀疏,故中点场强最小,往两边越密场强越大。
方向从正点荷指向负电荷。
(2)两点电荷的中垂线上分析:把正点荷、负点荷在中垂线上某点场强进行合成,合场强方向在连线上且由正电荷指向负电荷。
当A 点离中垂线中点越远,E 1、E 2大小越小,且夹角越大,所以合场强越小,又因为两边对称,可以中垂线上从中点经两边场强减小,方向与两点电荷的连线平行且由正电荷指向负电荷。
1.正电核电场线向外发散,负电荷电场线向内收缩,等势线总是和电场线垂直,在同一等势线上移动电荷,电场力不做功;2.电场力做正功,电势能减少,动能增加;电场力做负功,电势能增加,动能减少(不分正负电荷,通用)3.沿电场线方向,电势降落;沿电场线方向,电势降落最快。

电场与电势的电荷分布电场和电势是电学中非常重要的概念,它们与电荷分布密切相关。
本文将对电场和电势的基本概念进行介绍,并详细探讨不同电荷分布对电场和电势的影响。
1. 电场的定义及其计算方法电场是指某一点周围空间中由电荷引起的力的作用。
电场可以用矢量来表示,其大小和方向分别表示电场强度和力的方向。
根据库仑定律,电荷与电场之间的关系可以通过以下公式计算得出:E = k * (q/r^2)其中,E表示电场强度,k是库仑常量,q为电荷大小,r为电荷到某一点的距离。
2. 电场的叠加原理当存在多个电荷时,它们所产生的电场可以按照叠加原理求和。
即,总的电场强度等于各个电荷产生的电场强度的矢量和。
这可以通过将各个电荷的电场矢量相加得到。
3. 各种电荷分布的电场不同的电荷分布会导致不同的电场特性。
以下是几种常见的电荷分布情况:- 点电荷分布:点电荷是指空间中只有一个电荷。
对于点电荷分布,电场强度随着距离的增加而减小。
其电场强度的大小和方向由库仑定律决定。
- 匀强电场分布:在这种情况下,电场在空间各处方向和大小都相同。
如两个相同大小的点电荷,它们之间的电场强度大小和方向都相等。
- 线性电荷分布:指电荷沿直线分布,如无限长直导线。
对于无限长直导线,由于其对称性,电场强度大小与距离成反比关系。
- 平面电荷分布:指电荷在一平面上均匀分布,如平行板电容器。
对于平面电荷分布,电场强度在垂直于平面的方向上是均匀的,并且呈直线分布。
4. 电势的定义及其计算方法电势表示单位正电荷在电场中所具有的能量。
在电静力场中,电势可以通过单位正电荷所做的功来定义。
电势的计算可以使用以下公式:V = k * (q/r)其中,V表示电势,k是库仑常量,q为电荷大小,r为电荷到某一点的距离。
5. 电势的叠加原理与电场类似,电势也满足叠加原理。
多个电荷产生的电势可以按照叠加原理求和。
这意味着,总的电势等于各个电荷产生的电势的代数和。
6. 各种电荷分布的电势不同的电荷分布也会对电势产生不同的影响。

两个点电荷的场强和电势分布1. 引言嗨,大家好!今天我们来聊聊电荷的场强和电势分布。
乍一听可能有点复杂,但别急,我们一步一步来,保证让你轻松搞定这些概念。
2. 基本概念2.1 点电荷的场强想象一下你在海边,海浪拍打着沙滩。
电荷的场强就像那些海浪,它的力量随着离电荷的距离不同而变化。
我们通常用电场强度来描述这个力量,它指的是单位电荷在某点受到的力。
电场强度的计算公式其实也不复杂,只要记住一点:它和电荷的大小成正比,和距离的平方成反比。
这就像是靠近海浪的时候感觉更强烈,远离的时候就没那么劲儿了。
2.2 点电荷的电势接下来讲电势。
电势就像是你在山上站的位置,高一点的地方总是看得更远。
电势告诉我们电荷在某个位置的“高度”,也就是在那个点的能量水平。
对于点电荷,电势的计算也有个公式,和电荷的大小成正比,和距离的反比。
这个“高度”决定了电荷在电场中的能量。
3. 两个点电荷的场强和电势3.1 组合电场强度当有两个点电荷在一起时,它们的场强就像是两个人一起推一辆车。
每个电荷都在推动电场,在某个点的总场强就是这两个电荷场强的合成。
为了计算这个总场强,我们要把每个电荷产生的场强加起来,记得加上它们之间的相对位置的影响。
这个过程就像是把两个推力合并在一起,最终决定了车的移动方向和速度。
3.2 组合电势电势的组合则简单得多。
不同于场强,电势是可以直接加起来的。
就像你在山顶放一个行李,接着又把另一个行李也放上去,你的总能量就是两个行李的能量加起来。
每个电荷在某个点的电势可以简单地相加,得到总电势。
这就像你在某个点的“高度”是由两个电荷的“高度”叠加而成的。
4. 实际应用4.1 实验中的电荷在实验室里,我们经常需要用这些理论来计算和预测电荷的行为。
比如,当你有两个带电的物体时,利用这些公式可以帮你预测它们的相互作用。
通过这些计算,你能知道它们会怎么影响周围的空间,甚至可以设计出有趣的电磁实验。
4.2 日常生活中的电荷电荷的这些原理不仅仅是实验室里的东西,实际上,它们也影响到我们日常生活中的许多方面。
等量同种正点电荷
注意:电场线、等势面的特点和电场线与等势面间的关系:
①电场线的方向为该点的场强方向,电场线的疏密表示场强的大小。
②电场线互不相交,等势面也互不相交。
③电场线和等势面在相交处互相垂直。
④电场线的方向是电势降低的方向,而且是降低最快的方向。
⑤电场线密的地方等差等势面密;等差等势面密的地方电场线也密。
电容器动态变化的两类典型问题讨论
平行板电容器充电后,继续保持电容器两极板与电池两极相连接,若电容器的d 、S 、ε变化,将引起电容器的C 、Q 、U 、E 怎样变化:由于电容器始终连接在电池上,因此两板间的电压保持不变,可根据下列几式讨论C 、Q 、E 的变化情况
d
d U E d S kd SU CU Q d S kd S C 144∝=∝==∝= επεεπε 平行板电容器充电后,切断与电池的连接,若电容器的d 、S 、ε变化,将引起电容器的C 、Q 、U 、E 怎样变化:由于电容器充电后,切断与电池的连接,使电容器的带电量保持不变,可根据下列几式讨论C 、U 、E 的变化情况
S Q S kQ d kd
S Q Cd Q d S d S kdQ d kd d S kd S C εεππεεεππεεπε∝=⋅==∝=∝=44,4,4UE= 4SQ CQU=。
等量的点电荷形成的电场中的场强和电势特点一. 等量的同种电荷形成的电场的特点(以正电荷形成的场为例)设两点电荷的带电量均为q,间距为R,向右为正方向1.场强特点:在两个等量正电荷的连线上,由A点向B点方向,电场强度的大小先减后增,即中点O处, 场强最小为0;场强的方向先向右再向左, 除中点O外,场强方向指向中点O在两个等量正电荷连线的中垂线上,由O点向N(M)点方向,电场强度的大小先增后减;场强的方向由O点指向N(M)。
外推等量的两个负电荷形成的场结论:在两个等量负电荷的连线上,由A点向B点方向,电场强度的大小先减后增,中点O处, 场强最小为零;场强的方向先向左再向右(除中点O外)。
在等量负电荷的连线的中垂线上,由O点向N(M)点方向,电场强度的大小先增后减,场强的方向由N(M)指向O点2.电势特点:在两个等量正电荷的连线上,由A点向B点方向,电势先减后增,中点O处, 电势最小,但电势总为正。
在两个等量正电荷的连线的中垂线上,由O点向N(M)点方向,电势一直减小且大于零,即O点最大,N(M)点为零外推等量的两个负电荷形成的场在两个等量负电荷连线上,由A点向B点方向,电势先增后减,在中点O处, 电势最大但电势总为负;在两个等量负电荷连线的中垂线上,由O点向N(M)点方向,电势一直增大且小于零,即O点最小,N(M)点为零二:等量的异种电荷形成的电场的特点1.场强特点在两个等量异种电荷的连线上,由A点向B点方向,电场强度的大小先减小后增大,中点O处场强最小;场强的方向指向负电荷在两个等量异种电荷的连线的中垂线上,由O点向N(M)点方向,电场强度的大小一直在减小;场强的方向平行于AB连线指向负电荷一端2.电势特点:在两个等量异种电荷的连线上,由A点向B点方向,电势一直在减小,中点O处电势为零,正电荷一侧为正势,负电荷一侧为负势。
等量异种电荷连线的中垂线上任意一点电势均为零即等量异种电荷的连线的中垂线(面)是零势线(面)库仑定律内容表述:真空中两个静止点电荷之间的相互作用力的大小跟两个点电荷的电荷量的乘积成正比,跟它们的距离的二次方成反比.作用力的方向在两个点电荷的连线上公式: 静电力常量:k = 9.0×109 N·m2/C2库仑定律适用条件:真空中,点电荷点电荷——理想化模型,实际上是不存在的.但只要带电体本身的大小跟它们之间的距离相比可以忽略,带电体就可以看作点电荷.并非是体积小就能当点电荷(理想化研究方法)启示与小结:可以看出,万有引力公式和库仑定律公式在表面上很相似,只有质量和电荷量的区别,体现了科学的一种对称美,它们的实质区别是:首先万有引力公式计算出的力只能是相互吸引的力,绝没有相排斥的力.其次,由计算结果看出,电子和质子间的万有引力比它们之间的静电引力小的很多,因此在研究微观带电粒子间的相互作用时,主要考虑静电力,万有引力虽然存在,但相比之下非常小,所以可忽略不计电场:是力的作用媒介:电荷之间的相互作用是通过特殊形式的物质——电场发生的,电荷的周围都存在电场,电场的物质性是客观存在的,具有物质的基本属性——质量和能量。
点电荷的电势表达式
V = k q / r.
其中,V表示电势,k是库仑常数(8.9875 x 10^9 N
m^2/C^2),q是电荷量,r是距离。
这个表达式描述了点电荷在空间中产生的电势,它告诉我们电
荷大小和距离对电势的影响。
电势是描述电场的重要物理量,它表
示单位正电荷在电场中所具有的势能。
点电荷的电势表达式可以帮
助我们理解电荷之间的相互作用和电场的分布。
除了点电荷的电势表达式,我们还可以通过电势的梯度来计算
电场强度,从而进一步了解电场的性质和行为。
电势和电场是电磁
学中的重要概念,它们对于理解电荷之间的相互作用和电磁现象具
有重要意义。
通过研究点电荷的电势表达式,我们可以深入了解电场的特性,并且可以应用这些知识来解决实际问题,比如电场中的电荷运动、
电场能量的转换等。
因此,点电荷的电势表达式是电磁学中的重要
基础知识,它对于我们理解和应用电场理论具有重要意义。
点电荷电势的公式在物理学中,点电荷电势的公式可是一个相当重要的知识点。
咱们先来说说啥是点电荷。
想象一下,在一个大大的空间里,有一个小小的带电粒子,它自己孤零零地待在那儿,周围没有其他电荷干扰,这个小小的带电粒子就叫做点电荷。
点电荷电势的公式是:φ = kQ / r 。
这里的φ就是电势,k 是静电力常量,约等于 9.0×10^9 N·m²/C²,Q 表示点电荷的电荷量,r 是距离点电荷的距离。
那这个公式到底咋用呢?我给您举个例子。
比如说有一个带电荷量为 +5×10^(-6) C 的点电荷,您想知道距离它 3 米处的电势是多少。
这时候,您就可以把数字代入公式啦。
k 是 9.0×10^9 N·m²/C²,Q 是5×10^(-6) C,r 是 3 米,也就是 3 m 。
那电势φ 就等于9.0×10^9×5×10^(-6)÷3 ,算出来就是 1.5×10^4 V 。
再比如说,有一次我在给学生们讲这个知识点的时候,有个调皮的小家伙就问我:“老师,这公式有啥用啊?难道我们在生活中还能到处碰到点电荷不成?”我笑着跟他说:“孩子,你可别小瞧这公式。
你想想看,咱们家里用的电,其实就是电荷在电线里流动产生的。
虽然电线里的电荷分布不是简单的点电荷,但这个公式背后的原理可是能帮助工程师们设计出更安全、更高效的电路呢!”这个公式不仅能帮助我们计算简单情况下的电势,还能让我们更深入地理解电场的性质。
比如说,当r 越来越大时,电势φ会越来越小,这就说明电场的强度随着距离的增加而减弱。
而且啊,理解点电荷电势的公式对于学习更复杂的电磁学知识也特别重要。
就像盖房子,这就是咱们的基石,如果基石不牢固,后面的知识大厦可就摇摇欲坠啦。
总之,点电荷电势的公式虽然看起来简单,但其蕴含的物理意义和实际应用可是非常广泛和重要的。
一、场强分布图
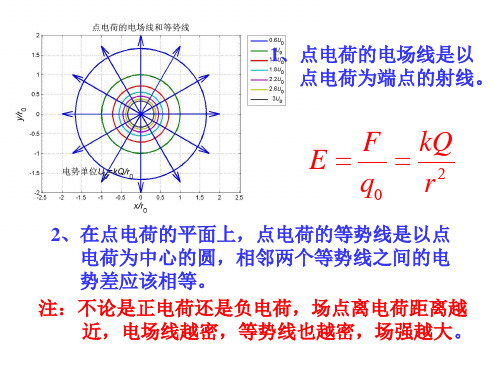
点电荷的电场线
等量异种点电荷电场线等量同种正电荷电
场线
二、列表比较
下面均以无穷远处为零电势点,场强为零。
孤
立的正点电荷电场
线
直线,起于正电荷,终止于无穷远。
场强
离场源电荷越远,场强越小;与场源电荷等距的各点组
成的球面上场强大小相等,方向不同。
电势
离场源电荷越远,电势越低;与场源电荷等距的各点组
成的球面是等势面,每点的电势为正。
等势
面
以场源电荷为球心的一簇簇不等间距的球面,离场源电
荷越近,等势面越密。
孤立电场
线
直线,起于无穷远,终止于负电荷。
如有侵权请联系告知删除,感谢你们的配合!。