江苏省高考数学第一轮复习单元试卷13：直线与圆锥曲线的位置关系

2020高考数学冲刺复习考点45 直线与圆锥曲线的位置关系1．已知抛物线C ：22(0)y px p =>，点F 为抛物线的焦点，焦点F 到直线3430x y -+=的距离为1d ，焦点F 到抛物线C 的准线的距离为2d ，且1235d d =. （1）求抛物线C 的标准方程；（2）若在x 轴上存在点M ，过点M 的直线l 分别与抛物线C 相交于P ，Q 两点，且2211PMQM+为定值，求点M 的坐标.【答案】（1）24y x =（2）(2,0) 【解析】解：（1）由题意知，焦点F 的坐标为,02p ⎛⎫ ⎪⎝⎭，则133362510pp d ++==，2d p =， 又363105p p +=，解得：2p =. 故抛物线C 的标准方程为24y x =.（2）设点M 的坐标为(,0)t ，设点P ，Q 的坐标分别为11(,)x y ，22(,)x y ， 显然直线l 的斜率不为0. 设直线l 的方程为x my t =+. 联立方程24x my t y x=+⎧⎨=⎩，消去x ，并整理得2440y my t --=， 则()2160m t ∆=+>且124y y m +=，124y y t =-.由1||PM ==，2||QM y ==.有()()222222121111||||11PM QM m y m y +=+++()()()2222122222222121682116121y y m t t m m y y m t m t +++===+++.若2211||||PM QM +为定值，必有2t =.所以当2211||||PM QM +为定值时，点M 的坐标为(2,0).2．（江苏省南通市2019届高三模拟练习卷四模）如图，已知F 是抛物线C ：24y x =的焦点，过E(﹣l ，0)的直线l 与抛物线分別交于A ，B 两点（点A ，B 在x 轴的上方）．（1）设直线AF ，BF 的斜率分別为1k ，2k ，证明：120k k +=； （2）若∆ABF 的面积为4，求直线l 的方程． 【答案】(1)见解析；(2)210x +=. 【解析】（1）当直线l 的斜率为0时，直线与抛物线只有一个交点，不合题意．当直线l 的斜率不为0时，设直线l 的方程为x ＝my ﹣1，A （x 1，y 1），B （x 2，y 2）， 联立抛物线方程可得得y 2﹣4my+4＝0，可得y 1+y 2＝4m ，y 1y 2＝4 ∴121212y y k k x 1x 1+=+=--()()()()()1212121222242402222my y y y m mmy my my my -+⨯-⨯==----. （2）S △ABF ＝S △EFB ﹣S △EFA ＝|y 1﹣y 2|()221212416164y y y y m +-=-=．解得m ＝2±（负值舍去）． ∴直线l 的方程为：210x +=．3．（江苏省南通市2019届高三模拟练习卷四模）如图，在平面直角坐标系xOy 中，椭圆C ：22221x y a b+=(a＞b ＞0)经过点(0，3-，点F 是椭圆的右焦点，点F 到左顶点的距离和到右准线的距离相等．过点F 的直线l 交椭圆于M ，N 两点．（1）求椭圆C 的标准方程；（2）当MF ＝2FN 时，求直线l 的方程；（3）若直线l 上存在点P 满足PM·PN ＝PF 2，且点P 在椭圆外，证明：点P 在定直线上． 【答案】（1）22143x y +=；（25250x y ±-=；（3）见解析. 【解析】（1）设椭圆的截距为2c ，由题意，b 3由点F 到左顶点的距离和到右准线的距离相等，得a+c ＝2a c c-，又a 2＝b 2+c 2，联立解得a ＝2，c ＝1．∴椭圆C 的标准方程为22143x y +=；（2）当直线l 与x 轴重合时，M （﹣2，0），N （2，0），此时MF ＝3NF ，不合题意； 当直线l 与x 轴不重合时，设直线l 的方程为x ＝my+1，M （x 1，y 1），N （x 2，y 2），联立22my 1x y 143x =+⎧⎪⎨+=⎪⎩，得（3m 2+4）y 2+6my ﹣9＝0．△＝36m 2+36（m 2+4）＞0．122634m y y m +=-+ ①，1229y y 3m 4=-+②，由MF ＝2FN ，得y 1＝﹣2y 2③， 联立①③得，1222126,3434m my y m m =-=++， 代入②得，()22227293434m m m-=-++，解得25m =5250x y ±=；（3）当直线l 的斜率为0时，则M （2，0），N （﹣2，0），设P （x 0，y 0）， 则PM•PN ＝|（x 0﹣2）（x 0+2）|，∵点P 在椭圆外，∴x 0﹣2，x 0+2同号，又()()()()2220000PF x 1,x 2x 2x 1=-∴-+=-，解得052x =． 当直线l 的斜率不为0时，由（2）知，1212226m 9y y ,y y 3m 43m 4+=-=-++， 22210200PM 1m y y ,PN 1m y y ,PF 1m y =+-=+-=+．∵点P 在椭圆外，∴y 1﹣y 0，y 2﹣y 0同号， ∴PM•PN ＝（1+m 2）（y 1﹣y 0）（y 2﹣y 0）＝()()221201201my yy y y y ⎡⎤+-++⎣⎦()()2222002269113434m m y m y m m ⎛⎫=++-=+ ⎪++⎝⎭，整理得032y m =，代入直线方程得052x =．∴点P 在定直线52x =上． 4．（江苏省南通市2019届高三适应性考试）已知抛物线C ：22(0)y px p =>的焦点为F ，过F 且斜率为43的直线l 与抛物线C 交于A ，B 两点，B 在x 轴的上方，且点B 的横坐标为4.（1）求抛物线C 的标准方程；（2）设点P 为抛物线C 上异于A ，B 的点，直线PA 与PB 分别交抛物线C 的准线于E ，G 两点，x 轴与准线的交点为H ，求证：HG HE ⋅为定值，并求出定值.【答案】（1）24y x =（2）见证明【解析】（1）由题意得：(,0)2pF ， 因为点B 的横坐标为4，且B 在x 轴的上方， 所以8)B p ， 因为AB 的斜率为43，4342=-，整理得：80p +=，即0=，得2p =， 抛物线C 的方程为：24y x =.（2）由（1）得：(4,4)B ，(1,0)F ，淮线方程1x =-， 直线l 的方程：4(1)3y x =-， 由24(1)34y x y x ⎧=-⎪⎨⎪=⎩解得14x =或4x =，于是得1(,1)4A -. 设点2(,)4n P n ，又题意1n ≠±且4n ≠±,所以直线PA ：41114y x n ⎛⎫+=- ⎪-⎝⎭，令1x =-，得41n y n +=--， 即41n HE n +=--， 同理可得：444n HG n -=+， 444414n n HG HE n n +-⋅=-⋅=-+. 5．（江苏省苏州市2019届高三高考模拟最后一卷）已知椭圆C ：22221(0)x y a b a b+=>>的左、右焦点分别为1F ，2F ，离心率为12，点P 是椭圆C 上的一个动点，且12PF F ∆（1）求椭圆C 的方程；（2）设斜率不为零的直线2PF 与椭圆C 的另一个交点为Q ，且PQ 的垂直平分线交y 轴于点1(0,)8T ，求直线PQ 的斜率.【答案】（1）22143x y +=（2）12或32【解析】(1)因为椭圆离心率为12，当P 为C 的短轴顶点时，12PF F △所以22212122c a a b c c b ⎧=⎪⎪=+⎨⎪⎪⨯⨯=⎩，所以21a b c =⎧⎪=⎨⎪=⎩，故椭圆C 的方程为:22143x y +=.（2）设直线PQ 的方程为()1y k x =-，当0k ≠时，()1y k x =-代入22143x y +=，得:()22223484120k x k x k +-+-=.设()()1122,,,P x y Q x y ，线段PQ 的中点为()00,N x y ，212024234x x k x k+==+，()1200231234y y k y k x k +-==-=+ 即22243,3434k k N k k ⎛⎫- ⎪++⎝⎭因为TN PQ ⊥，则1TN PQ k k ⋅=-，所以222314381443k k k k k --+⋅=-+，化简得24830k k -+=，解得12k =或32k =，即直线PQ 的斜率为12或32.6．（江苏省扬州中学2019届高三4月考试）已知抛物线方程24y x =，F 为焦点，P 为抛物线准线上一点，Q 为线段PF 与抛物线的交点，定义:()PFd P FQ=. （1）当8(1)3P --，时，求()d P ； （2）证明:存在常数a ，使得2()d P PF a =+.（3）123,,P P P 为抛物线准线上三点，且1223PP P P =，判断13()()d P d P +与22()d P 的关系.【答案】（1）83；（2）证明见解析；（3）()()()1322d P d Pd P+>. 【解析】（1）因为8443(1)233PFk y x==⇒=-.联立方程24(1)1344Qy xxy x⎧=-⎪⇒=⎨⎪=⎩，则1083()534PFd PQF⎧=⎪⎪⇒=⎨⎪=⎪⎩.（2）当()1,0P-，易得2()2a d P PF=-=，不妨设()1,PP y-，0Py>，直线:1PF x my=+，则2Pmy=-，联立214x myy x=+⎧⎨=⎩，2440y my--=，224(4)16221Qm my m m++==++，()222212()||212221PPQy m d P PF m yy m m m+ -=-+=+++2212122m m m+-+=-+=.（3）设()()()1122331,,1,,1,P y P y P y---，则()()()13224d P d P d P+-⎡⎤⎣⎦1322PF P F P F =+-2221324424y y y =+++-+ 222131344242y y y y +⎛⎫=+++-+ ⎪⎝⎭()22213134416y y y y =+++-++，因为()()222213134416y y y y ⎡⎤+++-++⎣⎦22131224428y y y y =++--，又因()()()()2222213131313444480y y y y y y y y ++-+=+->，所以()()()1322d P d P d P +>.7．（江苏省南京金陵中学、海安高级中学、南京外国语学校2019届高三第四次模拟考试）已知在平面直角坐标系xOy 中，椭圆C ：22221x y a b+=（a ＞b ＞0）离心率为2，其短轴长为2．（1）求椭圆C 的标准方程；（2）如图，A 为椭圆C 的左顶点，P ，Q 为椭圆C 上两动点，直线PO 交AQ 于E ，直线QO 交AP 于D ，直线OP 与直线OQ 的斜率分别为k 1，k 2，且k 1k 2＝12-，,AD DP AE λ==u u ur u u u r u u u r EQ μuuu r （λ，μ为非零实数），求λ2+μ2的值．【答案】（1）2212x y +=；（2）1 【解析】（1）因为短轴长2b ＝2，所以b ＝1，又离心率e ＝2c a =a 2﹣b 2＝c 2，解得a ＝2，c ＝1，则椭圆C 的方程为22x +y 2＝1； （2）由（1）可得点 A（﹣2，0），设P （x 1，y 1），D （x 0，y 0），则y 1＝k 1x 1，y 0＝k 2x 0， 由AD DP λ=u u u r u u u r可得x 0+2＝λ（x 3B x 、﹣x 0），y 0＝λ（y 1﹣y 0），即有x 0＝11021,1x y y λλλλ-+=+，k 1x 1＝y 1＝1λλ+y 0＝1λλ+k 2x 0＝k 2（x 1﹣2λ）， 两边同乘以k 1，可得k 12x 1＝k 1k 2（x 1﹣2λ）＝﹣12（x 1﹣2λ）， 解得x 1＝()()11221122,1212y k k k λλ=++，将P （x 1，y 1）代入椭圆方程可得λ2＝22112k +， 由AE EQ μ=u u u r u u u r可得μ2＝2122212k 11212k k =++，可得λ2+μ2＝1． 8．（江苏省七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第三次调研考试）如图，在平面直角坐标系xoy 中，已知椭圆22221y x C a b+=：（0a b >>）的上顶点为()0,3A ，圆2224a O x y +=：经过点()01M ，．（1）求椭圆C 的方程；（2）过点M 作直线1l 交椭圆C 于P ，Q 两点，过点M 作直线1l 的垂线2l 交圆O 于另一点N ．若△PQN 的面积为3，求直线1l 的斜率．【答案】（1）13422=+y x ；（2）12± 【解析】（1）因为椭圆C 的上顶点为(03A ，，所以3b =22214O x y a +=：经过点()01M ，，所以2a =． 所以椭圆C 的方程为13422=+y x ．（2）若1l 的斜率为0，则PQ =，2MN =， 所以△PQN的面积为3，不合题意，所以直线1l 的斜率不为0． 设直线1l 的方程为1y kx =+，由221431x y y kx ，⎧+=⎪⎨⎪=+⎩消y 得()2234880k x kx ++-=， 设()11P x y ，，()22Q x y ，，则1x，2x所以PQ =12x =-=. 直线2l 的方程为11y x k=-+，即0x ky k+-=，所以MN = 所以△PQN 的面积MN PQ S ⋅=21132==， 解得12k =±，即直线1l 的斜率为12±． 9．（江苏省苏锡常镇四市2019届高三教学情况调查二）在平面直角坐标系xOy 中，已知抛物线C ：24y x=的焦点为F ，过F 的直线l 交抛物线C 于A ，B 两点． （1）求线段AF 的中点M 的轨迹方程；（2）已知△AOB 的面积是△BOF 面积的3倍，求直线l 的方程．【答案】（1）221y x =-；（2）)1y x =±-【解析】（1）设线段AF 的中点的坐标为(),M x y ，()11,A x y 由抛物线C 的方程24y x =可得：焦点()1,0F由中点坐标公式可得：1110,22x y x y ++== 即：1121,2x x y y =-=又()11,A x y 在抛物线24y x =上，所以2114y x =，将1121,2x x y y =-=代入上式可得：()()22421y x =- 整理得：221y x =-所以线段AF 的中点M 的轨迹方程为：221y x =- （2）依据题意作出图形，如下：设()()1122,,,A x y B x y ，且1y 与2y 的取值一正、一负因为△AOB 的面积是△BOF 面积的3倍，所以直线AB 的斜率存在， 且OAF ∆的面积是OBF ∆面积的2倍， 即：1211222OF y OF y ⨯⨯=⨯⨯⨯，整理得：122y y =- 设直线AB 的方程为：()1y k x =-联立直线与抛物线方程可得：()241y xy k x ⎧=⎪⎨=-⎪⎩，整理得：204k y y k --=.所以124y y k+=，124y y ⋅=- 由121212244y y y y y y k ⎧⎪=-⎪⋅=-⎨⎪⎪+=⎩解得：22k =±.所以直线AB 的方程为：()221y x =±-10．（江苏省苏锡常镇四市2019届高三教学情况调查二）如图，在平面直角坐标系xOy 中，已知椭圆C ：22221x y a b +=(a ＞b ＞0)的左、右顶点分别为A 1(﹣2，0)，A 2(2，0)，右准线方程为x ＝4．过点A 1的直线交椭圆C 于x 轴上方的点P ，交椭圆C 的右准线于点D ．直线A 2D 与椭圆C 的另一交点为G ，直线OG 与直线A 1D 交于点H ．（1）求椭圆C 的标准方程；（2）若HG ⊥A 1D ，试求直线A 1D 的方程；（3）如果11A H A P λ=u u u u r u u u u r，试求λ的取值范围．【答案】（1）22143x y +=；（2）)62y x =+；（3）13,35⎛⎫ ⎪⎝⎭【解析】（1）由题可得：2a =，又椭圆右准线方程为x ＝4，所以24a c =，解得：1225，又222a b c =+，解得：23b =所以椭圆C 的标准方程为：22143x y +=.（2）设()11,G x y （10y <）,则2112GA y k x =-且2211143x y +=所以直线GD 的方程为：()1122y y x x =-- 联立直线GD 的方程与准线方程4x =可得：()11224y y x x x ⎧=-⎪-⎨⎪=⎩，整理得：1122y y x =-，所以1124,2y D x ⎛⎫⎪-⎝⎭， 所以()()111112024232A Dy y x k x --==---.又HG ⊥A 1D ，所以11HG A D k k ⋅=-，即：()1111132y yx x ⋅=--联立()22111111143132x y y y x x ⎧+=⎪⎪⎨⎪⋅=--⎪⎩可得：112,3x y ==. (D ∴所以()10426A D k ==--.所以直线1A D的方程为：()26y x =+. （3）设()4,D m ，(),P P P x y ，(),G G G x y ，(),H H H x y ，其中0m > 直线1A D 的方程为：()26my x =+ 联立椭圆方程可得：()2214326x y m y x ⎧+=⎪⎪⎨⎪=+⎪⎩，解得2254227P m x m -=+ 直线2A D 的方程为：()22my x =- 联立椭圆方程可得：()2214322x y m y x ⎧+=⎪⎪⎨⎪=-⎪⎩，解得22263G m x m -=+，263G m y m -=+ 所以直线OG 的方程为：2626my x m -=-联立直线OG 的方程与直线1A D 的方程可得：()226626my x my x m ⎧=+⎪⎪⎨-⎪=⎪-⎩，解得：226215H m x m -=+ 所以2125422,27P m A P y m ⎛⎫-=+ ⎪+⎝⎭u u u r ,212622,15H m A H y m ⎛⎫-=+ ⎪+⎝⎭u u u u r 又11A H A P λ=u u u u v u u u u v ，所以2222625422,2,1527H P m m y y m m λ⎛⎫⎛⎫--+=+ ⎪ ⎪++⎝⎭⎝⎭所以222262542221527m m m m λ⎛⎫--+=⨯+ ⎪++⎝⎭整理得：()222271121315315m m m λ+⎛⎫==+ ⎪++⎝⎭因为21515m +>，所以111213315λ⎛⎫<<+ ⎪⎝⎭，整理得：1335λ<< 11．（江苏省南通市2019届高三下学期4月阶段测试）已知()()2,0,2,0,A B C D 点、-依次满足()12,.2AC AD AB AC ==+u u u v u u u v u u u v u u u v（1）求点D 的轨迹；（2）过点A 作直线l 交以A B 、为焦点的椭圆于M N 、两点，线段MN 的中点到y 轴的距离为45，且直线l 与点D 的轨迹相切，求该椭圆的方程；（3）在（2）的条件下，设点Q 的坐标为()1,0，是否存在椭圆上的点P 及以Q 为圆心的一个圆，使得该圆与直线,PA PB 都相切，如存在，求出P 点坐标及圆的方程，如不存在，请说明理由【答案】（1）以原点为圆心，1为半径的圆；（2）22184x y +=； （3）存在点P ，其坐标为(或(2,,使得直线12,PF PF 与以Q 为圆心的圆()2211x y -+=相切 【解析】（1）设()()00,,,C x y D x y ，则()()002,,4,0AC x y AB =+=u u u v u u u v ()003,2,22x y AD x y ⎛⎫⇒=+=+⎪⎝⎭u u u v 则：00222x x y y =-⎧⎨=⎩ 代入()2220024AC x y u u u v =++=得：221x y +=∴点D 的轨迹是以原点为圆心，1为半径的圆（2）由题意可知直线l 斜率存在，设直线l 的方程为()2y k x =+……①椭圆的方程()22222144x y a a a +=>-……②由l1= 213k ⇒=将①代入②得：()222222224244440a k a x a k x a k a a +-++-+= 又213k =，可得()2224233404a x a x a a -+-+=设()11,M x y ，()22,N x y21224235a x x a ∴+=-=⨯- 28a ⇒=∴椭圆方程为：22184x y +=（3）假设存在椭圆上的一点()00,P x y ，使得直线,PA PB 与以Q 为圆心的圆相切 则Q 到直线,PA PB 的距离相等，又()()2,0,2,0,A B -则()000:220PA x y y x y --+=，()000:220PB x y y x y +--= 则12d d ===化简整理得：220008403280x x y -++= P Q 点在椭圆上 220028x y ∴+=解得：02x =或08x =（舍）02x =时，0y = 1r ∴=∴椭圆上存在点P，其坐标为(或(2,使得直线12,PF PF 与以Q 为圆心的圆()2211x y -+=相切．12．（江苏省苏州市2019届高三下学期阶段测试）在平面直角坐标系xOy 中，椭圆C的参数方程为,(),x y tsin ααα⎧=⎪⎨=⎪⎩为参数．在极坐标系(与直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴正半轴为极轴)中，直线l的方程为πsin()4ρθ-(1)求直线l 的直角坐标方程和椭圆C 的普通方程； (2)若直线l 与椭圆C 有公共点，求t 的取值范围．【答案】（1）20y x --=，(22213x y t t +=≠（2）((1][1+),-∞-∞U U U【解析】（1）由题意知π2ρsin θ4⎛⎫-= ⎪⎝⎭y x 20--=，由()αx y t sin αα⎧=⎪⎨=⋅⎪⎩为参数，得(222x y 1t 3t +=≠.(2)由22220x y 13t y x --=⎧⎪⎨+=⎪⎩消去y 得()322t 3x 12x 123t 0+++-=.因为直线l 与椭圆C 有公共点，所以()()222Δ124t 3123t 0=-+-≥,即()42tt 00t -≥≠．所以t 的取值范围是t 1t 1≥≤-或，所以t的取值范围是(][(),1∞∞-⋃-⋃⋃+.13．（江苏省七市2019届(南通、泰州、扬州、徐州、淮安、宿迁、连云港)高三第二次调研考试）如图所示，在平面直角坐标系xOy 中，已知椭圆C 1：2214x y +=，椭圆C 2：22221(0)x y a b a b +=>>，C 2与C 1的长轴∶1，离心率相同． （1）求椭圆C 2的标准方程；（2）设点P 为椭圆C 2上一点．① 射线PO 与椭圆C 1依次交于点A B ，，求证：PAPB为定值； ② 过点P 作两条斜率分别为12k k ，的直线12l l ，，且直线12l l ，与椭圆C 1均有且只有一个公共点，求证：12k k ⋅为定值．【答案】（1）22182x y +=；（2）①见解析，②见解析. 【解析】（1）设椭圆C 2的焦距为2c，由题意，a =，c a =，222a b c =+，解得b =C 2的标准方程为22x y 182+=。

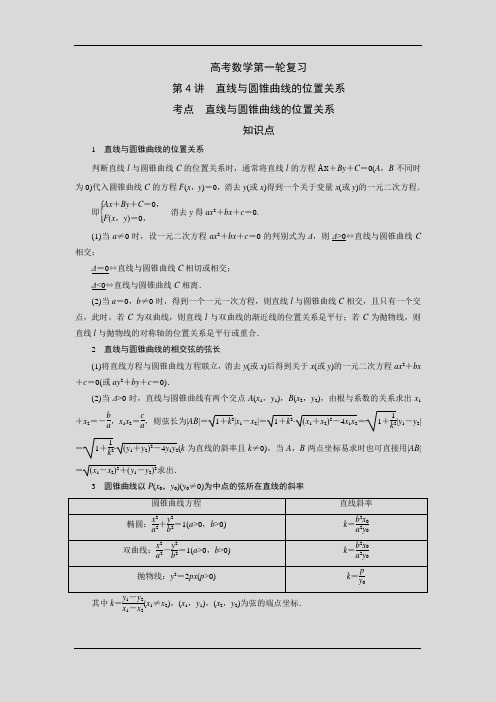
高考数学第一轮复习第4讲 直线与圆锥曲线的位置关系 考点 直线与圆锥曲线的位置关系知识点1 直线与圆锥曲线的位置关系判断直线l 与圆锥曲线C 的位置关系时，通常将直线l 的方程Ax ＋By ＋C ＝0(A ，B 不同时为0)代入圆锥曲线C 的方程F (x ，y )＝0，消去y (或x )得到一个关于变量x (或y )的一元二次方程．即⎩⎪⎨⎪⎧Ax ＋By ＋C ＝0，F (x ，y )＝0，消去y 得ax 2＋bx ＋c ＝0. (1)当a ≠0时，设一元二次方程ax 2＋bx ＋c ＝0的判别式为Δ，则Δ>0⇔直线与圆锥曲线C 相交；Δ＝0⇔直线与圆锥曲线C 相切或相交； Δ<0⇔直线与圆锥曲线C 相离．(2)当a ＝0，b ≠0时，得到一个一元一次方程，则直线l 与圆锥曲线C 相交，且只有一个交点，此时，若C 为双曲线，则直线l 与双曲线的渐近线的位置关系是平行；若C 为抛物线，则直线l 与抛物线的对称轴的位置关系是平行或重合．2 直线与圆锥曲线的相交弦的弦长(1)将直线方程与圆锥曲线方程联立，消去y (或x )后得到关于x (或y )的一元二次方程ax 2＋bx ＋c ＝0(或ay 2＋by ＋c ＝0)．(2)当Δ>0时，直线与圆锥曲线有两个交点A (x 1，y 1)，B (x 2，y 2)，由根与系数的关系求出x 1＋x 2＝－b a ，x 1x 2＝ca ，则弦长为|AB |＝1＋k 2|x 1－x 2|＝1＋k 2·(x 1＋x 2)2－4x 1x 2＝1＋1k2|y 1－y 2|＝1＋1k2·(y 1＋y 2)2－4y 1y 2(k 为直线的斜率且k ≠0)，当A ，B 两点坐标易求时也可直接用|AB |＝(x 1－x 2)2＋(y 1－y 2)2求出．3 圆锥曲线以P (x 0，y 0)(y 0≠0)为中点的弦所在直线的斜率圆锥曲线方程 直线斜率 椭圆：x 2a 2＋y 2b 2＝1(a >0，b >0)k ＝b 2x 0a 2y 0 双曲线：x 2a 2－y 2b2＝1(a >0，b >0)k ＝b 2x 0a 2y 0 抛物线：y 2＝2px (p >0)k ＝p y 0其中k ＝y 1－y 2x 1－x 2(x 1≠x 2)，(x 1，y 1)，(x 2，y 2)为弦的端点坐标．注意点直线与圆锥曲线的相切与只有一个公共点的关系直线与椭圆(圆)只有一个公共点是直线与椭圆(圆)相切的充要条件，而直线与双曲线(抛物线)只有一个公共点，只是直线与双曲线(抛物线)相切的必要不充分条件.入门测1．思维辨析(1)直线l与椭圆C相切的充要条件是：直线l与椭圆C只有一个公共点．()(2)直线l与双曲线C相切的充要条件是：直线l与双曲线C只有一个公共点．()(3)直线l与抛物线C相切的充要条件是：直线l与抛物线C只有一个公共点．()(4)如果直线x＝ty＋a与圆锥曲线相交于A(x1，y1)，B(x2，y2)两点，则弦长|AB|＝1＋t2|y1－y2|.()(5)若抛物线C上存在关于直线l对称的两点，则需满足直线l与抛物线C的方程联立消元后得到的一元二次方程的判别式Δ>0.()2．椭圆ax2＋by2＝1与直线y＝1－x交于A，B两点，过原点与线段AB中点的直线的斜率为32，则ab的值为()A.32 B.233C.932 D.23273．直线l经过抛物线y2＝4x的焦点F，与抛物线相交于A，B两点，若|AB|＝8，则直线l的方程为________．解题法[考法综述] 直线与圆锥曲线位置关系的判断、相交弦的弦长计算、中点弦问题等是考查热点，同时与函数、数列、平面向量等知识综合考查，难度较大．命题法1 直线与圆锥曲线的位置关系典例1 (1)若直线y ＝kx ＋2与双曲线x 2－y 2＝6的右支交于不同的两点，则k 的取值范围是( )A.⎝⎛⎭⎫－153，153 B.⎝⎛⎭⎫0，153 C.⎝⎛⎭⎫－153，0 D.⎝⎛⎭⎫－153，－1 (2)若直线l ：y ＝(a ＋1)x －1与曲线C ：y 2＝ax 恰好有一个公共点，则实数a 的取值为( ) A.⎩⎨⎧⎭⎬⎫－1，－45，0B ．{－1,0}C.⎩⎨⎧⎭⎬⎫－1，－45D.⎩⎨⎧⎭⎬⎫－45，0 【解题法】 直线与圆锥曲线位置关系的判断(1)直线与圆锥曲线相交或相离时，可直接联立直线与曲线的方程，结合消元后的一元二次方程求解．(2)直线与圆锥曲线相切时，尤其是对于抛物线与双曲线，要结合图形，数形结合求解． (3)当条件中含有参数时，要注意对参数进行讨论，尤其是在双曲线与抛物线中，必须要保证联立后的方程为二次方程才能由“Δ”进行判定．命题法2 直线与圆锥曲线的弦长问题典例2 已知椭圆E 的中心在坐标原点、对称轴为坐标轴，且抛物线x 2＝－42y 的焦点是它的一个焦点，又点A (1，2)在该椭圆上．(1)求椭圆E 的方程；(2)若斜率为2的直线l 与椭圆E 交于不同的两点B 、C ，当△ABC 的面积最大时，求直线l 的方程．【解题法】 直线与圆锥曲线相交时弦长的求法(1)定义法：过圆锥曲线的焦点的弦长问题，利用圆锥曲线的定义可优化解题．(客观题常用) (2)点距法：将直线的方程与圆锥曲线的方程联立，求出两交点的坐标，再运用两点间距离公式求弦长．(不常用)(3)弦长公式法：它体现了解析几何中的设而不求的思想，其实质是利用两点之间的距离公式以及一元二次方程根与系数的关系．(常用方法)命题法3 中点弦问题典例3 平面直角坐标系xOy 中，过椭圆M ：x 2a 2＋y 2b 2＝1(a >b >0)右焦点的直线x ＋y －3＝0交M 于A ，B 两点，P 为AB 的中点，且OP 的斜率为12.(1)求M 的方程；(2)C ，D 为M 上两点，若四边形ACBD 的对角线CD ⊥AB ，求四边形ACBD 面积的最大值．【解题法】弦中点问题的解题策略(1)涉及直线与圆锥曲线相交弦的中点和弦所在直线的斜率问题时，常用“点差法”“设而不求法”，并借助一元二次方程根的判别式、根与系数的关系、中点坐标公式及参数法求解．但在求得直线方程后，一定要代入原方程进行检验．(2)点差法求解弦中点问题的基本步骤为：①设点：即设出弦的两端点坐标．②代入：即代入圆锥曲线方程．③作差：即两式相减，再用平方差公式把上式展开．④整理：即转化为斜率与中点坐标的关系式，然后求解．对点练1．过点P(－2,0)的直线与抛物线C：y2＝4x相交于A、B两点，且|P A|＝12|AB|，则点A到抛物线C的焦点的距离为()A.53 B.75C.97D．22．设F为抛物线C：y2＝3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，O为坐标原点，则△OAB的面积为()A.334 B.938C.6332 D.943.已知点A(－2,3)在抛物线C：y2＝2px的准线上，过点A的直线与C在第一象限相切于点B，记C的焦点为F，则直线BF的斜率为()A.12 B.23C.34D.434．已知F 为抛物线y 2＝x 的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，OA →·OB →＝2(其中O 为坐标原点)，则△ABO 与△AFO 面积之和的最小值是( )A ．2B ．3 C.1728D.105．在平面直角坐标系xOy 中，P 为双曲线x 2－y 2＝1右支上的一个动点．若点P 到直线x －y ＋1＝0的距离大于c 恒成立，则实数c 的最大值为________．6．设F 为抛物线C ：y 2＝4x 的焦点，过点P (－1,0)的直线l 交抛物线C 于A ，B 两点，点Q 为线段AB 的中点．若|FQ |＝2，则直线l 的斜率等于________．7．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，点(2，2)在C 上．(1)求C 的方程；(2)直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M .证明：直线OM 的斜率与直线l 的斜率的乘积为定值．8．已知椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)过点(0，2)，且离心率e ＝22.(1)求椭圆E 的方程；(2)设直线l ：x ＝my －1(m ∈R )交椭圆E 于A ，B 两点，判断点G ⎝⎛⎭⎫－94，0与以线段AB 为直径的圆的位置关系，并说明理由．9．已知点A (0，－2)，椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，F 是椭圆E 的右焦点，直线AF的斜率为233，O为坐标原点．(1)求E的方程；(2)设过点A的动直线l与E相交于P，Q两点，当△OPQ的面积最大时，求l的方程．10．圆x2＋y2＝4的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为P(如图)．双曲线C1：x2a2－y2b2＝1过点P且离心率为 3.(1)求C1的方程；(2)椭圆C2过点P且与C1有相同的焦点，直线l过C2的右焦点且与C2交于A，B两点，若以线段AB为直径的圆过点P，求l的方程．11．如图，已知两条抛物线E1：y2＝2p1x(p1>0)和E2：y2＝2p2x(p2>0)，过原点O的两条直线l1和l2，l1与E1，E2分别交于A1，A2两点，l2与E1，E2分别交于B1，B2两点．(1)证明：A1B1∥A2B2；(2)过O作直线l(异于l1，l2)与E1，E2分别交于C1，C2两点．记△A1B1C1与△A2B2C2的面积分别为S1与S2，求S1S2的值．已知抛物线y2＝4x的焦点为F，过F作两条相互垂直的弦AB，CD，设弦AB，CD的中点分别为M，N.求证：直线MN恒过定点．课时练基础组1.抛物线y 2＝4x 的焦点为F ，准线为l ，经过F 且斜率为3的直线与抛物线在x 轴上方的部分相交于点A ，AK ⊥l ，垂足为K ，则△AKF 的面积是( )A ．4B ．3 3C ．4 3D ．82．已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)上一点C ，过双曲线中心的直线交双曲线于A ，B 两点，记直线AC ，BC 的斜率分别为k 1，k 2，当2k 1k 2＋ln |k 1|＋ln |k 2|最小时，双曲线离心率为( ) A. 2 B. 3 C.2＋1D ．23．斜率为1的直线l 与椭圆x 24＋y 2＝1相交于A 、B 两点，则|AB |的最大值为( )A ．2 B.455C.4105D.81054.直线y ＝kx －2与抛物线y 2＝8x 交于A 、B 两点，且AB 中点的横坐标为2，则k 的值是________．5．已知两定点M (－1,0)，N (1,0)，若直线上存在点P ，使|PM |＋|PN |＝4，则该直线为“A 型直线”．给出下列直线，其中是“A 型直线”的是________(填序号)．①y ＝x ＋1；②y ＝2；③y ＝－x ＋3；④y ＝－2x ＋3.6．已知焦点在y 轴上的椭圆C 1：y 2a 2＋x 2b 2＝1经过点A (1,0)，且离心率为32.(1)求椭圆C 1的方程；(2)过抛物线C 2：y ＝x 2＋h (h ∈R )上点P 的切线与椭圆C 1交于两点M 、N ，记线段MN 与P A 的中点分别为G 、H ，当GH 与y 轴平行时，求h 的最小值．7. 已知圆O ：x 2＋y 2＝49，直线l ：y ＝kx ＋m 与椭圆C ：x 22＋y 2＝1相交于P 、Q 两点，O 为原点．(1)若直线l 过椭圆C 的左焦点，与圆O 交于A 、B 两点，且∠AOB ＝60°，求直线l 的方程； (2)若△POQ 的重心恰好在圆上，求m 的取值范围．8．已知F 1、F 2是双曲线x 2－y 215＝1的两个焦点，离心率等于45的椭圆E 与双曲线x 2－y 215＝1的焦点相同，动点P (m ，n )满足|PF 1|＋|PF 2|＝10，曲线M 的方程为x 22＋y 22＝1.(1)求椭圆E 的方程；(2)判断直线mx ＋ny ＝1与曲线M 的公共点的个数，并说明理由；当直线mx ＋ny ＝1与曲线M 相交时，求直线mx ＋ny ＝1截曲线M 所得弦长的取值范围．9．如图所示，已知抛物线C ：y 2＝4x 的焦点为F ，直线l 经过点F 且与抛物线C 相交于A ，B 两点．(1)若线段AB 的中点在直线y ＝2上，求直线l 的方程； (2)若线段|AB |＝20，求直线l 的方程．10．已知点A 、B 的坐标分别是(－1,0)、(1,0)．直线AM ，BM 相交于点M ，且它们的斜率之积为－2.(1)求动点M 的轨迹方程；(2)若过点N ⎝⎛⎭⎫12，1的直线l 交动点M 的轨迹于C 、D 两点，且N 为线段CD 的中点，求直线l 的方程．11．已知定点G (－3,0)，S 是圆C ：(x －3)2＋y 2＝72上的动点，SG 的垂直平分线与SC 交于点E ，设点E 的轨迹为M .(1)求M 的方程；(2)是否存在斜率为1的直线l ，使得l 与曲线M 相交于A ，B 两点，且以AB 为直径的圆恰好经过原点？若存在，求出直线l 的方程；若不存在，请说明理由．12．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为63，F 为椭圆在x 轴正半轴上的焦点，M ，N 两点在椭圆C 上，且MF →＝λFN →(λ>0)，定点A (－4,0)．(1)求证：当λ＝1时，MN →⊥AF →； (2)若当λ＝1时有AM →·AN →＝1063，求椭圆C 的方程； (3)在(2)的条件下，M ，N 两点在椭圆C 上运动，当AM →·AN →·tan ∠MAN 的值为63时，求出直线MN 的方程．能力组13已知F 1、F 2是双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右两个焦点，以线段F 1F 2为直径的圆与双曲线的一条渐近线交于点M ，与双曲线交于点N (设点M 、N 均在第一象限)，当直线MF 1与直线ON 平行时，双曲线的离心率的取值为e 0，则e 0所在的区间为( )A ．(1，2)B ．(2，3)C ．(3，2)D ．(2,3)14．已知中心在坐标原点的椭圆和双曲线有公共焦点(左、右焦点分别为F 1、F 2)，它们在第一象限的交点为P ，△PF 1F 2是以PF 1为底边的等腰三角形．若|PF 1|＝10，椭圆与双曲线的离心率分别为e 1，e 2，则e 1e 2的取值范围是( )A ．(0，＋∞)B.⎝⎛⎭⎫13，＋∞C.⎝⎛⎭⎫15，＋∞D.⎝⎛⎭⎫19，＋∞15如图，F 是椭圆的右焦点，以点F 为圆心的圆过原点O 和椭圆的右顶点，设P 是椭圆上的动点，点P 到椭圆两焦点的距离之和等于4.(1)求椭圆和圆的标准方程；(2)设直线l 的方程为x ＝4，PM ⊥l ，垂足为M ，是否存在点P ，使得△FPM 为等腰三角形？若存在，求出点P 的坐标；若不存在，请说明理由．16．如图，设椭圆的中心为原点O ，长轴在x 轴上，上顶点为A ，左，右焦点分别为F 1，F 2，线段OF 1，OF 2的中点分别为B 1，B 2，且△AB 1B 2是面积为4的直角三角形．(1)求该椭圆的离心率和标准方程；(2)过B1作直线l交椭圆于P，Q两点，使PB2⊥QB2，求直线l的方程．。

第十三单元 直线与圆锥曲线的位置关系一.选择题. (1) 椭圆141622=+y x 上的点到直线22=-+y x 的最大距离是( )A 3B 11C22D 10 (2) 过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点，它们的横坐标之和等于5，则这样的直线( )A 有且仅有一条B 有且仅有两条C 有无穷多条D 不存在(3) 设双曲线12222=-by a x (0<a<b)的半焦距c, 直线l 过(a, 0), (0, b)两点. 已知原点到直线l 的距离为43c,则双曲线的离心率为( )A 2B 3C 2D 332(4) 如果椭圆193622=+y x 的弦被点(4，2)平分，则这条弦所在的直线方程是 ( ) A 02=-y x B 042=-+y x C 01232=-+y x D 082=-+y x(5)过双曲线2x 2-y 2-8x +6=0的由焦点作直线l 交双曲线于A 、B 两点, 若|AB|=4, 则这样 的直线有 ( )A 4条B 3条C 2条D 1条(6) 已知定点A 、B 且|AB|=4，动点P 满足|PA|－|PB|=3，则|PA|的最小值是 ( )A21 B23 C27 D 5(7) 直线l 交椭圆4x 2+5y 2=80于M 、N 两点, 椭圆的上顶点为B 点, 若△BMN 的重心恰好落在椭圆的右焦点上, 则直线l 的方程是 ( )A 5x +6y -28=0B 5x +6y -28=0C 6x +5y -28=0D 6x -5y -28=0 (8) 过抛物线2y ax =(a>0)的焦点F 作一直线交抛物线于P 、Q 两点，若线段PF 与FQ 的长分别为p 、q ，则11p q+等于 ( )A2a B 12aC 4aD4a(9) 已知双曲线13622=-y x 的焦点为F 1、F 2，点M 在双曲线上且MF 1⊥x 轴，则F 1到直线F 2M 的距离为( ) A563 B665 C56 D65(10) 点P （-3，1）在椭圆)0(12222>>=+b a by a x 的左准线上，过点P 且方向为)5,2(-=的光线，经直线2-=y 反射后通过椭圆的左焦点，则这个椭圆的离心率为( )A 33B31 C22D21二.填空题(11) 椭圆192522=+y x 的两焦点为F 1，F 2，一直线过F 1交椭圆于P 、Q ，则△PQF 2的周长为 ___________. (12) 若直线l 过抛物线2y ax =(a>0)的焦点，并且与y 轴垂直，若l 被抛物线截得的线段长为4，则a=_______(13) 过点)1,3(-M 且被点M 平分的双曲线1422=-y x 的弦所在直线方程为 .(14) 已知F 1、F 2是椭圆42x +y 2=1的两个焦点, P 是该椭圆上的一个动点, 则|PF 1|·|PF 2|的最大值是 . 三.解答题(15) 如图，O 为坐标原点，过点P （2，0）且斜率为k 的直线l 交抛物线y 2=2x 于M （x 1,y 1）,N(x 2, y 2)两点． （1）写出直线l 的方程； （2）求x 1x 2与y 1y 2的值； （3）求证：OM ⊥ON ．(16) 已知椭圆C ：22a x ＋22by ＝1（a ＞b ＞0）的左．右焦点为F 1、F 2，离心率为e. 直线l ：y ＝e x ＋a 与x 轴．y 轴分别交于点A 、B ，M 是直线l 与椭圆C 的一个公共点，P 是点F 1关于直线l 的对称点，设AM ＝λAB .（Ⅰ）证明：λ＝1－e 2； （Ⅱ）若43=λ，△PF 1F 2的周长为6；写出椭圆C 的方程.(17) 已知中心在原点的双曲线C 的右焦点为（2，0），右顶点为)0,3(（1）求双曲线C 的方程； （2）若直线2:+=kx y l 与双曲线C 恒有两个不同的交点A 和B ，且2>⋅（其中O 为原点）. 求k 的取值范围.(18) 如图，已知椭圆的中心在坐标原点，焦点12,F F 在x 轴上，长轴12A A 的长为4，左准线l 与x 轴的交点为M ，|MA 1|∶|A 1F 1|＝2∶1． (Ⅰ)求椭圆的方程；(Ⅱ)若点P 为l 上的动点，求∠F 1PF 2最大值参考答案一选择题: 1.D[解析]：设椭圆141622=+y x 上的点P （4cos θ，2sin θ）则点P 到直线022=-+y x 的距离d=5|2)4sin(24|5|2sin 4cos 4|-+=-+πθθθ105|224|max =--=d2.B[解析]：过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点，若直线AB 的斜率不存在，则横坐标之和等于2，不适合。

. 直线与圆锥曲线的位置关系
.已知为椭圆的两个焦点，过的直线交椭圆于、两点若
，则．
.过抛物线的焦点作倾角为的直线，与抛物线分别交于、两点（在轴左侧），则．
.已知椭圆（＞＞）的右焦点为，右准线为，离心率过顶点(，)作,垂足为，则直线的斜率等于.
.双曲线（，）的左、右焦点分别是，过作倾斜角为的直线交双曲线右支于点，若垂直于轴，则双曲线的离心率为.
.已知椭圆的中心为坐标原点，短轴长为，一条准线方程为：＝.
()求椭圆的标准方程；
()设为坐标原点，是椭圆的右焦点，点是直线上的动点，过点作的垂
线与以为直径的圆交于点，求证：线段的长为定值．
.过点(，)的椭圆的离心率为，椭圆与轴交于两点、，过点的直线与椭圆交于另一点，并与轴交于点，直线与直线交于点．
（）当直线过椭圆右焦点时，求线段的长；
（Ⅱ）当点异于点时，求证：为定值．
.已知抛物线:上横坐标为的点到焦点的距离为.
（Ⅰ）求抛物线的方程；
（Ⅱ）设直线与抛物线交于两点，，且（，且为常数）.过弦的中点作平行于轴的直线交抛物线于点，连结、得到.
（）求证：；
（）求证：的面积为定值.
【回顾反思】
．直线与圆锥曲线的位置关系。

12. 直线与圆锥曲线的位置关系1.设F 1、F 2为椭圆2214x y +=的左右焦点，过椭圆中心任作一直线与椭圆交于P ，Q 两点，当21PF PF ⋅=_________时，四边形PF 1QF 2的面积最大．2. 以双曲线12x 2－4y 2=3的焦点为焦点，过直线l ：y =x +3上一点P ，且长轴最短的椭圆方程是___________．3. 已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率是63，过椭圆上一点M 作直线MA ，MB 交椭圆于A ，B 两点，且斜率分别为k 1，k 2，若点A ，B 关于原点对称，则k 1k 2的值为________．4. 设点F 1、F 2分别为椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的左、右两焦点，直线l 为右准线．若在椭圆上存在点M ，使MF 1，MF 2，点M 到直线l 的距离d 成等比数列，则此椭圆离心率e 的取值范围是________． 5. 已知双曲线2222b y a x -=1的右焦点是F ，右顶点是A ,虚轴的上端点是B ，AB ·AF =6-43，∠BAF =150°.（1）求双曲线的方程；（2）设Q 是双曲线上的点，且过点F 、Q 的直线l 与y 轴交于点M ，若+2=0，求直线l 的斜率.6. 已知C B A ,,均在椭圆)1(1:222>=+a y ax M 上，直线AB 、AC 分别过椭圆的左右焦点1F 、2F ，当120AC F F ⋅=时，有21219AF AF AF=⋅. (Ⅰ)求椭圆M 的方程;(Ⅱ)设P 是椭圆M 上的任一点，EF 为圆()12:22=-+y x N 的任一条直径，求⋅的最大值.7. 已知定点C （-1，0）及椭圆x 2+3y 2=5,过点C 的动直线与椭圆相交于A ，B 两点.（1）若线段AB 中点的横坐标是-21，求直线AB 的方程；（2）在x 轴上是否存在点M ，使MA ·MB 为常数？若存在，求出点M 的坐标；若不存在，请说明理由.【回顾反思】12．直线与圆锥曲线的位置关系1. -22. 22154x y +=3. 设A (x 0，y 0)，B (－x 0，－y 0)，则x 20a 2＋y 20b 2＝1，再设 M (x 1，y 1)，则x 21a 2＋y 21b 2＝1，所以k 1·k 2＝y 1－y 0x 1－x 0·y 1＋y 0x 1＋x 0＝y 21－y 20x 21－x 20＝－b 2a 2＝－a 2－c 2a 2＝－1＋e 2＝－1＋69＝－13. 4. 因为MF 22＝MF 1·d ，且MF 2d＝e ，所以MF 1＝e ·MF 2.设M (x 0，y 0)，则有 a ＋ex 0＝e (a －ex 0)，解得x 0＝a(e －1)e (1＋e ).又因为－a ≤x 0≤a ，所以1－e ≤e ＋e 2， 所以2－1≤e ＜1.5. （1）由条件知A(a,0),B(0,b),F(c,0)AB ·AF =（-a, b)·(c-a,0)=a(a-c)=6-43 cos ∠BAF=)()(a c c c a a AF AB AF AB --==-c a =cos150°=-23. ∴a=23c,代入a(a-c)=6-43中得c=22. ∴a=6,b 2=c 2-a 2=2,故双曲线的方程为12622=-y x . (2)∵点F 的坐标为（22，0）.∴可设直线l 的方程为y=k(x-22),令x=0，得y=-22k ，即M(0,-22k)设Q （m,n ），则由MQ +2QF =0得(m,n+22k)+2(22-m,-n)=(0,0).即(42-m,22k-n)=（0,0).即⎪⎩⎪⎨⎧==k n m 2224，∵12622=-n m . ∴2)22(6)24(22k -=1，得k 2=1213，k=±639.· ·6. 解:(1)因为120AC F F ⋅=，所以有12AC F F ⊥所以12AF F ∆为直角三角形；1122cos AF F AF AF ∴∠=则有22212121221199cos 9AF AF AF AF F AF AF AF AF ⋅=∠=== 所以，123AF AF = a 2=+，123,22a a AF AF ∴== 在12AF F ∆中有2221212AF AF F F =+即)1(4223222-+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛a a a ，解得22=a 所求椭圆M 方程为1222=+y x (2)()()-⋅-=⋅ ()()()1222-=--=-⋅--=NP NF NP NP NF NP NF 从而将求PF PE ⋅的最大值转化为求2的最大值. P 是椭圆M 上的任一点，设()00,y x P ，则有122020=+y x 即202022y x -= 又()2,0N ，所以()()10222020202+--=-+=y y x NP . 而[]1,10-∈y ,所以当10=y 时，2取最大值9故PF PE ⋅的最大值为8.7. （1）依题意，直线AB 的斜率存在，设直线AB 的方程为y=k(x+1), 将y=k(x+1)代入x 2+3y 2=5,消去y 整理得(3k 2+1)x 2+6k 2x+3k 2-5=0.设A （x 1,y 1）,B(x 2,y 2),则⎪⎩⎪⎨⎧+-=+>-+-=∆.136,0)53)(13(4362221224k k x x k k k 由线段AB 中点的横坐标是-21， ① ②得221x x +=-13322+k k =-21,解得k=±33，适合①. 所以直线AB 的方程为x-3y+1=0,或x+3y+1=0.(2)假设在x 轴上存在点M （m ，0），使·为常数. （ⅰ）当直线AB 与x 轴不垂直时，由（1）知 x 1+x 2=-13622+-k k ,x 1x 2=135322+-k k . ③ 所以MA ·MB =（x 1-m ）(x 2-m)+y 1y 2=(x 1-m)(x 2-m)+k 2(x 1+1)(x 2+1)=(k 2+1)x 1x 2+(k 2-m)(x 1+x 2)+k 2+m 2.将③代入，整理得·=135)16(22+--k k m +m 2 =133142)13)(312(22+--+-k m k m +m 2 =m 2+2m-31-)13(31462++k m . 注意到·是与k 无关的常数，从而有 6m+14=0，m=-37，此时·=94.（ⅱ）当直线AB 与x 轴垂直时，此时点A ，B 的坐标分别为⎪⎪⎭⎫ ⎝⎛-32,1、⎪⎪⎭⎫ ⎝⎛--32,1， 当m=-37时，亦有·=94.综上，在x 轴上存在定点M ⎪⎭⎫ ⎝⎛-0,37，使·为常数.。

直线与圆锥曲线的位置关系(1)从几何角度看：要特别注意当直线与双曲线的渐进线平行时，直线与双曲线只有一个交点；当直线与抛物线的对称轴平行或重合时，直线与抛物线也只有一个交点。

(2)从代数角度看：设直线L的方程与圆锥曲线的方程联立得到ax°+bx+c=0.①.若a=0，当圆锥曲线是双曲线时，直线L与双曲线的渐进线平行或重合；当圆锥曲线是抛物线时，直线L与抛物线的对称轴平行或重合。

1、圆锥曲线的范围问题有两种常用方法：（1）寻找合理的不等式，常见有△＞0和弦的中点在曲线内部；（2）所求量可表示为另一变量的函数，求函数的值域。

2、圆锥曲线的最值、定值及过定点等难点问题。

直线与圆锥曲线的位置关系：(1)从几何角度来看，直线和圆锥曲线有三种位置关系：相离、相切和相交，相离是直线和圆锥曲线没有公共点，相切是直线和圆锥曲线有唯一公共点，相交是直线与圆锥曲线有两个不同的公共点，并特别注意直线与双曲线、抛物线有唯一公共点时，并不一定是相切，如直线与双曲线的渐近线平行时，与双曲线有唯一公共点，但这时直线与双曲线相交；直线平行（重合）于抛物线的对称轴时，与抛物线有唯一公共点，但这时直线与抛物线相交，故直线与双曲线、抛物线有唯一公共点时可能是相切，也可能是相交，直线与这两种曲线相交，可能有两个交点，也可能有一个交点，从而不要以公共点的个数来判断直线与曲线的位置关系，但由位置关系可以确定公共点的个数．(2)从代数角度来看，可以根据直线方程和圆锥曲线方程组成的方程组解的个数确定位置关系．设直线l的方程与圆锥曲线方程联立得到ax2+bx+c=0．①若a=0，当圆锥曲线是双曲线时，直线l与双曲线的渐近线平行或重合；当圆锥曲线是抛物线时，直线l与抛物线的对称轴平行或重合．②若当Δ>0时，直线和圆锥曲线相交于不同两点，相交．当Δ=0时，直线和圆锥曲线相切于一点，相切．当Δ<0时，直线和圆锥曲线没有公共点，相离．直线与圆锥曲线相交的弦长公式：若直线l与圆锥曲线F(x，y)=0相交于A，B两点，求弦AB的长可用下列两种方法：(1)求交点法：把直线的方程与圆锥曲线的方程联立，解得点A，B 的坐标，然后用两点间距离公式，便得到弦AB的长，一般来说，这种方法较为麻烦．(2)韦达定理法：不求交点坐标，可用韦达定理求解．若直线l的方程用y=kx+m或x=n表示．。