红对勾理科数学10-3
- 格式:ppt
- 大小:4.89 MB
- 文档页数:59

人教版高中数学高一必修一答案目录•第一章线性方程与不等式•第二章函数基础•第三章函数的初等函数•第四章三角函数•第五章数列•第六章概率第一章线性方程与不等式1. 解答:(1)解:因为$$ \\begin{aligned} x+y&=-2\\\\ 2x-y&=1 \\end{aligned} $$(2)解得:$$ \\begin{aligned} x&=-\\frac{3}{5}\\\\ y&=-\\frac{7}{5} \\end{aligned} $$(3)所以方程的解为$x=-\\frac{3}{5}$,$y=-\\frac{7}{5}$。
(2)解:因为$$ \\begin{aligned} 2x+y&=-3\\\\ 3x-2y&=4 \\end{aligned} $$(3)解得:$$ \\begin{aligned} x&=-\\frac{11}{5}\\\\ y&=\\frac{7}{5} \\end{aligned} $$(4)所以方程的解为$x=-\\frac{11}{5}$,$y=\\frac{7}{5}$。
2. 解答:(1)解:根据题意,2x−3<4,移项得2x<7,再除以2得$x<\\frac{7}{2}$,所以不等式的解集为$x<\\frac{7}{2}$。
(2)解:根据题意,$3x+2\\leq 5$,移项得$3x\\leq 3$,再除以3得$x\\leq 1$,所以不等式的解集为$x\\leq 1$。
第二章函数基础1. 解答:(1)解:由题意,函数x(x)的定义域是$x\\geq -3$,根据函数的图象可得:当$x\\geq -3$时,x(x)的值为正;当x<−3时,x(x)的值为负。
(2)解:由题意,函数x(x)的定义域是$x\\leq 2$,根据函数的图象可得:当$x\\leq 2$时,x(x)的值为负;当x>2时,x(x)的值为正。
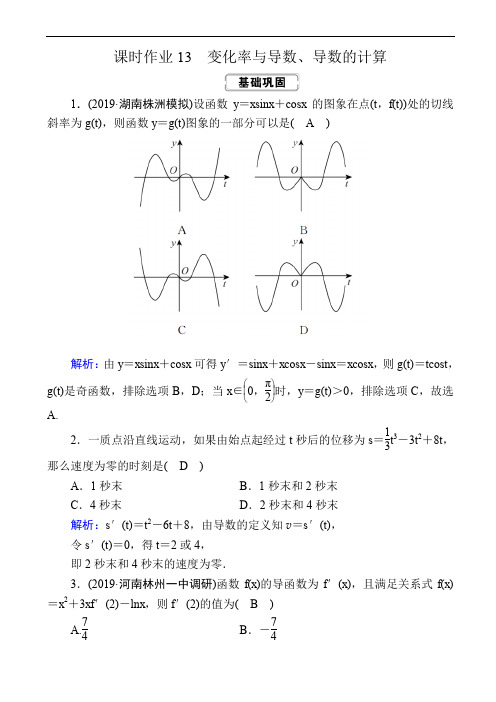
课时作业13 变化率与导数、导数的计算1.(2019·湖南株洲模拟)设函数y =x sin x +cos x 的图象在点(t ,f (t ))处的切线斜率为g (t ),则函数y =g (t )图象的一部分可以是( A )解析:由y =x sin x +cos x 可得y ′=sin x +x cos x -sin x =x cos x ,则g (t )=t cos t ,g (t )是奇函数,排除选项B ,D ;当x ∈⎝ ⎛⎭⎪⎫0,π2时,y =g (t )>0,排除选项C ,故选A.2.一质点沿直线运动,如果由始点起经过t 秒后的位移为s =13t 3-3t 2+8t ,那么速度为零的时刻是( D )A .1秒末B .1秒末和2秒末C .4秒末D .2秒末和4秒末解析:s ′(t )=t 2-6t +8,由导数的定义知v =s ′(t ),令s ′(t )=0,得t =2或4, 即2秒末和4秒末的速度为零.3.(2019·河南林州一中调研)函数f (x )的导函数为f ′(x ),且满足关系式f (x )=x 2+3xf ′(2)-ln x ,则f ′(2)的值为( B )A.74B .-74C.94D .-94解析:∵f (x )=x 2+3xf ′(2)-ln x ,∴f ′(x )=2x +3f ′(2)-1x ,令x =2,得f ′(2)=4+3f ′(2)-12, 解得f ′(2)=-74,故选B.4.(2019·广西五市联考)已知e 为自然对数的底数,曲线y =a e x +x 在点(1,a e +1)处的切线与直线2e x -y -1=0平行,则实数a =( B )A.e -1eB.2e -1e C.e -12eD.2e -12e解析:∵y ′=a e x +1,∴切线的斜率为y ′|x =1=a e +1, 又切线与直线2e x -y -1=0平行, ∴a e +1=2e ,解得a =2e -1e .5.(2019·广州模拟)设函数f (x )=x 3+ax 2,若曲线y =f (x )在点P (x 0,f (x 0))处的切线方程为x +y =0,则点P 的坐标为( D )A .(0,0)B .(1,-1)C .(-1,1)D .(1,-1)或(-1,1) 解析:∵f (x )=x 3+ax 2,∴f ′(x )=3x 2+2ax ,∵曲线y =f (x )在点P (x 0,f (x 0))处的切线方程为x +y =0,∴3x 20+2ax 0=-1,∵x 0+x 30+ax 20=0,解得x 0=±1, ∴当x 0=1时,f (x 0)=-1, 当x 0=-1时,f (x 0)=1.故选D.6.(2019·广东深圳模拟)设函数f (x )=x +1x +b ,若曲线y =f (x )在点(a ,f (a ))处的切线经过坐标原点,则ab =( D )A .1B .0C .-1D .-2解析:由题意可得,f (a )=a +1a +b ,f ′(x )=1-1x 2,所以f ′(a )=1-1a 2,故切线方程是y -a -1a -b =⎝⎛⎭⎪⎫1-1a 2(x -a ),将(0,0)代入得-a -1a -b =⎝⎛⎭⎪⎫1-1a 2(-a ),故b =-2a ,故ab =-2,故选D.7.(2019·乐山模拟)已知函数f (x )=e 2x -2e x +ax -1,曲线y =f (x )上存在两条斜率为3的切线,则实数a 的取值范围为( B )A .(3,+∞) B.⎝⎛⎭⎪⎫3,72C.⎝ ⎛⎭⎪⎫-∞,72 D .(0,3)解析:f (x )=e 2x -2e x +ax -1的导函数为f ′(x )=2e 2x -2e x +a ,由题意可得2e 2x -2e x +a =3的解有两个,即有⎝ ⎛⎭⎪⎫e x -122=7-2a 4,即为e x =12+7-2a 2或e x =12-7-2a 2,即有7-2a >0且7-2a <1,解得3<a <72.8.(2016·山东卷)若函数y =f (x )的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y =f (x )具有T 性质.下列函数中具有T 性质的是( A )A .y =sin xB .y =ln xC .y =e xD .y =x 3解析:设函数y =f (x )图象上的两点分别为(x 1,y 1),(x 2,y 2),且x 1≠x 2,则由题意知只需函数y =f (x )满足f ′(x 1)·f ′(x 2)=-1即可.y =f (x )=sin x 的导函数为f ′(x )=cos x ,则f ′(0)·f ′(π)=-1,故函数y =sin x 具有T 性质;y =f (x )=ln x 的导函数为f ′(x )=1x ,则f ′(x 1)·f ′(x 2)=1x 1x 2>0,故函数y =ln x 不具有T 性质;y=f (x )=e x 的导函数为f ′(x )=e x ,则f ′(x 1)·f ′(x 2)=e x 1+x 2>0,故函数y =e x 不具有T 性质;y =f (x )=x 3的导函数为f ′(x )=3x 2,则f ′(x 1)·f ′(x 2)=9x 21x 22≥0,故函数y =x 3不具有T 性质.故选A.9.(2019·大庆模拟)函数f (x )=x e x 的图象在点P (1,e)处的切线与坐标轴围成的三角形面积为 e4 .解析:f ′(x )=e x +x e x =e x (x +1), ∴切线斜率k =f ′(1)=2e ,∴曲线y =f (x )在(1,e)处的切线方程为y -e =2e(x -1), 即y =2e x -e.∵y =2e x -e 与坐标轴交于点(0,-e),⎝ ⎛⎭⎪⎫12,0,∴y =2e x -e 与坐标轴围成的三角形面积S =12×e ×12=e4.10.(2019·上饶模拟)若点P 是曲线y =x 2-ln x 上任意一点,则点P 到直线y=x -2解析:由题意知y =x 2-ln x 的定义域为(0,+∞),当点P 是曲线的切线中与直线y =x -2平行的直线的切点时,点P 到直线y =x -2的距离最小,如图所示.故令y ′=2x -1x =1,解得x =1, 故点P 的坐标为(1,1).故点P 到直线y =x -2的最小值d min =|1-1-2|2= 2.11.已知函数f (x )=x 3+(1-a )x 2-a (a +2)x +b (a ,b ∈R ).(1)若函数f (x )的图象过原点,且在原点处的切线斜率为-3,求a ,b 的值; (2)若曲线y =f (x )存在两条垂直于y 轴的切线,求a 的取值范围. 解:f ′(x )=3x 2+2(1-a )x -a (a +2).(1)由题意,得⎩⎪⎨⎪⎧f (0)=b =0,f ′(0)=-a (a +2)=-3,解得b =0,a =-3或a =1.(2)因为曲线y =f (x )存在两条垂直于y 轴的切线,所以关于x 的方程f ′(x )=3x 2+2(1-a )x -a (a +2)=0有两个不相等的实数根,所以Δ=4(1-a )2+12a (a +2)>0, 即4a 2+4a +1>0,所以a ≠-12.所以a 的取值范围为⎝⎛⎭⎪⎫-∞,-12∪⎝⎛⎭⎪⎫-12,+∞.12.(2019·福州质检)设函数f (x )=ax -bx ,曲线y =f (x )在点(2,f (2))处的切线方程为7x -4y -12=0.(1)求f (x )的解析式;(2)证明:曲线y =f (x )上任一点处的切线与直线x =0和直线y =x 所围成的三角形的面积为定值,并求此定值.解:(1)方程7x -4y -12=0可化为y =74x -3. 当x =2时,y =12.又f ′(x )=a +bx 2, 于是⎩⎪⎨⎪⎧2a -b 2=12,a +b 4=74,解得⎩⎪⎨⎪⎧a =1,b =3.故f (x )=x -3x .(2)证明:设P (x 0,y 0)为曲线上任一点,由y ′=1+3x 2,知曲线在点P (x 0,y 0)处的切线方程为 y -y 0=⎝ ⎛⎭⎪⎫1+3x 20(x -x 0), 即y -⎝⎛⎭⎪⎫x 0-3x 0=⎝ ⎛⎭⎪⎫1+3x 20(x -x 0).令x =0,得y =-6x 0,从而得切线与直线x =0的交点坐标为⎝⎛⎭⎪⎫0,-6x 0.令y =x ,得y =x =2x 0,从而得切线与直线y =x 的交点坐标为(2x 0,2x 0).所以点P (x 0,y 0)处的切线与直线x =0,y =x 所围成的三角形的面积为S =12⎪⎪⎪⎪⎪⎪-6x 0|2x 0|=6. 故曲线y =f (x )上任一点处的切线与直线x =0,y =x 所围成的三角形的面积为定值,且此定值为6.13.(2019·达州二诊)已知曲线C 在动点P (a ,a 2+2a )与动点Q (b ,b 2+2b )(a <b <0)处的切线互相垂直,则b -a 的最小值为( A )A .1B .2 C. 2D .- 2解析:由题意可得曲线y =x 2+2x 上存在两点处的切线互相垂直,由y =x 2+2x 的导数为y ′=2x +2,可得(2a +2)(2b +2)=-1,由a +1<b +1,可得a +1<0,且b =1-4(a +1)-1,b -a =1-4(a +1)+(-a -1)≥2·(-a -1)·1-4(a +1)=2×12=1,当且仅当1-4(a +1)=-a -1,即a =-32,b =-12时等号成立,所以b -a 的最小值为1.14.(2019·安徽江南十校联考)若曲线C 1:y =x 2与曲线C 2:y =e xa (a >0)存在公共切线,则a 的取值范围为( D )A .(0,1)B.⎝ ⎛⎭⎪⎫1,e 24 C.⎣⎢⎡⎦⎥⎤e 24,2 D.⎣⎢⎡⎭⎪⎫e 24,+∞ 解析:曲线y =x 2在点(m ,m 2)的切线斜率为2m ,曲线y =e xa (a >0)在点⎝ ⎛⎭⎪⎫n ,1a e n 的切线斜率为1a e n ,如果两条曲线存在公共切线,那么2m =1a e n.又由直线的斜率公式得到2m =m 2-1a enm -n,则有m =2n -2,则由题意知4n -4=1a e n 有解,即y =4x-4,y =1a e x 的图象有交点.若直线y =4x -4与曲线y =1a e x相切,设切点为(s ,t ),则1a e s =4,且t =4s -4=1a e s ,可得切点为(2,4),此时1a =4e 2,故要使满足题意,需1a ≤4e 2,则a ≥e 24,故a 的取值范围是a ≥e 24.故选D.15.已知曲线y =1e x +1,则曲线的切线斜率取得最小值时的直线方程为 x+4y -2=0 .解析:y ′=-e x(e x +1)2=-1e x +1e x +2, 因为e x>0,所以e x+1e x ≥2e x×1e x =2(当且仅当e x=1e x ,即x =0时取等号),则e x+1e x +2≥4,故y ′=-1e x +1e x +2≥-14(当x =0时取等号). 当x =0时,曲线的切线斜率取得最小值,此时切点的坐标为⎝⎛⎭⎪⎫0,12,切线的方程为y -12=-14(x -0),即x +4y -2=0.16.(2019·安徽淮南一模)已知函数f (x )=x 2-ln x . (1)求函数f (x )在点(1,f (1))处的切线方程;(2)在函数f (x )=x 2-ln x 的图象上是否存在两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间⎣⎢⎡⎦⎥⎤12,1上?若存在,求出这两点的坐标,若不存在,请说明理由.解:(1)由题意可得f (1)=1,且f ′(x )=2x -1x ,f ′(1)=2-1=1,则所求切线方程为y -1=1×(x -1),即y =x .(2)假设存在两点满足题意,且设切点坐标为(x 1,y 1),(x 2,y 2),则x 1,x 2∈⎣⎢⎡⎦⎥⎤12,1,不妨设x 1<x 2,结合题意和(1)中求得的导函数解析式可得⎝ ⎛⎭⎪⎫2x 1-1x 1⎝ ⎛⎭⎪⎫2x 2-1x 2=-1,又函数f ′(x )=2x -1x 在区间⎣⎢⎡⎦⎥⎤12,1上单调递增,函数的值域为[-1,1],故-1≤2x 1-1x 1<2x 2-1x 2≤1,据此有⎩⎪⎨⎪⎧2x 1-1x 1=-1,2x 2-1x 2=1,解得x 1=12,x 2=1⎝ ⎛⎭⎪⎫x 1=-1,x 2=-12舍去, 故存在两点⎝ ⎛⎭⎪⎫12,ln2+14,(1,1)满足题意.。

课时作业73 离散型随机变量及其分布列一、选择题1.已知随机变量ξ的分布列为:则ξA .0.7 B .-1 C .0D .1解析:因为P (ξ=-1)=0.7,P (ξ=0)=0.2,P (ξ=1)=0.1,所以ξ最可能出现的值是-1.故选B.答案:B2.某射手射击所得环数X 的分布列为A .0.28B .0.88C .0.79D .0.51解析:P (X >7)=P (X =8)+P (X =9)+P (X =10) =0.28+0.29+0.22=0.79. 答案:C3.离散型随机变量X 的概率分布规律为P (X =n )=an (n +1)(n =1,2,3,4),其中a 是常数,则P ⎝⎛⎭⎪⎫12<X <52的值为( ) A.23 B .34 C.45D .56解析:由⎝ ⎛⎭⎪⎫11×2+12×3+13×4+14×5×a =1,知45a =1,解得a =54. 故P ⎝⎛⎭⎪⎫12<X <52=P (1)+P (2)=12×54+16×54=56. 答案:D4.设某项试验的成功率是失败率的2倍,用随机变量X 去描述1次试验的成功次数,则P (X =0)等于( )A .0B .12 C.13D .23解析:设X 的分布列为即“X =0”p ,则成功率为2p .由p +2p =1,则p =13,故应选C.答案:C5.带活动门的小盒子里有采自同一巢的20只工蜂和10只雄蜂,现随机地放出5只做实验,X 表示放出的蜂中工蜂的只数,则X =2时的概率是( )A.C 120C 410C 530B .C 220C 310C 530C.C 320C 210C 530D .C 420C 110C 530解析:X 服从超几何分布,P (X =2)=C 220C 310C 530.答案:B6.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X 是一个随机变量,其分布列为P (X ),则P (X =4)的值为( )A.1220 B .2755 C.27220D .2125解析:由题意取出的3个球必为2个旧球1个新球,故P (X =4)=C 23C 19C 312=27220.答案:C 二、填空题7.若P (ξ≤x 2)=1-β,P (ξ≥x 1)=1-α,其中x 1<x 2,则P (x 1≤ξ≤x 2)等于________.解析:由分布列性质可有:P (x 1≤ξ≤x 2)=P (ξ≤x 2)+P (ξ≥x 1)-1=(1-β)+(1-α)-1=1-(α+β).答案:1-(α+β)8.从4名男生和2名女生中选3人参加演讲比赛,则所选3人中女生人数不超过1人的概率是________.解析:设所选女生人数为X ,则X 服从超几何分布,其中N =6,M =2,n =3,则P (X ≤1)=P (X =0)+P (X =1)=C 02C 34C 36+C 12C 24C 36=45.答案:459.已知随机变量ξ只能取三个值:x 1,x 2,x 3,其概率依次成等差数列,则公差d 的取值范围是________.解析:设ξ取x 1,x 2,x 3时的概率分别为a -d ,a ,a +d , 则(a -d )+a +(a +d )=1, ∴a =13, 由⎩⎪⎨⎪⎧13-d ≥013+d ≥0得-13≤d ≤13.答案:⎣⎢⎡⎦⎥⎤-13,13三、解答题10.从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸到的球中有红球(不放回),则试验结束.(1)求第一次试验摸到一个红球和一个白球的概率. (2)记试验次数为X ,求X 的分布列.解:(1)记“第一次试验摸到一个红球和一个白球”为事件A ,则P (A )=C 12C 16C 28=37.(2)由题意知X =1,2,3,4,P (X =1)=C 12C 16+C 22C 28=1328,P (X =2)=C 26C 28×C 14C 12+C 22C 26=928,P (X =3)=C 26C 28×C 24C 26×C 12C 12+C 22C 24=528,P (X =4)=C 26C 28×C 24C 26×C 22C 24×C 22C 22=128,所以X 的分布列为11.n 位校友(n >8且n ∈N *),其中女校友6位,组委会对这n 位校友登记制作了一份校友名单,现随机从中选出2位校友代表,若选出的2位校友是一男一女,则称为“最佳组合”.(1)若随机选出的2位校友代表为“最佳组合”的概率不小于12,求n 的最大值;(2)当n =12时,设选出的2位校友代表中女校友人数为ξ,求ξ的分布列.解:(1)由题意可知,所选2人为“最佳组合”的概率为C 1n -6C 16C 2n=12(n -6)n (n -1),则12(n -6)n (n -1)≥12,化简得n 2-25n +144≤0,解得9≤n ≤16,故n 的最大值为16. (2)由题意得,ξ的可能取值为0,1,2, 则P (ξ=0)=C 26C 212=522,P (ξ=1)=C 16C 16C 212=611,P (ξ=2)=C 26C 212=522,ξ的分布列为1.一位客人游览福州鼓山、福州永泰天门山、福州青云山这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设Y表示客人离开福州市时游览的景点数与没有游览的景点数之差的绝对值.求Y的分布列.解:分别记“客人游览福州鼓山”,“客人游览福州永泰天门山”,“客人游览福州青云山”为事件A1,A2,A3.因为事件A1,A2,A3是相互独立的,P(A1)=0.4,P(A2)=0.5,P(A3)=0.6.由于客人游览的景点数的可能取值为0,1,2,3,相应地,客人没有游览的景点数的可能取值为3,2,1,0,所以Y的所有可能取值为1,3.所以P(Y=3)=P(A1·A2·A3)+P(A1·A2·A3)=P(A1)P(A2)P(A3)+P(A1)P(A2)P(A3)=2×0.4×0.5×0.6=0.24,P(Y=1)=1-0.24=0.76,所以Y的分布列为2的三张卡片,现从这个盒子中,有放回地随机抽取两张卡片,记第一次抽取的卡片的标号为x,第二次抽取的卡片的标号为y,设O为坐标原点,点P的坐标为(x→|2,-2,x-y),记ξ=|OP(1)求随机变量ξ的最大值,并求“ξ取最大值”的概率.(2)求随机变量ξ的分布列.解:(1)因为x,y可能的取值为1,2,3,所以|x-2|≤1,|x-y|≤2,所以ξ=(x-2)2+(x-y)2≤5.且当x=1,y=3或x=3,y=1时,ξ=5,因此,随机变量ξ的最大值为5.又因为有放回地随机抽取两张卡片共有3×3=9种情况,所以P(ξ=5)=2 9.(2)ξ的所有可能取值为0,1,2,5.因为ξ=0时,x=2,y=2,ξ=1时,x=1,y=1;x=2,y=1;x=2,y=3;x=3,y=3. ξ=2时,x=1,y=2;x=3,y=2.所以P(ξ=0)=19,P(ξ=1)=4 9,P(ξ=2)=2 9,则随机变量ξ的分布列为。

课时作业31数系的扩充与复数的引入一、选择题1.若复数z=(a2+2a-3)+(a+3)i为纯虚数(i为虚数单位),则实数a的值是()A.-3 B.-3或1C.3或-1 D.1解析:若复数z为纯虚数,则需满足a2+2a-3=0且a+3≠0,解得a=1.不要忽视虚部不等于零的条件.答案:D2.(2014·重庆卷)复平面内表示复数i(1-2i)的点位于()A.第一象限B.第二象限C.第三象限D.第四象限解析:i(1-2i)=2+i,对应点为(2,1)位于第一象限.答案:A3.(2014·山东卷)已知a,b∈R,i是虚数单位,若a-i与2+b i 互为共轭复数,则(a+b i)2=()A.5-4i B.5+4iC.3-4i D.3+4i解析:由已知得,a=2,b=1,即a+b i=2+i,所以(a+b i)2=(2+i)2=3+4i,选D.答案:D4.(2014·湖南卷)满足z+iz=i(i为虚数单位)的复数z=()A.12+12iB.12-12i C .-12+12iD .-12-12i解析:由题可得z +i z =i ⇒z +i =z i ⇒z (1-i)=-i ⇒z =-i 1-i =12-12i ,故选B.答案:B5.(2014·安徽卷)设i 是虚数单位,z 表示复数z 的共轭复数.若z =1+i ,则zi +i·z =( )A .-2B .-2iC .2D .2i解析:zi +i z =1+i i +i(1-i)=1-i +i +1=2. 答案:C6.(2014·辽宁卷)设复数z 满足(z -2i)(2-i)=5,则z =( ) A .2+3i B .2-3i C .3+2iD .3-2i解析:z -2i =52-i =5(2+i )(2-i )(2+i )=5(2+i )5=2+i ,故z =2+3i ,从而选A.答案:A 二、填空题7.(2014·四川卷)复数2-2i1+i =________.解析:2-2i 1+i =2(1-i )2(1+i )(1-i )=-2i.答案:-2i8.已知a ,b ∈R ,i 是虚数单位.若(a +i)(1+i)=b i ,则a +b i =________.解析:(a +i)(1+i)=a -1+(a +1)i =b i ,由复数的运算法则可得⎩⎪⎨⎪⎧ a -1=0a +1=b 解得⎩⎪⎨⎪⎧a =1,b =2,所以a +b i =1+2i. 答案:1+2i9.已知定义在复数集C 上的函数满足f (x )=⎩⎨⎧1+x 3(x ∈R )|x1+i |(x ∉R ),则f (f (1-i))等于________.解析:由已知得f (1-i)=|1-i 1+i |=|-2i2|=|-i|=1,∴f (1)=1+13=2,即f (f (1-i))=2. 答案:2 三、解答题10.实数m 分别取什么数值时,复数z =(m 2+5m +6)+(m 2-2m -15)i.(1)与复数2-12i 相等;(2)与复数12+16i 互为共轭复数; (3)对应的点在x 轴上方.解:(1)根据复数相等的充要条件得⎩⎪⎨⎪⎧m 2+5m +6=2,m 2-2m -15=-12,解得m =-1. (2)根据共轭复数的定义得⎩⎪⎨⎪⎧m 2+5m +6=12,m 2-2m -15=-16,解得m =1. (3)根据复数z 对应点在x 轴上方可得m 2-2m -15>0, 解得m <-3或m >5.11.复数z 1=3a +5+(10-a 2)i ,z 2=21-a +(2a -5)i ,求z 1+z 2是实数,求实数a 的值.解:z 1+z 2=3a +5+(a 2-10)i +21-a +(2a -5)i =⎝ ⎛⎭⎪⎫3a +5+21-a +[(a 2-10)+(2a -5)]i =a -13(a +5)(a -1)+(a 2+2a -15)i.∵z 1+z 2是实数,∴a 2+2a -15=0.解得a =-5或a =3. ∵分母a +5≠0,∴a ≠-5,故a =3.1.复数z =|(3-i)i|+i 5(i 为虚数单位),则复数z 的共轭复数为( )A .2-iB .2+iC .4-iD .4+i解析:z =|1+3i|+i =2+i ,故共轭复数为2-i. 答案:A2.复数z =1+2i 2 0131-i 2 013(i 为虚数单位)的共轭复数在复平面上对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限解析:由i 4=1⇒i2 013=i4×503+1=i ,则z =1+2i 1-i =(1+2i )(1+i )(1-i )(1+i )=-1+3i 2⇒z =-12-32i ,所以点⎝ ⎛⎭⎪⎫-12,-32在第三象限. 答案:C3.在复平面内,复数11+i ,11-i (i 为虚数单位)对应的点分别为A ,B ,若点C 为线段AB 的中点,则点C 对应的复数为( )A.12 B .1 C.12iD .i解析:∵11+i =1-i (1-i )(1+i )=12-12i ,11-i =1+i (1-i )(1+i )=12+12i ,则A (12,-12),B (12,12),∴线段AB 的中点C (12,0),故点C 对应的复数为12,选A.答案:A4.设复数z =-3cos θ+2isin θ. (1)当θ=43π时,求|z |的值;(2)若复数z 所对应的点在直线x +3y =0上,求2cos 2θ2-12sin (θ+π4)的值.解:(1)∵θ=43π,∴z =-3cos 43π+2isin 43π=32-3i ,∴|z |=(32)2+(-3)2=212.(2)由条件得-3cos θ+3×2sin θ=0, ∴tan θ=12,原式=cos θsin θ+cos θ=1tan θ+1=23.。


课时作业13变化率与导数、导数的计算一、选择题1.函数y=x2cos x在x=1处的导数是()A.0 B.2cos1-sin1C.cos1-sin1 D.1解析:∵y′=(x2cos x)′=(x2)′cos x+x2(cos x)′=2x cos x-x2sin x,∴y′|x=1=2cos1-sin1.答案:B2.(2014·大纲卷)曲线y=x e x-1在点(1,1)处切线的斜率等于() A.2e B.eC.2 D.1解析:y′=e x-1+x·e x-1,∴y′|x=1=e0+1×e0=2.答案:C3.(2014·新课标全国卷Ⅱ)设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a=()A.0 B.1C.2 D.3解析:因为y′=a-1x+1,所以在点(0,0)处切线的斜率为a-1=2,解得a=3,故选D.答案:D4.设a为实数,函数f(x)=x3+ax2+(a-3)x的导函数为f′(x),且f′(x)是偶函数,则曲线y=f(x)在点(2,f(2))处的切线方程为()A .9x -y -16=0B .9x +y -16=0C .6x -y -12=0D .6x +y -12=0解析:f ′(x )=3x 2+2ax +a -3,由于f ′(x )是偶函数,所以a =0,此时f ′(x )=3x 2-3,f ′(2)=9,f (2)=2,所以曲线y =f (x )在点(2,f (2))处的切线方程为y -2=9(x -2),即9x -y -16=0.答案:A5.等比数列{a n }中,a 1=2,a 8=4,函数f (x )=x (x -a 1)·(x -a 2)…(x -a 8),则f ′(0)=( )A .212B .29C .28D .26解析:f ′(x )=(x -a 1)(x -a 2)…(x -a 8)+x [(x -a 1)(x -a 2)…(x -a 8)]′,故f ′(0)=a 1a 2…a 8=(a 1a 8)4=212.答案:A6.函数f (x )=-1b e ax(a >0,b >0)的图象在x =0处的切线与圆x 2+y 2=1相切,则a +b 的最大值是( )A .4B .2 2 C. 2D .2解析:f ′(x )=-a b e ax ,所以x =0处的切线斜率k =f ′(0)=-ab ,又f (0)=-1b ,所以切线方程为y +1b =-ab (x -0)即ax +by +1=0,由题意该直线与圆x 2+y 2=1相切,故1a 2+b 2=1即a 2+b 2=1,由a 2+b 2≥(a +b )22得a +b ≤2,故最大值为 2.答案:C二、填空题7.函数y =f (x )的图象在点P (3,f (3))处的切线方程为y =x +2,f ′(x )为f (x )的导函数,则f (3)+f ′(3)=________.解析:(3,f (3))在切线y =x +2上,∴f (3)=5,又f ′(3)=1,∴f (3)+f ′(3)=6.答案:68.(2014·江西卷)若曲线y =e -x 上点P 处的切线平行于直线2x +y +1=0,则点P 的坐标是________.解析:设P (x 0,y 0),∵y =e -x ,答案:(-ln2,2)9.若以曲线y =13x 3+bx 2+4x +c (c 为常数)上任意一点为切点的切线的斜率恒为非负数,则实数b 的取值范围是________.解析:y ′=x 2+2bx +4,∵y ′≥0恒成立, ∴Δ=4b 2-16≤0,∴-2≤b ≤2. 答案:[-2,2] 三、解答题10.已知函数f (x )=x 3+(1-a )x 2-a (a +2)x +b (a ,b ∈R ). (1)若函数f (x )的图象过原点,且在原点处的切线斜率为-3,求a ,b 的值;(2)若曲线y =f (x )存在两条垂直于y 轴的切线,求a 的取值范围. 解:f ′(x )=3x 2+2(1-a )x -a (a +2).(1)由题意得⎩⎪⎨⎪⎧f (0)=b =0,f ′(0)=-a (a +2)=-3,解得b =0,a =-3或1.(2)∵曲线y =f (x )存在两条垂直于y 轴的切线,∴关于x 的方程f ′(x )=3x 2+2(1-a )x -a (a +2)=0有两个不相等的实数根,∴Δ=4(1-a )2+12a (a +2)>0,即4a 2+4a +1>0, ∴a ≠-12.∴a 的取值范围是⎝ ⎛⎭⎪⎫-∞,-12∪⎝ ⎛⎭⎪⎫-12,+∞. 11.已知函数f (x )=x ,g (x )=a ln x ,a ∈R .若曲线y =f (x )与曲线y =g (x )相交,且在交点处有相同的切线,求a 的值及该切线的方程.解:f ′(x )=12x,g ′(x )=ax (x >0),由已知得:⎩⎨⎧x =a ln x 12x =a x,解得a =12e ,x =e 2.∴两条曲线交点的坐标为(e 2,e), 切线的斜率为k =f ′(e 2)=12e ,所以切线的方程为y -e =12e (x -e 2),即x -2e y +e 2=0.1.已知曲线y =ln x 的切线过原点,则此切线的斜率为( ) A .e B .-e C.1eD .-1e解析:y =ln x 的定义域为(0,+∞),设切点为(x 0,y 0),则有k =f ′(x 0)=1x 0,∴切线方程为y -y 0=1x 0(x -x 0),又切线过点(0,0),则x 0=e ,y 0=1,∴k =f ′(x 0)=1x 0=1e ,故选C.答案:C2.下列四个图象中,有一个是函数f (x )=13x 3+ax 2+(a 2-4)x +1(a ∈R ,a ≠0)的导函数y =f ′(x )的图象,则f (1)=( )A.103B.43 C .-23D .1解析:∵f (x )=13x 3+ax 2+(a 2-4)x +1(a ∈R ,a ≠0),则f ′(x )=x 2+2ax +(a 2-4),由a ≠0,结合导函数y =f ′(x )的图象知导函数图象为③,从而可知a 2-4=0,解得a =-2或a =2,再结合-a >0知a =-2,代入可得函数f (x )=13x 3+(-2)x 2+1,∴f (1)=-23,故选C.答案:C3.若直线l 与曲线C 满足下列两个条件:(ⅰ)直线l 在点P (x 0,y 0)处与曲线C 相切;(ⅱ)曲线C 在点P 附近位于直线l 的两侧,则称直线l 在点P 处“切过”曲线C .下列命题正确的是________.(写出所有正确命题的编号) ①直线l :y =0在点P (0,0)处“切过”曲线C :y =x 3②直线l :x =-1在点P (-1,0)处“切过”曲线C :y =(x +1)2 ③直线l :y =x 在点P (0,0)处“切过”曲线C :y =sin x④直线l :y =x 在点P (0,0)处“切过”曲线C :y =tan x ⑤直线l :y =x -1在点P (1,0)处“切过”曲线C :y =ln x 解析:对于①,y ′=3x 2,y ′|x =0=0,所以l :y =0是曲线C :y =x 3在点P (0,0)处的切线,画图可知曲线C :y =x 3在点P (0,0)附近位于直线l 的两侧,①正确;②中,y ′=2(x +1),x =-1,y ′=0,x =-1不是切线; ③中,y ′=cos x ,x =0,y ′=1,切线方程为y =x ,又x <0时,x <sin x ;x >0时,x >sin x ,符合;④中,y ′=⎝ ⎛⎭⎪⎫sin x cos x ′=cos 2x +sin 2x cos 2x =1cos 2x ,x =0,y ′=1,切线为y =x .当x >0时,x >tan x ;当x <0时,x <tan x ,符合;⑤中,y ′=1x ,x =1,y ′=1,切线方程为y =x -1.当x <1时,x -1>ln x ;当x >1时,x -1>ln x ,不满足(ⅱ).综述,①③④正确. 答案:①③④4.已知函数f (x )=ax 3+3x 2-6ax -11,g (x )=3x 2+6x +12和直线m :y =kx +9,又f ′(-1)=0.(1)求a 的值;(2)是否存在k 的值,使直线m 既是曲线y =f (x )的切线,又是y =g (x )的切线;如果存在,求出k 的值;如果不存在,说明理由.解:(1)因为f ′(x )=3ax 2+6x -6a ,所以f ′(-1)=0,即3a -6-6a =0,所以a =-2.(2)因为直线m 恒过点(0,9).设切点为(x 0,3x 20+6x 0+12),因为g ′(x 0)=6x 0+6.所以切线方程为y -(3x 20+6x 0+12)=(6x 0+6)(x -x 0),将点(0,9)代入得x0=±1.当x0=-1时,切线方程为y=9,当x0=1时,切线方程为y=12x +9.由f′(x)=0得-6x2+6x+12=0,即有x=-1,x=2.经检验,当x=2时,y=f(x)的切线方程为y=9,∴y=9是公切线,又由f′(x)=12得-6x2+6x+12=12,∴x=0或x=1,经检验,x=0或x=1不是公切线,∴k=0时y=9是两曲线的公切线.。
课时作业23 函数y =A sin(ωx +φ)的图象及应用一、选择题1.(2014·四川卷)为了得到函数y =sin(x +1)的图象,只需把函数y =sin x 的图象上所有的点( )A .向左平行移动1个单位长度B .向右平行移动1个单位长度C .向左平行移动π个单位长度D .向右平行移动π个单位长度解析:由y =sin x 得y =sin(x +1)只需向左平移1个单位即可. 答案:A2.函数f (x )=A sin(2x +φ)(A ,φ∈R )的部分图象如上图所示,那么f (0)=( )A .-12B .-1C .-32D .- 3解析:由图象知A =2,图象过点(π3,2), ∴2sin(π3×2+φ)=2, ∴2π3+φ=π2+2k π,k ∈Z , ∴φ=-π6+2k π,k ∈Z ,∴φ=-π6,∴f (0)=2sin(-π6)=-1. 答案:B3.(2014·安徽卷)若将函数f (x )=sin2x +cos2x 的图象向右平移φ个单位,所得图象关于y 轴对称,则φ的最小正值是( )A.π8B.π4C.3π8D.3π4解析:f (x )=sin2x +cos2x =2sin(2x +π4),向右平移φ个单位,得y =2sin(2x -2φ+π4)关于y 轴对称,则-2φ+π4=π2+k π,k ∈Z ,φ=-π8-k π2,k ∈Z ,φ的最小正值为38π.答案:C4.(2014·辽宁卷)将函数y =3sin(2x +π3)的图象向右平移π2个单位长度,所得图象对应的函数( )A .在区间[π12,7π12]上单调递减B .在区间[π12,7π12]上单调递增 C .在区间[-π6,π3]上单调递减 D .在区间[-π6,π3]上单调递增解析:平移后的函数为y =3sin[2(x -π2)+π3]=3sin(2x +π3-π)=3sin(2x -23π),增区间:-π2+2k π≤2x -23π≤π2+2k π,k ∈Z ,即π12+k π≤x ≤712π+k π,k ∈Z ,k =0时,π12≤x ≤712π,故选B.答案:B5.函数f (x )=A sin(ωx +φ)(A >0,ω>0)的图象如图所示,则f (1)+f (2)+f (3)+…+f (2 015)=( )A .0 B. 2 C.2+1D .1解析:由图象知φ=0,ω=2πT =π4,∴f (x )=2sin πx4,其图象关于(4,0),x =2,x =6对称,∴f (1)+f (2)+f (3)+…+f (8)=0,∵T =8,2 015=251×8+7,∴f (1)+f (2)+f (3)+…+f (2 015)=f (0)+f (1)+…+f (2 015)-f (0)=-f (0)=0.答案:A6.函数f (x )=sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,|φ|<π2的最小正周期是π,若其图象向右平移π6个单位后得到的函数为奇函数,则函数f (x )的图象( )A .关于点⎝ ⎛⎭⎪⎫π12,0对称B .关于直线x =π12对称 C .关于点⎝ ⎛⎭⎪⎫π6,0对称 D .关于直线x =π6对称解析:∵2πω=π,∴ω=2.∴f (x )=sin(2x +φ)向右平移π6个单位,得y =sin ⎝ ⎛⎭⎪⎫2x -π3+φ为奇函数, ∴-π3+φ=k π(k ∈Z ),∴φ=π3+k π(k ∈Z ), ∴φ=π3,∴f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3. ∵sin ⎝ ⎛⎭⎪⎫2×π12+π3=1,∴直线x =π12为函数的对称轴.故选B. 答案:B 二、填空题7.函数y =A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)在闭区间[-π,0]上的图象如图所示,则ω=________.解析:由图象可以看出32T =π, ∴T =23π=2πω,因此ω=3. 答案:38.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎢⎡⎦⎥⎤π6(x -6)(x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为________℃.解析:由题意得⎩⎨⎧a +A =28,a -A =18,∴⎩⎨⎧a =23,A =5,∴y =23+5cos ⎣⎢⎡⎦⎥⎤π6(x -6),x =10时,y =23+5×⎝ ⎛⎭⎪⎫-12=20.5.答案:20.59.若将函数y =tan ⎝ ⎛⎭⎪⎫ωx +π4(ω>0)的图象向右平移π6个单位长度后,与函数y =tan ⎝ ⎛⎭⎪⎫ωx +π6的图象重合,则ω的最小值为________. 解析:y =tan ⎝ ⎛⎭⎪⎫ωx +π4向右平移π6个单位长度后得到函数解析式为y =tan[ω(x -π6)+π4]=tan ⎝ ⎛⎭⎪⎫ωx -ωπ6+π4,显然当π4-πω6=π6+k π,k ∈Z 时,两图象重合,此时ω=12-6k ,k ∈Z .∵ω>0,∴k =0时,ω的最小值为12.答案:12 三、解答题10.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π4+1.(1)求它的振幅、最小正周期、初相;(2)画出函数y =f (x )在⎣⎢⎡⎦⎥⎤-π2,π2上的图象.解:(1)振幅为2,最小正周期T =π,初相为-π4. (2)图象如图所示.11.设函数f (x )=(sin ωx +cos ωx )2+2cos 2ωx (ω>0)的最小正周期为2π3.(1)求ω的值;(2)若函数y =g (x )的图象是由y =f (x )的图象向右平移π2个单位长度得到.求y =g (x )的单调增区间.解:(1)f (x )=sin 2ωx +cos 2ωx +2sin ωx cos ωx +1+cos2ωx =sin2ωx +cos2ωx +2=2sin ⎝ ⎛⎭⎪⎫2ωx +π4+2, 依题意得2π2ω=2π3,故ω=32. (2)依题意得g (x )=2sin ⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫x -π2+π4+2=2sin ⎝ ⎛⎭⎪⎫3x -5π4+2. 由2k π-π2≤3x -5π4≤2k π+π2(k ∈Z )解得23k π+π4≤x ≤23k π+7π12(k ∈Z ).故g (x )的单调增区间为⎣⎢⎡⎦⎥⎤23k π+π4,23k π+7π12(k ∈Z ).1.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如上图所示,则当t =1100秒时,电流强度是( )A .-5安B .5安C .53安D .10安解析:由图象知A =10,T 2=4300-1300=1100, ∴ω=2πT =100π.∴I =10sin(100πt +φ).⎝ ⎛⎭⎪⎫1300,10为五点中的第二个点, ∴100π×1300+φ=π2. ∴φ=π6.∴I =10sin ⎝ ⎛⎭⎪⎫100πt +π6, 当t =1100秒时,I =-5安.答案:A2.(2014·江苏卷)已知函数y =cos x 与y =sin(2x +φ)(0≤φ<π),它们的图象有一个横坐标为π3的交点,则φ的值是________.解析:由题意cos π3=sin ⎝ ⎛⎭⎪⎫2×π3+φ,即sin ⎝⎛⎭⎪⎫2π3+φ=12,2π3+φ=k π+(-1)k ·π6(k ∈Z ).因为0≤φ<π,所以φ=π6. 答案:π63.已知函数f (x )=sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2≤φ≤π2的图象上的两个相邻的最高点和最低点的距离为22,且过点⎝⎛⎭⎪⎫2,-12,则函数解析式f (x )=________.解析:据已知两个相邻最高和最低点距离为22,可得⎝ ⎛⎭⎪⎫T 22+(1+1)2=22,解得T =4,故ω=2πT =π2,即f (x )=sin ⎝ ⎛⎭⎪⎫πx 2+φ,又函数图象过点⎝ ⎛⎭⎪⎫2,-12,故f (2)=sin ⎝ ⎛⎭⎪⎫π2×2+φ=-sin φ=-12,又-π2≤φ≤π2,解得φ=π6,故f (x )=sin ⎝ ⎛⎭⎪⎫πx 2+π6.答案:sin ⎝⎛⎭⎪⎫πx 2+π64.已知函数f (x )=A sin(ωx +φ)(x ∈R ,A >0,ω>0,0<φ<π2)的部分图象如图所示,P 是图象的最高点,Q 为图象与x 轴的交点,O 为坐标原点.若OQ =4,OP =5,PQ =13.(1)求函数y =f (x )的解析式;(2)将函数y =f (x )的图象向右平移2个单位后得到函数y =g (x )的图象,当x ∈[0,3]时,求函数h (x )=f (x )·g (x )的值域.解:(1)由条件,cos ∠POQ =42+(5)2-(13)22×4×5=55,所以P (1,2).因为A =2,周期T =4×(4-1)=12, 又2πω=12,则ω=π6.将点P (1,2)代入f (x )=2sin(π6x +φ),得sin(π6+φ)=1,因为0<φ<π2,所以φ=π3,所以f (x )=2sin(π6x +π3).(2)由题意,可得g (x )=2sin π6x .所以h (x )=f (x )·g (x )=4sin(π6x +π3)·sin π6x =2sin 2π6x +23sin π6x ·cos π6x =1-cos π3x +3sin π3x =1+2sin(π3x -π6).当x∈[0,3]时,π3x-π6∈[-π6,5π6],所以sin(π3x-π6)∈[-12,1],所以函数h(x)的值域为[0,3].。