陕西省西安地区2011届高三八校联考试题数学理科(四)

西安地区：陕师大附中、西安高级中学、西安高新一中、西安交大附中、 西安市八十三中、西安一中、西安铁一中、西安中学、西工大附中“八校”联考2011届高三年级数学(理科)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分, 共150分, 考试时间120分钟. 注意事项:1. 答题前,考生务必先将自己的姓名、准考证号填写在答题纸上,认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题纸上的指定位置上。

2. 选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整，笔迹清楚。

3. 请按照题号各题的答案区域（黑色线框）内作答，超出答案区域书写的答案无效。

4. 保持纸面清洁，不折叠，不破损。

5. 做选考题时，考生按照题目要求作答，并用2B 铅笔在答题纸上把所选择题目对应的题号涂黑。

第Ⅰ卷(选择题 共50分)一. 选择题: (本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合{}{}2|4,|4,P x x Q x x x R =<=<∈, 则( ) A. P Q ⊆ B. Q P ⊆ C. R P Q ⊆ð D. R Q P ⊆ð2. 1iz i=-, 在复平面上对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限3. 设n S 为等比数列{}n a 的前n 项和, 2580,a a += 则52SS =( )A. 11B. 5C. 8-D. 11-4.已知函数()cos (0),f x x x ωωω=+> 若函数()y f x =的图象与直线2y =的相邻两个公共点间的距离为π, 则()f x 的单调递增区间是( )A. 5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦ k Z ∈B. 511,1212k k ππππ⎡⎤++⎢⎥⎣⎦k Z ∈ C. 2,63k k ππππ⎡⎤++⎢⎥⎣⎦ k Z ∈ D. ,36k k ππππ⎡⎤-+⎢⎥⎣⎦k Z ∈ 5. 已知函数1()ln xf x x e ⎛⎫=- ⎪⎝⎭, 若实数0x 是函数的零点, 且100x x <<, 则1()f x ( )A. 大于0B. 等于0C. 小于0D. 不大于06. 一空间几何体的三视图如图所示,则该几何体的体积为( )A. 2π+B. 4π+C. 2πD. 4π+7. 已知椭圆C 的方程是22221(0),x y a b a b+=>> 其左顶点为A , 左、右焦点分别为1F 、2F , D 是它短轴上的一个顶点,若1232DF DA DF =+, 则该椭圆的离心率为( ) A.12 B. 13 C. 14 D. 158. 已知,a b 是实数, 则“2a >, 且2b >”是“4a b +>, 且4ab >”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分又不必要条件9. 如果执行如图的程序框图, 输入正整数,n m 满足,n m ≥ 那么输出的P 等于( )A. 1m n C -B. 1m n A -C. m n CD. mn A10. 一条直线型生产线上从左往右依次有机器人1α, 2α, 3α,4α, 5α, 6α, 其中相邻两个的间隔距离均为2， 现在要在该生产线上选择一个位置放置工具箱, 若到六个机器人的距离之和最小的位置为最佳工具位置, 则最佳位置与机器人1α的距离需且只需满足( )A. 2d =B. 46d ≤≤C. 13d ≤≤D. 06d ≤≤第Ⅱ卷(非选择题 共100分)二. 填空题:(本大题共5小题, 每小题5分, 共25分. 把答案填写在题中的横线上.) 11. 圆222210x y x y +-++=的圆心到直线10x y -+=的距离是 .12. 若1()n x x+的展开式的二项式系数之和为64, 则展开式中常数项为 .13. 已知正数,x y 满足20,350x y x y -⎧⎨-+⎩≤≥则11()()42x y z =⋅的最小值为 .14. 如图所示, 在一个边长为1的正方形AOBC 内, 曲线2y x =和y =围成一个叶形图(阴影部分). 向正方形AOBC 内随机投一点(该点落在正方形AOBC内任一点是对等可能的), 则所投的点落在叶形图内部的概率是15. (考生注意: 请在下列三题中任选一题作答, 如果多做, 则按所做的第一题评分.)A. (不等式选做题)不等式112x x +>+的解集为 .B. (几何证明选做题)如图, 已知,EB EC 是O 的两条切线, ,B C 是切点. ,A D 是O 上两点, 如果46E ∠= ,32DCF ∠= , 则A ∠的度数为C. (坐标系与参数方程选做题) 已知直线3sin 40:1cos40x t l y t ⎧=+⎪⎨=-+⎪⎩(t 为参数), 则直线l 的倾斜角为三. 解答题: (本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤) 16. (本小题满分12分)已知数列{}n a 的前n 项和22.n S n n =+ 其中*n N ∈ (1)求数列{}n a 的通项公式; (2)设11,n n n b a a +=⋅ 记数列{}n b 的前n 项和为n T , 求证: 16n T <.17. (本小题满分12分)在ABC ∆中, 角,,A B C 所对的边的长分别是,,a b c 且1cos 3A =. (1)求2sin cos22B CA ++的值; (2)若a 求bc 的最大值.18. (本小题满分12分)如下图(1)所示,已知正方形AMCD 的边长为2, 延长AM , 使得M 为AB 的中点, 连结AC . 现将A D C ∆沿AC 折起, 使平面A D C ⊥平面ABC ,得到几何体,D ABC - 如图(2)所示. (1)求证: BC ⊥平面ACD ;(2)求平面ACD 与平面MCD 的夹角的余弦值.19. (本小题满分12分)为了推动21世纪高等院校科研的发展,从某市“交通大学”,“工业大学”,“电子科技大学”三所“211工程”重点院校的相关教师中, 用分层抽样的方法抽取若干人组成研究小组, 有关数据如下表. (单位:人)高校相关教师人数抽取人数交通大学54 x电子科技大学36 4工业大学18 y(1)求,x y的值;(2)若从“工业大学”,“电子科技大学”两所院校抽取的人中选2人为代表作专业报告. 求这2人中至少有一人是来自“工业大学”的概率.20. (本小题满分13分)在双曲线2222:1(0,0)x yC a ba b-=>>中, 过焦点垂直于实轴的弦长为焦点到一条渐近线的距离为1.(1)求该双曲线的方程;(2)若直线:(0,0)l y kx m k m=+≠≠与双曲线交于,A B两点, (,A B不是左右顶点), 且以AB为直径的圆过双曲线C 的右顶点.求证: 直线l过定点, 并求出该定点的坐标21. (本小题满分14分)已知函数().f x mx=(1)当1m=-时, 求函数()f x的最大值;(2)若()f x为定义域上的单调函数, 求实数m的取值范围;(3)当1m=时, 且10a b>≥≥, 证明: 4()()2. 3f a f ba b-<<-西安地区“八校”2011届高三联考 数学试题(理科)参考答案一. 选择题(每小题5分, 共50分)题号1 2 3 4 5 6 7 8 9 10 答案B B D D ACD A D B二. 填空题(每小题5分, 共25分) 11.12. 20 13. 116 14. 1315. A. 3(,2)(2,)2-∞--- B. 99 C. 50三. 解答题(本大题共6小题, 共75分) 16. (本小题满分12分)解: (1)由22n S n n =+得 1n =时, 113a S == ------------------------2分当2n ≥时, 221(2)[(1)2(1)]n n n a S S n n n n -=-=+--+- ------------3分 *21()n n N =+∈ -----------------------5分 显然13a =符合21n a n =+ 故21n a n =+*()n N ∈ -------------------6分 (2)1111[](21)(23)22123n b n n n n ==-++++ -----------------------7分∴121111111[()()()235572123n n T b b b n n =++⋅⋅⋅+=-+-+⋅⋅⋅+-++ ----------------9分11111[]2323646n n =-=-++ ----------------------11分 ∵1046n >+, 则16n T < -----------------------12分 17. (本小题满分12分) 解: (1) 由1cos 3A =得27cos22cos 19A A =-=- ---------------------2分故21cos()sin cos2cos222B C B C A A +-++=+ ---------------------3分 1cos cos22AA +=+ ----------------------------4分 11713()299+=+-=- ------------------------------6分 (2)∵2221cos 23b c a A bc +-== 且*,b c R ∈ ------------------8分故222b c bc +≥又a ∴2222331222b c a bc bc bc bc +--=-≥ -----------------------10分 从而13132bc -≥ ∴3223bc ≥ 故94bc ≤当且仅当32b c ==时, bc 取得最大值94--------------------------12分18. (本小题满分12分)解: 在图1中,可得AC BC == 从而222,AC BC AB +=故AC BC ⊥ 取AC 的中点O , 连结DO, 则DO AC ⊥, 又面ADC ⊥面ABC ,面ADC 面ABC AC =, DO ⊂面ACD ,从而OD ⊥平面ABC , ------------4分 ∴OD BC ⊥又,AC BC AC OD O ⊥= ,∴BC ⊥平面ACD ----------------------------6分另解: 在图1中,可得AC BC == 从而222,AC BC AB +=故AC BC ⊥ ∵面ADC ⊥面ABC ,面ADC 面ABC AC =, BC ⊂面ABC ,从而BC ⊥平面ACD . (2)建立空间直角坐标系O xyz -如图所示, 则(M C DCM CD ==----------------------8分 设1(,,)n x y z =为面CDM 的法向量,则1100n CM n CD ⎧⋅=⎪⎨⋅=⎪⎩即00==, 解得y x z x =-⎧⎨=-⎩ 令1x =-, 可得1(1,1,1)n =- 又2(0,1,0)n =为面ACD 的一个法向量∴121212cos ,||||n n n n n n ⋅<>==∴平面ACD 与平面MCD. ----------------------12分 19. (本小题满分12分)(1)由题意可得:5436184x y== 解得6,2x y == -------------------6分 (2)记事件A :从“工业大学” 、“电子科技大学”两所院校抽取的人中选2人为代表作专业报告,至少有一人来自“工业大学”,则A 包含基本事件的共1122429C C C ⋅+=种 ----------------------------9分另外从两所高校中共6人抽取2人作专业报告, 基本事件共有2615C =种,故93()155P A == -----------------12分 20. (本小题满分13分) 解: (1)由已知得2211b ab a ⎧=⎪⎪⇒=⎨=----------------4分∴双曲线的方程为2213x y -= -----------------5分(2)设1122(,),(,),A x y B x y 联立2233y kx mx y =+⎧⎨-=⎩得 222(13)63(1)0k x kmx m ---+= ----------------6分则2236k m ∆=2212(1)(13)0m k ++-> 化简得22130m k +->由韦达定理得21212223(1),1331bkm m x x x x k k ++==-- -------------------7分∵以AB 为直径的圆过双曲线的右顶点M∴0,MA MB ⋅=即1212(0x x y y += -------------------8分又2212121212()()()y y kx m kx m k x x km x x m =++=+++∴221212(1)()30k x x km x x m +++++=整理得2260m k ++=解得: m =或m =-均满足22130m k +-> -----------------10分当3m k =-时, :(l y k x =此时过定点(3,0)与已知矛盾,((3,0)为双曲线的右顶点)当m =-时, :(l y k x =-此时又过定点()符合题意.∴直线l 过定点,定点坐标为() --------------------------13分 21. (本小题满分14分)解: (1)1m =-时, 1()()2f x x x =>则1112()2112121212xf x x x x -'=⋅⋅-=-=+++ ----------------1分 令()0f x '=得0x =, 令()0f x '>得102x -<<, 令()0f x '<得0x >故()f x 在1(,0)2-上递增, 在(0,)+∞上递减 -----------------------2分所以max ()(0)0f x f == -----------------------3分(2)依题意()0f x '≥或()0f x '≤恒成立, 1(,)2x ∈-+∞ ----------------------4分∵1()ln(12)2f x mx x mx ==++∴11()()122f x m x x '=+>-+ ----------------------------5分 ∵1012x >+, 故不存在m R ∈,使得1()012f x m x'=++≤恒成立 ---------------6分 若()0f x '≥对一切1(,)2x ∈-+∞恒成立.则112m x -+≥对一切1(,)2x ∈-+∞恒成立 -----------------------------7分 ∵1012x-<+ ∴0m ≥ 此时1()012f x m x '=+>+对一切1(,)2x ∈-+∞恒成立 故当[0,)m ∈+∞时,()f x 为在定义域上的单调函数. ----------------------8分 (3)当1m =时,令411()()ln(12)323g x f x x x x =-=+- -------------------9分则112(1)()1233(12)x g x x x -'=-=++, 当[]0,1x ∈时, 总有()0g x '≥ 即()g x 在[]0,1上递增当01b a <≤≤时, ()()g b g a <即44()()4()()333f a f b f b b f a a a b --<-⇒>- ------------------------12分令1()()2ln(12),2h x f x x x x =-=+- 则由(1)知()h x 在[]0,1上递减∴()()h a h b <即()2()2,()()2()f a a f b b f a f b a b -<--<- ∵0a b ->, ∴()()2f a f b a b-<-综上可得4()()23f a f b a b-<<-成立, 其中01b a <≤≤ ------------------14分。

陕西省西安地区八校2010—2011学年高三下学期5月联考理科综合能力测试本试题分选择题和非选择题两部分．考试时间150分钟,满分300分．注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡上的指定位置上．2．选择题答案使用2B铅笔填涂,如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案用0．5毫米的黑色中性（签字)笔或碳素笔书写,字体工整，笔迹清楚．3．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效．4．保持卡面清洁，不折叠，不破损．5．做选考题时,考生按照题目要求作答，并用2B铅笔在答题卡上把所选题目对应的题号涂黑。

可能用到的相对原子质量：H一1、C一12、N一14、O-16、S一32、Na一23．第Ⅰ卷（选择题共126分）一、选择题:本小题包括13小题每小题6分，78分．在每小题给出的四个选项中，只有一个选项符合题目要求的。

1．若在显微镜下发现一种新的单细胞生物并需鉴定其类群,下列哪种特征可作为鉴定依据（)①组胞核的有无②核糖体的有无③叶绿体的有无④膜上磷脂的有无A．①③B．②④C．①④D．②③2．某成年雄性小鼠的初级精母细胞中有20个四分体，如取该小鼠的某种干细胞，放入含3H标记的胸腺嘧啶脱氧核苷酸的培养液中培养,当该细胞首次进入有丝分裂后期时（）A．被标记的同源染色体分向两极B．被标记的染色体是80条C．此时细胞内的基因表达很活跃D．此时细胞内含有2个染色体组3．下列关于动物稳态的说法中错误的是（) A．体液调节过程中,体温的降低是神经调节和体液调节共同作用的结果，体温升高只有神经调节参与B．大量流汗导致失水过多，可通过增加抗利尿激素的分泌进行调节C．甲状腺机能亢进的患者对氧气的需求量高于正常个体D．长期注射性激素可导致性腺的衰退4．关于细胞分化、衰老、凋亡和癌变的叙述中，错误的是（)A．癌变是正常细胞发生基因突变的结果B．个体发育过程中细胞的衰老对于生物体是有害的C．细胞分化将造成不同细胞间蛋白质种类有差异D．细胞凋亡对生物的个体发育、机体稳态的维持等有着重要作用5．有关群落演替的叙述正确的是（）A．森林遭受火灾后的地段上重新形成森林属于初生演替过程B．群落演替的根本原因在于群落内部，不受外界因素的影响C．群落自然演替是一个群落替代另一个群落的过程D．人类活动不能改变群落自然演替的速度和方向6．有一瓶酵母菌和葡萄糖的混合培养液,当通人不同浓度的氧气时,其产生的C2H5OH和CO2的量如下表所示：下列叙述错误的是（）A．氧浓度为a时只进行有氧呼吸B．b值对应的氧气浓度为零C．氧浓度为C时，经有氧呼吸产生的CO2为6molD．氧浓度为d时，有1／3的葡萄糖用于酒精发酵7．2007年诺贝尔化学奖授予德国化学家格哈德·埃特尔，以表彰他在界面化学研究领域取得的成就，下面实例中涉及到的变化都属于“界面化学”的范畴．其中正确的是（)A．在汽车上安装催化转化器，使一氧化碳在催化剂表面氧化为二氧化碳,可减少一氧化碳的排放B．泄漏在海洋中的原油可被海洋生物迅速分解而除去C．铁生锈是铁与空气中的氧气、水蒸气直接化合生成了水合氧化铁（Fe2O3、nH2O)的结果D．放置在空气中澄清石灰水表面出现的白色固体的主要成分是氢氧化钙8．研究发现，奥司他韦可以有效治疗H1Nl流感，奥司他韦分子式为C16H28N2O4·H3PO4，分子结构如图．下列有关奥司他韦的说法中正确的是（)A．含极性键，易溶于水，其水溶液有丁达尔效应B．分子中含有酯基、氨基、苯环等官能团C．1 mol该物质最多能与3molNaOH反应D．可以发生加成、取代、氧化反应9．下列表述中正确的是（）A．任何能使熵值减小的过程都能自发进行B．已知热化学方程式2SO 2（g)+O2（g）2SO3（g）；△H=-QkJ·mol —1（Q>0），则将2mol SO2(g）和1mol O2（g）置于一密闭容器中充分反应后放出QkJ的热量C．在Na2SO4溶液中加入过量的BaCl2后，溶液中不存在SO42—D．1mol NaOH分别和1mol CH3COOH、1molHNO3反应，后者比前者△H小10．常温下，在下列各组溶液中，加水稀释时c（H+）／c(OH-）值明显增大,且能大量共存的离子组是（）①K+、Cl-、NO3—、AlO2- ②K+、Fe2+、I—、SO42—③Ba2+、OH—、NO3—、Na+ ④Na+、Ca2+、Al3+、Cl—A．①② B．①③ C．②④ D．②③11．已知：2SO 2（g）+O2（g)2SO3(g):△H=-197kJ／mol．实验测得4molSO2参加上述反应放出354kJ热量，则SO2的转化率最接近于（）A．90% B．80％ C．50％D．40％12．下列表示溶液中发生反应的化学方程式或离子方程式错误的是（）A．5SO32—+6H++2MnO4-5SO42—+2Mn2++3H2OB．2KMnO4+HCOOK+KOH=2K2MnO4+CO2↑+H2OC．K2Cr2O7+6FeSO4+7H2SO4=Cr2（SO4)3+3Fe2(SO4）3+K2SO4+7H2O D．3Fe2++4H++NO3—=3Fe3++NO↑+2H2O13．NaHA是二元酸H2A的酸式盐，下列说法正确的是（) A．若NaHA的水溶液呈酸性，则二元酸H2A一定是强酸B．若NaHA的水溶液呈碱性，则HA—只发生水解C．无论H2A是强酸还是弱酸，NaHA溶液中Na+和HA—的个数之比都是1：1D．无论H2A是强酸还是弱酸,NaHA晶体中的阴阳离子个数比都是1：1二、选择题：本题共8小题,每小题6分，48分．在每小题给出的四个选项中,有的只有一个选项正确，有的有多个选项正确．全部选对的得6分.选对但不全的得3分,有选错的得0分．14．图中四幅图片涉及物理学史上的四个重大发现，其中说法不正确的有（）A．卡文迪许通过扭秤实验，测定出了万有引力恒量B．奥斯特通过实验研究,发现了电流周围存在磁场C．法拉第通过实验研究，总结出法拉第电磁感应定律D．牛顿根据理想斜面实验,提出力不是维持物体运动的原因15．把一钢球系在一根弹性绳的一端，绳的另一端固定在天花板上,先把钢球托起(如右图所示）,然后放手．若弹性绳的伸长始终在弹性限度内，关于钢球的加速度a、速度v随时间t变化的图象，下列说法正确的是( ）A．甲为a—t图象B．乙为a—t图象C．丙为v—t图象D．丁为v—t图象16．图示为全球定位系统（GPS）．有24颗卫星分布在绕地球的6个轨道上运行，它们距地面的高度都为2万千米。

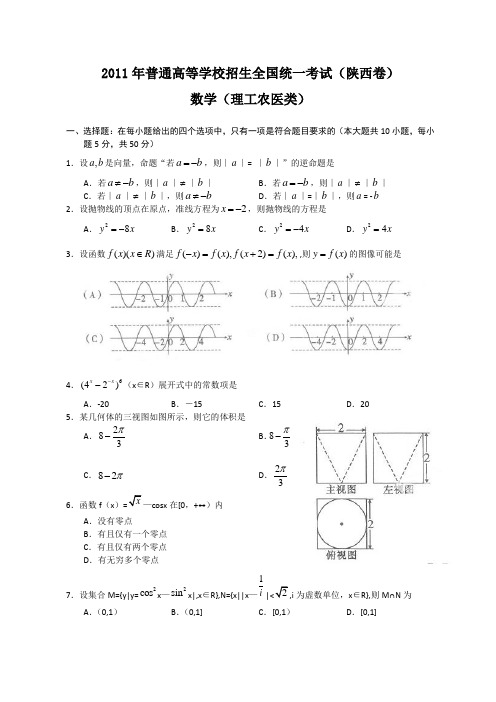
2011年普通高等学校招生全国统一考试（陕西卷）数学（理工农医类）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共10小题，每小题5分，共50分） 1．设,a b 是向量，命题“若a b =-，则∣a ∣= ∣b ∣”的逆命题是A ．若a b ≠-，则∣a ∣≠∣b ∣B ．若a b =-，则∣a ∣≠∣b ∣C ．若∣a ∣≠∣b ∣，则a b ≠-D ．若∣a ∣=∣b ∣，则a = -b 2．设抛物线的顶点在原点，准线方程为2x =-，则抛物线的方程是A ．28y x =-B ．28y x =C ．24y x =-D ．24y x =3．设函数()()f x x R ∈满足()(),(2)(),f x f x f x f x -=+=,则()y f x =的图像可能是4．6(42)xx --（x ∈R ）展开式中的常数项是 A ．-20 B ．－15C ．15D ．205．某几何体的三视图如图所示，则它的体积是A ．283π- B ．83π-C ．82π-D ．23π 6．函数f （x ）cosx 在[0，+∞）内A ．没有零点B ．有且仅有一个零点C ．有且仅有两个零点D ．有无穷多个零点7．设集合M={y|y=2cos x —2sin x|,x ∈R},N={x||x —1i为虚数单位，x ∈R},则M ∩N 为A ．（0,1）B ．（0,1]C ．[0,1）D ．[0,1]8．右图中，1x ，2x ，3x 为某次考试三个评阅人对同一道题的独立评分，P为该题的最终得分。

当126,9.x x ==p=8．5时，3x 等于A ．11B ．10C ．8D ．79．设（1x ，1y ），（2x ，2y ），…，（n x ，n y ）是变量x 和y 的n 个样本点， 直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以 下结论中正确的是 A ．x 和y 的相关系数为直线l 的斜率 B ．x 和y 的相关系数在0到1之间C ．当n 为偶数时，分布在l 两侧的样本点的个数一定相同D ．直线l 过点(,)x y10．甲乙两人一起去游“2011西安世园会”，他们约定，各自独立地从1到6号景点中任选4个进行游览，每个景点参观1小时，则最后一小时他们同在一个景点的概率是A ．136B ．19C ．536D ．1611．设若2lg ,0,()3,0,ax x f x x t dt x >⎧⎪=⎨+≤⎪⎩⎰((1))1f f =，则a = 12．设n N +∈,一元二次方程240x x n -+=有正数根的充要条件是n = 13．观察下列等式1=12+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49……照此规律，第n 个等式为 。

【本文作者】姓 名：雷春来工作单位：陕西省西乡县第二中学2011年普通高等学校招生全国统一考试(陕西卷)理科数学（必修+选修Ⅱ）第Ⅰ卷一、 选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共10小题，每小题5分，共50分）1、设,a b 是向量，命题“若a = -b ，则∣a ∣= ∣b ∣”的逆命题是 （ ）（A ）若a b ≠-，则∣a ∣≠∣b ∣ （B ）若a b =，则∣a ∣≠∣b ∣（C ）若∣a ∣≠∣b ∣，则∣a ∣≠∣b ∣ （D ）若∣a ∣=∣b ∣，则a = -b 2、设抛物线的顶点在原点，准线方程为2x =-，则抛物线的方程是 （ ）（A ）28y x =- （B ）28y x = (C) 24y x =- (D) 24y x =3.设函数()()f x x R ∈满足()(),(2)(),f x f x f x f x -=+=则()y f x =的图像可能（ ）4. 6(42)x x --（x ∈R ）展开式中的常数项是 （ ） （A ）-20 （B ）-15 （C ）15 （D ）205. 某几何体的三视图如图所示，则它的体积是（ ）（A ）283π- （B ）83π- (C) 82π- (D) 23π6. 函数f(x)= cos x x 在[0，+∞）内 （ ）（A ）没有零点 （B ）有且仅有一个零点（C ）有且仅有两个零点 （D ）有无穷多个零点7. 设集合M={y |22|cos sin |y x x =- ，x ∈R},N={x | 1||2x i-<，i 为虚数单位，x ∈R},则M ∩N 为（ ）(A)(0,1) (B)(0,1] (C)[0,1) (D)[0,1]8. 右图中，123,,x x x 为某次考试三个评阅人对同一道题的独立评分，P 为该题的最终得分。

当126,9x x ==，p=8.5时，3x等于 （ ）(A)11 (B)10 (C)8 (D)7 9. 设（1x ，1y ），（2x ，2y ），…，（n x ，n y ）是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是（ ）（A ）x 和y 的相关系数为直线l 的斜率（B ）x 和y 的相关系数在0到1之间（C ）当n 为偶数时，分布在l 两侧的样本点的个数一定相同（D ）直线l 过点(,)x y10．甲乙两人一起去游“2011西安世园会”，他们约定，各自独立地从1到6号景点中任选4个进行游览，每个景点参观1小时，则最后一小时他们同在一个景点的概率是（ ）（A ）136 （B ）19 （C ）536（D ）16 二、填空题：把答案填在答题卡相应题号后的横线上（本大题共5小题，每小题5分，共25分）11、设20lg ,0()3,0a x x f x x t dt x >⎧⎪=⎨+≤⎪⎩⎰，若((1))1f f =，则a = . 12、设n N +∈,一元二次方程240x x n -+=有正数根的充要条件是n = .13.观察下列等式 1=12+3+4=93+4+5+6+7=254+5+6+7+8+9+10=49……照此规律，第n 个等式为 .14.植树节某班20名同学在一段直线公路一侧植树，每人植一棵，相邻两棵树相距10米。

陕西省西安市八校高三数学联考（四）试题 理 新人教A 版【会员独享】第Ⅰ卷 （选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知复数z满足3)3i z i ⋅=，则z 等于（ ）A.32B. 34C. 32D. 34 2. 下列函数中，周期为1且是奇函数的是（ ）A. 21sin y x π=-B. sin(2)3y x ππ=+C. tan2y x π= D. sin cos y x x ππ=3. 设,a b 是非零向量，若函数()()()f x xa b a xb =+⋅-的图像是一条直线，则必有（ ） A. a b ⊥ B. a b ∥ C. ||||a b = D. ||||a b ≠4. 在等比数列{}n a 中，n S 为其前n 项和，已知546523,23a S a S =+=+，则此数列的公比q 为（ ） A. 2 B.3 Ｃ. 4 D. 55. 已知227x y A ==，且112x y+=，则A 的值是（ ）A. 7B.±6. 已知函数3()f x x x =+，则0a b +>是()()0f a f b +>的（ ） A. 充分非必要条件 B. 必要非充分条件C. 充分必要条件D. 既非充分也非必要条件7. 已知a 、b 均为正数，且满足2a b +=，则22S a b =++的最大值是（ ） A.72 B. 4 C. 5 D. 928. 体育老师把9个相同的足球放入编号为1,2,3的三个箱中，要求每个箱子放球的个数不少于其编号，则不同的方法有（ ）A.28种B.16种C.10种D. 42种9. 已知不等式组00220x y x y ≥⎧⎪≥⎨⎪+-≤⎩，表示平面区域D ，现在往抛物线22y x x =-++与两坐标轴正半轴围成的封闭区域内随机地抛掷一粒小颗粒，则该颗粒落到区域D内的概率为（）A.19B.15C.29D.31010. 对于(1,3)x∈. 不等式32236(6)x x x a+≥+恒成立，则实数a的取值范围（）A。

2011年普通高等学校招生全国统一考试（陕西卷）数学（理科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。

（本大题共10小题，每小题5分，共50分。

）1、设是向量，命题“若，则”的逆命题是（A）若则（B）若则（C）若则（D）若则【答案】D【解析】：交换一个命题的题设与结论，所得到的命题与原命题是（互逆）命题。

故选D2、设抛物线的顶点在原点，准线方程为，则抛物线的方程是（A）（B）（C）（D）【答案】B【解析】：设抛物线方程为，则准线方程为于是3、设函数满足，则的图像可能是【答案】B【解析】：由知为偶函数，由知周期为2。

故选B4、的展开式中的常数项是（A）（B）（C）（D）【答案】C【解析】：令，于是展开式中的常数项是故选C5、某几何体的三视图如图所示，则它的体积是（A）（B）（C）（D）【答案】A【解析】：由三视图可知该几何体为立方体与圆锥，立方体棱长为2，圆锥底面半径为1、高为2，所以体积为故选A6、．函数在内（A）没有零点（B）有且仅有一个零点（C）有且仅有两一个零点（D）有无穷个零点【答案】B【解析】：令，，则它们的图像如图故选B7、．设集合，则为（A）（B）（C）（D）【答案】C【解析】：由即由得即故选C 8、右图中，为某次考试三个评阅人对同一道题的独立评分，为该题的最终得分，当，时等于（A）（B）（C）（D）【答案】C【解析】：,由得故选C9．设，，，是变量x和y的n个样本点，直线是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是（A）x和y相关系数为直线l的斜率（B）x和y的相关系数在0到1之间（C）当n为偶数时，分布在l两侧的样本点的个数一定相同（D）直线过点【答案】D二、填空题：11．设，若，则【答案】1【解析】：12．设，一元二次方程有整数根的冲要条件是【答案】3或4【解析】：由韦达定理得又所以则13．观察下列等式照此规律，第个等式为【答案】【解析】：第个等式是首项为，公差1，项数为的等差数列，即14、植树节某班20名同学在一段直线公路一侧植树，每人植一棵，相邻两棵树相距10米，开始时需将树苗集中放置在某一树坑旁边，使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小，这个最小值为（米）。

上，，，所以)+∞1x >cos 1x ≤()f x x =-，所以函数1sin 02x x=+>()cos f x x =-ππ个进行游览，每个景点参观1小时，则最后一小时他们同在一个景点的概率是 （ ） （A ）（B ） （C ） （D ） 1361953616【解】选D 甲乙两人各自独立任选4个景点的情形共有（种）；最后一小时他们同在4466A A ⋅一个景点的情形有（种），所以．33556A A ⋅⨯33554466616A A P A A ⋅⨯==⋅二、填空题：把答案填在答题卡相应题号后的横线上（本大题共5小题，每小题5分，共25分）11．设，若，则 ．2lg 0()30ax x f x x t dt x >⎧⎪=⎨+⎪⎩⎰…((1))1f f =a =【解】因为，所以，又因为，10x =>(1)lg10f ==230()3af x x t dt x a =+=+⎰所以，所以，． 3(0)f a =31a =1a =【答案】112．设，一元二次方程有整数根的充要条件是 ． n N +∈240x x n -+=n =【解】，因为是整数，即为整数，所以41642nx ±-=24n =±-x 24n ±-4n-为整数，且，又因为，取，验证可知符合题意；反之4n …n N +∈1,2,3,4n =3,4n =3,4n =时，可推出一元二次方程有整数根． 240x x n -+=【答案】3或4 13．观察下列等式1=1 2+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49……Ｍ为PD 上一点，且，所以，且， 4||||5MD PD =p x x =54p y y =∵P 在圆上，∴，整理得，2225x y +=225()254x y +=2212516x y +=即C 的方程是．2212516x y +=（2）过点（3，0）且斜率为的直线方程是， 454(3)5y x =-设此直线与C 的交点为，，11(,)A x y 22(,)B x y 将直线方程代入C 的方程得：4(3)5y x =-2212516x y +=，化简得，∴，， 22(3)12525x x -+=2380x x --=13412x -=23412x +=所以线段AB 的长度是 22212121216||()()(1)()25AB x x y y x x =-+-=+-，即所截线段的长度是． 414141255=⨯=41518．（本小题满分12分） 叙述并证明余弦定理．【分析思路点拨】本题是课本公式、定理、性质的推导，这是高考考查的常规方向和考点，引导考生回归课本，重视基础知识学习和巩固． 【解】叙述:余弦定理：三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍。

2011届西安地区八校高三年级联考数学（理科）试题2011年4月第Ⅰ卷 （选择题 共50分）一、选择题：（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 设集合{}1,2A =，则满足{}1,2,3A B = 的集合B 的个数是A. 1B. 3C. 4D. 8 2. 方程221cos 2010sin 2010xy-=所表示的曲线为A. 焦点在x 轴上的椭圆B. 焦点在y 轴上的椭圆C. 焦点在x 轴上的双曲线D. 焦点在y 轴上的双曲线 3. 已知复数12z i =+，21z i =-，则12z z z =⋅在复平面上对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限 4. 在边长为1的等边A B C ∆中，设BC a = ，CA b = ，AB c = ，则a b b c c a ⋅+⋅+⋅=A. 32-B. 0C. 32D. 35. 如图在棱长为5的正方体1111ABCD A B C D -中，EF 是棱AB 上的一条线段，2EF =，Q 是11A D 中点，点P是棱11C D 上动点，则四面体PQEF 的体积A. 是变量且有最大值B. 是变量且有最小值C. 是变量且有最大值和最小值D. 是常量6. 如图，程序框图所进行的求和运算是A. 11112310+++⋅⋅⋅+B. 11113519+++⋅⋅⋅+C.111124620+++⋅⋅⋅+D.231011112222+++⋅⋅⋅+7. 函数()y f x =的图像经过原点，且它的导函数()y f x '=的图像是如图所示的一条直线，则()y f x =的图像不经过A. 第一象限B. 第二象限C. 第三象限D. 第四象限 8. 在区间,22ππ⎡⎤-⎢⎥⎣⎦上随机取一个数x ，则cos x 的值介于0到12之间的概率为A.13B.2πC.12D. 239. 在某校举行的数学竞赛中，全体参赛学生的竞赛成绩近似服从正态分布(70,100)N .已知成绩在90分以上（含90分）的学生有12名，若(2)0.9772Φ=，则此次参赛学生总人数约为A. 526B. 431C. 345D. 673 10. 观察下列三角形数表：其中从第2行起，每行一个数为其“肩膀”上两个数之和，则该数表的最后一行的数为A. 981012⨯B. 991012⨯C. 99992⨯D. 991002⨯第Ⅱ卷 （非选择题 共100分）二、填空题：（本大题共5小题，每小题5分.把答案填在答题卡相应题号的位置上） 11. 在101()2x x -的展开式中，4x 的系数为 .12. 设变量,x y 满足约束条件222y xx y x ⎧⎪+⎨⎪-⎩≥≤≥，则3z x y =-的最小值 .13. 设曲线ax y e =在点(0,1)处的切线与直线210x y ++=垂直，则a = . 14. 右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是 .15. （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分） A. （不等式选做题）函数|1||1|y x x =+--的最大值是 .B. （几何选讲选做题）如图，PA 切圆O 于点A ，割线PBC 经过圆心O ，1,O B P B == O A 绕点O逆时针转60 到O D ，则PD 的长为 .C. （极坐标与参数方程选做题）在极坐标系中，过圆6cos ρθ=的圆心，且垂直于极轴的直线的极坐标方程为 .三、解答题：（本大题共6小题，共75分.解答应写出文字说明、推理过程和演算步骤） 16. （本小题满分12分）已知函数()2sin()184f x x ππ=++.（Ⅰ）在所给的坐标纸上作出函数[](),2,14y f x x =∈-的图象（不要求作图过程） （Ⅱ）令()()()g x f x f x =+-，x R ∈，求函数()y g x =与x 轴交点的横坐标. 17. （本小题满分12分）已知实数列{}n a 为等比数列，其中71a =，且4a ，51a +，6a 成等差数列. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）是否存在正整数m ，使得当n m >时，1||2011n a <恒成立？若存在，求出m 的值构成的集合.若不存在，请说明理由.18. （本小题满分12分）某大学举办“我爱记歌词”校园歌手大赛，经过层层选拔，有5人进入决赛，决赛办法如下：选手先参加“千首电脑选歌”演唱测试，测试过关者即被授予“校园歌手”称号，否则参加“百首电脑选歌”演唱测试. 若“百首电脑选歌”演唱测试过关也被授予“校园歌手”称号，否则被彻底淘汰.若进入决赛的5人“千首电脑选歌”演唱测试过关的概率是0.5，“百首电脑选歌”演唱测试合格的概率是0.8，而且每个人每轮测试是否合格是相互独立的.试计算（结果精确到0.01）：（Ⅰ）恰好有两人参加“百首电脑选歌”演唱的概率； （Ⅱ）平均有几人参加“百首电脑选歌”演唱； （Ⅲ）至少一人被最终淘汰的概率. 19. （本小题满分12分）如图在三棱锥S A B C -中，SC ⊥平面ABC ，M 、N 分别是S B 和SC 的中点，设1M N AC ==，90ACB ∠= ，直线AM 与直线SC 所称的角为60（Ⅰ）求证：平面AM N ⊥平面SAC ；（Ⅱ）求二面角M A B C --的平面角的余弦值； （Ⅲ）求A N 和C M 所成角的余弦. 20. （本小题满分13分）设直线l 的方程为20x -=，点P 到点(1,0)F 的距离与点P 到直线l 的距离之比为2.（Ⅰ）求动点P 的轨迹Γ的方程；（Ⅱ）设定点B 的坐标为(0,1)，直线L 与轨迹Γ交于M ，N 两点.试探求点F 是否可以为B M N ∆的垂心？若可以，求出直线L 的方程；若不可以，请说明理由. 21. （本小题满分14分）已知函数21()log .21x f x x=+-（Ⅰ）求证：存在定点M ，使得函数()f x 图象上任意一点P 关于M 点对称的点Q 也在函数()f x 的图象上，并求出点M 的坐标；（Ⅱ）定义11121()()()(),n n i i n S f f f f n n n n-=-==++⋅⋅⋅+∑其中*n N ∈且2n ≥，求2011S ；（Ⅲ）对于（Ⅱ）中的n S ，求证：对于任意*n N ∈都有212311ln ln .n n S S nn-+->-。

2011年普通高等学校招生全国统一考试（陕西卷）数学（理工农医类）一．选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共10小题，每小题5分，共50分）1. 设,a b是向量，命题“若a b≠-，则∣a∣= ∣b∣”的逆命题是（）（A）若a b≠-，则∣a∣≠∣b∣（B）若a=—b，则∣a∣≠∣b∣（C）若∣a∣≠∣b∣，则a≠—b（D）若∣a∣=∣b∣，则a= -b 2.设抛物线的顶点在原点，准线方程为2x=-，则抛物线的方程是（）（A）28=-(D) 24=y xy xy xy x=-（B）28=(C) 243.设函数()()f x x R=的图像可能是-=+=,则()y f x∈满足()(),(2)(),f x f x f x f x（B）4. （x∈R展开式中的常数项是（）（A）-20 （B）-15 （C）15 （D）205. 某几何体的三视图如图所示，则它的体积是（）(A) 8—2π/3(B) 8—π/3(C) 8—2π(D) 2π/36.函数cosx在[0，+∞）内（）（A ）没有零点 （B ）有且仅有一个零点 （C ）有且仅有两个零点 （D ）有无穷多个零点 7. 设集合M={y |2cos x —2sin x |,x ∈R},N={x ||x —1i 为虚数单位，x ∈R},则M ∩N 为（ ）(A)(0,1) (B)(0,1] (C)[0,1) (D)[0,1]8.右图中，1x ，2x ，3x 为某次考试三个评阅人对同一道题的独立评分，P 为该题的最终得分。

当1x =6，2x =9，p=8.5时，3x 等于 （ ）(A)11 (B)10 (C)8 (D)79.设（1x ，1y ），（2x ，2y ），…，（n x ，n y ）是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是【D 】（A ）x 和y 的相关系数为直线l 的斜率 （B ）x 和y 的相关系数在0到1之间（C ）当n 为偶数时，分布在l 两侧的样本点的个数一定相同（D ）直线l 过点10.甲乙两人一起去游“2011西安世园会”，他们约定，各自独立地从1到6号景点中任选4个进行游览，每个景点参观1小时，则最后一小时他们同在一个景点的概率是【D 】 （A ）136 （B ）19 （C ）536（D ）16二、填空题（本大题共5个小题，每小题5分，共25分）11.设若((1))1f f =，则a = 112.设n N +∈,一元二次方程240x x n -+=有正数根的充要条件是n = 3或4 13.观察下列等式1=1 2+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49……照此规律，第n 个等式为 2(1)(2)...(32)(21)n n n n n ++++++-=-。

本试卷分第I卷(选择题）和第N卷(非选择题)两部分.共300分，考试时间150分钟.可能用到的相对原子质量：H-1C-12、O - 16、N - 14、S -32、Na -23、A1 -27、Ba -137第I卷(选择题共126分）一、选择题（本小题包括13小题.每小题只有一个选项符合题意）7.化学用语是学习化学的重要工具.下列用来表示物质变化的化学用语中，错误的是A.钢铁腐蚀时可能发生的正极反应：B.表示H2燃烧热的热化学方程式：C.纯碱水解的离子方程式：D溶液中加入过量澄清石灰水:8.某烃有两种或两种以上的同分异构体，其同分异构体中的某一种的一氯代物只有一种，则这种烃可能是：①分子具有7个碳原子的芳香烃②分子中具有4个碳原子的烷烃③分子中具有12个氢原子的烷烃④分子中具有8个碳原子的烷烃A.①②B.②③ c. ③④D.②④9.气态烃0.5MOL能与1MOL HCL加成，转变为氯代烷烃，加成后产物分子上的氢原子又可被3mol Cl2完全取代，则该烃可能是A. B. C. D.10.250C时，20. OOmL硫酸和硝酸的混合溶液，加入足量氯化钡溶液，充分反应后过滤、洗涤、烘干，可得0.466g沉淀.滤液跟2MOL/L NA O H溶液反应，共用去10. OOML碱液时恰好中和.下列说法中正确的是A.原混合液中B.原混合液中C.原混合液中PH =0 D原混合液中由水电离出的11.下列实验报告记录的实验现象正确的是12.气体X 可能含有中的一种或几种，已知X 通入；溶液时产生淡黄色沉淀，且沉淀不溶于稀硝酸；若将X通人澄清的石灰水中，却不见沉淀产生.对于气体X的成分，下列说法正确的是A.一定含有，可能含有B.—定不含C.一定不含和D.可能含有和13.MCFC型燃料电池可同时供应电和水蒸气，其工作温度为600¾-700¾，所用燃料为H2，电解质为熔融的.已知该电池的总反应为，则下列有关该电池的说法正确的是A.该电池的正极的反应式为：B.该电池负极的反应为：C.放电时向正极移动D.该燃料电池能量转化率很低第II卷(非选择题共174分）25.(14分)氮化铝（AlN)是一种新型无机材料，广泛应用于集成电路生产领域.某氮化铝中含有碳或氧化铝杂质，现用图I中的一些装置来进行检验，使氮化铝样品和NaOH溶液反应：，根据反应中所生成氨气的体积来测定样品中的氮化铝的质量分数，并根据实验现象来确定杂质的成分(实验中导管体积忽略不计）26题图(1)实验有关操作为:A、往烧瓶中放入适量的AIN样品:b、从分液漏斗往烧瓶中加人过量的浓NaOH; C、检验装置的气密性;d、测定收集到水的体积.正确的操作顺序为：______________________________.(2)本试验中（图I)检査装置气密性的方法是：______________________________.(3)广口瓶中的试剂X可选用______________________________.(填选项的标号）A.汽油B.酒精C.植物油D.⑷实验结束后，若观察到烧瓶中还有固体，则样品中含有的杂质是___________________ .(5)若实验中测得样品的质量为W g，氨气的体积为a L(标况下），则样品中AIN的质量分数为: _____.(6)有人改用图II装置进行同样实验，通过测定烧杯中硫酸的增重来确定样品中AIN的质量分数.你认为是否可行？ ____________________ .(填入“可行”、“不可行”）.原因是____________________27.(15分)A-J是中学化学中常见的几种物质，它们之间的转化关系如图所示.已知常温下A为固体单质，B为淡黄色粉末，C、F、I为气态单质，E在常温下为液体，且E可由C、F合成，J可用作杀菌消毒剂.回答下列问题：(1)B的化学式：_________________________，E的电子式_________________________.(2)写出反应⑤、⑦的离子方程式：⑤_______________，⑦____________________.(3)向AlCl3溶液中加入适量固体B，写出AlCl3与物质B按物质的量比2 _：3反应的化学方程式________________________________________.(4)以P t为电极电解滴加有少量酚酞的H饱和溶液，则在_____ _____ _____ _____ (填“阴、阳”）极附近溶液由无色变为红色，简述溶液变红的原因_________________________.28. (14分)一定温度下，在一个带有活塞的容积可变的密闭容器中（活塞的一端与大气相通），发生如下反应：若反应开始时充人2moIX和8molY，达到平衡后，测得平衡时混合气体的总物质的量为8.4mol,X的体积分数为w%.(1)写出该反应平衡常数的表达式____________________，并计算平衡时X的转化率_______________.(2)若增大压强，该反应的化学反应速率将_______________，该反应的K值将_____ _____ _____ _____ (均填“增大”“减小”或“不变”）.(3)保持上述反应温度不变，设a、b、c分别代表初始加人的X、Y、Z的物质的量，若反应达平衡后，混合气体中X的体积分数仍为，那么：若a =1，C =2，则b = __________，在此情况下反应起始时将向_______________方向进行.(4)保持上述反应温度不变，若按下列四种配比作为起始物质，达平衡后X的体积分数大于w％的是_______________.(填序号）A. B.C. D.37.[化学一选修物质结构与性质](15分）A、B、C、D、E都是短周期主族元素,原子序数依次增大，B、C同周期，A、D同主族，E的单质既可溶于稀硫酸又可溶于氢氧化钠溶液.A、B能形成两种在常温下呈液态的化合物甲和乙，原子个数比分别为2:1和1:1.根据以上信息回答下列1 -3问：(1)C和D的离子中，半径较小的是_____ _____ (填离子符号).(2)实验室在测定C的气态氢化物的相对分子质量时，发现实际测定值比理论值大出许多，其原因是__________•(3)C、D、E可组成离子化合物D x E6其晶胞（晶胞是在晶体中具有代表性的最小重复单元)结构如图所示，阳离子D+(用0表示)位于正方体的棱的中点和正方体内部；阴离子（用示）位于该正方体的顶点和面心，该化合物的化学式是____________________________•(4)Mn、Fe均为第四周期过渡元素，两元素的部分电离能数据列于下表：回答下列问题：(5) Mn元素价电子层的电子排布式为_____________________,比较两元素的I2 J3可知，气态Mn2 +再失去一个电子比气态Fe2+再失去一个电子难.对此的解释是______________ ；(2) Fe原子或离子外围有较多能量相近的空轨道而能与一些分子或离子形成配合物.①与Fe原子或离子形成配合物的分子或离子应具备的结构特征是_____________________②六氰合亚铁离子中的配体CN-中c原子的杂化轨遣类型是______________写出一种与CN-互为等电子体的单质分子的路易斯结构式_____________________；38.[化学一选修有机化学基础](15分）下列是A、B、C、D、E、F、G、H 及丙二酸（）间转化反应的关系图.A是一种链状羧酸，分子式为；F中含有由七个原子构成的环;H是一种高分子化合物.请填写下列空白：(1)A中官能团的名称_____________________.(2)C的结构简式：_____________________ ；F的结构简式：_____________________.(3)请写出下列化学方程式：①A→H__________________________________________.②B与NaOH溶液的反应_____________________，其反应类型是 _____________________.(4)G与银氨溶液反应的化学方程式为__________________________________________.(5)苹果酸是丙二酸的某种同系物的轻基取代产物.元素分析证明该酸中C、H、0的质量比为:24:3:40;该酸蒸气的密度是同温同压下氢气密度的67倍，该酸分子结构中没有支链.写出苹果酸的结构简式________________________________________________________；.参考答案及评分标准第I卷（选择题,共126分）。