地质参数参考取值

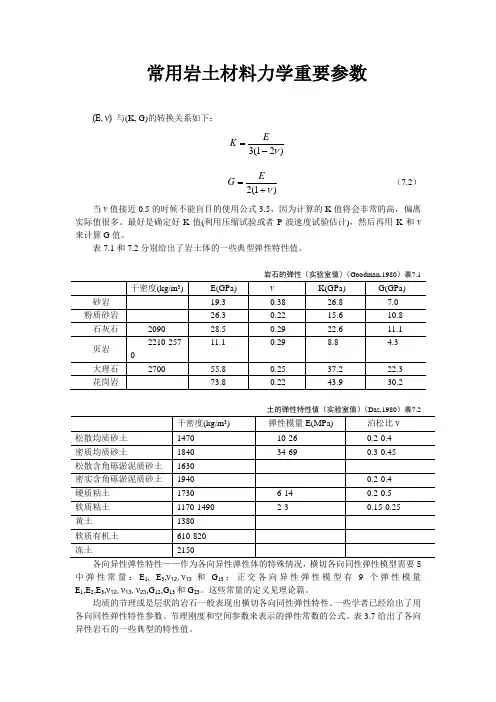
常用岩土材料力学重要参数(E, ν) 与(K, G)的转换关系如下：)21(3ν-=E K )1(2ν+=E G （7.2） 当ν值接近0.5的时候不能盲目的使用公式3.5，因为计算的K 值将会非常的高，偏离实际值很多。

最好是确定好K 值(利用压缩试验或者P 波速度试验估计)，然后再用K 和ν来计算G 值。

表7.1和7.2分别给出了岩土体的一些典型弹性特性值。

岩石的弹性（实验室值）（Goodman,1980）表7.1土的弹性特性值（实验室值）（Das,1980）表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况，横切各向同性弹性模型需要5中弹性常量：E 1, E 3,ν12,ν13和G 13；正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3,ν12,ν13,ν23,G 12,G 13和G 23。

这些常量的定义见理论篇。

均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。

一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。

表3.7给出了各向异性岩石的一些典型的特性值。

横切各向同性弹性岩石的弹性常数（实验室）表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ，如果土粒是可压缩的，则要用到比奥模量M 。

纯净水在室温情况下的K f 值是2 Gpa 。

其取值依赖于分析的目的。

分析稳态流动或是求初始孔隙压力的分布状态（见理论篇第三章流体-固体相互作用分析），则尽量要用比较低的K f ，不用折减。

这是由于对于大的K f 流动时间步长很小，并且，力学收敛性也较差。

在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ，渗透系数k 以及K f 有如下关系：'f f kK n t ∝∆ （7.3） 对于可变形流体（多数课本中都是将流体设定为不可压缩的）我们可以通过获得的固结系数νC 来决定改变K f 的结果。

f 'K n m k C +=νν（7.4）其中3/4G K 1m +=ν f 'k k γ=其中，'k ——FLAC 3D 使用的渗透系数 k ——渗透系数，单位和速度单位一样（如米/秒）f γ——水的单位重量考虑到固结时间常量与νC 成比例，我么可以将K f 的值从其实际值（Pa 9102⨯）减少，利用上面得表达式看看其产生的误差。

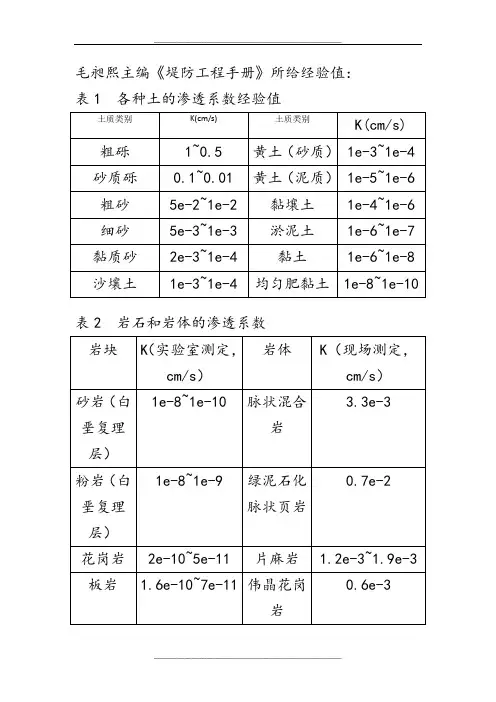
毛昶熙主编《堤防工程手册》所给经验值：表1 各种土的渗透系数经验值
表2 岩石和岩体的渗透系数
角砾岩 4.6e-10 褐煤层 1.7e-2~2.39e-2 方解岩 9.3e-8~7e-10 砂岩 1e-2 灰岩
1.2e-7~7e-10
泥岩
1e-4 白云岩 1.2e-8~4.6e-9 鳞状片岩 1e-2~1e-4
砂岩 1.2e-5~1.6e-7 1个吕荣单位裂隙宽度0.1mm 间距1m 和
不透水岩块的岩体
0.8e-4
砂泥岩 2e-6~6e-7
细粒砂岩 2e-7
蚀变花岗岩
0.6e-5~1.5e-5 表3 各种岩土的给水度
岩土类别 渗透系数K
（cm/s ）
孔隙率n 给水度
资料来源
砾 240 0.371 0.354
瑞士工学研究所
粗砾 160 0.431 0.338 砂砾 0.76 0.327 0.251 砂砾 0.17 0.265 0.182 砂砾 7.2e-2 0.335 0.161 中粗砂 4.8e-2 0.394 0.18 含黏土的
1.1e-4
0.397
0.0052
表4 各种岩土的压缩弹性模量E及单位储存量S的值
郑春苗，Gordon D.Bennett 著《地下水污染物迁移模拟》所给经验值：
表5 不同岩石类型的渗透系数取值范围
表6 不同地质材料的单位给水度
表7 不同地质材料的孔隙率
朱学愚，钱孝星著《地下水水文学》所给经验值表8 典型孔隙率数值。

一、可信度系数根据《《矿业权评估收益途径评估方法修改方案》说明》：“对于经济基础储量，即探明的（可研）经济基础储量（111b）、探明的（预可研）经济基础储量（121b）、控制的经济基础储量（122b）、（332），全部参与评估计算，不采用可信度系数进行调整。

推断的内蕴经济资源量（333）可参考 (预)可行性研究、矿山设计或矿产资源开发利用方案取值。

(预)可行性研究、矿山设计或矿产资源开发利用方案中未予设计利用，但资源储量在矿业权有效期（或评估年限）开发范围内的，可信度系数在0.5～0.8范围中取值，具体取值应按矿床 (总体)地质工作程度、推断的内蕴经济资源量 (333)与其周边探明的或控制的资源储量关系、矿种及矿床勘探类型等确定。

矿床地质工作程度高的，或 (333)资源量的周边有高级资源储量的，或矿床勘探类型简单的，可信度系数取高值；反之，取低值。

”无需做更多地质工作即可供开发利用的地表出露矿产（如建筑材料类矿产），估算的资源储量均视为111b或122，全部参与评估计算。

预测的资源量（334）不参与评估计算。

1、评估报告中显示，《详查报告》中控制的内蕴经济资源量（332）全部参与评估计算；又根据《可行性研究报告》，推断的内蕴经济资源量（333）全部设计利用，故不再进行可信度系数调整，全部参与本次评估计算。

（333）资源量全部作为设计利用的资源量参数是合理有据的。

二、含矿系数含矿系数（ore coefficient）（又名：含矿率）是矿床或矿体、矿段、块段中的工业可采部分与整个矿床或矿体、矿段、块段之比。

在某些矿产的储量计算时，为除去无矿地段，提高储量计算精度而使用的校正系数，其计算方法及数值虽与含矿率相同，但两者的地质意义却不同。

矿化连续的矿体其含矿系数为1或近于1;含矿系数愈小，矿化愈不连续。

对于一些矿化连续程度很低，工业可采地段分布极不规则、在勘探和储量计算时难以分别圈定的矿体，则必须引用含矿系数来校正矿产储量，使其比较切合矿床的实际情况。

各类岩土参数变异系数限制值-概述说明以及解释1.引言1.1 概述在概述部分，你可以写一些关于岩土参数变异系数的基本背景和重要性的内容。

可以参考以下写作示例：概述岩土参数的变异性是指在不同地质条件下，不同取样点或试验结果中存在的差异。

由于岩土参数的变异性，其数值在不同地点、不同试验中可能会有较大差别。

岩土参数的变异性对于土木工程的设计和施工具有重要影响。

岩土参数变异系数是衡量岩土参数变异性的一种指标。

它是通过统计分析大量试验数据得出的，反映了岩土参数数值的分散程度。

岩土参数变异系数越大，代表相同性质的岩土在不同地点或试验中的数值差异越大。

相反，岩土参数变异系数越小，代表变异性较低，岩土参数的数值变化较为稳定。

岩土参数变异系数的研究对于岩土工程的设计和施工具有重要意义。

首先，岩土参数的变异性可能会导致工程设计出现一定的风险。

因此，在进行工程设计时，需要充分考虑岩土参数的变异性，并在设计过程中设置合理的安全系数，以确保工程的可靠性和安全性。

其次，岩土参数变异系数在岩土工程施工和监测中也具有重要作用。

合理评估岩土参数的变异性可以帮助工程师更准确地确定施工方案和监控指标，从而提高施工质量和工程效益。

本文将探讨各类岩土参数的变异性，并分析其变异系数的限制值。

通过研究各类岩土参数的变异性限制值，有助于合理评估其可靠性和安全性，并为岩土工程的设计和施工提供科学依据。

此外，本文还将探讨实际应用中需考虑的因素，为岩土工程实践提供一些参考和建议。

1.2文章结构文章结构部分的内容可以针对以下几个方面进行撰写：1.2 文章结构：本文分为引言、正文和结论三大部分。

引言部分主要对文章进行开场介绍，概述了本文的主题和意义，并介绍了文章的结构框架。

正文部分分为2.1小节和2.2小节。

2.1小节将详细介绍各类岩土参数的意义和作用，包括常见的岩土参数如抗剪强度、含水量、孔隙比等在工程中的应用和重要性。

通过对各类岩土参数的解释和实际案例的介绍，读者可以对这些参数的定义、计算方法和工程中的应用有更加深入的理解。

岩土体物理力学参数在边坡稳定性定量分析中，岩土体的物理力学参数往往直接控制着稳定系数和支护工程量。

常规的获取参数的方法主要有试验法、经验法、工程地质类比法、反演分析法等。

此外，当边坡稳定受成组结构面和岩桥共同控制时，仍常采用结构面连通率，即采用结构面和岩桥强度进行加权平均来求取潜在滑移面的综合抗剪强度。

以下对两种参数获取方法进行简单介绍。

1.试验法试验法一般可分为室内试验和现场试验两类。

现场试验试件尺寸一般较大，多为（50～70）cm×（50～70）cm，它能保持岩土体的原始状态，并能反映结构面二、三级起伏差对强度的影响，但加工困难，周期长，试验费用相对较高。

室内试验试件一般较小，多为扰动样，存在尺寸效应问题，但取样简单，可以开展各种不同工况下的试验，如三轴直剪试验、饱和固结快剪试验、饱和固结排水剪试验、慢剪试验等。

室内试验由于试验周期短，费用相对较低，可以大量开展。

目前，随着取样技术的发展，已具备取原状样的条件，且可在刚性伺服机上开展试验，能有效地确定有效正应力，控制剪切速度，试验成果较为真实可靠。

2.经验估算法可根据一些经验公式，如利用Hoek-Brown强度准则确定岩体的综合抗剪强度。

一般是在工程前期和缺乏试验的地区应用，该方法存在的问题是岩石强度权重偏大，应用在坚硬和极坚硬岩石中时，确定的抗剪强度常常偏高。

8.5.2 选择原则对于一些不重要或者工程前期缺乏试验资料的边坡，可通过经验法和工程地质类比法，初步确定岩土体的物理力学参数，以此估算边坡的稳定性和支护工程量。

对于一些已经失稳或正在变形的边坡，采用反演分析法来获取岩土体的物理力学参数是一种最有效的办法，但由于此时的抗剪强度已不是常规物理意义上的抗剪强度，而是岩土体抗剪强度参数、边界条件、地下水条件等因素的综合反映，因此，在应用时应严格注意条件的相似性。

同时，应考虑在工程有效期内工作条件的可能变化趋势对强度参数的影响，并适当进行调整。

对结构设计影响较大的地质勘察报告参数浅析目前，房地产业已进入低利润时代，房地产企业普遍认识到成本控制的重要性，并开展了很多深入的研究。

例如，针对在建安成本中占很大比重的土建结构成本控制，各大房地产企业已经总结出很多行之有效的经验和措施。

但是，作为结构设计依据之一的地质勘察报告，却没有引起足够的重视。

地勘报告中的一些指标，对结构设计计算影响很大，这些指标的细微变化，就可能使结构内力、位移、配筋计算结果产生差异，从而对成本造成影响。

下面，本文就对这些指标进行介绍和分析。

一、地下水位及抗浮设计水位：工程设计中常用的水位有防水设计水位和抗浮设计水位。

1、防水设计水位：指地下水的最大水头，用于确定建筑外防水和地下室的抗渗等级。

《北京地区建筑地基基础勘察设计规范》(DBJ-01-501-92)第4.1.5条规定：对防水要求严格的地下室或地下构筑物，其设防水位可按历史最高地下水位确定；对防水设计要求不严格的地下室或地下构筑物，其设防水位可按照3-5年的最高水位及勘察时的实测静止水位确定。

而在《地下工程防水技术规范》（GB50108）中规定：单建式的地下工程应采用全封闭、部分封闭防排水设计，附建式的全地下或半地下工程的防水设防高度，应高出室外地坪高程500mm以上。

也就是说，国标规范中规定不管地下水位高度多少，均按高出室外地坪500以上进行防水设防。

显然，这种做法偏于保守。

建议根据地下室的防水等级及重要性等级，在+0.500米和历史最高水位之间，采取防水砂浆、防水混凝土等防水措施；在历史最高水位以下，水压力经常作用的部位，采取防水卷材等较严格的防水措施。

2.抗浮设计水位众所周知，地下室抗浮是个非常严峻的问题，抗浮设计水位的选择对工程成本影响巨大。

《高层建筑岩土工程勘察规程》（JGJ72—2004，J366—2004）对抗浮设防水位给予了明确的定义：抗浮设防水位——地下室抗浮评价计算所需的，保证抗浮设防安全和经济合理的场地地下水位。

中粗粒砂岩岩体容重取值标准中粗粒砂岩岩体容重取值标准的深入探讨1. 引言中粗粒砂岩作为一种常见的岩石类型，它的容重在地质调查和工程设计中具有重要的意义。

容重是指岩石单位体积内所含的质量，是岩石强度和稳定性的重要参数之一。

在工程领域中，准确的中粗粒砂岩容重取值标准对于土木工程建设的安全性和稳定性至关重要。

本文将深入探讨中粗粒砂岩岩体容重取值标准的背景、必要性以及影响因素，并提出一种有效的评估方法。

2. 背景和必要性中粗粒砂岩广泛存在于地质构造复杂地区，例如山地、丘陵等地形，对于这些地区进行工程建设时，需要了解该地区的地质特征，特别是中粗粒砂岩的容重。

容重的取值标准不仅影响到地质勘察和土木工程设计，还直接关系到工程建设的安全性和经济性。

3. 影响因素中粗粒砂岩岩体容重受多种因素的影响。

岩石的化学组成会影响其容重，例如矿物成分及含量的差异会导致容重的变化。

岩石的结构性质，包括孔隙度、压实度以及颗粒间的结合情况，也会对容重产生影响。

环境条件，如湿度、温度等，也可能对中粗粒砂岩的容重产生一定影响。

4. 中粗粒砂岩容重取值标准的评估方法为了准确评估中粗粒砂岩的容重，我们可以采用以下方法：(1) 野外实地取样和试验：通过野外实地取样和试验的方式，可以直接获取中粗粒砂岩的样本，并进行密度测定。

该方法可以获得较为准确的容重取值，但需要较高的成本和人力投入。

(2) 统计分析法：通过分析已有的文献和实验数据，可以进行统计分析，得出大量数据的统计规律，并根据这些规律估算中粗粒砂岩容重的取值标准。

这种方法成本相对较低，但对于容重取值的准确性会有一定的影响。

5. 个人观点和理解对于中粗粒砂岩岩体容重取值标准的评估，我认为应该充分考虑多种因素的综合影响，并且在评估方法中要有一定的可信度和准确性。

在工程实践中，应根据具体工程需求和可行性，选择合适的方法来评估容重取值标准。

在研究和实践中，也需要进一步探讨和完善中粗粒砂岩岩体容重的评估方法，以提高工程设计和建设的安全性和经济效益。

(水利水电)部分常用岩土物理力学参数经验数值-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN使用说明：1、资料涉及各行各业；2、资料出处为黄底加粗字体的为最新版本内容。

可按规范适用范围选择使用；3、资料出处非黄底加粗字体的为引用资料，很多为老版本，参考用。

水利水电工程部分岩土物理力学参数经验数值1岩土的渗透性（1）渗透系数《地下铁道、轻轨交通岩土工程勘察规范》GB50307-1999 139~140页土体的渗透系数值2《水利水电工程水文地质勘察规范》SL373-2007 62~63页岩土体渗透性分级Lu：吕荣单位，是1MPa压力下，每米试段的平均压入流量。

以L/min计摘自《水利水电工程地质勘察规范》GB50287-99 附录J 66页表F 岩土体渗透性分级3《水利水电工程地质勘察规范》（GB50487-2008）109页附录F （2）单位吸水量各种构造岩的单位吸水量（ω值）上表可以看出：同一断层内，一般碎块岩强烈透水；压碎岩中等透水；断层角砾岩弱透水；糜棱岩和断层泥不透水或微透水。

摘自高等学校教材天津大学《水利工程地质》第三版 113页坝基（肩）防渗控制标准4注：透水率1Lu（吕荣）相当于单位吸水量0.01摘自高等学校教材天津大学《水利工程地质》第三版 118页。

（3）简易钻孔抽注水公式1）简易钻孔抽水公式根据水位恢复速度计算渗透系数公式1.57γ(h2-h1)K= ———————t (S1+S2)式中：γ---- 井的半径；h1---- 抽水停止后t1时刻的水头值；h2---- 抽水停止后t2时刻的水头值；S1、S2---- t1或t2时刻从承压水的静止水位至恢复水位的距离；H---- 未抽水时承压水的水头值或潜水含水层厚度。

《工程地质手册》第三版 927页2）简易钻孔注水公式当l/γ＜4时0.366Q 2lK= ———— lg ———Ls γ式中：K—渗透系数（m/d）；l---试验段或过滤器长度（m）；Q---稳定注水量（m3/d）；s---孔中水头高度（m）；γ---钻孔或过滤器半径（m）。

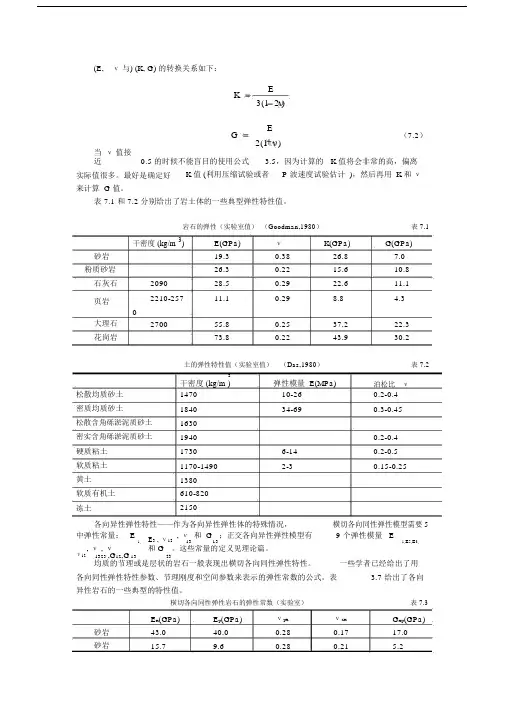
(E, ν与) (K, G) 的转换关系如下：KE3(1 2 )GE（7.2）2(1 )当 ν值接近0.5 的时候不能盲目的使用公式 3.5，因为计算的 K 值将会非常的高，偏离实际值很多。

最好是确定好K 值 (利用压缩试验或者P 波速度试验估计 )，然后再用 K 和 ν来计算 G 值。

表 7.1 和 7.2 分别给出了岩土体的一些典型弹性特性值。

岩石的弹性（实验室值） （Goodman,1980） 表 7.1干密度 (kg/m 3)E(GPa) ν K(GPa)G(GPa)砂岩 19.3 0.38 26.8 7.0 粉质砂岩26.30.22 15.6 10.8石灰石 2090 28.5 0.29 22.6 11.1页岩 2210-25711.10.298.84.3大理石 270055.8 0.25 37.2 22.3花岗岩73.80.2243.930.2土的弹性特性值（实验室值） （Das,1980）表 7.2松散均质砂土 密质均质砂土松散含角砾淤泥质砂土 密实含角砾淤泥质砂土硬质粘土 软质粘土 黄土软质有机土冻土3弹性模量 E(MPa)泊松比 ν 干密度 (kg/m ) 1470 10-260.2-0.41840 34-690.3-0.45163019400.2-0.41730 6-14 0.2-0.5 1170-1490 2-30.15-0.251380610-820 2150各向异性弹性特性——作为各向异性弹性体的特殊情况，横切各向同性弹性模型需要5 中弹性常量： E E 3 , ν12 , ν 和 G 13 ；正交各向异性弹性模型有9 个弹性模量 E1, 131,E 2,E 3,ν12 , ν , ν 和 G 23。

这些常量的定义见理论篇。

1323 ,G 12,G 13均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。

一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。

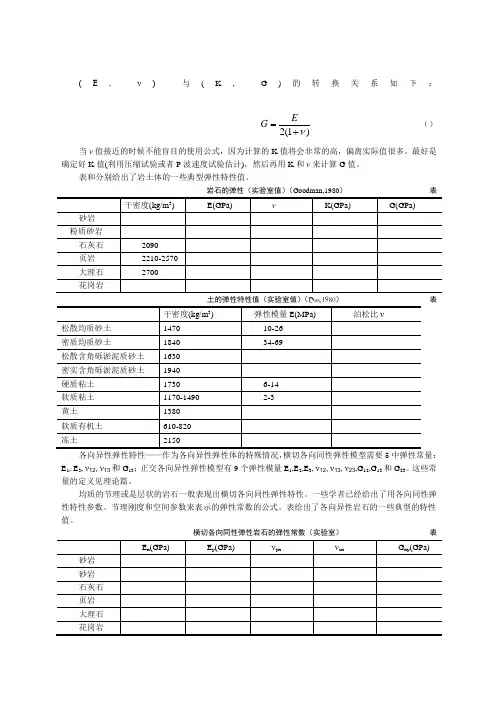
(E , ν) 与(K , G )的转换关系如下：)1(2ν+=EG （）当ν值接近的时候不能盲目的使用公式，因为计算的K 值将会非常的高，偏离实际值很多。

最好是确定好K 值(利用压缩试验或者P 波速度试验估计)，然后再用K 和ν来计算G 值。

表和分别给出了岩土体的一些典型弹性特性值。

岩石的弹性（实验室值）（Goodman,1980） 表土的弹性特性值（实验室值）（Das,1980） 表各向异性弹性特性——作为各向异性弹性体的特殊情况，横切各向同性弹性模型需要5中弹性常量：E 1, E 3, ν12,ν13和G 13；正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。

这些常量的定义见理论篇。

均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。

一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。

表给出了各向异性岩石的一些典型的特性值。

横切各向同性弹性岩石的弹性常数（实验室） 表流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ，如果土粒是可压缩的，则要用到比奥模量M 。

纯净水在室温情况下的K f 值是2 Gpa 。

其取值依赖于分析的目的。

分析稳态流动或是求初始孔隙压力的分布状态（见理论篇第三章流体-固体相互作用分析），则尽量要用比较低的K f ，不用折减。

这是由于对于大的K f 流动时间步长很小，并且，力学收敛性也较差。

在FLAC 3D 中用到的流动时间步长,? tf 与孔隙度n ，渗透系数k 以及K f 有如下关系：'f f k K nt ∝∆ （） 对于可变形流体（多数课本中都是将流体设定为不可压缩的）我们可以通过获得的固结系数νC 来决定改变K f 的结果。

f'K n m k C +=νν （）其中其中，'k ——FLAC 3D 使用的渗透系数k ——渗透系数，单位和速度单位一样（如米/秒） f γ——水的单位重量考虑到固结时间常量与νC 成比例，我么可以将K f 的值从其实际值（Pa 9102⨯）减少，利用上面得表达式看看其产生的误差。