函数的单调性

4.1、函数的单调性函数的单调性就是函数的一种增减性，主要看y 随x 的变化而发生的一种变化情况，简单的说当y 随x 的增大而增大时，就说y 是在相应的x 的取值范围内是增函数，对应的区间为其增区间；而当y 随x 的增大而减小时，我们就说y 是在相应的x 的取值范围内是减函数，对应的区间为其减区间。

A 、定义：一般地，设函数)(x f 的定义域为I 。

如果对于定义域I 内的某个区间D 上的任意两个自变量的值21,x x ，当21x x <时，都有)()(21x f x f <，那么就说函数)(x f 在区间D 上是增函数。

如果对于定义域I 内的某个区间D 上的任意两个自变量的值21,x x ，当21x x <时，都有)()(21x f x f >，那么就说函数)(x f 在区间D 上是减函数。

如果函数)(x f y =在区间D 上是增函数或减函数，那么就说函数)(x f y =在这一区间上具有（严格的）单调性，区间D 叫做)(x f y =的单调区间。

B 、函数单调性的证明对于某区间内的函数的单调性，一般利用定义来证明，其基本步骤如下： （1）取值：设21,x x 为该区间内的任意两个值，并且21x x <；（2）作差变形：作差)()(21x f x f -，并利用因式分解、配方、有理化等方法向有利于判断差值的符号的方向变形；（3）定号：确定差值的符号，当符号不确定时，可考虑分类讨论； （4）下结论：根据函数的单调性的定义得出结论。

C 、函数单调性的判断判断函数单调性的常用方法有：（1）定义法：即“取值——变形——定号——下结论”；（2）图像法：先作出函数的图像，在利用图像的形象直观判断函数的单调性；（但应注意极值点及其拐点） （3）复合法：)(x f y =增 增 减 减（4）导数法：求出函数导数后，在令其导数大于零的x 的连续区间为其单调递增区间，令其导数小于零的x 的连续区间为其单调递减区间；4.1.1、函数单调性的判断与证明A 、函数单调性的证明：1、证明函数12)(+-=x x f 在R 上是减函数。

证明函数单调性的方法证明一个函数的单调性是数学分析中的重要内容，它涉及到函数的增减性质，对于函数的研究具有重要意义。

在数学分析中，我们常常需要证明一个函数在某个区间上是单调递增或者单调递减的。

下面，我将介绍几种常见的方法来证明函数的单调性。

1. 导数法。

导数法是证明函数单调性常用的方法之一。

对于给定的函数f(x)，如果它在某个区间上具有一阶导数，那么我们可以通过导数的正负来判断函数的单调性。

具体来说，如果在某个区间上f'(x)大于0，则函数在该区间上是单调递增的；如果f'(x)小于0，则函数在该区间上是单调递减的。

2. 函数的增减表。

函数的增减表是一种通过导数的符号来判断函数单调性的方法。

我们可以通过求出函数的导数，并列出导数的符号随着自变量的变化而变化的情况，从而得出函数在某个区间上的单调性。

通过增减表，我们可以清晰地看出函数的单调性，并进行证明。

3. 极值点和拐点。

对于一个函数f(x)，它的极值点和拐点也可以帮助我们证明函数的单调性。

如果在某个区间上f'(x)恒大于0，并且f''(x)恒大于0，那么函数在该区间上是单调递增的；如果f'(x)恒小于0，并且f''(x)恒小于0，那么函数在该区间上是单调递减的。

通过分析极值点和拐点，我们可以得出函数的单调性。

4. 函数图像法。

最直观的方法是通过函数的图像来观察函数的单调性。

我们可以通过绘制函数的图像，并观察函数在某个区间上的变化趋势，从而得出函数的单调性。

通过观察函数的图像，我们可以直观地理解函数的单调性，并进行证明。

综上所述，证明函数单调性的方法有多种多样，我们可以根据具体的函数和问题选择合适的方法进行证明。

在实际应用中，我们需要灵活运用这些方法，从而准确地判断函数的单调性，为数学分析和实际问题的解决提供有力的支持。

判断函数单调性的常用方法判断函数单调性的常用方法一、定义法设$x_1.x_2$是函数$f(x)$定义域上任意的两个数，且$x_1f(x_2)$，则此函数为减函数。

例如，证明：当$x>0$时，$x>\ln(1+x)$。

f'(x)=\frac{1}{1+x}>0$，所以$f(x)$为严格递增的。

因为$f(x)>\lim\limits_{x\to 0}-\ln(1+x)=-\ln(1+0)=0$，所以$x>\ln(1+x)$。

二、性质法除了用基本初等函数的单调性之外，利用单调性的有关性质也能简化解题。

若函数$f(x)。

g(x)$在区间$B$上具有单调性，则在区间$B$上有：⑴$f(x)$与$f(x)+C$（$C$为常数）具有相同的单调性；⑵$f(x)$与$c\cdot f(x)$当$c>0$时具有相同的单调性，当$c<0$时具有相反的单调性；⑷当$f(x)。

g(x)$都是增（减）函数，则$f(x)+g(x)$都是增（减）函数；⑸当$f(x)。

g(x)$都是增（减）函数，则$f(x)\cdot g(x)$当两者都恒大于时也是增（减）函数，当两者都恒小于时也是减（增）函数。

三、同增异减法是处理复合函数的单调性问题的常用方法。

对于复合函数$y=f[g(x)]$满足“同增异减”法（应注意内层函数的值域），可令$t=g(x)$，则三个函数$y=f(t)。

t=g(x)。

y=f[g(x)]$中，若有两个函数单调性相同，则第三个函数为增函数；若有两个函数单调性相反，则第三个函数为减函数。

注：（1）奇函数在对称的两个区间上有相同的单调性，偶函数在对称的两个区间上有相反的单调性；2）互为反函数的两个函数有相同的单调性；3）如果$f(x)$在区间$D$上是增（减）函数，那么$f(x)$在$D$的任一子区间上也是增（减）函数。

设单调函数$y=f(x)$为外层函数，$y=g(x)$为内层函数。

函数单调性知识点总结一、函数单调性知识结构【知识网络】1．函数单调性的定义，2．证明函数单调性；3．求函数的单调区间4．利用函数单调性解决一些问题；5．抽象函数与函数单调性结合运用二、重点叙述1. 函数单调性定义(一)函数单调性概念(1)增减函数定义一般地,设函数y=f(x)的定义域为I,对于定义域I内某个区间D上的任意两个自变量的值x1、x2 :如果当x1＜x2时,都有f(x1 ) ＜f(x2 ),那么就说函数y=f(x)在区间D上是增函数;如果当x1＜x2时,都有f(x1 ) ＞f(x2 ),那么就说函数y=f(x)在区间D上是减函数。

如果函数在区间D上是增函数或减函数,那么就说函数在这一区间具有(严格的)单调性,区间D叫做的单调区间。

(2)函数单调性的内涵与外延⑴函数的单调性也叫函数的增减性。

函数的单调性是对某个区间而言的,是一个局部概念。

⑵由函数增减性的定义可知:任意的x1、x2∈D,① x1＜x2 ,且f(x1 ) ＜f(x2 ),y=f(x)在区间D上是增函数;(可用于判断或证明函数的增减性)② y=f(x)在区间D 上是增函数,且x 1＜x 2 , f(x 1) ＜f(x 2 ) ;(可用于比较函数值的大小) ③ y=f(x)在区间D 上是增函数,且f(x 1) ＜f(x 2 ), x 1＜x 2 。

(可用于比较自变量值的大小) 2. 函数单调性证明方法证明函数单调性的方法有:定义法(即比较法);导数法。

实际上,用导数方法证明一般函数单调性是很便捷的方法,定义法是基本方法,常用来证明解决抽象函数或不易求导的函数的单调性。

(1)定义法:利用增减函数的定义证明。

在证明过程中,把数式的大小比较转化为求差比较(或求商比较)。

⑴转化为求差比较证明程序:①设任意的x 1 、x 2∈D,使x 1＜x 2 ; ②求差—变形—判断正负;此为关键步骤,变形大多要“因式分解”。

求差:; 变形:化简、因式分解; 判断:差的符号的正或负。

函数的单调性一、 函数单调性的的判断方法除了用差分法（又称定义法）判断函数的单调性外，常用的方法还是有以下几种：1.直接法直接法就是利用我们熟知的正比例函数、一次函数、反比例函数的单调性，直接判断函数的单调性，并写出它们的单调区间，熟记以下几种函数的单调性：(1)正比例函数(0)y kx k =≠：○1当0k >时，函数y kx =在定义域R 上是增函数；○2当0k <时，函数y kx =在定义域R 上是减函数.(2)反比例函数(0)k y k x =≠： ○1当0k >时，函数k y x=的单调递减区间是(,0),(0,)-∞+∞，不存在单调递增区间；○2当0k <时，函数k y x=的单调递增区间是(,0),(0,)-∞+∞，不存在单调递增区间.(3)一次函数(0)y kx b k =+≠：○1当0k >时，函数y kx b =+在定义域R 上是增函数；○2当0k <时，函数y kx b =+在定义域R 上是减函数.（4）二次函数2(0)y ax bx c a =++≠：○1当0a >时，函数2y ax bx c =++的图像开口向上，单调递减区间是(,]2b a -∞-，单调递增区间是[,)2b a-+∞；○2当0a <时，函数2y ax bx c =++的图像开口向下，单调递增区间是(,]2b a -∞-，单调递减区间是[,)2b a-+∞. 注意：3()y f x x ==在定义域R 上是增函数，其图像如右图：2.图像法画出函数图象，根据其图像的上升或下降趋势判断函数的单调性.3.运算性质法（1）函数()()f x af x 与，当0a >时有相同的单调性，当0a <时有相反的单调性；如函数()f x x =与3()3f x x -=-的单调性相反，函数()f x x =与3()3f x x =的单调性相同；（2）当函数()f x 恒为正（或恒为负）时()f x 与1()f x 有相反的单调性，如：函数1()0f x x =->((,0))x ∈-∞是递增函数，则111()x f x x==--在区间(,0)-∞是递减函数；（3）若()0f x ≥，则()f x与如：函数2()234f x x x =++，在定义域R 上，()0f x >，且()f x 是3(,]4-∞-上的递减函数，是3[,)4-+∞上的递增函数，所以函数=3(,]4-∞-上的递减函数，是3[,)4-+∞上的递增函数；（4）若()f x ，()g x 的单调性相同，则()()f x g x +的单调性与()f x ，()g x 的单调性相同.如211()x F x x x x -+==-+，令1(),()f x x g x x=-=，即 ()()()F x f x g x =+，因为函数()f x 在R 上单调递减，()g x 的单调递减区间是(,0),(0,-∞+∞），所以函数211()x F x x x x-+==-+的单调递减区间是 (,0),-∞(0,+∞）； (5) 若()f x ，()g x 的单调性相反，则()()f x g x -的单调性与()f x 的相同.因为()g x -与()f x 的单调性相同，所以()()f x g x -的单调性与()f x 的相同.二、抽象函数单调性的判定没有具体函数解析式的函数，我们称为抽象函数，判断抽象函数单调性是一类重要的题型，其解法采用差分法.实例1 已知定义在(0,)+∞上的函数()f x 对任意,(0,)x y ∈+∞，恒有()()()f xy f x f y =+，且当01x <<时()0f x >，判断()f x 在(0,)+∞上的单调性. 解 设,(0,),0x x h h +∈+∞>，则()()()[()]x f x h f x f x h f x h x h+-=+-⋅++ ()[()()]()x x f x h f f x h f x h x h =+-++=-++.01,()0,()0x x x f f x h x h x h<<∴>∴-<+++，()()0f x h f x ∴+-<，所以函数 ()f x 在(0,)+∞上的单调递减.二、 复合函数单调性的判定方法求复合函数(())y f g x =的单调性的步骤：（1） 求出函数的定义域；（2） 明确构成复合函数的简单函数（所谓简单函数即我们熟知其单调性的函数）:(),()y f u u g x ==;（3） 确定简单函数的单调性；（4） 若这两个函数同增或同减（单调性相同），则(())y f g x =为增函数；若这两个函数一增一减（单调性相异）则(())y f g x =为减函数简记为“同增异减”.实例2 求函数()f x =解：由解析式得2340x x +-≥，即函数的定义域为{|41}x x x ≤-≥或.令234t x x =+-，则y =y t =是增函数，而234t x x =+-在(,4]-∞上是减函数，在[1,)+∞上是增函数，∴函数()f x =[1,)+∞，递减区间为(,4]-∞.三、 单调性的应用1. 用函数的单调性比较大小利用函数的单调性及自变量的大小可以比较两个函数值的大小，即已知函数()y f x =在定义域的某个区间上为增函数，若对区间内的任意两个值12,x x 且 12x x <，则12()()f x f x <.减函数也有类似的性质.示例3 已知函数()y f x =在[0,)+∞上是减函数，试比较3()4f 与2(1)f a a -+的大小.解：221331()244a a a -+=-+≥，34∴与21a a -+都在区间[0,)+∞内.又()y f x =在区间[0,)+∞上是减函数，23()(1).4f f a a ∴≥-+ 注意：解答这类型的题目首先要判断函数的自变量是否在所给区间内.示例4 已知()f x 是定义在[1,1]-上的增函数，且(1)(13)f x f x -<-，求x 的取值范围.解()f x 是定义在[1,1]-上的增函数，且(1)(13)f x f x -<-，∴可得不等式组111,1131,113,x x x x -≤-≤⎧⎪-≤-≤⎨⎪-<-⎩即02,20,31.2x x x ⎧⎪≤≤⎪⎪≤≤⎨⎪⎪<⎪⎩解得102x ≤<，所以所求1[0,)2x ∈. 2. 用函数的单调性求最值在利用单调性求最值或值域时要注意以下结论：（1） 若()f x 在定义域[,]a b 是增函数，则当x a =时，()f x 取得最小值()f a 当x b =，()f x 取得最大值()f b 如图2.（2） 若()f x 在定义域[,]a b 是减函数，则当x a =时，()f x 取得最大值()f a ，当x b =，()f x 取得最小值()f b 如图3.（3）已知函数(),[,],y f x x a b a c b =∈<<，如果()f x 在[,]a c 上是单调递增（减）函数，在[,]c b 上是单调递减（增）函数，则()f x 在x c =时取得最大（小）值，在x a =或x b =时取得最小（大）值，如下图4,5.示例5 求函数32y x =--.解：令()32f x x =-，()g x =()()y f x g x =-.由题意得函数的定义域为(,2]-∞.()32f x x =-在(,2]-∞上递增，()g x =在(,2]-∞上递减，但()g x -=(,2]-∞上递增，∴32y x =-(,2]-∞上为递增函数，∴当2x =时，y 有最大值4.注意：研究函数最值时，先求定义域，再判断其单调性.3.利用单调性求参数的取值举例应用：课本40页例34.解含“f ”的不等式根据函数()y f x =在某区间上的单调性及函数值的大小，可以求自变量的取值范围即已知函数()y f x =在定义域内的某个区间上为增函数，若12()(),f x f x <则12x x <；若已知函数()y f x =在定义域内的某个区间上为减函数，若12()(),f x f x <则12x x >，就是增（减）函数定义的逆应用.示例6 已知函数()y f x =是R 上的减函数，且(23)(56)f x f x ->-，求实数x 的取值范围. 解：函数()y f x =是R 上的减函数，且(23)(56)f x f x ->-，2356x x ∴-<+，(3,)x ∴∈-+∞.函数的定义域和值域一、复合函数的定义域复合函数(())y f g x =的定义域，是函数()g x 的定义域中，使中间变量()u g x =属于函数()f u 的定义域全体.示例1 若函数()f x 的定义域为[1,4]，求函数(4)f x +的定义域. 解：函数()f x 的定义域为[1,4]，∴使得(4)f x +有意义的条件是144x ≤+≤,即30x -≤≤，则(4)f x +的定义域为[3,0]-.注意：这类型的题目简记为“对应法则相同，括号内的取值范围相同”. 示例2 已知(3)f x +的定义域为[0,3]，求函数()f x 的定义域. 解题分析：函数(3)f x +和()f x 中的x 并不是同一个量，若设3u x =+，则(3)f x +变成()f u ，那么u 的取值范围才是函数()f x 的定义域，即“对应法则相同，括号内的取值范围相同”.解：(3)f x +的定义域为[0,3]，03x ∴≤≤，则336x ∴≤+≤，所以 函数()f x 的定义域为[3,6].二、求函数值域的常用方法1.公式法：适用于初中所学的一次函数、二次函数、反比例函数及以后学习的基本初等函数，形如ax b y cx d +=+（0c ≠且分式不可约）的值域为{|}a y y c≠. 示例3 求函数311x y x -=+的值域 解：函数311x y x -=+，∴331y ≠≠，∴311x y x -=+的值域为{|3}y y ≠.2.图像法：适用于能画出图像的函数.如225((,2])y x x x =--∈-∞的图像如右图所示，所以值域为[6,)-+∞.3.不等式性质法（包括配方法、分离常数法、有界性法）适用于解析式只含“一个”x 或通过变形能化成只出现“一个”x 的函数，如1||,y x =-由||0x ≥，则1||1x -≤，可得(,1]y ∈-∞；又如2211172()24y x x x ==-+-+，因为2177()244x -+≥，所以2140177()24x <≤-+，所以4(0,]7y ∈. 示例4求函数23()(221)1x f x x x x -=-≤≤≠-+且的值域 解：232(1)55()2111x x f x x x x -+-===-+++，由221x x -≤≤≠-且，得 11310x x -≤+≤+≠且.令1t x =+，则130t t -≤≤≠且.结合反比例函数5y t=-的图像可知，当 130t t -≤≤≠且，即[1,0)(0,3]t ∈-时，55553t t-≤--≥或. ∴5555131x x -≤--≥++或.515()2()27131f x f x x x =-≤=-≥++或. ∴23()(221)1x f x x x x -=-≤≤≠-+且的值域为1-][7,)3∞+∞（，. 4.换元法：适用于无理式中含自变量的函. 示例5求函数y x =+.解：函数的定义域是{|1}x x ≤.t =，则[0,)t ∈+∞，2+1x t =-， 22212(21)2(1)2y t t t t t ∴=-++=--++=--+，0t ≥，结合二次函数的图像2y ∴≤，∴原函数的值域为∞（-，2].注意：解这类型的题目要注意函数的定义域,在利用换元法求函数值域时，一定要注意新变量t 的取值范围，若忽视了这点，就容易造成错误.5.判别式法：适用于形如22(,)ax bx c y a d dx ex f++=++不全为零且分式不可约的函数. 示例6 求函数2224723x x y x x +-=++的值域.解：由2224723x x y x x +-=++得2(2)2(2)370y x y x y -+-++=，当2y =时，方程无解；当2y ≠时，要使关于x 的方程有解，必须24(2)4(2)(37)0y y y ∆=---+≥， 解得9 2.2y -≤< ∴原函数的值域为92[-，2). 6.方程思想（包括判别式法、反解法）适用于可解出x 的解析式的函数.示例7 求函数2211x y x -=+的值域解：由2211x y x-=+得2(1)10y x y ++-=，当1y =-时，方程无解：当1y ≠-时，要使关于x 的方程有解，必须04(1)(1)0y y ∆=-+-≥，解得11y -≤≤.∴原函数的值域为[-1，1].示例7：求函数311x y x -=+的值域. 解：由311x y x -=+得1(1)31(3)103y y x x y x y x y ++=-⇒-++=⇒=--， 只要30,3y y -≠≠即，就有13y x y +=--.∴原函数的值域为{y |3}y ≠.。

函数的单调性，是指函数在其定义域内某一区间上的取值是递增或递减的性质。

不强调区间的情况下，所谓的单调函数是指，对于整个定义域而言，函数具有单调性。

单调性的判定方法主要有两种：定义法和导数法。

定义法利用的是函数的增减性，即如果对于定义域内的任意两个变量x1和x2，当x1<x2时，有f(x1)≤f(x2)，则称该函数在区间D上为增函数；如果对于定义域内的任意两个变量x1和x2，当x1<x2时，有f(x1)≥f(x2)，则称该函数在区间D上为减函数。

导数法则是利用函数的导数来判断其单调性，如果函数在某区间内的导数大于0，那么这个函数在这个区间就是单调递增的；如果函数在某区间内的导数小于0，那么这个函数在这个区间就是单调递减的。

六、 函数的单调性：㈠函数单调性的判定与证明：1、讨论函数f （x ）=12-x ax（a ＞0）在x ∈（－1，1）上的单调性.解：设－1＜x 1＜x 2＜1，则f （x 1）－f （x 2）=1211-x ax －1222-x ax=)1)(1(222122121221--+--x x ax x ax ax x ax =)1)(1()1)((22212112--+-x x x x x x a .∵－1＜x 1＜x 2＜1，∴x 2－x 1＞0，x 1x 2+1＞0，（x 12－1）（x 22－1）＞0.又a ＞0，∴f （x 1）－f （x 2）＞0，函数f （x ）在（－1，1）上为减函数. 练习1：利用单调性的定义证明函数y=12++x x 在(-1,+∞)上是减函数. 证明:设x 1＞x 2＞-1, 则y 1-y 2=)1)(1(121221122211++-=++-++x x x x x x x x . ∵x 1＞x 2＞-1,x 2-x 1＜0,x 1+1＞0,x 2+1＞0, ∴)1)(1(2112++-x x x x ＜0,即y 1-y 2＜0,y 1＜y 2.∴y=12++x x 在(-1,+∞)上是减函数. ㈡求函数的单调区间 Ⅰ定义法： 1、求函数y =x +x1的单调区间. Ⅱ导数法：求下列函数的单调区间 1、 432()3861f x x x x =-++解：3222()12241212(21)12(1)f x x x x x x x x x '=-+=-+=- 当0x ≥时单调递增,0x <时单调递减. 2、1()1f x x x =+- 解:21()1(1)f x x -'=+-故2222(1)12()(1)(1)x x xf x x x ---'==-- 则[0,1)(1,2]x ∈⋃时单调递减;(,0][2,)x ∈-∞⋃+∞时单调递增3、()f x =解：21()2f x '=2== 当9[,3)(0,)2x ∈--⋃+∞时单调递增，[3,0]x ∈-时单调递减。

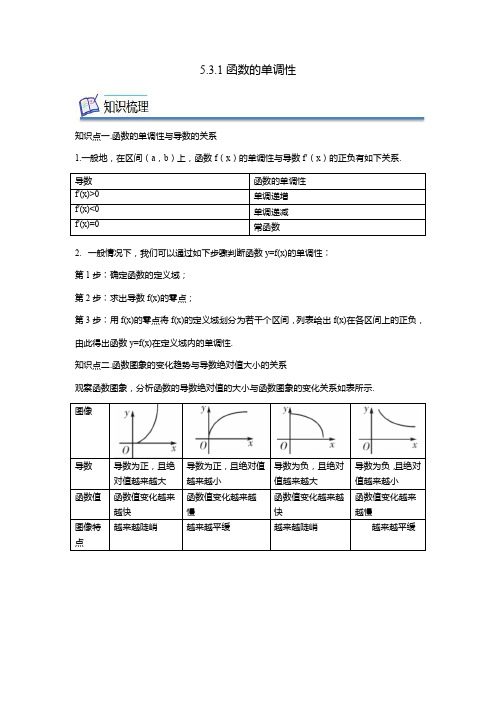
5.3.1函数的单调性知识点一.函数的单调性与导数的关系1.一般地，在区间（a，b）上，函数f（x）的单调性与导数f′（x）的正负有如下关系.导数函数的单调性f′(x)>0单调递增f′(x)<0单调递减f′(x)=0常函数2.一般情况下，我们可以通过如下步骤判断函数y=f(x)的单调性∶第1步∶确定函数的定义域；第2步∶求出导数f(x)的零点；第3步∶用f(x)的零点将f(x)的定义域划分为若干个区间，列表给出f(x)在各区间上的正负，由此得出函数y=f(x)在定义域内的单调性.知识点二.函数图象的变化趋势与导数绝对值大小的关系观察函数图象，分析函数的导数绝对值的大小与函数图象的变化关系如表所示.图像导数导数为正，且绝对值越来越大导数为正，且绝对值越来越小导数为负，且绝对值越来越大导数为负，且绝对值越来越小函数值函数值变化越来越快函数值变化越来越慢函数值变化越来越快函数值变化越来越慢图像特点越来越陡峭越来越平缓越来越陡峭越来越平缓题型1求不含参函数的单调区间【例题1】（2021·宁夏·海原县第一中学）函数f(x)=(x−3)e x的单调递减区间是（）A．(−∞,2]B．[0,3]C．[1,4]D．[2,+∞)【答案】A【分析】求函数的导数，利用函数单调性和导数之间的关系解不等式f′(x)<0进行求解即可.【详解】函数的导数f′x=e x+x−3e x=x−2e x由f′x<0得x−2e x<0，即x−2<0得x<2，即函数的单调递减区间为(−∞,2]，故选：A【变式1-1】1．（2022·云南·昆明一中模拟预测（理））设a为实数，函数f(x)=x3+(a−1)x2−(a+2)x，且f′(x)是偶函数，则f(x)的单调递减区间为（）A．(0,2)B．(−3,3)C．(−1,1)D．(−3,3)【答案】C【分析】求导，结合f′(x)是偶函数得到f′−x=f′x，求出a=1，从而根据f′(x)=3x2−3小于0，求出单调递减区间.【详解】因为f(x)=x3+(a−1)x2−(a+2)x，所以f′(x)=3x2+2(a−1)x−(a+2)，又因为f′(x)是偶函数，所以f′−x=f′x，即3−x2−2a−1x−a+2=3x2+2a−1x−a+2，故a−1=0，即a=1，所以f′(x)=3x2−3，令f′x<0，解得−1<x<1，所以f(x)的单调递减区间为(−1,1).故选：C．【变式1-1】2．（2022·安徽·长丰北城衡安学校高三开学考试）函数f x=x3−x2+x的单调递增区间为______.【答案】−∞,+∞【分析】求出导函数f′x，解不等式f′x≥0即可得到.【详解】由题意知，f x=x3−x2+x定义域为R，f′x=3x2−2x+1，且f′x=3x2−2x+1=3x+23>0在R上恒成立，所以，函数f x=x3−x2+x的单调递增区间为−∞,+∞.故答案为：−∞,+∞【变式1-1】3．（2022·广东·深圳实验学校光明部高三期中）己知函数f x=x2+5x+2ln x，则函数f x的单调递增区间是_____________．【答案】(0,+∞)【分析】利用导数法求单调区间即可【详解】函数f x=x2+5x+2ln x，其定义域x x>0，则f′x=2x+5+2×1x=2x2+5x+2x>0在0,+∞恒成立，所以函数f x的单调递增区间是0,+∞.故答案为：0,+∞.【变式1-1】4．（2022·全国·高三专题练习）设函数f(x)=e2x+ln x(x>0)，求f(x)的单调区间．【答案】f x的减区间为0,+∞.【分析】求出导函数f′(x)，由f′(x)>0得增区间，由f′(x)<0得减区间．【详解】f′x=−e2x2+1x=2x−e2x2，当0<x<e2，f′x<0，当x>e2，f′x>0，所以f x的减区间为0,f x+∞.【变式1-1】5．（2021·宁夏·海原县第一中学高二期中（文））已知函数f(x)=x3−x2−x+2.(1)求曲线f(x)在点2,f2处的切线方程；(2)求f(x)的单调区间.【答案】(1)7x−y−10=0(2)递增区间为(−∞,−13)，(1,+∞)；递减区间为−13,1【分析】（1）求出函数的导函数，再求得f'2=7与f2=4，利用点斜式可求得曲线f(x)在点2,f2处的切线方程；（2）由f′x=3x2−2x−1=x−13x+1，利用导函数f'(x)与函数f(x)的单调性的关系可得答案.【详解】（1）∵f x=x3−x2−x+2，∴f′x=3x2−2x−1=x−13x+1，∴f'2=7，又f2=4，∴曲线f(x)在点2,f2处的切线方程为y−4=7x−2，即7x−y−10=0；（2）∵f′x=3x2−2x−1=x−13x+1，∴当x∈−∞,−∪1,+∞时，f'(x)>0，当x∈−13,1时，f'(x)<0，∴f(x)在(−∞,−13)，(1,+∞)上单调递增，在−13,1上单调递减.∴f(x)的递增区间为(−∞,−13)，(1,+∞)；递减区间为−13,1.题型2含参函数单调区间◆类型1导数为1个根【例题2-1】（2022·上海市金山中学高二期末）已知函数f(x)=a ln x+bx(a,b∈R)．若a=1，求函数y=f(x)的单调区间；【答案】答案见解析.【分析】根据题意，分b≥0和b<0两种情况讨论求解即可；【详解】解：当a=1时，f(x)=ln x+bx，定义域为0,+∞，所以，f′(x)=1x+b=1+bx x，所以，b≥0时，f′(x)≥0在0,+∞上恒成立，故f(x)在0,+∞上单调递增，当b<0时，令f′(x)=0得x=−1b，所以，当x∈0,−f′(x)>0，f(x)单调递增；当x∈−1b,+∞时，f′(x)<0，f(x)单调递减；综上，b≥0时，f(x)在0,+∞上单调递增；b<0时，f(x)在0,上单调递增，在−1b,+∞上单调递减.【变式2-1】1．（2022·江苏·盐城经济技术开发区中学高三阶段练习）已知函数f x=ax−3ln x．讨论函数f x的单调性；【答案】当a≤0时，f(x)在(0,+∞)上单调递减；当a>0时，f(x)在(0,3a)上单调递减，在(3a,+∞)上单调递增【分析】对函数f x进行求导，然后对a进行分类讨论，根据导函数值的正负，得到函数的单调区间【详解】由f x=ax−3ln x，得f′(x)=a−3x=ax−3x，x>0，当a≤0时，f′(x)<0，∴f x在(0,+∞)上单调递减；当a>0时，f′(x)=ax−3x=a⋅(x−3a)x，由x>3a时，f′(x)>0，f x在(3a,+∞)上单调递增，由x<3a时，f′(x)<0，f(x)在(0,3a)上单调递减，∴综上所述，当a≤0时，f(x)在(0,+∞)上单调递减；当a>0时，f(x)在(0,3a)上单调递减，在(3a,+∞)上单调递增【变式2-1】2.（2007·山东·高考真题（理））设函数f x=ax−a+1ln x+1，其中a≥−1，求f x的单调区间．【答案】答案见解析【分析】求出函数f x的定义域，对实数a的取值进行分类讨论，分析导数的符号变化，由此可得出函数f x的增区间和减区间.【详解】函数f x=ax−a+1ln x+1的定义域为−1,+∞，f′x=a−a+1x+1=ax−1x+1.①当−1≤a≤0时，对任意的x>−1，f′x<0，此时，函数f x的减区间为−1,+∞，无增区间；②当a>0时，由f′x<0可得−1<x<1a，由f′x>0可得x>1a.此时，函数f x的减区间为−+∞.综上所述，当−1≤a≤0时，函数f x的减区间为−1,+∞，无增区间；当a>0时，函数f x的减区间为−+∞.【变式2-1】3．（2022·黑龙江·哈尔滨三中模拟预测）已知函数f x=e x−ax−1.讨论函数f(x)的单调性；【答案】答案见解析．【分析】求出导函数f′(x)分类讨论确定f′(x)的正负得单调性；【详解】f′(x)=e x−a，a≤0时，f′(x)>0恒成立，f(x)在R上是增函数，a>0时，x<ln a时，f′(x)<0，f(x)是减函数，x>ln a时，f′(x)>0，f(x)是增函数，综上，a≤0时，f(x)在R上是增函数，a>0时，f(x)在(−∞,ln a)上是减函数，在(ln a,+∞)上是增函数；【变式2-1】4．（2022·江苏苏州·高三阶段练习）已知函数f x=e ax−ax a∈R,a≠0,g x=b ln x−x b∈R.讨论函数f x的单调性；【答案】f x在−∞,0单调递减，在0,+∞单调递增【分析】由题意可得f′x=a e ax−a=a e ax−1，按a和x的取值分类讨论f′(x)的正负即可得到f x的单调性；【详解】由题意f′x=a e ax−a=a e ax−1,x∈R，令f′x=0，得x=0，当a>0时，若x>0，则ax>0,e ax>1，所以f′x>0，若x<0，则ax<0，e ax<1，所以f′x<0；当a<0时，若x>0，则ax<0,e ax<1，所以f′x>0，若x<0，则ax>0，e ax>1，所以f′x<0；综上f x在−∞,0单调递减，在0,+∞单调递增.【变式2-1】5．（2022·河南商丘·高三阶段练习（文））已知函数f x=x e x−ax2a∈R，g x=f′x+1−x e x，其中f′x是f x的导函数.讨论函数g x的单调性；【答案】当a≤0时，g x在R上单调递增；当a>0时，g x在−∞,ln a上单调递减，在ln a,+∞上单调递增.【分析】根据题意写出f′x，进而写出g x，对g x进行求导，根据导函数的正负判断原函数的单调性即可；【详解】f′x=x+1e x−2ax，g x=f′x+1−x e x=x+1e x−2ax+1−x e x= 2e x−2ax，g′x=2e x−2a，当a≤0时，对∀x∈R，g′x>0恒成立，故g x在R上单调递增；当a>0时，令g′x<0，解得x<ln a；令g′x>0，解得x>ln a，故g x在−∞,ln a上单调递减，在ln a,+∞上单调递增.◆类型2导数为2个根【例题2-2】（2022·湖南·长郡中学高二阶段练习）设函数f x=ax2+2a−1x−ln x a∈R.讨论f x的单调性；【答案】当a≤0时，f x在区间0,+∞上单调递减；当a>0时f x在区间+∞上单调递增【分析】求出函数的导数，分类讨论a的取值范围，根据导数的正负，即可得答案;【详解】由于f x=ax2+2a−1x−ln x a∈R，则定义域为(0,+∞)，可得：f′x=2ax+2a−1−1x==当a≤0时，∵x>0，∴f′x<0，故f x在区间0,+∞上单调递减；当a>0时，∵x>0，∴由f′x>0可得x>12a，由f′x<0得x<12a，故f x在区间+∞上单调递增.ax3a−1x2−2x−12.【变式2-2】1．（2022·山东淄博·高三期中）已知三次函数f x=1(1)当a=3时，求曲线y=f x在点1,f1处的切线方程，(2)讨论y=f x的单调性.【答案】(1)6x−y−5=0；(2)见解析.【分析】（1）求导可得f′x=9x2+5x−2，利用导数的几何意义，可得曲线y=f x在点1,f1处的切线斜率为f′(1)=12，f(1)=3，利用直线点斜式即可得解；（2）求导可得f′x=ax2+2a−1x−2=(ax−1)(x+2)，对参数a进行讨论即得解.【详解】（1）当a=3时，f x=x3+52x2−2x−12，f'x=3x2+5x−2，所以曲线y=f x在点1,f1处的切线斜率为f'(1)=6，又f(1)=1+52−2−12=1，y=6(x−1)+1，整理可得曲线y=f x在点1,f1处的切线方程为6x−y−5=0；（2）f′x=ax2+2a−1x−2=(ax−1)(x+2)，若a=0，由f′x=−(x+2)=0可得x=−2，当x∈(−∞,−2)时，f′(x)>0，f(x)为增函数，当x∈(−2,+∞)时，f′(x)<0，f(x)为减函数，当a>0时，f′x=(ax−1)(x+2)=0，可得x=1a或x=−2，所以f(x)在(−∞,−2),(1a,+∞)为增函数，在(−2,1a)上为减函数，当a<0时，若−12<a<0，f(x)在(−∞,1a),(−2,+∞)为减函数，在(1a,−2)上为增函数，若a=−12，f′(x)≤0，f(x)在R上为减函数，若a<−12，f(x)在(−∞,−2),(1a,+∞)为减函数，在(−2,1a)上为增函数，综上可得：若a=0，f(x)在(−∞,−2)上为增函数，在(−2,+∞)上为减函数，当a>0时，f(x)在(−∞,−2),(1a,+∞)为增函数，在(−2,1a)上为减函数，当a<0时，若−12<a<0f(x)在(−∞,1a),(−2,+∞)为减函数，在(1a,−2)上为增函数，若a=−12，f′(x)≤0，f(x)在R上为减函数，若a <−12，f (x )在(−∞,−2),(1a ,+∞)为减函数，在(−2,1a)上为增函数.【变式2-2】2．（2022·江苏省江浦高级中学高三阶段练习）已知函数f (x )=x 2−ax +1e x (a ∈R ).讨论f (x )的单调性；【答案】答案见解析【分析】根据f (x )的导函数零点间的大小关系进行分类讨论求解即可；【详解】由f ′(x )=−x 2+(a +2)x −a −1e x =−(x −1)(x −a −1)e x ，①当a +1=1，即a =0时，因为f ′(x )=−(x −1)2e x ≤0恒成立，故f (x )在(−∞，+∞)上为减函数；②当a +1>1，即a >0时，由f '(x )<0得，x <1或x >a +1；由f ′(x )>0得，1<x <a +1，所以f (x )在(−∞，1)和(a +1，+∞)上为减函数，在(1，a +1)上为增函数；③当a +1<1，即a <0时，由f ′(x )<0得，x <a +1或x >1；由f ′(x )>0得，a +1<x <1，所以f (x )在(−∞，a +1)和(1，+∞)上为减函数，在(a +1，1)上为增函数.综上：当a =0时，f (x )在(−∞，+∞)上为减函数；当a >0时，f (x )在(−∞，1)和(a +1，+∞)上为减函数，在(1，a +1)上为增函数；当a <0时，f (x )在(−∞，a +1)和(1，+∞)上为减函数，在(a +1，1)上为增函数.【变式2-2】3．（2022·四川省遂宁市教育局模拟预测（理））已知函数f (x )=x 3−a +32x 2+ax +b 讨论f x 的单调性；【答案】答案见解析；【分析】对二次函数f ′(x )=(3x −a )(x −1)零点分布情况分类讨论即可求解；【详解】因为f (x )=x 3−a +32x 2+ax +b ，∴f ′(x )=3x 2−(a +3)x +a =(3x −a )(x −1)．①若a >3，当1<x <a 3时，f ′x <0,当x <1或x >a 3时，f ′x >0，即f x 在(1,a 3)上单调递减，在(−∞,1)和(a 3,+∞)上单调递增；②若a =3，恒有f ′x ≥0．即f x 在定义域R 上单调递增；③若a <3，当a 3<x <1时，f ′x <0,当x <a 3或x >1时，f ′x >0，即f x 在(a 3,1)上单调递减，在(−∞,a 3)和(1,+∞)上单调递增.【变式2-2】4．（2022·山东聊城·高三期中）已知函数f x =x −a +2ln x −a +1x ．讨论函数f x 的单调性；【答案】答案见解析【分析】先求导函数f ′x ，讨论a 的范围，求解f ′x >0和f ′x <0的解集，写出单调区间．【详解】（1）f x =x −a +2ln x −a +1x 定义域为0,+∞，f′x =1−a +2x +a +1x 2=令f ′x =0，得x =1或x =a +1．当a +1≤0即a ≤−1时：x ∈0,1，f ′x <0，函数f x 在0,1上单调递减；x ∈1,+∞，f ′x >0，函数f x 在1，+∞单调递增；当0<a +1<1，即−1<a <0时：x ∈0,a +1，f ′x >0，函数f x 在0，a +1单调递增；x ∈a +1,1，f ′x <0，函数f x 在a +1,1上单调递减；x ∈1,+∞，f ′x >0，函数f x 在1，+∞上单调递增；当a +1=1即a =0时：x ∈0,+∞，f ′x ≥0，函数f x 在0，+∞单调递增；当a +1>1即a >0时：x ∈0,1，f ′x >0，函数f x 在0,1单调递增；x ∈1,a +1，f ′x <0，函数f x 在1,a +1上单调递减；x ∈a +1,+∞，f ′x >0，函数f x 在a +1,+∞上单调递增；综上：当a ≤−1时，单调递减区间有0,1，单调递增区间有1,+∞；当−1<a<0时，单调递减区间有a+1,1，单调递增区间有0,a+1，1,+∞；当a=0时，单调递增区间有0,+∞，无单调递减区间；当a>0时，单调递减区间有1,a+1，单调递增区间有0,1，a+1,+∞．【变式2-2】5．（2022·贵州·模拟预测（理））已知函数f x=x2e ax−1a≠0，g x=ln x+ bx+1.求函数f x的单调区间；【答案】答案见解析【分析】求得f'x，对a进行分类讨论，由此求得函数f x的单调区间.【详解】函数f x的定义域为R，f′x=x ax+2e ax，令f′x=0得x1=0，x2=−2a，①当a>0时，若x∈−∞,∪0,+∞，则f′x>0；若x∈−2a,0，则f′x<0，故f x在−∞,−0,+∞上单调递增，在−2a,0上单调递减；②当a<0时，若x∈0,则f′x>0；若x∈−∞,0∪−2a,+∞，则f′x<0，故f x在0,−∞,0，−2a,+∞上单调递减.◆类型3不能因式分解【例题2-3】（2022·浙江·慈溪中学高三期中）已知函数f x=mx3−mx−x ln x m∈R.若f x的导函数为g x，试讨论g x的单调性；【答案】答案见解析【分析】由f x可求g x，再根据g x的导函数，讨论参数的范围即可得出g x的单调性；【详解】解：由已知g x=f′x=3mx2−m−ln x−1，则g′x=6mx−1x=6mx2−1x(x>0)，①当m≤0时，g′x<0，得g x在0,+∞单调递减；②当m>0时，g′x=6mx2−1x=<0⇒0<x<得g x在0,+∞单调递增，综上：当m≤0时，函数g x在0,+∞单调递减；当m>0时，函数g x在+∞单调递增.【变式2-3】1．（2022·广西·桂林市第五中学高三阶段练习（文））已知函数f x=ln x−12ax2+ x,a∈R.(1)当a=2时，求函数y=f x在点1,f1处的切线方程；(2)求函数f x的单调区间.【答案】(1)y=0(2)答案见解析.【分析】（1）分别求f′(x)、f(1)、f′(1)，由点斜式方程可得切线方程；（2）先求f(x)的定义域再求导f′(x)，分类讨论a≤0与a>0时导数的正负来研究原函数的单调性.【详解】（1）当a=2时，f(x)=ln x−x2+x，则f(1)=0，∴f′(x)=1x−2x+1，∴f(x)在点(1,0)处的切线斜率k切线=f′(1)=0，∴f(x)在点(1,0)处的切线方程为y−0=0×(x−1)，即：y=0.（2）f(x)的定义域为(0,+∞)，f′(x)=1x−ax+1=−ax2+x+1x，①当a≤0时，f′(x)>0恒成立，∴f(x)的单调递增区间为(0,+∞)，无单调递减区间.②当a>0时，−ax2+x+1=0，Δ=1+4a>0，两根分别为x1=1−1+4a2a<0，x2=1+1+4a2a>0∴f′(x)>0⇒0<x<1+1+4a2a，f′(x)<0⇒x>1+1+4a2a∴f(x)的单调递增区间为(0,1+1+4a2a)，单调递减区间为(1+1+4a2a,+∞).综述：①当a≤0时，f(x)的单调递增区间为(0,+∞)，无单调递减区间；②当a>0时，f(x)的单调递增区间为，单调递减区间为+∞).【变式2-3】2．（2022·广东·佛山一中高三阶段练习）已知函数f x=12x2−2x−a ln x．讨论f x的单调性；【答案】答案见解析；【分析】根据一元二次方程根的判别式分类讨论求解即可；【详解】f x=12x2−2x−a ln x(x>0)⇒f′x=x−2−a x=x2−2x−a x，设x2−2x−a=0的判别式Δ=(−2)2+4a=4+4a，当Δ≤0时，即当a≤−1时，x2−2x−a≥0⇒f′(x)≥0，函数f x在(0,+∞)上单调递增；当Δ>0时，即当a>−1时，设方程x2−2x−a=0的两根为：1−1+a,1+1+a，当a≥0时，1−1+a≤0，当0<x<1+1+a时，f′x<0,f x单调递减，当x>1+1+a时，f′x>0,f x单调递增；当−1<a<0时，1−1+a>0当0<x<1−1+a时，f′x>0,f x单调递增，当1−1+a<x<1+1+a时，f′x<0,f x单调递减，当x>1+1+a时，f′x>0,f x单调递增，综上所述：当a≤−1时，函数f x在(0,+∞)上单调递增；当a≥0时，函数f x在(0,1+1+a)单调递减，在(1+1+a,+∞)单调递增；当−1<a<0时，函数f x在(0,1−1+a)，(1+1+a,+∞)单调递增，在(1−1+a,1+ 1+a)单调递减；【变式2-3】3．（2022·宁夏·青铜峡市宁朔中学高三期中（理））已知函数f x=e x ax2+x+ a a≥0.求函数f x的单调区间；【答案】见解析【分析】求导得到f′(x)=(ax+a+1)(x+1)e x，考虑a=0和a>0两种情况，根据导函数的正负判断函数的单调区间即可.【详解】函数f x的定义域为R，且f′(x)=(ax+a+1)(x+1)e x，当a=0时，f′(x)=e x(x+1)，当x>−1时，f′x>0，当x<−1时，f′x<0，所以函数f x 的单调递增区间为−1,+∞，单调递减区间为−∞,−1.当a >0时，f ′(x )=a (x +1)x +e x ，f ′x =0有两根－1，−a +1a，且−1>−a +1a，f′(x )=a (x +1)x +e x >0，则x ∈−∞,∪−1,+∞；f′(x )=a (x +1)x +e x <0，则x ∈−a +1a,−1；故函数f x 的单调递增区间为−∞,−−1,+∞，单调递减区间为−a +1a,−1.综上可知：当a >0时，函数f x 的单调递增区间为−∞,−1,+∞，单调递减区间为−a +1a,−1；当a =0时，函数f x 的单调递增区间为−1,+∞，单调递减区间为−∞,−1.【变式2-3】4．（2022·四川省内江市第六中学高三阶段练习（理））函数f x =a ln x −x 2+x ，g x =x −2⋅e x −x 2+m ．当a <0时，讨论函数y =f x 的单调性；【答案】答案见解析【分析】先求得f ′x ，对a 进行分类讨论，由此求得f x 的单调区间.【详解】函数f x =a ln x −x 2+x 定义域是0,+∞，f ′x =a x −2x +1=−2x 2+x +ax，①当a ≤−18时，Δ=1+8a ≤0，当x ∈0,+∞时，f ′x ≤0，即函数y =f x 的减区间为0,+∞，无递增区间；②当−18<a <0时，Δ=1+8a >0，令f ′x >0<x <又∵−18<a <0>0>0，此时函数y =f x 的减区间为+∞，综上所述，①当a ≤−18时，函数y =f x 的减区间为0,+∞，无递减区间；②当−18<a <0时，函数y =f x 的减区间为0,+∞，增区间为题型3已知单调区间求参数◆类型1已知单增单减求取值范围【例题3-1】若函数f x=x2−ax+ln x在区间1,e上单调递增，则实数a的取值范围是（）A．3,+∞B．−∞,3C．3,e2+1D．−∞,e2+1【答案】B【分析】根据函数的单调性与导函数之间的关系，将单调性转化为导函数恒大于或等于0，即可求解.【详解】依题意f′x=2x−a+1x≥0在区间1,e上恒成立，即a≤2x+1x在区间1,e 上恒成立.<x<e，则g′x=2−1x2=2x2−1x2>0，所以g x在1,e上单调递增，令g x=2x+则g x>3，所以a≤3.故选:B.【变式3-1】1．若函数f x=x3−3kx+1在区间1,+∞上单调递增，则实数k的取值范围是（）A．−∞,1B．−∞,1C．−1,+∞D．1,+∞【答案】B【分析】利用函数f x在区间(1,+∞)上的导函数为非负数，列不等式，解不等式即可求得k的取值范围.【详解】由题意得，f′(x)=3x2−3k=3(x2−k)≥0在区间(1,+∞)上恒成立，即k≤x2在区间(1,+∞)上恒成立，又函数y=x2在(1,+∞)上单调递增，得x2>1，所以k≤1，即实数k的取值范围是(−∞,1].故选：B【变式3-1】2．（多选）已知函数f x=12x2−a ln x+x在1,+∞上单调递增，则实数a 的所有可能取值是（）A．0B．1C．2D．3【答案】ABC【分析】由f′(x)≥0在1,+∞上恒成立，参变分离得a≤x2+x，结合二次函数求出最小值即可求解.【详解】由题意得f′(x)≥0在1,+∞上恒成立，即f′x=x−a x+1≥0，整理得a≤x2+x，即a≤x2+x min，又x2+x=x+−14在1,+∞上单调递增，则最小值为1+1=2，故a≤2，结合选项知，a可取0，1，2.故选：ABC.【变式3-1】3．若函数f(x)=12sin2x+a cos x在区间(0,π)上单调递增，则实数a的取值范围是（）A．(−∞,−1]B．[−1,+∞)C．(−∞,−1)D．[1,+∞)【答案】A【分析】依题意f′(x)=cos2x−a sin x≥0在(0,π)上恒成立，根据二倍角公式得到1−2sin x2−a sin x≥0，令t=sin x，即−2t2−at+1≥0，t∈0,1恒成立，参变分离可得a≤−2t+1t，再构造函数g t=−2t+1t，利用导数说明函数的单调性，即可求出函数的最小值，从而得解；【详解】解：∵f(x)=12sin2x+a cos x在区间(0,π)上是增函数，∴f′(x)=cos2x−a sin x≥0在(0,π)上恒成立，∴1−2sin2x−a sin x≥0，因为x∈(0,π)，所以sin x∈0,1令t=sin x，则t∈0,1，即−2t2−at+1≥0，t∈0,1，∴a≤−2t+1t，令g t=−2t+1t，t∈0,1，则g′t=−2−1t2<0，∴g t在0,1上单调递减，∴a≤g1=−1，即a∈−∞,−1，故选：A．【变式3-1】4．“函数y=ax−sin x在R上是增函数”是“a>0”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【分析】求导，根据导数恒大于等于0可得a的范围，然后判断可得.【详解】因为函数y=ax−sin x是增函数，所以y′=a−cos x≥0恒成立，即a≥cos x恒成立，所以a≥1>0反之a>0，函数的导数不一定大于0.故“函数y=ax−sin x在R上是增函数”是“a>0”的充分不必要条件.故选：A【变式3-1】5．若函数f(x)=ln(x+1)−mx在区间(0,+∞)上单调递减，则实数m的取值范围是（）A．(−∞,−1]B．(−∞,−1)C．(1,+∞)D．[1,+∞)【答案】D【分析】函数f(x)在区间(0,+∞)上单调递减，则导函数f′(x)≤0在区间(0,+∞)上恒成立,分离参数，即可求解.【详解】解：f(x)=ln(x+1)−mx,f′(x)=1x+1−m，则f′(x)=1x+1−m≤0在0,+∞上恒成立，即m≥1x+1恒成立，又y=1x+1在0,+∞上单调递减，故1x+1<1，所以m≥1，当m=1时，导数不恒为0，故选：D.【变式3-1】6．若函数f(x)=bx+2sin x在x∈则实数b的取值范围是（）A．b≥0B．b>0C．b≥−2D．b>−2【答案】A【分析】由f′(x)≥0【详解】由题意f′(x)=b+2cos x≥0b≥−2cos x，x∈y=−2cos x是增函数，y max=0（x=π2时取得），所以b≥0．【变式3-1】7．已知函数f x=13x3+a2x2+x+1上−∞,0，3,+∞单调递增，在1,2上单调递减，则实数a的取值范围为______.【答案】−103,−【分析】求导得到f′x=x2+ax+1，根据f x在−∞,0，3,+∞上单调递增，在1,2上单调递减，可得方程f′x=0的两个根分别位于区间0,1和2,3上，进而根据数形结合，列出相应的不等式组，即可求出实数a的取值范围【详解】由f x=13x3+a2x2+x+1，得f′x=x2+ax+1，因为f x在−∞,0，3,+∞上单调递增，在1,2上单调递减，所以方程f′x=0的两个根分别位于区间0,1和2,3上，所以f′0≥0f′1≤0f′2≤0f′3≥0，即1≥02+a≤02a+5≤03a+10≥0解得−103≤a≤−52故答案为：−103,◆类型2存在单增单减区间问题【例题3-2】已知函数f(x)＝lnx，g(x)＝12ax2＋2x.（1）若函数h(x)＝f(x)－g(x)存在单调递减区间，求实数a的取值范围；（2）若函数h(x)＝f(x)－g(x)在[1，4]上单调递减，求实数a的取值范围.【答案】（1）(－1，＋∞)；（2）[−716,+∞).【分析】（1）由函数h(x)在(0，＋∞)上存在单调减区间，则当x>0时，1x－ax－2<0有解，即a>1x2−2x有解，构造函数G(x)=1x2−2x，求出其最小值即可；（2）由h(x)在[1，4]上单调递减，可得当x∈[1，4]时，ℎ'(x)=1x−ax−2≤0恒成立，则a≥1x2−2x恒成立，构造函数G(x)=1x2−2x，求出其最大值即可【详解】h(x)＝ln x－12ax2－2x，x>0.∴h′(x)＝1x－ax－2.（1）若函数h(x)在(0，＋∞)上存在单调减区间，则当x>0时，1x－ax－2<0有解，即a>1x2−2x有解.设G(x)=1x2−2x，所以只要a>G(x)min.又G(x)=(1x−1)2−1，所以G(x)min＝－1.所以a>－1.即实数a的取值范围是(－1，＋∞).（2）由h(x)在[1，4]上单调递减，∴当x∈[1，4]时，ℎ'(x)=1x−ax−2≤0恒成立，则a≥1x2−2x恒成立，设G(x)=1x2−2x，所以a≥G(x)max.又G(x)=(1x−1)2−1，x∈[1，4]，因为x∈[1，4]，所以1x∈[14,1]，所以G(x)max＝−716(此时x＝4)，所以a≥−716.又当a＝−716时，ℎ'(x)=1x+716x−2=(7x−4)(x−4)16x，∵x∈[1，4]，∴ℎ'(x)=(7x−4)(x−4)16x≤0，当且仅当x＝4时等号成立.∴h(x)在[1，4]上为减函数.故实数a的取值范围是[−716,+∞).【点睛】此题考查导数的应用，注意函数的单调区间和在某区间上单调的区别，同时考查不等式恒成立问题转化为求函数的最值，属于中档题【变式3-2】1．若函数f(x)=ln x−12ax2−2x存在单调递减区间，则实数a的取值范围是________.【答案】(−1,+∞)【分析】先求导函数，递减小于0，再解含参数的不等式分类讨论即可.【详解】f′(x)=1x−ax−2=1−2x−ax2x，由题意知，f′(x)<0在(0,+∞)上有实数解，即ax2+2x−1>0有实数解，当a≥0时，显然满足，当a<0时，只需Δ=4+4a>0∴−1<a<0综上所述a>−1故答案为：(−1,+∞)【点睛】本题考查导函数的单调性，及含参数的不等式有解求参数的取值范围问题.【变式3-2】2．设f(x)=−13x3+12x2+ax.（1）若f(x)+∞上存在单调递增区间，求a的取值范围；（2）若f(x)+∞上单调递减，求a的取值范围.【答案】（1）a>−29；（2）a≤−29【分析】（1）f(x)+∞上存在单调递增区间，即f'(x)>0+∞上有解，只要f'(x)max>0即可；（2）f(x)+∞上单调递减，即f'(x)≤0+∞上恒成立，只要f'(x)max≤0即可；【详解】解：（1）f'(x)=−x2+x+a=−x+14+a，当x∈+∞时，f'(x)max=f'=29+a，则当x∈+∞时，令29+a>0，得a>−29，所以，当a>−29时，f(x)+∞上存在单调递增区间；（2）由（1）得当x∈+∞时，f'(x)max=f'=29+a，则当x∈+∞时，令29+a≤0，得a≤−29，所以，当a≤−29时，f(x)+∞上单调递减.【点睛】本题考查利用导数研究函数的单调性及函数在闭区间上的最值问题，正确理解导数与函数单调性的关系及准确求导是解决问题的基础.【变式3-2】3．已知函数f(x)=ln x−12ax2−2x+1,a∈R（1）若f(x)在x=2处的切线与直线2x+y=0垂直，求a的值；（2）若f(x)存在单调递减区间，求实数a的取值范围．【答案】（1）−1（2）(−1,+∞).【分析】（1）根据导数的几何意义，再利用两直线垂直的充要条件即可求解；（2）根据函数f(x)存在单调递减等价f′(x)<0在(0,+∞)上有解，转化为a>1−2x x2在(0,+∞)上有解，求g(x)=1−2x x2在(0,+∞)的最小值即可求解．【详解】（1）因为f(x)=ln x−12ax2−2x+1,a∈R，所以f'(x)=1x−ax−2,∴f′(2)=−2a−32,所以f(x)在x=2处的切线的斜率为k=f′(2)=−2a−32，因为f (x )在x =2处的切线与直线2x +y =0垂直，所以(−2a −32)×(−2)=−1，即−2a −32=12，解得a =−1．（2）因为f (x )=ln x −12ax 2−2x +1,所以f ′(x )=1x−ax −2，因为f (x )存在单调递减区间等价于f ′(x )=1x−ax −2<0在(0,+∞)上有解．即a >1−2xx 2在(0,+∞)上有解．令g (x )=1−2xx 2,(x >0),所以只需a >g (x )min ．因为g (x )=1−2xx 2=(1x)2−2(1x)=(1x−1)2−1≥−1,即g (x )min =−1,所以实数a 的取值范围为(−1,+∞)．【变式3-2】4．已知函数f (x )=−13x 3+12x 2+2ax ．(1)若函数f (x )+∞上存在单调增区间，求实数a 的取值范围．(2)若函数f (x ),1上单调递增，求实数a 的取值范围．【答案】(1)a >−19(2)a ≥0【分析】（1）即f ′x >0有解，参变分离得a >，最后根据二次函数性质求最值，即得实数a 的取值范围．（2）即f ′x >0恒成立，参变分离得a >，最后根据二次函数性质求最值，即得实数a 的取值范围．（1）f ′x =−x 2+x +2a ，由于f (x )+∞上存在单调增区间，故∃x 0∈+∞，f ′x 0>0，∴a >，由于y =x 2−x 2在+∞单调递增，且当x =23时，x 2−x2=−19∴a >−19（2）∀x ∈,1f ′x ≥0，由于y =x 2−x 2在+∞单调递增，故y =x 2−x 2在,1单调递增，当x =1时，x 2−x2=0a ≥，∴a ≥0．◆类型3已知单调区间问题【例题3-3】已知函数f x =ln x +x 2+ax ,1，则（）.A ．a ∈−∞,−3B ．a =−3C ．a =3D ．a ∈−∞,3【答案】B【分析】根据f x 得到f ′x ，再根据f x ,1，得到12和1是方程f ′x =0的两个根，代入解方程即可.【详解】由f x =ln x +x 2+ax 得f′x =2x 2+ax +1x，又f x ,1，所以12和1是方程2x 2+ax +1x=0的两个根，代入得a =−3.经检验满足题意故选：B.【变式3-3】1．已知函数f x =mx 3+3m −1x 2−m 2+1m >0的单调递减区间是0,4，则m =（）A ．3B ．13C ．2D ．12【答案】B【分析】利用导数结合韦达定理得出m 的值.【详解】函数f x =mx 3+3m −1x 2−m 2+1m >0，则导数f ′x =3mx 2+6m −1x令f ′x <0，即3mx 2+6m −1x <0，∵m >0，f x 的单调递减区间是0,4，∴0，4是方程3mx 2+6m −1x =0的两根，∴0+4=0×4=0，∴m =13故选：B.【变式3-3】2．已知函数f (x )=2x 3−mx 2+2(m >0)的单调减区间为(a ,b )，若b −a ≤2，则m 的最大值为______．【答案】6【分析】根据已知条件及导数的正负与函数单调性的关系即可求解.【详解】由f(x)=2x3−mx2+2(m>0)，得f′(x)=6x2−2mx(m>0)．令f′(x)<0,即6x2−2mx<0，解得0<x<m3，所以函数f(x)=2x3−mx2+2(m>0)的单调减区间为(0,m3)，所以b−a=m3≤2，解得m≤6，所以m的最大值为6．故答案为：6.【变式3-3】3．已知函数f x=ln x+x2+ax,1，则a的值为________．【答案】−3【分析】分析可知不等式2x2+ax+1<0,1，利用韦达定理可求得实数a的值.【详解】函数f x的定义域为0,+∞，且f′x=1x+2x+a=2x2+ax+1x，由题意可知，不等式2x2+ax+1<0,1，所以，12+1=−a2，解得a=−3.故答案为：−3.【变式3-3】4．（多选）若函数f x=ax3−3x2+x+1恰好有三个单调区间，则实数a的取值可以是（）A．−3B．−1C．0D．3【答案】AB【分析】将问题转化为导函数有两个零点问题，由判别式可解.【详解】当a=0时，f x=−3x2+x+1，显然不满足题意；当a≠0时，f′x=3ax2−6x+1，因为f x恰好有三个单调区间，所以f′x=3ax2−6x+1有两个零点，即Δ=36−12a>0，解得a<3，综上，a的取值范围为(−∞,0)∪(0,3).故选：AB◆类型4不单调问题【例题3-4】已知函数f x=1−x ln x+ax在1,+∞上不单调，则a的取值范围是（）A．0,+∞B．−∞,0C．0,+∞D．−∞,0【答案】A【分析】因为f (x )在1,+∞上不单调，故利用f ′x 在1,+∞上必有零点，利用a =ln x −1x+1，构造函数z (x )=ln x −1x +1，通过z (x )的范围，由此求得a 的取值范围.【详解】依题意f ′x =−ln x +1x+a −1，故f ′(x )在1,+∞上有零点，令g (x )=−ln x +1x+a −1，令g (x )=0，得a =ln x −1x +1，令z (x )=ln x −1x +1，则z ′(x )=1x +1x 2，由x >1，得z ′(x )>0，z (x )单调递增，又由z (1)=0，得z (x )>0，故a =z (x )>0，所以，a 的取值范围0,+∞故选：A【变式3-4】若函数()()11xf x e a x =--+在(0，1)上不单调，则a 的取值范围是（）A ．()2,1e +B ．[]2,1e +C ．(][),21,e -∞⋃++∞D ．()(),21,e -∞⋃++∞【答案】A 【解析】()(1)1x f x e a x =--+，()1x f x e a '∴=-+，若()f x 在(0,1)上不单调，则()'f x 在(0,1)上有变号零点，又()f x '单调递增，()()010f f ''∴<，即(11)(1)0a e a -+-+<，解得21a e <<+．a ∴的取值范围是(2,e +1)．故选：A ．题型4单调性与图象【例题4-1】函数()()22xf x x x e =-的图象大致是()A ．B ．C ．D ．【答案】B 【解析】函数()()22x f x x x e =-，则()()22xf x x e '=-，令()0f x '=，解得()f x 的两个极值点为AD ，且当0x <时，()f x 恒为正，排除C ，即只有B选项符合要求，故选：B.【变式4-1】1.函数()21ln 2f x x x =-的图象大致是（）.A ．B ．C ．D ．【答案】B 【解析】由题得，()1(0)f x x x x'=->，当(0,1)时，()0f x '>，函数()f x 为增函数，当(1,)+∞时，()0f x '<，函数()f x 为减函数，则当1x =时，()f x 取最大值，()112f =-，则B 选项正确.故选：B 【变式4-1】2.已知函数f (x )＝e x －(x ＋1)2(e 为2.71828…)，则f (x )的大致图象是（）A ．B ．C ．D ．【答案】C 【解析】函数()2(1)x f x e x ＝－+，当1x =-时，()1=110f ee -->＝，故排除A 、D ，又()22()20ln2x x f x e x f x e x '''=--=-=⇒=，，当0ln2x <<时，()(0())00f f f x x ''<''<∴<，，所以()f x 在()0,ln 2为减函数，故排除B,故选：C【变式4-1】3．函数f x =ax 3+bx 2+cx +d 的图象如图，则函数y =ax 2+32bx +c3的单调递增区间是()A ．−∞,−2B ．[12,+∞)C ．−2,3D ．[98,+∞)【答案】D【分析】由题可得d ＝0，不妨取a ＝1，求导，由题图可得f ′−2=f ′3=0，可求b ，c 的值，从而可求单调区间.【详解】解:由题图可知d ＝0.不妨取a ＝1，∵f x=x3+bx2+cx，∴f′x=3x2+2bx+c.由图可知f′−2=f′3=0，∴12－4b＋c＝0,27＋6b＋c＝0，∴b=−32，c=−18.∴y=x2−94x−6，y′=2x−94.当x＞98时，y′>0，∴y=x2−94x−6的单调递增区间为[98,+∞).故选:D.【变式4-1】4．已知函数f x的图象如图所示，则下列说法中错误的是A．f x在区间上单调递减B．f x在区间上单调递增C．当时，f′x>0D．当时，f′x=0【答案】C【详解】试题分析：由图像可知增区间为(1,4)，此时，减区间为(−∞,1),(4,+∞)此时f'(x)<0，所以x=1,x=4是极值点考点：函数单调性与极值【例题4-2】如图是y=f′x的图像，则函数y=f x的单调递减区间是（）A．−2,1B．−2,0,2,+∞C．−∞,−1D．−∞,−1,1,+∞【答案】B【分析】由导数与单调性的关系判断．【详解】由图象知−2<x<0或x>2时，f′(x)<0，因此减区间是(−2,0)，(2,+∞)．故选：B．【变式4-2】1．函数y=f(x)的导函数y=f′(x)的图象如图所示，给出下列命题：①−3是函数y=f(x)的极值点；②−1是函数y=f(x)的最小值点；③y=f(x)在区间(−3,1)上单调递增；④y=f(x)在x=0处切线的斜率小于零．以上正确命题的序号是（）A．①②B．③④C．①③D．②④【答案】C【分析】根据导函数图象可判定导函数的符号，从而确定函数的单调性，得到极值点，以及根据导数的几何意义可知在某点处的导数即为在该点处的切线斜率．【详解】根据导函数图象可知：当x∈−∞,−3时，f′x<0，在x∈−3,1时，f′x≥0，∴函数y=f x在−∞,−3上单调递减，在−3,1上单调递增，故③正确；则−3是函数y=f x的极小值点，故①正确；∵在−3,1上单调递增，∴−1不是函数y=f x的最小值点，故②不正确；∵函数y=f x在x=0处的导数大于0，∴切线的斜率大于零，故④不正确．故选：C．【变式4-2】2．已知函数f x与其导函数f′x的图象的一部分如图所示，则函数g x=的单调性（）A．在1,1单调递减B．在−1,2−3单调递减C．在2−3,1单调递减D．在1,2上单调递减【答案】B【分析】由导函数与原函数之间关系可确定两个图象的分属，由此可得g′x在不同区间内的正负，进而判断单调性，得到结果.【详解】∵f′x<0时，f x单调递减；f′x>0时，f x单调递增，∴已知图象中在−∞,0上单调递减，在0,+∞上单调递增，且有两个零点x=−1和x=1的是f′x，∵g′x=f′x−f x e x，由图象可知：当x∈−1,2−3时，f x>f′x；当x∈2−3,2时，f′x>f x；∴当x∈−1,2−3时，g′x<0；当x∈2−3,2时，g′x>0；∴g x在−1,1上不单调，A错误；在−1,2−3上单调递减，B正确；在2−3,1，1,2上单调递增，CD错误.故选：B.【变式4-2】3．已知f x是定义在R上的可导函数，y=e f′x的图象如下图所示，则y=f x的单调减区间是A．−∞,−1B．−∞,2C．0,1D．1,2【答案】B【详解】分析：先根据图像求出e f′(x)≤1，即得f′(x)≤0，也即得结果.详解：因为当x≤2时，e f′(x)≤1，所以当x≤2时，f′(x)≤0，所以y=f(x)的单调减区间是(−∞,2)，选B.点睛：函数单调性问题，往往转化为导函数符号是否变号或怎样变号问题，经常转化为解方程或不等式.题型5利用导数图象解不等式【例题5】定义域为R的可导函数的导函数y=f x为f′x，满足f x>f′x，且f0=1，则不等式f x<e x的解集为（）A．−∞,2B．2,+∞C．−∞,0D．0,+∞【答案】D【分析】根据条件构造函数F x=<1⇔F x<F0利用函数的单调性解不等式，即可得到结果．【详解】设F x=则F′x==f x>f′x，所以F′x<0，即函数F x在定义域上单调递减，因为f(0)=1，所以不等式f x<e x<1，等价于F(x)<F(0)，解得x>0，故不等式的解集为0,+∞.故选：D．【变式5-1】1．已知定义在R上的函数f x的导函数为f′x，若f′x<e x，且f2=e2+2，则不等式f ln x>x+2的解集是（）A．0,e2B．0,2C．−∞,e2D．−∞,2【答案】A【分析】设g x=f x−e x+2，求导可得g x在R上单调递减，再根据f ln x>x+2转化为g ln x>4，再结合g x的单调性求解即可.【详解】设g x=f x−e x+2，则g′x=f′x−e x.因为f′x<e x，所以f′x−e x<0，即g′x<0，所以g x在R上单调递减.。

高一函数的单调性的知识点函数是数学中的重要概念之一，而在高一阶段学习的数学中，函数的单调性是一个重要的知识点。

下面我们将详细介绍高一函数的单调性的相关知识。

一、函数的单调性定义函数的单调性是指函数在定义域上的变化趋势。

具体来说，若对于定义域上的任意两个数x₁和x₂，当x₁<x₂时，函数f(x₁)的值与函数f(x₂)的值之间的关系。

如果函数在定义域上满足这种关系，我们称之为函数的单调性。

二、单调递增与单调递减函数的单调性可分为单调递增和单调递减两种情况。

1. 单调递增函数f(x)在定义域上，当x₁<x₂时，如果f(x₁)≤f(x₂)，则函数f(x)是单调递增的。

例如，对于函数f(x)=x²，在整个实数范围上，无论取哪两个不相等的实数x₁和x₂，当x₁<x₂时，f(x₁)≤f(x₂)恒成立。

因此，函数f(x)=x²是单调递增的。

2. 单调递减函数f(x)在定义域上，当x₁<x₂时，如果f(x₁)≥f(x₂)，则函数f(x)是单调递减的。

例如，对于函数f(x)=1/x，在定义域(0，+∞)上，当x₁<x₂时，f(x₁)≥f(x₂)恒成立。

因此，函数f(x)=1/x是单调递减的。

三、判断函数的单调性的方法我们可以通过函数图像、导数和函数的增减性来判断函数的单调性。

1. 函数图像法通过画出函数的图像，观察图像随x的变化趋势，判断函数的单调性。

例如，对于函数f(x)=x³，我们可以绘制出函数的图像。

通过观察图像可知，当x₁<x₂时，f(x₁)≤f(x₂)恒成立，因此函数f(x)=x³是单调递增的。

2. 导数法对于一元函数f(x)，如果其导数f'(x)的值恒大于0（或小于0），则函数f(x)是单调递增的（或递减的）。

例如，对于函数f(x)=2x²-3x，我们首先求出其导数f'(x)=4x-3。

通过观察导数的值可知，f'(x)在整个实数范围上恒大于0，也就是说函数f(x)是单调递增的。

函数单调性怎么判断
1、导数法
首先对函数进行求导，令导函数等于零，得X值，判断X与导函数的关系，当导函数大于零时是增函数，小于零是减函数。

2、定义法
设x1，x2是函数f(x)定义域上任意的两个数，且x1＜x2，若f(x1)＜f(x2)，则此函数为增函数；反知，若f(x1)＞f(x2)，则此函数为减函数.
3、性质法
若函数f(x)、g(x)在区间B上具有单调性，则在区间B上有：
⑴f(x)与f(x)＋C（C为常数）具有相同的单调性；
⑵f(x)与c•f(x)当c＞0具有相同的单调性，当c＜0具有相反的单调性；
⑶当f(x)、g(x)都是增(减)函数，则f(x)＋g(x)都是增(减)函数；
⑷当f(x)、g(x)都是增(减)函数，则f(x)•g(x)当两者都恒大于0时也是增(减)函数，当两者都恒小于0时也是减(增)函数；
4、复合函数同增异减法
对于复合函数y＝f[g(x)]满足“同增异减”法(应注意内层函数的值域)，可令t＝g(x)，则三个函数y＝f(t)、t＝g(x)、y＝f[g(x)]中，若有两个函数单调性相同，则第三个函数为增函数；若有两个函数单调性相反，则第三个函数为减函数。

拓展资料：
1、奇函数在对称的两个区间上有相同的单调性，偶函数在对称的两个区间上有相反的单调性；
2、互为反函数的两个函数有相同的单调性；
3、如果f(x)在区间D上是增（减）函数，那么f(x)在D的任一子区间上也是增（减）函数.。

函数的单调性一、知识梳理＆方法总结1. 单调性的定义和证明(1) 单调性：当x 逐渐增加时，函数值y 逐渐减小；当x 逐渐增加时，函数值y 逐渐增加。

函数的这两种性质都叫做函数的单调性。

(2) 定义：一般地，对于给定区间I 上的函数()y f x =：① 如果对于属于这个区间I 的自变量的任意两个值12,x x ，当12x x <时，都有12()()f x f x <，那么就说函数()y f x =在这个区间上是单调增函数。

② 如果对于属于这个区间I 的自变量的任意两个值12,x x ，当12x x <时，都有12()()f x f x >，那么就说函数()y f x =在这个区间上是单调减函数。

(3) 如果函数()y f x =在某个区间I 上是增（减）函数，那么就说函数()y f x =在区间I 上是单调函数。

区间I 叫做函数()y f x =的单调区间。

若()f x 在区间D 上是增（减）函数，则()f x 在D 的任一子区间上也是增（减）函数 (4) 函数单调性的证明（证明某函数在指定区间上增减性的步骤）① 在该区间上任取12x x <② 作差12()()f x f x -，通过因式分解等恒等变形方法将差式化为若干因式的积或商．③ 由判断各因式的符号来确定差式的符号，从而得到12()()f x f x >（或12()()f x f x <）即()f x 的增减性依定义证明完毕．任取、做差、变形、定号、下结论。

(5) 函数单调性的两种等价定义设12,[,]x x a b ∈则①1212()()0()f x f x f x x x ->⇔-在[,]a b 上是增函数1212()()0()f x f x f x x x -<⇔-在[,]a b 上是减函数② 1212()[()()]0()x x f x f x f x -->⇔在[,]a b 上是增函数1212()[()()]0()x x f x f x f x --<⇔在[,]a b 上是减函数2. 四则运算的单调性增函数+)(x f 增函数)(x g 是增函数； 减函数+)(x f 减函数)(x g 是减函数； 增函数-)(x f 减函数)(x g 是增函数； 减函数-)(x f 增函数)(x g 是减函数。

函数的单调性xx年xx月xx日•函数的单调性概述•单调函数的性质•单调函数的应用目录•单调函数的证明•单调函数的扩展01函数的单调性概述•函数的单调性是指函数在某区间内单调递增或单调递减的性质。

如果函数在某区间内单调递增，则函数在该区间内的图形是上升的；如果函数在某区间内单调递减，则函数在该区间内的图形是下降的。

定义类型•函数的单调性主要有两种类型：单调递增和单调递减。

判断函数单调性的方法有多种，以下是其中两种常用的方法判断方法求导数法：如果函数在某区间内可导，且导数大于0，则函数在该区间内单调递增；如果函数在某区间内可导，且导数小于0，则函数在该区间内单调递减。

定义法：根据函数单调性的定义，如果对于任意的$x_{1},x_{2}$满足$x_{1}<x_{2}$时，都有$f(x_{1})\leq f(x_{2})$（单调递增）或$f(x_{1})\geq f(x_{2})$（单调递减），则函数在该区间内单调。

01020302单调函数的性质单调函数的定义域和值域定义域单调函数的定义域是实数集的子集，即定义域可以是全体实数、正实数、负实数或零。

值域单调函数的值域是定义域上的子集，即值域可以是全体实数、正实数、负实数或零。

奇函数如果一个函数满足f(-x)=-f(x)，则称该函数为奇函数。

在单调函数中，奇函数关于原点对称，即对于定义域内的任意x，都有f(-x)=-f(x)。

偶函数如果一个函数满足f(-x)=f(x)，则称该函数为偶函数。

在单调函数中，偶函数关于y轴对称，即对于定义域内的任意x，都有f(-x)=f(x)。

如果一个函数满足f(x+T)=f(x)，则称该函数为周期函数，其中T为该函数的周期。

在单调函数中，周期函数是指存在一个正实数T，使得对于定义域内的任意x，都有f(x+T)=f(x)。

最小正周期对于单调函数而言，其周期性意味着该函数存在最小正周期，即存在一个最小的正实数T，使得对于定义域内的任意x，都有f(x+T)=f(x)。