一次函数复习导学案

一次函数复习课导学案班级 姓名学习目标：1．使学生巩固一次函数的概念、图象及性质，引导学生对一次函数的重点知识有一个整体把握，2．进一步体会数学来源于生活又服务于生活，提高学生数学知识的应用意识。

3．通过学生亲自参与合作学习，锻炼其概括总结能力、分析能力、识图能力。

一．一次函数的定义一次函数的概念：如果函数______=y (b 、k 为常数，且k ______)，那么y 叫做x 的一次函数。

特别地，当b _____时，函数______=y (k ______)叫做正比例函数。

【练习】：求m 为何值时，关于x 的函数()312++=m x m y 是一次函数，并写出其函数关系式。

二．一次函数的图像*. 正比例函数()0≠=k kx y 的图象是过点（_____），(______)的_________。

*.一次函数()0≠+=k b kx y 的图象是过点（0，___),（____，0)的__________。

*.一次函数()0≠+=k b kx y 的图象与b 、k 符号的关系：k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0练习：一次函数2-3x y +=的图象不经过（ ）A 、第一象限B 、第二象限C 、第三象限D 、第四象限2.已知一次函数y=kx+b,y 随着x 的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )(A) (B) （C ） （D ）三．一次函数的性质一次函数()0≠+=k b kx y 的性质：⑴当k >0时，y 随x 的增大而_________。

⑵当k <0时，y 随x 的增大而_________。

【练习】：1、点A （5，1y ）和B （2，2y ）都在直线1+-=x y 上，则1y 与2y 的关系是（ ）A 、1y ≥2yB 、1y ＝2yC 、1y ＜2yD 、1y ＞2y2、已知一次函数y=(m+2)x+(m-3),(1)m 为何值时，直线经过原点？ (2)m 为何值时直线与y 轴交于（0,2）？(3)m 为何值时直线与x 轴交于（3,0）？四．一次函数表达式的确定：待定系数法：求一次函数y=kx+b 的解析式，可由已知条件给出的两对x 、y 的值，列出关于k 、b 的一次方程。

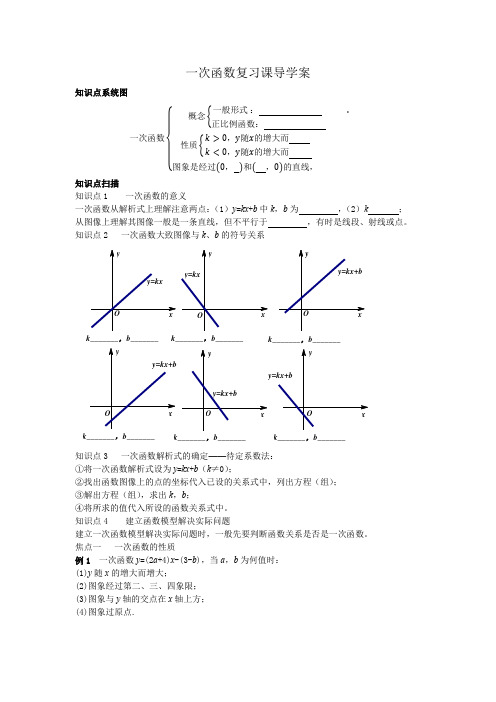
一次函数复习课导学案知识点系统图一次函数概念一般形式： .正比例函数：性质k >0，y 随x 的增大而k <0，y 随x 的增大而图象是经过 0， 和 ，0 的直线，知识点扫描知识点1 一次函数的意义一次函数从解析式上理解注意两点：（1）y =kx +b 中k ，b 为，（2）k ；从图像上理解其图像一般是一条直线，但不平行于，有时是线段、射线或点。

知识点2 一次函数大致图像与k 、b 的符号关系知识点3 一次函数解析式的确定——待定系数法： ①将一次函数解析式设为y =kx +b （k ≠0）；②找出函数图像上的点的坐标代入已设的关系式中，列出方程（组）； ③解出方程（组），求出k ，b ；④将所求的值代入所设的函数关系式中。

知识点4 建立函数模型解决实际问题建立一次函数模型解决实际问题时，一般先要判断函数关系是否是一次函数。

焦点一 一次函数的性质例1 一次函数y =(2a +4)x -(3-b )，当a ，b 为何值时： (1)y 随x 的增大而增大；(2)图象经过第二、三、四象限； (3)图象与y 轴的交点在x 轴上方； (4)图象过原点.k_______，b_______k_______，b_______k_______，b_______k_______，b_______k_______，b_______k_______，b_______焦点二 一次函数解析式的确定例2 如图所示，直线l 过A （0，-1）、B （1，0）两点，求直线l 的解析式。

焦点三 根据图像信息解题例3在社会主义新农村建设中，衢州某乡镇决定对A 、B 两村之间的公路进行改造，并有甲工程队从A 村向B 村方向修筑，乙工程队从B 村向A 村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务有甲工程队单独完成，直到公路修通．下图是甲乙两个工程队修公路的长度y （米）与施工时间x （天）之间的函数图象，请根据图象所提供的信息解答下列问题： （1）乙工程队每天修公路多少米？（2）分别求甲、乙工程队修公路的长度y （米）与施工时间x （天）之间的函数关系式． （3）若该项工程由甲、乙两工程队一直合作施工，需几天完成？焦点四 一次函数与几何综合例4 如图，在平面直角坐标系中，Rt △OAB 的直角边OA 在x 轴的正半轴上，点B 在第象限，将△OAB 绕点O 按逆时针方向旋转至△OA ′B ′，使点B 的对应点B ′落在y 轴的正半轴上，已知OB =2，∠BOA =30°． （1）求点B 和点A ′的坐标；（2）求经过点B 和点B ′的直线所对应的一次函数解析式，并判断点A 是否在直线BB ′上．例2图例4图课堂作业1.直线y =kx -1一定经过点（ ） A ．（1,0） B ．（1，k ） C ．(0, k ) D ．(0,-1)2.已知一次函数y =mx +n -2的图象如图所示，则m 、n 的取值范围是（ ）A ．m ＞0，n ＜2B ．m ＞0，n ＞2C ．m ＜0，n ＜2D ．m ＜0，n ＞2 3.一条直线y =kx +b 其中k +b =-5，kb =6，那么该直线经过（）A ．第二、四象限B ．第一、二、三象限C ．第一、三象限D ．第二、三、四象限 4.下列函数中，当x >0时，y 随x 的增大而增大的是（ ） A ．y =-x +1 B ．y =x 2-1 C ．y =1xD ．y =-x 2+1 5.已知一次函数y =kx +b 的图象经过点A （1，-1），B （-1,3）两点，则（ ） A ．k >0，b >0 B ．k >0，b <0 C ．k <0，b >0 D ．k <0，b <06.若实数a 、b 、c 满足a +b +c =0，且a <b <c ，则函数y =cx +a 的图象可能是（ ）A ．B ．C ．D ．7.一个矩形被直线分成面积为x ，y 的两部分，则y 与x 之间的函数图象只可能是（ ）A ．B ．C ．D ．8.将直线y =2x 向右平移1个单位后所得图象对应的函数关系式为（ ）A ．y =2x -1B ．y =2x -2C ．y =2x +1D ．y =2x +2 9.如图，函数y =2x 和y =ax +4的图象相交于点A （m ，3）,则不等式2x <ax +4的解集为（ ） A ． 32x <B ．x <3C ． 32x >D ．x >310. A 、B 两点在一次函数图象上的位置如图所示，两点的坐标分别为A （x +a ，y +b ）， B （x ，y ），下列结论正确的是（）第2题 第10题 第9题 第12题A ．a ＞0B ．a ＜0C ．b =0D ．ab ＜0 11. 下列关于一次函数y =-2x +1的说法：①y 随x 的增大而减小； ②图象与直线y =-2x 平行； ③图象与y 轴的交点坐标是(0，1)；④图象经过第一、二、四象限.其中正确的有（ ）个. A ．4B ．3C ．2 D ．1 12.如图，是函数y =3−x (0≤x ≤2)x −1 (2<x ≤4)的图象，请说说这个函数的最小值是A ．1B ．2C ．3D ．413.若一次函数y =kx +b ，当x 的值减小1，y 的值就减小2，则当x 的值增加2时，y 的值（） A ． 增加4 B ．减小4 C ． 增加2 D ．减小2 14.如图，是直线y =x -3的图象，点P （2，m ）在该直线的上方，则m 的取值范围是（ ） A . m ＞-3B . m ＞-1C . m ＞0D . m ＜3 15.如图，点A 的坐标为（-1，0），点B 在直线y =x 上运动，当线段AB 最短时，点B 坐标为（ ）A .（0，0）B .(11,22--)C ．(22-D .(22--)16.如图，一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完．假设每分钟的进水量和出水量是两个常数，容器内的水量y （单位：升）与时间x （单位：分）之间的部分关系．那么，从关闭进水管起多少分钟时该容器内的水恰好放完．17（1）对于一次函数y =−3x +4，当0≤x ≤2时，求对应函数值y 的取值范围； （2）对于一次函数y =3x −2，当−2≤y ≤4时，求对应的自变量x 的取值范围； （3）对于一次函数y =kx +b ，当0≤x ≤2时，对应函数值y 的取值范围为−2≤y ≤4，求k 、b 的值。

八年级数学复习《一次函数》导学案.doc1、第十四章一次函数复习学习目标：1.了解本章的学问结构；2.把握一次函数的概念、图象和性质；能用待定系数法确定一次函数解析式。

学习重点：一次函数的概念、图象和性质；能用待定系数法确定一次函数解析式学习难点：一次函数学问的运用。

【学问提要】一、函数与函数的图象1.叫变量，叫常量.2.函数定义：在一个改变过程中，假如有两个变量x与y，并且对于x的每一个确定的值，y都有确定的值与其对应，那么我们就说x是自变量，y是x的函数.3.函数的图象：对于一个函数，假如把自变量与函数的每对对应值分别作为点的，那么坐标平面2、内由这些点组成的图形，就是这个函数的图象。

4、描点法画图象的步骤：5.函数的三种表示方法：6、自变量的取值范围：〔1〕分式类：分母不为0，〔2〕根式类：开偶次方的被开方数大于等于0，〔3〕整式类：全体实数。

〔4〕实际类：使实际问题有意义。

例1、求以下函数中自变量x的取值范围〔1〕；〔2〕；〔3〕；〔4〕。

例2、以下四组函数中，表示同一函数的是〔〕A、y=x与y=B、y=x与y=C、y=x与y=x2/xD、y=x与y=例3、如下图的图象分别给出了x与y的对应关系，其中y是x的函数的是〔〕xyoAxyo3、BxyoDxyoC二、一次函数1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。

当b_____时，函数y=____(k____)叫做正比例函数。

2、正比例函数y=kx(k≠0)的图象是过点〔_____〕，(______)的。

3、一次函数y=kx+b(k≠0)的图象是过点〔0，___),〔____，0)的__________。

4.一次函数y=kx+b的图象是一条直线，其中k确定直线性，b确定直线与轴的交点位置.k和b确定了直线所在的象限,k0时，图象必过象限 4、；k0时，图象必过象限；b0,b0时，图象过象限;k0,b0时，图象过象限;k0k0B0B.yx2时，y1y2，则m的范围是11、直线y=3x+b与y轴的交点的纵坐标为-2，则这条直线肯定不过象限12、一次函数y=(m2-3)x-1和y=(m+2)x+(m2-3)的图像与y轴分别交于P，Q两点，若P、Q点关于x轴对称，则m=。

一次函数的图像和性质导学案班级：姓名：一、学习目标：1、会选取两个适当的点画一次函数的图像2、理解一次函数中k，b对函数图象的影响，掌握一次函数的性质。

二、重点难点：重点：通过画一次函数图像探究得出一次函数的性质难点：引导学生用数形结合法探究得出一次函数的性质。

三、学习过程：(一〕、复习、回忆：1.怎样画一次函数的图像？2.正比例函数的图像是什么形状？有哪些性质？① k＞0时， y随x的增大而_________，这时函数的图像从左到右_______；图象经过第_________象限② k＜O时， y随x的增大而_______ ，这时函数的图像从左到右_______.图象经过第__________象限(二〕、自主学习,合作探究：1、在同一直角坐标系内用两点法做出y=x+1，y=2x+1、y=-x+1，y=-2x+1的图像，1题）观察上面四个一次函数的图象，类比正比例函数y=kx(k≠0,k为常数)中 k的正负对图象的影响,探究一次函数y=kx+b (k≠0,k、b为常数)中K的正负对函数的影响，(小组交流分组展示)一次函数y=kx＋b〔k，b为常数，k≠0〕的性质k的正负决定_____________________________；① k＞0时， y随x的增大而_________，这时函数的图像从左到右_______；② k＜O时， y随x的增大而_______ ，这时函数的图像从左到右_______.2、在同一直角坐标系内用两点法做出y=x+1， y=x-1、y=-2x+1，y=-2x-1的图像， x ......y=x+1y=x-1y=-2x+1y=-2x-1观察上面四个一次函数的图象，探究一次函数y=kx+b (k≠0,k、b为常数)中b 的正负对函数的影响，(小组交流分组展示)b的正、负决定________________________；①当b＞0时，__________________________________②当b＜0时，___________________________________3,：探究K、b对函数y=kx+b的图象位置的影响如图〔l〕所示，当k＞0，b＞0时，直线经过第____________象限；y随x 的增大而_________1题）如图〔2〕所示，当k ＞0，b ＜O 时，直线经过第_____________象限. y 随x 的增大而_________如图〔3〕所示， 当k ﹤O ，b ＞0时，直线经过第____________象限； y 随x 的增大而_________如图〔4〕所示，当k ﹤O ，b ﹤O 时，直线经过第_____________象限, y 随x 的增大而_________三，当堂训练1、有以下函数：①y=2x+1,②y=-3x+4,③y=,④y=x-6;其中过原点的直线是________；函数y 随x 的增大而增大的是__________；函数y 随x 的增大而减小的是___________；图象在第一、二、三象限的是________。

教学课题一次函数综合复习--导学案教学目标考点分析1、掌握一次函数、正比例函数的概念、图象及其性质、表达式的求法；2、掌握一次函数及其图象的应用；3、掌握一次函数关于坐标轴及原点对称后的一次函数表达式。

重点难点重点：一次函数、正比例函数的概念、图象及其性质、表达式的求法；难点：一次函数及其图象的应用，关于坐标轴及原点对称后的一次函数表达式求法。

教学方法讲练结合法、启发式教学教学过程知识要点梳理1、一次函数的定义一次函数的一般形式：y=kx+b (k ,b为常数k≠0)当b=0时y=kx (k为常数k≠0）也叫正比例函数。

思考：y=(m－1)X 是一次函数，则m=___________2、一次函数的图象与性质（1）一次函数y=kx+b (k ,b为常数k≠0) 的图象是一条直线，与x轴的交点是______,（2）与y轴的交点是_______思考：画一次函数图象的常用方法？如何画y=2x+3的图像？（2）正比例函数y=kx (k为常数k≠0）的图象是经过点_______和（1，k）的一条直线。

（3）一次函数y=kx+b (k ,b为常数k≠0)的性质：当k＞0时，图象过_______象限，y随x的增大而______当k＜0时，图象过_______象限，y随x的增大而_____当b＞0时,图象与y轴交于_____半轴, 当b＜0时，图象与y轴交于_____半轴, 当b=0时呢？3、一次函数解析式的求法：常用方法：待定系数法一、选择题1、下列函数关系中表示一次函数的有（）①12+=xy②xy1=③xxy-+=21④ts60=⑤xy25100-=A.1个B.2个C.3个D.4个2、下列函数中，图象经过原点的为( )A．y=5x+1 B．y=-5x-1 C．y=-5xD．y=51-x3、下列各函数中，y是x的正比例函数的是（）A、y=3x2B、y=3xC、y=3xD、y=113x+4、下列语句不正确的是A、所有的正比例函数都是一次函数B、一次函数的一般形式是y=kx+bC、正比例函数和一次函数的图象都是直线D、正比例函数的图象是一条过原点的直线5．下列函数（1）y=2xπ (2)y=2x-1 (3)y=1x(4)y=2-1－3x (5)y=12-x中，是一次函数的有（）A、 4个 B、 3个 C、 2个 D、 1个6．点P关于x轴的对称点1P的坐标是（4，－8），则P点关于原点的对称点2P的坐标是（）A、（－4，－8）B、（4，8）C、（－4，8）D、（4，－8）1O OO O7．下面哪个点不在函数32+-=x y 的图像上（ ）A 、（-5，13）B 、（0.5，2）C 、（3，0）D 、（1，1） 8．下面函数图象不经过第二象限的为 （ ）(A) y=3x+2 (B) y=3x －2 (C) y=－3x+2 (D) y=－3x －2 9．已知P （x ，y ）在第四象限，且|x|=3，|y|=5，则P 点坐标为（ ） A 、 （3，5） B 、 （-3，5） C 、 （3，-5） D 、 （-3，-5） 10、若y=(m-2)x+(m 2-4)是正比例函数，则m 的取值是A 、2B 、-2C 、±2D 、任意实数 11、y=28(3)m m x--是正比例函数，则m 的值为 （ ）A 、±3B 、3C 、﹣3D 、任意实数 12、若23y x b =+-是正比例函数，则b 的值是 （ ）A. 0B.23C. 23-D. 32- 13、下列给出的四个点中，不在直线y ＝2x-3上的是 （ ）A.（1， -1）B.（0， -3）C.（2， 1）D.（-1，5） 14、直线b kx y +=经过A(0,2)和B(3,0)两点,那么这个一次函数关系式是( )(A)32+=x y (B)232+-=x y (C)23+=x y (D)1-=x y15、下列函数（1）y=πx (2)y=2x-1 (3)y=1x (4)y=2-1-3x (5)y=x 2-1中，是一次函数的有（ ）（A ）4个 （B ）3个 （C ）2个 （D ）1个16、 一次函数b ax y -=中，0,0><b a ，则它的图像可能是（ ）17、如图，线段AB 对应的函数表达式为（ ） A ．y=-32x+2 B ．y=-23x+2 C ．y=-23x+2（0≤x ≤3） D ．y=-23x+20（0<x<3）18、若m ＜0, n ＞0, 则一次函数y=mx －n 的图象不经过 （ ）A.第一象限B. 第二象限C.第三象限D.第四象限 19、已知函数y ＝3x +1，当自变量增加m 时，相应的函数值增加（ ） Ａ．3m +1 Ｂ．3m Ｃ．m Ｄ．3m －120下面图象中，关于x 的一次函数y ＝－mx －(m －3)的图象不可能是( ) 21、 一次函数b kx y +=与k bx y +=在同一坐标系中的图象大致是 ( )yyyy22、一次函数y=ax+b ，ab ＜0，则其大致图象正确的是（ ）23、一次函数y ＝kx ＋b 的图象经过(m ，1)、(－1，m)，其中m>1，则k 、b ( ) A ．k>0且b<0 B ．k>0且b>0 C ．k<0且b<0 D ．k<0且b>024、两条直线y 1＝ax ＋b 与y 2＝bx ＋a 在同一坐标系中的图象可能是下图中的 ( )二、填空题25、在函数① y=2x ②y=－3x+1 ③ y= x 2中， x 是自变量， y 是x 的函数， 一次函数有_______ 正比例函数有______, 26.某函数具有下列两条性质（1）它的图像是经过原点（0，0）的一条直线；（2）y 的值随x 值的增大而增大。

七年级第六章一次函数的图像和性质一、知识梳理：1.一次函数与正比例函数的概念形如的函数，叫做x的一次函数。

当b 时,一次函数也叫做正比例函数. k叫做比例系数。

对应练习:1.已知函数y=(m-3)xm-1+5，当m= 时，y是x的一次函数；2.已知函数y=（a+3）x-a+1为正比例函数，则a= 。

3.要使y=(m－2)xn－1+n是关于x的一次函数,m,n应满足 .二、直线与坐标轴交点问题：一次函数y=kx+b的图象与x轴交点的特点是：一次函数y=kx+b的图象与y轴交点的特点是：对应练习:1.直线y=2x-4与x轴的交点坐标是________，和y轴的交点坐标是________2.直线y=x-3与直线y=-5x+b都交y轴上同一点，则b的值为 _________三、一次函数y=kx+b的图象与性质：⑴正比例函数y=kx(k≠0)的图像是一条经过原点（0,0）和（1,k）的一条直线；一次函数y=kx+b(k≠0) 的图像是一条经和的一条直线。

⑵一次函数y=kx+b(k≠0) 的图像、性质与k、b的关系如下表所示：对应练习：1.在一次函数y=（2﹣k）x+1中，y随x的增大而增大，则k的取值范围为2.若一次函数y=kx+1（k为常数，k≠0）的图象经过第一、二、三象限，则的取值范围是D用待定系数法求函数表达式的一般步骤为：（1）设；（2）代；（3）解；（4）答。

1.已知一次函数的图象经过点(3,2)与（4,-3）.求这个一次函数的解析式．2.正比例函数经过点（-3,9），求此函数解析式.3.求下图中直线的函数表达式4.若y-2与x-2成正比例，当x=-2时,y=4,则x=_________时,y = -4。

五.一次函数与一次方程（组）和不等式（组）的关系：⑴当一次函数y=kx+b(k≠0)的值y=0时，相应自变量的值即为方程的解；⑵两个一次函数1122y k x b y k x b=+=+与的交点坐标就是他们所对应的的解对应练习：1. 如图，是在同一坐标系内作出的一次函数y1、y2的图象l1、l2，设y1＝k1x＋b1，y2＝k2x＋b2，则方程组⎩⎪⎨⎪⎧y1＝k1x＋b1y2＝k2x＋b2的解是_______.A、⎩⎪⎨⎪⎧x＝－2y＝2B、⎩⎪⎨⎪⎧x＝－2y＝3C、⎩⎪⎨⎪⎧x＝－3y＝3D、⎩⎪⎨⎪⎧x＝－3y＝4六、直线11bxky+=（01≠k）与22bxky+=（02≠k）的位置关系（1）两直线平行⇔21kk=且21bb≠（2）两直线相交⇔21kk≠（3）两直线重合⇔21kk=且21bb=（4）两直线垂直⇔121-=kk对应练习：1、直线y=kx+b与直线y=5-4x平行，且与直线y=-3(x-6)相交，交点在y轴上，求此直线解析式。

中考第一轮复习《一次函数》导学案复习目标 ：1. 清楚一次函数的意义及其图像的性质；会利用函数图象解决实际问题； 2．会求一次函数的解析式；3．理解一次函数与一元一次方程、一元一次不等式以及二元一次方程组的关系.复习重点:掌握一次函数的图象及性质，会利用待定系数法求一次函数的解析式．复习难点:1． 会利用函数图象解决实际问题．2． 理解一次函数与一元一次方程、一元一次不等式以及二元一次方程组的关系．数学思想方法：数形结合的思想方法，转化的思想方法，函数与方程的思想复习过程:一． 自主复习（知识梳理）1．正比例函数的一般形式是y=kx(k≠0)，一次函数的一般形式是y=kx+b(k≠0). 2. 一次函数y kx b =+的图象是经过（kb-，0）和（0，b ）两点的一条直线. 3. 一次函数y kx b =+的图象与性质4. 如果要求两条直线的交点坐标，你会采用的方法是 .5. 如果两条直线y =k 1x +b 1和y =k 2x +b 2平行，可以得到 .6. 求一次函数的解析式： （1）、设函数解析式为 （2）、代入已知两点的坐标或者x,y 的两组对应值，得到 （3）、解 （4）、写出函数解析式。

7. 求一次函数的图象与坐标轴围成的三角形或四边形的面积；一次函数在解决实际问题中的应用；用函数观点看方程（组）和不等式。

二．合作交流k ＞0，b ＞0k ＞0，b ＜0k ＜0，b ＞01．（2008重庆）如图，在直角梯形ABCD 中，DC ∥AB ，∠A=90°，AB=28cm ，DC=24cm ，AD=4cm ，点M 从点D 出发，以1cm/s 的速度向点C 运动，点N 从点B 同时出发，以2cm/s 的速度向点A 运动，当其中一个动点到达端点停止运动时，另一个动点也随之停止运动.则四边形AMND 的面积y （cm 2）与两动点运动的时间t （s ）的函数图象大致是（ ）2.（2007重庆） 已知，如图：在平面直角坐标系中，O 为坐标原点，四边形OABC 是矩形，点A 、C 的坐标分别为A （10，0）、C （0，4），点D 是OA 的中点，点P 在BC 边上运动，当△ODP 是腰长为5的等腰三角形时，点P 的坐标为 。

一次函数的复习(一）【学习目标】1.会画一次函数的图像，掌握它的性质2.会求一次函数图像与坐标轴的交点3.会根据图像利用待定系数法求解析式以及看图像解决问题。

【学习重难点】利用一次函数的图象和性质解题【课前自习】1.一次函数的一般形式是___________________________正比例函数的一般形式是________________________,2.画一次函数图像有三步:_______、________、________.3.已知一次函数y=2x+2,（1）比例系数K=_____,b=________(2) 在给出的直角坐标系中画出它的图像。

(3)从图像中可以看出它与 x 轴的交点坐标为______与y 轴的交点坐标为___________思考：你能找到求图像与坐标轴交点的方法吗？_______________________________________________（4）利用图像求出当22≤-x π时，y 的范围为________(5) 利用图像求出不等式022φ+x 的解为___________.若点P(b-1,b+1)在其上，求b 的值。

4. 已知一次函数)4()22(m x m y -+-=（m 为常数）（1）、当m 满足什么条件时，一次函数经过原点。

______________（2）、当m 满足什么条件时，y 随x 的增大而减小. _________________ 你还能提出什么问题来求m 的范围。

5.已知某一次函数图像如图所示，求出它的解析式。

思考：你认为第2,3题都用到了什么数学方法?______________.已知一次函数y = kx + b 关系满足下表(x 为自变量)， x…-2 -1 0 1 2 y …12 9 6 3 0则由表格可以看到，当x______时，0φb kx +在这一题中，我还可以知道：增减性，两点之间的距离，与坐标轴围成的三角形的面积，o 到直线的距离，通过平移过原点。

《一次函数》复习导学案复习目标：1、通过知识回顾和习题练习进一步明确一次函数和正比例函数的概念，熟练的应用待定系数法求出一次函数解析式。

2、通过知识表格，习题练习进一步明确一次函数的图象与性质，会熟练的应用性质去解决一些简单的问题。

3、通过知识表格，函数图象和习题练习进一步明确一次函数与一元一次方程、二元一次方程（组）和一元一次不等式组之间的关系，熟练的运用它们之间的关系解决一些简单的问题。

复习重点：1、熟练运用待定系数法求一次函数解析式。

2、熟练的运用一次函数的图像与性质去解决一些简单的问题。

复习难点熟练的运用一次函数与一元一次方程、二元一次方程（组）和一元一次不等式组之间的关系去解决一些简单数学问题。

学习过程知识点一：一次函数的概念与待定系数法求一次函数解析式。

（一）一次函数、正比例函数的概念形如________________________的函数叫做x 的一次函数，其中k 与b 是_______。

特别的，当b=0时，一次函数y=kx 也叫做________________，k 叫做_______________。

对应练习：1、下列语句不正确的是 （ ） A 、所有的正比例函数都是一次函数 B 、一次函数的一般形式是y=kx+bC 、正比例函数和一次函数的图象都是直线D 、正比例函数的图象是一条过原点的直线2、下列函数中，①y=31x ②y=-2+5x ③y=-x 1 ④ y=22x +2 ⑤y=32x-2⑥y=2∏x ，______________是一次函数；_______________正比例函数。

（只写序号） 3、当m=_____时，函数y=31m 2x -1是一次函数。

A 、1 B 、0 C 、-1 D 、-214、若y=(m-2)x+(2m -4)是正比例函数，则m 的取值是 （ ）A 、2B 、-2C 、±2D 、任意实数 （二）用待定系数法求一次函数解析式。