甘肃省庆阳二中2018-2019学年高二下学期第一次月考数学(文)试卷 Word版缺答案

答案）庆阳二中2018-2019学年度第二学期高二英语第一次月考卷命题人：杨 洁审题人：窦 洁第I 卷（选择题，共100分）第一部分：听力（共两节，满分30分） 第一节（共5小题，每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的 佳选项，并标在试卷的相应位置。

听完每段对话后，你都有 和阅读下一小题。

每段对话仅读一遍。

1. What is the woma n going to do this evening? A. Go to dinner. B. Visit her sister.C.Go to the airport.2. What does the woma n mea n?A. The man ager is sure to be at the office.B. She is won deri ng where to go.C. She ' d like to give her help.3. How ofte n did the woma n take the medici ne? A. Four times a day. B. Twice a day.4. Why doesn ' t the man take the suit? A. It is too big.B. It doesn' t fit him.5. What can be the result of the talk?A. The woma n can be off on Friday.B. The woma n should work on Friday.C. Noresult.第二节（共15小题，每小题1.5分，满分22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A 、B 、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各 个小题，每小题 5秒钟；听完后，各小题将给出 5秒钟的作答时间。

庆阳二中2018-2019学年度第一学期高二语文第三次月考卷注意事项：1.本试题命题范围：语文必修五、选修一2.满分150分，考试时间150分钟3.答题前填写好自己的姓名、班级、考号等信息4.请将答案正确填写在答题卡上一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1~3题。

中国书画作伪历史十分悠久，始于魏晋南北朝，隋唐五代已形成风气，宋时形成我国历史上第一个作伪高潮，元代稍有衰落，尤至明代达到顶峰。

明代书画作伪比之于前代，在手法和形式上又有新发展，除了仿制名家之作外，还有如挖掉旧款改署新款、在本无款的作品上添上名人款、赝品配真题跋等，几乎集中了我们现在已知的全部作伪方法。

但归纳起来不外乎摹、临、仿、造及对真迹改头换面等手段。

作伪的手法各种各样，一时古今名家之赝品充斥泛滥。

较普遍的一种手法是把原画改款、添款，也就是通常所说的“改头换面”。

有些作伪者，把明代院体画家作品的名款挖去，改成宋代某画家之名款，冒充宋画出售。

还有明代的一幅山水画《阔渚晴峰图》轴，此画原为宣德宫廷画家师法郭熙之作，为后人挖去原款，在右下角添上郭熙的伪款，企图当成北宋名家的山水画。

又如，明宫廷画师朱瑞的一幅人物故事画轴，原画左边中上部有“朱瑞”二字款，下面有印章二方。

作伪者将朱瑞二字挖去，印章也刮得模糊不清，把标签写成了宋代马远的《弘衣渡口图》。

但经过认真鉴定比较，看出其画法风格异于马远，时代风格又不相符，详细观察，发现画上方中部有“钦赐一樵图书”朱文方印，此乃皇帝钦赐朱瑞的专用印章，他人不能假借。

对于此种方法作伪，时人屡试不爽。

清顾复曾谈到明院体浙派画家，其中三人的画被改成宋人画的情况：“迩来三人之笔寥寥，说者谓洗去名款，竟作宋人款者，强半三人笔也。

”他就曾见到吕纪的《杏花双雀图》被改作宋代的黄筌款。

后来明代院体画传世稀少，甚至一些宫廷名手之作竟没有一件流传下来，究其原因，或许与这种改头换面，明画冒充宋画的作伪因素有很大关系。

庆阳二中2018-2019学年度第一学期高一数学第一次月考卷考试时间：120分钟注意事项：1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上。

一、选择题(每小题5分,共60分)1.设集合{}{}0,2,4,6,8,10,4,8A B ==,则A C B = ( ) A. {}4,8B. {}0,2,6C. {}0,2,6,10D.{}0,2,4,6,8,102.集合{|24}x N x +∈-<用列举法可表示为( ) A. {}0,1,2,3,4B. {}1,2,3,4C. {}0,1,2,3,4,5D.{}1,2,3,4,53.设集合{}{}21,2,4,40A B x x x m ==-+=,若{}1A B ⋂=,则B = ( ) A. {}1,3-B. {}1,0C. {}1,3D.{}1,54.下列命题:①空集没有子集; ②任何集合至少有两个子集; ③空集是任何集合的真子集; ④若,则A ≠∅,其中正确的有( ) A.0个B.1个C.2个D.3个5.已知集合{},,S a b c =中的三个元素可构成ABC ∆的三条边长,那么ABC ∆—定不是( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形6.集合(){},23|x y y x =+表示( )A.方程23y x =+B.点(),x yC.函数23y x =+图象上的所有点组成的集合D.平面直角坐标系中的所有点组成的集合7.已知集合{}{}233,||2,A x x x B x x =-<=≥则( ) A. A B ⊆B. B A ⊆C. R A C B ⊆D.B C A ⊇R8.满足的集合 P 的个数是 ( )A.2B.3C.4D.59.已知集合},B={1, m } ,A B=A, 则m =( )A.0B.0或3C.1D.1或310.下列函数中,在区间()0,+∞上是增函数的是( ) A. 11y x =+ B. 21y x =-C. y x =-D.23y x x =-11.函数1()f x x x=-的图象关于( ) A. y 轴对称B.直线y x =-对称C.坐标原点对称D.直线y x =对称12.一个面积为2100cm 的等腰梯形,上底长为xcm ,下底长为上底长的3倍,则把它的高y 表示成x 的函数为( ) A. ()500y x x =>B. ()1000y x x =>C. ()500y x x=> D.()1000y x x=> 二、填空题(每小题5分,共20分) 13.集合{}1,0,1-共有__________个子集.14.已知集合{}{}1,1,|10A B x ax =-=+=,若B A ⊆,则实数a 的取值集合为__________.15.已知()f x 为奇函数, ()()6,(1)3g x f x g =+-=,则(1)f =__________.16.已知23(0)()1(0)4(0)x x f x x x x ⎧+>⎪==⎨⎪+<⎩,则()()()4f f f -=__________.三、解答题(第17题10分;第18～22题每小题12分,共70分) 17.已知函数()12x f x =-. (1).求函数()f x 的定义域 (2).求()()13f f +-的值(3).求()1f a +的值(其中4a >-且1a ≠)18.已知函数()f x 为R 上的奇函数,且当0x >时, ()() 1?3?f x x x =-,试求函数()f x 的解析式.19.设定义在上的奇函数在区间上单调递减,若,求实数的取值范围.20.已知函数()mf x x x=+的图像过点(1,5)P . (1).求实数m 的值,并证明函数()f x 是奇函数;(2).利用单调性定义证明()f x 在区间[)2,+∞上是增函数.21.已知函数()222,[5,5]f x x ax x =++∈-.(1).当1a =-时,求函数的最大值和最小值;(2) 函数()y f x =在区间[]5,5-上是单调函数,求实数a 的取值范围.22.已知函数()221x f x x =+(1).分别求()122f f ⎛⎫+⎪⎝⎭, ()133f f ⎛⎫+ ⎪⎝⎭, ()144f f ⎛⎫+ ⎪⎝⎭的值; (2).归纳猜想一般性结论,并给出证明2018—2019第一学期高一数学参考答案一、选择题 1.答案：C解析：由补集的概念,得{}0,2,6,10A C B =,选C 2.答案：D解析：{|24}{|6}{1,2,3,4,5}.x N x x N x ++∈-<=∈<= 3.答案：C解析：∵{}1A B ⋂=∴1B ∈∴21410m -⨯+=∴3m =∵方程2430x x -+=的解为121,3x x ==∴{}1,3B =,故选C4.答案：B解析：因为①空集没有子集；错误②任何集合至少有两个子集；那么空集只有本身这一个子集， ③空集是任何集合的真子集；应该是非空集合的真子集，错误， ④若,则A ≠∅，成立，选B5.答案：D解析：因为集合中的元素具有互异性,可知a ,b ,c 任何两个都不可能相等,故选D 。

甘肃省庆阳二中2018-2019学年高二上学期第三次月考数学（理）试卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息；2．请将答案正确填写在答题卡上。

第1卷（选择题）一、选择题。

（每小题5分，共60分）1.双曲线的顶点到其渐近线的距离等于（）A. B. C. D.【答案】C【解析】试题分析：双曲线的顶点在其实轴上，而其实轴为轴，所以令，可得其两顶点为，而双曲线的渐近线为，利用点到直线的距离公式可求得顶点到渐近线的距离为所以本题正确选项为C.考点：双曲线的顶点，渐近线，点到直线的距离.2.已知，是椭圆的两个焦点，过的直线交椭圆于，两点，若的周长为，则椭圆方程为（）A. B.C. D.【答案】A【解析】因为的周长为，所以是椭圆的两焦点，椭圆方程为，故选A.3.已知中心在原点的双曲线C的右焦点为F(3,0)，离心率等于，则C的方程是( )A. B.C. D.【答案】B【解析】由题意可知，，，故双曲线的方程为，故选B.4.若,，且与的夹角为钝角,则的取值范围是( )A. B. C. D.【答案】B【解析】【分析】空间向量数量积等于各个坐标相乘之和，建立不等式，得到关于x的范围，即可。

【详解】,解得,故选B。

【点睛】本道题考查了空间数量积运算法则，较容易，对应坐标相乘再相加，建立不等式，即可。

5.如右图:在平行六面体中，为AC与BD的交点，若=，=，=.则下列向量中与相等的向量是 ( )A. B.C. D.【答案】A【解析】【分析】由题意可得化简得到结果．【详解】由题意可得故答案为：A【点睛】本题主要考查向量的加法减法法则,意在考查学生对这些知识的掌握水平和分析推理能力.6.双曲线（，）的左、右焦点分别是，过作倾斜角为的直线交双曲线右支于点，若垂直于轴，则双曲线的离心率为（）A. B. C. D.【答案】B【解析】试题分析：设，易求M坐标为，在三角形中，即，由得，答案选B. 考点：双曲线的性质7.已知点为抛物线上的动点,点在轴上的射影是,点坐标为,则的最小值是( )A. B. C. D.【答案】C【解析】【分析】本道题目通过绘图发现,要求最小值,转化为两点间距离最短,即可得出答案.【详解】如图,故,故最短距离为,,所以,所以,故选C.【点睛】本道题目考查了抛物线的性质,可以利用点P到准线距离,转化为两点间距离最短问题.8.设分别是椭圆，的左右焦点，过的直线与相交于两点，且成等差数列，则的长为（）A. B. C. D.【答案】C【解析】【分析】利用椭圆性质和等差数列性质，建立等式，即可计算的长。

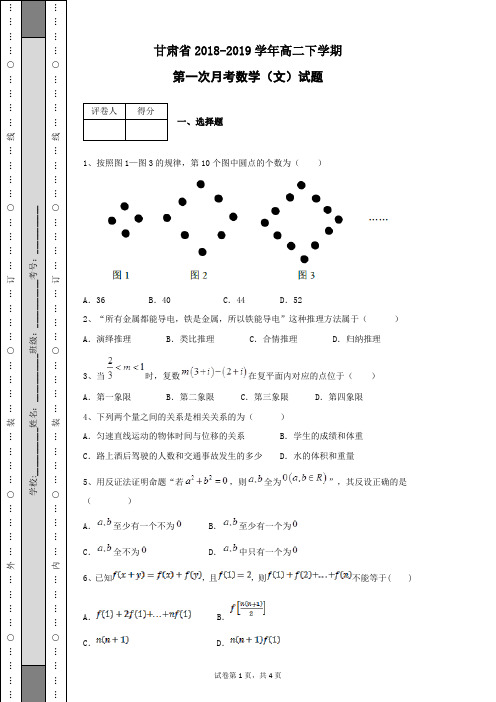
甘肃省2018-2019学年高二下学期第一次月考数学（文）试题一、选择题1、按照图1—图3的规律，第10个图中圆点的个数为（ ）A ．36B ．40C ．44D ．522、“所有金属都能导电，铁是金属，所以铁能导电”这种推理方法属于（ ） A ．演绎推理 B ．类比推理 C ．合情推理 D ．归纳推理3、当时，复数在复平面内对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 4、下列两个量之间的关系是相关关系的为（ ）A ．匀速直线运动的物体时间与位移的关系B ．学生的成绩和体重C ．路上酒后驾驶的人数和交通事故发生的多少D ．水的体积和重量 5、用反证法证明命题“若，则全为”，其反设正确的是（ ） A ．至少有一个不为 B ．至少有一个为 C ．全不为 D ．中只有一个为 6、已知，且，则不能等于( )A ．B ．C ．D ．7、已知呈线性相关关系的变量之间的关系如下表所示，则回归直线一定过点( ) A.B.C. D.8、复数的共轭复数是（ ）A ．B ．C ．D ．9、若复数为纯虚数（为虚数单位），则实数的值是（ ）A ．B ．或 C ．或D ．10、（ ） A ．B ．C ．D ．二、填空题11、已知，若，则_________。

12、若三角形内切圆半径为， 三边长分别为， 则三角形的面积；根据类比的思想，若四面体的内切球半径为，四个面的面积分别为，则四面体的体积为_________。

13、设复数 的模为，则________。

14、回归直线方程为，则时，的估计值为________。

三、解答题15、某种产品的广告费用支出（万元）与销售额（万元）之间有如下的对应数据：(1)画出散点图；(2)求回归直线方程；(3)据此估计广告费用为9万元时，销售收入的值。

参考公式：回归直线的方程，其中.16、用反证法证明：如果，那么。

17、甲乙两个班级均为40人，进行一门考试后，按学生考试成绩及 格与不及格进行统计，甲班及格人数为36人，乙班及格人数为24人． (1) 根据以上数据建立一个的列联表；(2) 试判断成绩与班级是否有关？参考公式：，其中18、求证：(1)；(2)。

甘肃省庆阳二中2018-2019学年高一语文下学期第一次月考试题（无答案）满分：150分考试时间：150分钟注意事项：1.本试卷命题范围：必修三第一、二单元2.满分150分，考试时间150分钟3.答题前填写好自己的姓名、班级、考号等信息4.请将答案正确填写在答题卡上一、现代文阅读(35分)（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

人类社会存在于一定的时间和空间中。

空间是固定、具体的，而时间则需要通过某种办法加以测定和标识。

人们测定和标识时间的参照最初是感知和观察到的物候和气候的变化。

什么时间月圆了、月缺了，什么时候气候转暖，种子发芽、庄稼生长了……这些变化就被我们的先人用来作为早期测定时间的依据。

时间是人类用以描述物质运动或事件发生过程的一个参数。

人们为了更准确地衡量、计算、记录时间，就要进一步选择具有普适性、恒久性和周期循环性的参照物。

于是，太阳、月亮、谷物的成熟期等，就成为了优选的参照系。

人类很早就学会观察日月星辰，用以测量时间。

大约在纪元前五千年，人们利用指时杆观察日影。

纪元前11世纪，已经有了关于日晷和漏壶的记载。

详细记录时间的钟表的发明，大约是13世纪下半叶的事情了。

协调和规范各民族或国家群体内部公共时间制度的，是各国的特定历法。

世界现行历法最为普遍的有：以地球围绕太阳旋转的周期作为参照物的太阳历或称阳历，我国当今使用的公历就是这一历法，作为我们传统时间制度组成部分的二十四节气的制定，实质上也是以地球围绕太阳旋转的周期作为参照物的；还有以月球围绕地球旋转周期为参照物的太阴历或称阴历；我国自夏代开始使用、后经汉武帝太初元年修订的兼顾太阳历和太阴历确定的历法是阴阳合历，即所谓“夏历”“农历”，或俗称的“阴历”“旧历”。

这样说来，我们的夏历是既参照了对月亮的观察，又参照了对太阳的观察而制定的。

我们的民间传统节日体系，例如春节、元宵节等都是依据过去千百年来通行的阴阳合历而确定的。

甘肃省庆阳二中2018-2019学年高一数学下学期第一次月考试题（无答案）考试时间：120分钟注意事项：1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上。

一、单项选择（每小题5分，共60分） 1.以下赋值语句书写正确的是（ ） A ．2a =B ．1a a =+C ．2a b *=D ．1a a +=2.(程序如图）程序的输出结果为（ ） A. 3，4 B. 7，7 C. 7，8D. 7，113.(1)某学校为了了解2017年高考数学学科的考试成绩，在高考后对1 200名学生进行抽样调查，其中文科200名考生，理科800名考生，艺术和体育类考生共200名，从中抽取120名考生作为样本．(2)从10题与方法配对合理的是（ ） A. (1)Ⅲ，(2)Ⅰ B. (1)Ⅰ，(2)C. (1)Ⅱ，(2)ⅠD. (1)Ⅲ，(2)Ⅱ4.阅读图1的程序框图. 若输入5n =, 则输出k 的值为（ A ．2 B ．3 C ．4 D ．55.三位八进制数能表示的最大十进制数是（ ） A. 399B.999C.511D. 5996.某学校高一、高二、高三年级的学生人数分别为1800，1800,2400人，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高三年级抽取的学生人数为 ( ) A.25 B.30C.15D.207.学校为了解学生在课外读物方面的支出情况,抽取了n 个同学进行调查,结果显示这些同学的支出都在[10,50)(单 位:元),其中支出在[)30,50(单位:元)的同学有67人,其频率分布直方图如右图所示,则n 的值为（ ） A ．100B ．120C ．130D ．3908.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50), [50,60), [60,70), [70,80), [80,90), [90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为（ ） A ．588B ．480C ．450D ．1209.在样本频率分布直方图中，一共有n 个小矩形，若中间一个小矩形的面积等于其余n －1个小矩形面积之和的14，且样本容量为160，则中间一组的频数是（ ） A. 32B. 20C.40D.2510.宋元时期数学名著《算数启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等. 如图是源于其思想的一个程序框图，若输入的,a b 分别为5,2，则输出的n =（ ） A. 2B. 3C. 4D. 511.读下边的程序，当输出的y 的范围大于1时，则输入的x 值的取值范围是( )A ．(－∞，－1)B ．(1，＋∞)C ．(－∞，－1)∪(1，＋∞)D ．(－∞，0)∪(0，＋∞)12.执行如图所示的程序框图后，输出的值为4，则P 的取值范围是（ ）A ．715816P <≤ B ．1516P > C ．715816P ≤<D ．3748P <≤二、填空题（每小题5分，共20分）13.261和319的最大公约数是_________________.14.把“五进制”数转化为“七进制”数： ()5321=__________()715.某人连续五周内收到的包裹数分别为3，2，5，1，4，则这5个数据的标准差为 ．16.阅读下边的程序框图，若输出S 的值为－14，则判断框内可填写三、解答题（17题10分，其余各12分，共60分）17.用秦九韶算法求多项式x x x x x x x x f ++++++=234567234567)( 当3=x 时的值。

庆阳二中2017-2018学年度第一学期高二数学第一次月考卷考试范围：必修5第一章，第二章考试时间：100分钟注意事项：1．答题前填写好自己的姓名、班级、考号等信息；2．请将答案正确填写在答题卡上第1卷一、选择题：1. 若为钝角三角形,三边长分别为，则的取值范围是( )A. B.C. D.【答案】D2. 在中,，那么满足条件的( )A. 有一个B. 有两个C. 不存在D. 不能确定【答案】C【解析】由正弦定理可得：，满足条件的不存在，满足条件的不存在，故选C.3. 已知数列,前项和，第项满足，则( )A. B. C. D.【答案】B【解析】略4. 已知数列的前项和，第项满足，则( )A. B. C. D.【解析】当时，；当时，，也适合，，，故选C.5. 一个各项均为正数的等比数列,其任何项都等于后面两项之和,则其公比是( )A. B. C. D.【答案】D【解析】由任何项都等于后面两项之和可得，，解得，故选D.6. 和的等差中项为( )A. B. C. D.【答案】C【解析】设和的等差中项为，，和的等差中项为，故选C.7. 在等差数列中，，则的值是( )A. B. C. D.【答案】A【解析】为等差数列，设首项为，公差为，，①，②由①-②得，即，故选A.【方法点睛】本题主要考查等差数列的通项公式、等差数列的前项和公式，属于中档题. 等差数列基本量的运算是等差数列的一类基本题型，数列中的五个基本量，一般可以“知二求三”，通过列方程组所求问题可以迎刃而解，另外，解等差数列问题要注意应用等差数列的性质（）与前项和的关系，利用整体代换思想解答.8. 已知数列满足，则( )A. B. C. D.【解析】试题分析：由题意得，所以，故此数列的周期为，所以．考点：数列的递推公式．【方法点晴】本题主要考查了数列的递推关系式的应用，其中解答中根据数列的首项和数列的递推关系式，可计算得出的值，着重考查了学生的分析问题和解答问题的能力，以及学生的应变能力和不完全归纳法，可能大部分学生想直接求解数列的通项公式，然后求解，但此法不通，很难入手，属于易错题型．9. 在中,若,则是( )A. 直角三角形B. 等边三角形C. 钝角三角形D. 等腰直角三角形【答案】B【解析】略10. 在等差数列中,，则( )A. B. C. D.【答案】B【解析】试题分析：因为,又因为，所以，故答案D.考点：等差数列通项公式.11. 等差数列的前项和为,如果，那么( )A. B. C. D.【答案】B【解析】试题分析：，又，所以，．故选B．考点：等差数列的前项和．12. 若是等差数列,则下列数列中仍为等差数列的个数有( )①；②；③；④；⑤.A. 个B. 个C. 个D. 个【解析】试题分析：设的公差为,则,;;;．则由等差数列的定义可知①、③、④、⑤仍然是等差数列．考点：等差数列的定义．二、填空题：13. 在中,，且，则_____.【答案】或【解析】由余弦定理：，，，即，解得，或，故答案为或.【思路点睛】本题主要考查余弦定理解三角形，属于简单题.对余弦定理一定要熟记两种形式：（1）；（2），同时还要熟练掌握运用两种形式的条件.另外，在解与三角形、三角函数有关的问题时，还需要记住等特殊角的三角函数值，以便在解题中直接应用.14. 在中,角的对边分别为，已知,则_____.【答案】【解析】由正弦定理：，得，从而，，故答案为.15. 在如下数表中,已知每行、每列中的数都成等差数列,那么位于表中的第行第列的数是_____.【答案】【解析】试题分析：从表格可知，第n行的等差数列的首项为n，公差也为n，根据等差数列的通项公式，其位于第n+1个数是n+(n-1)n= n+n2，所以位于下表中的第n行第n+1列的数是n+n2.考点：等差数列的通项公式，观察与归纳的能力.16. 已知等差数列的公差为,且,,若,则______.【答案】【解析】，即，根据等差数列的性质得时，,故答案为.三、解答题：17. 在公差为的等差数列中,已知,且成等比数列.（1）求；（2）若，求.【答案】（1）或,或；（2）.【解析】试题分析：（1）由已知条件，且成等比数列，列方程求出公差，则通项公式可求；（2）利用（1）中的结论，得到等差数列的前项对于等于，后面的项小于，所以分类讨论求时，两种情况，分别求得的和即可.试题解析：（1）由题意,得,∴,∴或.∴或。

甘肃省庆阳市高二下学期数学月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2019高二上·南宁月考) 已知集合，，则（）A .B .C .D .2. （2分）下列函数中，既是偶函数又在区间上单调递增的函数为（）A .B .C .D .3. （2分） (2019高一上·上海月考) 设 ,则“ ”是“ 且”的（）A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既非充分又非必要条件4. （2分） (2019高一上·峨山期中) 如果二次函数y＝x2+mx+（m+3）有两个不同的零点，则m的取值范围是（）A . ｛-2,6｝B . （-2,6）C . [-2,6]D . (-∞，-2)∩(6，+∞)5. （2分） (2016高一上·黑龙江期中) 设全集为R，函数的定义域为M，则∁RM为（）A . [﹣1，1]B . （﹣1，1）C . （﹣∞，﹣1]∪[1，+∞）D . （﹣∞，﹣1）∪（1，+∞）6. （2分） (2019高一上·辽源期中) 定义在R上的奇函数f(x)，满足f ＝0，且在(0，＋∞)上单调递减，则xf(x)＞0的解集为（）A .B .C .D .7. （2分） (2016高三上·连城期中) 函数f（x）=x3+bx2+cx+d图象如图，则函数的单调递减区间为（）A . （﹣∞，﹣2）B . [3，+∞）C . [﹣2，3]D . [ ）8. （2分） (2020高二下·哈尔滨期末) 为做好社区新冠疫情防控工作，需将四名志愿者分配到甲、乙、丙三个小区开展工作，每个小区至少分配一名志愿者，则不同的分配方案共有（）种A . 36B . 48C . 60D . 169. （2分）设x ， y ， z都是正实数，a＝x＋， b＝y＋， c＝z＋，则a ， b ， c三个数（）．A . 至少有一个不大于2B . 都小于2C . 至少有一个不小于2D . 都大于210. （2分）设函数y=f（x）的定义域为D，若对于任意x1、x2∈D，当x1+x2=2a时，恒有f（x1）+f（x2）=2b，则称点（a，b）为函数y=f（x）图象的对称中心．研究函数f（x）=x+sinπx﹣3的某一个对称中心，并利用对称中心的上述定义，可得到的值为（）A . ﹣4031B . 4031C . ﹣8062D . 806211. （2分） (2018高一上·佛山期末) 已知偶函数在单调递减，则使得成立的的取值范围是（）A .B .C .D .12. （2分）小明站在点观察练车场上匀速行驶的小车的运动情况，小车从点出发的运动轨如图所示.设小明从点开始随动点变化的视角为，练车时间为，则函数的图象大致为（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2018高二下·赣榆期末) 复数（为虚数单位）的模为________.14. （1分）(2017·抚顺模拟) 设函数f（x）= ，则f（3）+f（4）=________．15. （1分）函数f（x）=﹣x3+mx2+1（m≠0）在（0，2）内的极大值为最大值，则m的取值范围是________．16. （1分） (2017高一下·西安期末) 用火柴棒按图的方法搭三角形：按图示的规律搭下去，则所用火柴棒数an 与所搭三角形的个数n之间的关系式可以是________．三、解答题 (共6题；共60分)17. （10分）已知函数f（x）=x2+3x|x﹣a|，其中a∈R．（1）当a=2时，把函数f（x）写成分段函数的形式，并画出函数f（x）的图象；（2）指出a=2时函数f（x）单调区间，并求函数在[1，3]最大值和最小值．18. （10分）(2017·巢湖模拟) 2017年存节期间，某服装超市举办了一次有奖促销活动，消费每超过600 元（含600元），均可抽奖一次，抽奖方案有两种，顾客只能选择其中的一种．方案一：从装有10个形状、大小完全相同的小球（其中红球3个，黑球7个）的抽奖盒中，一次性摸出3个球，其中奖规则为：若摸到3个红球，享受免单优惠；若摸到2个红球，则打6折；若摸到1个红球，则打7折；若没摸到红球，则不打折．方案二：从装有10个形状、大小完全相同的小球（其中红球3个，黑球7个）的抽奖盒中，有放回每次摸取1球，连摸3次，每摸到1次红球，立减200元．（1）若两个顾客均分别消费了 600元，且均选择抽奖方案一，试求两位顾客均享受免单优惠的概率；（2）若某顾客消费恰好满1000元，试从概率的角度比较该顾客选择哪一种抽奖方案更合算．19. （10分） (2015高三上·广州期末) 如图所示，在四棱柱ABCD﹣A1B1C1D1中，底面ABCD是梯形，AD∥BC，侧面ABB1A1为菱形，∠DAB=∠DAA1 ．（1）求证：A1B⊥AD；（2）若AD=AB=2BC，∠A1AB=60°，点D在平面ABB1A1上的射影恰为线段A1B的中点，求平面DCC1D1与平面ABB1A1所成锐二面角的余弦值．20. （10分）(2018·沈阳模拟) 随着移动互联网的发展，与餐饮美食相关的手机APP软件层出不穷为调查某款订餐软件的商家的服务情况，统计了10次订餐“送达时间”，得到茎叶图如下：时间：分钟（1）请计算“送达时间”的平均数与方差；（2）根据茎叶图填写下表：送达时间35分钟以内包括35分钟超过35分钟频数A B频率C D在答题卡上写出A，B，C，D的值；（3）在问的情况下，以频率代替概率现有3个客户应用此软件订餐，求出在35分钟以内包括35分钟收到餐品的人数X的分布列，并求出数学期望．21. （10分） (2020高二下·北京期中) 已知：直线与抛物线（a为常数）交于两点，且抛物线在点A，B处的切线互相垂直．（1）求a的值；（2）求两条切线交点的横坐标（用k表示）．22. （10分）(2020·盐城模拟) 设函数 . （1）若a＝0时，求函数的单调递增区间；（2）若函数在x＝1时取极大值，求实数a的取值范围；（3）设函数的零点个数为m ，试求m的最大值.参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、22-3、。

庆阳二中2018-2019学年度第一学期高二语文第三次月考卷注意事项：1.本试题命题范围：语文必修五、选修一2.满分150分，考试时间150分钟3.答题前填写好自己的姓名、班级、考号等信息4.请将答案正确填写在答题卡上一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1~3题。

中国书画作伪历史十分悠久，始于魏晋南北朝，隋唐五代已形成风气，宋时形成我国历史上第一个作伪高潮，元代稍有衰落，尤至明代达到顶峰。

明代书画作伪比之于前代，在手法和形式上又有新发展，除了仿制名家之作外，还有如挖掉旧款改署新款、在本无款的作品上添上名人款、赝品配真题跋等，几乎集中了我们现在已知的全部作伪方法。

但归纳起来不外乎摹、临、仿、造及对真迹改头换面等手段。

作伪的手法各种各样，一时古今名家之赝品充斥泛滥。

较普遍的一种手法是把原画改款、添款，也就是通常所说的“改头换面”。

有些作伪者，把明代院体画家作品的名款挖去，改成宋代某画家之名款，冒充宋画出售。

还有明代的一幅山水画《阔渚晴峰图》轴，此画原为宣德宫廷画家师法郭熙之作，为后人挖去原款，在右下角添上郭熙的伪款，企图当成北宋名家的山水画。

又如，明宫廷画师朱瑞的一幅人物故事画轴，原画左边中上部有“朱瑞”二字款，下面有印章二方。

作伪者将朱瑞二字挖去，印章也刮得模糊不清，把标签写成了宋代马远的《弘衣渡口图》。

但经过认真鉴定比较，看出其画法风格异于马远，时代风格又不相符，详细观察，发现画上方中部有“钦赐一樵图书”朱文方印，此乃皇帝钦赐朱瑞的专用印章，他人不能假借。

对于此种方法作伪，时人屡试不爽。

清顾复曾谈到明院体浙派画家，其中三人的画被改成宋人画的情况：“迩来三人之笔寥寥，说者谓洗去名款，竟作宋人款者，强半三人笔也。

”他就曾见到吕纪的《杏花双雀图》被改作宋代的黄筌款。

后来明代院体画传世稀少，甚至一些宫廷名手之作竟没有一件流传下来，究其原因，或许与这种改头换面，明画冒充宋画的作伪因素有很大关系。