下载文档原格式
高考数学条件概率知识点高考中，数学是一门重要的科目，而其中又涉及到概率这个重要的数学分支。
在概率中，条件概率是一个重要的概念，它可以帮助我们更好地理解和应用概率。
接下来，我们将深入探讨高考数学中的条件概率知识点。
首先，我们来了解一下条件概率的定义。
条件概率是指在一个条件下发生某一事件的概率。
用数学的语言来描述就是：对于两个事件A和B，已知事件B发生的条件下，事件A发生的概率称为事件A在条件B下的条件概率，记作P(A|B)。
其中，P(A|B)的计算方式为P(A|B)= P(AB)/P(B)。
这里P(AB)表示事件A和B同时发生的概率，P(B)表示事件B发生的概率。
条件概率常常用于解决含有条件约束的概率问题。
举个例子来说，假设有一个罐子里装有两种颜色的球，红球和白球。
已知罐子里有20个球，其中10个红球，10个白球。
现在从罐子中随机抽取一个球，已知这个球是红球，问该球是白球的概率是多少？对于这个问题，首先我们要明确已知条件：已知抽取的球是红球。
设事件A表示抽取的球是白球，事件B表示抽取的球是红球。
现在我们要求的是事件A在事件B条件下发生的概率P(A|B)。
根据条件概率的定义，我们可以得到P(A|B) = P(AB)/P(B)。
进一步分析，P(AB)表示抽取的球既是红球又是白球的概率，显然是不存在的，所以P(AB) = 0。
又因为已知抽取的球是红球，所以P(B) = 10/20 = 1/2。
因此，根据条件概率的计算公式，可以得到P(A|B) = 0/(1/2) = 0。
因此，抽取的球是红球的条件下，该球是白球的概率为0。
除了条件概率的计算，还有一些与条件概率相关的概念和定理。
其中一个重要的概念是独立事件。
如果两个事件A和B满足P(A|B) =P(A)，或者等价地说P(B|A) = P(B)，那么我们称事件A和事件B是相互独立的。
简而言之，两个事件满足条件概率的定义，且条件概率等于事件自身的概率，那么这两个事件就是相互独立的。
高三条件概率知识点总结高中数学中的概率是一个重要的章节，而条件概率是其中的一个核心知识点。
在高三阶段，学生们需要对条件概率进行全面的学习和理解。
本文将从条件概率的定义和性质、条件概率的计算方法、条件概率的应用等方面对这一知识点进行总结和归纳。
一、条件概率的定义和性质条件概率是指在事件B已经发生的条件下，事件A发生的概率。
用数学符号表示为P(A|B)。
条件概率的定义和性质需要我们对概率的基本概念有一定的了解。
条件概率的定义可以表示为：P(A|B) = P(AB) / P(B)。
其中，P(B) ≠ 0。
条件概率的性质有以下几个方面：互斥性、非互斥性、独立性和非独立性。
互斥性是指在两个事件的发生过程中，其中一个事件的发生将排除另一个事件的发生。
非互斥性则相反。
独立性是指两个事件的发生与否不会相互影响，而非独立性则表示相反的情况。
二、条件概率的计算方法条件概率的计算主要有两种方法：频率法和几何法。
频率法是根据历史数据或实验结果来计算条件概率。
几何法则是通过几何图形进行计算。
在使用频率法计算条件概率时，我们需要先进行事件的分类和计数，然后使用P(A|B) = N(A∩B) / N(B)的公式进行计算。
其中，N(A∩B)表示A和B同时发生的次数，N(B)表示事件B发生的总次数。
几何法则是通过事件发生的几何图形进行计算。
可以通过画出事件A和B在样本空间中的区域，来计算两个事件之间的重叠面积。
通过求出重叠面积与事件B的面积之比，即可得到条件概率。
三、条件概率的应用条件概率在实际生活中有着广泛的应用。
其中一个经典的应用是贝叶斯定理。
贝叶斯定理是一种根据已知的结果来推断事件的概率的方法。
在实际应用中，我们通常会通过贝叶斯定理来进行医学诊断、市场预测等方面的分析。
另一个应用是在赌博游戏中的运用。
比如，在扑克牌游戏中，根据已知的手牌和公共牌，可以通过条件概率来计算自己手中牌型的概率，从而根据概率来做出合理的决策。
此外，条件概率还可以应用于信息论和统计学等领域。
对条件概率的几点认识
条件概率一词指的是一个随机变量的概率，这个随机变量的值取决于另一个随机变量的值，换句话说，条件概率是在某一条件下给定变量的概率。
条件概率无处不在，它们随处可见，用于评估概率分布。
在数学上，条件概率是指在满足一定条件的前提下，某个事件发生的概率。
它可以利用一
系列变量的不同状态，然后通过计算指定变量状态组合下事件发生的概率，来表达概率模型。
许多概率和统计模型依赖于条件概率以衡量随机变量之间的相互关系。
它们可以用来计算某种情况下的概率分布，以及相互之间的关系，如果事件A发生，会对另一个事件B的
发生有什么影响。
条件概率可以被用来表示某种条件下某种事件发生的概率，这可以帮助我们更好地理解导
致这种事件发生的内部因素。
从更宏观的角度来看，条件概率可以帮助我们识别某种趋势，通过揭示两两事件之间的联系，我们可以更全面地了解概率。
总的来说，条件概率是一个重要的概率概念，它可以帮助我们去观察不同的事件之间的关系，并准确估计出发生某种事件的概率。
浅谈条件概率从狄青的100枚铜币谈起——浅谈条件概率教学过程的设计汕头市金山中学林琪条件概率是人教A版选修2-3第二章2.2.1的内容，是学生在已学习古典概型与几何概型的基础上又一类型的概率问题。
条件概率是概率论中的一个重要概念，它是推导独立事件概率公式的前提，也是继续学习事件的独立性等概率知识的基础，正确理解概念是解题的关键，所以学好这一节，对后续概率的学习有着铺垫作用。
而条件概率又是比较难理解的概念，在新课的讲授过程学生总会有这样或那样的疑惑。
下面我就如何把条件概率这节课讲“懂”，使学生真正把知识学好学透彻，浅谈我的一点见解。
1.寻找条件概率——狄青的100枚铜币在我们生活的世界上，充满着不确定性，从流星坠落，到大自然的千变万化，从婴儿诞生，到世间万物的繁衍生息，都充满奇异的随机现象。
我们能根据现在预测未来吗？或者一切都能心想事成吗？这可以从狄青的100枚铜币谈起。
话说北宋庆历、皇祐年间，大将狄青奉旨征讨侬智高时，来到桂林以南。
当时南方有崇拜鬼神的风俗，于是，他拿了100枚铜币向神许愿，说：“如果这次出征能够打败敌人，那么把这些铜币扔到地上，钱面定然会全部朝上。
”左右官员都诚惶诚恐，力劝主帅放弃这个念头——因为经验告诉他们，这种尝试是注定要失败的。
他们担心最终弄不好，反而会动摇部队的士气。
可是，狄青对此概然不理，固执如牛。
在千万人的注视下，他突然举手一挥，把铜币全部扔到地上。
结果这100枚铜币的面，竟然鬼使神差般全部朝上。
这时，全军欢呼，声音响彻山村原野。
由于士兵个个认定有神灵护佑，在战斗中奋勇争先，迅速赢得了胜利。
最后回师时，狄青的僚属们一看才发现那些铜币的两面都是一样的。
实际上，聪明的狄青便是注意到人们在观察随机现象时，往往过于相信自身的经验，而忽视了前提条件。
对于狄青来说，100个钱面全部朝上，原本是个必然事件，但在别人看来，却是几乎不可能出现的。
因此，观察一种现象，不能忽视它的前提。
条件概率的思考条件概率是指在已知某一事件发生的前提下，另一个事件发生的概率。
例如，已知某人患有高血压，那么在这个前提下，他患有心脏病的概率就是条件概率。
我们可以用条件概率来研究各种现实问题，例如天气、疾病流行等等。
在处理这些问题时，我们需要注意以下几点：1. 事件的独立性两个事件的独立性指的是它们之间的发生没有任何关系，互相独立。
例如，抛硬币的结果和一只老虎在森林中的位置就是独立的事件。
如果两个事件互相独立，那么它们的条件概率就是它们各自的概率的乘积。
这可以用以下公式表示：P(A|B) = P(A) * P(B)其中，P(A)和P(B)是两个事件发生的概率。
2. 全概率公式有时候，我们需要求某个事件发生的概率，但是这个概率又依赖于其他多个事件的概率。
这时候，我们可以利用全概率公式来求解。
全概率公式如下：P(A) = ∑ P(A|B) * P(B)其中，B是一组互斥的事件，它们的并集包含了样本空间中所有的可能结果。
应用全概率公式的一个例子是：我们可以通过已知的数据和概率，预测一个市场营销活动的成功率。
3. 贝叶斯公式在某些情况下，我们已知一个事件发生的条件概率以及发生另一个事件的概率，但是我们希望知道从后者发生的条件下，前者发生的概率。
这时候，我们可以使用贝叶斯公式。
贝叶斯公式如下：P(A|B) = P(B|A) * P(A) / P(B)其中，A和B都是事件，P(A|B)是在B条件下A发生的概率，P(B|A)是在A条件下B发生的概率，P(A)和P(B)则是A和B各自发生的概率。
贝叶斯公式的应用场景包括预测疾病的概率、判断嫌疑对象的罪行概率等。
综上所述，条件概率是个十分有用的概念。
在解决各种实际问题时，我们需要根据问题本身的性质，选择使用全概率公式或贝叶斯公式。
通过对条件概率的掌握，我们可以对世界有一种更深入的理解，并且更好地应对各种情况。
浅谈认识对条件概率的两点认识1. 引言1.1 认识条件概率的背景条件概率是概率论中的一个重要概念，指的是在已知一定条件下某一事件发生的概率。
认识条件概率的背景可以追溯到古希腊数学家欧几里得提出的概率论概念。
随着数学和统计学的发展，条件概率逐渐成为解决实际问题中不确定性和随机性的重要工具。
在现代社会，随着大数据和人工智能技术的快速发展，人们对条件概率的认识变得越来越重要。
在金融、医疗、工程等领域，条件概率被广泛应用于风险评估、疾病诊断、系统设计等方面。
对条件概率的深入理解不仅可以帮助人们更好地处理不确定性问题，还可以提高决策的准确性和效率。
了解条件概率的背景及其重要性，对于提高个人的数学素养和解决实际问题具有重要意义。
深入研究条件概率的定义、计算方法、应用范围以及与其他概率理论的关系，有助于我们更好地运用条件概率解决实际问题，同时也有助于对条件概率的认识不断完善，不断提升自身的数学水平和思维能力。
1.2 目的引言：认识条件概率作为概率论中的重要概念，掌握其基本知识和运用方法，是提高数学能力和解决实际问题的关键。
本文旨在通过对条件概率的深入探讨，帮助读者加深对条件概率的理解，掌握条件概率的计算方法，了解条件概率在实际问题中的应用范围，以及探讨条件概率与独立事件、贝叶斯定理之间的关系。
通过本文的学习，读者将能够更好地应用条件概率解决实际问题，提高解决问题的能力和效率。
认识到对条件概率的理解是一个不断完善和深化的过程，从而在日常生活和工作中更好地运用条件概率进行分析和决策。
希望通过本文的阐述，读者能够对条件概率有更全面和深入的认识，从而提高数学思维和解决实际问题的能力。
2. 正文2.1 条件概率的定义条件概率是指在某一条件下，事件发生的可能性。
通常用P(A|B)表示，在事件B已经发生的情况下，事件A发生的概率。
条件概率的定义可以用数学公式表示为P(A|B) = P(A∩B) / P(B)，其中P(A∩B)表示事件A和事件B同时发生的概率，P(B)代表事件B发生的概率。
条件概率的通俗解释
条件概率是一种描述在某一特定条件下，某事件发生的概率。
简单来说，就是事件A在另一事件B已经发生条件下的发生概率。
条件概率表示为P(A|B)，其中"A|B" 的含义是"A 发生且B 已经发生"。
举个例子，假设有一个袋子里面有红球和蓝球，总共10个球。
现在，如果你知道里面有5个红球和5个蓝球，那么随机取出一个红球的概率是5/10，即0.5。
但是，如果你先随机取出一个蓝球，然后再从剩下的球中随机取出一个红球，这个概率就是条件概率。
这个条件概率的计算公式是：P(A|B) = P(A∩B)/P(B)。
其中，P(A ∩B)表示事件A和事件B同时发生的概率，P(B)表示事件B发生的概率。
以刚才的例子来说，P(A∩B)就是先取出一个蓝球（P(B)=1/2），然后再从剩下的球中取出一个红球（P(A∩B)=4/9），所以
P(A|B)=(4/9)/(1/2)=8/9。
条件概率在实际生活中有很多应用，比如医学诊断、天气预报、保险赔率计算等。
理解并正确使用条件概率，可以帮助我们更好地理解和预测事物的发展。
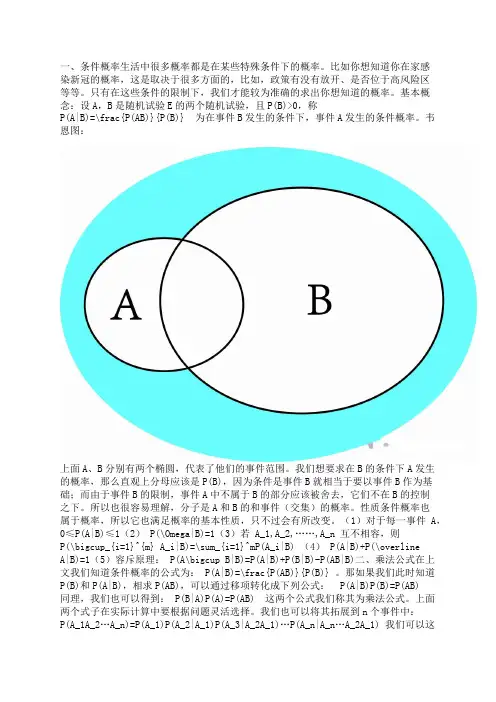
一、条件概率生活中很多概率都是在某些特殊条件下的概率。
比如你想知道你在家感染新冠的概率，这是取决于很多方面的，比如，政策有没有放开、是否位于高风险区等等。
只有在这些条件的限制下，我们才能较为准确的求出你想知道的概率。
基本概念：设A，B是随机试验E的两个随机试验，且P(B)>0，称P(A|B)=\frac{P(AB)}{P(B)} 为在事件B发生的条件下，事件A发生的条件概率。
韦恩图：上面A、B分别有两个椭圆，代表了他们的事件范围。
我们想要求在B的条件下A发生的概率，那么直观上分母应该是P(B)，因为条件是事件B就相当于要以事件B作为基础；而由于事件B的限制，事件A中不属于B的部分应该被舍去，它们不在B的控制之下。
所以也很容易理解，分子是A和B的和事件（交集）的概率。
性质条件概率也属于概率，所以它也满足概率的基本性质，只不过会有所改变。
（1）对于每一事件A，0≤P(A|B)≤1（2） P(\Omega|B)=1（3）若A_1,A_2,……,A_n 互不相容，则P(\bigcup_{i=1}^{m} A_i|B)=\sum_{i=1}^mP(A_i|B) （4） P(A|B)+P(\overlineA|B)=1（5）容斥原理： P(A\bigcup B|B)=P(A|B)+P(B|B)-P(AB|B)二、乘法公式在上文我们知道条件概率的公式为： P(A|B)=\frac{P(AB)}{P(B)} 。
那如果我们此时知道P(B)和P(A|B)，相求P(AB)，可以通过移项转化成下列公式： P(A|B)P(B)=P(AB)同理，我们也可以得到： P(B|A)P(A)=P(AB) 这两个公式我们称其为乘法公式。
上面两个式子在实际计算中要根据问题灵活选择。
我们也可以将其拓展到n个事件中：P(A_1A_2…A_n)=P(A_1)P(A_2|A_1)P(A_3|A_2A_1)…P(A_n|A_n…A_2A_1) 我们可以这样理解：$P(A_1)$是假设A1正确，$P(A_2|A_1)$是假设A1正确的情况下A2正确，以此类推三、全概率公式有限划分基本概念：设 \Omega 为随机试验E的样本空间，B1，B2 ，…，Bn为E的一组事件，若(1) Bi∩Bj =f ,i ≠ j(2) B_1∪B_2 ∪…∪B_n=\Omega则称B1，B2，…，Bn 为 \emptyset 的一个有限划分，或称完备事件组。
条件概率定义条件概率，也称为条件期望，是概率论中描述不确定性的一种基本概念。
它以某种程度反映事件或结果发生的概率，准确地表达事件间的联系，并建立统计关联或因果关系。
条件概率是统计学中最重要的一种概率样式，它表示了某种事件发生的条件下，另一种事件发生的概率。
为了清晰地表述条件概率的定义，假设有两个事件A和B，其中P（A）是A事件发生的概率，P（B）是B事件发生的概率。
如果要确定A事件发生的条件下B事件发生的概率，我们可以定义的条件概率为P（B|A）。
这里的“|”表示“条件”的意思，即P（A）是P（B|A）的条件。
因此，条件概率P（B|A）表示A事件发生的条件下，B事件发生的概率。
根据条件概率的定义，条件概率可以分为两种形式：（1）全概率定理：P（A B）= P（A）+ P（B|A），即两个事件A、B的总概率等于A事件发生的概率加上A事件发生的条件下B事件发生的概率。
（2）贝叶斯公式：P（A|B）= P（B|A）* P（A）/ P（B）。
根据以上定义，可以看出，条件概率是一个衡量不确定性的重要概念。
它可以用来计算不同结果出现的概率，并基于先验知识和已知信息给出有效的决策。
条件概率的应用条件概率是统计学中应用最广泛的概念之一，它在几乎所有的统计领域都有广泛的应用。
例如，在市场营销领域，条件概率可以用来预测市场营销活动的成功程度，也可以用来分析竞争对手的行动策略；在统计推断中，条件概率可以用来衡量不同的数据背景下的统计模型的拟合程度；在概率编程中，条件概率可以用来演示一定程度上的规则，并用来预测系统的行为；在保险领域，条件概率可以用来预测产品发生保险风险的概率和费用；在金融领域，条件概率可以用来预测投资于某只股票的期望收益率以及发生市场振荡的概率等。
此外，条件概率还被应用于计算机视觉领域，特别是用于图像识别和分类等。
由于图像的不同部分的特征是不同的，因此可以使用条件概率来计算图像中不同部分特征的相关性，以及这些特征之间发生复杂模式的概率。
条件概率理解
嘿，朋友！今天咱就来好好唠唠条件概率这个玩意儿，你可得竖起耳朵听好喽！
咱先说个例子哈，就比如彩票，你买了一张彩票，中头奖的概率那可是
相当低。
但如果我告诉你，这张彩票是从某个特定的机器里出来的，而这个机器之前出过头奖，那你会不会觉得你中奖的概率好像瞬间就增加了呢？这就是条件概率！
再举个例子，你想啊，假如你知道一个人总是很守时，那么你是不是就
会觉得他这次也会大概率守时呢？就好像你和朋友约好出去玩，他平常都不怎么迟到，这次你就会更相信他会按时出现。
咱生活中到处都是条件概率的影子呢！比如你看天气预报说第二天有雨，那你出门带伞的可能性就会大大提高，因为这个“第二天有雨”的条件改变了你对“带不带伞”这件事的概率判断。
嘿，你想想是不是这个理儿？条件概率就像一个隐藏的小开关，一旦打开，事情的可能性就变了。
可以说它就像是给我们的判断加上了一层滤镜。
我记得有一次，我和几个朋友一起玩猜硬币的游戏。
我们都先猜正面，
然后有个朋友说他知道这枚硬币之前连续三次都是正面，这时候，大家瞬间觉得这次还是正面的概率好像大了很多呢！
我觉得啊，理解条件概率真的超级重要！它能让我们更理性地看待事情，而不是盲目地去判断。
不然的话，我们可能就会做出一些不太明智的决定。
所以，咱可得好好琢磨琢磨这个条件概率，让它为我们的生活服务呀！怎么样，你是不是也觉得条件概率很有意思呢？是不是也对它有了更深的理解呢？。
目录摘要 (1)关键词 (1)Abstract (1)Key Words (1)引言 (1)1.条件概率的定义及意义 (1)1.1条件概率的定义 (1)1.2几何直观意义 (1)1.3 概率直观意义 (2)2.条件概率的性质及算法 (2)2.1 条件概率的性质 (2)2.2条件概率的算法 (3)3.条件概率系列公式的关系探讨 (4)3.1乘法公式 (4)3.2全概率公式 (4)3.3贝叶斯公式 (5)3.4 系列公式使用的技巧 (5)3.5例题解析 (6)4.结束语 (9)参考文献 (10)浅谈条件概率学生姓名：李青烨 学号：20090401057 数学与计算机科学系 数学与应用数学 指导老师：王瑞瑞 职称：讲师摘 要：条件概率是“概率论与数理统计”课程的重要知识之一，文章从条件概率的定义及意义、性质及算法和条件概率系列公式的联系，以及公式使用的规则和技巧，这三方面来分析、探讨条件概率．关键词：条件概率;乘法公式;全概率公式;贝叶斯公式Abstract : Conditional probability is one of the important knowledge of the probability theory and mathematical statistics course, This article analyses and discusses conditional probability from meaning of conditional probability , quality, algorithm , the connection of serial formulas of conditional probability and some rules and skills about the using of these formulas.Key Words : Conditional probability ；Multiply formula ；Probability formula ； Bayesian formula引言概率论与数理统计是研究随机现象的数量规律性的学科，而条件概率又是概率论与数理统计一个重要知识点．本文从条件概率的定义及意义、性质及算法和条件概率系列公式的联系，乘法公式、全概率公式和贝叶斯公式使用的规则和技巧，这三方面来分析、探讨条件概率．1.条件概率的定义及意义1.1条件概率的定义若),,(P F Ω是一个概率空间，F B ∈，且0)(>B P 则对任意的F A ∈，称(|)P A B)()(B P AB P =为已知事件B 发生的条件下，事件A 发生的条件概率． 条件概率的意义，可以从以下二个方面来阐述. 1.2几何直观意义我们可以用单位正方形来表示样本空间Ω,用正方形内任一封闭曲线围成的图形表示事件，而把图形的面积理解为相应事件的概率．设Ω⊆Ω⊆B A , (见图1）事件A 的无条件概率(或称为绝对概率)为)|()(Ω=A P A P .(注意1)(=ΩP )．几何直观上，相当于A 在空间Ω中所占的比例.图1 条件概率的维恩图对于条件概率)()()|(B P AB P B A P =，实际上是仅局限于B 事件这个范围来考察A 事件发生的概率，几何直观上，相当于A 在B 内的那部分AB 在B 中所占的比例． 1.3 概率直观意义条件概率)|(B A P 与无条件概率)(B P 亦可解释为后验概率，)(B P 可解释为试验前人们根据以往积累的资料和经验，对事件B 发生的(绝对)可能性大小的认识．而现在经过试验，我们获得了A 事件已发生的这个新信息．那么，这个新的信息将要求我们并且有助于我们重新审视或估价事件B 发生的可能性大小的重新认识，故可解释为后验概率．2.条件概率的性质及算法2.1 条件概率的性质如果0)(>A P ，条件概率具有如下性质： (1) 对任意事件B ，有 0)|(≥A B P ；(2) 1)|(=ΩA P ,(|)0P A ∅=；(3) 对任意可列个两两互不相容事件 ,,,,21n A A A 有()∑∑∞=∞==11|)|(i i i i A A P A A P ；(4) 对于一般的事件1A 与2A ，有);|()|()|()|(212121A A A P A A P A A P A A A P -+=(5) ;1)|()|(=+A B P A B P(6) 当A B ⊂ 时，有)()()|(A P B P A B P = ；当A B ⊃时，有.1)|(=A B P2.2条件概率的算法条件概率的计算通常有两种方法：一种是利用条件概率公式 )()()|(A P BA P A B P =在原样本空间Ω中计算；二种是根据直观在缩小的样本空间中直接计算，即就是在 附加条件 “事件A 已经发生”的情况下，直接计算事件B 发生的概率即可得)|(A B P . 例１ 掷二颗骰子,已知二颗骰子点数之和为7,求其中有一颗为1点的概率．【分析】 容易判断这是一个条件概率，下面用两种方法计算，一种是按条件概率公式在原样本空间中计算，一种是在缩小的样本空间中计算.法一 设A ={二颗骰子点数之和为7}，B ={二颗中有一颗为1点}，于是所求 概率为,)()()|(A P BA P A B P =由于样本空间}6,2,1,),,{( ==Ωj i j i 中基本事件总数为36，)},1,6(),6,1{(=AB )},1,6(),2,5(),3,4(),4,3(),5,2(),6,1{(=A 故由古典概率公式,61366)(,181362)(====A P AB P 所以)|(A B P ,3161181==法二 将两颗骰子点数之和为7的所有可能情况，即事件A 作为样本空间，此 时基本事件总数为6；有利事件数，即在A 中有一个为1点的情况共有2种，故)|(A B P ,3162==3.条件概率系列公式的关系探讨条件概率系列公式即条件概率、乘法公式、全概率公式和贝叶斯公式．这四个公式是以条件概率公式为起点，以乘法公式和全概率公式为媒介，以贝叶斯公式为终点的一组关联公式，是沿着一条路子走下来的，是一棵藤上开着的四朵美丽的花． 3.1乘法公式设),,(P F Ω是一个概率空间，F B A ∈,由条件概率公式 )()()|(A P AB P A B P =知 (1) 当)|()()(,0)(A B P A P AB P A P =>, (2) 当)|()()(,0)(B A P B P AB P B P =>. (3) 概率乘法公式可以推广到多个事件的情形:如果,0)(121>-n A A A P F A A n ∈,,1 ,2≥n 则有)|()|()|()()(12121312121-=n n n A A A A P A A A P A A P A P A A A P . 概率论的重要研究课题之一是希望从已知的简单事件的概率推算出未知的复杂事件的概率．为达到这个目的，经常把一个复杂事件分解为若干个互不相容的简单事件之和，再通过分别计算这些简单事件的概率．最后，利用概率的可加性得到最终结果．这里，全概率公式起着重要作用． 3.2全概率公式全概率公式是指若n A A A ,,,21 为一完备事件组,()0i P A > ),,2,1( =i 则对于任意事件B ,有)|()()(1i ni i A B P A P B P ∑==，全概率公式的直观意义是:某事件B 的发生有各种可能的原因i A ),,2,1( =i 并且这些原因两两不能同时发生,如果B 是由原因i A 所引起的,若B 发生时,i BA 必同时发生,因而()P B 与()i P BA ),2,1( =i 有关,且等于其总和11()()(|)n ni i i i i P BA P A P B A ===∑∑,全概率的全就是总和的含义,当然这个总和要能求出来,需已知概率()i P BA 或已知各原因i A 发生的概率()i P A 及在i A 发生的条件下B 的条件概率(|)i P B A ),,2,1( =i 通俗地说,事件B 发生的可能性,就是其原因i A 发生的可能性与在i A 发生的条件下事件B 发生的可能性的乘积之和. 3.3贝叶斯公式贝叶斯公式是指若n A A A ,,,21 为一完备事件组,且()0i P A > ( ,2,1=i ),则对任何概率非零的事件B ,有1()(|)()(|)(|)()()(|)i i i i i njjj P A P B A P A P B A P A B P B P A P B A ===∑.在理论研究和实际中还会遇到一类问题,这就是需要根据试验发生的结果找原因,看看导致这一试验结果的各种可能的原因中哪个起主要作用,解决这类问题的方法就是使用贝叶斯公式.贝叶斯公式的意义是导致事件B 发生的各种原因可能性的大小,称之为后验概率. 3.4 系列公式使用的技巧条件概率公式作为这组系列公式的头一个．还是较好理解和掌握的，一般从题目当中能判断出要求的目标是事件是否具有附加条件，从而选择正确的公式． 是否使用乘法公式，判断起来也较容易，但是具体使用时，存在公式(2)与公式(3)的选择问题．其实，用乘法公式计算)(AB P 时，哪一个事件先发生，就选择以那个事件为条件的公式，如事件A 先发生，就选择公式(2)，计算)(AB P ．应用全概率公式的关键是建立样本空间的正确划分(即构造一个正确的完备事件组)，然后计算各个概率和条件概率．最后代入全概率公式．全概率公式是求复杂事件概率的有利工具．贝叶斯公式往往与全概率公式同时使用，全概率公式一般用于“由因求果”问题，而贝叶斯公式一般用于 “执果寻因”问题，在使用时要分清是什么问题，确定应用哪个公式．3.5例题解析例 2 一袋中有r 只红球，t 只白球，每次从袋中任取一只球，观察后放回并且放入a 只同色球．若在袋中连续取球四次，求第一，二次取到红球且第三,四次取到白球的概率．解：以)4,3,2,1(=i A i 表示第i 次取到红球事件，则所求事件的概率为：)(4321A A A A P =t r r + a t r a r +++ a t r t 2++ a t r a t 3+++ =.)3)(2)()(()()(a t r a t r a t r t r a t t a r r +++++++++例3 设一人群中有37.5％的人血型A 为型，20.9％的人为B 型，33.7％的人为O 型，7.9％的人为AB 型，已知能允许输血的血型配对如表1，现在在人群中任选一人为输血者，再选一个为受血者，问输血能成功的概率是多少？ 表1 输血者 受血者A BAB OA√ × × √ B× √ × √ AB√ √ √ √ O×××√( 其中√表示允许输血，×表示不允许输血.)【分析】 实验过程可分成两个阶段进行，第一阶段是选择输血者，其结果共有四种情况，但具体出现哪一个未知；第二阶段是选择受血者，其结果共有两个:发生的概率，故用全概率公式.解：设)4,3,2,1(=i B i 表示“从人群中任选一人，其血型分别为AB B A ,,和O 型” ，S 表示“受血者输血成功” ，由已知条件知%,9.20)(%,5.37)(21==B P B P%,7.33)(%,9.7)(43==B P B P另外，由血型配对表知，若输血者血型为A 型，则受血者可以是A 型或AB 型,于是成功的概率为 %,4.45)()()|(311=+=B P B P B S P类似可得%,8.28)()()|(322=+=B P B P B S P%,9.7)()|(33==B P B S P.1%100)()|(414===∑=i i B P B S P由全概率公式得.5737.0)|()()(41==∑=i i i B S P B P S P例4 设在n 张彩票中有k 张奖券，求第三个人摸到奖券的概率是多少？解: 设i A 表示事件“第i 人摸到奖券”，n i ,,2,1 =，现在目的是求)(3A P ,因为k 不确定所以用数学归纳法.又因1A 与1A 是两个概率大于0 的事件：,1=k,1)(,1)(11nn A P n A P -==,11)|(,0)|(1212-==n A A P A A P由全概率公式得)|()()|()()(1211212A A P A P A A P A P A P +=11101-⋅-+⋅=n n n n ,1n =)|()()|()()|()()(213212321313A A A P A A P A A P A P A A P A P A P ++=2112100-⋅--⋅-++=n n n n n.1n = 用类似的方法可得.1)(...)(4nA P A P n=== ,2=k ,2)(,2)(11nn A P n A P -==)|()()|()()(1211212A A P A P A A P A P A P +=122112-⋅-+-⋅=n n n n n ,2n =+++=)|()()|()()|()()(2132121321213213A A A P A A P A A A P A A P A A A P A A P A P)|()(21321A A A P A A P1322221122122210--⋅-⋅-+-⋅-⋅-+--⋅⋅-+=n n n n n n n n n n n n n.2n = 用类似的方法可得 .2)()(4n A P A P n ===有归纳法得当有)(n k ≤张奖券，则可得.)()()(21n kA P A P A P n ==== 这说明购买彩票时，不论先买后买，中彩机会是均等的.例5 用某种试剂检查食品的卫生情况，记事件B 为 “被检查的食品不卫生”，事件A 为“试验呈阳性”，由经验知：A P (|99.0)=B ,P (A |B )=0.95；而已知04.0)(=B P ．现检查出一批食品的结果呈阳性．求这些食品确实不卫生的概率．解： 这是一个执果寻因问题，已知试验结果呈阳性，可能是确实不卫生也可是试验有误．由贝叶斯公式，得)|(A B P =)()(A P AB P = )|()()|()()|()(B A P B P B A P B P B A P B P + =.452.005.096.099.004.099.004.0=⨯+⨯⨯本题说明，虽然概率)|(B A P 与P (A |B )都较高，但以此来确定食品不卫生仍然是不够正确的．4.结束语概率论与数理统计是研究随机现象的数量规律性的学科，条件概率是概率论中一个既重要又实用的概念，本文主要介绍了条件概率的意义、性质，算法和条件概率系列公式，探讨了乘法公式、全概率公式和贝叶斯公式三者之间的关系、使用的规则和技巧.全概率公式提供了计算复杂事件概率的一条有效途径，使一个复杂事件的概率计算问题化繁为简，在乘法公式和全概率公式的基础上得出了贝叶斯公式，为解决实际问题提供了方法，使我可以在遇到很多概率问题时熟练的应用和使用全概率公式和贝叶斯公式，这体现了全概率公式和贝叶斯公式在应用和实践中的重要的作用.参考文献[1] 魏宗舒等编．概率论与数理统计教程[M]．北京：高等教育出版社，1983．[2] 复旦大学编．概率论[M]．北京：人民教育出版，1979．[3] 复旦大学教研室.概率论[M].北京:高等教育出版社,1979.[4] 孙清华赵德修．新编概率论与数理统计题解[M]．武汉：华中科技大学出版社，2000．[5] 濮晓龙等编.概率论与数理统计教程[M].北京：高等教育出版社，2004.[6] 来向荣程维虎编.简明概率论教程[M].北京：北京工业大学出版社，2001．[7] 曹显兵编．概率论与数理统计学习指导[M]．北京：世界图书出版公司，2003．[8] 缪铨生.概率与数理统计[M].上海: 华东师范大学出版社,1997.[9] 章昕.概率统计辅导[M].北京:机械工业出版社,2002.10。
