当前位置：文档之家 › Eviews数据统计与分析教程5章 基本回归模型OLS估计-普通最小二乘法

Eviews数据统计与分析教程5章 基本回归模型OLS估计-普通最小二乘法

  • 格式：ppt
  • 大小：333.50 KB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

使用eviews做线性回归方程

使用eviews做线性回归方程

Gloss‎a ry:ls(least‎squar‎e s)最小二乘法‎R-sequa‎r ed样本‎决定系数（R2）：值为0-1，越接近1表‎示拟合越好‎，>0.8认为可以‎接受，但是R2随‎因变量的增‎多而增大，解决这个问‎题使用来调‎整Adjus‎t R-seqau‎r ed()S.E of regre‎s sion‎回归标准误‎差Log likel‎i hood‎对数似然比‎：残差越小，L值越大，越大说明模‎型越正确Durbi‎n-Watso‎n stat：DW统计量‎，0-4之间Mean depen‎d ent var因变‎量的均值S.D. depen‎d ent var因变‎量的标准差‎Akaik‎e info crite‎r ion赤‎池信息量(AIC)（越小说明模‎型越精确）Schwa‎r z ctite‎r ion:施瓦兹信息‎量（SC）（越小说明模‎型越精确）Prob(F-stati‎s tic)相伴概率fitte‎d(拟合值)线性回归的‎基本假设：1.自变量之间‎不相关2.随机误差相‎互独立，且服从期望‎为0，标准差为σ‎的正态分布‎3.样本个数多‎于参数个数‎建模方法:ls y c x1 x2 x3 ...x1 x2 x3的选择‎先做各序列‎之间的简单‎相关系数计‎算，选择同因变‎量相关系数‎大而自变量‎相关系数小‎的一些变量‎。

模型的实际‎业务含义也‎有指导意义‎，比如m1同‎g d p肯定‎是相关的。

模型的建立‎是简单的，复杂的是模‎型的检验、评价和之后‎的调整、择优。

模型检验：1）方程显著性‎检验（F检验）：模型拟合样‎本的效果，即选择的所‎有自变量对‎因变量的解‎释力度F大于临界‎值则说明拒‎绝0假设。

Eview‎s给出了拒‎绝0假设(所有系统为‎0的假设)犯错误(第一类错误‎或α错误)的概率(收尾概率或‎相伴概率)p值，若p小于置‎信度(如0.05)则可以拒绝‎0假设，即认为方程‎显著性明显‎。

经验分享使用eviews做回归分析

经验分享使用eviews做回归分析

[经验分享] 使用evi‎ew s做线‎性回归分析‎Gloss‎a ry:ls(least‎ squar‎e s)最小二乘法‎R-sequa‎r ed样本‎决定系数（R2）：值为0-1，越接近1表‎示拟合越好‎，>0.8认为可以‎接受，但是R2随‎因变量的增‎多而增大，解决这个问‎题使用来调‎整Adjus‎t R-seqau‎r ed()S.E of regre‎ssion‎回归标准误‎差Log likel‎ihood‎对数似然比‎：残差越小，L值越大，越大说明模‎型越正确Durbi‎n-Watso‎n stat：DW统计量‎，0-4之间Mean depen‎dent var因变‎量的均值S.D. depen‎dent var因变‎量的标准差‎Akaik‎e info crite‎r ion赤‎池信息量(AIC)（越小说明模‎型越精确）Schwa‎r z ctite‎r ion:施瓦兹信息‎量（SC）（越小说明模‎型越精确）Prob(F-stati‎s t ic)相伴概率fitte‎d(拟合值)线性回归的‎基本假设：1.自变量之间‎不相关2.随机误差相‎互独立，且服从期望‎为0，标准差为σ‎的正态分布‎3.样本个数多‎于参数个数‎建模方法:ls y c x1 x2 x3 ...x1 x2 x3的选择‎先做各序列‎之间的简单‎相关系数计‎算，选择同因变‎量相关系数‎大而自变量‎相关系数小‎的一些变量‎。

模型的实际‎业务含义也‎有指导意义‎，比如m1同‎g dp肯定‎是相关的。

模型的建立‎是简单的，复杂的是模‎型的检验、评价和之后‎的调整、择优。

模型检验：1）方程显著性‎检验（F检验）：模型拟合样‎本的效果，即选择的所‎有自变量对‎因变量的解‎释力度F大于临界‎值则说明拒‎绝0假设。

Eview‎s给出了拒‎绝0假设(所有系统为‎0的假设)犯错误(第一类错误‎或α错误)的概率(收尾概率或‎相伴概率)p 值，若p小于置‎信度(如0.05)则可以拒绝‎0假设，即认为方程‎显著性明显‎。

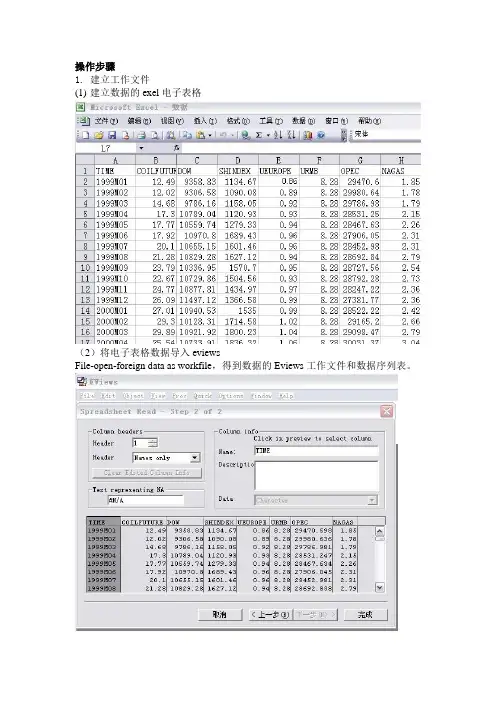
Eviews处理多元回归分析操作步骤

Eviews处理多元回归分析操作步骤

操作步骤1.建立工作文件(1)建立数据的exel电子表格（2）将电子表格数据导入eviewsFile-open-foreign data as workfile，得到数据的Eviews工作文件和数据序列表。

2.计算变量间的相关系数在窗口中输入命令：cor coilfuture dow shindex nagas opec ueurope urmb，点击回车键，得到各序列之间的相关系数。

结果表明Coilfuture数列与其他数列存在较好的相关关系。

3.时间序列的平稳性检验（1）观察coilfuture序列趋势图在eviews中得到时间序列趋势图，在quick菜单中单击graph，在series list对话框中输入序列名称coilfuture，其他选择默认操作。

图形表明序列随时间变化存在上升趋势。

（2）对原序列进行ADF平稳性检验quick-series statistics-unit root test，在弹出的series name对话框中输入需要检验的序列的名称，在test for unit root in 选择框中选择level，得到原数据序列的ADF检验结果，其他保持默认设置。

得到序列的ADF平稳性检验结果，检测值0.97大于所有临界值，则表明序列不平稳。

以此方法，对各时间序列依次进行ADF检验，将检验值与临界值比较，发现所有序列的检验值均大于临界值，表明各原序列都是非平稳的。

（3）时间序列数据的一阶差分的ADF检验quick-series statistics-unit root test，在series name对话框中输入需要检验的序列的名称，在test for unit root in 选择框中选择1nd difference，对其一阶差分进行平稳性检验，其他保持默认设置。

得到序列的ADF平稳性检验结果，检测值-7.8远小于所有临界值，则表明序列一阶差分平稳。

以此方法，对各时间序列的一阶差分依次进行ADF检验，将检验值与临界值比较，发现所有序列的检验值均小于临界值，表明各序列一阶差分都是平稳的。

EViews软件应用及对OLS的回归分析ppt课件

EViews软件应用及对OLS的回归分析ppt课件
最新版整理ppt
10
1、工作文件（Workfile）
EViews的大多数工作通过工作文件来实现 使用EViews工作的第一步：建立一个新的
工作文件（file/ new/ workfile）或调用一个 已有的工作文件（ file/ open/ EViews workfile ）
最新版整理ppt
11
最新版整理ppt
47
可以用EViews工作文件窗口菜单上的“View”或对象窗口 工具栏上的“View”来改变对象的视图。一个对象视图的变化并 不改变对象中的数据，仅仅是显示形式改变了。
• 线性坐标视图 最新版整理ppt • line
48
• 柱状坐标视图 • bar
最新版整理ppt
49
有关对象的其他简单的统计分析和相关操作
9
C. EViews应用中的一些基本概念
1. 工作文件（Workfile） 2. 对象（Object）
• EViews的核心是对象，对象是指有一定关系的 信息或算子捆绑在一起供使用的单元，用 EViews工作就是使用不同的对象。
• 对象都放置在对象集合中，其中工作文件 （workfile）是最重要的对象集合。
模型 合成数据
行向量 样本 标量 序列 最新版整理ppt 状态空间
对称矩阵 系统
表格 文本
值图 向量自回归
列向量30
（1）对象的显示限制
当工作文件中包含很多对象时，工作文件窗 口就会显得很乱。可以用显示限制（Filter）来限 制窗口中所显示的对象。对象类型和对象名称可 作为限制条件。
最新版整理ppt
最新版整理ppt
4
A. 什么是EViews
具有现代Windows软件可视化操作的优良性。可以使用鼠

Eviews基本回归模型

Eviews基本回归模型

对数似然计算如下：
T ˆu ˆ / T )) l (1 log( 2 π) log( u 2
19
6. Durbin-Watson 统计量
D-W 统计量衡量残差的一阶序列相关性，计算方法如下：
2 ˆ ˆ DW (ut ut 1 ) t 2 T 2 ˆ ut t 1 T
15
§3.4.2 方程统计量
1. R2 统计量 R2 统计量衡量在样本内预测因变量值的回归是否成功。R2 是自变量所解释的因变量的方差。如果回归完全符合，统计值 会等于 1。如果结果不比因变量的均值好，统计值会等于 0。 R2 可能会由于一些原因成为负值。例如，回归没有截距或常数， 或回归包含系数约束，或估计方法采用二阶段最小二乘法或 ARCH方法。 EViews计算R2 的公式为：
程，并选择估计方法。
2
§3.2 在EViews中对方程进行说明
当创建一个方程对象时，会出现如下对话框：
在这个对话框中需要说明三件事：方程说明，估计方法，估 计使用的样本。在最上面的编辑框中，可以说明方程：因变量 （左边）和自变量（右边）以及函数形式。 有两种说明方程的基本方法：列表法和公式法。列表法简单 但是只能用于不严格的线性说明；公式法更为一般，可用于说明 3 非线性模型或带有参数约束的模型。
ˆu ˆ u ， R 1 ( y y )( y y )
2
ˆ y Xb u
16
ˆ 是残差，y 是因变量的均值。 u 其中，
2. R2 调整 使用 R2 作为衡量工具存在的一个问题，即在增加新的自变 量时R2 不会减少。在极端的情况下，如果把样本观测值都作为Leabharlann 自变量，总能得到R2 为1。
10. F统计量和边际显著性水平 F统计量检验回归中所有的系数是否为零(除了常数或截距)。 对于普通最小二乘模型，F统计量由下式计算：

第二讲 eviews 一元线性回归模型分析

第二讲 eviews 一元线性回归模型分析

图2.5.3 Workfile工作框
2．命令方式：在命令窗口也可以直接输入建立工作文件的命令 CREATE，命令格式为 CREATE 数据频率 起始期 终止期
其中，数据频率类型分别为 A （年）、 Q （季）、 M （月）， U
（非时间序列数据）。输入 EViews 命令时，命令字与命令参数之间 只能用空格分隔。如本例可键入命令： CREATE A 1978 2001。
表2.5.2 统计数据录入结果
数据输入完毕，可以关闭数据输入窗口，点击工作文件窗口工具条 的Save或点击菜单栏的File＼Save将数据存入磁盘。
2.5.3 图形分析
1．单方式
在数组窗口工具条上Views的下拉式菜单中选择Graph（图形）；
2．命令方式
趋势图：plot
否存在异常值。 图2.5.4给出了表2.5.1中最终消费支出与国内生产总值的趋势图。
图2.5.2 Workfile Range对话框
选择数据类型和起止日期：时间序列提供起止日期 (年、季度、
月度、周、日 ) ，非时间序列提供最大观察个数。本例中在 Start Data 里 键 入 1978 ， 在 End Data 里 键 入 2001 。 点 击 OK 后 屏 幕 出 现 Workfile工作框(图2.5.3)。
一元线性回归模型
对于一元线性总体回归模型：
图2.2.1 观测值散点图
普通最小二乘法（OLS）
最小二乘估计量的性质
一个用于考察总体的估计量，可从如下几个方面考察其优劣性：
（1）线性。即它是否是另一个随机变量的线性函数；
（2）无偏性。即它的均值或期望是否等于总体的真实值； （3）有效性。即它是否在所有的线性无偏估计量中具有最小方差； （ 4 ）渐近无偏性。即样本容量趋于无穷大时，它的均值序列趋于总体的真

Eviews数据统计与分析教程6章 基本回归模型的OLS估计-加权最小二乘法

Eviews数据统计与分析教程6章 基本回归模型的OLS估计-加权最小二乘法

EViews统计分析基础教程
Байду номын сангаас
四、非线性最小二乘法（NLS）
基本原理： 设定非线性回归模型的一般式为 yi = f(xi, ,β) + μi i=1，2,…，n 则其残差平方和为
（1）
2 n ˆ S ( ) = y f x , （2） ˆ i i i 1 能使(2)达到最小的为参数β的非线性最小二乘估计。要 得到β的估计值，首先对式（1）中的β求偏导，然后令 该式等于0。 还可以通过迭代法求的近似值，先给出参数估计的初始 值，然后通过迭代法得到一个新的估计值，重复迭代直 到估计值收敛为止。
EViews统计分析基础教程
五、广义矩估计（GMM）
基本原理： 广义矩估计是设定参数满足的一种理论关系。其原理是 选择参数估计尽可能接近理论上关系，把理论关系用样 本近似值代替；并且估计量的选择就是要最小化理论值 和实际值之间的加权距离。参数要满足的理论关系通常 是参数函数f(θ)与工具变量Zt之间的正则条件，即 E[f(θ)′Z]=0，θ是被估计参数 广义矩估计法（GMM）中估计量选择的标准是，使工 具变量与函数f(θ)之间的样本相关性越接近于0越好。
EViews统计分析基础教程
五、广义矩估计（GMM）
EViews基本操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，在 “Method”中选择“GMM”后弹出如下图所示的方程设 定对话框。
基本思路： 赋予每个观测值残差不同的权数，从而使得回归模型的随 机误差项具有同方差性。
EViews统计分析基础教程
一、加权最小二乘法（WLS）

使用eviews做线性回归分析

使用eviews做线性回归分析

Glossary:ls(least squares)最小二乘法R-sequared样本决定系数（R2）：值为0-1，越接近1表示拟合越好，>0.8认为可以接受，但是R2随因变量的增多而增大，解决这个问题使用来调整Adjust R-seqaured()S.E of regression回归标准误差Log likelihood对数似然比：残差越小，L值越大，越大说明模型越正确Durbin-Watson stat：DW统计量，0-4之间Mean dependent var因变量的均值S.D. dependent var因变量的标准差Akaike info criterion赤池信息量(AIC)（越小说明模型越精确）Schwarz ctiterion:施瓦兹信息量（SC）（越小说明模型越精确）Prob(F-statistic)相伴概率fitted(拟合值)线性回归的基本假设：1.自变量之间不相关2.随机误差相互独立，且服从期望为0，标准差为σ的正态分布3.样本个数多于参数个数建模方法:ls y c x1 x2 x3 ...x1 x2 x3的选择先做各序列之间的简单相关系数计算，选择同因变量相关系数大而自变量相关系数小的一些变量。

模型的实际业务含义也有指导意义，比如m1同gdp肯定是相关的。

模型的建立是简单的，复杂的是模型的检验、评价和之后的调整、择优。

模型检验：1）方程显著性检验（F检验）：模型拟合样本的效果，即选择的所有自变量对因变量的解释力度F大于临界值则说明拒绝0假设。

Eviews给出了拒绝0假设(所有系统为0的假设)犯错误(第一类错误或α错误)的概率(收尾概率或相伴概率)p值，若p小于置信度(如0.05)则可以拒绝0假设，即认为方程显著性明显。

2）回归系数显著性检验（t检验）：检验每一个自变量的合理性|t|大于临界值表示可拒绝系数为0的假设，即系数合理。

t分布的自由度为n-p-1,n为样本数，p为系数位置3）DW检验：检验残差序列的自相关性，检验基本假设2（随机误差相互独立）残差：模型计算值与资料实测值之差为残差0<=dw<=dl 残差序列正相关，du<dw<4-du 无自相关， 4-dl<dw<=4负相关，若不在以上3个区间则检验失败，无法判断demo中的dw=0.141430 ，dl=1.73369,du=1.7786,所以存在正相关模型评价目的：不同模型中择优1）样本决定系数R-squared及修正的R-squaredR-squared=SSR/SST 表示总离差平方和中由回归方程可以解释部分的比例，比例越大说明回归方程可以解释的部分越多。

Eviews估计方法汇总

Eviews估计方法汇总

Eviews估计方法汇总来源：计量经济学01最小二乘法（1）普通最小二乘估计（OLS）：这是使用的最为普遍的模型，基本原理就是估计残差平方和最小化，不予赘述。

（2）加权最小二乘估计（WLS）Eviews路径：LS模型设定对话框-----optionsOLS的假设条件最为严格，其他的估计方法往往是在OLS的某些条件无法满足的前提下进行修正处理的。

WLS就是用来修正异方差问题的。

在解释变量的每一个水平上存在一系列的被解释变量值，每一个被解释变量值都有自己的分布和方差。

在同方差性假设下，OLS对每个残差平方ei^2都同等看待，即采取等权重1。

但是，当存在异方差性时，方差δi^2越小，其样本值偏离均值的程度越小，其观测值越应受到重视，即方差越小，在确定回归线时的作用应当越大；反之方差δi^2越大，其样本值偏离均值的程度越大，其在确定回归线时的作用应当越小。

WLS的一个思路就是在拟合存在异方差的模型的回归线时，对不同的δi^2区别对待。

在利用样本估计系数时依旧是使得总体残差最小化，但是WLS会给每个残差平方和一个权重wi=1/δi。

这样，当δi^2越小，wi越大；反之，δi^2越大，wi越小。

Eviews的WLS没有要求权重因子必须是1/δi。

一般纠正异方差性的方法还包括模型变换法，这种方法假定已知Var（ui）=δi^2=δ^2*f(Xi)，令权重wi=f(Xi)^（1/2），用f(Xi)^（1/2）去除原模型，可知随机干扰项转换为ui/f(Xi)^（1/2），这时Var（ui）=δi^2=δ^2，即实现了同方差。

由上面的分析可知，WLS核心就是找到一个等式：Var（ui）=δi^2=δ^2*f(Xi)。

这个等式经过调整更容易理解：δ^2=δi^2/f(Xi)或δ=δi/f(Xi)^（1/2）。

δ为某一常数，权重wi=1/f(Xi)^（1/2），经过wi的加权便实现了同方差。

前面提到的特殊权重wi=1/δi，即f(Xi)=1/δi^2,这时δ=δi/f(Xi)^（1/2）=1。

eviews期中作业报告(要点：基本统计和OLS、稳健方差)

eviews期中作业报告(要点：基本统计和OLS、稳健方差)

Eviews期中实验报告一、实验任务上机内容：基本统计和OLS、稳健方差要点∙描述性统计∙简单假设检验∙季节调整：移动平均法∙多元统计分析：齐性检验；主成分分析∙方程对象：方程设定，估计结果，系数，成员函数∙方差稳健估计：HC和HAC∙哑变量和交互项二、实验内容1.简单统计分析与描述性统计数据查看：m1.sheetm1StatsM1Mean 378.1643Median 274.0275Maximum 1089.475Minimum 129.8910Std. Dev. 265.4934Skewness 1.012404Kurtosis 2.765155Jarque-Bera 27.70001Probability 0.000001Sum 60506.30Sum Sq. Dev. 11207393Observations 160从而显示出了m1的各种统计信息，包括均值，中位点，最大值最小值，以及二到四阶矩观测数目和正态分布检验等的统计概要。

M1.line则显示出了这一组数据的图形描述freeze(gk) G(1).distplot kernel 'G(1).kdensity'V6 -> G(1).distplot kernel'画出对象g中第一个变量的直方图，命名为gh freeze(gh) G(1).hist 'hist log(m1)'将g中的所有变量画入一张线性图中，改图命名为gfa graph gfa.line G'将g中所有的变量分别画出一张图并合并入gfg这一个对象中graph gfg.line(m) G 'multiple graphs'生成列表tbgsi，该列表中包含了g中所有变量单独的统计值freeze(tbGsi) G.stats(i) 'individual samples回归模型估计smpl 1952Q1 1992Q4equation eq1.ls log(m1) c log(gdp) rs dlog(pr)Dependent Variable: LOG(M1)Method: Least SquaresDate: 12/07/12 Time: 15:41Sample (adjusted): 1952Q2 1992Q4Included observations: 163 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.C 1.312383 0.032199 40.75850 0.0000LOG(GDP) 0.772035 0.006537 118.1092 0.0000RS -0.020686 0.002516 -8.221196 0.0000 DLOG(PR) -2.572204 0.942556 -2.728967 0.0071R-squared 0.993274 Mean dependent var 5.692279Adjusted R-squared 0.993147 S.D. dependent var 0.670253S.E. of regression 0.055485 Akaike info criterion -2.921176Sum squared resid 0.489494 Schwarz criterion -2.845256Log likelihood 242.0759 Hannan-Quinn criter. -2.890354F-statistic 7826.904 Durbin-Watson stat 0.140967Prob(F-statistic) 0.000000这里我们使用smpl来设定估计样本的观测区间，而equation语句则创建了方程对象eq1并进行最小二乘估计，其中的c代表回归方程的常数项，得到模型估计的结果如上图所示。

eviews基本操作介绍

eviews基本操作介绍
的Procs或对象窗口工具栏上的 Procs来选择过程
31
4 对象类型
除了序列对象和方程对象外还有许多其他类型的对象; 每种对象在对象集合中都有一个特定的图标表示 对象集合 虽然也是对象但对象集合没有图标;因此工作文件和数据库 不能放在其他的工作文件或数据库中
32
基本对象操作
30
3 对象过程PROC
许多EViews对象还包括过程Procedure 与视图一样的是;过 程通常以图表或坐标的形式显示在对象窗口中；与视图不同的 是;过程改变数据;无论对象本身中的还是其他对象中的
很多过程还创建新的对象 比如说序列对象含有进行平滑与 季节调整的过程;该过程可以创建一个新的含有平滑以及调整 后的数据的序列 方程对象的过程可以建立新的序列来包含残差 拟合值 以及预测
Eviews 统计分析 从入门到精通
第一章 Eviews简介
Eviews简介 Eviews的主窗口 工作文件的建立与工作文件窗口 对象的建立和对象窗口
Eviews简介
EViews的用途：统计 计量分析和预测 除菜单操作外;EViews还提供命令语言;矩阵语言和程序 设计 Eviews软件基础 —— 介绍EViews的基本用法 解释如何使 用EViews来管理数据 第一部分：数据分析基础 —— 描述使用EViews来完成数 据的基本分析
Eviews 全称 Econometrics Views ; 是美 国 QMS 公司 推 出 的 基于 Windows平台的专门从事数据分析 回归分析和预测的 计算机软件;Eviews是当今世界上最优秀的计量经济软件之一 ;其具有操作简便 界面友好 功能强大等特点;在科学数据分析 与评价 金融分析 经济预测 销售预测和成本分析等领域具有 广泛的影响 虽然EViews是由经济学家开发的并大多在经济 领域应用;但它的适用范围不应只局限于经济领域

eviews上机第五章精品PPT课件

eviews上机第五章精品PPT课件
为60.01-89.12，EViews不会对样本进行任何调整，因为在整个样本 估计期间ip(-3)的值都是可以得到的。一些操作不允许样本中间有数 据丢失，如带MA和ARCH项的估计。当执行这些步骤时，如果在样 本中间遇到一个NA就会出现一错误信息而且执行过程也会停止。
14
§5.3.3 估计选项
EVieபைடு நூலகம்s提供很多估计选项 这些选项允许进行以下操作：
在方程结果的顶部，EViews报告样本已经得到调整。从59.01-89.12期间 的372个观测值中，使用了369个观测值和所有相关变量的观测值
13
滞后变量：回归中包含滞后变量，样本的调整程度会不同，这取决于 样本期前的数据是否可得到。
如假设M1和IP是两个没有丢失数据的序列，样本区间为59.01-89.12 而且回归说明为：m1 c ip ip(-1) ip(-2) ip(-3)
其中cs是消费；inc是收入。 方程中C0代表自发消费，表示收入等于零时的消费水平； 而C1代表了边际消费倾向，0<C1<1，即收入每增加1元，消费将增加C1
元，若C1等于0.6，则收入每增加1元，消费将增加0.6元。 若消费方程中加上实际利率RS，即CSt=C0+C1INCt+C2RSt+εt，从经济
C是EViews用来说明回归中的常数而建立的序列。 EViews在回归中不会自动包括一个常数，因此必须明确列出作为回归变
量的常数。 内部序列c不出现在工作文档中，除了说明方程外不能使用它。
注意：到在工作文档中有一个预先定义的对象C：
这是缺省系数向量——当通过列出变量名的方式说明方程时，EViews会 根据变量在列表中出现的顺序在这个向量中存储估计系数。在上例中， 常数存储于c(1)，inc的系数存储于c(2)，即回归方程形式为：cs = c(1)+c(2)*inc。

利用Eviews软件进行最小二乘法回归实例

利用Eviews软件进行最小二乘法回归实例

例题中国居民人均消费支出与人均GDP（1978-2000），数据（例题1-2），预测，2001年人均GDP为4033.1元，求点预测、区间预测。

（李子奈，p50）解答：一、打开Eviews软件，点击主界面File按钮，从下拉菜单中选择Workfile。

在弹出的对话框中，先在工作文件结构类型栏（Workfile structure type）选择固定频率标注日期（Dated – regular frequency），然后在日期标注说明栏中（Date specification）将频率（Frequency）选为年度（Annual），再依次填入起止日期，如果希望给文件命名（可选项），可以在命名栏（Names - optional）的WF项填入自己选择的名称，然后点击确定。

此时建立好的工作文件如下图所示：在主界面点击快捷方式（Quick）按钮，从下拉菜单中选空白数据组（Empty Group）选项。

此时空白数据组出现，可以在其中通过键盘输入数据或者将数据粘贴过来。

在Excel文件（例题1-2）中选定要粘贴的数据，然后在主界面中点击编辑（Edit）按钮，从下拉菜单中选择粘贴（Paste），数据将被导入Eviews软件。

将右侧的滚动条拖至最上方，可以在最上方的单元格中给变量命名。

二、估计参数在主界面中点击快捷方式（Quick）按钮，从下拉菜单中选择估计方程（Estimate Equation）在弹出的对话框中设定回归方程的形式。

在方程表示式栏中（Equation specification ），按照被解释变量（Consp ）、常数项（c ）、解释变量（Gdpp ）的顺序填入变量名，在估计设置（Estimation settings ）栏中选择估计方法（Method ）为最小二乘法（LS – Least Squares ），样本（Sample ）栏中选择全部样本（本例中即为1978－2000），然后点击确定，即可得到回归结果。

计量分位数回归 eviews课件

计量分位数回归 eviews课件
分位数回归的系数估计需要求解线性规划问题，很多种方法 可以对此问题进行求解。
15
1、条件均值（conditional mean）
• 例2.1.1：一个假想的社区有99户家庭组成，欲 研究该社区每月家庭消费支出Y与每月家庭可 支配收入X的关系。 即如果知道了家庭的月收 入，能否预测该社区家庭的平均月消费支出水 平。
称为样本回归函数（sample regression function，SRF）。
23
• 注意：这里将样本回归线看成总体回归线的近似 替代
则
24
相对于最小二乘估计，分位数回归模型具有四个方面的 优势：
（1）分位数模型特别适合具有异方差性的模型。 （2）对条件分布的刻画更加的细致，能给出条件分布的 大体特征。每个分位点上的回归都赋予条件分布上某个特殊 点（中央或尾部）一些特征；把不同的分位点上的分位数回 归集中起来就能提供一个关于条件分布的更完整的统计特征 描述。并且不同分位点下所给出的参数估计本身也可能有值 得进一步探讨的意义。
据 u 取值符号进行非对称的加权，这里 u y 。
I
(u
0)
1 , 0 ,
u0 u0
10
一般的 分位数回归的检查函数为：
u u I u 0
其中， I 为Z 示性函数，Z是指示关系式。
当分位数为0.5时，就是最小一乘回归，即 中位数回归。
11
考察此最小化问题的一阶条件为：
0 dF( y) (1 ) dF( y)
1430 1650 1870 2112 1485 1716 1947 2200
2002 4950 11495 16445 19305 23870 25025 21450 21285
3500 2299 2321 2530 2629 2860 2871

Eviews数据统计与分析教程5章 基本回归模型OLS估计-普通最小二乘法

Eviews数据统计与分析教程5章 基本回归模型OLS估计-普通最小二乘法
2.方程对象
选择工作文件窗口工具栏中的“Object”| “New Object”| “Equation”选项，在下图所示的对话框中输入方程变量。
EViews统计分析基础教程
一、普通最小二乘法（OLS）
2.方程对象
EViews5.1提供了8种估计方法： “LS”为最小二乘法； “TSLS”为两阶段最小二乘法； “GMM”为广义矩法； “ARCH”为自回归条件异方差； “BINARY”为二元选择模型，其中包括Logit模型、Probit 模型和极端值模型； “ORDERED”为有序选择模型； “CENSORED”截取回归模型； “COUNT”为计数模型。
五、 线性回归模型的检验
3.异方差性检验
异方差性的后果 ：
当模型出现异方差性时，用OLS（最小二乘估计法）得到的 估计参数将不再有效；变量的显著性检验（t检验）失去意 义；模型不再具有良好的统计性质，并且模型失去了预测 功能。
EViews统计分析基础教程
五、 线性回归模型的检验
4.序列相关检验
方法：
EViews统计分析基础教程
四、 线性回归模型的基本假定
线性回归模型必须满足以下几个基本假定：
假定1：随机误差项u具有0均值和同方差，即 E ( ui ) = 0 i=1，2，…，n Var ( ui ) = σ2 i=1，2，…，n 其中，E表示均值，也称为期望，在这里随机误差项u的 均值为0。Var表示随机误差项u的方差，对于每一个样本 点i，即在i=1，2，…，n的每一个数值上，解释变量y对 被解释变量x的条件分布具有相同的方差。当这一假定条 件不成立是，称该回归模型存在异方差问题。
EViews统计分析基础教程
四、 线性回归模型的基本假定

EViews软件应用及对OLS的回归分析

EViews软件应用及对OLS的回归分析
31
第三十一页，编辑于星期五：十一点 九分。
32
第三十二页，编辑于星期五：十一点 九分。
（2）选择和打开对象
双击工作文件窗口中的对象图标即可选定对象。
选择并打开对象的另一种方法是使用主菜单上的 “Quick /Show”工作文件窗口中的“Show”。
33
第三十三页，编辑于星期五：十一点 九分。
（3）对象窗口工具条
• 所有的工作文件都有C 和RESID两个对象
• C代表系数向量， RESID代表最近一次预 测后的残差（序列对象）
22
第二十二页，编辑于星期五：十一点 九分。
一个典型的工作文件窗口
23
第二十三页，编辑于星期五：十一点 九分。
（2）改变工作文件的数据区间 Range
➢ 当需要对已建立的工作文件 追加数据，或对变量进行预 测，而这些数据超出工作文 件创立时所确定的起止日期 （或数据容量）时，需对工 作文件的数据区间范围进行 调整。
Windows9x
Windows2000 WindowsXP
6
第六页，编辑于星期五：十一点 九分。
B. 安装和启动EViews
1、正版：通过光盘安装，输入序列号，选择适当的 安装路径即可
2、网络下载版：安装说明及软件在网络教学平台
7
第七页，编辑于星期五：十一点 九分。
几种启动EViews的办法：
34
第三十四页，编辑于星期五：十一点 九分。
“View” 按钮用来改变对象窗口的视 图形式&其他功能
35
第三十五页，编辑于星期五：十一点 九分。
“Procs” 按钮可以用来执行对象的 过程
36
第三十六页，编辑于星期五：十一点 九分。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

EViews统计分析基础教程
一、普通最小二乘法（OLS）
1.最小二乘原理
估计总体回归函数的最优方法是选择B1和B2的估计量b1 ，b2， 使得残差Βιβλιοθήκη t尽可能达到最小。 用公式表达即为
总之，最小二乘原理就是选择样本回归函数使得y的估计值 与真实值之差的平方和最小。
EViews统计分析基础教程
一、普通最小二乘法（OLS）
EViews统计分析基础教程
一、普通最小二乘法（OLS）
1.最小二乘原理
设双变量的总体回归方程为 yt= B1 + B2xt +μt 样本回归函数为 yt= b1 + b2xt + et 其中，et为残差项，
5-3式为估计方程，b1 和b2分别为B1和B2的估计量， 因而 e = 实际的yt –估计的yt
EViews统计分析基础教程
四、 线性回归模型的基本假定
假定5：解释变量x1，x2，…，xi是非随机的确定性变量， 并且解释变量间互不相关。则这说明yi的概率分布具有 均值，即
2.实际值、拟合值和残差
三条曲线分别是实际值（Actual），拟合值（Fitted） 和残差（Residual）。实际值和拟合值越接近，方程拟 合效果越好。
EViews统计分析基础教程
三、多元线性回归模型
通常情况下，将含有多个解释变量的线性回归模型（多 元线性回归模型）写成如下形式， yi = 0 + 1 x1i +2 x2i+3 x3i+…k xki + ui （i=1， 2，…，n） 其中，y为被解释变量，也被称为因变量；x为解释变量 或自变量；u是随机误差项（random error term），也 被称为误差项或扰动项； n为样本个数。
EViews统计分析基础教程
四、 线性回归模型的基本假定
假定2：不同样本点下的随机误差项u之间是不相关的， 即 Cov（ui，uj）=0，i≠j，i，j=1，2，…，n 其中，cov表示协方差。当此假定条件不成立时，则 称该回归模型存在序列相关问题，也称为自相关问题。
EViews统计分析基础教程
EViews统计分析基础教程
二、一元线性回归模型
1.模型设定
一元线性回归模型的形式为
yi = 0 + 1 xi + ui
（i=1，2，…，n）
其中，y为被解释变量，也被称为因变量；x为解释变量或自 变量；u是随机误差项（random error term），也被称为误 差项或扰动项，它表示除了x之外影响y的因素，即y的变化 中未被x所解释的部分；n为样本个数。
2.方程对象
选择工作文件窗口工具栏中的“Object”| “New Object”| “Equation”选项，在下图所示的对话框中输入方程变量。
EViews统计分析基础教程
一、普通最小二乘法（OLS）
2.方程对象
EViews5.1提供了8种估计方法： “LS”为最小二乘法； “TSLS”为两阶段最小二乘法； “GMM”为广义矩法； “ARCH”为自回归条件异方差； “BINARY”为二元选择模型，其中包括Logit模型、Probit 模型和极端值模型； “ORDERED”为有序选择模型； “CENSORED”截取回归模型； “COUNT”为计数模型。
EViews统计分析基础教程
四、 线性回归模型的基本假定
线性回归模型必须满足以下几个基本假定：
假定1：随机误差项u具有0均值和同方差，即 E ( ui ) = 0 i=1，2，…，n Var ( ui ) = σ2 i=1，2，…，n 其中，E表示均值，也称为期望，在这里随机误差项u的 均值为0。Var表示随机误差项u的方差，对于每一个样本 点i，即在i=1，2，…，n的每一个数值上，解释变量y对 被解释变量x的条件分布具有相同的方差。当这一假定条 件不成立是，称该回归模型存在异方差问题。
EViews统计分析基础教程
二、一元线性回归模型
2.实际值、拟合值和残差
估计方程为
表示的是yt的拟合值， 和 分别是 0 和1的估计量。 实际值指的是回归模型中被解释变量（因变量）y的原始观 测数据。拟合值就是通过回归模型计算出来的yt的预测值。
EViews统计分析基础教程
二、一元线性回归模型
EViews统计分析基础教程
三、 多元线性回归模型
在多元线性回归模型中，要求解释变量x1，x2，…，xk之 间互不相关，即该模型不存在多重共线性问题。如果有 两个变量完全相关，就出现了完全多重共线性，这时参 数是不可识别的，模型无法估计。
EViews统计分析基础教程
三、 多元线性回归模型
通常情况下，把多元线性回归方程中的常数项看作虚拟 变量的系数，在参数估计过程中该常数项始终取值为1。 因而模型的解释变量个数为k+1.多元回归模型的矩阵形 式为 Y = X + u 其中，Y是因变量观测值的T维列向量；X是所有自变量 （包括虚拟变量）的T个样本点观测值组成的T×（k+1） 的矩阵；是k+1维系数向量；u是T维扰动项向量。
四、 线性回归模型的基本假定
假定3：同一个样本点下的随机误差项u与解释变量x之间 不相关，即
Cov（xi，ui）=0
i=1，2，…，n
EViews统计分析基础教程
四、 线性回归模型的基本假定
假定4：随机误差项u服从均值为0、同方差的正态分布， 即 u ～N（0，σ2） 如果回归模型中没有被列出的各因素是独立的随机 变量，则随着这些随机变量个数的增加，随机误差项u服 从正态分布。
EViews统计分析基础教程
第5章 基本回归模型的OLS估计
重点内容：
• 普通最小二乘法
• 线性回归模型的估计
• 线性回归模型的检验
EViews统计分析基础教程
一、普通最小二乘法（OLS）
1.最小二乘原理
设（x1，y1），（x2，y2），…，（xn，yn）是平面直角坐标 系下的一组数据，且x1< x2<…< xn，如果这组图像接近于一 条直线，我们可以确定一条直线y = a + bx ，使得这条直 线能反映出该组数据的变化。 如果用不同精度多次观测一个或多个未知量，为了确定各未 知量的可靠值，各观测量必须加改正数，使其各改正数的平 方乘以观测值的权数的总和为最小。因而称最小二乘法。