人教新课标版数学高二人教A选修4-1试题 3.2平面与圆柱面的截线

主动成长夯基达标1.梯形ABCD中,AB∥CD,若梯形不在平面α内,则它在α内的射影是（）A.平行四边形B.梯形C.一条线段D.一条线段或梯形思路解析:当梯形所在的平面平行于投射线时,梯形在α上的射影是一条线段;当梯形所在的平面与投射线不平行时,梯形在α上的射影是一个梯形.答案:D2.如果一个三角形的平行投影仍是一个三角形,则下列结论正确的是（）A.内心的平行投影还是内心B.重心的平行投影还是重心C.垂心的平行投影还是垂心D.外心的平行投影还是外心思路解析:如果三角形的平行投影仍是三角形,但三角形的形状通常将发生变化,此时三角形的各顶点、各边的位置也会发生变化,而重心、垂心、外心这些由顶点和边确定的点通常随着发生变化,而内心则始终是原先角平分线的交点,所以仍是新三角形的内心.答案:A3.如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是（）A.(0,+∞)B.(0,2)C.(1,+∞)D.(0,1)思路解析:将所给方程转化为标准形式,根据焦点的位置即可获得实数k的取值范围.将所给方程x2+ky2=2转化为标准形式,即22x+122=ky,因为焦点在y轴上,所以有22>k,于是0 <k <1.答案:D走近高考4.如图3-2-5,设P为△ABC所在平面外一点,点O为P在平面ABC上的射影,若PA =PB =PC,则O为△ABC的心.图3-2-5思路解析:连结AO、BO、CO,则AO、BO、CO分别为PA、PB、PC在平面ABC内的射影.又∵PA =PB =PC,由射影长定理,则OA =OB =OC,∴O为△ABC的外心.答案:外5.在平面解析几何中,我们学过用方程表示直线、圆等图形,将椭圆上的点满足的条件用坐标表示出来,也可以得到椭圆的方程,试建立适当的坐标系,求长轴为2a,短轴为2b（a>b）,焦距为2c 的椭圆的方程.思路解析:以长轴所在直线为x 轴建立坐标系,也可以以长轴所在直线为y 轴建立坐标系.解:以长轴所在直线为x 轴建立坐标系,其方程为a x 2+12=by ;以长轴所在直线为y 轴建立坐标系,其方程为b x 2+12=ay .。

[核心必知]1．平面与圆柱面的截线(1)椭圆组成元素：F1，F2叫椭圆的焦点；F1F2叫椭圆的焦距；AB叫椭圆的长轴；CD叫椭圆的短轴．如果长轴为2a，短轴为2b，那么焦距2c(2)如图(1)，AB、CD是两个等圆的直径，AB∥CD，AD、BC与两圆相切，作两圆的公切线EF，切点分别为F1、F2，交BA、DC的延长线于E、F，交AD于G1，交BC于G2.设EF与BC、CD的交角分别为φ、θ.①G 2F 1＋G 2F 2＝AD ；②G 1G 2＝AD ；③G 2F 1G 2E＝cos φ＝sin θ. (3)如图(2)，将两个圆拓广为球面，将矩形ABCD 看成是圆柱面的轴截面，将EB 、DF拓广为两个平面α、β，EF 拓广为平面γ，则平面γ与圆柱面的截线是椭圆．即得定理1：圆柱形物体的斜截口是椭圆．2．平面与圆锥面的截线(1)如图，AD 是等腰三角形底边BC 上的高，∠BAD ＝α，直线l 与AD 相交于点P ，且与AD 的夹角为β⎝⎛⎭⎫0<β<π2，则：①β>α，l 与AB (或AB 的延长线)、AC 相交；②β＝α，l 与AB 不相交；③β<α，l 与BA 的延长线、AC 都相交．(2)定理2：在空间中，取直线l为轴，直线l′与l相交于O点，夹角为α，l′围绕l旋转得到以O为顶点，l′为母线的圆锥面．任取平面π，若它与轴l的交角为β(当π与l平行时，记β＝0)，则①β>α，平面π与圆锥的交线为椭圆；②β＝α，平面π与圆锥的交线为抛物线；③β<α，平面π与圆锥的交线为双曲线．[问题思考]用平面截球面和圆柱面所得到的截线分别是什么形状？提示：联想立体图形及课本方法，可知用平面截球面所得截线的形状是圆；用平面截圆柱面所得截线的形状是圆或椭圆．已知圆柱底面半径为3，平面β与圆柱母线夹角为60°，在平面β上以G1G2所在直线为横轴，以G1G2中点为原点，建立平面直角坐标系，求平面β与圆柱截口椭圆的方程．[精讲详析]本题考查平面与圆柱面的截线．解答本题需要根据题目条件确定椭圆的长轴和短轴．过G1作G1H⊥BC于H.∵圆柱底面半径为3，∴AB＝2 3.∵四边形ABHG1是矩形，∴AB＝G1H＝2 3.在Rt△G1G2H中，G1G2＝G1Hsin∠G1G2H＝2332＝4.又椭圆短轴长等于底面圆的直径23，∴椭圆的标准方程为x 24＋y 23＝1.——————————————————借助条件中已经建立的直角坐标系，通过相关平面图形转换确定椭圆的长、短轴的长是关键．1．平面内两个定点的距离为8，动点M 到两个定点的距离的和为10，求动点M 的轨迹方程．解：以两点的连线段所在的直线为x 轴，线段的中垂线为y 轴建立直角坐标系，则由椭圆的定义知，动点的轨迹是椭圆，设所求椭圆方程为x 2a 2＋y 2b2＝1.∵2a ＝10，2c ＝8，∴a ＝5，c ＝4.则b 2＝9.故所求椭圆的方程为x 225＋y 29＝1.证明：定理2的结论(1)，即β>α时，平面π与圆锥的交线为椭圆．[精讲详析] 本题考查平面与圆锥面的截线．解答本题需要明确椭圆的定义，利用椭圆的定义证明．如图，与定理1的证明相同，在圆锥内部嵌入Dandelin双球，一个位于平面π的上方，一个位于平面π的下方，并且与平面π及圆锥均相切．当β>α时，由上面的讨论可知，平面π与圆锥的交线是一个封闭曲线．设两个球与平面π的切点分别为F1、F2，与圆锥相切于圆S1、S2.在截口的曲线上任取一点P，连接PF1、PF2.过P作母线交S1于Q1，交S2于Q2，于是PF1和PQ1是从P到上方球的两条切线，因此PF1＝PQ1.同理，PF2＝PQ2.所以PF1＋PF2＝PQ1＋PQ2＝Q1Q2.由正圆锥的对称性，Q1Q2的长度等于两圆S1、S2所在平行平面间的母线段的长度而与P的位置无关，由此我们可知在β>α时，平面π与圆锥的交线是以F1、F2为焦点的椭圆．——————————————————由平面中，直线与等腰三角形两边的位置关系拓广为空间内圆锥与平面的截线之后，较难入手证明其所成曲线的形状，尤其是焦点的确定更加不容易，但可以采用与上节中定理1的证明相同的方法，即Dandelin双球法，这时较容易确定椭圆的焦点，学生也容易入手证明，使问题得到解决.2．在空间中，取直线l为轴，直线l′与l相交于O点，夹角为α，l′围绕l旋转得到以O为顶点，l′为母线的圆锥面，任取平面π，若它与轴l的交角为β(当π与l平行时，记β＝0)，求证：β＝α时，平面π与圆锥的交线是抛物线．证明：如图，设平面π与圆锥内切球相切于点F1，球与圆锥的交线为圆S，过该交线的平面为π′，π与π′相交于直线m.在平面π与圆锥的截线上任取一点P，连接PF1.过点P 作P A⊥m，交m于点A，过点P作π′的垂线，垂足为B，连接AB，则AB⊥m，∴∠P AB 是π与π′所成二面角的平面角．连接点P与圆锥的顶点，与S相交于点Q1，连接BQ1，则∠BPQ 1＝α，∠APB ＝β.在Rt △APB 中，PB ＝P A cos β.在Rt △PBQ 1中，PB ＝PQ 1cos α.∴PQ 1P A ＝cos βcos α.又∵PQ 1＝PF 1，α＝β，∴PF 1P A＝1， 即PF 1＝P A ，动点P 到定点F 1的距离等于它到定直线m 的距离，故当α＝β时，平面与圆锥的交线为抛物线．本课时考点在高考中很少考查．本考题以选择题的形式考查了平面与圆柱面的截线的形状，是高考命题的一个新动向．[考题印证]已知半径为2的圆柱面，一平面与圆柱面的轴线成45°角，则截线椭圆的焦距为( )A ．22B ．2C ．4D ．4 2[命题立意] 本题主要考查平面与圆柱面的截线问题，同时考查椭圆的相关性质．[解析]选C由题意知，椭圆的长半轴长a＝2sin 45°＝22，短半轴长b＝2，则半焦距c＝a2－b2＝8－4＝2.所以焦距2c＝4.一、选择题1．下列说法不．正确的是()A．圆柱面的母线与轴线平行B．圆柱面的某一斜截面的轴面总是垂直于直截面C．圆柱面与斜截面截得的椭圆的离心率与圆柱面半径无关，只与母线和斜线面的夹角有关D．平面截圆柱面的截线椭圆中，短轴长即为圆柱面的半径解析：选D显然A正确，由于任一轴面过轴线，故轴面与圆柱的直截面垂直，B正确，C显然正确，D中短轴长应为圆柱面的直径长，故不正确．2．过球面上一点可以作球的()A．一条切线和一个切平面B．两条切线和一个切平面C．无数条切线和一个切平面D．无数条切线和无数个切平面解析：选C过球面上一点可以作球的无数条切线，并且这些切线在同一个平面内，过球面上一点可以作一个球的切平面．3．球的半径为3，球面外一点到球心的距离为6，则过该点的球的切线和过切点的半径所成的角为()A．30°B．60°C．90°D．不确定解析：选C由平面内圆的切线垂直于过切点的半径，我们推广到空间中仍有球的切线垂直于过切点的球的半径，因为切线与过切点的半径仍相交，故可以转化为平面图形，因而可以利用平面图形的性质来解决．4．一圆锥面的母线和轴线成30°角，当用一与轴线成30°的不过顶点的平面去截圆锥面时，所截得的截线是()A．椭圆B．双曲线C．抛物线D．两条相交直线解析：选C如图可知应为抛物线．二、填空题5．一平面与半径为3的圆柱面截得椭圆，若椭圆的两焦球球心的距离为10，则截面与圆柱面母线的夹角的余弦值为________．解析：因为两焦球的球心距即为椭圆的长轴长，所以2a＝10，即a＝5.又椭圆短轴长2b＝6，即b＝3，∴c＝4.故e＝cos φ＝ca＝45.答案：456．一平面与圆柱面的母线成45°角，平面与圆柱面的截线椭圆的长轴长为6，则圆柱面的半径为________．解析：由2a ＝6，即a ＝3，又e ＝cos 45°＝22， 得b ＝c ＝ea ＝22×3＝322，即为圆柱面的半径． 答案：3227．设圆锥面V 是由直线l ′绕直线l 旋转而得，l ′与l 交点为V ，l ′与l 的夹角为α(0°<α<90°)，不经过圆锥顶点V 的平面π与圆锥面V 相交，设轴l 与平面π所成的角为β，则：当________时，平面π与圆锥面的交线为圆；当________时，平面π与圆锥面的交线为椭圆；当________时，平面π与圆锥面的交线为双曲线；当________时，平面π与圆锥面的交线为抛物线．答案：β＝90° α<β<90° β<α β＝α8．半径分别为1和2的两个球的球心距为12，则这两个球的外公切线的长为______，内公切线的长为______．解析：设两个球的球心为O1，O2，外公切线的切点为A、B，则有|AB|＝O1O22－（R1－R2）2＝122－（2－1）2＝143，设内公切线的切点分别为C、D，则|CD|＝O1O22－（R1＋R2）2＝122－（2＋1）2＝144－9＝135＝315.答案：143315三、解答题9．一平面截圆锥的截线为椭圆，椭圆的长轴长为8，长轴的两端点到顶点的距离分别是6和10，求椭圆的离心率．解：如图所示为截面的轴面，则AB＝8，SB＝6，SA＝10，则∠SBA ＝π2，cos ∠ASB ＝35， cos ∠BSP ＝cos 12∠ASB ＝1＋cos ∠ASB 2＝255. ∴cos ∠SPB ＝sin ∠BSP ＝55，∴e ＝cos ∠SPB cos ∠BSP ＝12. 10．如图，上面一个Dandelin 球与圆锥面的交线为圆S ，记圆S 所在的平面为π′，设π与π′的交线为m .在椭圆上任取一点P ，连接PF 1，在π中过P 作m 的垂线，垂足为A ，过P 作π′的垂线，垂足为B ，连接AB 是P A 在平面π′上的射影．若Rt △ABP 中，∠APB ＝β.求平面π与π′所成二面角的大小．解：由已知PB ⊥π′，平面π′∩平面π＝m .∴m ⊥PB .又P A ⊥m ，∴m ⊥面P AB ，∴∠P AB 是π与π′所成二面角的平面角．又∠APB ＝β，∴∠P AB ＝π2－β.11．定长为3的线段AB 的两个端点在抛物线y 2＝x 上移动，设线段AB 的中点为M ，求点M 到y 轴的最短距离．解：设A (x 1，y 1)，B (x 2，y 2)，则AF ＝x 1＋14，BF ＝x 2＋14，若AB 过F ，则AF ＋BF ＝AB ， 此时点M 到y 轴距离为32－14＝54； 若AB 不过F ，则AF ＋BF >AB ，即x 1＋14＋x 2＋14>3，x 1＋x 2>52， 从而M 的横坐标x 1＋x 22>54， 显然弦AB 过焦点F 时，M 到y 轴距离最短．设过F 的直线方程为y ＝k ⎝⎛⎭⎫x －14， 联立⎩⎪⎨⎪⎧y 2＝x ，y ＝k ⎝⎛⎭⎫x －14，则k 2x 2－⎝⎛⎭⎫k 22＋1x ＋k 216＝0. ∵x M ＝54，∴k ＝±22，即直线存在． ∴点M 到y 轴最短距离为54.。

一平行射影二平面与圆柱面的截线三平面与圆锥面的截线．了解平行射影的含义，体会平行射影．．会证明平面与圆柱面的截线是椭圆(特殊情况是圆)．(重点)．会用双球证明定理、定理.(难点)[基础·初探]教材整理射影阅读教材～，完成下列问题．．正射影给定一个平面α，从一点作平面α的垂线，垂足为点′，称点′为点在平面α上的正射影．一个图形上各点在平面α上的正射影所组成的图形，称为这个图形在平面α上的正射影．．平行射影设直线与平面α相交(如图--)，称直线的方向为投影方向．过点作平行于的直线(称为投影线)必交α于一点′，称点′为沿的方向在平面α上的平行射影．一个图形上各点在平面α上的平行射影所组成的图形，叫做这个图形的平行射影．图--下列说法正确的是( )．平行射影是正射影．正射影是平行射影．同一个图形的平行射影和正射影相同．圆的平行射影不可能是圆【解析】正射影是平行射影的特例，不正确；对于同一图形，当投影线垂直于投影面时，其平行射影就是正射影，否则不相同，故不正确；当投影线垂直于投影面且圆面平行于投影面时，圆的平行射影是圆，不正确；只有正确．【答案】教材整理两个定理阅读教材～，完成下列问题．．椭圆的定义平面上到两个定点的距离之和等于定长的点的轨迹叫做椭圆．．两个定理定理：圆柱形物体的斜截口是椭圆．定理：在空间中，取直线为轴，直线′与相交于点，夹角为α，′围绕旋转得到以为顶点，′为母线的圆锥面．任取平面π，若它与轴的交角为β(当π与平行时，记β＝)，则()β>α，平面π与圆锥的交线为椭圆；()β＝α，平面π与圆锥的交线为抛物线；()β<α，平面π与圆锥的交线为双曲线．下列说法不正确的是( )。

A 选修4选修41第三讲圆锥曲线性质的探讨二平面与圆柱面的截线 测试题 2019.91,下列命题中正确的是（ ）A ．过平面外一点作此平面的垂面是唯一的B ．过直线外一点作此直线的垂线是唯一的C ．过平面的一条斜线作此平面的垂面是唯一的D ．过直线外一点作此直线的平行平面是唯一的2,由422=+=y x x y 和圆所围成的较小图形的面积是( )A ．πB ．4πC ．43πD ．23π3,设数列{}n a 的前n 项和S n ，且12+-=n a n ，则数列}{n S n 的前11项的和为（ ）A ．-45B ．-50C ．-55D ．-664,设则的值为（ ）A ．B ．C ．、中较小的数D ．、中较大的数5,某工厂有甲、乙、丙、丁四类产品的数量成等比数列，共计3000件，现要用分层抽样的方法从中抽取150件进行质量检测，其中乙、丁两类产品抽取的总数为100件，则甲类产品总共有（ ）⎩⎨⎧<>-=)0(1)0(1)(x x x f )(2)()()(b a b a f b a b a ≠-⋅--+a b a b a bA. 100件B. 200件C. 300件D. 400件6,某工厂有甲、乙、丙、丁四类产品的数量成等比数列，共计3000件，现要用分层抽样的方法从中抽取150件进行质量检测，其中乙、丁两类产品抽取的总数为100件，则甲类产品总共有（ ）A. 100件B. 200件C. 300件D. 400件7,已知函数)20,0)(sin()(πϕωϕω≤<>+=x x f ，且此函数的图象如图所示，则点),(ϕωP 的坐标是（ ） A.)2,2(π B.)4,2(π C.)2,4(π D.)4,4(π8,命题:p 不等式0]1)1(lg[>+-x x 的解集为{}10|<<x x ；命题:q 在ABC ∆中，B A >是B A sin sin >成立的必要不充分条件.则（ ）A.p 真q 假B.p 且q 为真C.p 或q 为假D.p 假q 真9,已知数列是等差数列，是等比数列，且,．（1）求数列的通项公式；（2）求数列的前10项和．{}n a {}n b 112,a b ==454b =12323a a a b b ++=+{}n b {}n a 10S10,已知向量, 向量，且与的夹角为，其中A 、B 、C 是的内角．（1）求角B 的大小； （2）求 的取值范围．测试题答案1, C2, A3, D4, D5, B6, B7, B8, A9, 解（1）（2）10, 解：（1） m =，且与向量n = （2，0）所成角为，又()m sin B,1cos B =-()n 2,0=m n 3πABC ∆C A sin sin +132-⨯=n n b 29010=S ()B B cos 1,sin -3π∴3sin cos 1=-B B ∴cos 1B B +=∴21)6sin(=+πB π<<B 0∴6766πππ<+<B ∴656ππ=+B ∴32π=B（2）由（1）知，，A+C= ===，，32π=B ∴3π∴C A sin sin +)3sin(sin A A -+πA A cos 23sin 21+)3sin(A +π 30π<<A ∴3233πππ<+<A ∴)3sin(A +π⎥⎦⎤ ⎝⎛∈1,23∴C A sin sin +⎥⎦⎤ ⎝⎛∈1,23。

二平面与圆柱面的截线课时过关·能力提升基础巩固1下列说法不正确的是()A.圆柱面的母线与轴线平行B.圆柱面的某一轴截面垂直于直截面C.圆柱面与斜截面截得的椭圆的离心率与圆柱面半径无关,只与母线和斜截面的夹角有关D.平面截圆柱面的截线椭圆中,短轴长即为圆柱面的半径A正确;由于任一轴截面过轴线,故轴截面与圆柱的直截面垂直,B正确;C显然正确;D中短轴长应为圆柱面的直径长,故不正确.2已知平面β与一圆柱斜截口(椭圆)的离心率为,则平面β与圆柱母线的夹角是()A. 0°B.60°C.45°D.90°β与母线夹角为φ,则cosφ=,故φ= 0°.3如果椭圆的两个焦点将长轴分成三等份,那么,这个椭圆的两条准线间的距离是焦距的() A.9倍 B.4倍 C.12倍 D.18倍2a,2b,2c,由已知,得=2c,即a=3c,故两条准线间的距离为=18c.4一组底面为同心圆的圆柱被一平面所截,截口椭圆具有() A.相同的长轴 B.相同的焦点C.相同的准线D.相同的离心率,所以长轴不同.嵌入的Dandelin球不同,则焦点不同,准线也不同,而平面与圆柱的母线夹角相同,故离心率相同.5若椭圆的一个顶点与两个焦点构成等边三角形,则此椭圆的离心率是()A.5B.4C. D.2a,2b,2c,由已知a=2c,得,即e=.6两个圆柱的底面半径分别为R,r(R>r),平面π与它们的母线的夹角分别为α,β(α<β<90°),斜截口椭圆的离心率分别为e1,e2,则()A.e1>e2B.e1<e2C.e1=e2D.无法确定e1=cosα,e2=cosβ,又α<β<90°时,cosα>cosβ,∴e1>e2.7已知圆柱的底面半径为2,平面π与圆柱的斜截口椭圆的离心率为,则椭圆的长半轴是() A.2 B.4C. 6D.42a,2b,2c.由题意,知b=2,-,则-4,解得a=4.8已知平面π截圆柱体,截口是一条封闭曲线,且截面与底面所成的角为45°,此曲线是,它的离心率为.9已知椭圆两条准线间的距离为8,离心率为,则Dandelin球的半径是.4,,解得 , ,∴b=-.∴Dandelin球的半径为.10如图,设两个焦点的距离F1F2=2c,两个端点的距离G1G2=2a,求证:l1与l2之间的距离为.,设椭圆上任意一点P,过点P作PQ1⊥l1于点Q1,过点P作PQ2⊥l2于点Q2.连接PF1,PF2.∵e=,∴PF1=PQ1,PF2=PQ2.由椭圆定义,知PF1+PF2=2a,∴PQ1+PQ2=2a.∴PQ1+PQ2=,即l1与l2之间的距离为.能力提升1如图,过点F1作F1Q⊥G1G2,若△QF1F2为等腰直角三角形,则椭圆的离心率为()A.B.-C.2-D.-12a,2b,2c.∵△QF1F2是等腰直角三角形,∴QF1=F1F2=2c,QF2=2 c.由椭圆的定义,得QF1+QF2=2a,∴e=-1.2已知圆柱的底面半径为r,平面α与圆柱母线的夹角为 0°,则它们截口椭圆的焦距是() A.2r B.4r C.r D.3r,过点G2作G2H⊥AD,H为垂足,则G2H=2r.在Rt△G1G2H中,=2r×2=4r,G1G2=60°∴长轴2a=G1G2=4r,短轴2b=2r.∴焦距2c=2-=2×r=2r.3一平面截圆柱(圆柱底面半径为1,高足够长)的侧面,得到一个离心率是的二次曲线,该曲线两焦点之间的距离为()A. B.2 C.3 D.e=<1,∴曲线是椭圆,且e=cosθ=,θ= 0°,φ=60°(φ是底面与截面的夹角).∴ 60°=,∴2a==4,∴a=2.又,∴c=.∴2c=2.★4如图,已知A为左顶点,F是左焦点,l交OA的延长线于点B,点P,Q在椭圆上,有PD⊥l于点D,QF⊥AO,则椭圆的离心率是①;②;③;④;⑤.其中正确的是()A.①②B.①③④C.②③⑤D.①②③④⑤符合离心率定义;②过点Q作QC⊥l于C,∵QC=FB,∴符合离心率定义;③∵AO=a,BO=,∴,故也是离心率;④∵AF=a-c,AB=-a,∴-,∴是离心率;-⑤∵FO=c,AO=a,∴是离心率.∴①②③④⑤的表述均正确,故选D.5已知圆柱底面半径为b,平面π与圆柱母线的夹角为 0°,在圆柱与平面交线上有一点P到一准线l1的距离是b,则点P到另一准线l2对应的焦点F2的距离是.=4b,∴c=4- b.,椭圆短轴长为2b,长轴长2a=0°∴e=或e= 0°=.设点P到焦点F1的距离为d,则,∴d=b.又PF1+PF2=2a=4b,∴PF2=4b-PF1=4b-b=5b.6如图,已知PF1∶PF2=1∶3,AB=12,G1G2=20,求PQ的长.2a,短轴长为2b,焦距为2c,.由椭圆定义,知PF1+PF2=G1G2=20,由已知可得a=10,b=6,c=-=8,e=45又PF1∶PF2=1∶3,则PF1=5,PF2=15.,由离心率定义,得45.∴PQ= 54★7如图,在圆柱O1O2内嵌入双球,使它们与圆柱面相切,并且和圆柱的斜截面相切,切点分别为F1,F2.求证:斜截面与圆柱面的截线是以点F1,F2为焦点的椭圆.,设点P为曲线上任一点,连接PF1,PF2,则PF1,PF2分别是两个球面的切线,切点分别为F1,F2,过点P作母线,与两球面分别相交于点K1,K2,则PK1,PK2分别是两球面的切线,切点为K1,K2.根据切线长定理的空间推广,知PF1=PK1,PF2=PK2,所以PF1+PF2=PK1+PK2=K1K2.由于K1K2为定值,故点P的轨迹是以F1,F2为焦点的椭圆.。

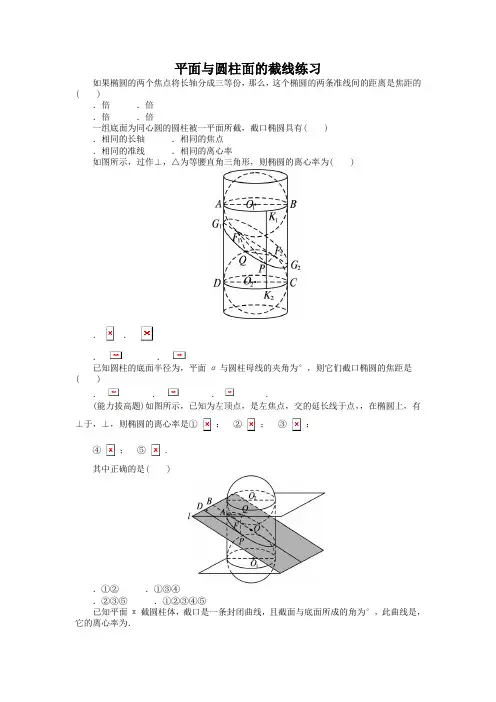
平面与圆柱面的截线练习
如果椭圆的两个焦点将长轴分成三等份，那么，这个椭圆的两条准线间的距离是焦距的( )
．倍．倍
．倍．倍
一组底面为同心圆的圆柱被一平面所截，截口椭圆具有( )
．相同的长轴．相同的焦点
．相同的准线．相同的离心率
如图所示，过作⊥，△为等腰直角三角形，则椭圆的离心率为( )
．．
．．
已知圆柱的底面半径为，平面α与圆柱母线的夹角为°，则它们截口椭圆的焦距是( )
．．．．
(能力拔高题)如图所示，已知为左顶点，是左焦点，交的延长线于点，，在椭圆上，有⊥于，⊥，则椭圆的离心率是①；②；③；
④；⑤.
其中正确的是( )
．①② ．①③④
．②③⑤ ．①②③④⑤
已知平面π截圆柱体，截口是一条封闭曲线，且截面与底面所成的角为°，此曲线是，它的离心率为．
已知椭圆两条准线间的距离为，离心率为，则球的半径是．
已知圆柱底面半径为，平面π与圆柱母线的夹角为°，在圆柱与平面交线上有一点到一准线的距离是，则点到另一准线对应的焦点的距离是．
如图所示，已知∶＝∶，＝，＝，求.
参考答案
答案：设椭圆的长轴长，短轴长，焦距分别为，，，由已知，得，即＝，故两条准线间的距离为＝.
答案：因为底面半径大小不等，所以长轴不同.
嵌入的球不同，则焦点不同，准线也不同，
而平面与圆柱的母线夹角相同，故离心率相同.
答案：设椭圆的长轴长，短轴长，焦距分别为，，.
∵△是等腰直角三角形，
∴＝＝，＝.
由椭圆的定义，得＋＝，
∴.
答案：如图，过点作⊥，为垂足，则.
在△中，
×，。

课时跟踪检测(十一) 平行射影 平面与圆柱面的截线 平面与圆锥面的截线一、选择题1．一条直线在一个面上的平行投影是( )A ．一条直线B ．一个点C ．一条直线或一个点D ．不能确定解析：选C 当直线与面垂直时，平行投影可能是点．2．△ABC 的一边在平面α内，一顶点在平面α外，则△ABC 在面α内的射影是( )A ．三角形B ．一直线C ．三角形或一直线D ．以上均不正确解析：选D 当△ABC 所在平面平行于投影线时，射影是一线段，不平行时，射影是三角形．3．下列说法不．正确的是( ) A ．圆柱面的母线与轴线平行B ．圆柱面的某一斜截面的轴面总是垂直于直截面C ．圆柱面与斜截面截得的椭圆的离心率与圆柱面半径无关，只与母线和斜线面的夹角有关D ．平面截圆柱面的截线椭圆中，短轴长即为圆柱面的半径解析：选D 显然A 正确，由于任一轴面过轴线，故轴面与圆柱的直截面垂直，B 正确，C 显然正确，D 中短轴长应为圆柱面的直径长，故不正确．4．设圆锥的顶角(圆锥轴截面上两条母线的夹角)为120°，当圆锥的截面与轴成45°角时，则截得二次曲线的离心率为( ) A.22 B. 2C ．1D.12 解析：选B 由题意知α＝60°，β＝45°，满足β<α，这时截圆锥得的交线是双曲线，其离心率为e ＝cos 45°cos 60°＝ 2. 二、填空题5．用平面截球面和圆柱面所得到的截线形状分别是________、________.解析：联想立体图形及课本方法，可得结论．要注意平面截圆柱面所得的截线的不同情况．答案：圆 圆或椭圆6．有下列说法：①矩形的平行射影一定是矩形；②梯形的平行射影一定是梯形；③平行四边形的平行射影可能是正方形；④正方形的平行射影一定是菱形；其中正确命题是________．(填上所有正确说法的序号)解析：利用平行射影的概念和性质进行判断．答案：③7．在底面半径为6的圆柱内有两个半径也为6的球面，两球的球心距为13.若作一个平面与这两个球面相切，且与圆柱面相交成一椭圆，则椭圆的长轴长为________．和球O2都相切的平解析：如图，为圆柱的轴截面，AB为与两球O面与轴截面的交线，由对称性知AB过圆柱的几何中心O.由O1O⊥OD，O1C⊥OA，故∠OO1C＝∠AOD，且O1C＝OD＝6，所以Rt△OO1C≌Rt△AOD，则AO＝O1O.故AB＝2AO＝2O1O＝O1O2＝13.显然AB即为椭圆的长轴，所以椭圆的长轴长13.答案：13三、解答题8．△ABC是边长为2的正三角形，BC∥平面α，A，B，C在α的同侧，它们在α内的射影分别为A′，B′，C′，若△A′B′C′为直角三角形，BC与α间的距离为5，求A到α的距离．解：由条件可知A′B′＝A′C′，∴∠B′A′C′＝90°.设AA′＝x，在直角梯形AA′C′C中，A′C′2＝4－(5－x)2，由A′B′2＋A′C′2＝B′C′2，得2×[4－(x－5)2]＝4，x＝5±2.即A到α的距离为5±2.9．若圆柱的一正截面的截线为以3为半径的圆，圆柱的斜截面与轴线成60°，求截线椭圆的两个焦点间的距离．解：设椭圆长半轴为a，短半轴为b，半焦距为c，则b＝3，a ＝b cos 60°＝3×2＝6，∴c 2＝a 2－b 2＝62－32＝27.∴两焦点间距离2c ＝227＝6 3.10.如图所示，圆锥侧面展开图扇形的中心角为2π，AB ，CD 是圆锥面的正截面上互相垂直的两条直径，过CD 和母线VB 的中点E 作一截面，求截面与圆锥的轴线所夹的角的大小，并说明截线是什么圆锥曲线．解：设⊙O 的半径为R ，母线VA ＝l ，则侧面展开图的中心角为2πR l ＝2π，∴圆锥的半顶角α＝π4.连接OE ，∵O ，E 分别是AB ，VB 的中点，∴OE ∥VA ，∴∠VOE ＝∠AVO ＝π4.又∵AB ⊥CD ，VO ⊥CD ，∴CD ⊥平面VAB .∴平面CDE ⊥平面VAB .即平面VAB 为截面CDE 的轴面，∴∠VOE 为截面与轴线所夹的角，即为π4.又∵圆锥的半顶角与截面与轴线的夹角相等，故截面CDE 与圆锥的截线为一抛物线．。

人教新课标A版选修4-1数学3.2平面与圆柱面的截线同步检测B卷姓名:________ 班级:________ 成绩:________一、选择题 (共14题；共28分)1. （2分） (2017高二上·绍兴期末) 如图，AB是平面a的斜线段，A为斜足，若点P在平面a内运动，使得△ABP的面积为定值，则动点P的轨迹是（）A . 圆B . 椭圆C . 一条直线D . 两条平行直线2. （2分）已知圆柱的底面半径为2，高为3，用一个与底面不平行的平面去截，若所截得的截面为椭圆，则椭圆的离心率的最大值为（）A . 1B .C .D .3. （2分）如图，一个底面半径为R的圆柱被与其底面所成角为θ（00＜θ＜900）的平面所截，截面是一个椭圆．当θ为30°时，这个椭圆的离心率为（）A .B .C .D .4. （2分）如图，一个底面半径为R的圆柱被与其底面所成角是30°的平面所截，截面是一个椭圆，则该椭圆的离心率是（）A .B .C .D .5. （2分）某舞台灯光设计师为了在地板上设计图案，他把一端向下发光的光源和支架之间的角度固定为θ角，支架的一端固定在地板的中心位置，支架的另一端固定在天花板的适当位置，当光源围绕支架以θ角快速旋转时，地板上可能出现的图案有（）A . 椭圆B . 抛物线C . 圆D . 以上均有可能6. （2分）已知平面β与一圆柱斜截口（椭圆）的离心率为 ,则平面β与圆柱母线的夹角是（）A . 30°B . 60°C . 45°D . 90°7. （2分）两个圆柱的底面半径分别为R,r（R>r）,平面π与它们的母线的夹角分别为α,β（α<β<90°）,斜截口椭圆的离心率分别为e1,e2,则（）A . e1>e2B . e1<e2C . e1=e2D . 无法确定8. （2分）已知圆柱的底面半径为2,平面π与圆柱的斜截口椭圆的离心率为 ,则椭圆的长半轴是（）A . 2B . 4C .D .9. （2分）一组底面为同心圆的圆柱被一平面所截,截口椭圆具有（）A . 相同的长轴B . 相同的焦点C . 相同的准线D . 相同的离心率10. （2分）如图,过点F1作F1Q⊥G1G2,△QF1F2为等腰直角三角形,则椭圆的离心率为（）A .B .C . 2-D . -111. （2分）已知圆柱的底面半径为r,平面α与圆柱母线的夹角为60°,则它们截口椭圆的焦距是（）A . 2 rB . 4 rC . rD . 3r12. （2分）一平面截圆柱（圆柱底面半径为1,高足够长）的侧面,得到一个离心率是的二次曲线,该曲线两焦点之间的距离为（）A .B . 2C . 3D .13. （2分）如图,已知A为左顶点,F是左焦点,l交OA的延长线于点B,点P,Q在椭圆上,有PD⊥l于点D,QF⊥AO,则椭圆的离心率是① ;② ;③ ;④ ;⑤其中正确的是（）A . ①②B . ①③④C . ②③⑤D . ①②③④⑤14. （2分）工人师傅在如图1的一块矩形铁皮上画一条曲线，沿曲线剪开，将所得到的两部分卷成圆柱状，如图2，然后将其对接，可做成一个直角的“拐脖”，如图3．工人师傅所画的曲线是（）A . 一段圆弧B . 一段抛物线C . 一段双曲线D . 一段正弦曲线二、填空题 (共7题；共12分)15. （1分）(2017·武威模拟) 如图所示，一个圆柱形乒乓球筒，高为20厘米，底面半径为2厘米．球筒的上底和下底分别粘有一个乒乓球，乒乓球与球筒底面及侧面均相切（球筒和乒乓球厚度均忽略不计）．一个平面与两个乒乓球均相切，且此平面截球筒边缘所得的图形为一个椭圆，则该椭圆的离心率为________．16. （2分）一平面截球面产生的截面形状是________ ；它截圆柱面所产生的截面形状是________ ．17. （3分）底面直径为10的圆柱被与底面成60°的平面所截，截口是一个椭圆，该椭圆的长轴长________ ，短轴长________ ，离心率为________ ．18. （1分）如图，一个底面半径为R的圆柱被与其底面所成角为θ（0°＜θ＜90°）的平面所截，截面是一个椭圆，当θ为30°时，这个椭圆的离心率为________ ．19. （1分）一只半径为R的球放在桌面上，桌面上一点A的正上方相距（+1）R处有一点光源O，OA与球相切，则球在桌面上的投影﹣﹣﹣﹣﹣﹣椭圆的离心率为________ ．20. （3分）底面直径为12cm的圆柱被与底面成30°的平面所截，截口是一个椭圆，该椭圆的长轴长________ ，短轴长________ ，离心率为________ ．21. （1分）工人师傅在如图1的一块矩形铁皮的中间画了一条曲线，并沿曲线剪开，将所得的两部分卷成圆柱状，如图2，然后将其对接，可做成一个直角的“拐脖”，如图3．对工人师傅所画的曲线，有如下说法：（1）是一段抛物线；（2）是一段双曲线；（3）是一段正弦曲线；（4）是一段余弦曲线；（5）是一段圆弧．则正确的说法序号是________三、解答题 (共4题；共20分)22. （5分）如图，圆柱的轴截面ABCD是正方形，点E在底面的圆周上，AF⊥DE，F是垂足．（1）求证：AF⊥DB；（2）如果圆柱与三棱锥D﹣ABE的体积的比等于3π，求直线DE与平面ABCD所成的角．23. （5分）如图，底面半径为1，高为2的圆柱，在A点有一只蚂蚁，现在这只蚂蚁要围绕圆柱由A点爬到B点，问蚂蚁爬行的最短距离是多少？24. （5分）一个圆柱形容器里装有水，放在水平面上，现将容器倾斜，这时水面是一个椭圆，当圆柱的母线AB与地面所成角时，椭圆的离心率是多少？25. （5分）用一与底面成30°角的平面去截一圆柱，已知圆柱的底面半径为4，求截面椭圆的方程．参考答案一、选择题 (共14题；共28分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、填空题 (共7题；共12分)15-1、16-1、17-1、18-1、19-1、20-1、21-1、三、解答题 (共4题；共20分)第11 页共13 页第12 页共13 页22-1、23-1、24-1、25-1、第13 页共13 页。

学业分层测评(十一)(建议用时：45分钟)[学业达标]一、选择题1．在空间，给出下列命题：(1)一个平面的两条斜线段相等，那么它们在平面上的射影相等；(2)一条直线和平面的一条斜线垂直，必和这条斜线在这个平面上的射影垂直；(3)一条斜线和它在平面内的射影所成的锐角是这条斜线和平面内过斜足的所有直线所成的一切角中最小的角；(4)若点P到△ABC三边所在的直线的距离相等，则点P在平面ABC上的射影是△ABC的内心．其中正确的命题是( )A．(3) B．(3)(4)C．(1)(3) D．(2)(4)【解析】由平行投影变换的性质知，当两条线段共线、平行或两线段是过同一点的平面的斜线段时，才有(1)正确，在(2)中这条直线可能在平面外，(3)显然正确，(4)中P点有可能是△ABC的旁心．【答案】 A2．如果一个三角形的平行射影仍是一个三角形，则下列结论正确的是( )A．内心的平行射影还是内心B．重心的平行射影还是重心C．垂心的平行射影还是垂心D．外心的平行射影还是外心【解析】 三角形的重心是三条中线的交点，三角形平行射影后各边的中点位置不会变，故其中线的交点，即重心仍是三角形的重心，而内心、外心、垂心都有可能改变．故只有B 正确．【答案】 B3．已知圆锥面的轴截面为等腰直角三角形，用一个与轴线成30°角的不过圆锥顶点的平面去截圆锥面时，所截得的截线的离心率为( )【导学号：07370054】A.62 B.63 C.32D.22【解析】 ∵圆锥的轴截面为等腰直角三角形，∴母线与轴线的夹角α＝45°.又截面与轴线的夹角β＝30°，即β＜α，∴截线是双曲线，其离心率e ＝cos βcos α＝cos 30°cos 45°＝32＝62.【答案】 A4．椭圆x 24＋y 2＝1的长轴为A 1A 2，短轴为B 1B 2，将坐标平面沿y轴折成一个二面角，使A 1点在平面B 1A 2B 2上的射影恰是该椭圆的一个焦点，则此二面角的大小是( )A ．30°B ．45°C ．60°D ．120°【解析】 设所成的二面角为α， 因为a ＝2，b ＝1，c ＝3，所以cos α＝c a ＝32，所以α＝30°.【答案】 A5．设平面π与圆柱的轴的夹角为β(0°<β<90°)，现放入Dandelin 双球使之与圆柱面和平面π都相切，若已知Dandelin 双球与平面π的两切点的距离恰好等于圆柱的底面直径，则截线椭圆的离心率为( )A.12B.22C.33D.32【解析】 Dandelin 双球与平面π的切点恰好是椭圆的焦点，圆柱的底面直径恰好等于椭圆的短轴长，由题意知，2b ＝2c ，所以e ＝c a ＝c b 2＋c 2＝c 2c ＝22.【答案】 B 二、填空题 6．有下列说法：①矩形的平行射影一定是矩形； ②梯形的平行射影一定是梯形； ③平行四边形的平行射影可能是正方形； ④正方形的平行射影一定是菱形．其中正确命题有________________．(填上所有正确说法的序号) 【解析】 利用平行射影的概念和性质进行判断． 【答案】 ③7．在梯形ABCD 中，AB ∥CD ，若梯形不在α内，则它在α上的射影是________．【解析】 如果梯形ABCD 所在平面平行于投影方向，则梯形ABCD在α上的射影是一条线段．如果梯形ABCD 所在平面不平行于投影方向，则平行线的射影仍是平行线，不平行的线的射影仍不平行，则梯形ABCD 在平面α上的射影仍是梯形．【答案】 一条线段或一个梯形8．一平面与圆柱面的母线成45°角，平面与圆柱面的截线椭圆的长轴长为6，则圆柱面内切球的半径为________．【解析】 由2a ＝6，得a ＝3，又e ＝cos 45°＝22，∴c ＝e ·a ＝22×3＝322，∴b ＝a 2－c 2＝32－92＝322，∴圆柱面内切球的半径r ＝322.【答案】 322三、解答题9．已知点A (1,2)在椭圆x 216＋y 212＝1内，F 的坐标为(2,0)，在椭圆上求一点P ，使|PA |＋2|PF |最小．【解】 如图所示，∵a 2＝16，b 2＝12，∴c 2＝4，c ＝2，∴F 为椭圆的右焦点，并且离心率为24＝12.设P 到右准线的距离为d ， 则|PF |＝12d ，d ＝2|PF |，∴|PA |＋2|PF |＝|PA |＋d .由几何性质可知，当P 点的纵坐标(横坐标大于零)与A 点的纵坐标相同时，|PA |＋d 最小，把y ＝2代入x 216＋y 212＝1，得x ＝463⎝ ⎛⎭⎪⎪⎫x ＝－463舍去， 即点P ⎝⎛⎭⎪⎪⎫463，2为所求． 10．在空间中，取直线l 为轴．直线l ′与l 相交于O 点，夹角为α.l ′绕l 旋转得到以O 为顶点，l ′为母线的圆锥面．任取平面π，若它与轴l 的交角为β.试用Dandelin 双球证明：当β＝α时，平面π与圆锥的交线为抛物线.【导学号：07370055】【证明】 如图：设Dandelin 双球与圆锥面的交线为圆S . 记圆所在的平面为π′，π与π′的交线为m . 在平面π与圆锥面的交线上任取一点P ， 设平面π与Dandlin 球的切点为F ，连接PF .在平面π中过P 作m 的垂线，垂足为A ，过P 作π′的垂线，垂足为B ，连接AB ，则AB 为PA 在平面π′上的射影．显然，m ⊥AB ，故∠PAB 是平面π与平面π′所成的二面角的平面角．在Rt △APB 中，∠APB ＝β， 则PB ＝PA ·cos β. ① 又设过点P 的母线交圆S 于点Q ， 则PQ ＝PF .在Rt △PBQ 中，PB ＝PQ ·cos α， ∴PB ＝PF ·cos α.②由①②得PF PA ＝PB cos α×cos βPB ＝cos βcos α.因为α＝β，所以PFPA＝1，即曲线任一点P 到定点F 的距离恒等于P 到定直线m 的距离．故点P 的轨迹为抛物线．[能力提升]1．一平面与圆柱面的母线成45°角，平面与圆柱面的截线椭圆的长轴为6，则圆柱面的半径为( )A. 2B. 3 C ．2 2D.322【解析】 由2a ＝6，即a ＝3，又e ＝cos 45°＝22，故b ＝c ＝ea ＝22×3＝322，即为圆柱面的半径．【答案】 D2．设圆锥的顶角(圆锥轴截面上两条母线的夹角)为120°，当圆锥的截面与轴成45°角时，则截得二次曲线的离心率为( )A.22B. 2 C ．1D.12【解析】 由题意知α＝60°，β＝45°，满足β<α，这时截圆锥得的交线是双曲线，其离心率为e ＝cos 45°cos 60°＝ 2.【答案】 B3．在底面半径为6的圆柱内有两个半径也为6的球面，两球的球心距为13.若作一个平面与这两个球面相切，且与圆柱面相交成一椭圆，则椭圆的长轴长为__________．【解析】 如图，为圆柱的轴截面，AB 为与两球O 1和球O 2都相切的平面与轴截面的交线．由对称性知AB 过圆柱的几何中心O .由O 1O ⊥OD ，O 1C ⊥OA ，故∠OO 1C ＝∠AOD ，且O 1C ＝OD ＝6，所以Rt △OO 1C ≌Rt △AOD ，则AO ＝O 1O . 故AB ＝2AO ＝2O 1O ＝O 1O 2＝13.显然AB 即为椭圆的长轴，所以AB ＝13. 【答案】 34.如图3­1­7，圆柱被平面α所截．已知AC 是圆柱口在平面α上最长投影线段，BD 是最短的投影线段，EG ＝FH ，EF ⊥AB ，垂足在圆柱的轴上，EG 和FH 都是投影线，分别与平面α交于点G ，H .图3­1­7(1)比较EF ，GH 的大小；(2)若圆柱的底面半径为r ，平面α与母线的夹角为θ，求CD . 【解】 (1)∵EG 和FH 都是投影线，∴EG ∥FH .又EG ＝FH ， ∴四边形EFHG 是平行四边形， ∴EF ＝GH .(2)如图，过点D 作DP ⊥AC 于点P ， 则在Rt △CDP 中，有： sin ∠DCP ＝DP CD. 又∠DCP ＝θ，DP ＝2r ， ∴CD ＝2rsin θ.。

学业分层测评(十一)(建议用时：45分钟)[学业达标]一、选择题1．在空间，给出下列命题：(1)一个平面的两条斜线段相等，那么它们在平面上的射影相等；(2)一条直线和平面的一条斜线垂直，必和这条斜线在这个平面上的射影垂直；(3)一条斜线和它在平面内的射影所成的锐角是这条斜线和平面内过斜足的所有直线所成的一切角中最小的角；(4)若点P到△ABC三边所在的直线的距离相等，则点P在平面ABC上的射影是△ABC的内心．其中正确的命题是()A．(3)B．(3)(4)C．(1)(3) D．(2)(4)【解析】由平行投影变换的性质知，当两条线段共线、平行或两线段是过同一点的平面的斜线段时，才有(1)正确，在(2)中这条直线可能在平面外，(3)显然正确，(4)中P点有可能是△ABC的旁心．【答案】 A2．如果一个三角形的平行射影仍是一个三角形，则下列结论正确的是() A．内心的平行射影还是内心B．重心的平行射影还是重心C．垂心的平行射影还是垂心D．外心的平行射影还是外心【解析】三角形的重心是三条中线的交点，三角形平行射影后各边的中点位置不会变，故其中线的交点，即重心仍是三角形的重心，而内心、外心、垂心都有可能改变．故只有B正确．【答案】 B3．已知圆锥面的轴截面为等腰直角三角形，用一个与轴线成30°角的不过圆锥顶点的平面去截圆锥面时，所截得的截线的离心率为()【导学号：07370054】A.62 B.63C.32 D.22【解析】∵圆锥的轴截面为等腰直角三角形，∴母线与轴线的夹角α＝45°.又截面与轴线的夹角β＝30°，即β＜α，∴截线是双曲线，其离心率e＝cos βcos α＝cos 30°cos 45°＝32＝62.【答案】 A4．椭圆x24＋y2＝1的长轴为A1A2，短轴为B1B2，将坐标平面沿y轴折成一个二面角，使A1点在平面B1A2B2上的射影恰是该椭圆的一个焦点，则此二面角的大小是()A．30°B．45°C．60°D．120°【解析】设所成的二面角为α，因为a＝2，b＝1，c＝3，所以cos α＝ca ＝32，所以α＝30°.【答案】 A5．设平面π与圆柱的轴的夹角为β(0°<β<90°)，现放入Dandelin双球使之与圆柱面和平面π都相切，若已知Dandelin双球与平面π的两切点的距离恰好等于圆柱的底面直径，则截线椭圆的离心率为()A.12 B.22C.33 D.32【解析】Dandelin双球与平面π的切点恰好是椭圆的焦点，圆柱的底面直径恰好等于椭圆的短轴长，由题意知，2b＝2c，所以e＝ca ＝cb2＋c2＝c2c＝22.【答案】 B二、填空题6．有下列说法：①矩形的平行射影一定是矩形；②梯形的平行射影一定是梯形；③平行四边形的平行射影可能是正方形；④正方形的平行射影一定是菱形．其中正确命题有________________．(填上所有正确说法的序号)【解析】利用平行射影的概念和性质进行判断．【答案】③7．在梯形ABCD中，AB∥CD，若梯形不在α内，则它在α上的射影是________．【解析】如果梯形ABCD所在平面平行于投影方向，则梯形ABCD在α上的射影是一条线段．如果梯形ABCD所在平面不平行于投影方向，则平行线的射影仍是平行线，不平行的线的射影仍不平行，则梯形ABCD在平面α上的射影仍是梯形．【答案】一条线段或一个梯形8．一平面与圆柱面的母线成45°角，平面与圆柱面的截线椭圆的长轴长为6，则圆柱面内切球的半径为________．【解析】由2a＝6，得a＝3，又e＝cos 45°＝2 2，∴c＝e·a＝22×3＝32 2，∴b＝a2－c2＝32－92＝322，∴圆柱面内切球的半径r＝322.【答案】32 2三、解答题9．已知点A(1,2)在椭圆x216＋y212＝1内，F的坐标为(2,0)，在椭圆上求一点P，使|P A|＋2|PF|最小．【解】如图所示，∵a2＝16，b2＝12，∴c2＝4，c＝2，∴F为椭圆的右焦点，并且离心率为24＝1 2.设P到右准线的距离为d，则|PF|＝12d，d＝2|PF|，∴|P A|＋2|PF|＝|P A|＋d.由几何性质可知，当P点的纵坐标(横坐标大于零)与A点的纵坐标相同时，|P A|＋d最小，把y＝2代入x216＋y212＝1，得x ＝463⎝ ⎛⎭⎪⎫x ＝－463舍去， 即点P ⎝ ⎛⎭⎪⎫463，2为所求．10．在空间中，取直线l 为轴．直线l ′与l 相交于O 点，夹角为α.l ′绕l 旋转得到以O 为顶点，l ′为母线的圆锥面．任取平面π，若它与轴l 的交角为β.试用Dandelin 双球证明：当β＝α时，平面π与圆锥的交线为抛物线.【导学号：07370055】【证明】 如图：设Dandelin 双球与圆锥面的交线为圆S . 记圆所在的平面为π′，π与π′的交线为m . 在平面π与圆锥面的交线上任取一点P ， 设平面π与Dandlin 球的切点为F ，连接PF .在平面π中过P 作m 的垂线，垂足为A ，过P 作π′的垂线，垂足为B ，连接AB ，则AB 为P A 在平面π′上的射影．显然，m ⊥AB ，故∠P AB 是平面π与平面π′所成的二面角的平面角．在Rt △APB 中，∠APB ＝β， 则PB ＝P A ·cos β. ①又设过点P 的母线交圆S 于点Q ， 则PQ ＝PF .在Rt △PBQ 中，PB ＝PQ ·cos α， ∴PB ＝PF ·cos α.②由①②得PF P A ＝PB cos α×cos βPB ＝cos βcos α. 因为α＝β，所以PFP A ＝1，即曲线任一点P 到定点F 的距离恒等于P 到定直线m 的距离．故点P 的轨迹为抛物线．[能力提升]1．一平面与圆柱面的母线成45°角，平面与圆柱面的截线椭圆的长轴为6，则圆柱面的半径为( )A.2B. 3 C ．2 2D.322【解析】 由2a ＝6，即a ＝3，又e ＝cos 45°＝22， 故b ＝c ＝ea ＝22×3＝322，即为圆柱面的半径． 【答案】 D2．设圆锥的顶角(圆锥轴截面上两条母线的夹角)为120°，当圆锥的截面与轴成45°角时，则截得二次曲线的离心率为( )A.22B. 2 C ．1D.12【解析】 由题意知α＝60°，β＝45°，满足β<α，这时截圆锥得的交线是双曲线，其离心率为e ＝cos 45°cos 60°＝ 2.【答案】 B3．在底面半径为6的圆柱内有两个半径也为6的球面，两球的球心距为13.若作一个平面与这两个球面相切，且与圆柱面相交成一椭圆，则椭圆的长轴长为__________．【解析】如图，为圆柱的轴截面，AB为与两球O1和球O2都相切的平面与轴截面的交线．由对称性知AB过圆柱的几何中心O.由O1O⊥OD，O1C⊥OA，故∠OO1C＝∠AOD，且O1C＝OD＝6，所以Rt△OO1C≌Rt△AOD，则AO＝O1O.故AB＝2AO＝2O1O＝O1O2＝13.显然AB即为椭圆的长轴，所以AB＝13.【答案】 34.如图3-1-7，圆柱被平面α所截．已知AC是圆柱口在平面α上最长投影线段，BD是最短的投影线段，EG＝FH，EF⊥AB，垂足在圆柱的轴上，EG和FH 都是投影线，分别与平面α交于点G，H.图3-1-7(1)比较EF，GH的大小；(2)若圆柱的底面半径为r，平面α与母线的夹角为θ，求CD.【解】(1)∵EG和FH都是投影线，∴EG∥FH.又EG＝FH，∴四边形EFHG是平行四边形，∴EF＝GH.(2)如图，过点D作DP⊥AC于点P，则在Rt△CDP中，有：sin∠DCP＝DP CD.又∠DCP＝θ，DP＝2r，∴CD＝2rsin θ.。

课堂探究探究一椭圆的度量性质圆柱形物体的斜截口是椭圆，因此，椭圆的度量性质与底面半径、截面及母线夹角密切相关．【典型例题1】已知一圆柱面的半径为3，圆柱面的一截面的两焦球的球心距为12，求截面截圆柱面所得的椭圆的长轴长、短轴长、两焦点间距离和截面与母线所夹的角．思路分析：根据题意可知长轴长及短轴长，进而求出离心率，从而得出截面与母线的夹角．解：易知长半轴长a ＝122＝6，短半轴长b ＝r ＝3，两焦点间距离2c ＝2a 2－b 2＝262－32＝6 3.椭圆离心率e ＝c a ＝32. 设截面与母线的夹角为φ，则cos φ＝32.∴φ＝π6. 综上，截面截圆柱面所得的椭圆的长轴长为12，短轴长为6，两焦点间距离为63，截面与母线所夹的角为π6. 探究二探讨椭圆的性质探究圆柱体的斜截口——椭圆的性质，要熟知Dandelin 双球与圆柱及其截平面的关系，综合应用切线长定理、三角形的相似与全等，解直角三角形，以及平行射影的性质．【典型例题2】如图所示，已知球O 1，O 2分别切平面β于点F 1，F 2，P 1P 2为⊙O 1的一条直径，Q 1，Q 2分别为P 1，P 2在平面β内的平行射影，G 1G 2＝2a ，Q 1Q 2＝2b ，G 1G 2与Q 1Q 2垂直平分，求证：F 1F 2＝2a 2－b 2.证明：如图，过G1作G1H⊥BG2，H为垂足，则四边形ABHG1是矩形．∴G1H＝AB.∵Q1，Q2分别是P1，P2的平行射影，∴P1Q1P2Q2.∴P1Q1Q2P2是平行四边形．∴Q1Q2＝P1P2，即Q1Q2等于底面直径．∴G1H＝AB＝Q1Q2＝2b.又由切线长定理，知G1A＝G1F1＝G2F2，G2F1＝G2B，∴G2F1－G2F2＝G2B－G1A.又G1A＝BH，∴G2F1－G2F2＝G2B－BH.∴F1F2＝G2H.在Rt△G1G2H中，G2H＝(2a)2－(2b)2＝2a2－b2，故F1F2＝2a2－b2.。

平面与圆柱面的截线练习1如果椭圆的两个焦点将长轴分成三等份，那么，这个椭圆的两条准线间的距离是焦距的( )A ．9倍B ．4倍C ．12倍D ．18倍2一组底面为同心圆的圆柱被一平面所截，截口椭圆具有( )A ．相同的长轴B ．相同的焦点C ．相同的准线D ．相同的离心率3如图所示，过F 1作F 1Q ⊥G 1G 2，△QF 1F 2为等腰直角三角形，则椭圆的离心率为( )A ．2 B ．12C ．21 4已知圆柱的底面半径为r ，平面α与圆柱母线的夹角为60°，则它们截口椭圆的焦距是( )A ．B ．CD ．3r5(能力拔高题)如图所示，已知A 为左顶点，F 是左焦点，l 交OA 的延长线于点B ，P ，Q 在椭圆上，有PD ⊥l 于D ，QF ⊥AO ，则椭圆的离心率是①PF PD ； ②QF BF ； ③AO BO ； ④AF AB ； ⑤FO AO. 其中正确的是( )A ．①②B ．①③④C ．②③⑤ D．①②③④⑤6已知平面π截圆柱体，截口是一条封闭曲线，且截面与底面所成的角为45°，此曲线是__________，它的离心率为__________．7已知椭圆两条准线间的距离为8，离心率为12，则Dandelin球的半径是__________．8已知圆柱底面半径为b，平面π与圆柱母线的夹角为30°，在圆柱与平面交线上有一点P到一准线l1，则点P到另一准线l2对应的焦点F2的距离是__________．9如图所示，已知PF1∶PF2＝1∶3，AB＝12，G1G2＝20，求PQ.参考答案1答案：A 设椭圆的长轴长，短轴长，焦距分别为2a，2b，2c，由已知，得223ac=，即a＝3c，故两条准线间的距离为22218a cc c=＝18c.2 答案：D 因为底面半径大小不等，所以长轴不同.嵌入的Dandelin球不同，则焦点不同，准线也不同，而平面与圆柱的母线夹角相同，故离心率相同.3 答案：D 设椭圆的长轴长，短轴长，焦距分别为2a，2b，2c. ∵△QF1F2是等腰直角三角形，∴QF1＝F1F2＝2c，QF2＝. 由椭圆的定义，得QF1＋QF2＝2a，∴212cea====.4答案：A 如图，过点G2作G2H⊥AD，H为垂足，则G2H=2r.在Rt△G1G2H中，G1G2=2cos60G H︒=2r×2=4r，∴长轴2a＝G1G2＝4r，短轴2b＝2r.∴焦距2c＝2==.5答案：D ①PFPD符合离心率定义；②过点Q作QC⊥l于C，∵QC＝FB，∴QF QFBF QC=符合离心率定义；③∵AO＝a，BO＝2ac，∴2AO a caBO ac==，故AOBO也是离心率；④∵AF＝a－c，AB＝2aac-，∴2AF a c caAB aac-==-，∴AFAB是离心率；⑤∵FO＝c，AO＝a，∴FO cAO a=是离心率.6 答案：椭圆27由题意知24,1,2acca⎧=⎪⎪⎨⎪=⎪⎩解得2,1,ac=⎧⎨=⎩∴b==.8答案：52b由题意知，椭圆短轴为2b，长轴长2a＝2sin30b︒＝4b，∴c=.∴22eb==或e＝cos 30°＝2.设P到F1的距离为d，2=，∴d＝32b.又PF1＋PF2＝2a＝4b，∴PF2＝4b－PF1＝4b－32b＝52b.9答案：解：设椭圆长轴为2a，短轴为2b，焦距为2c，由已知可得a＝10，b＝6，c＝8，45cea==. 由椭圆定义，知PF1＋PF2＝G1G2＝20，又PF1∶PF2＝1∶3，则PF1＝5，PF2＝15.由离心率定义，得145PFPQ=，∴PQ＝254.。