同济大学结构力学第五章-4(温度变化)
- 格式:ppt
- 大小:345.50 KB
- 文档页数:13

5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ=== 钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b得()223212ϕααλλλ⎡=++⎢⎣ ()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ= (或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+-⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896xϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604yϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。

结构力学温度引起的变形引言:在结构力学中,温度是一种重要的外部因素,它会对结构体产生影响,导致结构发生变形。
本文将从温度引起的结构变形的机理、影响因素以及应对措施等方面进行探讨。
一、温度引起的结构变形机理温度变化会导致结构内部的材料产生热胀冷缩现象,从而引起结构体的变形。
具体机理可分为以下两个方面:1. 热胀冷缩效应温度升高会使结构材料内部的原子振动加剧,原子间的平均距离增大,导致材料体积膨胀;而温度降低则会使原子振动减弱,原子间的平均距离缩小,导致材料体积收缩。
这种热胀冷缩效应使得结构体在温度变化过程中产生变形。
2. 温度梯度引起的热应力当结构体不均匀受热或受冷时,不同部位的温度变化不一致,形成温度梯度。
温度梯度会导致结构体内部产生热应力,从而引起结构变形。
热应力的大小与材料的热膨胀系数有关,热膨胀系数越大,结构变形越明显。
二、温度引起结构变形的影响因素温度引起的结构变形受到多种因素的影响,主要包括以下几个方面:1. 材料的热膨胀系数不同材料的热膨胀系数不同,热膨胀系数越大,结构变形越明显。
因此,在结构设计中,需要根据材料的热膨胀系数合理选择材料,以减小结构变形。
2. 结构的几何形状结构的几何形状对温度引起的结构变形有一定影响。
例如,薄长结构在温度变化时容易发生弯曲变形,而厚短结构则更容易发生收缩变形。
因此,在结构设计中,需要根据结构的几何形状合理选择材料和构造方式,以减小结构变形。
3. 温度变化的速率温度变化的速率越快,结构变形越明显。
因此,在结构设计和使用过程中,需要尽量避免温度变化的剧烈波动,以减小结构变形。
三、温度引起结构变形的应对措施为了减小或控制温度引起的结构变形,可以采取以下措施:1. 智能温控系统通过安装智能温控系统,监测结构体的温度变化,并根据变化情况调节环境温度,以减小结构变形。
2. 优化结构设计在结构设计过程中,可以通过合理选择材料、构造方式和几何形状,以及采取适当的支撑和补强措施,来降低结构在温度变化下的变形。

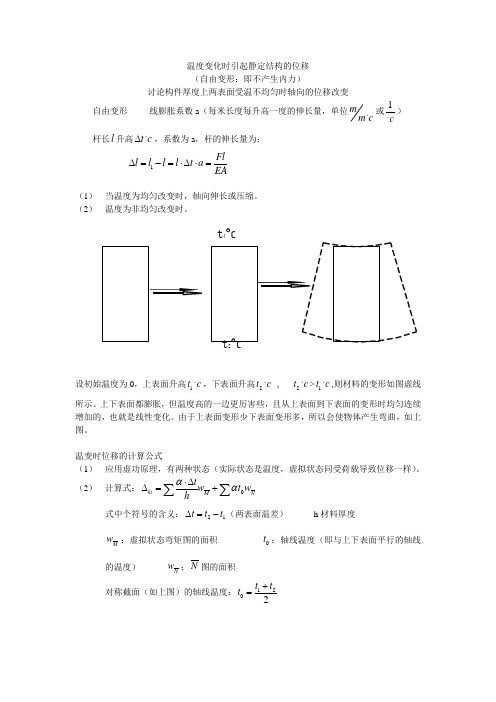
温度变化时引起静定结构的位移 (自由变形:即不产生内力)讨论构件厚度上两表面受温不均匀时轴向的位移改变自由变形 线膨胀系数a (每米长度每升高一度的伸长量,单位m m c。
或1c。
)杆长l 升高t c ∆。
,系数为a ,杆的伸长量为:(1) 当温度为均匀改变时,轴向伸长或压缩。
(2) 温度为非均匀改变时。
设初始温度为0,上表面升高1t c 。
,下表面升高2t c 。
, 2t c 。
>1t c 。
,则材料的变形如图虚线所示。
上下表面都膨胀,但温度高的一边更厉害些,且从上表面到下表面的变形时均匀连续增加的,也就是线性变化。
由于上表面变形少下表面变形多,所以会使物体产生弯曲,如上图。
温变时位移的计算公式(1) 应用虚功原理,有两种状态(实际状态是温度,虚拟状态同受荷载导致位移一样)。
(2) 计算式:0ki M N t w tw hαα⋅∆∆=+∑∑式中个符号的含义:21t t t ∆=-(两表面温差) h 材料厚度M w :虚拟状态弯矩图的面积 0t :轴线温度(即与上下表面平行的轴线的温度) N w :N 图的面积 对称截面(如上图)的轴线温度:1202t t t +=1F l l l l l t a E A∆=-=⋅∆⋅=t 1°c非对称截面(如下图)的轴线温度:12210h t h t t h+=M t w ∆⨯:有正负区别,温度产生的变形使构件受拉测和虚拟力产生的变形使构件受拉测在同一侧为正,不同侧为负0N t w ⨯: 有正负区别,0t 为温度升高对应N 为拉力时为正。
总之虚拟力产生的效果和温度产生的效果一样时为正例:截面为对称图形,线膨胀系数0.000012m m cα=。
,h=0.6m(对称截面),外侧20c -。
,内侧30c +。
,求cy ∆。
h1h2t1t2h线轴tt 1=-206m6mC解:建虚拟状态,并画M和N图。
6m6mMN整理数据:2150(t t t c ∆=-=。

5-1试找出下列结构中的零力杆(在零力杆上打上“0”记号)5-2 已知平面桁架的几何尺寸和载荷情况如题5-2图所示,用节点法计算桁架各杆的内力。
解:(a)、零力杆:74,76,65,68,43分析节点4,得P N -=45分析节点5,得 2- 1P N P N ==552,(b)、零力杆:26,61,63,48,83,85,37,71分析节点7:P N -=75 分析节点5:5254P N =1221233234434554N N N N N N N N =======(c)、支座反力:均为0分析节点1: P N P N 2,31512-== 分析节点2: P N P N 2,32523== 分析节点3: P N 235-= 分析节点4: 04543==N N (d)、零力杆:12,15,52,83,43,49支座反力:P R P R P R y x y 3.1,8.0,3.2223=-==分析节点5: P N 8.056-=分析节点6: P N P N -=-=6267,8.0 分析节点9: P N P N 6.0,26.09893=-= 分析节点8: P N 6.087=分析节点3: P N P N 1.1,27.13237=-= 分析节点7: P N 23.072-=5-3 用分解成平面桁架的方法求如题5-3图所示空间桁架各杆的内力。
解:零力杆:26,48,34,24,28122152316213337317383N P a N P P cN P N P N P N P NP ==-=-=-===-3 5-4 已知平面桁架的几何尺寸和受载情况如题5-4图所示。
求图中用粗线所示的杆件①,②,③的内力。
解:(a)、零力杆如图所示1340,3P M N ==∑由得 3210,M N P ==-∑由得310,3y F N P ==∑由得 (b)、2140,2M N P ==∑由得230,x F N P ==-∑由得250,y F N ==∑由得(c)、支座反力:均为0,结构简化为:PN F P N F PN M x y 31,032,032,03213====-==∑∑∑得由得由得由5-5 求如题5-5图所示平面桁架的内力。
结构力学自测题(第五单元力法)姓名学号一、是非题(将判断结果填入括弧:以 O 表示正确,以X表示错误)1、图示结构用力法求解时,可选切断杆件2、4后的体系作为基本结构。
()12345a b ab2、图示结构中,梁AB的截面EI为常数,各链杆的E A1相同,当EI增大时,则梁截面D 弯矩代数值M D增大。
()`C3、图 a 所示结构,取图 b 为力法基本体系,线胀系数为α,则∆1=tt l h-322α()。
()lo+2t1X(a)(b)4、图示对称桁架,各杆EA l,相同,N PAB=2。
()5、图 a 所示梁在温度变化时的M图形状如图 b 所示,对吗 ( )(a)(b)0C 图 -50C +15M二、选 择 题 ( 将 选 中 答 案 的 字 母 填 入 括 弧 内 )【1、图 a 所 示 结构 ,EI = 常数 ,取 图 b 为 力 法 基 本 体 系,则 下 述 结 果 中 错 误的是:A .δ230= ;B .δ310= ;C .∆20P = ;D .δ120= 。
()llll/2(a)P (b)2、图 示 连 续 梁 用 力 法 求 解 时 ,最 简 便 的 基 本 结 构 是 : A .拆 去 B 、C 两 支 座 ;B .将 A 支 座 改 为 固 定 铰 支 座 ,拆 去 B 支 座 ;C .将 A 支 座 改 为 滑 动 支 座 ,拆 去 B 支 座 ;D .将 A 支 座 改 为 固 定 铰 支 座 ,B 处 改 为 完 全 铰 。
()}3、图 示 结 构 H B 为 :A .P ; B .-P 2 ; C .P ; D .-P 。
()4、图 示 两 刚 架 的 EI 均 为 常 数 ,并 分 别 为 EI = 1 和 EI = 10,这 两 刚 架 的 内 力 关 系 为:()A .M 图 相 同;B .M 图 不 同;C .图 a 刚 架 各 截 面 弯 矩 大 于 图 b 刚 架 各 相 应 截 面 弯 矩;D .图 a 刚 架 各 截 面 弯 矩 小 于 图 b 刚 架 各 相 应 截 面 弯 矩。
2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)【W=5×3 - 4×2 – 6=1>0几何可变(c)】有一个多余约束的几何不变体系(d)|2-3 试分析图示体系的几何构造。
(a)/W=3×3 - 2×2 – 4=1>0可变体系(ⅡⅢ) (b);Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变-(b)~(ⅠⅢ)(ⅡⅢ)几何不变~W=4×3 -3×2 -5=1>0几何可变体系(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体@(e)(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系…(f)?(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(g):(h)|二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)%(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)!Ⅲ(ⅡⅢ)(ⅠⅢ)`3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)%aa *a a2P F a 2P F a4P F Q34P F 2P F(b)"2020Q10/326/310(c){2m6m`4m2m3m2m2m3m3m4m18060(d)]7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)3m2m2m2m2m2m 2m2m4kNm%6m1k N /m2kNCB{242018616MQ18(b),30303011010QM 2106m10kN>3m3m40kNmAB CD:45MQ(d)…444444/32MQN3m3m6m)2m2m(e))4481``(f)#222220M…4m2m3m4m/3-4试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)—(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学温度引起的变形引言:在工程设计和实际应用中,结构的温度变化往往是一个不可忽视的因素。
温度的变化会导致结构的热胀冷缩,从而引起结构的变形。
本文将从结构力学的角度来探讨温度引起的变形现象。
一、热胀冷缩原理温度的变化会导致物质的体积发生变化,即热胀冷缩现象。
当物体受热时,其内部分子的热运动加剧,分子之间的距离增大,从而使物体的体积膨胀。
相反,当物体受冷时,其内部分子的热运动减弱,分子之间的距离缩小,物体的体积收缩。
这种热胀冷缩现象是由物体内部分子的热运动引起的。
二、温度引起的结构变形温度的变化会导致结构的变形,主要表现为以下几个方面:1. 线膨胀温度的升高会导致结构中的线材或线性构件发生膨胀,从而引起结构的线膨胀变形。
线材的线膨胀系数是一个重要的参数,它描述了材料在单位温度变化下长度的变化率。
当温度升高时,线材的长度会随之增加,从而引起结构的变形。
2. 面膨胀温度的变化也会导致结构中的面材或面构件发生膨胀,从而引起结构的面膨胀变形。
面材的面膨胀系数描述了材料在单位温度变化下面积的变化率。
当温度升高时,面材的面积会随之增加,从而引起结构的变形。
3. 体膨胀温度的变化还会导致结构中的体材或体构件发生膨胀,从而引起结构的体膨胀变形。
体材的体膨胀系数描述了材料在单位温度变化下体积的变化率。
当温度升高时,体材的体积会随之增加,从而引起结构的变形。
4. 热应力温度的变化引起的结构变形还会产生热应力。
热应力是由于温度不均匀引起的,当结构中的不同部位受到不同温度影响时,会产生内部应力,从而引起结构的变形。
热应力会对结构的强度和稳定性产生影响,需要在设计和施工过程中予以考虑。
结论:温度的变化会导致结构的热胀冷缩现象,从而引起结构的变形。
这种变形主要体现在线膨胀、面膨胀、体膨胀和热应力等方面。
在结构设计和施工过程中,需要充分考虑温度引起的变形现象,采取合适的措施来控制和补偿结构的变形,确保结构的安全可靠运行。
通过深入研究结构力学温度引起的变形现象,可以为工程设计和实际应用提供科学依据和技术支持。