同济大学朱慈勉结构力学第10章结构动.知识题目解析
- 格式:doc
- 大小:4.17 MB
- 文档页数:36
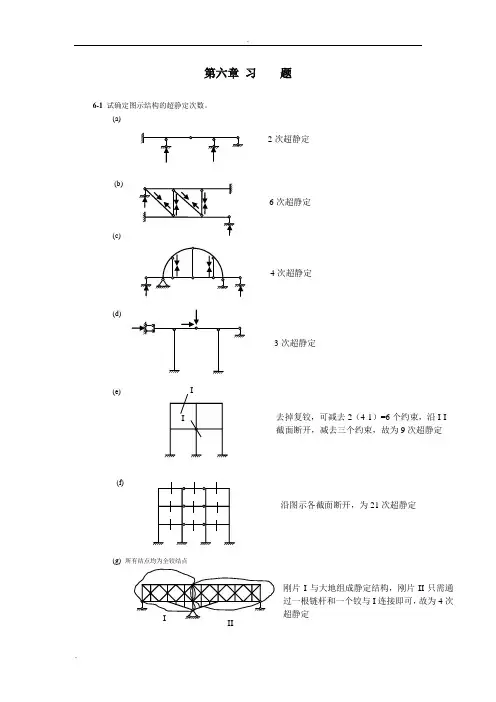
第六章 习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误,为可变体系。
+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解:基本结构为:1Mp M01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a 2a4a4a3m6m6m810810计算1M,由对称性知,可考虑半结构。
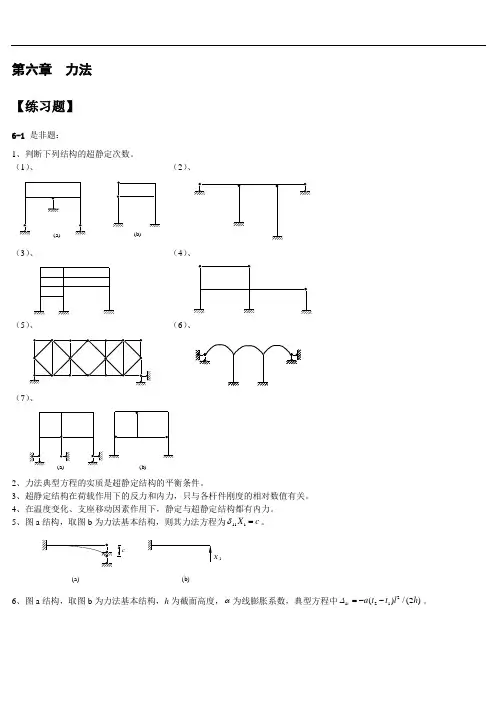
第六章 力法【练习题】6-1 是非题:1、判断下列结构的超静定次数。
(1)、 (2)、(a)(b)(3)、 (4)、(5)、 (6)、(7)、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力,只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下,静定与超静定结构都有内力。
5、图a 结构,取图b 为力法基本结构,则其力法方程为δ111X c =。
(a)(b)X 16、图a 结构,取图b 为力法基本结构,h 为截面高度,α为线膨胀系数,典型方程中∆12122t a t t l h =--()/()。
t 21t lA h (a)(b)X 17、图a 所示结构,取图b 为力法基本体系,其力法方程为。
(a)(b)16-2 用力法作图示结构的M 图。
3m m6-3 用力法作图示排架的M 图。
已知 A = 0.2m 2,I = 0.05m 4,弹性模量为E 0。
q6-4 用力法计算并作图示结构M 图。
EI =常数。
a a6-5 用力法计算并作图示结构的M 图。
ql /26-6 用力法计算并作图示结构的M 图。
q3 m4 m6-7 用力法计算图示结构并作出M 图。
E I 常数。
(采用右图基本结构。
)l 2/3l /3/3l /36-8 用力法计算图示结构并作M 图。
EI =常数。
3m3m6-9 用力法计算图示结构并作M 图。
EI =常数。
2m2m 2m2m6-10 用力法计算图示结构并作M 图。
EI =常数。
l lql l6-11 用力法计算并作图示结构M 图。
E I =常数。
6-12 用力法计算图示结构并作弯矩图。
161kN m m m m6-13 已知EI = 常数,用力法计算并作图示对称结构的M 图。
l l6-14 用力法计算并作图示结构的M 图。
EI =常数。
a a6-15 用力法作图示结构的 M 图 。
EI = 常数。
2q l6-16 用力法作M 图。

2003年春,记得田宗漱老教授在中国科学院研究生院的有限元课上曾提及一件事,国内某项重点工程的甲方单位委托国内多家科研机构背靠背地分头对该项目进行了整体结构分析,后来结果汇总到一起,专家组经过反复的研究论证,判定国内一家985高校的计算团队给出的结果是错的,因其采用的一些计算假定不符合实际情况。
一所名校的专业仿真团队,耗费数月时间,投入大量人力,对这个项目的分析竟以失败的结果而告终。
这个真实发生的事情说明,实际工程问题往往都是难度比较大的问题。
专业团队小心翼翼地计算,花费数月时间尚且出错,那么可想而知,对于大量研发力量薄弱的中小企业,缺乏专业经验,有些甚至没有专职分析人员的情况下,要真正地具备仿真分析能力会有多困难。
那么,工程问题的有限元分析,到底难在哪里呢?这是一个很大的题目,本文仅结合几个具体的算例和个人认识作简单讨论,希望能抛砖引玉,引起广大分析人员的思考。
01首先,来看第一个算例。
如图1所示,一个100mm×100mm×1000mm 的长方块体,材质为结构钢,弹性模量200GPa,泊松比0.3,屈服强度200MPa,理想塑性(不考虑硬化),材料应力应变关系如图2所示。
整个构件轴向受压。
图1 轴压柱形构件图2 理想塑性材料模型读者可能会说,一个构件单轴受压,这能有什么问题?计算中采用了图中所示的一端固定(ANSYS Mechanical中的Fixed Support),另一端位移加载的方式进行模拟,顶部向下加载位移量0.8mm。
计算结果表明,构件的中上部接近单轴应力状态,从轴向变形来看,名义轴向应变绝对值仅为0.0008,并未达到单轴屈服应变0.001 (fy/E),Von-Mises等效应力几乎等于轴向应力,即0.0008×200GPa≈160MPa。
但是由于泊松效应,底面附近位置实际上是处于复杂的三轴应力状态,而且这一看似再平常不过的固定约束还引起了应力奇异。

第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。




第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。

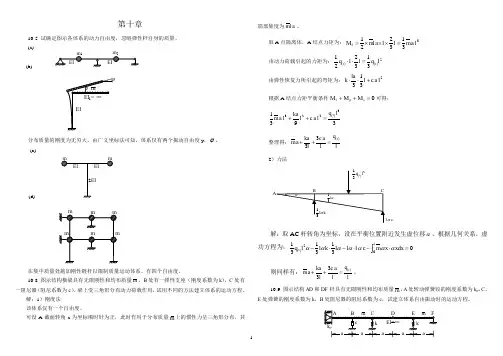
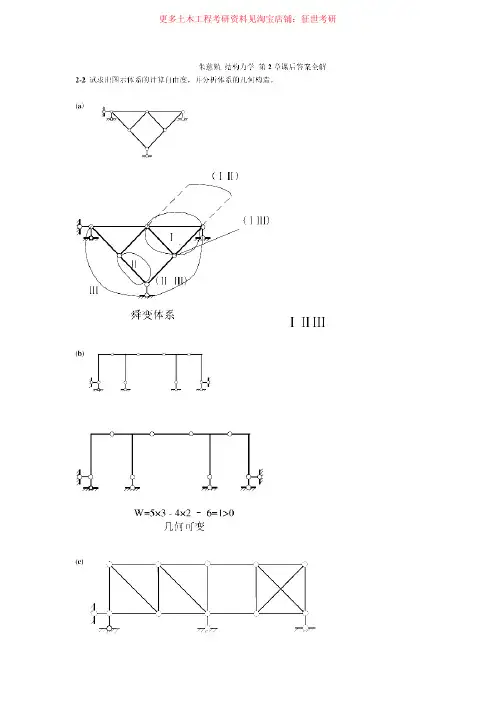
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
混凝土结构理论作业(受弯部分)混凝土结构设计原理(第四版)第一部分简答题P69 思考题——3.2 3.4 3.6 第二部分计算题P70 习题——3.1,3.2,3.4 在3.1 题目的基础上,增加如下4 问,题目间互相独立(1)其他条件不变,若a). 将f c 提高10%,重新计算所需的A s1 ; b). 将f y 提高10%,重新计算所需的A s2 ; c). 将b 提高10%,重新计算所需的A s3 ; d). 将h 提高10%,重新计算所需的A s4 ; 对比A s1 、A s2 、A s3 、A s4 与A s (原计算面积)的关系,说明哪个因素影响最大,为什么?(2)其他条件不变,若在此梁的拉区配置3φ18,请问此梁的极限受弯承载力M 为多少?(3)若已知压区配置了2φ16 的钢筋,重新计算所需要的钢筋面积A s5 ,并与A s (原计算面积)进行对比。
(4)若此题截面变成如下图情况,重新计算所需要的钢筋面积A s6 ,并与原计算面积A s 进行对比。
550 1 0 0 5 0 0 第三部分证明题或公式推导题(后两题选作,建议学有余力的同学完成,可增加对课本知识的理解)(1)推导ξ b 与ρ b 或称ρ max 之间的关系(即推导书本中P49 的公式3-19),并计算C25 及C30 混凝土情况下HPB235、HRB335、HRB400 钢筋的ρ max 数值。
(2)推导超筋梁的钢筋应力σ s 与相对受压区高度ξ 之间的关系。
(假设平截面假定仍然成立,用几何关系和物理关系,利用σ s =E s ε s 及ε s 与ε cu ,x,h 0 之间的关系进行推导)(3)A、B 二梁其他参数完全相同,唯有配筋量不同,其中A 梁为超筋梁,B 梁为适筋梁。
证明:A 梁的极限抗弯承载力M uA 大于B 梁的极限抗弯承载力M uB 。
第六章 习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误,为可变体系。
+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解:基本结构为:1Mp M01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a 2a4a4a3m6m6m810810计算1M,由对称性知,可考虑半结构。
同济大学朱慈勉 结构力学 第10章 结构动..习题答案10-1 试说明动力荷载与移动荷载的区别。
移动荷载是否可能产生动力效应?10-2 试说明冲击荷载与突加荷载之间的区别。
为何在作厂房动力分析时,吊车水平制动力可视作突加荷载?10-3 什么是体系的动力自由度?它与几何构造分析中体系的自由度之间有何区别?如何确定体系的 动力自由度?10-4 将无限自由度的振动问题转化为有限自由度有哪些方法?它们分别采用何种坐标? 10-5 试确定图示各体系的动力自由度,忽略弹性杆自身的质量。
(a) (b)EI 1=∞EImyϕ分布质量的刚度为无穷大,由广义坐标法可知,体系仅有两个振动自由度y ,ϕ。
(c)(d)在集中质量处施加刚性链杆以限制质量运动体系。
有四个自由度。
10-6 建立单自由度体系的运动方程有哪些主要方法?它们的基本原理是什么? 10-7 单自由度体系当动力荷载不作用在质量上时,应如何建立运动方程?10-8 图示结构横梁具有无限刚性和均布质量m ,B 处有一弹性支座(刚度系数为k ),C处有一阻尼器(阻尼系数为c ),梁上受三角形分布动力荷载作用,试用不同的方法建立体系的运动方程。
解:1)刚度法该体系仅有一个自由度。
可设A 截面转角a 为坐标顺时针为正,此时作用于分布质量m 上的惯性力呈三角形分布。
其端部集度为..ml a 。
取A 点隔离体,A 结点力矩为: (3)121233I M ml a l l mal =⨯⨯⨯=由动力荷载引起的力矩为:()()2121233t t q l l q l ⋅⋅= 由弹性恢复力所引起的弯矩为:.2133la k l c al ⋅⋅+ 根据A 结点力矩平衡条件0I p s M M M ++=可得:()3 (322)1393t q l ka m al l c al ++=整理得:()...33t q ka c a m a l l l++= 2)力法.cα解:取AC 杆转角为坐标,设在平衡位置附近发生虚位移α。
同济大学朱慈勉 结构力学 第10章 结构动..习题答案10-1 试说明动力荷载与移动荷载的区别。
移动荷载是否可能产生动力效应?10-2 试说明冲击荷载与突加荷载之间的区别。
为何在作厂房动力分析时,吊车水平制动力可视作突加荷载?10-3 什么是体系的动力自由度?它与几何构造分析中体系的自由度之间有何区别?如何确定体系的 动力自由度?10-4 将无限自由度的振动问题转化为有限自由度有哪些方法?它们分别采用何种坐标? 10-5 试确定图示各体系的动力自由度,忽略弹性杆自身的质量。
(a) (b)EI 1=∞EImyϕ分布质量的刚度为无穷大,由广义坐标法可知,体系仅有两个振动自由度y ,ϕ。
(c)(d)在集中质量处施加刚性链杆以限制质量运动体系。
有四个自由度。
10-6 建立单自由度体系的运动方程有哪些主要方法?它们的基本原理是什么? 10-7 单自由度体系当动力荷载不作用在质量上时,应如何建立运动方程?10-8 图示结构横梁具有无限刚性和均布质量m ,B 处有一弹性支座(刚度系数为k ),C处有一阻尼器(阻尼系数为c ),梁上受三角形分布动力荷载作用,试用不同的方法建立体系的运动方程。
解:1)刚度法该体系仅有一个自由度。
可设A 截面转角a 为坐标顺时针为正,此时作用于分布质量m 上的惯性力呈三角形分布。
其端部集度为..ml a 。
取A 点隔离体,A 结点力矩为: (3)121233I M ml a l l mal =⨯⨯⨯=由动力荷载引起的力矩为:()()2121233t t q l l q l ⋅⋅= 由弹性恢复力所引起的弯矩为:.2133la k l c al ⋅⋅+ 根据A 结点力矩平衡条件0I p s M M M ++=可得:()3 (322)1393t q l ka m al l c al ++=整理得:()...33t q ka c a m a l l l++= 2)力法.cα解:取AC 杆转角为坐标,设在平衡位置附近发生虚位移α。
根据几何关系,虚功方程为:() (20111)0333l t q l l k l l l c m x xdx ααααααα-⋅-⋅-⋅=⎰则同样有:()...33t q ka c a m a l l l++=。
10-9 图示结构AD 和DF 杆具有无限刚性和均布质量m ,A 处转动弹簧铰的刚度系数为k θ,C 、E 处弹簧的刚度系数为k ,B 处阻尼器的阻尼系数为c ,试建立体系自由振动时的运动方程。
t )解:取DF 隔离体,0FM=∑:..2220.2322324a R a mx dx ka R ma ka αααα⋅=+⇒=+⎰取AE 隔离体:0AM=∑...32220430ak mx dx ca ka Ra θαααα++++=⎰将R 代入,整理得:..32251504R ma ka k θααα=++= 10-10 试建立图示各体系的运动方程。
(a)解:(1)以支座B 处转角作为坐标,绘出梁的位移和受力图如下所示。
图中惯性力为三角形分布,方向与运动方向相反。
(t )..α(2)画出p M 和1M 图(在B 点处作用一附加约束)ll 2m (t )()324t l M α-()t pM3EI l1M(3)列出刚度法方程113EIk l=,()..3124p t m R l M α=- 1110p k R α+=代入1p R 、11k 的值,整理得:()..432472t M EIm l l αα+=(b) 解:11=1M 图21P =2l2M 图 试用柔度法解题此体系自由度为1 。
设质量集中处的竖向位移y 为坐标。
y 是由动力荷载()p t F和惯性力矩I M 共同引起的。
11112()p ty M F δα=+由图乘法:321112233l l l EI EIδ=⋅=l 2 l2312/252622248l l l l l l EI EIδ⎛⎫=⨯⋅+⋅=⎪⎝⎭ 惯性力矩为..m y l -()33..5348p t l l y m yl F EIEI⎛⎫=⋅-+ ⎪⎝⎭ 经整理得,体系运动方程为:()..33516p t EI m y y F l+=。
10-11 试求图示各结构的自振频率,忽略杆件自身的质量。
(a)解:21M 图图乘得:31111225222223236a a a f a a a a EI EI⎛⎫=⨯⨯⨯⨯⨯+⨯⨯⨯=⎪⎝⎭ ω=(b)在集中质量处施加垂直力P ,使质量发生竖向单位位移,可得弹簧处位移为23。
由此根据弯矩平衡可求得49P k =。
ω== (c)l 2 l2l 2l2 2aa a解:可以将两个简支梁视为两个并联的弹簧。
上简支梁柔度系数为()332486l l EI EI=下简支梁柔度系数为396l EI于是两者并联的柔度系数为331696102l EI EI EIl δ==+并ω==(d)解:在原结构上质量运动方向加上一根水平支杆后,施加单位水平位移后画得弯矩图如下。
水平支杆中力为33013EI l ,即1133013EIk l =。
ω(e)忽略水平位移解:4a4a3a1M图22112455272213362a a af aEA EA EA⎛⎫⎛⎫=⨯⨯+⨯⨯+⨯=⎪ ⎪⎝⎭⎝⎭ω=(f)解:3323321M图2M图M图31312331323162130.0149743223323221933219364ll l l l l l lEI EIδ⎛⎫=⨯⨯⨯+⋅⋅⨯⨯+⨯⨯=⎪⎝⎭ω==10-12 为什么说自振周期是结构的固有性质?它与结构哪些固有量有关?关系如何?10-13 试说明有阻尼自由振动位移时程曲线的主要特点。
此时质量往复一周所用的时间与无阻尼时相比如何?10-14 什么是阻尼系数、临界阻尼系数、阻尼比和振幅的对数递减率?为什么阻尼对体系在冲击荷载作用下的动力响应影响很小?10-15 设已测得某单自由度结构在振动10周后振幅由1.188mm减小至0.060mm,试求该结构的阻尼比ξ。
l2l2解:0475.006.0188.1ln 201ln 21==≈+ππξn k k y y n10-16 设有阻尼比ξ=0.2的单自由度结构受简谐荷载F P (t )= F t θsin 作用,且有ωθ75.0=。
若阻尼比降低至ξ=0.02,试问要使动位移幅值不变,简谐荷载的幅值应调整到多大?解:2222222411ωθξωθω+⎪⎪⎭⎫ ⎝⎛-⋅=m F A 已知ξ从0.2降低至0.02. ωθ75.0=,t F F θsin 1=,A 不变。
12222221827.016902.0416911692.041691F F F F =⇒⋅⋅+⎪⎭⎫ ⎝⎛-⋅⋅+⎪⎭⎫ ⎝⎛-=F 简谐荷载的幅值应调整到0.827F 。
10-17 试说明动力系数的含义及其影响因素。
单自由度体系质量动位移的动力系数与杆件内力的动力系数是否相同?10-18 什么是共振现象,如何防止结构发生共振?10-19 试求图示梁在简谐荷载作用下作无阻尼强迫振动时质量处以及动力荷载作用点的动位移幅值,并绘制最大动力弯矩图。
设36ml EI =θ。
(a)解:由力法可知,单位荷载作用在B 点引起33l EI位移。
ωθ=()32221sin sin 31t F Fl y t t EI m θθθωω=⋅=--即幅值为33Fl EI当幅值最大时,弯矩也最大。
Flmax M 图t θ sin l(b)解:1M 图 2M 图(1)求结构运动方程如所示弯矩图,图乘后,333112212215,,24348l l l f f f f EI EI EI====()..11121112..3sin sin 245sin 2I t C y f F f F t f m y f F tEI F y y tm ml θθθ⎛⎫=+=-+ ⎪⎝⎭+=其中2*3245,2EI P F ml ω==稳态解:()*222331sin 1512 =sin 124145 =sin 36t CP y tm Flt EI Fl tEIθωθωθθ=⋅-⋅-所示结构的运动方程为()35=sin 36t C Fl y t EIθC 点最大动位移幅值为3536Fl EI(2)求B 点的动位移反应()()..21222122sin sin I t B t B y f F f P t f m y f P t θθ⎛⎫=+=-+ ⎪⎝⎭()*2221sin 1t BP y t m θωθω=⋅-()*..22221sin 1t BP yt m θθωθω=-⋅-2l2l t θ sin()()32*212222232322232222235=sin 361sin 1551 =sin 48231251 =1sin 33217132 =3t C t B Fl y tEI y f P Pf tl lP P t EI EI Pl t EI Pl EI θθθωθωθθωθωθθωθωθ⎡⎤⎛⎫⎢⎥ ⎪⎢⎥ ⎪=⋅⋅+⎢⎥ ⎪- ⎪⎢⎥⎝⎭⎣⎦⎡⎤⎢⎥⋅⋅⋅+⎢⎥⎢⎥-⎢⎥⎣⎦⎛⎫⎪ ⎪⋅⋅+ ⎪- ⎪⎝⎭-22233sin 11214 =sin 31283121 =sin 288t Pl tEI Pl tEIωθθωθθ⎛⎫⎪⎪ ⎪- ⎪⎝⎭⋅⋅B 点的动位移幅值为3121288Pl EI(3)绘制最大动力弯矩图221M 图 2M 图 ()33max 2212135122812883696A Pl EI Pl EI M Pl EI EI l l =⨯+⨯= ()3max 212131212881922C Pl EI M Pl EI l =⨯=121192Pl 28196Pl最大动力弯矩图10-20 试求图示集中质量体系在均布简谐荷载作用下弹簧支座的最大动反力。
设杆件为无限刚性,弹簧的刚度系数为k 。
2l 2l l解:α若()t q 为静力荷载,弹簧中反力为ql 89。
已知图示体系为静定结构,具有一个自由度。
设为B 点处顺时针方向转角α为坐标。
建立动力方程:⎰=⋅+⋅+l xdx q l l k l m l l m l 230....2332322αααααααq k m l q l k l m 8989..2222..=+⇒=+αααααα2211ωθμ-=则弹簧支座的最大动反力为l 891122⋅-ωθ。
10-21 设图a 所示排架在横梁处受图b 所示水平脉冲荷载作用,试求各柱所受的最大动剪力。
已知EI =6×106N ·m 2,t 1=0.1s ,F P0=8×104N 。
(a)解:求排架自振频率,横梁无限刚性,则各排架水平侧移相同。