齿轮啮合精选ppt

格式：ppt
大小：2.44 MB
文档页数：18

下载文档原格式

渐开线标准圆柱齿轮的啮合传动课件

模数
表示齿轮尺寸的一个参数，模数越大，齿轮尺
寸越大。
压力角
表示齿轮受力的一个参数，压力角越大，齿轮
传递的扭矩越大。
齿数
表示齿轮上齿的个数，齿数越多，齿轮的传动
比越精确。
齿高
表示齿轮的高度，齿高越大，齿轮的承载能力
越强。
渐开线标准圆柱齿轮的加工与设计
加工方法
采用滚齿机或铣床等设备，按照设计图纸进行加工。
05
渐开线标准圆柱齿轮的应用与发展
齿轮在机械传动中的应用
齿轮是机械传动中常用的元件，能够实现旋转运动和力的传递。
在各种机械设备中，如汽车、飞机、机床等，齿轮广泛应用于变速器、减速器、传动装置等部件
中。
齿轮的传动效率高、工作可靠、使用寿命长，因此在工业生产和
日常生活中得到了广泛应用。
齿轮技术的发展趋势
良好的润滑可以减小齿轮的摩擦和磨损，提高齿轮的使用寿命和工作效率。根据齿轮的工作条件和要求，选择合适的润滑方式和润滑剂。
维护
定期对齿轮进行检查和维护，及时发现和处理存在的问题，可以保证齿轮的正常运转和使用寿命。维护内容包括检查齿面磨损、齿隙变化、润滑情况等，以及更换损坏或磨损严重的齿轮。
CHAPTER
材料选择
选择高强度、耐磨性好的材料，如合金钢、不锈钢等。
设计原则
根据传动需求和工况条件，合理选择齿轮参数，确保齿轮传动的平稳、可靠。
CHAPTER
03
齿轮的啮合传动
齿轮的啮合方式
平面啮合
两齿轮的齿面在同一个平面上接触，传递扭矩时，齿面接触线是一条直线。
空间啮合
斜齿啮合
两齿轮的齿面在空间中相交，齿面接触线是一条斜线，这种啮合方式可以减小齿轮噪音和振动。

齿轮啮合原理ppt

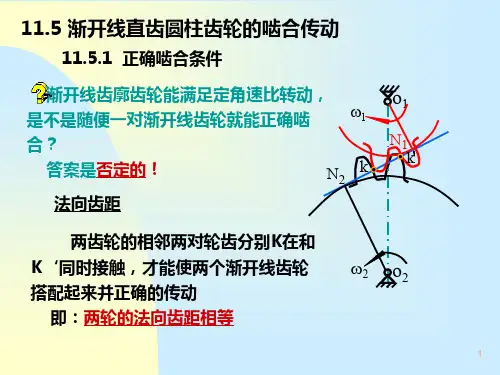
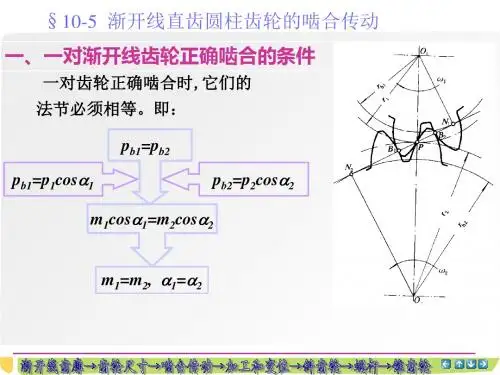
而是点M和N处的两条切线之间的夹角。当点N趋近于点 M时，比值 s 的极限称为曲线在点M处的曲率。
平面曲线
2 几种特殊的平面曲线
2.1 笛卡尔叶形线 2.2 心脏线 2.3 圆内摆线 2.4 阿基米德螺旋线
齿轮啮合原理
平面曲线
2.1 笛卡尔叶形线
方程式： x3 y3 3axy
齿轮啮合原理
一般认为，构成机械零件的基本元素是点、直线、圆、椭圆和曲线。当前运用计算机视觉技术对机械零件的检测和识别，绝大部分只是对零件的点、直线、圆和椭圆的研究，而其他形式的曲线的检测和识别研究却比较少。
平面曲线
齿轮啮合原理
3.4 在道路设计中的应用
已知：平面曲线的方程式 F(x, y) 0
和P点的坐标 x0, y0
切线
则：平面曲线的法线为：
y y0
Fy x0, y0
x x0 Fx x0, y0
切点P
曲线C
法线
平面曲线
齿轮啮合原理
1.4 平面曲线的曲率
用矢量函数 r sC2 ，s E 表示的曲线，式中s是曲线的弧
长。曲线上分别与s和（s+ s）对应的两个相邻的点M和N。
b
全曲线长：L = 6a
曲线所围成的面积： S 3 a3
8
平面曲线
齿轮啮合原理
2.4 阿基米德螺旋线
曲线为一动点以常速沿一射线运动，而这一射线又以定角速度绕极点转动时，该动点所描成的轨迹.曲线由两支曲线组成，它们关于x轴对称。
方程式： a
a v
弧长：LOM
a 2
2 1 Arsh
3
a2 y2
极值点：C,
D
3 4
a,
3

《齿轮机构啮合传动》课件

齿轮机构啮合传动的应用
应用
齿轮机构啮合传动广泛应用于各种机械传动系统和工业领域，如汽车、航空、船舶、能源、化工等。
举例
汽车发动机中的曲轴与凸轮轴之间的啮合传动，实现发动机的工作循环；风力发电机中的齿轮箱，将风能转化为电能；船舶推进器中的齿轮传动，驱动螺旋桨旋转等。
02
齿轮机构啮合传动的类型
业领域，如汽车、飞机、机床等。
蜗杆蜗轮传动
总结词
具有减速、自锁和传递大扭矩的特点，常用于精密设备和自动化控制系统。
详细描述
蜗杆蜗轮传动是一种特殊的齿轮类型，其特点是蜗杆和蜗轮相互啮合，传递旋转运动和扭矩。与直齿圆柱齿轮、斜齿圆柱齿轮和圆锥齿轮相比，蜗杆蜗轮传动具有减速、自锁和传递大扭矩的特点，常用于精密设备和自动化控制系统。这种传动方式广泛应用于各
BIG DATA EMPOWERS TO CREATE A NEW ERA
《齿轮机构啮合传动》ppt
课件
• 齿轮机构啮合传动的概述 • 齿轮机构啮合传动的类型 • 齿轮机构啮合传动的特性 • 齿轮机构啮合传动的优化设计 • 齿轮机构啮合传动的未来发展
目录
CONTENTS
01
齿轮机构啮合传动的概述
BIG DATA EMPOWERS TO CREATE A NEW
ERA
直齿圆柱齿轮传动
总结词
最常见的齿轮类型，两个直齿圆柱齿轮相互啮合，传递扭矩和旋转运动。
详细描述
直齿圆柱齿轮传动是最常见的齿轮类型，其特点是两个直齿圆柱齿轮相互啮合，通过传递扭矩和旋转运动来驱动机械设备。这种传动方式广泛应用于各种工业领域，如汽车、飞机、机床等。
圆锥齿轮传动
总结词
适用于传递垂直或倾斜方向的扭矩和旋转运动，具有较高的承载能力和可靠性。

12694_齿轮啮合传动ppt课件

根据齿轮工作条件选择合适的润滑方式和密封结构，保证齿轮传动的可靠性和寿命。
2024/1/27
16
调试过程检查项目清单
齿轮啮合间隙检查
通过压铅法或塞尺法测量齿轮啮合间隙，确保间隙在规定范围内。
齿轮啮合接触斑点检查
涂色法检查齿轮啮合接触斑点，确保接触斑点分布均匀且符合规定要求。
齿轮传动噪音检查
2024/1/27
12
热处理工艺对性能影响
淬火
提高齿轮的硬度和耐磨性，但可能导致变形和开裂。
2024/1/27
回火
消除淬火应力，提高齿轮的韧性和综合力学性能。
渗碳淬火
提高齿轮表面的硬度和耐磨性，同时保持心部的韧性。
氮化处理
提高齿轮表面的硬度和耐磨性，同时改善其耐腐蚀性。
13
精度等级评定标准
控制齿轮箱内外压差和温度变化在允许范围内。
提高齿轮箱设计和制造质量，确保密封性能符合要求。
2024/1/27
25
06 性能测试与评价标准
2024/1/27
26
静态性能测试项目和方法
齿轮精度检测
使用齿轮测量中心或万能测齿仪等设备，对齿轮的各项精度指标进行测量，包括齿距、齿形、齿
向等。
2024/1/27
2024/1/27
11
常用加工方法介绍
01
02
03
04
铣齿
利用铣刀按照齿轮的齿形进行切削加工，适用于单件或小批
量生产。
滚齿
通过滚刀与齿坯的相对运动，实现齿轮齿形的加工，生产效率高，适用于大批量生产。
插齿
利用插齿刀按照齿轮的齿形进行切削加工，适用于内齿轮和
模数较大的齿轮加工。

《啮合传动原理部分》课件

根据应用需求，选择合适的材料和工艺，提高传动部件的寿
命和可靠性。
THANKS FOR WA化设计提供依据。
04
啮合传动的维护与保养
啮合传动的润滑
01
02
03
润滑的重要性
良好的润滑是保证啮合传动正常运行的关键，可以减小摩擦和磨损，提高传动效率和使用寿命。
润滑剂的选择
根据不同的啮合传动方式和工况条件，选择合适的润滑剂，如润滑油、润滑脂等。
润滑方式
常见的润滑方式包括油浴润滑、喷油润滑、油雾润滑等，应根据实际情况选择合适的润滑方式。
效率计算公式
根据定义，啮合传动效率的计算公式为输入功率与输出功率的比值，可以通过实验测量或理论计算得出。
啮合传动的功率计算
功率定义
在啮合传动中，功率是指单位时间内完成的功或转换的能量。它是衡量系统工作能力的重要参数。
功率计算公式
根据定义，功率的计算公式为功或能量转换速率，可以通过测量输入和输出功率来计算。
传动系统优化的重要目标。
02
优化策略
为了提高效率和功率，可以采取多种优化策略，包括改进齿轮设计、提
高制造精度、优化润滑方案、采用高性能材料等。这些措施可以降低摩
擦和能量损失，提高系统的效率和功率。
03
实验研究
为了深入了解啮合传动效率和功率的关系，可以通过实验研究来测试不
同条件下的效率和功率性能。通过实验数据的分析，可以揭示各种因素
02
啮合传动的基本原理
齿轮的工作原理
齿轮的工作原理
齿轮通过一对齿廓的啮合实现动力的传递。当两个齿轮相互咬合时，一个齿轮的旋转方向会带动另一个齿轮的旋转，从而实现动
力的传递。

渐开线直齿圆柱齿轮的啮合传动ppt课件

ω2
重要结论：a’cosaα’’c= oascαosα’
O2
提问：对于规范齿轮，有能够α’ <α吗？
特别留意： ▲分度圆和压力角是单个齿轮就有的；
▲节圆和啮合角是两个齿轮啮合后才出现的.
(3)齿轮齿条传动
规范安装： r1’ = r1 ，α’＝α 节线与分度线重合;
非规范安装： N1N2 线与齿廓垂直，且与基圆相切，
故在齿轮上，节点位置不变，有：
节圆与分度圆重合，
r 1 ’ = α ’ ＝重要结论！
r1
α
节线与分
度线不重
O1 合
O1
ra1
ω1
r1 rf1
ra1
ω1
r1 rf1
1
1
N1
N1 α’=α
B2
α’=α
潘存云教授
无穷远
潘存云教授 B2
N2 B1P v2 2
N 2
B1P v
2
2
1.3一对轮齿的啮合过程轮齿在从动轮顶圆与N1N2 线交点B2处进入啮合，自动轮
rb
根切
r
B2
N 1
N’1 K
α 潘存云教授
M
α B1 P
1 2 发生根切
34
结论：刀具齿顶线与啮合线的交点B2落在极限啮合点 N1的右上方，必发生根切。
根切条件为： PB2>PN1
O1
rb
α
r
B2
N 1
潘存云教授
P
✓在齿齿渐条高一开型样线的刀情齿况具下轮比，刀不齿具齿发轮越生多型，根刀越容切具易发的更生最根切少齿数容易发生根切。凡齿条刀不
[ε]的引荐值：
运用场所普通机械制造业汽车迁延机

齿轮啮合PPT课件

1
2
z1(tga1 tg ' ) z2 (tga2 tg ' )
a

arccos
rb ra
arccosrb
r
而
cosa

rb ra

r cos
r ha

z cos
z 2ha*
可见重合度与齿数有关而与模数无关
当齿数趋向无穷多，齿轮变成齿条时，重合度增大，在直齿圆柱齿轮中 max = 1.98
理论啮合线—— 线段N1N2
o1
ra
1
N2 B1
rb2
o2
1 rb1
B2N1
ra
2
2
6
齿轮传动是依靠两轮的轮齿依次啮合而实现的。如图所示，齿轮1是
o1
主动轮，齿轮2是从动轮，齿轮的啮合是从主动轮的齿根推动从动轮的
ra
齿顶开始的，因此初始啮合点是从
1
动轮齿顶与啮合线的交点B2点，一直啮合到主动轮的齿顶与啮合线的交点B1点为止，由此可见B1B2是实
15
顶隙的作用有两个：一是可以避免一个齿轮的齿顶与另一个齿轮齿槽底部发生顶死现象，二是为了贮存润滑油以润滑齿廓表面
当安装中心距不等于标准中心距(即非标淮安装)时，节圆半径要发生变化，但分度圆半径是不变的，这时分度圆与节圆分离。啮合线位置变化．啮合角也不再等于分度圆上的压力角。此时的中心距为
s1 e2 s2 e1
14
1.外啮合传动
齿轮啮合时相当于一对节圆作纯滚动，在标准齿轮分度圆上的齿厚等于齿槽宽
即s＝e＝πｍ／2 而两轮要正确啮合必须保证ｍl＝ｍ2，所以若要保证无侧隙啮合，就要求分度圆与节圆重合。这样的安装称为标准安装．此时的中心距称为标准中心距。

齿轮机构啮合传动-PPT文档资料

r r ( r r ) cos a a cos a b 1 b 2 1 2
r r ( r r ) cos a a cos a b 1 b 2 1 2
两轮中心距与啮合角的关系：
a cos a a cos a
§10-5 渐开线直齿圆柱齿轮的啮合传动
（1）外啮合传动
B B PB PB 1 2 1 2
mz 1 PB r (tg tg ) cos (tg tg ) 1 b 1 a 1 a 1 2
aa1=arccosrb1/ra1
aa
a aa
mz PB r (tg tg ) 2 cos (tg tg ) 2 b 2 a 2 a 2 2
N1、N2 —— 啮合极限点。
§10-5 渐开线直齿圆柱齿轮的啮合传动 2. 连续传动条件
实际啮合线段≥法向齿距
重合度——实际啮合线段
与法向齿距的比值，用a
表示。
B1 B 2 a pb
连续传动条件—— 重合轮的啮合传动 3.重合度的计算
§10-5 渐开线直齿圆柱齿轮的啮合传动一、一对渐开线齿轮正确啮合的条件
一对齿轮正确啮合时,它们的
法节必须相等。即：
pb1=pb2
pb1=p1cosa1
pb2=p2cosa2
m1cosa1=m2cosa2 m1=m2, a1=a2
§10-5 渐开线直齿圆柱齿轮的啮合传动正确啮合条件 m1 = m2 = m
§10-5 渐开线直齿圆柱齿轮的啮合传动
一对标准齿轮，当c = c*m 时，中心距 :
ar cr a 1 f2
* * * * (r h m )c m (r h m c m ) 1 a 2 a

齿轮机构的齿廓啮合基本规律、特点和类型41页PPT

Thank you
齿轮机构的齿廓啮合基本规律、特点和类型
46、法律有权打破平静。——马·格林 47、在一千磅法律里，没有一盎司仁爱。— —英国
48、法律一多，公正就少。——托·富勒 49、犯罪总是以惩罚相补偿；只有处罚才能使犯罪得到偿能得到法律的保护。—— 威·厄尔
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

若如图中虚线所示，前一对齿到达 B1点时，后一·对齿已经啮合多时，此时B1B2＞Ｐｂ。由此可见，齿轮连续传动的条件为
B1B2 Pb 1
ε称为重合度，它表明同时参与啮合轮
齿的对数。 ε大表示每对齿的负荷小，负荷变动量也小，传
动平稳。因此ε是衡量齿轮传动质量的指标之一
.
8
渐开线直齿圆柱齿轮的啮合传动
.
1
机械设计基础 ——齿轮传动
两轮法向齿距不等时
❖ 两轮法向齿距不等时（ pn1≠pn2 ），轮齿发生干涉，两轮不能正确啮合传动
❖
两轮法向齿距相等时（
合传动
.
pn1=pn2
），两轮能正确啮
2
由渐开线性质可知，法向齿距等于两轮基圆上的齿距，因此，要使两轮正确啮合，必须满足：
可得：
pb1 pb2
r1'
a P a'
b b'
•正确安装中心距：无侧隙啮合的中心距称为正确安装中心距。
· 无侧隙啮合传动条r2'件
一齿轮轮齿的节圆齿厚必须等于另一齿轮节圆齿槽宽。
s1 e2 s2 e1
.
13
1.外啮合传动
齿轮啮合时相当于一对节圆作纯滚动，在标准齿轮分度圆上的齿厚等于齿槽宽
即s＝e＝πｍ／2 而两轮要正确啮合必须保证ｍl＝ｍ2，所以若要保证无侧隙啮合，就要求分度圆与节圆重合。这样的安装称为标准安装．此时的中心距称为标准中心距。
渐开线齿轮传动的重合度
齿轮传动是依靠两轮的轮齿依次啮合而实现的。
具体啮合及重合度的概念观看右图演示。
图11.10所示为ε＝1.3的情况，当前一对齿在c点啮合时，后一对齿在B2点接触，从此时开始两对齿同时啮合，直到前一对齿到达Bl点，后一对齿到达D点为止。因此，啮合线上的B1C和DB2区间是双齿啮合区。从D点开始到C点只有一对齿啮合，是单齿啮合区。所以ε＝1.3 表明在齿轮转过一个基圆齿距的时间内有30％的时间是双齿啮合，70％的时间是单齿啮合
a
arccosrb ra
arccosrb
r
而
coasrra brrco h aszzc 2oh a *s
可见重合度与齿数有关而与模数无关
当齿数趋向无穷多，齿轮变成齿条时，重合度增大，在
直齿圆柱齿轮中 max = 1.98
.
12
11.5.3 正确安装
· 无侧隙啮合传动一个齿轮齿厚的两侧齿
廓与其相啮合的另一个齿轮的齿槽两侧齿廓在两条啮合线上均紧密相切接触。
11.5 渐开线直齿圆柱齿轮的啮合传动
11.5.1 正确啮合条件
渐开线齿廓齿轮能满足定角速比转动，
是不是随便一对渐开线齿轮就能正确啮
1
o1
合？答案是否定的！
N1
N2 k
k
法向齿距
两齿轮的相邻两对轮齿分别K在和 K‘同时接触，才能使两个渐开线齿轮搭配起来并正确的传动
即：两轮的法向齿距相等
2 o2
pb1 pb2 o2
齿轮的传动比计算可为：
i12 1 2rr1 21 1rrb b1 2rr1 2c co ossrr1 2zz1 2
.
4
11.5.2 渐开线齿轮传动的重合度
在齿轮啮合过程中，如果前一对齿轮到达B1点，终止啮合，而后一对齿轮还没有在啮合线上进入啮合，则这对齿轮就不能接传动比连续活动，从而破坏了传动的平稳性
也就是说：满足正确啮合条件只是连续传动的必要条件而不是充分条件。为了保证连续传动，还必须研究齿轮传动的重合度
.
5
一对轮齿在啮合线上啮合的起始点—— 从动轮2的齿顶圆与啮合线N1N2的交点B2
一对轮齿在啮合线上啮合的终止点—— 主动轮的齿顶圆与啮合线N1N2的交点B1。
实际啮合线—— 线段B1B2
p bm 1co 1 sm 2co 2s
由于渐开线齿轮的模数和压力角α
均为标准值，所以两轮的正确啮合条
件是：
m1 m2 m
1 2
即：两轮的模数相等，两轮的压力角相等
.
3
1 o1
N1
N2 k
k
pb1 pb2
2 2
o1
N1
N2 k
k 2
k1
pb1 pb2 o2
o1
N2 k
N1 k2 k1
但无论是标准安装还是非标准安装，其传动比都为一恒值
.
15
2.齿轮齿条传动
渐开线齿条的几何特点
齿轮齿条啮合
p se
n
n
齿形角
hf ha
齿顶线分度线齿根线
（1）同侧齿廓为互相平行的直线.。
（2）凡与齿条分度线平行的任一直线上的齿距和模数都等于分
度线上的齿距和模数。
（3）齿条齿廓上各点的压力角均相等，且数值上等齿条齿形角。
.
10
重合度的物理意义( 1.3) Pn
0.3Pn
0.7Pn
双对齿
啮合区
B1
K'
单对齿啮合区
Pn
1.3Pn
二对齿啮合区长度
实际应用中，
.
0.3Pn
双对齿
啮合区
K
B2
许用重合度，见表11.5
11
➢ε的计算公式
a B P 1 B n2 2 1z 1 (tg a 1 tg ') z2 (tg a 2 tg ')
理论啮合线—— 线段N1N2
o1
ra1
N2 B1
rb2 o2
1 rb1
B2N1
ra2 2
.
6
齿轮传动是依靠两轮的轮齿依次啮合而实现的。如图所示，齿轮1是
o1
主动轮，齿轮2是从动轮，齿轮的啮
合是从主动轮的齿根推动从动轮的齿顶开始的，因此初始啮合点是从
ra1
动轮齿顶与啮合线的交点B2点，一
直啮合到主动轮的齿顶与啮合线的交点B1点为止，由此可见B1B2是实
此时两齿轮在径向方向留有间隙c，其值为一齿轮的齿根高减去另一齿轮的齿顶高，c＝ｃ*ｍ称为标准顶隙
.
14
顶隙的作用有两个：一是可以避免一个齿轮的齿顶与另一个齿轮齿槽底部发生顶死现象，二是为了贮存润滑油以润滑齿廓表面
当安装中心距不等于标准中心距(即非标淮安装)时，节圆半径要发生变化，但分度圆半径是不变的，这时分度圆与节圆分离。啮合线位置变化．啮合角也不再等于分度圆上的压力角。此时的中心距为
N2 B1
际啮合线长度。显然，随着齿顶圆的增大， B1B2线可以加长，但不会
rb2
超过N1、N2点，N1、N2点称为啮
合极限点，N1N2是理论啮合线长度。
o2
当B1B2恰好等于Pb时，即前一对齿
在B1点即将脱离，后一对齿刚好在B
２点接触时，齿轮能保证连续传动。
1 rb1
B2N1
ra2 2
.
7
但若齿轮2的齿顶圆直径稍小，它与啮合线的交点在B２´，则B1B２´＜Ｐｂ。此时前一对齿即将分离，后一对齿尚未进入啮合，齿轮传动中断；