格网模型 1
- 格式:doc
- 大小:136.00 KB
- 文档页数:4



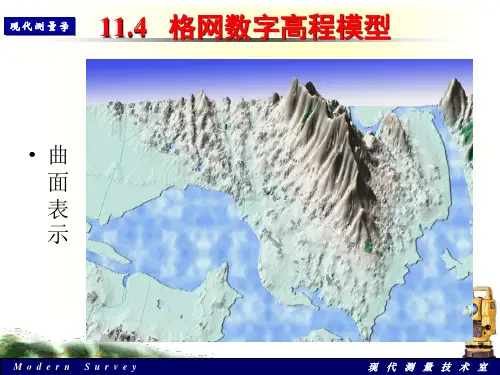
不规则三角网(TIN)Ⅰ 数字高程模型(DEM)地球表面高低起伏,呈现一种连续变化的曲面,这种曲面无法用平面地图来确切表示。
于是我们就利用一种全新的数字地球表面的方法——数字高程模型的方法,这种方法已被普遍广泛采用。
数字高程模型即DEM(Digital Elevation Model),是以数字形式按一定结构组织在一起,表示实际地形特征空间分布的模型,也是地形形状大小和起伏的数字描述。
DEM有三种主要的表示模型:规则格网模型,等高线模型和不规则三角网。
格网(即GRID)DEM在地形平坦的地方,存在大量的数据冗余,在不改变格网大小情况下,难以表达复杂地形的突变现象,在某些计算,如通视问题,过分强调网格的轴方向。
不规则三角网(简称TIN,即Triangulated Irregular Network)是另外一种表示数字高程模型的的方法(Peuker等,1978),它既减少了规则格网带来的数据冗余,同时在计算(如坡度)效率方面又优于纯粹基于等高线的方法。
不规则三角网能随地形起伏变化的复杂性而改变采样点的密度和决定采样点的位置,因而它能够避免地形起伏平坦时的数据冗余,又能按地形特征点如山脊,山谷线,地形变化线等表示数字高程特征。
Ⅱ TIN的基本知识在TIN中,满足最佳三角形的条件为:尽可能的保证三角形的三个角都是锐角,三角形的三条边近似相等,最小角最大化。
TIN 是基于矢量的数字地理数据的一种形式,通过将一系列折点(点)组成三角形来构建。
形成这些三角形的插值方法有很多种,例如Delaunay 三角测量法或距离排序法。
ArcGIS 支持Delaunay 三角测量方法。
TIN 的单位是英尺或米等长度单位,而不是度分秒。
当使用地理坐标系的角度坐标进行构建时,Delaunay 三角测量无效。
创建TIN 时,应使用投影坐标系(PCS)。
TIN 模型的适用范围不及栅格表面模型那么广泛,且构建和处理所需的开销更大。
获得优良源数据的成本可能会很高,并且,由于数据结构非常复杂,处理TIN 的效率要比处理栅格数据低。

一、名词解释(10小题,每小题3分,共30分)。
1.地理信息系统(GIS):是在计算机软、硬件系统支持下,对整个或部分地球表层(包括大气层)的有关地理分布数据进行采集、储存、管理、运算、分析、显示和描述的技术系统。
简言之,地理信息系统是对空间数据进行采集、编辑、存储、分析和输出的计算机信息系统。
2.地理信息:是指表征地理圈或地理环境固有要素或物质的数量、质量、分布特征、联系和规律等的数字、文字、图像和图形等的总称。
3.地理数据:是以地球表面空间位置为参照,描述自然、社会和人文景观的数据。
4.不规则三角网模型(TIN):简称TIN,它根据区域有限个点集将区域划分为相连的三角面网络,区域中任意点落在三角面的顶点、边上或三角形内。
5.拓扑关系:指网结构元素结点、弧段、面域之间的空间关系。
6.拓扑结构:指在点、线和多边形之间建立关联,以及彻底解决邻域和岛状信息处理问题而必须建立的数据结构。
7.空间数据结构:是指适合于计算机系统存储、管理和处理的地学图形的逻辑结构。
8.矢量数据结构:是利用几何学中的点、线、面及其组合体来表示地理实体空间分布的一种数据组织方式。
9.栅格数据结构:指将空间分割成有规则的网络,在各个网格上给出相应的属性值来表示地理实体的一种数据组织形式。
10.空间数据编码:指将数据分类的结果用一种易于被计算机和人识别的符号系统表示出来的过程。
11. Delaunay三角网:即由狄洛尼三角形组成的三角网,狄洛尼三角形有三个最邻近的点连接而成,这三个相邻点对应的V oronoi多边形有一个公共的顶点,此顶点同时也是狄洛尼三角形外接圆的圆心。
12. V oronoi多边形:由连接两邻点直线的垂直平分线组成的连续多边形组成的图形。
13.坐标变换:采用一定的数学方法将一种坐标系的坐标变换为另一种坐标系的坐标的过程。
14.数据精度:是考察数据质量的一个方面,即对现象描述的详细程度。
15.空间数据库:是地理信息系统在计算机物理存储介质上存储的与应用相关的地理空间数据的总和。

第十三讲网格模型一. 慨述怎样将现实中的一个物体,比如,一只花瓶,一个足球,甚至一架大的战斗机,在电脑屏幕上显示呢?我们一般会这样做:1. 先把该物体放在一个虚拟的三维坐标系中,该坐标称为局部坐标系(Local Space), 一般以物体的中心作为坐标原点,采用左手坐标系。
2. 然后,对坐标系中的物体进行点采样(Point Sample), 这些采样点按一定顺序连接成为一系列的小平面(三角形或共面的四边形,五边形等),这些小平面称为图元(Primitive), 3D 引擎会处理每一个图元,称为一个独立的渲染单位。
这样取样后的物体看起来像是由许许多多的三角形,四边形或五边形组成的,就像网一样,我们称为一个网格(Mesh).这个采样过程又可称为物体的3D建模。
当然现在都有功能非常强大的3D建模工具,例如,3D Max, 3D Cool等建模工具,省去了我们这方面的许多工作。
3. 我们纪录这些顶点数据和连线情况到一个文件中,3D引擎读取这些数据,依次渲染每一个图元,就能在显示屏幕上再现物体。
当然了,取样的点越多,再现的物体也会越逼真,要处理的数据量也越大。
二. D3D中的网格(Mesh)1、子集和属性缓存网格模型都由一个或多个子集(subset)组成,其中每个子集都具有一组相同材质、纹理和绘制状态等属性的三角形集合。
为了区分网格中的不同子集,每个子集都被指定了一个唯一的属性ID,而且网格中的每个三角形也被指定了该三角形所属子集的属性ID。
在mesh中的每个三角形都与一个属性ID相关联,表示该三角形属于该子集。
例如,上图中组成地板的三角形具有属性ID0,它表示这些三角形属于子集0。
同样,组成墙的三角形具有属性ID1,它表示这些三角形属于子集1。
三角形的属性ID存储在mesh的属性缓存中,它是一个DWORD数组。
因为每个面对应属性缓存中的一项,所以属性缓存中的项目数等于mesh中的面的个数。
属性缓存中的项目和索引缓存中定义的三角形一一对应。


基本概念此教学将提供您使用流道和冷却系统来建构网格的快速概观,可产生简易的模型并将它导出到Moldex3D Project 进行分析。
流程分为五部分:建立模穴网格、建立流道系统、建立模座、建立冷却水路,以及导出网格模型。
下列图表的简图用于说明此流程。
此矩型固体的维度为 2 mm * 20 mm * 10 mm。
若您要在阅读此教学时依照以下步骤操作,请使用「Rhino 工具栏」(Rhino Toolbar) 中的立方体(Box) 来建立此模型。
1. 建立模穴网格(Create Cavity Mesh)1.撒点单击Node Seeding来设定模型表面的网格尺寸。
在快显对话框中将[Initial Mesh Size] )设为2mm。
2.建立表面网格单击Create Surface Mesh来在模型上建立表面网格。
在快显对话框中,选取Pure triangle,然后单击Generate来建立表面网格。
2. 建立流道系统(Create Runner System)1.描绘流道的线条单击多重直线(Polyline)来描绘定义流道配置的线形对象。
2.指定流道属性单击Attribute Setting来设定流道的直径。
在Attribute下拉式清单中选取Cold Runner。
将正面直径设为 1 mm,背面直径设为 2 mm。
然后单击OK来完成设定。
结果显示如下。
3.描绘代表进浇点的点单击单点(Point)来描绘流道线条末端的点。
4.指定进浇点的属性单击Attribute Setting来将点的属性设为进浇点(Melt Entrance)。
5.建立流道实体网格单击Create Runner System Mesh来建立流道的实体网格。
3. 建立模穴实体网格(Create Cavity Solid Mesh)建立塑件的tetra 实体网格单击[Create Tetra ]来建立塑件的四面体实体网格。
在快显对话框中,将其属性设为[Cavity (Part ) Solid Mesh]。

D*名词解释DOM数字正射影像图:(Digital Orthophoto Map,缩写DOM)是利用数字高程模型(DEM)对经扫描处理的数字化航空像片,经逐像元进行投影差改正、镶嵌,按国家基本比例尺地形图图幅范围剪裁生成的数字正射影像数据集。
它是同时具有地图几何精度和影像特征的图像,具有精度高、信息丰富、直观真实等优点。
DEM数字高程模型:(Digital Elevation Model,缩写DEM)是在某一投影平面(如高斯投影平面)上规则格网点的平面坐标(X,Y)及高程(Z)的数据集。
DEM的格网间隔应与其高程精度相适配,并形成有规则的格网系列。
根据不同的高程精度,可分为不同类型。
为完整反映地表形态,还可增加离散高程点数据。
DLG数字线划地图:(Digital Line Graphic,缩写DLG)是现有地形图要素的矢量数据集,保存各要素间的空间关系和相关的属性信息,全面地描述地表目标。
DRG数字栅格地图:(Digital Raster Graphic,缩写DRG)是现有纸质地形图经计算机处理后得到的栅格数据文件。
每一幅地形图在扫描数字化后,经几何纠正,并进行内容更新和数据压缩处理,彩色地形图还应经色彩校正,使每幅图像的色彩基本一致。
数字栅格地图在内容上、几何精度和色彩上与国家基本比例尺地形图保持一致。
DTM数字地面模型DTM(Digital Terrain Models)即数字地面模型,它是地形起伏的数字表达,它由对地形表面取样所得到的一组点的x、y、Z坐标数据和一套对地面提供连续的描述的算法组成。
简单地说,数字地面模型是按一定结构组织在一起的数据组,它代表着地形特征的空间分布。
DTM是建立地形数据库的基本数据,可以用来制作等高线图、坡度图、专题图等多种图解产品。
---------------------------------数字地形模型(DTM)与地形分析在这个论坛里发现有朋友常问这些问题,所以特把有些资料贴出来,希望对大家有帮助,更希望大家支持我,有时间到我家做客/bbs/数字地形模型(DTM)与地形分析导读:DEM和DTM主要用于描述地面起伏状况,可以用于提取各种地形参数,如坡度、坡向、粗糙度等,并进行通视分析、流域结构生成等应用分析。

无刻度直尺网格作图的基本模型及应用《义务教育数学课程标准(2022年版)》对尺规作图的内容及要求有所加强,其地位又得到了一定提升。
尺规作图蕴含丰富的推理,是发展学生推理能力的良好载体,而“无刻度直尺网格作图”是尺规作图的基础。
本文将在9×9的网格下讨论三种基本模型和四种复合模型。
在网格作图中,我们把两条相交直线叫做格点的“母线”。
若两条母线都是网格线,则交点叫格点;若两条母线中只有一条网格线,则交点叫次格点;若两条母线都不是网格线,则交点叫一般点。
我们要过一个点作一条线的平行线或垂线,当点是格点时,我们很轻松的通过平移完成,当点不是格点时,我们通常通过平移“生成”点的母线来完成。
一、基本作图1、过点作平行线①如图1,过C点作CD平行且等于AB解答:C是格点,只需要找到C的对应点D,因A到B的平移方式是横左2纵下3,则A到B的平移方式也是横左2纵下3。
总结:若点是格点,直接通过平移到对应点,并且平移横纵不变(下文中平移方式不变就不再强调)。
②如图2,过E点作EF平行且等于AB解答:E是次格点,先找到母线AC的对应母线BD,再找到E的对应点F。
总结:若点是次格点,先通过平移非网格线的那条母线到对应母线,再找到对应点。
③如图3,过E点作EF平行且等于AB解答:E是一般点,先找到两条母线的对应母线,再找到E的对应点F。
总结:若点是一般点,先通过平移两条母线到对应母线,再找到对应点。
变式:如图4,过E点作AB的平行线交BC于点F解答:我们除了用平移的方法作平行线,还可以利用X、A型相似作平行。
因为E是AC的一个三等分点,可以先连接BC,再利用相似找BC对应的三等分点F。
2、过点作垂线①如图5,过C点作CD垂直且等于AB解答:C是格点,只需要找到C的对应点D,因A到B的平移方式是横左2纵下3,则C到D的平移方式是横左3纵上2。
总结:若点是格点,直接通过旋转得到对应点,并且旋转横纵交换。
②如图6,过E点作EF垂直且等于AB解答:E是次格点,先过A点作AB的垂线AC(横纵交换),再过次格点E点作AC的平行线EF。
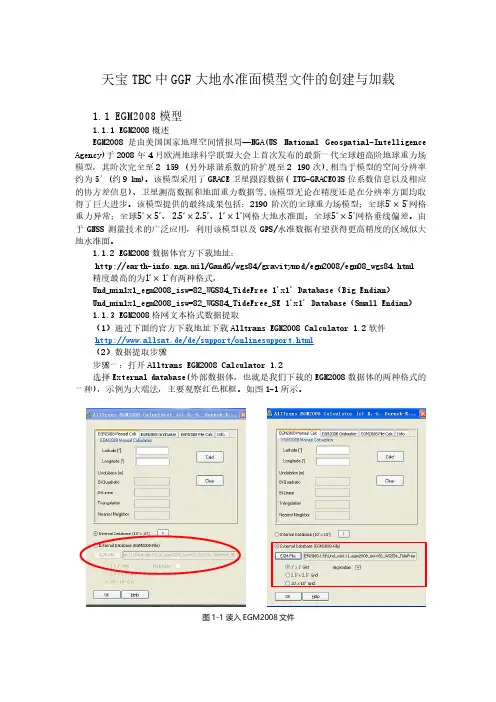
天宝TBC 中GGF 大地水准面模型文件的创建与加载1.1 EGM2008模型1.1.1 EGM2008概述EGM2008是由美国国家地理空间情报局—NGA(US National Geospatial-Intelligence Agency)于2008年4月欧洲地球科学联盟大会上首次发布的最新一代全球超高阶地球重力场模型,其阶次完全至2 159 (另外球谐系数的阶扩展至2 190次),相当于模型的空间分辨率约为5′(约9 km)。
该模型采用了GRACE 卫星跟踪数据( ITG-GRACE03S 位系数信息以及相应的协方差信息)、卫星测高数据和地面重力数据等,该模型无论在精度还是在分辨率方面均取得了巨大进步。
该模型提供的最终成果包括:2190阶次的全球重力场模型;全球5‘×5’网格重力异常;全球5‘×5’、 2.5‘×2.5’、1‘×1’网格大地水准面;全球5‘×5’网格垂线偏差。
由于GNSS 测量技术的广泛应用,利用该模型以及GPS/水准数据有望获得更高精度的区域似大地水准面。
1.1.2 EGM2008数据体官方下载地址:/GandG/wgs84/gravitymod/egm2008/egm08_wgs84.html 精度最高的为1‘×1’有两种格式,Und_min1x1_egm2008_isw=82_WGS84_TideFree 1'x1' Database (Big Endian ) Und_min1x1_egm2008_isw=82_WGS84_TideFree_SE 1'x1' Database (Small Endian )1.1.3 EGM2008格网文本格式数据提取(1)通过下面的官方下载地址下载Alltrans EGM2008 Calculator 1.2软件 http://www.allsat.de/de/support/onlinesupport.html(2)数据提取步骤步骤一:打开Alltrans EGM2008 Calculator 1.2 选择External database(外部数据体,也就是我们下载的EGM2008数据体的两种格式的一种),示例为大端法,主要观察红色框框。
地理信息系统中常⽤的空间数据模型有哪些?之前在百度知道上看到了这个问题——“地理信息系统中常⽤的空间数据模型有哪些?”今天就针对这个问题做了⼀些整理,看看能不能帮到⼤家。
空间数据模型是指利⽤特定的数据结构来表达空间对象的空间位置、空间关系和属性信息;是对空间对象的数据描述。
空间数据模型是地理信息系统的基础,它不仅决定了系统数据管理的有效性,⽽且是系统灵活性的关键。
⽬前,与GIS设计有关的空间数据模型主要有⽮量模型,栅格模型,数字⾼程模型,⾯向对象模型,⽮量和栅格的混合数据模型等。
前⾯四种模型属于定向性模型,在模型设计时只包括与应⽤⽬标有关的实体及其相互关系,⽽混合模型的设计则包括所有能够指出的实体及其相互关系。
就⽬前的应⽤现状⽽⾔,⽮量模型、栅格模型、数字⾼程模型相当成熟(⽬前成熟的商业化GIS主要采⽤这三类模型),⽽其它模型,特别是混合模型则处于⼤⼒发展之中。
⼀、⽮量模型(vector model)⽮量模型是利⽤边界或表⾯来表达空间⽬标对象的⾯或体要素,通过记录⽬标的边界,同时采⽤标识符(Identifier)表达它的属性来描述空间对象实体。
⽮量模型能够⽅便地进⾏⽐例尺变换、投影变换以及图形的输⼊和输出。
⽮量模型处理的空间图形实体是点(point)、线(line)、⾯(area)。
⽮量模型的基本类型起源于“Spaghetti”模型。
在Spaghetti模型中,点⽤空间坐标对表⽰,线由⼀串坐标对表⽰,⾯是由线形成的闭合多边形。
CAD等绘图系统⼤多采⽤Spaghetti模型。
GIS的⽮量数据模型与Spaghetti模型的主要区别是,前者通过拓扑结构数据来描述空间⽬标之间的空间关系,⽽后者则没有。
在⽮量模型中,拓扑关系是进⾏空间分析的关键。
在GIS的拓扑数据模型中,与点、线、⾯相对应的空间图形实体主要有结点(node)、弧段(arc)、多边形(polygon),多边形的边界被分割成⼀系列的弧和结点,结点、弧、多边形间的空间关系在数据结构或属性表中加以定义。
如何进行地理空间数据的模型建立与分析地理空间数据是指带有地理位置信息的数据,其记录了地球上不同区域的各种属性。
在如今数据驱动的社会中,地理空间数据的模型建立与分析对于城市规划、交通管理、环境保护等方面具有重要意义。
本文将介绍如何进行地理空间数据的模型建立与分析,以帮助读者更好地理解和应用这一领域的知识。
一、地理空间数据的模型建立地理空间数据的模型建立是指将真实世界的地理信息通过抽象和建模的方式转化为计算机可以处理的形式。
从数据形式上来说,地理空间数据可以分为矢量数据和栅格数据两种类型。
1. 矢量数据建模矢量数据是通过点、线、面等几何要素来表示地理对象的数据形式。
在矢量数据建模中,常用的数据模型包括欧几里得模型和拓扑模型。
欧几里得模型是一种基于空间坐标的数据模型,通过确定空间中的点、线、面的位置和相对关系来描述地理要素。
在欧几里得模型中,地理要素的属性信息和几何信息被分开存储,常用的数据格式有Shapefile和GeoJSON等。
拓扑模型是一种基于地理实体之间的拓扑关系来描述地理要素的数据模型。
在拓扑模型中,地理要素的几何信息和属性信息被统一存储,可以更好地描述地理要素之间的关系。
常用的拓扑模型有面邻接关系模型和图结构模型等。
2. 栅格数据建模栅格数据是将地理空间划分为规则的像素网格,并将地理要素的属性信息以栅格的形式进行存储。
在栅格数据建模中,常用的数据模型有格网模型和格网金字塔模型。
格网模型是一种将地理空间划分为等大小的像素网格,每个像素网格存储一个值来表示地理要素的属性信息。
格网模型适用于连续变量的表示,如高程数据和遥感影像等。
格网金字塔模型是一种将地理空间划分为多个层级的像素网格,每个层级的像素网格存储了不同分辨率的地理要素属性信息。
格网金字塔模型适用于多尺度分析,可以在不同层级上对地理要素进行分析。
二、地理空间数据的分析地理空间数据的分析是指通过空间统计、空间交互和空间模拟等方法对地理空间数据进行解释和预测的过程。
2.4.2格网电离层模型
广域增强系统(WAAS)是由美国航空航天局为提高GPS 卫星导航系统在本地区的位置服务精度与可靠性而提出并且成功实施运行的系统,WAAS 建议采用格网电离层模型,其能够为单频接收机用户提供大范围、实时与精确的电离层延迟误差改正。
WAAS 把复杂的电离层视为距离地面约350公里的薄层,并把它作为地面站点及用户接收机共同的参考面。
并将电离层参考面按55⨯的间隔划分成大量的网格单元。
在广域增强系统的覆盖范围内分布着一定数目的基准观测站以及一个主控站,各基准观测站根据观测到的GPS 资料,实时地分离出卫星和接收机的仪器偏差与电离层延迟数据,然后提取出各电离层穿刺点处的精确垂向电离层延迟数据信息;主控站整合网络覆盖区域内所有观测基准站所有可视卫星的电离层穿刺点处的精确电离层TEC 信息,并通过一定的算法计算出电离层参考面上所有网格结点处的电离层垂向总电子含量(VTEC),建立覆盖整个网络服务区的电离层格网模型,并分析格网模型的模型精度;主控站再将所有网格结点的电离层延迟数据以一定格式生成电文经由GEO 卫星播发给服务区域内的用户,用户接收机首先计算各可视卫星穿刺点的位置坐标,根据各穿刺点落入的网格单元所对应的GEO 卫星播发的格网点电离层延迟信息,按照一定算法解算出各可视卫星伪距观测中的电离层延迟误差量[26,36-37]。
(1)网格结点电离层的解算[38]
广域增强系统主控站首先接收其网络覆盖区域内的所有观测基准站发送的实时电离层延迟误差信息,其中包括所有基准站可视卫星电离层穿刺点的位置坐标及各穿刺点的电离层VTEC 信息,然后采用距离反比例加权算法解算出WAAS 整个网络覆盖区域内的所有网格结点的VTEC 值。
距离反比例加权法是基于空间相关性原理而来的,根据距离的远近赋予不同的权重系数,即所测穿刺点距离该格点越近权重值越大,越远权重值越小,然后整合相应格网点周围四个网格内的穿刺点VTEC 信息来估算出网格结点的垂直电离层延迟误差, 如图2.1。
计算公式如下:
111/00i n n ion ij j
i i ij ij ion i ion ij D d DR d d D D d ==⎧<<⎪=⎨⎪=⎩∑∑ (2-4-1)
-1
()cos [sin sin cos cos cos()]ij i j i j i j d R H ϕϕϕϕλλ=++- (2-4-2) 式中,DR 表示距离阈值,作用是对监测站数据进行筛选;(,)i i ϕλ为格网点
i 的地理经纬度;(,)j j ϕλ为穿刺点j 的地理经纬度;R 为地球半径,H 为电离层单层模型高度。
图2.1 主控站网格点算法示意图
(2)用户穿刺点电离层的解算
WAAS 系统中的用户计算电离层延迟的方法与主控站和基准站的算法相似,不同的是最终电离层延迟误差的获取是来自于对同步卫星广播电离层延迟数据的内插。
具体流程如下:
1) 确定可视卫星电离层穿刺点位置,其中用户的位置由用户接收机提供概略位置,但并不影响电离层延迟误差的解算。
基本公式,参考文献38.
2) 用户电离层穿刺点垂直延迟误差的获取
虽然用户接收机可以接收到来自同步卫星转发的WAAS 网格点的垂直电离层延迟数据,然而对于用户来说,其所有的电离层穿刺点不可能同时或时刻都在网格结点上,所以需要利用广播的电离层延迟数据对各个穿刺点进行内插解算。
内插法的一般公式为
1(,)n V
V u i u u
i i T W x y T ==∑ (2-4-3)
式中,V u T 为待求值;(,)i u u W x y 为加权函数;,u u x y 为待求点位置的函数;n
为参加计算的已知点的个数;V i T 为已知的边界条件。
加权函数(,)W x y 有很多种不同的表达形式。
其中最为常用的的三种:双线性加权法、距离倒数加权和Junkins 加权法。
Junkins 法与倒数法相比较而言,接收机的计算负荷不高,和双线性法相比来说,Junkins 的空间相关性更强,要强调的一点是其为WAAS 文件规范中所推荐的方法,所以本文在对用户电离层穿刺点进行电离层解算时采用Junkins 法。
Junkins 的权函数计算公式为
22(,)(,)(9664)W x y f x y x y x y xy ==--+ (2-4-4) 计算矩形四点加权时的加权函数为
1234(,)(,)
(,)(1,)
(,)(1,1)
(,)(,1)W x y f x y W x y f x y W x y f x y W x y f x y ==-=--=- (2-4-5)
矩形内插法的计算公式为
4
1(,)(,)V
IPP IPP IPP i IPP IPP Gi i I W x y I ϕλ==∑ (2-4-6)
式中,V IPP I 为待求点(穿刺点)的垂直电离层延迟;,IPP IPP ϕλ为穿刺点的纬度和经度;(,)i IPP IPP W x y 为Junkins 加权函数;,IPP IPP x y 为电离层穿刺点位置与相关网格结点的位置的函数;Gi I 为网格结点的电离层垂直延迟误差量,通过导航电文播发而来。
,IPP IPP x y 的计算如图2.2所示,
21
IPP IPP x λλλ∆=- (2-4-7) 21IPP IPP y ϕϕϕ∆=
- (2-4-8) 1IPP IPP λλλ∆=- (2-4-9) 1IPP IPP ϕϕϕ∆=- (2-4-10) 1λ,2λ,1ϕ,2ϕ,IPP λ∆,IPP ϕ∆的含义如图所示。
图2.2 IPP x ,IPP y 的计算示意图。