质心运动定理讲解

质心运动定理
质心运动定理是质点系动量定理的另一种形式,可由质点系动量定理直接导出。

即将P＝Mvc代入质点系动量定理dP/dt＝∑Fe，得：Mdvc/dt＝∑Fe或Mac ＝∑Fe——称为质心运动定理.(∵ac＝dvc/dt)
即：质点系的质量M与质心加速度ac的乘积等于作用于质点系所有外力的矢量和(外力主矢量)。

可见：只有外力才能改变质点系质心的运动。

定理的推论
根据这个定理可推知：
①质点系的内力不能影响它的质心的运动；例如跳水运动员自跳板起跳后，不论他在空中再做何种动作，采取何种姿势，由于外力(重力)并未改变，所以运动员的质心在入水前仍沿抛物线轨迹运动；
②如果作用于质点系上外力的矢量和始终为零，则质点系的质心作匀速直线运动或保持静止；
③若作用于质点系上外力的矢量和在某轴上的投影始终为零，则质点系质心在该轴上的坐标匀速变化或保持不变。

质心运动守恒定理
质心运动守恒定理，也称为质心运动定理，是物理学中的一个重要定理，用于描述系统总质量的质心在不受外力作用时的运动特性。

质心是一个系统的所有质点的质量加权平均位置。

在不受外力作用的情况下，质心的运动有一个重要的特性：系统的质心以恒定的速度直线运动。

质心运动守恒定理的表述如下：
在一个封闭系统中，如果系统内部没有外力作用，那么系统的质心将以恒定的速度沿着直线运动。

这意味着，如果一个系统内部没有物体离开或进入，系统的总质量保持不变，而且系统的质心在运动过程中不会改变速度或方向。

质心运动守恒定理是一个非常有用的工具，特别在研究大规模物体组成的系统时，如行星运动、天体运动等。

需要注意的是，如果系统受到外力作用，那么质心运动守恒定理将不再适用，质心的运动将会受到外力的影响。

因此，在具体问题中，需要根据情况来判断是否可以应用质心运动守恒定理。

1/ 1。

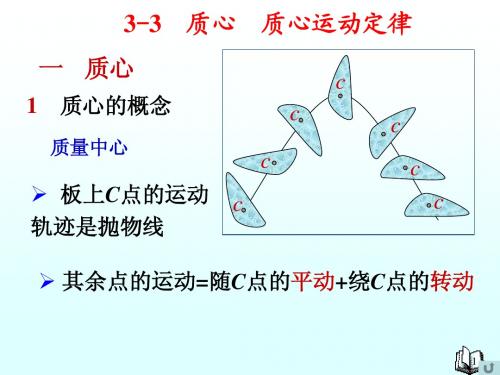
质心与质心运动定律一、质心1. 定义我们先来回顾一下牛顿第二定律:是对单个质点而言的,由于质点系内各质点的运动情况各不相同,加速度也各不相同,并不能简单的等效于 (M是体系的总质量),但对质点系而言,确实存在一个特殊点C,而使成立,这个ac是该特殊点C的加速度.这个特殊点称为质心.2. 质心的位置如果将质点系各质点参量记为mi 、ri、vi、xi、yi、zi……，质点系质心记为C则对于由两个质点构成的简单质点系，质心在它们连线上，将这两个质点的质量分别记为m1和m2，间距记为l，那么质心与两者的间距依次为：二、质心运动定律1.质心动量定理：外力对体系的冲量等于质心动量的增量。

2.质心运动定律：体系总质量与质心加速度的乘积等于外力的矢量和，或者说，在诸外力作用下，体系质心的加速度等于质量为体系总质量的质点在这些外力共同作用下的加速度。

对一个质点系而言，同样可以应用牛顿第二定律。

三、习题1.试求匀质三角形板的质心位置。

答案：三条中线的焦点：即几何中的重心2. 试求匀质三角形框架的质心位置。

答案：三边中点构成的小三角形的内心。

3. 一轻弹簧两端各系有质量分别为m和2m的物块，用系于质量为m的物块上的细线悬挂在支点O上，如图。

今将细线突然剪断，求该瞬时体系质心的加速度。

答案：g。

4. 用质心运动定理解：长为l、总质量为m的柔软绳索盘放在水平台面上。

用手将绳索的一端以恒定速率vo向上提起，求当提起高度为x时手的提力F。

5. 如图所示，用劲度系数为k的轻弹簧连接质量分别为m1、m2的木块，放在光滑的水平面上。

让第一个木块紧靠竖直墙，在第二个木块的侧面上施加水平压力，将弹簧压缩l长度。

撤去这一压力后，试求系统质心可获得的最大加速度值和最大速度值。

多说两句：体系的总动量为：质心的动能为：质点系相对质心的动能为：质点系的总动能为：（克尼希定理）☆在使用质心参照系时要特别主要克尼希定理的使用！。

质心运动定理质心运动定理，也称为质心定理或重心定理，是指在一个系统中，质心的运动轨迹与被控制的物体或系统所受的力的性质有关系。

简言之，就是一个物体或系统中质心位置的变化量与作用在系统上的合力的大小和方向成正比。

质心运动定理是物理学中一个非常基本的定理，其具体表述为：一个物体或系统中的质心所受的外力F，可以完全等效于作用在系统上质量为整个系统质量的质点上，该质点运动的加速度与整个系统的质心所受的加速度相等，即：F = MA其中F为作用在系统上的合力，M为整个系统的质量，A为整个系统的质心所受的加速度。

质心运动定理的意义非常重要，它为研究物体或系统的运动提供了很有用的计算工具。

在实际应用中，质心运动定理可以用于分析和预测物体或系统的运动轨迹、速度和加速度等。

此外，质心运动定理还被广泛应用于机器人控制、流体动力学、宇航学和机械设计等领域。

为更好地理解质心定理的实际意义，以下我们将介绍一些具体的应用场景：1. 火箭的运动轨迹计算火箭运动轨迹计算是质心运动定理的典型应用之一。

在火箭发射过程中，产生的反推力会使火箭向上加速，而重力则会使其向下偏转。

此时，可以用质心运动定理来计算火箭的运动轨迹。

火箭的运动可以看作是由两个质点组成的系统：一个是火箭自身，另一个是喷气口所排出的燃料。

如果将整个系统看作一个质点，它所受的外力就是火箭发射过程中的反推力。

根据质心运动定理，可以将这个质点的运动加速度确定为整个系统的质心运动加速度。

然后，我们可以根据质心位置的变化率来计算火箭在空间中的位置和速度。

如果将质心坐标系与地球坐标系对齐，就可以得到火箭的运动轨迹。

2. 物体保持平衡在某些情况下，我们需要确定一个物体的重心位置，才能使其保持平衡。

例如，在建筑工地上，建筑工人需要确定装满土壤的草坪车的重心位置，才能确保它不会侧翻。

我们可以通过质心运动定理来计算草坪车的重心位置。

首先，我们需要将草坪车看作一个较大的系统，将其质心位置确定在车身的中心。