质心运动定理
- 格式:docx
- 大小:37.56 KB
- 文档页数:3

质心运动定理
质心运动定理是质点系动量定理的另一种形式,可由质点系动量定理直接导出。
即将P=Mvc代入质点系动量定理dP/dt=∑Fe,得:Mdvc/dt=∑Fe或Mac =∑Fe——称为质心运动定理.(∵ac=dvc/dt)
即:质点系的质量M与质心加速度ac的乘积等于作用于质点系所有外力的矢量和(外力主矢量)。
可见:只有外力才能改变质点系质心的运动。
定理的推论
根据这个定理可推知:
①质点系的内力不能影响它的质心的运动;例如跳水运动员自跳板起跳后,不论他在空中再做何种动作,采取何种姿势,由于外力(重力)并未改变,所以运动员的质心在入水前仍沿抛物线轨迹运动;
②如果作用于质点系上外力的矢量和始终为零,则质点系的质心作匀速直线运动或保持静止;
③若作用于质点系上外力的矢量和在某轴上的投影始终为零,则质点系质心在该轴上的坐标匀速变化或保持不变。

质心运动守恒定理
质心运动守恒定理,也称为质心运动定理,是物理学中的一个重要定理,用于描述系统总质量的质心在不受外力作用时的运动特性。
质心是一个系统的所有质点的质量加权平均位置。
在不受外力作用的情况下,质心的运动有一个重要的特性:系统的质心以恒定的速度直线运动。
质心运动守恒定理的表述如下:
在一个封闭系统中,如果系统内部没有外力作用,那么系统的质心将以恒定的速度沿着直线运动。
这意味着,如果一个系统内部没有物体离开或进入,系统的总质量保持不变,而且系统的质心在运动过程中不会改变速度或方向。
质心运动守恒定理是一个非常有用的工具,特别在研究大规模物体组成的系统时,如行星运动、天体运动等。
需要注意的是,如果系统受到外力作用,那么质心运动守恒定理将不再适用,质心的运动将会受到外力的影响。
因此,在具体问题中,需要根据情况来判断是否可以应用质心运动守恒定理。
1/ 1。
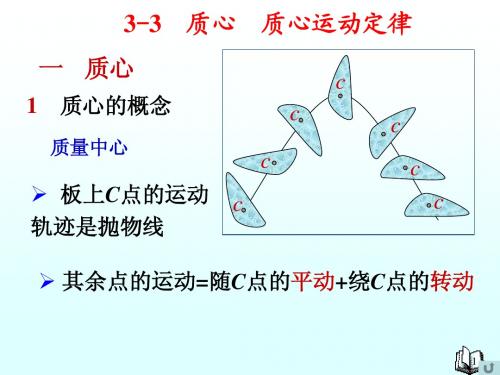

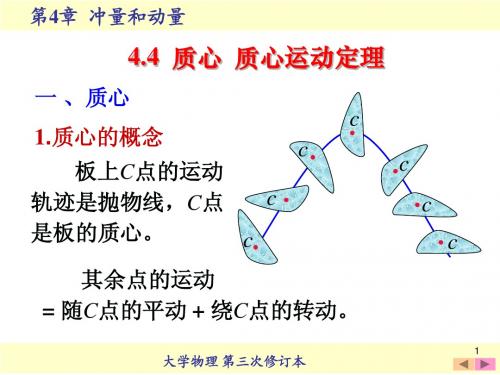

质心运动定理讲解
质心运动定理指的是质点系的质心以恒定的速度沿着直线运动,
且其所受合外力等于其质量与加速度的积。
这个定理结合了牛顿第二
定律和质点系的质心公式,表达了质心运动的关键性质。
牛顿第二定律指出,物体受到的合外力等于其质量乘以加速度。
对于质点系,可以将其看成一个由若干个质点组成的系统。
此时,质
点系的质心可以看作是其所有质点质量之和的加权平均值。
因此,如
果我们知道了质点系受到的合外力,就可以计算出质点系的总加速度,从而推导出质心的运动规律。
具体来说,如果质点系受到的合外力为F,质点系的质量为M,
质心的速度为v,则根据牛顿第二定律有F=Ma。
又根据质点系的质心
公式,有Mv=Σmivi,其中Σmivi表示所有质点的质量与速度之积之和。
这里我们假设质点系并不发生转动,因此质心的速度与角速度均
为常数。
将上述两个式子联立,可以得到Mv=F/a,也就是质心的加速度与外力和质点系质量之比相等。
因此,质心的运动可以看成是一个受到
恒定加速度的匀加速直线运动,其速度随时间线性增加。
总之,质心运动定理给出了描述质点系运动的一个关键性质。
通
过计算质心的加速度,我们可以推导出质心的运动规律,从而了解整
个质点系的运动情况。




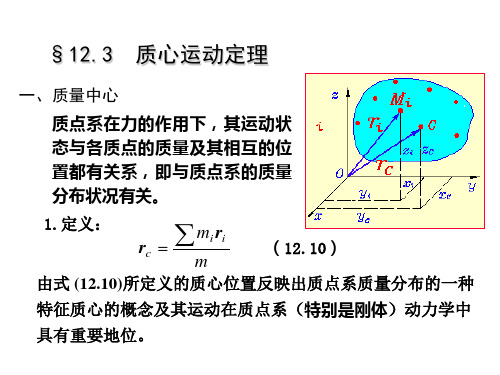



质心运动定理公式
《质心运动定理公式》是物理学中一个重要的定理,它描述了质点在牛顿力学中的运动规律。
它指出,在牛顿力学中,一个质点的运动轨迹是一个椭圆,其中质心是椭圆的中心,它是质点的动量的守恒定律的结果。
质心运动定理的公式为:质点的轨迹方程为:
x²/a²+y²/b²=1,其中a为椭圆的长轴,b为椭圆的短轴,x为质点的横坐标,y为质点的纵
坐标。
质心运动定理公式的发现对物理学的发展具有重要意义,它可以用来描述质点运动的轨迹,也可以用来解释物体运动的规律,比如太阳系中行星的运动轨迹就是椭圆,它们的轨迹就是质心运动定理的结果。
此外,质心运动定理公式也可以用来描述其他物理现象,比如电子在原子核中的运动轨迹也是椭圆,它们的运动轨迹也是质心运动定理的结果。
质心运动定理公式是一个重要的定理,它可以用来描述物体运动的规律,为物理学的发展做出了重要贡献。

质心运动定理讲解
质心运动定理是物理学中的一个重要定理,它描述了一个物体的质心在外力作用下的运动规律。
质心是一个物体的所有质点的平均位置,它是一个重要的物理量,可以用来描述物体的运动状态。
根据质心运动定理,一个物体的质心在外力作用下的运动规律可以用以下公式表示:
F = ma
其中,F表示物体所受的外力,m表示物体的质量,a表示物体的加速度。
这个公式表明,一个物体所受的外力越大,它的加速度就越大,质心的运动速度也就越快。
质心运动定理的应用非常广泛,它可以用来解释很多物理现象。
例如,当一个物体受到一个施加在它上面的力时,它的质心会向着力的方向运动。
这个现象可以用质心运动定理来解释,因为当一个物体受到外力时,它的质心会受到相同的力,从而产生加速度,导致质心运动。
质心运动定理还可以用来解释物体的旋转运动。
当一个物体旋转时,它的质心也会随着旋转,但是质心的运动速度和旋转速度是不同的。
这个现象可以用质心运动定理来解释,因为当一个物体旋转时,它的质心会受到向心力的作用,从而产生向心加速度,导致质心运动。
质心运动定理是物理学中一个非常重要的定理,它可以用来解释很多物理现象。
通过理解和应用质心运动定理,我们可以更好地理解物体的运动规律,从而更好地掌握物理学知识。

质心运动定理表达式
质心运动定理是一种在物理学中使用的定理,它定义了一个物体在受外力作用时,其运动轨迹对于半径等于质心处运动轨迹的投影是什么。
质心运动定理的数学表达式是:速度矢量的和等于两个外力矢量的和乘以质心距离的倒数(P2-P1)。
质心运动定理可以在物理学中应用于多种情况。
例如,在分析多部件系统的运动特性时,可以使用质心运动定理来描述它们之间的运动关系。
比如,可以用质心运动定理来求解车轮系统中每个部件的运动关系,也可以用它来研究悬挂系统中悬挂点与质心之间的运动特性。
此外,质心运动定理还可以用来描述复杂的摩擦力学系统中物体之间的运动特性;还有,它还可用来检验重力势能场和摩擦力场影响的运动特性,以及多体系统中的动力学。
另外,质心运动定理还被广泛应用于船舶分析和控制系统的设计中,并可以用来确定摇杆系统的运动特性,并对船只在自由和受控状态下的运动进行预测和模拟。
总而言之,质心运动定理是一种在多种应用领域都有重要应用的定理,可以用来查明受外力作用时物体的移动历程。
正是有了这个定理,我们才能更加清楚的掌握复杂物理问题,从而做出更好的解决方案。
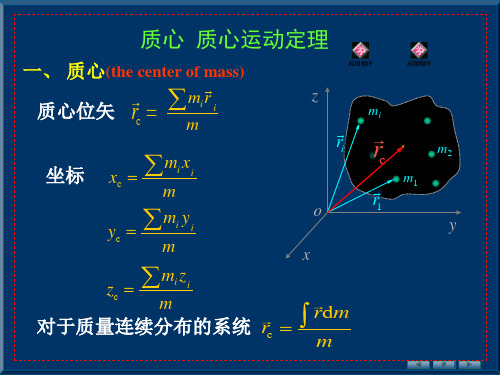
质心运动定理
质心运动定理,也称为质心定理或重心定理,是指在一
个系统中,质心的运动轨迹与被控制的物体或系统所受的力的性质有关系。
简言之,就是一个物体或系统中质心位置的变化量与作用在系统上的合力的大小和方向成正比。
质心运动定理是物理学中一个非常基本的定理,其具体
表述为:一个物体或系统中的质心所受的外力F,可以完全等
效于作用在系统上质量为整个系统质量的质点上,该质点运动的加速度与整个系统的质心所受的加速度相等,即:
F = MA
其中F为作用在系统上的合力,M为整个系统的质量,A
为整个系统的质心所受的加速度。
质心运动定理的意义非常重要,它为研究物体或系统的
运动提供了很有用的计算工具。
在实际应用中,质心运动定理可以用于分析和预测物体或系统的运动轨迹、速度和加速度等。
此外,质心运动定理还被广泛应用于机器人控制、流体动力学、宇航学和机械设计等领域。
为更好地理解质心定理的实际意义,以下我们将介绍一
些具体的应用场景:
1. 火箭的运动轨迹计算
火箭运动轨迹计算是质心运动定理的典型应用之一。
在
火箭发射过程中,产生的反推力会使火箭向上加速,而重力则会使其向下偏转。
此时,可以用质心运动定理来计算火箭的运动轨迹。
火箭的运动可以看作是由两个质点组成的系统:一个是火箭自身,另一个是喷气口所排出的燃料。
如果将整个系统看作一个质点,它所受的外力就是火箭发射过程中的反推力。
根据质心运动定理,可以将这个质点的运动加速度确定为整个系统的质心运动加速度。
然后,我们可以根据质心位置的变化率来计算火箭在空间中的位置和速度。
如果将质心坐标系与地球坐标系对齐,就可以得到火箭的运动轨迹。
2. 物体保持平衡
在某些情况下,我们需要确定一个物体的重心位置,才能使其保持平衡。
例如,在建筑工地上,建筑工人需要确定装满土壤的草坪车的重心位置,才能确保它不会侧翻。
我们可以通过质心运动定理来计算草坪车的重心位置。
首先,我们需要将草坪车看作一个较大的系统,将其质心位置确定在车身的中心。
然后,通过计算草坪车车身上各个部位的质量,可以确定它的质心位置。
如果草坪车上装载的土壤质量分布不均,就需要重新计算它的重心位置以确保平衡。
3. 确定机器人运动规划
机器人运动规划是质心运动定理在工业自动化领域中的应用。
在机器人的运动控制中,我们可以使用质心运动定理来确定机器人的运动规划,以完成非常复杂的工作任务。
例如,在对汽车进行喷漆时,机器人需要准确地控制喷枪的运动轨迹和速度,以便均匀地喷涂整个汽车表面。
为了确定机器人的运动规划,我们可以将机器人看作为一个质点,在计算机视觉系统的控制下,根据质心运动定理,确定机器人的运动加速度和位置变化,从而实现运动规划。
此外,根据质心运动定理,我们还可以优化机器人的运动路径,
以最大限度地提高工厂的生产效率和质量。
4. 测量物体质量
在一些实验室实验中,我们需要测量物体的质量。
根据质心运动定理,我们可以将一个物体看作系统中的一个质点,通过施加一个已知的力F,测量它在水平方向上的加速度和质心位置变化。
根据质心定理,我们可以计算该物体的质量M。
综上所述,质心运动定理是物理学中的一个非常重要的定理,它与世界上所有物体和系统的运动有着直接的关系。
在实际应用中,质心运动定理已经被广泛应用于机器人控制、流体动力学、宇航学和机械设计等领域,并在各种实验室实验中起着关键作用。