2015.6北京市初三二模数学26题归类

2015北京中考数学二模各区29题（含答案）昌平29. 在平面直角坐标系xOy 中，给出如下定义：形如()()2y a x m a x m =-+-与()()2y a x m a x m =---的两个二次函数的图象叫做“兄弟抛物线”． （1）试写出一对兄弟抛物线的解析式 与 ； （2）判断二次函数2y x x =-与232y x x =-+的图象是否为兄弟抛物线，如果是，求出a 与m 的值，如果不是，请说明理由；（3）若一对兄弟抛物线各自与x 轴的两个交点和其顶点构成直角三角形，其中一个抛物线的对称轴为直线2x =且开口向上，请直接写出这对兄弟抛物线的解析式．备用图朝阳29.如图，顶点为A （－4,4）的二次函数图象经过原点（0,0），点P 在该图象上，OP 交其对称轴l 于点M ，点M 、N 关于点A 对称，连接PN ，ON .（1）求该二次函数的表达式；（2）若点P 的坐标是（－6,3），求△OPN 的面积； （3）当点P 在对称轴l 左侧的二次函数图象上运动时，请解答下面问题：① 求证：∠PNM ＝∠ONM ；② 若△OPN 为直角三角形，请直接写出所有符合 条件的点P 的坐标.丰台29.对某一个函数给出如下定义：如果存在实数M ，对于任意的函数值y ，都满足y M ≤，那么称这个函数是有上界函数，在所有满足条件的M 中，其最小值称为这个函数的上确界．例如，图中的函数是有上界函数，其上确界是2． （1）分别判断函数1y x=-（0x ＜）和23y x =-（2x ＜） 是不是有上界函数？如果是有上界函数，求其上确界； （2）如果函数2y x =-+ （,a x b b a ≤≤＞）的上确界是b ，且这个函数的最小值不超过21a +，求a 的取值范围；（3）如果函数222y x ax =-+（15x ≤≤）是以3为上确界的 有上界函数，求实数a 的值.怀柔29. 阅读理解：学习了三角形全等的判定方法:“SAS ”，“ASA ”，“AAS ”，“SSS ”和直角三角形全等的判定方法“HL ”后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA ”的情形进行研究．我们不妨将问题用符号语言表示为：在△ABC 和△DEF 中，AC =DF ，BC =EF ，∠A =∠D . 初步探究：如图1，已知AC=DF, ∠A =∠D ,过C 作CH ⊥射线AM 于点H ，对△ABC 的CB 边进行分类，可分为“CB<CH ，CB=CH ，CH<CB<CA ，”三种情况进行探究．深入探究： 第一种情况，当BC<CH 时，不能构成△ABC 和△DEF ．第二种情况，（1）如图2，当BC=CH 时，在△ABC 和△DEF 中，AC =DF ，BC =EF ，∠A =∠D ，根据 ，可以知道Rt △ABC ≌Rt △DEF ．HNANA第三种情况，（2）当CH<BC<CA 时，△ABC 和△DEF 不一定全等．请你用尺规在图1的两个图形中分别补全△ABC 和△DEF,使△DEF 和△ABC 不全等（表明字母，不写作法，保留作图痕迹）．（3）从上述三种情况发现，只有当BC=CH 时，才一定能使△ABC ≌△DEF ． 除了上述三种情况外，BC 边还可以满足什么条件，也一定能使△ABC ≌△DEF ？写出结论,并利用备用图证明.石景山29．对于平面直角坐标系xOy 中的点(),P m n ，定义一种变换：作点(),P m n 关于y 轴对称的点'P ，再将'P 向左平移()0k k >个单位得到点'k P ，'k P 叫做对点(),P m n 的k 阶“ℜ”变换．（1）求()3,2P 的3阶“ℜ”变换后3'P 的坐标；（2）若直线33y x =-与x 轴，y 轴分别交于,A B 两点，点A 的2阶“ℜ”变换后得到点C ，求过,,A B C 三点的抛物线M 的解析式； （3）在（2）的条件下，抛物线M 的对称轴与x 轴交于D ，若在抛物线M 对称轴上存在一点E ，使得以,,E D B 为顶点的三角形是等腰三角形，求点E 的坐标．房山29.如图1，若抛物线L 1的顶点A 在抛物线L 2上，抛物线L 2的顶点B 也在抛物线L 1上(点A 与点B 不重合)，我们把这样的两抛物线L 1、L 2互称为“友好”抛物线. （1）一条抛物线的“友好”抛物线有_______条.A . 1 B. 2 C. 3 D. 无数 （2）如图2，已知抛物线L 3：2284y x x =-+与y 轴交于点C ，点C 关于该抛物线对称轴的对称点为D ，请求出以点D 为顶点的L 3的“友好”抛物线L 4的表达式;（3）若抛物线21()y a x m n =-+的“友好”抛物线的解析式为22()y a x h k =-+,请直接写出1a 与2a 的关系式为 .ANH图2图1平谷29．定义：如图1，平面上两条直线AB 、CD 相交于点O ，对于平面内任意一点M ，点M 到直线AB 、CD 的距离分别为p 、q ，则称有序实数对（p ，q ）是点M 的“距离坐标”．根据上述定义，“距离坐标”为（0,0）点有1个，即点O ． （1）“距离坐标”为（1，0）点有 个；（2）如图2，若点M 在过点O 且与直线CD 垂直的直线l 上时，点M 的“距离坐标”为（p ，q ），且∠BOD =120°．请画出图形，并直接写出p ，q 的关系式； （3）如图3，点M 的“距离坐标”为（1，且∠AOB =30°，求OM 的长．顺义29．如图，在平面直角坐标系xOy 中，抛物线223y x bx c =-++与x 轴交于A ，B 两点，其中B （6，0），与y 轴交于点C （0，8），点P 是x 轴上方的抛物线上一动点（不与点C 重合）． （1）求抛物线的表达式；（2）过点P 作PD ⊥x 轴于点D ，交直线BC 于点E ，点E 关于直线PC 的对称点为'E ，若点'E 落在y 轴上（不与点C 重合），请判断以P ，C ，E ，'E 为顶点的四边形的形状， 并说明理由； （3）在（2）的条件下直接写出点P 的坐标．图1O D C B A 图2 图3备用图西城29．对于平面直角坐标系xOy 中的点P 和图形G ，给出如下定义：在图形G 上若存在两点M ，N ，使△PMN 为正三角形，则称图形G 为点P 的τ型线，点P 为图形G 的τ型点， △PMN 为图形G 关于点P 的τ型三角形．（1）如图1，已知点(0,A ，(3,0)B ，以原点O 为圆心的⊙O 半径为1．在A ，B两点中，⊙O 的τ型点是____，画出并回答⊙O 关于该τ型点的τ型三角形；（画 出一个即可）（2）如图2，已知点(0,2)E ，点(,0)F m （其中m ＞0）．若线段EF 为原点O 的τ型线，且线段EF 关于原点O 的τ，求m 的值； （3）若(0,2)H -是抛物线2y x n =+的τ型点，直接写出n 的取值范围．东城29．定义：如果一条直线能够将一个封闭图形的周长和面积平分，那么就把这条直线称作这个封闭图形的等分线。

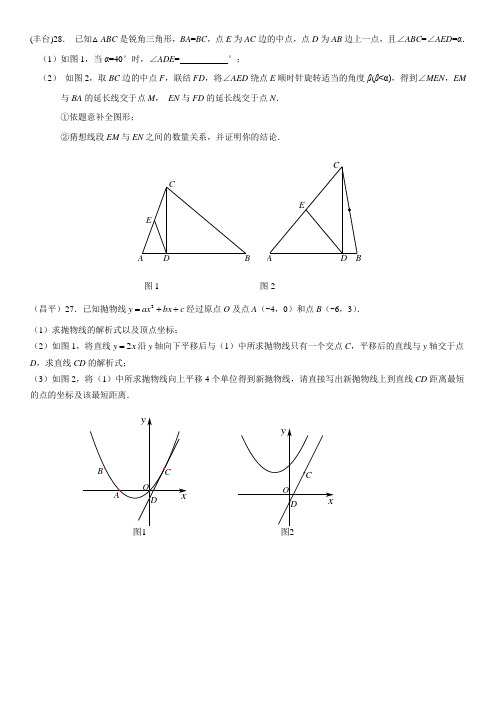
(丰台)28． 已知△ABC 是锐角三角形，BA =BC ，点E 为AC 边的中点，点D 为AB 边上一点，且∠ABC =∠AED =α． （1）如图1，当α=40°时，∠ADE = °；（2） 如图2，取BC 边的中点F ，联结FD ，将∠AED 绕点E 顺时针旋转适当的角度β(β<α)，得到∠MEN ，EM与BA 的延长线交于点M ， EN 与FD 的延长线交于点N ． ①依题意补全图形；②猜想线段EM 与EN 之间的数量关系，并证明你的结论．A B ECD D CEBA图1 图2（昌平）27．已知抛物线2y ax bx c =++经过原点O 及点A （-4，0）和点B （-6，3）． （1）求抛物线的解析式以及顶点坐标；（2）如图1，将直线2y x =沿y 轴向下平移后与（1）中所求抛物线只有一个交点C ，平移后的直线与y 轴交于点D ，求直线CD 的解析式；（3）如图2，将（1）中所求抛物线向上平移4个单位得到新抛物线，请直接写出新抛物线上到直线CD 距离最短的点的坐标及该最短距离．yx图1BACD Oyx图2CD O（朝阳）28．数学活动课上，老师提出这样一个问题:如果AB =BC ,∠ABC =60°,∠APC =30°,连接PB ，那么P A 、PB 、PC 之间会有怎样的等量关系呢？ 经过思考后，部分同学进行了如下的交流：小蕾：我将图形进行了特殊化，让点P 在BA 延长线上（如图1），得到了一个猜想: P A 2+PC 2=PB 2 .小东：我假设点P 在∠ABC 的内部，根据题目条件，这个图形具有“共端点等线段”的特点，可以利用旋转解决问题，旋转△P AB 错误！未找到引用源。

后得到△P′CB ,并且可推出△PBP′ ,△PCP ′ 错误！未找到引用源。

错误！未找到引用源。

分别是等边三角形、直角三角形，就能得到猜想和证明方法. 这时老师对同学们说，请大家完成以下问题： （1）如图2，点P 在∠ABC 的内部，①P A =4，PC =23，PB= .②用等式表示P A 、PB 、PC 之间的数量关系，并证明.（2）对于点P 的其他位置，是否始终具有②中的结论？若是，请证明；若不是，请举例说明.26.【阅读学习】 刘老师提出这样一个问题：已知α为锐角，且tan α=13，求sin2α的值．小娟是这样解决的：如图1，在⊙O 中，AB 是直径，点C 在⊙O 上，∠BAC =α，所以∠ACB =90°，tan α=BC AC =13． 易得∠BOC =2α．设BC =x ，则AC =3x ，则AB =10x ．作CD ⊥AB 于D ，求出CD = （用含x 的式子表示），可求得sin2α=CDOC= ． 【问题解决】已知，如图2，点M 、N 、P 为圆O 上的三点，且∠P =β，tan β =12，求sin2β的值.图12ααOAD C B图2βMNPO图1图2（门头沟）26．阅读下面的材料：小明遇到一个问题：如图1，在□ABCD 中，点E 是边BC 的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G . 如果3AF EF =，求CDCG的值． 他的做法是：过点E 作EH ∥AB 交BG 于点H ，那么可以得到△BAF ∽△HEF ． 请回答：（1）AB 和EH 之间的数量关系是 ，CG 和EH 之间的数量关系是 ，CDCG的值为 ． （2）参考小明思考问题的方法，解决问题：如图2，在四边形ABCD 中，DC ∥AB ，点E 是BC 延长线上一点，AE 和BD 相交于点F ．如果2AB CD =，23BC BE =，求AFEF的值． HG F ECDBAFECB AD图1 图2（门头沟）28．如图1，在△ABC 中，CA =CB ，∠ACB =90°，D 是△ABC 内部一点，∠ADC =135°，将线段CD 绕点C 逆时针旋转90°得到线段CE ，连接DE ． （1）① 依题意补全图形；② 请判断∠ADC 和∠CDE 之间的数量关系，并直接写出答案．（2）在（1）的条件下，连接BE ，过点C 作CM ⊥DE ，请判断线段CM ，AE 和BE 之间的数量关系，并说明理由．（3）如图2，在正方形ABCD 中，AB =2，如果PD =1，∠BPD =90°，请直接写出点A 到BP 的距离．DAB CPDC AB图1 图2（顺义）27．已知关于x 的方程()2230x m x m +-+-=． （1）求证：方程()2230x m x m +-+-=总有两个实数根； （2）求证：抛物线()223y x m x m =+-+-总过x 轴上的一个定点；（3）在平面直角坐标系xOy 中，若（2）中的“定点”记作A ，抛物线()223y x m x m =+-+-与x 轴的另一个交点为B ， 与y 轴交于点C ，且△OBC 的面积小于或等于8，求m 的 取值范围．28．如图，△ABC 中，∠BAC =90°，AB =AC ，边BA 绕点B 顺时针旋转α角得到线段BP ，连结P A ，PC ，过点P 作PD ⊥AC 于点D ．（1）如图1，若α=60°，求∠DPC 的度数； （2）如图2，若α=30°，直接写出∠DPC 的度数；（3）如图3，若α=150°，依题意补全图，并求∠DPC 的度数．图3PCAB DD图2图1ABPCBCPAxyO。

x 的请回答：（1） 当k ＝1时，使得原等式成立的x 的个数为 _______； （2） 当0＜k ＜1时，使得原等式成立的x 的个数为_______； （3） 当k ＞1时，使得原等式成立的x 的个数为 _______． 参考小明思考问题的方法，解决问题：关于x 的不等式240 ()x a a x+-<＞0只有一个整数解，求a 的取值范围．26．（1）小明遇到下面一道题：如图1，在四边形ABCD 中，AD ∥BC ，∠ABC =90º，∠ACB =30º，BE ⊥AC 于点E ，且=CDE ACB ∠∠．如果AB =1，求CD 边的长．小明在解题过程中发现，图1中，△CDE 与△ 相似，CD 的长度等于，线段CD 与线段 的长度相等；他进一步思考：如果ACB α∠=（α是锐角），其他条件不变，那么CD 的长度可以表示为CD = ；（用含α的式子表示）)（2）受以上解答过程的启发，小明设计了如下的画图题：在Rt △OMN 中，∠MON =90º，OM ＜ON ，OQ ⊥MN 于点Q ，直线l 经过点M ，且l ∥ON ．请在直线l 上找出点P 的位置，使得NPQ ONM ∠=∠．请写出你的画图步骤，并在答题卡上完成相应的画图过程．（画出一个即可，保留画图痕迹，不要求证明）26 .阅读材料如图1，若点P 是⊙O 外的一点，线段PO 交⊙O 于点A,则PA 长是点P 与⊙O 上各点之间的最短距离.图1 图2 证明：延长PO 交⊙O 于点B ，显然PB>PA .如图2，在⊙O 上任取一点C （与点A ，B 不重合），连结PC ，OC .,,,,PO PC OC PO PA OA OA OC PA PC <+=+=∴<且∴PA 长是点P 与⊙O 上各点之间的最短距离.由此可以得到真命题：圆外一点与圆上各点之间的最短距离是这点到圆心的距离与半径的差.请用上述真命题解决下列问题．(1)如图3，在Rt △ABC 中，∠ACB =90°，AC =BC =2，以BC 为直径的半圆交AB 于D ，P 是上的一个动点，连接AP ，则AP长的最小值是．图3(2)如图4，在边长为2的菱形ABCD 中，∠A =60°，M 是AD 边的中点，点N 是AB 边上一动点，将△AMN 沿MN 所在的直线翻折得到△MN A '，连接C A ',①求线段A ’M 的长度; ②求线段C A '长的最小值.26．问题背景：在△ABC 中，AB ，BC ，AC ，求这个三角形的面积．小军同学在解答这道题时，先建立了一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC （即△ABC 三个顶点都在小正方形的顶点处），如图1所示．这样不需要求出△ABC 的高，借用网格就能计算出它的面积．图4图1 图2 （1）请你直接写出△ABC 的面积________； 26．阅读下面材料：小玲遇到这样一个问题：如图1，在等腰三角形ABC 中，AC AB =，︒=∠45BAC ，22=BC ，BC AD ⊥图3小玲发现：分别以AB ，AC 为对称轴，分别作出△ABD ，△ACD 的轴对称图形，点D 的对称点分别为E ，F ，延长EB ，FC 交于点G ，得到正方形AEGF ，根据勾股定理和正方形的性质就能求出AD 的长．（如图2）请回答：BG 的长为，AD 的长为； 参考小玲思考问题的方法，解决问题：如图3，在平面直角坐标系xOy 中，点()0,3A ，()4,0B ，点P 是△OAB 的外角的角平分线AP 和BP 的交点，求点P 的坐标．CBAE图1 图226．阅读下面材料：小凯遇到这样一个问题：如图1，在四边形ABCD 中，对角线AC 、BD 相交于点O ， AC =4，BD =6，∠AOB =30°，求四边形ABCD 的面积．小凯发现，分别过点A 、C 作直线BD 的垂线，垂足分别为点E 、F ，设AO 为m ，通过计算△ABD 与△BCD 的面积和使问题得到解决（如图2）．请回答：（1）△ABD 的面积为 （用含m 的式子表示）． （2）求四边形ABCD 的面积．参考小凯思考问题的方法，解决问题：如图3，在四边形ABCD 中，对角线AC 、BD 相交于 点O ，AC =a ，BD =b ，∠AOB =α（0°＜α＜90°），则四边形ABCD 的面积为 （用含a 、b 、α的式子表示）．26.【阅读学习】 刘老师提出这样一个问题：已知α为锐角，且tan α=13，求sin2α的值．小娟是这样解决的：如图1，在⊙O 中，AB 是直径，点C 在⊙O 上，∠BAC =α，所以∠ACB =90°，tan α=BCAC=13．易得∠BOC =2α．设BC =x ，则AC =3x ，则AB．作CD ⊥AB 于D ，求出CD = （用含x 的式子表示），可求得sin2α=CDOC= ． 【问题解决】已知，如图2，点M 、N 、P 为圆O 上的三点，且∠P =β，tan β =12，求sin2β的值.图1图2图326． 如图，在平面直角坐标系xOy 中，矩形ABCD 各边都平行于坐标轴，且A （-2，2），C（3，-2）．对矩形ABCD 及其内部的点进行如下操作：把每个点的横坐标乘以a ，纵坐标乘以b ，将得到的点再向右平移k （0k >）个单位，得到矩形''''A B C D 及其内部的点（''''A B C D 分别与ABCD 对应）．E （2，1）经过上述操作后的对应点记为'E ． （1）若a =2，b =-3，k =2，则点D 的坐标为 ，点'D 的坐标为 ； （2）若'A （1，4），'C （6，-4），求点'E 的坐标．26．阅读下面的材料：小明遇到一个问题：如图1，在□ABCD 中，点E 是边BC 的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G . 如果3AF EF =，求CDCG的值． 他的做法是：过点E 作EH ∥AB 交BG 于点H ，那么可以得到△BAF ∽△HEF ． 请回答：（1）AB 和EH 之间的数量关系是 ，CG 和EH 之间的数量关系是 ，图1图2CDCG的值为 ． （2）参考小明思考问题的方法，解决问题：如图2，在四边形ABCD 中，DC ∥AB ，点E 是BC 延长线上一点，AE 和BD 相交于点F ．如果2AB CD =，23BC BE =，求AFEF的值．图1 图226.在平面内，将一个图形以任意点O 为旋转中心，逆时针．．．旋转一个角度θ，得到图形'G ，再以O 为中心将图形放大或缩小得到图形''G ，使图形''G 与图形G 对应线段的比为k ，并且图形G 上的任一点P ，它的对应点''P 在线段'OP 或其延长线上；我们把这种图形变换叫做旋转相似变换，记为()O θ,k ，其中点O 叫做旋转相似中心，θ叫做旋转角，叫做相似比. 如图1中的线段''OA 便是由线段OA 经过()302︒O ,得到的.（1）如图2，将△ABC 经过☆ ()901,︒后得到△'''A B C ，则横线上“☆”应填下列四个点()00O ，、()01D ，、()0E ，-1、()12C ，中的点 . （2）如图3，△ADE 是△ABC 经过()A θ,k 得到的，90︒=EAB ∠，12cos EAC =∠ 则这个图形变换可以表示为(),A .HG F ECDBAFECB A D G 'G k图2图3O26．如图1，在□ABCD 中，点E 是BC 边上的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G ，若AB =6，3AF EF =，求DG 的长．小米的发现，过点E 作交BG 于点H （如图2），经过推理和计算能够使问题得到解决．则DG = .如图3，四边形ABCD 中，AD ∥BC ，点E 是射线DM 上的一点，连接BE 和AC 相交于点F ，若BC aAD =，CD bCE =，求BFEF的值（用含EH AB ∥,a 图1图2图326．如图①，P 为△ABC 内一点，连接P A 、PB 、PC ，在△P AB 、△PBC 和△P AC 中，如果存在一个三角形与△ABC 相似，那么就称P 为△ABC 的自相似点．（1）如图②，已知Rt △ABC 中，∠ACB =90°，∠ACB ＞∠A ，CD 是AB 上的中线，过点B 作BE ⊥CD ，垂足为E ，试说明E 是△ABC 的自相似点． （2）如图③，在△ABC 中，∠A ＜∠B ＜∠C ．①利用尺规作出△ABC 的自相似点P （不写出作法，保留作图痕迹）；②如果△ABC 的内心P 是该三角形的自相似点，请直接写出该三角形三个内角的度数．BBC①②CBC③答案26. (本小题满分5分)解：（1）当k＝1时，使1 ；…………………………………….（2）当0＜k＜1时，2 ；（3）当k＞1时，使1 ．…..解决问题：将不等式240 (x a ax+-<研究函数2(0)y x a a=+>与函数4yx=∵函数4yx=的图象经过点A(1,4)，B函数2y x=的图象经过点C(1,1)，D若函数2(y x=+3a=，结合图象可知，当03a<<时，关于x的不等式24(0)x a ax+<>只有一个整数解．也就是当03a<<时，关于x的不等式240()x a ax+-<＞0只有一个整数解. ……………………5分26.解：（1）CAD BC. ……………………………………………………………3分1tan α.……………………………………………………………………………4分 （2）方法1：如图8，以点N 为圆心，ON 为半径作圆，交直线l 于点1P ，2P ，则点 1P ，2P 为符合题意的点.……………………………………………… 5分 方法2：如图9，过点N 画NO 的垂线1m ，画NQ 的垂直平分线2m ，直线1m 与2m 交于点R ，以点R 为圆心，RN 为半径作圆，交直线l 于点1P ，2P ，则点1P ，2P 为符合题意的点. ……………………………………… 5分26. 解：（1）△ABC 的面积是4.5；…….2分（2）如右图: …….4分△MNP 的面积是7. …….5分26．解：BG 的长为2，AD 的长为22+；…………………2分如图，过点P 分别作x PC ⊥轴于点C ，y PD ⊥轴于点D ，AB PE ⊥于点E …………………3分∵AP 和BP 是△OAB 的外角的角平分线 ∴CAP EAP ∠=∠，EBP DBP ∠=∠ ∴PD PE PC ==∴四边形OCPD 是正方形，AE AC =，BE BD =…………4分∴DO PD CP OC === ∵()0,3A ，()4,0B ∴5=AB∴12=++=+BO AB OA OD OC∴6==OD OC ,∴6==PD CP ∴()6,6P ……………………5分26. 解：（1）32m ；……………………………………………………………………………1分（2）由题意可知∠AEO =90°．∵ AO = m ，∠AOB =30°， ∴AE =12m ．∴S △ABD =m AE BD 2321=⋅． 同理，CF =1(4)2m -．∴S △BCD =m CF BD 23621-=⋅．…………………………………………………2分 ∴S 四边形ABCD = S △ABD ＋S △BCD 6=．…………………………………………………3分解决问题：αsin 21⋅ab ．………………………………………………………………5分 26．解：10103xCD =． ……………………………………………………………………… 1分Sin2α=CD OC=53． ……………………………………………………………………… 2分 如图，连接NO ，并延长交⊙O 于Q ,连接MQ ，MO ，作NO MH ⊥于H ． 在⊙O 中，∠NMQ =90°． ∵ ∠Q=∠P =β，ＯＭ＝ＯＮ，∴ ∠MON=2∠Q=2β． ………………………………………… 3分∵ tan β=21，∴ 设MN =k ，则MQ =2k ，∴ NQ =k MQ MN 522=+．∴ OM=21NQ=k 25． ∵ MH NQ MQ MN S NMQ ⋅=⋅=∆2121， ∴ MH k k k ⋅=⋅52 ． ∴MH=k 552． ………………………………………………………………………………… 4分 在MHORt ∆中，sin2β=sin ∠MON =5425552==kkOM MH ． …………………………………… 5分26． 解：（1）D （3，2），'D （8，-6），..................................................................................2分 （2）依题可列：21,3 6.a k a k -+=⎧⎨+=⎩则a =1，k =3，2b =4，b =2，.........................................................4分（a ，b ，k 求出一个给1分） ∵点E （2，1），∴'E （5，2）．.....................................................................................................5分26．（本小题满分5分）解：（1）AB =3EH ，CG =2EH ，32.………………………………………………3分 （2）如图，过点E 作EH ∥AB 交BD 的延长线于点H .∴ EH ∥AB ∥CD ． ∵ EH ∥CD ， ∴23CD BC EH BE ==， ∴ CD =23EH ． 又∵2AB CD=，∴ AB =2CD =43EH ．∵ EH ∥AB ，∴ △ABF ∽△EHF ． ∴4433AF AB EH EH EF EH ===．……………………………………5分 26.（1）E ………………………………………………………………………………2分 （2）60,k︒………………………………………………………5分26．答案：DG =2；……………………………………………………………………………………2 如图（画图正确，正确标出点E 、F ）………………………………………………………………3 过E 作EG ∥AD ，延长CA 交于点G ∴△CAD ∽△CGE ．∴AD CDGE CE=． ∵CD bCE =，HF E CB AD∴ADb GE=．∴AD bEG=． (4)∵AD∥BC，∴BC∥EG．∴△GEF∽△CBF．∴BC BF EG EF=．∵BC aAD=，∴BC abEG=．∴BFabEF= (5)26.解：⑴在Rt△ABC中，∠ACB＝90°，CD是AB上的中线，∴12CD AB=，∴CD=BD．∴∠BCE＝∠ABC．……………………………….(1分)∵BE⊥CD，∴∠BEC＝90°，∴∠BEC＝∠ACB．……………………………….(2分)∴△BCE∽△ABC．∴E是△ABC的自相似点．………………………….(3分)⑵①作图略．（方法不唯一）……………………….(5分)②连接PB、PC．∵P为△ABC的内心，∴12PBC ABC∠=∠，12PCB ACB∠=∠．∵P为△ABC的自相似点，∴△BCP∽△ABC．∴∠PBC＝∠A，∠BCP＝∠ABC=2∠PBC =2∠A，∠ACB＝2∠BCP=4∠A．∵∠A+∠ABC+∠ACB＝180°．∴∠A+2∠A+4∠A＝180°．∴1807A∠=．∴该三角形三个内角的度数分别为1807、3607、7207．…………….(6分)。

北京市东城区2014--2015学年第二学期综合练习（二）数 学 试 卷 2015.6学校 班级 姓名 考号一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个是符合题意的.1．如图，数轴上有A ，B ，C ，D 四个点，其中到原点距离相等的两个点是 A ．点B 与点DB ．点A 与点CC ．点A 与点DD ．点B 与点C2.据统计，中国每年浪费的食物总量折合粮食约为50 000 000 吨，将50 000 000用科学记数法表示为 A ． 5×107B ． 50×106C ． 5×106D ． 0.5×1083. 下列运算正确的是A ．236a a a ⋅= B ．336a a a += C ．22a a -=- D ．326()a a -= 4．甲、乙、丙、丁四名运动员参加了射击预选赛，他们射击的平均环数－x 及其方差2s 如下表所示．如果选出一个成绩较好且状态稳定的人去参赛，应选运动员A ．甲B ．乙C ．丙D ．丁5. 如图，已知⊙O 的半径为13，弦AB 长为24，则点O 到AB 的距离是 6．已知一个布袋里装有2个红球，3个白球和a 个黄球，这些球除颜色外其余都相同．若从此布袋里任意摸出1个球，该球是红球的概率为13，则a 等于 A ．1B ． 2C ．3D ． 47. 如图，将△ABC 沿BC 方向向右平移2cm 得到△DEF ，若△ABC 的周长为16cm ，则四边形ABFD 的周长为8．如图，在已知的△ABC 中，按以下步骤作图：①分别以B ，C 为圆心，以大于12BC 的长为半径作弧，两弧相交于点M ，N ；②作直线MN 交AB 于点D ，连接CD ．若CD =AC ，∠B =25°，则∠ACB 的度数为 A ． 90°B ． 95°C ． 100°D ． 105°9．如果三角形的一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是A B，10. 如图，矩形ABCD 中，AB =3，BC =4，动点P 从A 点出发，按A →B →C 的方向在AB 和BC 上移动，记P A =x ，点D 到直线P A 的距离为y ，则y 关于x 的函数图象大致是A ．B ．C ．D ．二、填空题（本题共18分，每小题3分）11x 的取值范围是 ．12．如图，AB //CD ，∠D = 27°，∠E =36°．则∠ABE 的度数是 ．13．一次函数y kx b =+ 的图象经过第一、二、三象限且经过(0,2)点.任写一个满足上述条件的一次函数的表达式是_________________.14．小刚用一张半径为24cm 的扇形纸板做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm ，那么这张扇形纸板的面积是_________________2cm ．第12题图 第14题图15. 如图，菱形ABCD 的对角线AC ，BD 相交于点O ，AC ＝8，BD ＝6，以AB 为直径作一个半圆，则图中阴影部分的面积为 ．16．如图，已知A 1，A 2，……，A n ，A n ＋1在x 轴上，且OA 1＝A 1A 2＝A 2A 3＝……＝A n A n ＋1＝1，分别过点A 1，A 2，……，A n ，A n ＋1作x 轴的垂线交直线y ＝x 于点B 1，B 2，……，B n ，B n ＋1，连接A 1B 2，B 1A 2，BAF CDEA 2B 3，B 2A 3，……，A n B n ＋1，B n A n ＋1，依次相交于点P 1，P 2，P 3，……，P n ，△A 1B 1P 1，△A 2B 2P 2，……，△A n B n P n 的面积依次为S 1，S 2，……，S n ，则S 1= ，S n = ． 三、解答题（本题共30分，每小题5分）17.计算：(101π8sin 454-⎛⎫+- ⎪⎝⎭18．如图，点A ，F ，C ，D 在同一直线上，点B 和点E 分别在直线AD 的两侧，且AB DE =，BC EF ∥， 求证：AF =DC .19．若实数a 满足2210a a --=，计算4(1)(1)2(2)a a a a +--+的值. 20. 已知关于x 的方程21(1)(1)04k x k x ---+=有两个相等的实数根，求实数k 的值．21． A ，B 两个火车站相距360km ．一列快车与一列普通列车分别从A ，B 两站同时出发相向而行，快车的速度比普通列车的速度快54km/h ，当快车到达B 站时，普通列车距离A 站还有135km ．求快车和普通列车的速度各是多少？22．如图，一次函数1y k x b =+的图象经过A （0，﹣2），B （1，0）两点，与反比例函数2k y x=的图象在第一象限内的交点为M （m ，4）． （1）求一次函数和反比例函数的表达式；（2）在x 轴上是否存在点P ，使AM ⊥MP ？若存在，求出点P 的坐标；若不存在，说明理由．四、解答题（本题共20分，每小题5分）23．如图，矩形ABCD 中，点O 为AC 的中点，过点O 的直线分别与AB ，CD交于点E ，F ，连接BF 交AC 于点M ，连接DE ，BO.若∠COB =60°，FO =FC .求证：（1）四边形EBFD 是菱形；（2）MB : OE=3：2 .24．以下是根据全国人力资源和社会保障部公布的相关数据绘制的统计图的一部分，请你根 据图中信息解答下列问题：（1）2015年全国普通高校毕业生人数年增长率约是多少？（精确到0.1%） （2）2013年全国普通高校毕业生人数约是多少万人？（精确到万位） （3）补全折线统计图和条形统计图．25．如图，已知AB 是⊙O 的直径，C 是⊙O 上一点，∠BAC 的平分线交⊙O 于点D ，交⊙O 的切线BE 于点E ，过点D 作DF ⊥AC ，交AC 的延长线于点F ．（1）求证：DF 是⊙O 的切线；（2）若DF =3，DE =2．①求BEAD值；②求FAB 26 .阅读材料如图1，若点P 是⊙O 外的一点，线段PO 交⊙O 于点A,则PA 长是点P 与⊙O 上各点之间的最短距离.图1 图2 证明：延长PO 交⊙O 于点B ，显然PB>PA .如图2，在⊙O 上任取一点C （与点A ，B 不重合），连结PC ，OC .∴PA 长是点P 与⊙O 上各点之间的最短距离.由此可以得到真命题：圆外一点与圆上各点之间的最短距离是这点到圆心的距离与半径的差. 请用上述真命题解决下列问题．(1)如图3，在Rt △ABC 中，∠ACB =90°，AC =BC =2，以BC 为直径的半圆交AB 于D ，P 是上的一个动点，连接AP ，则AP 长的最小值是 ． 图3(2)如图4，在边长为2的菱形ABCD 中，∠A =60°，M 是AD 边的中点，点N 是AB 边上一动点，将△AMN 沿MN 所在的直线翻折得到△MN A '，连接C A ',①求线段A ’M 的长度; ②求线段C A '长的最小值.五．解答题（本题共22分，第27题7分，第28题7分，第29题8分）27．在平面直角坐标系中，抛物线2+3y ax bx =+()0≠a 与x 轴交于点A （-3,0）、B （1,0）两点， D 是抛物线顶点，E 是对称轴与x 轴的交点.(1)求抛物线的解析式;(2)若点F 和点D 关于x 轴对称, 点P 是x 轴上的一个动点，过点P 作PQ ∥OF 交抛物线于点Q ，是否存在以点O ,F ,P ,Q 为顶点的平行四边形？若存在，求出点P 坐标;若不存在，请说明理由. 28. 如图1，在ABC Rt △中，90ACB ∠=︒，E 是边AC 上任意一点(点E与点A ，C 不重合)，以CE 为一直角边作ECD Rt △，90ECD ∠=︒，图连接BE ，AD .(1) 若CA CB =，CE CD =，①猜想线段BE ，AD 之间的数量关系及所在直线的位置关系，直接写出结论；②现将图1中的ECD Rt △绕着点C 顺时针旋转锐角α，得到图2，请判断①中的结论是否仍然成立，若成立，请证明；若不成立，请说明理由；(2) 若8CA =，6CB =，3CE =，4CD =，ECD Rt △绕着点C 顺时针旋转锐角α，如图3，连接BD ，AE ，计算22BD AE +的值.29．定义：如果一条直线能够将一个封闭图形的周长和面积平分，那么就把这条直线称作这 个封闭图形的等分线。

2015 年北京市昌平区初三二模数学 2015．6一、选择题（共10 道小题，每题 3 分，共 30 分）以下各题均有四个选项，其中只有一个．．是吻合题意的．1．小超同学在“百度”找寻引擎中输入“中国梦，我的梦”，能找寻到与之相关结果的条数是1650000，这个数用科学记数法表示为A ．16510 4B．1.65 105C． 1.65 106D． 0.165 1072．如图，数轴上有A， B， C，D 四个点，其中表示- 3 的相反数的点是A B C D-3-2-1 0 1 2 3 A．点 A B．点 B C．点 C D．点 D3．用 5 个完满相同的小正方体组合成以下列图的立方体图形，它的主视图为A B C D4.四张质地、大小相同的卡片上，分别画上以以下列图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是中心对称图形的概率为直角三角形平行四边形矩形圆113A.B. C. D .12445．如图，直线AB∥ CD ，Rt△ DEF 如图放置，∠ EDF =90 °，若∠ 1+∠ F=70 °，F则∠ 2 的度数为A 1BA． 20°B． 25°C． 30°D ．40°E2C D6．五一期间（ 5 月 1 日 -7 日），昌平区每天最高温度（单位：℃）情况以下列图，则表示最高温度的这组数据的中位数是A．24B ．25C． 26 D． 27P7．如图， A， B，P 是半径为 2 的⊙ O 上的三点，∠ APB＝ 45°，则弦 AB 的长为O A．2B．4C．2D．22AB8．小明在学习之余去买文具，打算购买 5 支单价相同的签字笔和3本单价相同的笔录本，期间他与售货员对话以下：小明：您好，我要买 5 支签字笔和 3 本笔录本．售货员：好的，那你应该付52 元．小明：刚刚我把两种文具的单价弄反了，以为要付44元．请你判断在单价没有弄反的情况下，购买 1 支签字笔和 1 本笔录本应付A ．10 元 B．11 元 C． 12 元 D．13 元9．如图，在已知的△ABC 中，按以下步骤作图：①分别以B，C 为圆心，以大于1BC 的长为半径作弧，两弧订交于M 2两点 M，N；②作直线 MN 交 AB 于点 D，连接 CD ．BD 若 CD =AC，∠ A=50°，则∠ ACB 的度数为NA ．90° B． 95°C． 100° D． 105°10. 如图，正方形 ABCD 的边长为 5，动点 P 的运动路线为 AB→ BC，动点 Q 的运动路A线为 BD ．点 P 与 Q 以相同的平均速度分别从A， B 两点同时出发，当一个点到达PB CAD QC终点停止运动时另一个点也随之停止．设点P 运动的行程为x，△ BPQ 的面积为y，则以下能大体表示y 与 x 的函数关系的图象为y y y y11111510 x1510 x1510 x1510 xA B C D二、填空题（共 6 道小题，每题 3 分，共18 分）11．分解因式：my29m.12．若关于 x 的一元二次方程kx22x 10 有实数根，则k的取值范围是．A 13．已知：如图，在△ ABC 中，点 D 为 BC 上一点， CA=CD ， CF 均分∠ ACB，E F交 AD于点 F，点 E 为 AB 的中点．若EF=2，则 BD =．B CD14．把方程x26x 3 0 变形为2k 的形式，其中h，k为常数，则kx h．15．在阳光体育课上，小腾在打网球，以下列图，网高 0.9m，球恰巧打过网，而且落在离网6m 的地址上，则球拍击球的高度h =m．0.9m h6m4m16. 以下列图，是一张直角三角形纸片，其中有一个内角为30 ，最小边长为2，点 D 、E 分别是一条直角边和斜边的中点，先将纸片沿DE 剪开，尔后再将两部分拼成一个四边形，则所得四边形的周长是．三、解答题（共 6 道小题，每题 5 分，共 30 分）17．计算：( 2015 1)027 3tan 30131．18．如图，AB AD，AE AC，E C，DE BC．E求证： AD AB ．D CAB19．求不等式4x3≤x的负整数解．220.已知x24x 1 0 ，求代数式 2x( x 3) (x 1) 23的值．21. 如图，在平面直角坐标系中，一次函数y kx b 与反比率函数 y6A 1 ，m，的图象交于xB n ， 3 两点，一次函数y kx b 的图象与y轴交于点C ．y（ 1）求一次函数的剖析式；（ 2）点P是x轴上一点，且△ BOP的面积是△ BOC面积的2倍，求点P的坐标．ACO xB22.自从 2012 年 9 月 1 日昌平区首批50 辆纯电动出租车正式运营以来，电动出租车以绿色环保碰到市民的广泛欢迎，给市民的生活带来了很大方便．下表是行驶15 公里以内一般燃油出租车和纯电动出租车的运营价格：车型起步公里数起步价格超出起步公里数后的单价一般燃油型313 元 2.3 元/公里纯电动型38元2元/公里老张每天从家去单位打出租车上班（行程在15 公里以内），结果发现正常情况下乘坐纯电动出租车比燃油出租车平均每公里节约0.8 元，求老张家到单位的行程是多少公里？四、解答题（共 4 道小题，每题 5 分，共 20 分）23．如图，在矩形ABCD 中， AB=3， BC=6，对角线交于点O．将△ BCD 沿直线 BD 翻折，获取△ BED．（ 1）画出△ BED ，连接 AE；（ 2）求 AE 的长．A DOB C24．我区某学校为了提升学生的体艺涵养，准备开设空手道、素描、剪纸三项活动课程，为认识学生对各项活动的兴趣，随机抽取了部分学生进行检查（每人从中必定采用一项，且只能选一项），将检查结果绘制成下面两个统计图，请你结合图中信息解答问题.（1）将条形统计图补充完满；（2）本次抽样检查的样本容量是 ____________；（ 3）已知该校有1200 名学生，请你依照样本估计全校学生中喜欢剪纸的人数.25．如图， AB 是⊙ O 的直径．半径 OD 垂直弦 AC 于点 E．F 是 BA 延长线上一点，CDB BFD ．（ 1）判断 DF 与⊙ O 的地址关系，并证明；C （ 2）若 AB=10， AC=8，求 DF 的长．DEF A O B26.【阅读学习】刘老师提出这样一个问题：已知α为锐角，且 tan α=1，求 sin2α的值．3小娟是这样解决的：如图 1，在⊙ O 中， AB 是直径，点 C 在⊙ O 上，∠ BAC=α，所以∠ ACB=90°， tan α=BC= 1 ．AC3易得∠ BOC =2α．设 BC=x ，则 AC=3x ，则 AB= 10 x ．作 CD ⊥AB 于 D ，求出 CD =（用含 x 的式子表示），可求得 sin2α=CD=．OC【问题解决】已知，如图 2，点 M 、 N 、 P 为圆 O 上的三点，且∠P=β， tan β= 1，求 sin2β的值 .2CMβP2αBαA NDOO图1 图2五、解答题（共 3 道小题，第 23， 24 小题各 7 分，第 25 小题 8 分，共 22 分）27．已知抛物线 y ax 2 bx c 经过原点 O 及点 A （ - 4， 0）和点 B （ - 6，3）．（ 1）求抛物线的剖析式以及极点坐标；（ 2）如图 1，将直线 y 2x 沿 y 轴向下平移后与（ 1）中所求抛物线只有一个交点C ，平移后的直线与 y轴交于点 D ，求直线 CD 的剖析式；（ 3）如图 2，将（ 1）中所求抛物线向上平移4 个单位获取新抛物线，请直接写出新抛物线上到直线 CD距离最短的点的坐标及该最短距离．yyBCCAOxODxD图1图228.如图，在平行四边形ABCD 中， AB=5，BC=12 ，对角线交于点O，∠ BAD 的均分线交BC 于 E、交 BD 于 F，分别过极点 B、 D 作 AE 的垂线，垂足为 G、 H ，连接 OG、OH．（ 1）补全图形；（2）求证： OG=OH ；（3）若 OG⊥ OH，直接写出∠ OAF 的正切值．A DOFB CE29. 在平面直角坐标系xOy 中，给出以下定义：形如 y a x m 22a x m 与 y a x m a x m 的两个二次函数的图象叫做“兄弟抛物线”．（ 1）试写出一对兄弟抛物线的剖析式与；（ 2）判断二次函数y x2x 与 y x 23x 2 的图象可否为兄弟抛物线，若是是，求出 a 与 m 的值，如果不是，请说明原由；（ 3）若一对兄弟抛物线各自与x 轴的两个交点和其极点构成直角三角形，其中一个抛物线的对称轴为直线x 2 且张口向上，请直接写出这对兄弟抛物线的剖析式．yO x备用图昌平区 2015 年初三年级第二次一致练习数学参照答案及评分标准 2015.6一、（共10 道小，每小 3 分，共 30 分）号12345678910答案C D A C A B D C D B 二、填空（共 6 道小，每小 3 分，共 18 分）号111213141516答案m(y+3)( y-3)k≤1，且 k≠046 1.58或4+23三、解答（共 6 道小，每小 5 分，共 30 分）117．解：(20151)027 3tan3013=133333 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分3=13333= 443．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分18．明：∵AB AD，AE AC，E∴EAC DAB 90 ,即 EAD DACCAB DAC ．D C∴∠ EAD =∠CAB．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分在△ ADE 和△ ABC 中，A BE C，EAD，CABDE BC，∴△ ADE ≌△ ABC ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分∴ AD=AB ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分19 ．解：去分母，得 4 x 6 ≤2 x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2分.移 ，合并，得x ≤ 2．系数化 1，得x ≥ - 2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分所以原不等式的 整数解2， 1．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分20．解： 2x(x3) ( x 1)2 32x 2 6 x x 2 2 x 13 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分x 2 4x 2 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分∵ x 2 4x 1 0，∴ x 2 4x 1 ，∴ 原式 =1+2=3. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分21．解：（ 1）∵点 A 1 ，m ， B n ， 3 在反比率函数 y6的 象上，x∴ m=6, n=2.∴ A1 ，6 ， B2 ，3 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分∵一次函数 y kxb 的 象 A 1 ，6 ， B 2， 3两点，6 k ，2 分∴2k ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3b.解方程 ，得k3, b 3.∴一次函数的剖析式y=- 3x+3. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分（ 2）∵一次函数 y=-3 x+3 与 y 交点 C(0 ， 3), 且 B(2 ， -3)∴ △BOC 面 3. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分∵ P 是 x 上一点，且 △ BOP 的面 是 △BOC 面 的 2 倍，∴ P ( a,0), ∴1a 36 ，解得， a4 .2∴点 P 的坐 （ 4, 0）或（ - 4, 0）. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分22．解： 小明家到 位的行程是x 千米．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分 依 意，得 13 2.3(x 3) 8 2( x 3)0.8 x ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分 解 个方程，得x 8. 2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分答：小明家到 位的行程是 8.2 千米．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分四、解答 （共4 道小 ，每小5 分，共 20 分）23．（ 1）如 ， 全 形．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分E（ 2）解： 接 CE 交 BD 于点 F ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分∵将△ BCD 沿直 BD 翻折，获取△ BED ，ADF∴ BD 垂直均分 CE ．O∵矩形 ABCD ， AB=3，BC=6，BC∴ BEDBCD 90 ， DE DC AB3， EB BC 6.∴ BD BE 2DE 262 323 5 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分∴ OD1BD3 5 .22∵cos EDBDF DEDE，BD∴ DF3 3 ． 35∴ DF3 5 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分5∴ OFODDF9 5 ．10∵ BD 垂直均分 CE ， O AC 中点，∴ AE=2OF =95 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分524．解：（ 1） 全条形 ，如 所示．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分（ 2） 100． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分（ 3）∵ 本中喜 剪 的人数30 人， 本容量 100，∴估 全校学生中喜 剪 的人数：1200×30=360 人．100答：全校学生中喜 剪 的有360 人．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分25．解：（ 1） DF 与⊙ O 相切．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分C∵ CDBCAB ，D 又∵CDBBFD ，EF A O B∴CAB BFD ．∴ AC ∥ DF ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分∵半径 OD 垂直于弦 AC 于点 E ， ∴ OD DF ． ∴ DF 与⊙O 相切．（ 2）∵半径 OD 垂直于弦⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯AC 于点 E ， AC =8，3 分∴AE1AC184．22∵ AB 是⊙ O 的直径， ∴OA OD1AB1105 ．22在 Rt AEO 中， OEOA 2 AE 2 52 42 3． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分∵ AC ∥DF ，∴OAE ∽ OFD ． ∴ OEAE ． ODDF ∴34 ． 5DF∴ DF 20⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分．33 10x1 分26．解： CD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10Sin2α=CD32 分= ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯OC5如 ， 接 NO ，并延 交⊙ O 于 Q , 接 MQ ， MO ，作 MH NO 于H ．在⊙ O 中，∠ NMQ =90 °． ∵∠ Q= ∠P=β，ＯＭ＝ＯＮ，∴∠ MON= 2∠ Q= 2β．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分 M∵ tan β= 1，βPNHOQ2∴ MN=k ， MQ=2k ，∴NQ= MN 2MQ 25k ．∴OM=1 NQ=5k ．22∵SNMQ1MN MQ1NQ MH ，22∴ k 2k5k MH ．∴ MH=2 5 k ． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分52 5 k4MH55 分在 Rt MHO 中， sin2β=sin ∠ MON =5k ． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯OM52五、解答 （本 共 22 分，第 277 分，第 287 分，第 298 分）27．解：（1）∵ 抛物0, 0 ， 4 ,0 ， 6 ,3 三点，c 0∴ 16a4b 0, ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分36a 6b 3.a1，4解得b ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分1c．∴ 抛物 的剖析式y2x ．1 x41 21 24x 4 41 2∵ yxxxx 2 1444∴抛物 的 点坐2 , 1 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分（ 2） 直 CD 的剖析式 y2x m ，依照 意，得1x 2 x2xm ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分4化 整理，得 x 2 4x 4m0 ，由16 16m0 ，解得 m1，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分∴直 CD 的剖析式 y 2 x 1．（ 3）点的坐2 , 7 ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分最短距离4 5 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 7 分528．解：（ 1）ADG OFBE CH⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分（ 2）ADG OFBE CHP明：如 ，延AE 、 DC 交于点 P ． ∵四 形ABCD 是平行四 形，∴ AD//BC ， AB//CD ．∴∠ DAE =∠ AEB ，∠ BAE =∠DPA ． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分∵ AE 均分∠ BAD ，∴∠ DAE =∠ BAE ，∴∠ BAE=∠ AEB ，∠ DAE =∠DPA ． ∴ BA=BE ， DA =DP ， ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分又∵ BG ⊥ AE ， DH ⊥ AE ，∴ G AE 中点， H AP 中点． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分又 ∵ O AC 中点，AD=BC ，∴ OG1 1 BC BE 1 AB ，CE2AD22OH1 1 CD1 AB ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分CPDP AD222∴ OG=OH ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分（ 3） 7．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分1729．解：（ 1）答案不唯一，只要两个剖析式 出相同的a 和相同的 m 即可（每空各 1分）⋯⋯ 2分（2）是兄弟抛物 ，原由以下．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分∵ yx 2xx 121 ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分xy x 23x2x 2x1 ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分1∴二次函数 y x 2 x 与 y x 23x 2 的 象是兄弟抛物 ．此 a 1 ， m 1 ． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分 （3） y2( x 1)( x3) ， y 2( x3)( x5) ；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分2 222或 y2(x3)(x5) ， y 2( x5)( x7) ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分2222。

2015北京市怀柔区初三二模 在答题卡上，选择题用一、选择题（本题共30分，每小题3分）下列各题均有四个选项，其中只有一个．．是符合题意的． 1．如图，数轴的单位长度为1，如果点A ，B 表示的数的绝对值相等，那么点A 表示的数是A. 4B. 0C. -2D. -42．2014年3月5日，李克强总理在政府工作报告中指出：2013年全国城镇新增就业人数 约13 100 000人，创历史新高．将数字13 100 000用科学记数法表示为 A ．13.1×106B ．1.31×107C ．1.31×108D ．0.131×1083．正八边形的内角和等于A. 720°B. 1080°C. 1440°D.1880° 4. 下列各式计算正确的是A ．23523a a a +=B ．235()a a = C ．623a a a ÷= D ．235a a a ⋅=5. 以下问题，不适合用普查方法的是A.了解某种酸奶中钙的含量B.了解某班学生的课外作业时间C.公司招聘职员，对应聘人员的面试 C. 旅客上飞机前的安检6．一个不透明的口袋中，装有5个红球，2个黄球，1个白球，这些球除颜色外其余都相同，从口袋中随机摸一个球，则摸到红球的概率为 A ．18B ．38C ．58D ．347．如图，A ，B 两点分别位于一个池塘的两端，小明想用绳子 测量A ，B 间的距离，但绳子不够长，一位同学帮他想了一个 主意：先在地上取一个可以直接到达A ，B 的点C ，找到AC ，BC的中点D ，E ，并且测出DE 的长为10m ，则A ，B 间的距离为A ．15mB ．25mC ．30mD ．20mx8. 在四边形ABCD 中，AB ∥DC , AD ∥BC ，如果添加一个条件，即可推出该四边形是矩形，那么这个条件可以是 A ．90D =∠B ．AB CD =C ．AD BC = D ．BC CD =9. 一元二次方程x 2﹣2x +m =0总有实数根，则m 应满足的条件是A. m ＞1B. m =1 B. m ＜1C. m ≤110．小丽早上从家出发骑车去上学，途中想起忘了带昨天晚上完成的数学作业，于是打电话让妈妈马上从家里送来，同时小丽也往回骑，遇到妈妈后停下说了几句话，接着继续骑车去学校．设小丽从家出发后所用时间为t ，小丽与学校的距离为S ．下面能反映S 与t 的函数关系的大致图象是二、填空题（本题共18分，每小题3分）11．如图，生活中都把自行车的几根梁做成三角形的支架，这是因为三角形具有_________________性．12．分解因式x 3-9x=__________.13．矩形，菱形，正方形都是特殊的四边形，它们具有很多共性，如___________.（填一条即可）.14. 如图，Rt △ABC 中，AB =9，BC =6，∠B =90°， 将△ABC 折叠，使A 点与BC 的中点D 重合， 折痕为MN ，则线段BN 的长为__________. 15. 观察下列一组坐标：（a,b ），(a,c)，(b,c)，(b,a)，(c,a)，(c,b),(a,b),(a,c)…… ，它们是按一定规律排列的，那么第9个坐标是 ，第2015个坐标是 ． 16.已知等腰△ABC 中，AD⊥BC 于点D ，且AD=21BC ，则△ABC 底角的度数为__________． 三、解答题（本题共30分，每小题5分）17．如图，点C ，D 在线段BF 上，AB DE ∥，AB DF =，BC=DE ．求证：AC=FE ．FEDCBA18.计算：011(2)2cos30()2π--+︒+19.解不等式组：20．先化简，再求值：2(2)(21)(21)4(1)x x x x x +++--+，其中x =21.列方程或方程组解应用题:周末小明和爸爸准备一起去商场购买一些茶壶和一些茶杯，了解情况后发现甲、乙两家商场都在出售两种同样品牌的茶壶和茶杯，定价相同，茶壶每把定价30元，茶杯每把定价5元，且两家都有优惠．甲商场买一送一大酬宾（买一把茶壶送一只茶杯）；乙商场全场九折优惠．小明的爸爸需茶壶5把，茶杯若干只（不少于5只）．当去两家商场付款一样时，求需要购买茶杯的数量. 22．大星发超市进了一批成本为8元/个的文具盒。

北京市西城区2015年初三数学二模试卷2015.6一、选择题(本题共30分，每小题3分)1．2015年羊年除夕夜的10点半，在央视春晚送红包的活动中，微信“摇一摇”峰值的摇动次数达到8.1亿次/分钟，送出微信红包120 000 000个．将120 000 000用科学记数法表示应为A. 90.1210⨯B. 71.210⨯C. 81.210⨯D. 71210⨯2．如图，BD ∥AC ，AD 与BC 交于点E ，如果∠BCA =50°，∠D =30°， 那么∠DEC 等于A. 75°B. 80°C. 100°D. 120° 3．64的立方根是A. 8±B. 4±C. 8D. 4 4．函数y 的取值范围是A.2x ≠B. x ≥2C. x ＞2D. x ≥2-5．如图，△ABC 中，D ，E 两点分别在AB ，AC 边上，且DE ∥BC ， 如果23AD AB =，AC =6，那么AE 的长为A. 3B. 4C. 9D. 126．某居民小区开展节约用电活动，该小区100户家庭4月份的节电情况如下表所示．那么4月份这100户家庭的节电量（单位：千瓦时）的平均数是A. 35B. 26C. 25D. 20 7. 若一个正六边形的半径为2，则它的边心距等于8．如图，△ABC 的边AC 与⊙O 相交于C ，D 两点，且经过圆心O ，边AB 与⊙O 相切，切点为B ．如果∠A =34°，那么∠C 等于A ．28°B ．33° C ．34° D ．56° 9．如图，将正方形OABC 放在平面直角坐标系xOy 中，O 是原点，若点A 的坐标为，则点C 的坐标为xA ．B ．(-C ．(D ．(1)-10．在平面直角坐标系xOy 中，点M 的坐标为(,1)m ．如果以原点为圆心，半径为1的⊙O 上存在点N ，使得45OMN ∠=︒，那么m 的取值范围是A ．1-≤m ≤1 B. 1-＜m ＜1 C. 0≤m ≤1 D. 0＜m ＜1 二、填空题(本题共18分，每小题3分)11．若2(2)0m ++ 则m n -= ．12．若一个凸n 边形的内角和为1080︒，则边数n = ． 13．两千多年前，我国的学者墨子和他的学生做了小孔成像的实验．他的做法是，在一间黑暗的屋子里，一面墙上开一个小孔，小孔对面的墙上就会出现外面景物的倒像．小华在学习了小孔成像的原理后，利用如下装置来验证小孔成像的现象．已知一根点燃的蜡烛距小孔20cm ，光屏在距小孔30cm 处，小华测量了蜡烛的火焰高度为2cm ，则光屏上火焰所成像的高度为______cm ． 14．请写出一个图象的对称轴是直线1x =，且经过(0,1)点的二次函数的表达式： ______．15．如图，在平面直角坐标系xOy 中，直线3y x =与双曲线nyx =（n ≠0）在第一象限的公共点是(1,)P m ．小明说：“从图象上可以看出，满足3nx x>的x 的取值范围是1x >．”你同意他的观点吗？答： ．理由是 ．16．如图，在平面直角坐标系xOy 中，点D 为直线2y x =上且在第一象限内的任意一点，1DA ⊥x 轴于点1A ，以1DA 为边在1DA 的右侧作正方形111A B C D ；直线1OC 与边1DA 交于点2A ，以2DA 为边在2DA 的右侧作正方形222A B C D ；直线2OC与边1DA 交于点3A ，以3DA 为边在3DA 的右侧作正方形333A B C D ，……，按这种方式进行下去，则直线1OC 对应的函数表达式为 ，直线3OC 对应的函数表达式为 .三、解答题(本题共30分，每小题5分)17．如图，△ABC 是等边三角形，D ，E 两点分别在AB ，BC 的延长线上，BD =CE ，连接AE ，CD ．求证：∠E ＝∠D ．18．计算：1012cos 30()1(3)3π-++--.19．已知2540x x --=，求代数式(2)(2)(21)(2)x x x x +----的值．20．解方程：231233x x x x-=--．21．列方程（组）解应用题：某超市的部分商品账目记录显示内容如下：求第三天卖出牙膏多少盒．22．已知关于x的函数2(3)3=+--．y mx m x（1）求证：无论m取何实数，此函数的图象与x轴总有公共点；（2）当m＞0时，如果此函数的图象与x轴公共点的横坐标为整数，求正整数m的值．四、解答题(本题共20分，每小题5分)23．如图，将平行四边形纸片ABCD按如图方式折叠，使点C与点A重合，点D的落点记为点D′ ，折痕为EF，连接CF．（1）求证：四边形AFCE是菱形；（2）若∠B=45°，∠FCE=60°，AB=D′F的长．24.1949年以来，北京市人口结构变迁经历了5个阶段，从2001年至今已进入第五个阶段——人口膨胀增长阶段.以下是根据北京市统计局2015年1月的相关数据制作的统计图.根据以上信息解决下列问题：（1）以下说法中，正确的是（请填写所有正确说法的序号）①从2011年至2014年，全市常住人口数在逐年下降；②2010年末全市常住人口数达到近年来的最高值；③ 2014年末全市常住人口比2013年末增加36.8万人；④从2011年到2014年全市常住人口的年增长率连续递减.（2）补全“2014年末北京市常住人口分布图”，并回答：2014年末朝阳、丰台、石景山、海淀四区的常住人口总数已经达到多少万人？（3）水资源缺乏制约着北京市的人口承载能力，为控制人口过快增长，到2015年底，北京市要将全市常住人口数控制在2180万以内（即不超过2180万）.为实现这一目标，2015年的全市常住人口的年增长率应不超过．（精确到0.1%）25．如图1，AB为⊙O的直径，弦CD⊥AB于点E，点F在线段ED上．连接AF并延长交⊙O于点G，在CD的延长线上取一点P，使PF=PG．（1）依题意补全图形，判断PG与⊙O的位置关系，并证明你的结论；（2）如图2，当E为半径OA的中点，DG∥AB，且OA时，求PG的长．26．（1）小明遇到下面一道题：如图1，在四边形ABCD中，AD∥BC，∠ABC=90º，∠ACB=30º，BE⊥AC于点E，且=∠∠．如C D E A C B果AB=1，求CD边的长．小明在解题过程中发现，图1中，△CDE与△相似，CD的长度等于，线段CD与线段的长度相等；∠=（α是锐角），其他条件不变，那么CD的长度可以表示为他进一步思考：如果ACBαCD= ；（用含α的式子表示）（2）受以上解答过程的启发，小明设计了如下的画图题：在Rt△OMN中，∠MON=90º，OM＜ON，OQ⊥MN于点Q，直线l经过点M，且l∥ON．请在直线l上找出点P的位置，使得NPQ ONM∠=∠．请写出你的画图步骤，并在答题卡上完成相应的画图过程．（画出一个即可，保留画图痕迹，不要求证明）五、解答题(本题共22分，第27题7分，第28题7分，第29题8分) 27． 已知一次函数1y kx b =+（k ≠0）的图象经过(2,0)，(4,1)两点，二次函数 2224y x ax =-+（其中a ＞2）． （1）求一次函数的表达式及二次函数图象的顶点坐标（用含a 的代数式表示）； （2）利用函数图象解决下列问题： ①若25=a ，求当10y >且2y ≤0时，自变量x 的取值范围； ②如果满足10y >且2y ≤0时的自变量x 的取值范围内恰有一个整数，直接写出a 的取值范围．28．正方形ABCD的边长为3，点E，F分别在射线DC，DA上运动，且DE=DF．连接BF，作EH ⊥BF所在直线于点H，连接CH.（1）如图1，若点E是DC的中点，CH与AB之间的数量关系是；（2）如图2，当点E在DC边上且不是DC的中点时，（1）中的结论是否成立？若成立给出证明；若不成立，说明理由；（3）如图3，当点E，F分别在射线DC，DA上运动时，连接DH，过点D作直线DH的垂线，交直线BF于点K，连接CK，请直接写出线段CK长的最大值．29．对于平面直角坐标系xOy中的点P和图形G，给出如下定义：在图形G上若存在两点M，N，使△PMN为正三角形，则称图形G为点P的τ型线，点P为图形G的τ型点，△PMN为图形G关于点P的τ型三角形．（1）如图1，已知点(0,A，(3,0)B，以原点O为圆心的⊙O的半径为1．在A，B两点中，⊙O的τ型点是____，画出并回答⊙O关于该τ型点的τ型三角形；（画出一个即可）（2）如图2，已知点(0,2)F m（其中m＞0）．若线段EF为原点O的τ型线，E，点(,0)且线段EF关于原点O的τ，求m的值；（3）若(0,2)H-是抛物线2=+的τ型点，直接写出n的取值范围．y x n。

2015北京各区中考数学25题汇编及答案25．如图，Rt △ABC 中，∠A =90°，以AB 为直径的⊙O 交BC 于点D ，点E 在⊙O 上， CE =CA ， AB ，CE 的延长线交于点F ． （1） 求证：CE 与⊙O 相切；（2） 若⊙O 的半径为3，EF =4，求BD 的长．25．如图1，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，点F 在线段ED 上．连接AF 并延长交 ⊙O 于点G ，在CD 的延长线上取一点P ，使PF=PG ．（1）依题意补全图形，判断PG 与⊙O 的位置关系，并证明你的结论；（2）如图2，当E 为半径OA 的中点，DG ∥AB，且OA PG 的长．25．如图，已知AB 是⊙O 的直径，C 是⊙O 上一点，∠BAC 的平分线交⊙O 于 点D ，交⊙O 的切线BE 于点E ，过点D 作DF ⊥AC ，交AC 的延长线于点F ． （1）求证：DF 是⊙O 的切线；F（2）若DF =3，DE =2．①求值；②求FAB ∠的度数．25．如图，点A B C D E 、、、、在⊙O 上，AB CB ⊥于点B ，tan 3D =，2BC=，H为CE 延长线上一点，且AH =CH =（1）求证：AH 是⊙O 的切线；（2）若点D 是弧CE 的中点，且AD 交CE 于点F ，求EF 的长．25．如图，⊙O 是△ABC 的外接圆，AB= AC ，BD 是⊙O的直径，P A ∥BC ，与DB 的延长线交于点P ，连接AD ． （1）求证：P A 是⊙O 的切线；（2）若BC =4 ，求AD 的长．25．如图，△ABC 中，AB =AC ，点D 为BC 上一点，且AD =DC ，过A ，B ，D 三点作⊙O ，AE是⊙O 的直径，连结DE ． （1）求证：AC 是⊙O 的切线；BEADCC（2）若4sin 5C =，AC =6，求⊙O 的直径．25．如图，AB 是⊙O 的直径．半径OD 垂直弦AC 于点E ．F 是BA 延长线上一点，CDB BFD ∠=∠．（1）判断DF 与⊙O 的位置关系，并证明； （2）若AB =10，AC =8，求DF 的长．25．如图，AB 是⊙O 的直径，以AB 为边作△ABC ，使得AC = AB ，BC 交⊙O 于点D ，联结OD ，过点D 作⊙O 的切线，交AB 延长线于点E ，交AC 于点F ．25．如图，⊙O 为△ABC 的外接圆，BC 为⊙O 的直径，AE 为⊙O 的切线，过点B 作BD ⊥AE 于D ．（1）求证：∠DBA =∠ABC ；（2）如果BD =1，tan ∠BAD =12，求⊙O 的半径．25.如图，AB 是⊙O 的直径，点C 是⊙O 上一点， AD ⊥ DC 于D , 且AC 平分∠DAB ，延长DC 交AB 的延长线于点P ，弦CE 平分∠ACB ，交AB 于点F ，连接BE ． （1）求证：PD 是⊙O 的切线； （2）若tan ABC =43∠，BE =PC 的长．25．如图，△ABC 内接于⊙O ，OC ⊥AB 于点E ，点D 在OC 的延长线上，且∠B =∠D =30°.（1）求证：AD 是⊙O 的切线；（2）若AB =求⊙O 的半径．25．如图，已知，⊙O 为△ABC 的外接圆，BC 为直径，点E 在AB 边上，过点E 作EF ⊥BC ，延长FE 交⊙O 的切线AG 于点G ． （1）求证：GA =GE ．PE（2）若AC =6，AB =8，BE =3，求线段OE 的长．答案25．(本小题满分5分) 证明：连接OE ，OC ．在△OEC 与△OAC 中， ,,,OE OA OC OC CE CA =⎧⎪=⎨⎪=⎩F∴△OEC ≌△OAC ． (1)分∴∠OEC =∠OAC ．∵∠OAC =90°，∴∠OEC =90°． ∴OE ⊥CF 于E ． ∴CF与⊙O相切．………………………………………………………………………………...2分（2）解：连接AD ．∵∠OEC =90°， ∴∠OEF =90°． ∵⊙O 的半径为3， ∴OE =OA=3．在Rt △OEF 中，∠OEF =90°，OE = 3，EF = 4，∴5OF ，………………………………………………………………………3分3tan 4OE F EF ==． 在Rt △F AC 中，∠F AC =90°，8AF AO OF =+=， ∴tan 6AC AF F =⋅=．…………………………………………………………………………4分∵AB 为直径，∴AB =6=AC ，∠ADB =90°． ∴BD =2BC． 在Rt △ABC 中，∠BAC =90°，∴BC =F∴BD=．…………………………………………………………………………………….5分25. 解：（1）补全图形如图5所示. ………………………………………………………… 1分 答：PG 与⊙O 相切. 证明：如图6，连接OG .∵ PF =PG ， ∴ ∠1=∠2.又∵OG =OA ， ∴ ∠3=∠A .∵ CD ⊥AB 于点E ， ∴ ∠A +∠AFE =90°. 又∵∠2 =∠AFE ，∴ ∠3+∠1=90°. ……………………… 2分 即 OG ⊥PG . ∵ OG 为⊙O 的半径，∴ PG 与⊙O 相切. …………………… 3分（2）解：如图7，连接CG . ∵ CD ⊥AB 于点E ，∴ ∠OEC =90°. ∵ DG ∥AB ，∴∠GDC =∠OEC =90°. ∵∠GDC 是⊙O 的圆周角， ∴ CG 为⊙O 的直径. ∵ E 为半径OA 的中点， ∴ 22OA OCOE ==. ∴ ∠OCE =30°即∠GCP =30°.又∵∠CGP =90°，2CG OA ==A∴tan 4PG CG GCP =⋅∠==. …………………………… 5分25. （1）连结OD ， ∵AD 平分∠BAC ∴∠DAF ＝∠DAO ∵OA =OD ∴∠OAD ＝∠ODA ∴∠ DAF ＝∠ODA ∴AF ∥OD ．┉┉1分 ∵DF ⊥AC ∴OD ⊥DF ∴DF 是⊙O 的切线┉┉2分 （2）①连接BD ∵直径AB ， ∴∠ADB =90° ∵圆O 与BE 相切 ∴∠ABE =90°∵∠DAB +∠DBA =∠DBA +∠DBE =90° ∴∠DAB =∠DBE ∴∠DBE =∠F AD ∵∠BDE=∠AFD =90° ∴△BDE ∽△AFD ∴32==DF DE AD BE ┉┉3分 ②连接OC ，交AD 于G 由①，设BE =2x ，则AD =3x ∵△BDE ∽△ABE ∴BE DE AE BE =∴xx x 22232=+∵AB BC ⊥于点B∴AC 是⊙O 的直径…………………………………1分 ∵D ACB ∠=∠，∴tan tan 3D ACB =∠= 在Rt ABC ∆中，2BC =，∴36AB BC == 由勾股定理AC =在CAH ∆中，由勾股定理逆定理：22250AC AH CH +==∴90CAH ∠=°即CA AH ⊥∴AH 是⊙O 的切线…………………………………2分 （2）解：∵点D 是弧CE 的中点∴EAD DAC ∠=∠…………………………………3分 ∵AC 是⊙O 的直径 ∴AE CH ⊥∴90H EAH H HCA ∠+∠=∠+∠=° ∴EAH HCA ∠=∠∴EAD EAH DAC HCA ∠+∠=∠+∠ 即AFH HAF ∠=∠∴HF HA =∵CA AH ⊥AE CH ⊥∴2AH EH CH =⨯可得EH = ∴EF =5分25.（1）证明：连接OA 交BC 于点E ，由AB =AC 可得OA ⊥BC ．………………………1分C B∵PA ∥BC ， ∴∠PAO =∠BEO =90°. ∵OA 为⊙O 的半径，∴PA 为⊙O 的切线. …………………………… 2分 （2）解：根据（1）可得CE =21BC=2． Rt △ACE 中，122=-=CE AC AE . ………………………………3分∴tan C =21=CE AE ． ∵BD 是直径，∴∠BAD =90°．…………………………………………………………4分 又∵∠D =∠C ， ∴AD =52tan =DAB.………………………………………………………5分25． （1）证明：∵AB =AC ，AD =DC ，∴∠1=∠C =∠B ，..................................................1分 又∵∠E =∠B ，∴∠1=∠E ， ∵AE 是⊙O 的直径，∴∠ADE =90°， ∴∠E +∠EAD =90°， ∴∠1+∠EAD =90°，∴AC 是⊙O 的切线．...........................................2分 （2）解：过点D 作DF ⊥AC 于点F ， ∵DA =DC ，AC =6， ∴CF =12AC =3，..................................... ............3分 ∵4sin 5E =，∴4sin 5C =， ∴在Rt △DFC 中，DF =4，DC =5， ∴AD =5，∵∠ADE =∠DFC =90°，∠E =∠C ，∴△ADE ∽△DFC ，.............................................4分C∴AD DFAE DC =， ∴545AE =， ∴AE =254，∴⊙O 的直径为254．....................5分25．解：（1）DF 与⊙O 相切． ∵CAB CDB ∠=∠， 又∵CDB BFD ∠=∠，∴BFD CAB ∠=∠． ∴AC ∥DF ． ………………………………… 2分∵半径OD 垂直于弦AC 于点E ，∴DF OD ⊥． ∴DF 与⊙O 相切． ………………………………… 3分 （2）∵半径OD 垂直于弦AC 于点E ，AC =8，∴482121=⨯==AC AE ． ∵AB 是⊙O 的直径， ∴5102121=⨯===AB OD OA ． 在AEORt ∆中，3452222=-=-=AE OA OE ． ……………………………………… 4分∵AC ∥DF ， ∴OAE ∆∽OFD ∆． ∴DF AEOD OE = ． ∴DF453=． ∴321DF CEB A O320=DF ． ………………………………………………… 5分25．（1）证明：联结AD ．∵AB 是⊙O 的直径，∴∠ADB =90°，AD ⊥BC .∵AC = AB ，∴12∠=∠．…….1分 ∵OA OD =，∴13∠=∠． ∴23∠=∠，∴OD ∥AC ．…….2分（2）∵AC = AB =10，∴B C ∠=∠．∴cos C=cos 5ABC ∠=． 在Rt △ABD 中，∠ADB =90°，cos 5BD ABC AB ∠==， ∴BDCD = BD….3分∵EF 为⊙O 的切线，∴OD ⊥EF ，由∵OD ∥AC ，∴∠DFC =90°. …….4分 在Rt △CDF 中，cos C=5CF CD =，∴CF =2．∴AF =8． ∵OD ∥AC ，∴ODE ∆∽AFE ∆．∴OE OD AE AF =．∴OB BE ODAB BE AF+=+． ∵152OB OA OD AB ====,∴103BE =．…….5分 25．（本小题满分5分）（1）证明：连接OA .（如图）∵ AE 为⊙O 的切线，BD ⊥AE ， ∴ ∠DAO =∠EDB =90°. ∴ DB ∥AO .∴ ∠DBA =∠BAO . …………1分 又 ∵OA =OB ， ∴ ∠ABC =∠BAO .∴ ∠D B A =∠A B C . ………………………………………………2分（2）在Rt △ADB 中，∠ADB =90°，C∵ BD =1，tan ∠BAD =12， ∴ AD =2，……………………………………………………………………3分由勾股定理得AB .∴ cos ∠DBA 又∵ BC 为⊙O 的直径， ∴ ∠BAC =90°. 又∵∠DBA =∠ABC .∴ cos ∠ABC = cos ∠DBA∴ 5.cos ABBC ABC===∠…………………………………………4分 ∴ ⊙O 的半径为5.2…………………………………………………………5分25.解：（1）∵ OC =OA∴ ∠CAO =∠OCA ∵ AC 平分∠DAB ∴ ∠DAC =∠CAO ， ∴ ∠ACO =∠DAC ． ∴ OC ∥AD ．…………………………………………………………………….1分 ∵ AD ⊥PD ， ∴OC ⊥PD ． ∴ PD 是⊙O 的切线……………………………………………………………...2分（2）连接AE ．∵CE 平分∠ACB ，∴AE BE =，∴AE BE == ∵AB 为⊙O 的直径， ∴∠AEB =90°．在Rt △ABE 中，14AB =………………………………………3分 ∵ ∠P AC =∠PCB ，∠P =∠P ， ∴ △P AC ∽△PCB ， ∴ PC AC PB BC =．…………………………………………………………………..4分 又∵4tan 3ABC =∠，∴43AC PCBC PB==， 设PC =4k ，PB =3k ，则在Rt △POC 中，PO =3k +7，OC =7，∵ PC 2+OC 2=OP 2， ∴()()2224737k k +=+， ∴ 126,0k k ==(舍去)．∴ PC =4k =4×6=24． …………………………………………………………..5分25证明：（1）连接OA .∵∠B =∠D =30°，∴∠AOC =2∠B =60°，……………………….(1分) ∴∠OAD =180°-∠AOD -∠D =90°，…………….(2分) 即OA ⊥AD ,∴AD 是⊙O 的切线.……………….(3分)（2）∵OA =OC ,∠AOC =60°，∴△ACO 是等边三角形， ∵CO ⊥AB ∴ ……………………….(4分)在Rt △ABC 中∴⊙O 的半径为6.……………………………….(5分)1122AE AB ==⨯=sin sin60AEACE AC∠==︒6AC ===。

中考统一练习㈡数 学 2015．5考生须知1．本试卷共6页，共五道大题，25个小题，满分120分。

考试时间120分钟。

2．在试卷和答题卡上认真填写学校名称、姓名和考试编号。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．考试结束，请将本试卷和答题卡一并交回。

一、选择题（共8道小题，每小题4分，共32分） 下列各题均有四个选项，其中只有一个．．是符合题意的． 1．21-的倒数是（ ）. A .2 B .2- C .21D . 21-2．根据中国汽车工业协会的统计，2011年上半年的中国汽车销量约为932.5万辆，同比增速3.35%．将932.5万辆用科学记数法表示为（ ）辆A ．93.25×105B ．0.9325×107C ．9.325×106D ．9.325×1023．若一个正多边形的每个内角都为135°，则这个正多边形的边数是（ ）. A .9 B .8 C .7 D .6 4．下列运算正确的是（ ）.A .22a a a =⋅B .22=÷a aC . 22423a a a +=D . ()33a a -=-5．如图所示，直线a ∥b ，直线c 与直线a ，b 分别相交于点A 、点B ，AM ⊥b ，垂足为点M ，若∠1=58°，则∠2的度数是（ ）．A .22B .30C .32D .426．某校抽取九年级的8名男生进行了1次体能测试，其成绩分别为90，75，90，85， 75，85，95，75，（单位：分）这次测试成绩的众数和中位数分别是 （ ）．A ．85，75B ．75，85C ．75，80D ．75，757．已知圆锥的底面半径为3，母线长为4，则圆锥的侧面积等于（ ）.A ．15πB ．14π C．13π D ．12π8．过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体，其正确展开图为( ) .A B C D 二、填空题（共4道小题，每小题4分，共16分）第5题图2a bcMB A 19．在函数3+=x y 中，自变量x 的取值范围是 .10．若()022=++-a b a ，则=+b a .11．把代数式142-+m m 化为()b a m ++2的形式，其中a 、b 为常数，则a +b = ． 12．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0）…根据这个规律探索可得，第20个点的坐标是__________；第90个点的坐标为____________．三、解答题（共6道小题，每小题5分，共30分） 13．()33602120---+︒-πcos解：14．解方程：2132+=+-a a a解：15． 已知4+=y x ，求代数式2524222-+-y xy x 的值.解：16．如图，在△ABC 中，AD 是中线，分别过点B 、C 作AD 及其延长线的垂线BE 、CF ，垂足分别为点E 、F ．求证：BE =CF ． 证明：17．如图，某场馆门前台阶的总高度CB 为0.9m ，为了方便残疾人行走，该场馆决定将其中一个门的门前台阶改造成供轮椅行走的斜坡，并且设计斜坡的倾斜角A ∠为8°，请计算从斜坡起点A 到台阶最高点D 的距离（即斜坡AD 的长）.（结果精确到0.1m ，参考数据：sin 8°≈0.14,cos 8°≈0.99,tan 8°≈0.14）C ABD解：18．如图，平面直角坐标系中，直线AB 与x 轴交于点A （2，0），与y 轴交于点B ，点D 在直线AB 上．⑴求直线AB 的解析式；⑵将直线AB 绕点A 逆时针旋转30°，求旋转后的直线解析式．解：⑴⑵四、解答题（共4道小题，每小题均5分，共20分）19．如图1，已知平行四边形ABCD 中，对角线AC BD ，交于点O ，E 是BD 延长线上的点，且ACE △是等边三角形． ⑴求证：四边形ABCD 是菱形；⑵如图2，若2AED EAD ∠=∠，AC =6．求DE 的长．OBEACD OB EACD图1 图2 证明：⑴ ⑵ 20． 如图，⊙O 中有直径AB 、EF 和弦BC ，且BC 和EF 交于点D ，点D 是弦BC 的中点，CD =4，DF =8.⑴求⊙O 的半径及线段AD 的长； ⑵求sin ∠DAO 的值. 解：⑴ ⑵21．图①、图②反映是某综合商场今年1-4月份的商品销售额统计情况．观察图①和图②，解答下面问题：y x31D B O A FED BOA C⑴来自商场财务部的报告表明，商场1-4月份的销售总额一共是280万元，请你根据这一信息补全图①；⑵商场服装部4月份的销售额是多少万元；⑶小华观察图②后认为，4月份服装部的销售额比3月份减少了．你同意他的看法吗？为什么？ 解：⑴ ⑵ ⑶22．⑴阅读下面材料并完成问题：已知：直线AD 与△ABC 的边BC 交于点D ，①如图1，当BD =DC 时，则S △ABD ________S △ADC ．(填“=”或“＜”或“＞”)DBCADBCABCAD图1 图2 图3②如图2，当BD =21DC 时，则=∆ABD S ADC S ∆ ． ③如图3，若AD ∥BC ,则有ABC S ∆ DBC S ∆ ．(填“=”或“＜”或“＞”)⑵请你根据上述材料提供的信息，解决下列问题：过四边形ABCD 的一个顶点画一条直线，把四边形ABCD 的面积分成1︰2的两部分．（保留画图痕迹）BCAD五、解答题（共3道小题，23题7分，24题8分，25题7分，共22分）23．已知：关于x 的方程mx 2－3(m －1)x ＋2m －3=0.⑴当m 取何整数值时，关于x 的方程mx 2－3(m －1)x ＋2m －3=0的根都是整数； ⑵若抛物线32)1(32-+--=m x m mx y 向左平移一个单位后，过反比例函数)0(≠=k xky 上的一点（-1,3），①求抛物线32)1(32-+--=m x m mx y 的解析式； ②利用函数图象求不等式0>-kx x k 的解集.解：⑴⑵①② 24．探究问题：已知AD 、BE 分别为△ABC 的边BC 、AC 上的中线，且AD 、BE 交于点O .⑴△ABC 为等边三角形，如图1，则AO ︰OD = ；⑵当小明做完⑴问后继续探究发现，若△ABC 为一般三角形（如图2），⑴中的结论仍成立，请你给予证明.⑶运用上述探究的结果，解决下列问题：如图3，在△ABC 中，点E 是边AC 的中点，AD 平分∠BAC , AD ⊥BE 于点F ，若AD =BE =4. 求：△ABC 的周长.ODE ABCOE DBCA1 2 3 4 4 3 2 1xy O -1 -2 -3 -4 -4 -3-2-1D CF B EA图1 图2 图3解：⑴⑵⑶25．如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P．已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）．⑴求c、b（可用含t的代数式表示）；⑵当t>1时，抛物线与线段AB交于点M．在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；⑶在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接．．写出t的取值范围．解：⑴⑵⑶参考答案一、选择题1 2 3 4 5 6 7 8 B C B D C B DB二、填空题9、x ≥-3 10、-4 11、-3 12、（6，4）；（13，1） 三、解答题（共6道小题，每小题5分，共30分） 13．解：原式=3121232-+⨯----------------------------------------4分 =3---------------------------------------5分14．解：()()()()32322-=+-++a a a a a ---------------------------------------1分a a a a a364222-=--++ ---------------------------------------2分 24=a ---------------------------------------3分 21=a ---------------------------------------4分是原方程的根经检验：21=a∴是原方程的根21=a ---------------------------5分15．44=-∴+=y x y x 解：---------------------------------------1分原式=2524222-+-y xy x ---------------------------------------2分()2522--=y x ---------------------------------------4分7254242=-⨯==-时，原式当y x ---------------------------------------5分 16．证明： AD 是中线∴BD=CD ---------------------------------------1分 分别过点B 、C 作AD 及其延长线的垂线BE 、CFCFD E ∠=∠∴---------------------------------------2分中和在CFD BED ∆∆ ⎪⎩⎪⎨⎧∠=∠=∠=∠CDF BDE CDBD CFD E ()AAS CFD BED ∆≅∆∴-------------------------------4分 CF BE =∴---------------------------------------5分17．解：E AB DE D 于点作过⊥---------------------------------------1分 ，于B AB CB ⊥ DC ∥AB∴.90==CB DE ---------------------------------------2分A DE AD AED Rt sin =∆ 中，在---------------------------------------4分∴m AD 4.614.09.0≈= EC AD B∴从斜坡起点A 到台阶最高点D 的距离约为6.4m 。

2015年房山区中考二模数学一、选择题（本题共30分，每小题3分）下列各题均有四个选项，其中只有一个．．是符合题意的．用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑． 1. 4的算术平方根是A ．16B ．2C ．﹣2D ．±22. 舌尖上的浪费让人触目惊心! 据统计，中国每年浪费的食物总量折合成粮食约为50000000000千克，把50000000000用科学记数法表示为 A ．5×1010B ． 50×109C ． 5×109D ．0.5×10113. 计算62a a ÷的结果是A.3a B .4a C . 8a D. 12a4. 如图，BC ⊥AE 于点C ，CD ∥AB ，∠B =55°，则∠DCE 等于A.35°B. 45°C.55°D.65°5.在下列图形中，既是轴对称图形又是中心对称图形的是6.如图，AB 为⊙O 的直径，弦CD ⊥AB ，垂足为点E ，连接OC ， 若CD =6，OE =4，则OC 等于A ．3B ．4C ．5D ．67.有11名同学参加了书法比赛，他们的成绩各不相同．若其中一位同学想知道自己能否进入前6名，则他不仅要知道自己的成绩，还要知道这11名学生成绩的 A.方差 B.平均数 C.众数D.中位数EDCBAA B C D8. 如图，AD 、BE 是△ABC 的两条中线，则EDC ABC S S △△：等于 A ．1:2 B ．2:3 C ．1:3 D ．1:49. 学校组织春游，每人车费4元．一班班长与二班班长的对话如下：由上述对话可知，一班和二班的人数分别是A ． 45，42B ．45，48C ．48，51D ．51，4210. 如图，在矩形A BCD 中，AB =2，点E 在边AD 上，∠ABE =45°，BE=DE ，连接BD ，点P 在线段DE 上，过点P 作PQ ∥BD 交BE 于点Q ，连接QD ．设PD =x ，△PQD 的面积为y ，则能表示y 与x 函数关系的图象大致是二、填空题（本题共18分，每小题3分）11. 分解因式: =________________.12.若分式12x -有意义，则x 的取值范围是________________． 13.如图，正方形ABCD 和正方形CEFG 中，点D 在CG 上，BC =1，CE =3，点H 是AF 的中点，那么CH 的长是.14.如图1，将长为20cm ，宽为2cm 的长方形白纸条，折成图2所示的图形并在其一面着色，则着色部分的面积为cm 2.A B C DEDCBA 8822+-x x 图115.如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．“杨辉三角”中有许多规律，如它的每一行的数字正好对应了()na b +（n 为非负整数）的展开式中a 按次数从大到小排列的项的系数．例如，()2222a b a ab b +=++展开式中的系数1、2、1恰好对应图中第三行的数字．请认真观察此图，写出()3a b +的展开式()3a b += ．16．正方形111A B C O ，2221A B C C ，3332A B C C ，…，按如图所示的方式放置．点1A ，2A ，3A ，…，和点1C ，2C ，3C ，…，分别在直线1y x =+和x 轴上，则点B 1的坐标是; 点B n 的坐标是 ．（用含n 的代数式表示）三、解答题（本题共30分，每小题5分）17101()6sin 60(22)2---.18．已知0132=-+x x ，求)1(3)1()2(422---++x x x x 的值.19．已知：如图，C 是AE 的中点，BC =DE ，BC ∥DE ．求证：∠B =∠D 20. 解方程：32322x x x +=+-21.如图，矩形OABC , A （0，5），C （4，0）,正比例函数)0(≠=m mx y 的图象经过点B ． （1）求正比例函数的表达式；（2）反比例函数4(0)y x x=>的图象与正比例函数的图象和边BC 围成的阴影区域BNM 如图所示,请直接写出阴影区域中横纵坐标都是整数的点的坐标（不包括边界）．22.列方程或方程组解应用题几个小伙伴打算去音乐厅看演出，他们准备用360元钱购买门票．下面是两个小伙伴的对话：根据对话中的信息，请你求出这些小伙伴的人数．四、解答题（本题共20分，每小题5分）23.已知：如图，在矩形ABCD 中，E 是BC 边上一点，DE 平分ADC ∠，EF ∥DC 交AD 边于点F ，连结BD .(1) 求证：四边形FECD 是正方形;(2)若BE ED ==1，求tan DBC ∠的值.24.网瘾低龄化问题已经引起社会各界的高度关注，有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查，绘制出以下两幅统计图．请根据图中的信息，回答下列问题：E BC（1）这次抽样调查中共调查了 人; （2）请补全条形统计图；（3）扇形统计图中18﹣23岁部分的圆心角的度数是 ；（4）据报道，目前我国12﹣35岁网瘾人数约为2000万，请估计其中12﹣23岁的人数． 25.如图，AB 是⊙O 的直径，点C 是⊙O 上一点， AD ⊥ DC 于D , 且AC 平分∠DAB ，延长DC 交AB 的延长线于点P ，弦CE 平分∠ACB ，交AB 于点F ，连接BE ． （1）求证：PD 是⊙O 的切线； （2）若tan ABC =43∠，BE =PC 的长．26.在平面内，将一个图形G 以任意点O 为旋转中心，逆时针．．．旋转一个角度θ，得到图形'G ，再以O 为中心将图形'G 放大或缩小得到图形''G ，使图形''G 与图形G 对应线段的比为k ，并且图形G 上的任一点P ，它的对应点''P 在线段'OP 或其延长线上；我们把这种图形变换叫做旋转相似变换，记为()O θ,k ，其中点O 叫做旋转相似中心，θ叫做旋转角，k叫做相似比. 如图1中的线段''OA 便是由线段OA 经过()302︒O ,得到的.（1）如图2，将△ABC 经过☆ ()901,︒后得到△'''A B C ，则横线上“☆”应填下列四个点()00O ，、()01D ，、()0E ，-1、()12C ，中的点 . （2）如图3，△ADE 是△ABC 经过()A θ,k 得到的，90︒=EAB ∠，12cos EAC =∠ 则这个图形变换可以表示为(),A .OPE五、解答题（本题共22分，第27题7分，第28题7分，第29题8分） 27.已知关于x 的一元二次方程()23130kx k x +++= (k ≠0).（1）求证：无论k 取何值，方程总有两个实数根；（2）点()()120,0A x B x ，、在抛物线()2313y kx k x =+++上，其中12x x ＜0＜，且12x x 、和k 均为整数，求A ，B 两点的坐标及k 的值；（3） 设（2）中所求抛物线与y 轴交于点C ，问该抛物线上是否存在点E ，使得ABEABCS S=，若存在，求出E 点坐标，若不存在，说明理由.28.在△ABC 中，AB ＝BC=2，∠ABC ＝90°，BD 为斜边AC 上的中线，将△ABD 绕点D 顺时针旋转α(0°＜α＜180°)得到△EFD ，其中点A 的对应点为点E ，点B 的对应点为点F . BE 与FC 相交于点H .（1）如图1，直接写出BE 与FC 的数量关系：____________; （2）如图2，M 、N 分别为EF 、BC 的中点.求证：MN =22FC ; （3）连接BF ，CE ，如图3，直接写出在此旋转过程中，线段BF 、CE 与AC 之间的数量关系： .yx11O29.如图1，若抛物线L 1的顶点A 在抛物线L 2上，抛物线L 2的顶点B 也在抛物线L 1上(点A 与点B 不重合)，我们把这样的两抛物线L 1、L 2互称为“友好”抛物线. （1）一条抛物线的“友好”抛物线有_______条.A . 1 B. 2 C. 3 D. 无数 （2）如图2，已知抛物线L 3：2284y x x =-+与y 轴交于点C ，点C 关于该抛物线对称轴的对称点为D ，请求出以点D 为顶点的L 3的“友好”抛物线L 4的表达式;（3）若抛物线21()y a x m n =-+的“友好”抛物线的解析式为22()y a x h k =-+,请直接写出1a图2图1图32015年房山区初中毕业会考试卷数学参考答案和评分参考一、选择题（本题共30分，每小题3分，）1.B2.A3.B4.A5.A6.C7.D8.D9.B 10.C 二、填空题（本题共18分，每小题3分）11. 2(x -2)2 12. 2x ≠13.14. 36 15.322333a a b ab b +++16. ()111B ， ,()121,2n n n B -- (分别为1分，2分)三、解答题（本题共30分，每小题5分）17．原式=621+-………………………………………………………………4分 =1 …………………………………………………………………………………5分18．原式331284222+-+-++=x x x x x ………………………………………………3分4622++=x x ……………………………………………………………………4分 ∵0132=-+x x ， ∴132=+x x .∴原式4)3(22++=x x=2×1+4=6 …………………………………………………… 5分19．∵C 是AE 的中点，∴AC ＝CE .…………………………………………………………………………1分 ∵BC ∥DE ，∴∠ACB =∠E . …………………………………………………………………2分 在△ABC 和△CDE 中，⎪⎩⎪⎨⎧=∠=∠=CE AC E ACB DE BC ，∴△ABC ≌△CDE . ………………………………………………………………4分 ∴∠B =∠D . ………………………………………………………………………5分20.3(2)2(2)3(2)(2)x x x x x -++=+- ……………………………………………………1分223624312x x x x -++=-……………………………………………………………2分4x =………………………………………………………………3分经检验：4x =是原方程的解.…………………………………………………………4分 ∴原方程的解是4x =. ………………………………………………………………5分21.（1）B (4，5)………………………………………………………………………………1分正比例函数解析式:x y 45=……………………………………………………3分 （2）（3，3），（3，2）……………………………………………………………………5分22.解：设小伙伴的人数为x 人 ……………………………………………………………1分根据题意，得：360x -2×60% = 360-72x ………………………………………………………….2分解得 x =8 ……………………………………………………………3分经检验x =8是原方程的根且符合题意．……………………………………………4分答：小伙伴的人数为8人． ……………………………………………5分四、解答题（本题共20分，每小题5分）23.(1)∵矩形ABCD∴AD//BC ，∠ADC=∠C =90° ∵EF//DC∴四边形FECD 为平行四边形 ………………………………………………………1分 ∵DE 平分∠ADC∴∠ADE=∠CDE ∵AD//BC∴∠ADE=∠DEC ∴∠CDE=∠DEC∴CD =CE ……………………………………………………………………….2分 又∵∠C =90°∴ 平行四边形FECD 是正方形 ………………………………………………….3分(2)∵四边形FECD 是正方形，ED =∴CD =CE=2， ……………………………………………………………………….4分 ∴BC=BE+EC=1+2=3∴2tan 3DC DBC BC ==∠……………………………………………………………….5分24. （1）1500 ………………………………………………………………………………1分（2）…………………………………………………2分（3）108° ……………………………………………………………………………3分 （4）万人1000%502000=⨯ ………………………………………………………5分25.解：（1）∵ OC =OA∴ ∠CAO =∠OCA ∵ AC 平分∠DAB ∴ ∠DAC =∠CAO ， ∴ ∠ACO =∠DAC ． ∴ OC ∥AD ．…………………………………………………………………….1分 ∵ AD ⊥PD ， ∴OC ⊥PD ． ∴ PD 是⊙O 的切线……………………………………………………………...2分（2）连接AE ．∵CE 平分∠ACB ，∴AE BE =，∴AE BE == ∵AB 为⊙O 的直径， ∴∠AEB =90°．在Rt △ABE 中，14AB ………………………………………3分 ∵ ∠P AC =∠PCB ，∠P =∠P ， ∴ △P AC ∽△PCB ， ∴PC ACPB BC=．…………………………………………………………………..4分 又∵4tan 3ABC =∠， ∴43AC PCBC PB==， 设PC =4k ，PB =3k ，则在Rt △POC 中，PO =3k +7，OC =7，∵ PC 2+OC 2=OP 2， ∴()()2224737k k +=+， ∴ 126,0k k ==(舍去)．∴ PC =4k =4×6=24． …………………………………………………………..5分26.（1）E ………………………………………………………………………………2分 （2）60,k︒………………………………………………………5分五、解答题（本题22分，第27题7分，第28题7分，第29题8分）27. （1）∵()()222Δ=3112961310k k k k k +-=-+=-≥∴方程总有两个实数根.……………………………………………………2分 （2）由求根公式得：()()31312k kx k-+?=∴3x =-或1x k=- ∵12x x 、和k 均为整数∴=1k ± 又∵120x x ＜＜∴1k =-…………………………………………………………………………3分 ∴A (-3,0), B (1,0) ……………………………………………………4分 （3）()()()2,3131，，--+---…………………………………………7分28.（1）=BE CF ． ………………………………………………………………2分 （2）证明：如图2，∵AB =BC ，∠ABC =90°，BD 为斜边中线 ∴BD =AD =CD =12AC ，BD ⊥AC∵ △EFD 是由△ABD 旋转得到的，∴DE =DF =DB =DC ，∠EDF =∠ADB =∠BDC =90° ∴∠EDF +∠BDF =∠BDC +∠BDF ，即∠BDE =∠FDC ∴△BDE ≌△FDC ∴BE =FC 且∠1=∠2 又∵∠3=∠4∴FHE FDE ︒==90∠∠ ,即BE CF ⊥…………………………………………3分 连接BF ，取BF 中点G ，连接MG 、NG . ∵M 为EF 中点，G 为BF 中点，N 为BC 中点 ∴MG ∥BE ，MG =12BE ；NG ∥FC ，NG =12FC又∵EB =FC ，BE ⊥FC ∴MG =NG ，∠MGN =90° ∴△MGN 为等腰直角三角形 ∴MN =22FC …………………………………………………………………5分 图2（3）222BF CE AC += ……………………………………………………………7分29. (1) D ……………………………………………………………………………………2分(2) 由L 3:2284y x x =-+=2(x -2)2-4∴C (0，4) ，对称轴为x =2，顶点坐标（2，-4）………………………………3分 ∴点C 关于对称轴x =2的对称点D （4，4）……………………………………4分 设L 4：()2y a x h k =-+将顶点D (4，4)代入得，()244y a x =-+ 再将点（2，-4）代入得，-4=4a +4 解得：a = -2L 3的友好抛物线L 4的解析式为：()2244y x =--+…………………………6分 (3) 12a a =-（或120a +a =）………………………………………………………8分。