当前位置：文档之家 › 第十一章时间数列预测方法

第十一章时间数列预测方法

  • 格式：ppt
  • 大小：709.00 KB
  • 文档页数：70

下载文档原格式

  / 70

合集下载

第11章 时间序列预测法 《市场调查与预测》PPT课件

第11章 时间序列预测法 《市场调查与预测》PPT课件
返回目录
11.3 移动平均法
二次移动平均法的预测步骤：
返回目录
11.3 移动平均法
11.3.3加权移动平均法 加权移动平均法，是对市场现象观察值按距离预测期的远近，给予不同的权数，
并求其按加权计算的移动平均值，以移动平均值为基础进行预测的方法。
Ft1
ft yt ft1 yt1 ft ft1
f y tn1 tn1 ftn1
返回目录
11.4 指数平滑法
11.4.1指数平滑法的含义及特点 指数平滑法是由移动平均法改进而来的，是一种特殊的加权移动平均法，也称为
指数加权平均法。 这种方法既有移动平均法的长处，又可以减少历史数据的数量。
返回目录
11.4 指数平滑法
11.4.1指数平滑法的含义及特点 指数平滑法主要具有以下几方面的特点：
中，移动平均法主要用来有效的消除不规则变动和季节变动对原序列的影响。 （4）移动平均采用奇数项移动能一次对准被移动数据的中间位置，若采用偶数
项移动平均，一次移动平均后的数值将置于居中的两项数值之间。 （5）移动周期至少为一个周期，并且是对不同时间的观察值进行修匀。
返回目录
11.3 移动平均法
11.3.1一次移动平均法 一次移动平均法也称为简单移动平均法，它是利用过去若干期实际的平均值，来
11.4.2指数平滑法的应用 指数平滑法在市场预测中的应用主要有一次指数平滑法和二次指数平滑法[271页字号]。 1.一次指数平滑法 一次指数平滑法，也称为单重指数平滑法，它是指对市场现象观察值计算一次平滑值，并
以一次指数平滑值为基础，估计市场现象的预测值的方法。
返回目录
11.4 指数平滑法
【例11-6】
返回目录
11.5 趋势延伸法

简述时间数列预测法的种类

简述时间数列预测法的种类

简述时间数列预测法的种类时间数列预测法是指通过对历史时间序列的分析，预测未来时间序列的方法。

根据其预测方法的不同，时间数列预测法可以分为以下几种：
1.简单移动平均法：以时间序列中过去一段时间的平均值作为未来一段时间的预测值，适用于波动较小的时间序列。

2.加权移动平均法：对不同时间点的数据赋予不同的权重，以反映不同时期的重要性，适用于波动较大的时间序列。

3.指数平滑法：通过对历史数据进行指数加权，降低较早数据的权重，提高较近数据的权重，以适应时间序列的变化趋势。

4.趋势线分析法：根据时间序列的变化趋势，通过拟合趋势线来预测未来的数值变化，适用于时间序列具有明显趋势的情况。

5.线性回归分析法：通过建立时间序列的回归方程，根据时间序列的历史数据和自变量的变化情况，预测未来时间序列的值。

6.ARIMA模型法：是基于时间序列的自回归、滑动平均和差分三个方面进行建模，可以对任意时间序列进行预测。

1/ 1。

趋势预测法

趋势预测法
(2)以观察期的每月平均值作为预测期对应月份 的预测值。
当时间序列资料在年度内变动显著，或呈季节性变化 时，如果用上一种方法求得预测值，其精确度难以保证。
例：假设某商品最近四年的每月销售量如表5.1 所示，在95%的可靠程度下,预测2008年的每月 销售量。
①如果以2007年的每月平均值作为2008年的每 月预测值；
零售量为：
y ˆ19 84 7 034 .8 4 7 5 5.7 3(万 8 5) 米
直线趋势延伸法的特点
• （1）直线趋势预测法仅适用于预测目标时间序列 呈现直线长期趋势变动情况。
• （2）它对时间序列资料一律同等看待，在拟合中 消除了季节、不规则、循环三类变动因素的影响
• （3）反映时间序列资料长期趋势的平均变动水平 。
②以四年的每月平均值335.7干元作为2008年的 每月预测值，标准差为：
Sx1
B 2.78 41
B （ 33 .4 3 33 .7 ） 25 （ 33 .5 6 33 .7 ） 25 （ 33 .7 3 33 .7 ） 25 （ 33 .2 9 33 .7 ） 25 2.1 38
在95％的可靠程度下，2008年每 月预测值区间为335.7土1.96x2.78， 即在330.25—341.15千元之间。
❖ 然后，计算某种可靠程度要求时的预测区间。
x tSx
①以2007年的月平均值339.2千元作为2008年 的每月预测值，标准差为：
Sx1
A 121
31.96181.703 11
在95%的可靠程度下，2008年每月预测区 间为339.2±1.96x17.03，即305.8—375.52千 元之间。
算术平均法，就是以观察期数据之和除以 求和时使用的数据个数(或资料期数)，求得 平均数。

第十一章时间数列预测方法

第十一章时间数列预测方法

第十一章时间数列预测方法例11.1 (11-1)（1）计算按5日扩大时距的时间数列和计算按5日平均日产量的时间数列，结果如下表Excel计算公式（3）5日移动平均数。

按下列步骤使用“移动平均”分析工具：1.选择工具菜单之数据分析选项, 在分析工具框中“移动平均”。

移动平均对话框将显示为下图所示，它带输入输出的提示。

1) 输入输入区域：B1:B31标志位于第一行间隔：52) 输出选项输出区域: C12. 单击确定，Excel将计算出结果显示在输出区域中。

例11.2 (11-2)(1)选择工具菜单之数据分析选项, 在分析工具框中“指数平滑”。

指数平滑对话框将显示为图所示，它带输入输出的提示。

1) 输入输入区域：B1:B13阻尼系树：0.2标志2) 输出选项输出区域: C2图表输出(2)．单击确定，Excel将计算出结果显示在输出区域中。

例11.3 (11-6)1．输入数据，绘制散点图2．点击图中数据点，在菜单“图表”中添加趋势线，在对话框中选择2阶多项式，并在选项中选中“显示公式”和“显示R平方值”例11.4 (11-7)1．求年合计和年平均：M2 = SUM(B2:M2)，。

N2 =A VERAGE(B2:M2)，。

2．求月合计和月平均：B6 =SUM(B2:B5)，。

B7 =A VERAGE(B2:B5)，。

3．求季节指数：B8 =B2/$O$2，。

例11.5 (11-7)1．计算线性趋势值T，D3 =FORECAST(B3,C$3:C$22,B$3:B$22)，FORECAST函数直接给出以B$3:B$22为自变量，C$3:C$22为因变量的线性回归的预测（估计）值，将公式拷贝到D22即的结果。

2．计算循环及不规则变动C·I（%）E3=C3/D3*100，。

3．用循环不规则变动的3项移动平均计算循环变动C(%)：F4=A VERAGE(E3:E5)，。

4．计算不规则变动I(%)：G4 =E4/F4*100，。

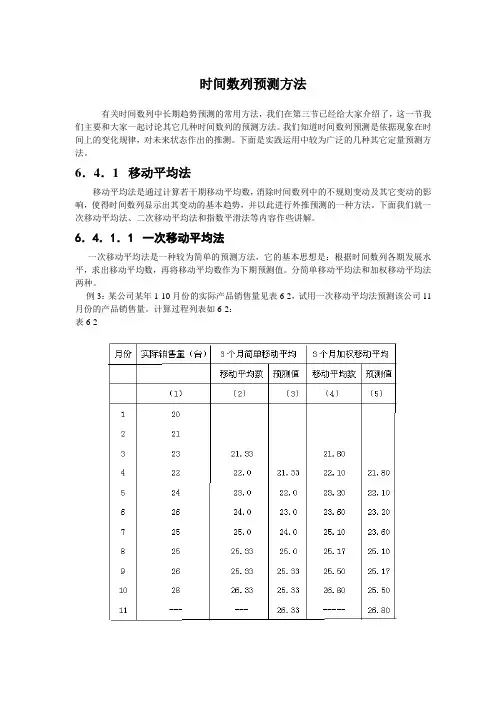
第十一章 时间数列预测方法

第十一章 时间数列预测方法
（五）计算题
1.对某地工业总产值1996～2000年的数据，配合不同的趋势方程式，得趋势值如下：
（1）判断两种趋势值数列各自所代表的趋势方程的类型？
（2）根据趋势值数列，写出原趋势方程式。
2.某企业历年利润资料如下：
要求用最小平方法预测该企业2001年的利润额。
3.某地区历年人口数字如下：
根据上述资料性质，拟合恰当趋势方程，并预测该地区2001年的人口数。
4.已知某地缝纫机销售量资料如下：
分析上述资料性质，拟合恰当的模型，并预测2001年的销售量。
ANSWER 11
（一）判断题
1.（×）
2.（×）
3.（√）
4.（√）
5.（×）
6.（×）
7.（×）
（二）单项选择题
1.①
2.④
3.④
4.③
5.②
6.④
7.②
8.①
（三）多项选择题
1.②④⑤
2.①④⑤
3.②③④⑤
7、循环变动和不规则变动分析预测常用的方Байду номын сангаас是剩余法。（）
（二）单项选择题
1、移动平均修匀时间数列所用的方法是（）。
简单算术平均法
加权算术平均法
调和平均法
几何平均法
2、最小平方法是要求（）。
A．
B．
C．
D．
3、二次抛物线所依据资料的特点是：（）。
定基发展速度大致相等
环比发展速度大致相等
逐期增长量近似一个常数
1200%
7、已知同一指标不同年度的数值顺序排列，欲求季节指数，则（）。
用按月平均法
用移动平均趋势剔除法
上述两种皆可以
上述两种皆不行

十一章节时间数列预测方法

十一章节时间数列预测方法


Y-T-S-C=I
若循环变动绝对数大于0为经济扩张期，小于0为经济收缩期， 等于0为无循环变动。
不规则变动绝对数等于0表示无影响，正值为正影响，负值为 负影响。
乘加型： Y=T×S+C×I
首先，测定趋势变动和季节变动值，得到循环、 不规则变动绝对额。
Y-T×S=C×I
其次，将循环变动和不规则变动值进行移动平均， 剔除不规则变动影响，测定循环变动绝对额。
1、时间数列预测分析的基本原理：
在长期趋势、季节变动、循环变动和不规则变 动四种因素中，先剔除其余几种因素的影响来 测定一种因素变动的影响；然后再结合起来测 定各种因素变动的综合影响。
2、各种因素变动的结构类型：
（1）乘法型 （2）加法型 （3）乘加型
Y=T×S×C×I Y=T+S+C+I Y=T×S+C×I
方法：用时距扩大后的总量指标编制时间数 列或平均数指标编制时间数列。
应用时距扩大法时需要注意以下几个问题：
1、扩大的时距多大为宜取决于现象自身的 特点。对于呈现周期波动的动态数列，扩大 的时距应与波动的周期相吻合；对于一般的 动态数列，则要逐步扩大时距，以能够显示 趋势变动的方向为宜。时距扩大太大，将造 成信息的损失。 2、扩大的时距要一致，相应的发展水平才 具有可比性。
四、最小平方法
最小平方法（最小二乘法）：以时间变 量为X，以指标值为Y，建立回归模型预 测。
1、直线模型 2、指数模型 3、二次曲线（抛物线）模型 4、双曲线模型
判断方法：将数据在坐标轴上以散点图或折
线图的形式画出来，以显示数据的变化趋势，通 过观察选择预测模型的方法。 如果数据的分布近似直线形状，就配合直线模 型进行预测。 如果数据的分布不属于直线型的，则应仔细观 察其分布是否近似于某一曲线（如抛物线、双曲 线、指数曲线、S曲线等），然后配合相应的曲 线模型进行预测。

时间数列预测方法

时间数列预测方法有关时间数列中长期趋势预测的常用方法，我们在第三节已经给大家介绍了，这一节我们主要和大家一起讨论其它几种时间数列的预测方法。

我们知道时间数列预测是依据现象在时间上的变化规律，对未来状态作出的推测。

下面是实践运用中较为广泛的几种其它定量预测方法。

6．4．1 移动平均法移动平均法是通过计算若干期移动平均数，消除时间数列中的不规则变动及其它变动的影响，使得时间数列显示出其变动的基本趋势，并以此进行外推预测的一种方法。

下面我们就一次移动平均法、二次移动平均法和指数平滑法等内容作些讲解。

6．4．1．1一次移动平均法一次移动平均法是一种较为简单的预测方法，它的基本思想是：根据时间数列各期发展水平，求出移动平均数，再将移动平均数作为下期预测值。

分简单移动平均法和加权移动平均法两种。

例3：某公司某年1-10月份的实际产品销售量见表6-2，试用一次移动平均法预测该公司11月份的产品销售量。

计算过程列表如6-2：表6-2注：表中第2列―3个月简单移动平均数‖是由原数列三个月的实际数之和除以3得到。

如，3月份的简单移动平均数=，并将此移动平均数作为4月份的预测值；3月份的加权移动平均数= 同样将它作为4月份的预测值。

这里的0.2，0.3，0.5分别是1、2、3、月份的权重，权重之和等于1。

这样赋值，主要是强调后期比前期对预测的影响要大些，权重也就大些。

其它各月预测值以此类推。

最后11月份的预测值，按简单移动平均法为26.33台，按加权移动平均法则为26.8台.相差无几。

进行移动平均预测法应注意以下问题：一次移动平均法适合于时间数列较为平缓，即现象变动幅度不大的近期预测，不适合作长时期的趋势预测；移动平均中的移动项数N的大小，对预测值有较大的影响，而且N的选取带有一定的经验性，实践中可多选几个方案加以比较，以确定最优的项数N；权数Wi的确定，需要预测者对数列作全面的了解和分析，根据经验和数列的变动规律来确定合适的Wi值。

第十一章时间数列预测方法


不规则变动分析
不规则变动是由一些不可估计 不可意料的原因引 起的变动;具有很大随机性
进行不规则变动分析可将时间数列剔除长期趋势 季节变动 循环变动;剩余的就是不规则变动
不规则变动也有乘法型 加法型和乘加型三种模型 分析
乘法型步骤
首先;用趋势季节变动值去除时间数列中的相应数 据;剔除长期趋势和季节变动影响;测定循环变动 和不规则变动
其次;将循环变动和不规则变动值进行移动平均; 剔除不规则变动影响;测定循环变动
最后;将长期趋势 季节变动 循环变动去除时间数 列中的实际数据;其商数就是不规则变动; 也可用 循环变动去除循环变动与不规则变动值;计算不规 则变动
乘法型模型
循环变动：
1 月 季资料：
C Y TSC I TSI TSI
首先;计算Y/T剔除长期趋势影响 其次;根据消除长期趋势后的比率计算同季平均数
和季节指数 案例分析 季节指数如果大于100%表示旺季;小于100%表示淡
季;在100%左右表示平季
加法型时间数列季节变动分析
这种分析是将原时间数列的实际数据减去长期趋 势值;剔除长期趋势影响；再同月季平均计算季节 差分析季节变动
最后;将长期趋势 季节变动 循环变动去除时间数列中的实际 数据;其商数就是不规则变动
Y/T×S×C=I
如果是以年为时间单位的数列;则不包含季节变动因素影响
Y=T×C×I
加法型模型：Y=T+S+C+I
首先;将时间数列中的实际数据减去趋势变动值;测定季节变动 循环变动和不规则变动的绝对额
YT=S+C+I
首先;测定长期趋势值T;用T去除时间数列各值;得到提出长期 趋势影响的时间数列
Y/T=S×C×I

时间数列分析与预测课件

季节性因素提取
根据季节性分解结果，提取季节性因素，用于预 测未来季节性变化趋势。
季节性预测
根据提取的季节性因素，结合历史数据，预测未 来季节性变化趋势。
03
时间数列的预测方法
简单平均预测法
定义
计算方法
简单平均预测法是指将时间序列的各个数 据点简单平均值作为预测值的方法。
将时间序列的各个数据点相加，再除以数 据点个数，得到平均值即为预测值。
优缺点
指数平滑预测法的优点是可以更好地捕捉到时间 序列的变化趋势，平滑效果较好；缺点是模型的 参数选择需要经验判断，且对数据的反应不够敏 感。
线性回归预测法
定义
计算方法
适用范围
优缺点
线性回归预测法是指利用历 史数据建立线性回归模型， 并以此模型作为预测值的方 法。
线性回归预测法通常采用最 小二乘法估计模型的参数， 即通过最小化残差平方和的 方法来估计模型的参数。
移动平均预测法通常采用加权 移动平均的方法计算，即根据 历史数据的远近赋予不同的权 重，再求加权平均值作为预测 值。
移动平均预测法适用于时间序 列数据有明显趋势的情况，尤 其适用于趋势变化较为平滑的 情况。
移动平均预测法的优点是可以 捕捉到时间序列的变化趋势， 对数据的反应较为敏感；缺点 是移动平均预测法的平滑效果 会受到数据波动性的影响，平 滑效果较差。
总结词
应用预测方法对时间数列进行未来趋势预测和波动预测。
详细描述
介绍常见的预测方法，如ARIMA模型、SARIMA模型、神经网络等，并给出实际 案例展示如何应用这些方法进行预测。
时间数列的模型选择与评估实例
总结词
根据实际数据特征和预测要求，选择合适的模型并进行评估。

时间序列预测法与运用

实际上是指各个观察指数的权重是相等 的。为1/n
二、加权平均法
概念：是指将时间数列的各个数据看作 对预测值有不同的影响程度，分别给各 个数据以不同的全数后计算出加权平均 数，并将其作为下期预测值的方法。
适用的关键：合理确定权数，附近的值 权重大，远期的值权重小。各个权重的 级差是根据预测者的经验来判断的。
一、无趋势变动的季节指数预测法； 二、含趋势变动的季节指数预测法； 见课本83页例题
第四节、趋势外推法
概念：是指根据时间数列呈现出的规律 性趋势向外推导，从而确定预测对象未 来值的预测方法。 准确度建立在外推模型能正确反映预测 对象的本质运动的基础上，并且向外推 导的时间不宜过长。 种类：直接作图法、直线趋势法、曲线 趋势外推法。
（一）、一次移动平均法
概念：是对时间数列按一定的观察期连 续计算平均值，取最后一个平均值作为 预测值的方法。 1、简单移动：直接以简单平均值数列中的 最后一个数值作为预测值。 2、加权移动：在移动跨越期内，对距离预 测期较远的数据给予较小的权数，反之 则给较大的权重，计算出加权移动平均 值数列，并以最后一个加权平均值作为 预测值。
一、直线趋势外推法
概念：是指对有线性变动趋势的时间数 列，拟合成直线方程进行外推预测的方 法。 直线方程的形式： Y=a+bt , 其中，a、b是模型参数，t为自变量，
一、直线趋势外推法
1、增减量预测法：是以上期实际值与上两 期之间的增减量之和，作为本期预测值 的一种预测方法；
2、平均增减量预测法：是先计算出整个时 间数列逐期增减量的平均数，再与上期 实际数相加，从而确定预测者的方法。
三、移动平均法
概念：是将观察期的统计数据，由远而 近地按照一定跨越期逐一求平均值，并 将最后一个平均值作为预测值的方法。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

预测值 Tt+1 -4.8 5.04 5.03 4.83 5.06
7月份库存量：
T6 1 S
(1) 6
5.05(百件)
均方误差：
MSE
( yt Tt ) 2 t 1

n
n
MSE最小的系数对应的时间数列趋势预测值为 最优
2）二次指数平滑法
一次指数平滑值： S t(1) yt (1 ) S t(11) ( 2) (1) ( 2) 二次指数平滑值： St St (1 )St 1 线性模型： Tt k a bk 其中： a 2 S (1) S ( 2 )
1 2 3 4 5 6 7 8
20 30 40 42 48 50 54 60
22.00 26.80 34.72 39.09 44.44 47.77 51.51 56.60
23.20 25.36 30.98 35.84 41.00 45.06 48.93 53.53
取初始值
20 30 S S 25 2 (1) ( 2) a8 2 S t S t 2 56.6 53.53 59.67
M t( 2 )
预测模型：
Tt k at bt k
其中： at 2 M t(1) M t( 2 )
2 (1) ( 2) bt (M t M t ) n 1
例：某商店某年商品销售额如下表：试用移动 平均法预测该年7月份销售额。（n=3）
单位：百万元
月份 t 1 2 3 4 5 6

yi yt yi a bt 最小值 ˆ
2

2
对上式求偏导数，并令其等于零，则
Q 2 ( y a bt ) 0 a Q 2 ( y a bt )(t ) 0 b
整理得未知参数a、b的求解方程：
y na b t 2 ty a t b t
即2002年人口数预计为84.63万元
一般情况下，若各观测值的环比发展 速度或环比增长速度大体相同，或各观测值 对数的一次差大体相同，可配合指数曲线。
2.二次曲线

当现象发展的趋势为抛物线形态时，则 配合二次曲线，即：
ˆ a bt ct 2 Y
根据最小二乘法，得方程：
y na b t c t 2 2 3 ty a t b t c t t 2 y a t 2 c t 4
第十一章时间数列分析预测
第一节时间数列预测的 基本理论
一、时间数列的构成要素与模型 构成要素： 长期趋势（T): 季节变动(S): 循环变动(C): 不规则变动(I):
模型： 乘法模型：Y=T*S*C*I
加法模型 ： Y=T+S+C+I
乘加模型： Y=Y*S+C*I
第二节长期趋势预测
一、长期趋势的修匀方法 1.时距扩大法和序时平均法： 2.移动平均法： 采用奇数项计算移动平均数，移动一次 采用偶数项计算移动平均数，移动二次 采用移动平均法修匀时间数列，可以消除 季节变动和不规则变动的影响。
5 6 7 8 9 10 11 12
48 52 54 50 55 56 51 58
51.0 51.3 52.0 53.0 53.7 54.0 55.0 ---
51.25
51.75
51.00
52.75
53.75
53.00
55.00
---
51.500 51.375 51.875 53.250 53.375 54.000 -----
1.9320 1.9369 1.9418 1.9468 1.9516 1.9564
拟合指数曲线：
11.6655 6 lg a 21 lg b 40.9148 21 lg a 91 lg b b 1.01132 a 84.555 ˆ Y ab t 84.555 1.01132 t ˆ12 84.555 (1.01132 )12 84.63(万元） Y
销售额 yt （n=3) 20 24 27 30 34 37 --23.7 27.0 30.3 33.7
M t(1)
M
( 2) t
at ----33.6 37.1
bt ----3.3 3.4
(n=3)
----27 30.3
若用一次移动平均数直接预测，则7月份销额
T61 M 6(1) 33.7(百万元）
指数曲线形式：
ˆ Y ab t
式中：a、b为未知常数。
将指数曲线线性化为对数直线形式：
lg y lg a t lg b ˆ
根据最小二乘法得标准方程如下：
lg y n lg a lg b t 2 t lg y lg a t lg b t
求出lga和lgb后，再取其反对数，即得常数a和b。
t t
b ( S t(1) S t( 2 ) ) 1
例：某商店某年各月销售额如下表：试运用指数 平滑法拟合直线模型预测9月份销售额 ( 0.6)
月份 销售额 t （万元）yt
S
(1) t
S
( 2) t
Tt 1
--19.00 30.40 44.07 47.22 53.04 54.55 57.96
(1) 0 ( 2) 0
(1) ( 2) b8 (St St ) 1
0. 6 (56.6 53.53) 4.605 1 0 .6
则：T 8 1 59.67 4.605 1 64.28(万元)
二、长期趋势的数学模型
(一)线性模型：ˆ a bt Y 其中未知参数a和b通常按最小平方法 （最小二乘法）求得。 最小平方法要求实际观察值（yi）与趋势 ˆ 值（Yt）的离差平方和为最小。 2 ( yi yt ) 最小值 ˆ 即：
1991 1992 1993 1994 1995 1996
1 2 3 4 5 6
一次 二次 环比 t2 差 差 增长 速度 （%） 1 0.98 1.1 4 0.97 -0.01 1.1 9 1.02 0.05 1.16 16 0.99 -0.03 1.1 25 0.98 -0.01 1.1 36
lgy
在一定条件下，移动平均法还可用于推断预测和 建模分析。 当事物的发展呈水平型变化时，可用以下预测模 型： (1)
Tt 1 M t
当事物的发展变化呈线性增长或下降趋势时， 需采用二次移动平均法，建模预测 二次移动平均公式：
1 1) M t(1) M t(1) M t(n1 n

一般情况下，若时间数列各观测值 的二次差或二级增长量大体相同，可配合 二次曲线。 若同一时间数列有几种趋势线可供 选择，则选方程估计标准差最小者为宜。 公式：
Sy

( y y) 2 ˆ nm
第三节季节变动的测定



季节变动---指事物因受自然条件或社会习俗等 因素影响，在一年内 随着季节的更 换而引起的比 较有规律变动。 测定季节变动一般需要掌握至少连续三个周期 以上的统计资料。 季节变动一般用季节指数（%）测定，其值围 绕100%上下波动。一般指数大于100%表示旺 季，低于100%表示淡季。
若用二次移动平均法建模预测，则7月份销售额
T61 a6 b6 1 37.1 3.4 1 40.5(百万元）
3.指数平滑法
1）一次指数平滑法
1 S t(1) yt (1 ) St(1)
Tt 1 St(1) yt (1 )Tt
上式表明t+1期的预测值是t 期实际值和预测值的加权平均数。 其中： (1) 为一次指数平滑值 S
设序时项数为n，则 N为奇数项时：
M i M i 1 M ni 1 Mt n
n为偶数项时：
Mi M n i M i 1 2 Mt 2 n
月份i 产量yi M i (n=3) M i (n=4) 移正M i （n=4) 1 50 ------2 3 4 45 52 53 49.0 50.0 51.0 50.0 49.5 --49.750 50.375
t
为权系数
(0 1)
yt 为 t 期实际观察值 Tt +1为期的一次指数平滑趋势预测值
任何时期指数平滑法的预测值同样也 是时间数列以前所有时期实际值的一个加 权平均数。
例：一个包含三个时期资料的时间数列
Y1 ，Y2 ， Y3 令
(1) T 1 S0 y1
T 2 S1(1) y1 (1 ) S 0(1) y1 (1 ) y1 y1 T 3 S 2(1) y 2 (1 ) S1(1) y 2 (1 ) y1 T 4 S 3(1) y 3 (1 ) S 2(1) y 3 (1 )y 2 (1 ) y1 y 3 (1 ) y 2 (1 ) 2 y1
年(t)
1（-9） 2（-7） 3（-5） 4（-3） 5（-1） 6（1） 7（3） 8（5） 9（7） 10（9） 合计
销售量/千辆(yt) 21.6 22.9 25.5 21.9 23.9 27.5 31.5 29.7 28.6 31.4 264.5
tyt
t2
21.6（-194.4） 1（81） 45.8（-160.3） 4（49） 76.5（-127.5） 9（25） 87.6（-65.7） 16（9） 119.5（-23.9） 25（1） 165（27.5） 36（1） 220.5（94.5） 49（9） 237.6（148.5） 64（25） 257.4（200.2） 81（49） 314（282.6） 100（81） 1545.5（181.5） 385（330）