第10章时间序列数据的基本回归分析

回归分析中的时间序列数据处理技巧时间序列数据在回归分析中起着重要的作用，它可以帮助我们预测未来的趋势和变化。

然而，时间序列数据处理并不是一件简单的事情，需要掌握一定的技巧和方法。

本文将介绍在回归分析中处理时间序列数据的一些技巧和方法。

时间序列数据的基本特征在进行时间序列数据处理之前，首先需要了解时间序列数据的基本特征。

时间序列数据是按时间顺序排列的数据序列，它包括趋势、季节性和随机性三个基本特征。

趋势是时间序列数据的长期变化趋势，季节性是周期性的变化趋势，而随机性则是不规律的波动。

对时间序列数据的趋势进行分析在回归分析中，我们通常需要对时间序列数据的趋势进行分析。

趋势分析可以帮助我们了解数据的长期变化趋势，从而进行未来的预测。

常用的趋势分析方法包括移动平均法、指数平滑法和趋势线法。

移动平均法是一种通过计算一定时间段内数据的平均值来消除随机波动，从而找出长期趋势的方法。

指数平滑法则是通过对数据赋予不同的权重来计算未来趋势的方法。

而趋势线法则是通过拟合一条直线或曲线来表示数据的长期变化趋势。

对时间序列数据的季节性进行分析除了趋势分析之外，我们还需要对时间序列数据的季节性进行分析。

季节性分析可以帮助我们找出数据的周期性变化规律，从而进行季节性调整。

常用的季节性分析方法包括周期性分解法、差分法和季节指数法。

周期性分解法是一种通过将数据分解为长期趋势、季节性和随机性三个部分来进行季节性分析的方法。

差分法则是通过对数据进行差分操作来消除季节性变化，从而得到平稳的数据。

而季节指数法则是通过计算季节指数来进行季节性调整的方法。

对时间序列数据的随机性进行分析最后，我们还需要对时间序列数据的随机性进行分析。

随机性分析可以帮助我们了解数据的不规律波动，从而进行随机性调整。

常用的随机性分析方法包括自相关性分析、白噪声检验和残差分析。

自相关性分析是一种通过计算数据的自相关系数来判断数据之间的相关关系的方法。

白噪声检验则是一种通过检验数据的残差序列是否符合白噪声过程来进行随机性分析的方法。

第10章时间序列预测从时间序列图可以看出，国家财政用于农业的支出额大体上呈指数上升趋势。

（2）年平均增长率为：。

（3）。

下表是1981年—2000年我国油彩油菜籽单位面积产量数据（单位：kg / hm2）年份单位面积产量年份单位面积产量1981 1451 1991 12151982 1372 1992 12811983 1168 1993 13091984 1232 1994 12961985 1245 1995 14161986 1200 1996 13671987 1260 1997 14791988 1020 1998 12721989 1095 1999 14691990 1260 2000 1519（1）绘制时间序列图描述其形态。

（2）用5期移动平均法预测2001年的单位面积产量。

（3）采用指数平滑法，分别用平滑系数a=和a=预测2001年的单位面积产量，分析预测误差，说明用哪一个平滑系数预测更合适？详细答案：（1）时间序列图如下：（2）2001年的预测值为：|（3）由Excel输出的指数平滑预测值如下表：年份单位面积产量指数平滑预测a= 误差平方指数平滑预测a=误差平方a=时的预测值为：比较误差平方可知，a=更合适。

下面是一家旅馆过去18个月的营业额数据月份营业额（万元）月份营业额（万元）1 295 10 4732 283 11 4703 322 12 4814 355 13 4495 286 14 5446 379 15 6017 381 16 5878 431 17 6449 424 18 660（1）用3期移动平均法预测第19个月的营业额。

（2）采用指数平滑法，分别用平滑系数a=、a=和a=预测各月的营业额，分析预测误差，说明用哪一个平滑系数预测更合适？（3）建立一个趋势方程预测各月的营业额，计算出估计标准误差。

详细答案：（1）第19个月的3期移动平均预测值为：（2）月份营业额预测a=误差平方预测a=误差平方预测a=误差平方1 2952 2833 3224 3555 2866 3797 3818 4319 42410 47311 47012 48113 44914 54415 60116 58717 64418 660合计————50236由Excel输出的指数平滑预测值如下表：a=时的预测值：，误差均方＝。

第九章时间序列数据的基本回归分析时间序列数据是指按照时间顺序排列的一系列数据观测值。

在实际应用中，时间序列数据广泛存在于经济学、金融学、气象学等领域，对于了解数据的趋势、季节性等特征具有重要意义。

时间序列数据的基本回归分析是通过建立回归模型，来研究时间序列数据中因变量与自变量之间的关系。

时间序列数据的回归分析可以分为简单回归和多元回归。

其中，简单回归是指只含有一个自变量的回归模型，多元回归是指含有多个自变量的回归模型。

下面将分别介绍这两种回归模型及其应用。

简单回归模型简单回归模型是时间序列数据回归分析中最基础的模型，其形式为：Y_t=α+βX_t+ε_t其中，Y_t表示时间为t时的因变量观测值，X_t表示时间为t时的自变量观测值，α和β分别是回归方程的截距项和斜率项，ε_t是误差项。

简单回归模型常用于分析两个变量之间的关系，并通过计算斜率项β的值来判断两个变量之间的线性相关程度。

如果β的值为正，则表示两个变量之间呈正相关关系；如果β为负，则表示两个变量之间呈负相关关系。

同时，可以通过计算误差项ε_t的方差来评估模型的拟合优度。

多元回归模型当考虑到多个自变量对因变量的影响时，可以使用多元回归模型。

其形式为：Y_t=α+β_1X_1,t+β_2X_2,t+...+β_kX_k,t+ε_t其中，Y_t表示时间为t时的因变量观测值，X_1,t,X_2,t,...,X_k,t表示时间为t时的自变量观测值，α和β_1,β_2,...,β_k分别是回归方程的截距项和各自变量的斜率项，ε_t是误差项。

多元回归模型相较于简单回归模型更能够适用于分析多个自变量与因变量之间的复杂关系。

在建模过程中，可以通过检验回归系数的显著性水平，来判断自变量对因变量的影响是否显著。

此外，还可以通过判断方程残差的波动性来评估模型的拟合优度。

时间序列数据的回归分析在实际应用中具有重要意义。

例如，经济学中常使用时间序列数据回归分析来研究GDP与通货膨胀率之间的关系；金融学中，可以利用时间序列数据回归分析来研究股票收益率与市场因素之间的关系。

时间序列数据差分GMM模型回归引言时间序列数据是在金融、经济学、气象学等领域中广泛应用的一种数据类型。

时间序列的特点是包含了时间顺序的信息，因此在分析和预测时常常需要考虑时间的影响。

时间序列数据的分析方法有很多种，其中一种常用的方法是差分GMM模型回归。

本文将深入探讨时间序列数据差分GMM模型回归的原理、应用和优势。

什么是时间序列数据差分GMM模型回归？时间序列数据差分GMM模型回归是一种利用差分和广义矩估计方法来建立模型并进行回归分析的方法。

差分是将时间序列数据转化为平稳序列的一种常用方法，平稳序列的特点是均值和方差不随时间变化。

广义矩估计方法（GMM）是一种通过选择适当的权重矩阵来估计参数的方法，可以解决估计过程中的异方差和内生性问题。

差分GMM模型回归可以用于分析和预测时间序列数据的关联性以及变量之间的影响关系。

它可以应用于金融数据中的股票价格预测、经济数据中的经济增长预测等问题。

通过对差分后的时间序列数据进行拟合和回归分析，可以得到关于时间序列数据的有用信息，从而做出准确的预测和决策。

差分GMM模型回归的原理1.差分：差分是将非平稳时间序列数据转化为平稳序列的一种方法。

差分的步骤是将当前观测值减去前一观测值，得到的差分序列具有无趋势和平稳性质。

差分的数学表达式如下：Δx t=x t−x t−1其中，Δx t表示第t时刻的差分值，x t表示第t时刻的原始观测值，x t−1表示第t−1时刻的原始观测值。

2.广义矩估计方法（GMM）：广义矩估计方法是一种利用样本矩和理论矩之间的差异来估计参数的方法。

在GMM中，通过选择适当的权重矩阵来优化估计的效果，可以解决估计过程中的异方差和内生性问题。

GMM的数学表达式如下：θ̂GMM=argming(θ)′Wg(θ)θ其中，θ̂GMM表示通过GMM方法得到的参数估计值，θ表示待估计的参数向量，g(θ)表示由样本矩和理论矩之间差异构成的矩方程，W表示选择的权重矩阵。

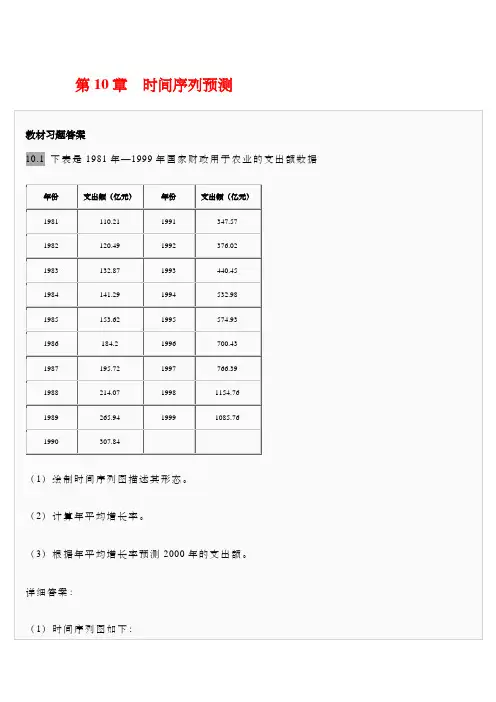
第10章时间序列预测从时间序列图可以看出，国家财政用于农业的支出额大体上呈指数上升趋势。

（2）年平均增长率为：。

（3）。

10.2 下表是1981年—2000年我国油彩油菜籽单位面积产量数据（单位：kg / hm2）年份单位面积产量年份单位面积产量1981 1451 1991 12151982 1372 1992 12811983 1168 1993 13091984 1232 1994 12961985 1245 1995 14161986 1200 1996 13671987 1260 1997 14791988 1020 1998 12721989 1095 1999 14691990 1260 2000 1519（1）绘制时间序列图描述其形态。

（2）用5期移动平均法预测2001年的单位面积产量。

（3）采用指数平滑法，分别用平滑系数a=0.3和a=0.5预测2001年的单位面积产量，分析预测误差，说明用哪一个平滑系数预测更合适？详细答案：（1）时间序列图如下：（2）2001年的预测值为：|（3）由Excel输出的指数平滑预测值如下表：2001年a=0.3时的预测值为：a=0.5时的预测值为：比较误差平方可知，a=0.5更合适。

10.3 下面是一家旅馆过去18个月的营业额数据月份营业额（万元）月份营业额（万元）1 295 10 4732 283 11 4703 322 12 4814 355 13 4495 286 14 5446 379 15 6017 381 16 5878 431 17 6449 424 18 660（1）用3期移动平均法预测第19个月的营业额。

（2）采用指数平滑法，分别用平滑系数a=0.3、a=0.4和a=0.5预测各月的营业额，分析预测误差，说明用哪一个平滑系数预测更合适？（3）建立一个趋势方程预测各月的营业额，计算出估计标准误差。

详细答案：（1）第19个月的3期移动平均预测值为：（2）月份营业额预测a=0.3误差平方预测a=0.4误差平方预测a=0.5误差平方1 2952 283 295.0 144.0 295.0 144.0 295.0 144.03 322 291.4 936.4 290.2 1011.2 289.0 1089.04 355 300.6 2961.5 302.9 2712.3 305.5 2450.35 286 316.9 955.2 323.8 1425.2 330.3 1958.16 379 307.6 5093.1 308.7 4949.0 308.1 5023.37 381 329.0 2699.4 336.8 1954.5 343.6 1401.68 431 344.6 7459.6 354.5 5856.2 362.3 4722.39 424 370.5 2857.8 385.1 1514.4 396.6 748.510 473 386.6 7468.6 400.7 5234.4 410.3 3928.711 470 412.5 3305.6 429.6 1632.9 441.7 803.112 481 429.8 2626.2 445.8 1242.3 455.8 633.513 449 445.1 15.0 459.9 117.8 468.4 376.914 544 446.3 9547.4 455.5 7830.2 458.7 7274.815 601 475.6 15724.5 490.9 12120.5 501.4 9929.416 587 513.2 5443.2 534.9 2709.8 551.2 1283.317 644 535.4 11803.7 555.8 7785.2 569.1 5611.718 660 567.9 8473.4 591.1 4752.7 606.5 2857.5合计——87514.7—62992.5—50236由Excel输出的指数平滑预测值如下表：a=0.3时的预测值：，误差均方＝87514.7。

研究生统计学教案：回归分析和时间序列分析1. 引言•统计学在现代社会中扮演着极为重要的角色，它可以帮助我们揭示数据背后的规律和趋势。

•在研究生阶段，统计学是一门必修课程，帮助学生理解统计方法的原理和应用。

2. 回归分析2.1 理论背景•回归分析是一种研究自变量与因变量之间关系的方法。

•通过建立一个数学模型来描述自变量对因变量的影响。

•最常见的回归模型是线性回归模型。

2.2 基本步骤1.数据收集：获取用于回归分析的数据集。

2.变量选择：确定自变量和因变量。

3.模型拟合：使用适当的统计软件进行回归模型拟合。

4.解释与评估：解释拟合结果并评估模型拟合程度。

2.3 应用领域1.经济学：通过回归分析来探讨经济指标之间的关系。

2.社会科学：研究人类行为和社会现象之间的相互作用。

3.医学研究：寻找风险因素或预测疾病发生概率。

4.市场营销：分析市场需求和消费者行为。

3. 时间序列分析3.1 理论背景•时间序列分析是一种统计方法，用于研究随时间变化的数据。

•它可以揭示数据的趋势、周期性和季节性。

3.2 基本步骤1.数据收集：获取包含时间变化信息的数据集。

2.数据预处理：对数据进行平滑处理，去除趋势和季节性成分。

3.模型拟合：基于历史数据建立合适的时间序列模型。

4.预测与评估：使用已有模型对未来数据进行预测，并评估模型拟合程度。

3.3 应用领域1.经济学：预测经济指标如GDP、通货膨胀率等。

2.气象学：预测天气变化和气候演变。

3.财务管理：分析股市走向和金融市场波动性。

4.销售预测：帮助企业确定销售计划和库存管理。

4. 总结•回归分析和时间序列分析是研究生统计学课程中的重要内容。

•回归分析用于研究自变量对因变量的影响关系，并解释其变异性。

•时间序列分析适用于研究随时间变化的数据，预测未来趋势和波动性。

•这两种方法在各个学科领域具有广泛的应用，帮助我们理解数据并做出合理决策。

第10章时间序列数据的基本回归分析10.1复习笔记一、时间序列数据的性质时间序列数据与横截面数据的区别：（1）时间序列数据集是按照时间顺序排列。

（2）时间序列数据与横截面数据被视为随机结果的原因不同。

①横截面数据应该被视为随机结果，因为从总体中抽取不同的样本，通常会得到自变量和因变量的不同取值。

因此，通过不同的随机样本计算出来的OLS估计值通常也有所不同，这就是OLS统计量是随机变量的原因。

②经济时间序列满足作为随机变量是因为其结果无法事先预知，因此可以被视为随机变量。

一个标有时间脚标的随机变量序列被称为一个随机过程或时间序列过程。

搜集到一个时间序列数据集时，便得到该随机过程的一个可能结果或实现。

因为不能让时间倒转重新开始这个过程，所以只能看到一个实现。

如果特定历史条件有所不同，通常会得到这个随机过程的另一种不同的实现，这正是时间序列数据被看成随机变量之结果的原因。

（3）一个时间序列过程的所有可能的实现集，便相当于横截面分析中的总体。

时间序列数据集的样本容量就是所观察变量的时期数。

二、时间序列回归模型的例子1．静态模型假使有两个变量的时间序列数据，并对y t和z t标注相同的时期。

把y和z联系起来的一个静态模型（staticmodel）为：10 1 2 t t t y z u t nββ=++=⋯，，，，“静态模型”的名称来源于正在模型化y 和z 同期关系的事实。

若认为z 在时间t 的一个变化对y 有影响，即1t t y z β∆=∆，那么可以将y 和z 设定为一个静态模型。

一个静态模型的例子是静态菲利普斯曲线。

在一个静态回归模型中也可以有几个解释变量。

2．有限分布滞后模型（1）有限分布滞后模型有限分布滞后模型（finitedistributedlagmodel，FDL）是指一个或多个变量对y 的影响有一定时滞的模型。

考察如下模型：001122t t t t ty z z z u αδδδ--=++++它是一个二阶FDL。