数学模型人在雨中奔跑速度与淋雨量的关系
- 格式:docx
- 大小:166.53 KB
- 文档页数:8

摘要本文在给定的降雨条件下,分别建立相应的数学模型,分析人体在雨 中奔跑时淋雨多少与奔跑速度、降雨方向等因素的关系.得出结论:若雨迎面落下,则以最大的速度跑完全程淋雨量最少;若雨从背后落下,则以降雨速度的水平分量时奔跑时淋雨量最少.关键词:降雨方向 速度 淋雨量一 问题的提出要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,建立数学模型讨论人是否跑得越快,淋雨量越少.讨论:(1)若不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量;(2)雨从迎面吹来,雨线与跑步方向在同一平面内时速度多大,总淋雨量最小; (3)雨从背面吹来,雨线方向与跑步方向在同一平面内时速度v 多大,总淋雨量最少;(4)若雨线方向与跑步方向不在同一平面内,模型会有什么变化.二 模型假设及符号说明2.1 把人体视为长方体,身高m a 5.1=(颈部以下),宽度 m b 5.0=,厚度 m c 2.0=.淋雨总量用CL 来记;2.2 降雨大小用降雨强度 h wcm /来描述,降雨强度指单位时间平面上的降下水的厚度;风速保持不变:2.3 距离为 m d 1000=,跑步的最大速度为s m v m /5=. 雨速s m u /4=.记跑步速度为v .2.4 文中所涉及到的降雨量是指从天空降落到地面上的雨水,未经蒸发、渗透、流失而在水面上积聚的水层深度,它可以直观地表示降雨的多少.淋雨量是指人在雨中行走时全身所接收到得雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积.三 模型建立3.1模型一的建立:若不考虑雨的方向,设降雨淋遍全身,即此时人的前后左右和上方都将淋雨,以最大速度跑步淋雨的面积bc ac ab S ++=22 (1)雨中奔跑的时间mv d t = (2) 总淋雨量t S w C ⨯⨯⨯=-2103600(3) (3)式是理想速度奔跑模型.3.2模型二的建立:若考虑降雨方向,雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ,淋湿的部位只有前面和顶部,分两部分计算淋雨量.若记雨滴的密度为p (1)p ≤,表示在一定的时间在单位体积的空间内,有雨滴所占的空间的比例系数.即up w =图1顶部的淋雨量:θcos 1vbcdw C = (4) 前表面的淋雨量:)]sin ([2v u p vdab C +=θ (5) 总淋雨量: ])sin (cos [21u v u ab bc v dw C C C ++=+=θθ (6) (6)式即为模型二3.3模型三的建立若雨从背面吹来,雨线方向与跑步方向在同一平面内,且与人体的夹角为α. 如图2建立总淋雨量与速度v 及参数θ,,,,,,w u d c b a 之间的关系图2雨速水平分量αsin u ,方向与v 相同,合速度为: v u -αsin ,则总淋雨量:()()()()⎪⎪⎩⎪⎪⎨⎧>+-=-+≤-+=-+=αααωααωαααωααωsin ,sin cos sin cos sin ,sin cos sin cos u v vav a c u u bd v u v a cu u bd u v v av a c u u bd v v u a cu u bd C (7) 即为模型三.四 模型求解4.1模型一的求解:将数据代入模型中,解得:22.2m S =L t 200=L C 444.2=4.2模型二的求解:将数据代入模型中,解得:0=θ时,L C 153.1=030=θ时,L C 555.1=4.3模型三的求解:由(7)可知:若0sin cos <-ααa c 即ac >αtan ,则αsin u v =时C 最小 将数据代入模型中,解得:L C s m v 242.0,2,5.12.0tan ,300≈=>=αα五 模型分析与总结5.1模型一的分析: 由理想奔跑速度模型知,淋雨量与速度成反比. 即跑得越快淋雨量越少. 但分析结果可知:人在雨中跑了s t 200=即3分20秒,身上却淋了2.444升的雨水,相当于5瓶可乐的水量,这是不可思议的!因此这个模型描述雨中奔跑的淋雨量不符合实际,因为没考虑雨速的大小和方向.使问题过于简化.5.2模型二的分析:雨速大小和方向不变,雨速与人的夹角090=θ,则以最大速度奔跑时淋雨量最少.5.3模型三的分析:若,0sin cos <-ααa c 即a c >αtan ,则a c >αtan 时C 最小.总结:根据以上模型得知我们在雨中奔跑时并非跑得越快,淋雨量最少,淋雨量的多少还取决于雨速大小和方向.六 模型的改进方向在以上的假设中,雨线方向与跑步方向是在同一平面内,若雨线方向与跑步方向不在同一平面内,则可将雨速方向分解为与人跑速度同向的速度和与人跑速度方向垂直的速度. 同向速度即平面共面,可看成模型II 的情况,垂直速度可看成模型一情况.在以上的假设中,人以沿直线奔跑,若人以沿折线奔跑,则可将折线分段考虑,同样可分解成模型一或模型二.在以上的假设中,人看成长方体,若人看成是圆柱体,情况又发生改变,而实际问题中的限制性因素远远超过这些,因此此文的分析方法仍存在一定的局限性,有待改进和提高.参考文献[1] 姜启源,谢金星,叶俊. 数学模型(第四版)[M].北京:高等教育出版社,2011:58-67.。
下雨天跑得快和跑得慢淋的雨物理题
这个问题不但是一道物理问题,还是一道经典的数学建模问题,可以通过建立数学模型来对此进行求解。
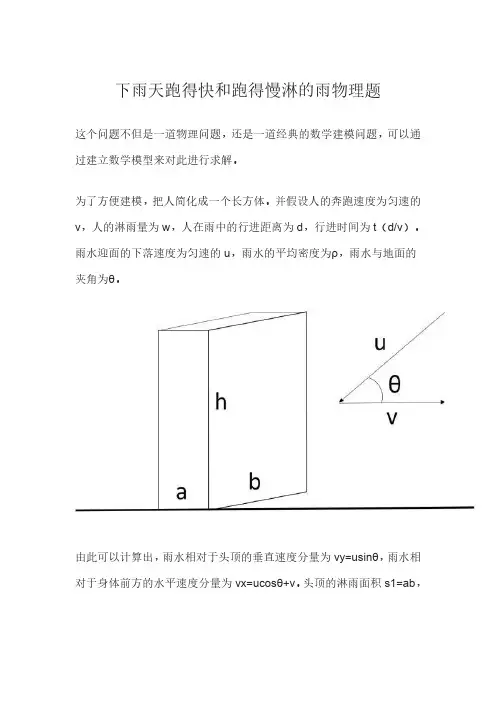
为了方便建模,把人简化成一个长方体。
并假设人的奔跑速度为匀速的v,人的淋雨量为w,人在雨中的行进距离为d,行进时间为t(d/v)。
雨水迎面的下落速度为匀速的u,雨水的平均密度为ρ,雨水与地面的夹角为θ。
由此可以计算出,雨水相对于头顶的垂直速度分量为vy=usinθ,雨水相对于身体前方的水平速度分量为vx=ucosθ+v。
头顶的淋雨面积s1=ab,
身体的淋雨面积s2=bh。
因此,人的总淋雨量就是头顶淋雨量和身体前方淋雨量之和。
头顶的淋雨量为:
身体前方的淋雨量为:
总的淋雨量为:
显然,w/v<0,这意味着随着速度v的增加,淋雨量w在逐渐减小。
并且如果人的身体与雨水平行,理论上只有头部会受到淋雨。
因此,在最为理想的情况下,对于没有带伞的人来说,在雨中奔跑的速度越快,并且身体的倾斜方向刚好跟雨水平行,那么,这个人所淋到的雨水是最少的。
为了便于计算,模型做了很多简化,最终得出的结论也是符合实际的。
关于在雨中是应该跑的慢还是跑的快,可以考虑两种极端的情况。
一种是在雨中以接近于零的速度运动,还有一种是在雨中以接近光速的速度运动。
显然,运动相同的距离,在雨中运动的时间越短,所淋到的雨水也会越少。

淋雨量与跑步速度关系探究摘要本文就“淋雨量与跑步速度关系”的问题建立了数学模型,从实际情况出发对不同条件下速度和淋雨量关系做出分析探究。
针对问题一:因为已经假设雨淋遍全身,且不考虑雨的方向,当人以最大速度跑步时,可由题中的已知条件,直接列方程求解。
针对问题二:利用最优化原理,以雨从迎面吹来时的“淋雨量—速度”图像为指标,利用了几何中的面积公式及物理中速度的分解等知识,建立出一个动态规划模型,结合题目中的已知条件,列出方程求解。
针对问题三:解决方法和问题二相同,通过绘制出雨从背面吹来时的“淋雨量—速度”图像,方便快速直观地得到两者关系。
利用了第二问已知的几何中的面积公式及物理中速度的分解等知识,列出方程求解即可得到相应结论。
针对问题四:结合问题三的结论,做出相应的图像,即可清楚地得出总降雨量最小的点。
针对问题五:将简单的平面问题升华为空间问题,但处理方法和问题二基本相同,只是增加了空间角,本质没有区别。
关键词:总淋雨量aMathematic1.问题分析本文讨论的是跑步快慢与淋雨量的关系。
总的淋雨量即为人体的各个面上的淋雨量之和。
每个面上的淋雨量等于单位面积,单位时间的淋雨量与面积以及时间的乘积。
面积由已知各边长乘积得出,时间为总路程与人前行速度的比值。
再由速度分解,合成,相对速度等知识确定各面淋雨量公式,列出总的方程,根据各变量关系,得出最优解。
当雨线方向和跑步方向不在同一平面时,我们设出雨线方向角,按照上述方法将其分解,同样可以解决问题。
2.问题的重述要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,说明是否跑得越快,淋雨量越少。
将人体简化成一个长方体,解释不考虑雨的方向,雨从迎面吹来,雨从背面吹来,雨线方向与跑步方向不在同一平面内的总淋雨量时的模型变化,已知总的淋雨量等于人体的各个面上的淋雨量之和。
每个面上的淋雨量等于单位面积,单位时间的淋雨量与面积以及时间的乘积。
面积由已知各边长乘积得出,时间为总路程与人前行速度的比值,再由速度分解,合成,相对速度等知识确定各面淋雨量公式,列出总的方程即可求解。

淋雨问题数学建模一、题目:淋雨问题要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变。
试建立数学模型讨论是否跑得越快,淋雨量越少。
二、问题假设(合理的假设)1 将人体看成一个长方体;2 雨速为常数且方向不变;3 降雨量为一定值;4 考虑雨的方向与人体前进的方向在同一平面内;三、符号的假定:身高(颈部以下):a=1.5米身宽:b=0.5 身厚: c=0.2米跑步距离:d=1000米跑步速度:v 跑步最大速度:=5v m sm雨速:u=4m s降雨量:w=4cm h总淋雨量:Q雨迎面吹来与人的夹角:θ雨背面吹来与人的夹角:α雨侧面吹来与人的夹角:γ有效淋雨面积:s 以人为参考系时的相对雨速:v四、问题分析:(1)不考虑雨的方向,设降雨淋遍全身,以最大的速度跑步,估计跑完全程的总淋雨量。
分析:雨垂直下落,人以速度v前行,此时降雨淋遍全身(如图1所示)(图1)(2)雨迎面吹来,雨线与跑步的方向在同意平面内,且与人体的夹角为θ。
分析:雨迎面吹来,雨线与跑步方向在同一平面内,与人的正面夹角为θ,此时后背淋不到雨(如图2所示)(图2)(3)雨从背面吹来,雨线方向与跑步方向在同一平面内,与人体的夹角为α。
分析:雨从背面吹来,雨线方向与跑步方向在同一平面内,与人背面体的夹角为α,此时正面淋不到雨(如图3所示)。
面淋不到雨(如图3所示)图 3我们知道当人在雨中前行的时候,人和雨相对地面都是运动的,故知人与雨是相对运动的。
为此我们选择人作为参考系,再考虑雨的相对速度及其与人体方向(即与人体夹角θ、α)对总淋雨量的影响。
(4)雨线的方向与跑步方向不在同一平面内。
分析:雨线的方向与跑步方向不在同一平面内时,与人侧面的夹角为γ,人体只有顶部与一个侧面淋到雨(如图4所示)(图4) 五、模型的建立先考虑现有一块土地面积为s ,雨垂直降落,雨速及方向不变,且降雨量为一常数w ,则有时间t 内该土地的淋雨量为 Q stw =。

淋雨量模型一、问题概述要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少。
将人体简化成一个长方体,高a=(颈部以下),宽b=,厚c=,设跑步的距离d=1000m,跑步的最大速度v m=5m/s,雨速u=4m/s,降雨量ω=2cm/h,及跑步速度为v,按以下步骤进行讨论[17]:(1)、不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量;(2)、雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ,如图1.建立总淋雨量与速度v及参数a,b,c,d,u,ω,θ之间的关系,问速度v多大,总淋雨里最少。
计算θ=0,θ=30°的总淋雨量.(3)、雨从背面吹来,雨线方向跑步方向在同一平面内,且与人体的夹角为α,如图2.建立总淋雨量与速度v及参数a,b,c,d,u,ω,α之间的关系,问速度v多大,总淋雨量最小。
计算α=30°的总淋雨量.(说明:题目中所涉及的图形为网上提供)(4)、以总淋雨量为纵轴,速度v为横轴,对(3)作图(考虑α的影响),并解释结果的实际意义.(5)、若雨线方向跑步方向不在同一平面内,试建立模型二、问题分析淋雨量是指人在雨中行走时全身所接收到得雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积。
可得:淋雨量(V)=降雨量(ω)×人体淋雨面积(S)×淋浴时间(t)①时间(t)=跑步距离(d)÷人跑步速度(v)②由①②得:淋雨量(V)=ω×S×d/v三、模型假设四、(1)、将人体简化成一个长方体,高a=(颈部以下),宽b=,厚c=.设跑步距离d=1000m,跑步最大速度v m=5m/s,雨速u=4m/s,降雨量ω=2cm/h,记跑步速度为v;(参考)(2)、假设降雨量到一定时间时,应为定值;(3)、此人在雨中跑步应为直线跑步;(4)、问题中涉及的降雨量应指天空降落到地面的雨,而不是人工,或者流失的水量,因为它可以直观的表示降雨量的多少;五、模型求解:(一)、模型Ⅰ建立及求解:设不考虑雨的方向,降雨淋遍全身,则淋雨面积:S=2ab+2ac+bc雨中奔跑所用时间为:t=d/v总降雨量V=ω×S×d/vω=2cm/h=2×10-2/3600 (m/s) 将相关数据代入模型中,可解得:S=(㎡)V= (cm3)= (L)(二)、模型Ⅱ建立及求解:若雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ.,则淋雨量只有两部分:顶部淋雨量和前部淋雨量. (如图1)设雨从迎面吹来时与人体夹角为θ. ,且 0°<θ<90°,建立a ,b ,c ,d ,u ,ω,θ之间的关系为:(1)、考虑前部淋雨量:(由图可知)雨速的水平分量为θsin u ⋅且方向与v 相反,故人相对于雨的水平速度为:()v sin u +⋅θ则前部单位时间单位面积淋雨量为:u /v sin u )(+⋅⋅θω又因为前部的淋雨面积为:b a ⋅,时间为: d/v于是前部淋雨量V 2为 :()()[]()v /d u /v sin u V 2⋅+⋅⋅⋅⋅=θωb a即:()()v u /v sin u a V 2⋅+⋅⋅⋅⋅=θωd b ①(2)、考虑顶部淋雨量:(由图可知)雨速在垂直方向只有向下的分量, 且与v 无关,所以顶部单位时间单位面积淋雨量为()θωcos ⋅,顶部面积为()c b ⋅ ,淋雨时间为()v /d ,于是顶部淋雨量为:v /cos b V 1θω⋅⋅⋅⋅=d c ②由①②可算得总淋雨量 :()()v u /v sin u a v /cos c b V V V 21⋅+⋅⋅⋅⋅⋅+⋅⋅⋅⋅=+=θωθωd b d代入数据求得:v 1800v 875.1sin 5.7cos V ⋅++=θθ 由V (v)函数可知:总淋雨量(V )与人跑步的速度(v )以及雨线与人的夹角(θ)两者有关。


淋雨量模型
每当下雨而人们又忘记带雨伞不得以要淋雨时,大家脑海中总会思考起这样一个问题:淋雨时走得越快淋雨少,还是走得越慢淋雨少呢?
有人认为走得快淋雨少,因为走得快用时少,从正上方降落到头上的雨滴就少;也有人认为走得慢淋雨少,因为走得快人正前方淋到的雨就多,而且正前方的淋雨面积肯定比正上方的大。
那么在固定行程时到底怎样才能淋雨最少呢?现在我们建立一个数学模型来研究一下这个问题。
设出参数:
人的前进速度:V人
雨滴下落的速度:V雨(2-9m/s)
风的速度:V风(矢量,迎风则合速度为相加,顺风为相减)
人的前进方向与风向的夹角:α
将人体设定为一个长方体:
厚度为a,宽度为b,高为h(0<a<b<h<2.5m)
人的行走距离:s
单位体积包含的雨量为n(kg/m³)(当地气象预报平均降雨量为k(mm/h),则n=k/v雨/3600)
单位均为国际单位
则淋雨量M分为三面:正面,侧面,顶面
M正=nbh*(V人+V风*cosα)*s/V人
M侧=nah*V风sinα*s/V人
M顶=nab*V雨*s/V人
总淋雨量M=ns*bh+ns*(bh*V风*cosα+ah*V风sinα+ab*V 雨)/V人
从公式可以看出总的淋雨量去除常数项部分后,和人的前进速度
成反比例关系;逆风时的速度为加,逆风的淋雨量要比顺风的淋雨量大。
当风速为0时,公式变为:
M=ns*(bh+ab*V雨/V人)
则淋雨量只和人的速度及降雨速度相关。
带入一些数据我们可以算一下平时都淋了多少雨。

目录摘要 (3)问题提出 (3)模型假设 (4)符号说明 (4)模型建立 (5)模型求解 (6)结果分析 (8)参考文献 (9)摘要本模型建立了在雨中奔跑时淋雨最少与奔跑速度,雨量,降雨方向,路程远近的关系,从而得出在雨中如何奔跑才会淋雨最少的方法。
关键词:淋雨量,降雨的大小,降雨的方向,路程的远近,奔跑的速度一、问题提出要在雨中从沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少。
将人体简化成一个长方体,高a=1.50米(颈部以下),宽b=0.5米,厚c=0.2m。
v=5m/s,雨速u=4m/s,降雨量w=2cm/h,记设跑步距离d=1000m,跑步最大速度m跑步速度为v,按一下步骤进行讨论[17](1)不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,,估计跑完全程的总林雨量。
(2)雨从迎面吹来,雨线跑步方向在同一平面以内,且与人体的夹角为θ,如图一,建立总淋雨量与速度v及参数a,b,c,d,u,w,θ,之间的关系,问速度v多大,总淋雨量最少,计算θ=0,θ=30时总淋雨量。
(3)雨从背面吹来,雨线方向与跑步方向在同一平面内,且与人体的夹角为α,如图2.建立总淋雨量与速度v及参数a,b,c,d,u,w,α之间的关系,问速度v为多大时,总淋雨量最小。
(4)以总林雨量为纵轴,速度v为横轴,对(3)作图(考虑α的影响),并解释结果的实际意义。
(5)若雨线方向与跑步方向不在同一平面内,模型会有什么变化。
二、模型假设(1)、假设人体为一个长方体;(2)、假设雨速为一个常数,且方向保持不变;(3)、假设人跑步的速度为匀速;(4)、假设产生的影响各个因素相互独立。
三、符号的说明D :人在雨中行走的距离(m )图1 图2t :人在雨中行走的时间(s )v :人在雨中行走的速度(m/s )c b a ,,:人的高度,宽度和厚度(m )w :降雨量(降雨强度,单位时间平面上的降下雨水的厚度,m/s )C :淋雨的总量(L )S:淋雨面积(2m )u :雨滴落下的速度(m/s)p :雨滴的密度(1,1=≤p p 时意味着大雨倾盆)θ:降雨的角度(雨滴落下的方向与行走的方向之间的夹角)四、模型建立问题一:不考虑降雨的角度影响:模型一:当不考虑降雨角度时,假设淋雨的部位时全身所有部位,因此淋雨的面积为)(2ac ab bc S ++=。

人在雨中奔跑的速度与淋雨量的关系摘要:本文通过分析人在雨中奔跑的速度与淋雨量之间存在的关联,针对不同的降雨方向,将人简化为长方体模型,建立了奔跑速度与总淋雨量的优化模型。
针对问题一,假设雨水淋遍全身且不考虑雨的方向,通过简单的模型分析得到跑完全程的总淋雨量。
针对问题二,考虑雨从迎面打来,雨线方向与奔跑方向在同一铅直平面,通过分析淋雨部位、竖直方向雨速和水平方向雨相对于人的速度,建立了总淋雨量的模型,又对模型进行了函数的单调性分析,得知总淋雨量最少时奔跑速度最大。
针对问题三,考虑雨从后面打来,雨线方向与奔跑方向在同一铅直平面,通过分析淋雨部位、竖直方向速度和水平方向上的相对速度,针对不同情况,建立了总淋雨量的模型,又对模型进行了函数单调性的分析讨论,得出了总淋雨量最少时的奔跑速度。
针对问题五,针对雨线方向与跑步方向不在同一平面内的情况,对雨速进行空间直角坐标分解,结合问题三,分析模型发生的变化。
关键词:跑步速度;总淋雨量;相对速度;单调性分析;矢量分解一、问题重述对于行人来说,下雨天最糟糕的情况莫过于出门在外雨伞没带。
在这种情况下,人们习惯用快跑来摆脱困境。
归根结底,“跑得越快淋雨就越少”的观点只是一种感性认识。
因此,考虑通过建模来科学分析两者之间的关系。
对于下列四个问题,分别给出奔跑速度与淋雨量之间的定性分析。
问题1:在不考虑雨线方向的情况下,计算以最大速度跑完全程的淋雨量。
问题2:考虑雨从迎面打来,且与跑步方向在同一铅直面上,雨线与人体的夹角为α。
建立总淋雨量与奔跑速度的模型,进而求总淋雨量最少时的速度。
问题3:考虑雨从背面打来,且与跑步方向在同一铅直面上,雨线与人体的夹角为β。
建立总淋雨量与奔跑速度的模型,进而求总淋雨量最少时的速度。
问题5:考虑雨线方向与跑步不在同一铅直面上时,模型的变化。
二、问题分析问题1,将人简化为长方体模型,不考虑雨的方向,设降雨淋遍全身,分析人的淋雨面积共五个面分别为前面、背部、顶部、左侧面和右侧面。

论文题目:淋雨量与人在雨中奔跑速度的关系目录一.摘要 ................................................................................二.问题的重述....................................................................三.问题分析 .........................................................................四.建模假设 .........................................................................五.模型的建立......................................................................六.模型的评价......................................................................七.参考文献 .........................................................................一.摘要本模型是研究人的淋雨量与人在雨中奔跑的速度的关系。
由于人在雨中行走的过程比较复杂,我们只能将人体简化为一个长方体建立模型,进行讨论。
本题中采用了优化模型,通过将人分为几个平面,分别求得各个平面所接受的淋雨量,然后求其加和的方法求解。
在问题一中,因为已经假设降雨淋遍全身,且人以最大的速度跑步。
所以根据已知条件,直接列出方程进行求解。
在问题二中,我们利用最优化原理,建立出一个动态规划模型。
雨迎面吹来,雨线方向与跑步方向在同一平面,人淋雨面积为前方和头顶面积之和。

淋雨量模型一、问题概述要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少。
将人体简化成一个长方体,高a=1.5m(颈部以下),宽b=0.5m,厚c=0.2m,设跑步的距离d=1000m,跑步的最大速度v=5m/s,雨速u=4m/s,降雨量ωm:=2cm/h,及跑步速度为v,按以下步骤进行讨论[17](1)、不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量;(2)、雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ,如图1.建立总淋雨量与速度v及参数a,b,c,d,u,ω,θ之间的关系,问速度v多大,总淋雨里最少。
计算θ=0,θ=30°的总淋雨量.(3)、雨从背面吹来,雨线方向跑步方向在同一平面内,且与人体的夹角为α,如图2.建立总淋雨量与速度v及参数a,b,c,d,u,ω,α之间的关系,问速度v多大,总淋雨量最小。
计算α=30°的总淋雨量.(说明:题目中所涉及的图形为网上提供)(4)、以总淋雨量为纵轴,速度v为横轴,对(3)作图(考虑α的影响),并解释结果的实际意义.(5)、若雨线方向跑步方向不在同一平面内,试建立模型二、问题分析淋雨量是指人在雨中行走时全身所接收到得雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积。
可得:淋雨量(V)=降雨量(ω)×人体淋雨面积(S)×淋浴时间(t)①时间(t)=跑步距离(d)÷人跑步速度(v)②由①②得:淋雨量(V)=ω×S×d/v三、模型假设(1)、将人体简化成一个长方体,高a=1.5m(颈部以下),宽b=0.5m,厚c=0.2m.=5m/s,雨速u=4m/s,降雨量ω=2cm/h,设跑步距离d=1000m,跑步最大速度vm记跑步速度为v;(参考)(2)、假设降雨量到一定时间时,应为定值;(3)、此人在雨中跑步应为直线跑步;(4)、问题中涉及的降雨量应指天空降落到地面的雨,而不是人工,或者流失的水量,因为它可以直观的表示降雨量的多少;四、模型求解:(一)、模型Ⅰ建立及求解:设不考虑雨的方向,降雨淋遍全身,则淋雨面积:S=2ab+2ac+bc雨中奔跑所用时间为:t=d/v总降雨量V=ω×S×d/vω=2cm/h=2×10-2/3600 (m/s) 将相关数据代入模型中,可解得:S=2.2(㎡)V=0.00244446 (cm³)=2.44446 (L)(二)、模型Ⅱ建立及求解:若雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ.,则淋雨量只有两部分:顶部淋雨量和前部淋雨量. (如图1)设雨从迎面吹来时与人体夹角为θ.,且0°<θ<90°,建立a,b,c,d,u,ω,θ之间的关系为:(1)、考虑前部淋雨量:(由图可知)雨速的水平分量为θu⋅且方向与v相反,sin故人相对于雨的水平速度为:()v⋅θsinu+则前部单位时间单位面积淋雨量为:u /v sin u )(+⋅⋅θω又因为前部的淋雨面积为:b a ⋅,时间为: d/v于是前部淋雨量V 2为 :()()[]()v /d u /v sin u V 2⋅+⋅⋅⋅⋅=θωb a即:()()v u /v s i n u a V 2⋅+⋅⋅⋅⋅=θωd b ①(2)、考虑顶部淋雨量:(由图可知)雨速在垂直方向只有向下的分量, 且与v 无关,所以顶部单位时间单位面积淋雨量为()θωcos ⋅,顶部面积为()c b ⋅ ,淋雨时间为()v /d ,于是顶部淋雨量为:v /c o s b V 1θω⋅⋅⋅⋅=d c ②由①②可算得总淋雨量 :()()v u /v sin u a v /cos c b V V V 21⋅+⋅⋅⋅⋅⋅+⋅⋅⋅⋅=+=θωθωd b d代入数据求得:v1800v875.1sin 5.7cos V ⋅++=θθ由V (v)函数可知:总淋雨量(V )与人跑步的速度(v )以及雨线与人的夹角(θ)两者有关。
数学建模淋雨量与跑步速度
情景重现
下雨天忘了带雨伞,要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑的越快,淋雨越少,将人体简化为长方体,高a=1.5米(颈部以下),宽b=0.5米,厚c=0.2米,设跑步距离d=100米,跑步最大速度=5米/秒,雨速u=4米/秒,降雨量w=2cm/h,记跑步速度为)
基本假设
(1)风速始终保持不变
(2)降雨速度和降雨强度保持不变
(3)跑完全程的速度始终不变
符号的约定
a人的身高(颈部以下)(已知)
b人的宽度(已知)
c人的厚度(已知)
d全程距离(知)
Vm跑步最大速度(已知)
u雨速(已知)
w降雨量(已知)
v人跑步的速度(未知)
C身上被淋的雨水总量(升)(未知)
I降水强度(单位时间平面上降下雨水的厚度)(厘米/时)
模型的建立
结论
通过对以上模型的分析我们可以知道,在雨中行走时要使身上淋的雨水最少,除了要考虑降雨角度外,还好考虑降雨速度,即是根据降雨角度和降雨速度来选择自己在雨中的行走速度,具体做法如下:
(1)如果雨是迎着前进的方向落下,应该以最大的速度跑完全程..
(2)如果雨是从背后落下,这时应该控制在雨中的速度,让它刚好等于落雨速度的水平分量.。
雨中行走模型摘要:在实际的日常生活中,人在雨中移动,根据不同的雨速及风向等因素求出相应的移动速度,用数学分析的方法建立数学模型,使人在一定的移动距离下淋雨量最小。
关键词:人速雨速风向面积体积淋雨量1 问题的复述在雨中沿直线从一处跑到另一处,雨速为常数且方向不变,讨论人跑的速度与淋雨量的关系。
将人体简化成一个长方体,高a=1.5m(颈部以下),宽b=0.5m,厚,雨速u=4m/s,降雨量c=0.2m。
设跑步距离d=1000m,跑步最大速度=5m/sw=2cm/h,记跑步速度为v。
主要因素:淋雨量,降雨的大小,降雨的方向(风),路程的远近,行走的速度2问题的分析考虑到人(或物体)在雨中A地走到B地,其距离为L,为方便起见我们认为在雨中行走的这一段时间雨速不变的情况下,并且无其他因素的限制与影响下的移动,在此前提下建立数学模型找出最优的速度,才能使淋雨量最小。
3合理的假设3.1雨速在相当长的一段时间里是不变的,其中包括矢量速度的大小和方向3.2人(或物体)可以理想化为一个长方体。
3.3在一定的时间里降雨量是不变的,即为一个常值3.4可以建立空间直角坐标系使人的行走速度只在x方向有分量4符号的说明L :人从A地走到B地的距离V:雨的速度V X,V Y V Z :V在空间直角坐标系中x,y,z方向上的速度的分量t:时间变量v:人(或物体)的移动速度R(u)单位时间里的淋雨量K:比例系数5模型的建立人(或物体)的表面比较复杂,为简化模型我们设前侧,顶的面积之比为a:b:c,使在空间直角坐标系中人行走的v={u,0,0},V={V X,V Y,V Z},由此可以知道在雨中行走的时间为t=L/u。
在上述的假设下,我们容易有数学分析中的曲面积分的通量的概念和空间向量之间的关系知单位时间里的淋雨量是与(|u-V X|,|0-V Y|,|0-V Z|).(a,b,c)=a|u-V X|+b|0-V Y|+c|0-V Z|成正比的。
数学模型论文学校:班级:姓名:学号:雨中行走问题摘要当我们在雨中冒雨行走时总会下意思的加快速度,似乎跑得越快淋雨量就会越小。
但事实上会是这种情况吗?在这里,我们将给予综合性的考虑,来解释不同情况下的淋雨量。
在不考虑风向的情况下,若人的全身都受到雨淋,理所当然人跑的越快所淋的雨就会越少。
那么模型也可算出淋雨量。
当雨线从正面和人的跑步方向在同一平面时,并且考虑风向的影响,雨线方向和竖直方向成θ角。
因为迎着雨的方向跑,所以全身都会淋到雨,由于有夹角,可以将雨分成竖直方向和水平方向两部分。
便可根据题的要求解出模型。
当雨线从后面和人的跑步方向在同一平面时,并且考虑风向的影响,雨线方向和竖直方向成α角。
因为背着雨的方向跑,所以全身不一定都会淋到雨。
可分几种情况分别来说。
关键词人速;雨速;风向;夹角1.问题的重述当人们在雨中行走时,是不是走的越快就会淋越少的雨呢?对于这个问题,建立合理的数学模型。
讨论一下,在不考虑风向时,人的淋雨量为多少;进而进一步讨论一下,在考虑雨线方向与人的跑步方向在同一平面内成不同角度时的淋雨量。
2.问题的分析当人在雨中行走时,是否跑的越快所淋的雨量就越少那,答案当然不是。
人在雨中所淋到的雨量和风向有关,因为风向的不同会导致雨线和人成不同的角度。
从而使人所淋到的雨量有所不同。
3.模型的假设与符号说明3.1模型的假设(1)把人体视为长方体,身高h米,身宽w米,身厚d米,淋雨总量C升。
(2)把降雨强度视为常量,记为:I(cm h)。
(3)风速保持不变。
v m s跑完全程D。
(4)以定速度()3.2符号说明h人体的身高(m)w 人体的宽度(m)d 人体的厚度(m)D 人跑步的全程(m)v 人跑步的速度(m/s)i 降雨强度(cm/h)c 人在跑步中的淋雨总量(L)s 人在雨中会被雨淋的面积 (㎡)t 人在雨中跑步的时间 (s)v 雨滴下落速度 (m/s)θ 雨滴反方向与人速度方向的夹角ρ 雨滴密度4.模型的建立与求解(1)不考虑雨的方向,此种情况,人的前后左右都会淋雨。
《数学模型与数学实验》摘要本文在给定的降雨条件下,分别建立相应的数学模型,分析人体在雨中行走时淋雨多少与行走速度、降雨方向等因素的关系。
其中文中所涉及到的降雨量是指从天空降落到地面上的雨水,未经蒸发、渗透、流失而在水面上积聚的水层深度,它可以直观地表示降雨的多少。
淋雨量,是指人在雨中行走时全身所接收到得雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积。
针对问题一,设降雨淋遍全身不考虑雨的方向,经简化假设得人淋雨面积为前后左右及头顶面积之和。
针对问题二,雨迎面吹来,雨线方向与行走方向在同一平面,人淋雨面积为前方和头顶面积之和。
因各个方向上降雨速度分量不同,故分别计算头顶和前方的淋雨量后相加即为总的淋雨量。
据此可列出总淋雨量W与行走速度v之间的函数关系。
分析表明当v时,淋雨量最少。
行走速度为max针对问题三,雨从背面吹来,雨线与行走方向在同一平面内,人淋雨量与人和雨相对速度有关。
列出函数关系式分析并求解。
关键词淋雨量;降雨的大小;降雨的方向(风);路程的远近;行走的速度;雨滴下落的速度,角度;降雨强度;一、问题重述生活中的我们常常会遇到下雨而没带雨具的时刻,我们在那时会有很多选择,其中之一就是淋雨,往往好多人会在雨中快走或奔跑而使自己身体淋雨量最小化,但往往很多人会感觉到淋雨量并不会因为快走或奔跑而减少多少,反而有时候淋雨量倒有所增加,淋雨量和速度等有关参数的关系如何,是否人走得越快雨淋得越少,让我们假设一数学模型模拟计算真实情况。
当我们在雨中从一处沿直线跑到另一处时,如果雨速为常数,走的时候身体的动作的大小和暴露在雨中的面积大小影响着淋雨的多少,并且行走速度也同样影响着淋雨量Q,将人体简化成一个长方体,高a=1.5米,宽b=0.5米,厚c=0.2m,行走距离D,雨速u,降雨量I,行走速度为ν。
1、当我们不考虑风,即雨滴垂直下落时,淋雨量和人行走速度之间的关系2、当雨滴从前方(斜的)下落时,即雨滴与人体的夹角为θ,建立总淋雨量与速度v及其它参数之间的关系,此时速度与淋雨量的关系3、当雨从人的背面吹来,即雨滴与人体的夹角为θ,建立总淋雨量与速度v之间的关系二、模型的假设与符号说明2.1 基本假设1、假设人行走的路线是直线;2、不考虑风的方向(即假定前后左右都淋雨),这是一种较为理想的假设,主要为了建模的方便,并且假设雨滴的速度为常数;3、为计算淋雨面积的方便,把人体表面积看成长方体,长用a表示,宽用b表示,厚度用c 表示,且abc都是定值。
人在雨中奔跑速度与淋雨量问题班级:数学(2)班 学号:1107022037 姓名:张柯摘要 在雨速和方向都不变的情形下讨论雨中行走问题,分析人体在雨中行走时淋雨多少与行走速度、降雨方向等因素的关系,建立相应的数学模型,使得被雨水淋湿的程度最低.得出不考虑雨的方向,淋雨总量(22)/Q wd ab ac bc =++v .即人走的越快淋雨量越少.因此在这种情况下应以最大速度行走.考虑风向时[cos (sin )]bpd Q uc a u v vθθ=++.当夹角θ一定,淋雨量Q 随着v 的变大而变小,即人走的越快淋雨量越少. 关键词 淋雨量,数学模型,最优淋雨量正文1 问题的提出1.1 不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的淋雨量.1.2 雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体夹角为θ,跑步速度v 为多大时淋雨量最小.2 合理假设2.1 假设人在雨中沿直线的方向奔跑且匀速.2.2 假设雨的速度为常数、雨的方向及降雨量即降雨强度不变.2.3 假设风速和风向保持不变.2.4 假设不考虑人表面不平整和衣服的原因对雨水的吸收量,将人 体简化为一长方体.2.5 假设雨线方向与人跑步方向在同一平面内.2.6 变量的限定表一变量表3 模型的构建3.1 不考虑雨方向淋雨总量模型图 1 雨水与人关系模型图不考虑雨的方向,如图1人以最大的速度奔跑,雨淋遍全身.前后面及两侧面与上面受淋雨面积分别为2ab,2ac,bc.淋雨的总面积22=,在雨中历经的时间w cm hS ab ac bc=++,降雨量2/t=/d v,淋雨总量为=Q Swt故=++v(1)(22)/Q wd ab ac bc3.2 考虑风向淋雨总量模型雨迎面吹来,雨线方向与行走方向在同一平面内且与人体夹角为θ,如图2所示.根据实际情况估计人体淋雨可分为头顶和前左右几个方向上.雨迎面吹来时,由于雨相对于人的速度有变化,因此人单位时间内接收雨量变化,且与相对速度成正比.据此,推算出前后侧上单位时间接受雨量.同理,头顶部位接雨量与雨速垂直于头顶平面的分速度成正比.分别计算出头顶侧与前侧单位时间接雨量,并分别乘以各自面积以及时间d v,从而得到头顶及两侧淋雨的总量.即人体总的淋雨量.据此可得Q 与v 之间关系.图 2 雨水与人关系模型图顶部淋雨量为顶部淋雨面积bc 与降雨强度pu 以及淋雨时间d v的乘积,故1Q =c o s d b c p u v θ (2) 前方淋雨量为前侧淋雨面积ba 与降雨强度(sin )p u v θ+以及淋雨时间d v的乘积,故 2Q =(s i n )d b a p u v vθ+ (3) 因此,淋雨总量c o s (s i n )d d Q bcpu bap u v v v θθ=++ [c o s (s i n )]bpd Q uc a u v vθθ=++ (4)4 模型的求解4.1 不考虑降雨方向的情况下,将100d =米,最大速度为max 5/v m s =,雨速为4/u m s =,降雨量为2/w cm h =带入,则跑完全程的淋雨量为Q 0.002(22)/3ab ac bc =++ (5)4.2 考虑降雨方向即风向,其模型应用了雨滴速度的分解及相对运动速度的概念,得出总的淋雨量为c o s (s i n )d d Q bcpu bap u v v v θθ=++ (6) [cos (sin )]bpd Q uc a u v vθθ=++ (7)其中假设夹角θ一定,淋雨量Q 随着v 的变大而变小,即人走的越快淋雨量越少.5 结果分析5.1 根据不考虑雨的方向,雨淋遍全身即人的前面、后面 、左面、右面和上面淋雨建立了相应的模型.(22)/Q Swt wd ab ac bc v ==++ (8)从模型中可以看出淋雨总量Q 随着v 的变大而变小,即人走越快淋雨量越小.5.2 雨迎面吹来,雨线方向与行走方向在同一平面内且与人体夹角为θ,应用雨滴速度的分解及相对运动速度的概念建立了相应的数学模型.cos (sin )[cos (sin )]d d Q bcpu bap u v v vbpd Q uc a u v v θθθθ=++=++ (9)其中假设夹角 一定,淋雨量Q随着v的变大而变小,即人走的越快淋雨量越少.6 模型的评价通过对题目的分析求解,可知道人在雨中奔跑的淋雨量不仅与跑步速度有关,还与雨线与人跑步方向的夹角,雨速以及人跑步速度等因素有关.文章中并未对雨从背面吹来的情况进行研究,建出相应的模型.,文章还忽略了降雨密度不均匀,风向不稳定等次要因素,以便更好的对问题进行分析和研究.但在实际问题中的限制性因素远远超过这些,因此文章的分析方法仍存在一定的局限性,有待改进和提高.参考文献[1] 刘锋.葛照强.数学建模[M].南京:南京大学出本社,2005.[2]全国大学生数学建模竞赛组委会.全国大学生数学建模竞赛优秀论文汇编[C].北京:中国物价出版社,2002.[3] 党林立.孙晓群.主编数学建模简明教程[M]西安电子科技大学出版社.。
人在雨中奔跑的速度与淋雨量的关系摘要:本文通过对人在雨中奔跑速度与淋雨量的分析,运用统计分析和分类讨论的方法,得出人在雨中奔跑时最佳的奔跑速度与淋雨量的关系。
因此从以下方面分析:一,设降雨淋遍全身不考虑雨的方向,经简化假设得人淋雨面积为前后左右及头顶面积之和。
二,雨迎面吹来,雨线方向与跑步方向在同一平面,人淋雨面积为前方和头顶面积之和。
因各个方向上降雨速度分量不同,故分别计算头顶和前方的淋雨量后相加即为总的淋雨量。
据此可列出总淋雨量W 与跑步速度v 之间的函数关系。
分析表明当跑步速度为maxv 时,淋雨量最少。
并计算出当雨与人体的夹角θ=0、θ=30°时淋雨量三,雨从背面吹来,雨线与跑步方向在同一平面内,人淋雨量与人和雨相对速度有关。
列出函数关系式分析并求解,可知当人速度v=2m s 时淋雨量最少四,列出淋雨量W 和跑步速度v 之间的函数关系式,利用MATLAB 画出α分别为0°,10°,….90°的曲线图。
五,雨线与人跑步方向不在同一平面内,则考虑人的淋雨面积为前后左右以及头顶。
分别列式表示,总的淋雨量即为三者之和。
1、问题的重述要在雨中的一处沿直线跑到另一处,若雨速为常数且保持方向不变,试建立数学模型讨论是否跑得越快淋雨量越少。
将人简化为一个长方体,高 1.5/a m s =(颈部以下),宽0.5b m =,厚0.2c m =,设跑步距离1000d m =,跑步最大速度5/m v m s =,雨速4/u m s =,降雨量2/w cm h =,记跑步速度为v 。
问题一,不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量。
问题二,雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ,如图1,建立总淋雨量与速度v 及参数,,,,,,a b c d u w θ之间的关系,问速度多大,总淋雨量最少,计算0,30oθθ==时的总淋雨量。
问题三,与从背面吹来,雨线方向与跑步方向在同一平面内,且与人体的夹角为α,如图2.建立总淋雨量与速度v 及参数,,,,,,a b c d u w θ之间的关系,问速度多大,总淋雨量最少,计算30oθ=时的总淋雨量。
问题四,以总淋雨量为纵轴,速度v 为横轴,对(3)作图(考虑α的影响),并解释结果的实际意义。
问题五,若雨线方向与跑步方向不在同一平面内,模型会有什么样的变化。
2、问题的分析问题一,将人体简化成长方体,雨以降雨量w 均匀地淋遍全身,求出人接受雨的总 面积,人以最大速度跑步,并计算淋雨时间、单位时间、单位面积上的降雨量,求出人跑完全程的总淋雨量W 。
问题二,雨迎面吹来,雨线方向与跑步方向在同一平面内且与人体夹角为θ,如图1所示。
根据分析可以得到人在头部及身体前面淋雨,计算模型中长方体的面积,再根据人的速度和跑步路程得出时间t,进而求出在人体总的淋雨量.据此可得W 与v 之间关系,并能求出θ=0和θ=30°时的总淋雨量。
图1问题三,雨从背面吹来,雨线与跑步方向在同一平面内且与人体夹角为α,如图2图二所示。
左右方向上淋雨量为0。
头顶上单位时间内接收雨的量1w 与雨速垂直方向上的分量成正比,1W 为头顶面积bc 与时间的d/v 以及1w 之积。
当sin v u θ<时,前方不受雨,前后方向上单位时间内淋雨量2w 与人前进方向上人相对于雨的速度(usin θ-v )成正比,据此推算出2W ;而当sin v u θ<时,后方不受雨,由于人速已经高于雨速,这时前面会向前撞上雨滴,即2w 与sin v u θ-成正比。
2W 为人体前面积ab 和跑步时间d/v 顶淋雨量以及2w 之积。
由此可计算出总的淋雨量。
12W W W =+,据此可得W 与v 之间关系,并能求出α=30°时的总淋雨量。
问题四以总淋雨量W 为纵轴、速度ν为横,针对问题三的求解,利用MATLAB 作出当α分别为0°,10°,20°,30°,40°,50°,60°,70°,80°,90°时的曲线图并加以分析。
问题五,如图三,为人体模型的俯视图。
需要分三部分计算,在前后面上,雨垂直方向分速度为cos u β,相对速度为sin cos v u θβ-,乘上垂直受雨的面积ab 以及时间dv 即为前后侧受雨量2W 。
因为垂直于左右面人的分速度为0,左右两面上相对速度为sin sin u θβ乘上面积ac 以及时间dv极为左右受雨量3W .而头顶受雨与雨速和人速夹角大小无关,因此1W 仍按(2)、(3)问的算法做。
由123W W W W =++可得雨量求法公式。
图33、模型的假设与符号说明、模型的假设1、把人体视为长方体,人体行走过程中的震荡引起的误差可忽略不计。
ν大小与方向恒定,即沿直线匀速前进。
2、问题1中不考虑雨下落的方向,假设为自由落体。
人体各个方向均匀接受雨量,即单位时间、单位面积上接受雨量恒定。
3、问题2、3雨线与跑步方向在同一平面内,并且雨线与人体夹角不变。
在此过程中左右两侧因与雨速平行而不沾雨。
4、假设雨的密度相同,雨滴大小、形状相同,雨速均匀不变5、假设单位时间内接收雨的量与雨速成正比。
、符号说明h :人的身高w :宽度d :厚度v :速度θ:降雨下落方向与人的夹角W :淋雨总量I :降雨大小(降雨强度) D :路程4、模型的建立与求解问题一:不考虑雨的方向,因为降雨量w 均匀地淋遍全身,所以在将人体简化成长方体的情况下,忽略次要因素,人以最大速度跑步,根据淋雨时间、单位时间、单位面积上的降雨量等有关条件,列出总淋雨量W 的求解公式如下: ()max22d W ab bc ac w v =++,利用MATLAB 编程求解,可得: 0.0024W ≈3m 问题二:将降落在人体上的雨滴分成两部分,1s (顶部)2s(前面),人体接收的雨量和头顶面积、头顶部分与雨滴垂直下落方向分量1u 、行走时间有关。
列式求解如下: 头顶:11cos u u s bc==θ假设降雨量w 与与点密度(均匀不计)淋雨量与人相对速度有关,所以:111111cos cos cos w u w w d bcdw W w s t w bcv v∝====θθθ正面:2sin v v u=+θ而222222212sin sin sin sin v u uw v w wv uw w u v abdW w s t wu v bd av W W W w c a v u +∝=+=⎛⎫== ⎪⎝⎭⎛⎫=+=++ ⎪⎝⎭θθθ+1θ利用MATLAB 编程求解,可得:当v =5m/s 时,淋雨量W 最小;当θ=0°时,W = 3m ,当θ=30°时,W =3m图4图5问题三:将降落在人体上的雨滴分成两部分,1s (顶部)2s (前后两面),1s 面积为1s bc= 假设:1w 与雨点密度,雨点与人的相对速度成正比而雨点均匀分布。
头顶:111111cos cos cos w v v u w w ds w t bcw vααα∝=∴===1W正面:当sin u v α<时,人速大于垂直于人前后面的雨速,雨会沾到人的前面2222sin sin w v v u v v u w w uαα∝-=-∴=2sin v u dW wab u vα-=当sin u v ≥θ时,人速小于垂直于人前后面的雨速,雨会沾到人的后面2222sin sin w v u v v u vw w uαα∝-=-∴=2sin u v dW wab u vα-=,因为12W W W =+ 所以[][]cos sin sin cos sin sin bcw d u v d wab u v v u v W bcw d v u d wab u v v u v αααααα⨯⨯-⎧+⨯⎪⎪=⎨⨯⨯-⎪+⨯≤⎪⎩>编程求解可得:当v =2m/s 时,总淋雨量最少;雨线方向与人体夹角为30°时,淋雨量为3m 。
问题四: 合速度sin u v α-总淋雨量 [][]cos sin sin cos sin sin bcw d u vd wab u v v u v W bcw d v u d wab u v v u v αααααα⨯⨯-⎧+⨯⎪⎪=⎨⨯⨯-⎪+⨯≤⎪⎩>若ccos α-asin α<0,即:tan α>c/a,则v=usin α时,W 最小。
否则,V=m v 时,W 最小。
(如下图)α当a=30°,tanα>,v=2m/s,W ≈升最小,可与v=Vm,≈升相比。
分析结果的实际意义可知,当雨从背面吹来,只要α不太小,满足tanα>c/a,即:α>时,v=usinα,W最小。
此时人体背面不淋雨,只有顶部淋雨。
问题五:该问题中,只举例研究雨从正侧面吹来。
设雨线与跑步速度方向夹角为δ。
作图如下:W1=bcdwsinδcosβ/v雨速水平分量 ucosδ(方向与v相反)合速度 ucosδ+v 单位面积时间的淋雨量ω(ucosδ+v)/uW2=abdω(ucosδ+v)/uvW3=acdwsinδsinβ/vW=W1+W2+W3=bcdwsinδcosβ/v+abdw(ucosδ+v)/uv+acdwsinδsinβ/v由以上式子可知,当v 最大时,W最小。
其他情况与问题二处理类似,利用速度分解和合成,可以解决。
本质并无区别。
5、模型的评价、模型优点通过模型的建立,对雨的各个方向进行了讨论,比较客观得出了人的速度与淋雨量的关系。
同时应用了matlab等软件的得到了比较准确的结果,并与实际情况相比较,忽略次要干扰,得到了比较满意的结果。
、模型改进此模型将人近似类比为长方体,与人体的实际形状有较大的差异,经分析后发现可以将人类比于一个长方体加一个球;并且文章没有考虑到人在奔跑时雨淋到身上并不是准确的直线,而是会发生偏折。
参考文献:l、中国大学生数学建模竞赛,李大潜主编,高等教育出版社(1998) 2、数学建模案例分析,白其岭主编,海洋出版社,(2000年,北京)小组成员:熊俞超辛晓云。