非线性控制系统数字仿真
- 格式:pptx
- 大小:271.18 KB
- 文档页数:13




控制系统数字仿真题库一、填空题1. 定义一个系统时,首先要确定系统的边界;边界确定了系统的范围,边界以外对系统的作用称为系统的输入,系统对边界以为环境的作用称为系统的输出。
2.系统的三大要素为:实体、属性和活动。
3.人们描述系统的常见术语为:实体、属性、事件和活动。
4.人们经常把系统分成四类,它们分别为:连续系统、离散系统、采样数据系统和离散-连续系统。
5、根据系统的属性可以将系统分成两大类:工程系统和非工程系统。
6.根据描述方法不同,离散系统可以分为:离散时间系统和离散事件系统。
7. 系统是指相互联系又相互作用的实体的有机组合。
8.根据模型的表达形式,模型可以分为物理模型和数学模型二大类,其中数学模型根据数学表达形式的不同可分为二种,分别为:静态模型和动态模型。
9、采用一定比例按照真实系统的样子制作的模型称为物理模型,用数学表达式来描述系统内在规律的模型称为数学模型。
10.静态模型的数学表达形式一般是代数方程和逻辑关系表达式等,而动态模型的数学表达形式一般是微分方程和差分方程。
11.系统模型根据描述变量的函数关系可以分类为线性模型和非线性模型。
12 仿真模型的校核是指检验数字仿真模型和数学模型是否一致。
13.仿真模型的验证是指检验数字仿真模型和实际系统是否一致。
14.计算机仿真的三个要素为:系统、模型与计算机。
15.系统仿真的三个基本活动是系统建模、仿真建模和仿真试验。
16.系统仿真根据模型种类的不同可分为:物理仿真、数学仿真和数学-物理混合仿真。
17.根据仿真应用目的的不同,人们经常把计算机仿真应用分为四类,分别为:系统分析、系统设计、理论验证和人员训练。
18.计算机仿真是指将模型在计算机上进行实验的过程。
19. 仿真依据的基本原则是:相似原理。
20. 连续系统仿真中常见的一对矛盾为计算速度和计算精度。
21.保持器是一种将离散时间信号恢复成连续信号的装置。
22.零阶保持器能较好地再现阶跃信号。
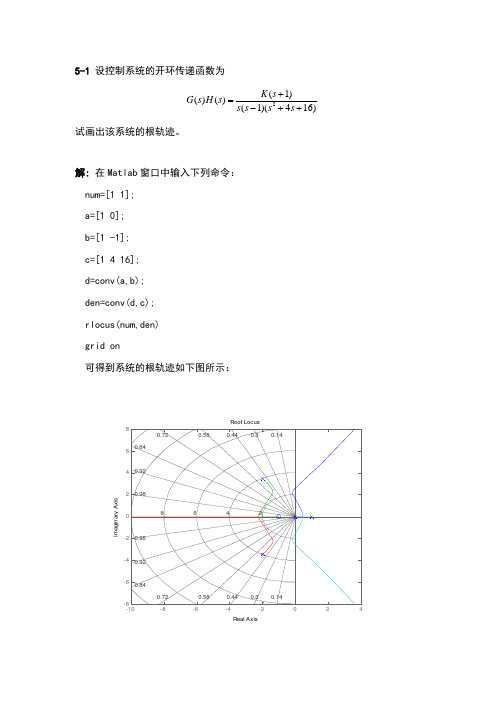
5-1 设控制系统的开环传递函数为2(1)()()(1)(416)K s G s H s s s s s +=-++试画出该系统的根轨迹。
解: 在Matlab 窗口中输入下列命令: num=[1 1]; a=[1 0]; b=[1 -1]; c=[1 4 16]; d=conv(a,b); den=conv(d,c); rlocus(num,den) grid on可得到系统的根轨迹如下图所示:5-2 某反馈控制系统的开环传递函数为()()()()24420KG s H s s s s s =+++ 试绘制其根轨迹。
解:在MATLAB 命令窗口中输入下列命令: num=1;den=conv(conv([1,0],[1,4]),[1,4,20]); rlocus(num,den) grid on 运行结果为:5-3.已知某系统传递函数为2180(1)100()11(1)[()20.31]40200200s W s s s s +=++⨯⨯+ 试绘制其伯德图。
解:分子分母同乘100*200得到280200(100)()(2.5100)(20.3200)200s W s s s s ⨯+=++⨯+在Matlab 窗口中输入下列命令:k=80*200; num=[1 100]; a=[ 100];b=[(1/200) 2* 200]; den=conv(a,b); w=logspace(-1,1,100); [m,p]=bode(k*num,den,w); subplot(2,1,1);semilogx(w,20*log10(m)); grid;xlabel('Frequency(rad/sec)'); ylabel('Gain(dB)'); subplot(2,1,2); semilogx(w,p); grid;xlabel('Frequency(rad/s)'); ylabel('Phase(deg)'); 可绘制该系统的伯德图如下所示。

一、实验目的本次实验旨在通过数字仿真技术,对线性连续控制系统和非线性环节控制系统进行仿真分析,验证控制系统的性能和稳定性,并加深对控制系统理论的理解。
二、实验环境1. 软件环境:MATLAB R2020a、Simulink2. 硬件环境:计算机三、实验内容1. 线性连续控制系统的数字仿真(1)系统描述本次实验选取两个线性连续控制系统,分别为G(S) = 10/S(S+1)和G(S) = 4/S^2 2.828S。
(2)参数设置输入信号:阶跃信号,阶跃时间:0;初值:0;终值:1迟滞环节:迟滞时间:0开环传递函数:G(S) = 10/S(S+1),G(S) = 4/S^2 2.828S反馈环节传递函数:H(S) = 1(3)仿真结果与分析通过Simulink对两个系统进行仿真,得到如下结果:系统1:G(S) = 10/S(S+1)阶跃响应曲线如图1所示,系统在t=0s时刻开始输入阶跃信号,经过一段时间后达到稳态值。
相轨迹曲线如图2所示,系统在相平面上的运动轨迹呈现出稳定的闭环运动。
系统2:G(S) = 4/S^2 2.828S阶跃响应曲线如图3所示,系统在t=0s时刻开始输入阶跃信号,经过一段时间后达到稳态值。
相轨迹曲线如图4所示,系统在相平面上的运动轨迹呈现出稳定的闭环运动。
2. 非线性环节控制系统的数字仿真(1)系统描述本次实验选取非线性环节控制系统,为Wk(s) = 10/s(s+1),并对其进行饱和死区特性的仿真。
(2)参数设置输入信号:阶跃信号,阶跃时间:0;初值:0;终值:1饱和死区:非线性的上下限为(-2,2),幅值为5和10(3)仿真结果与分析通过Simulink对非线性环节控制系统进行仿真,得到如下结果:阶跃响应曲线如图5所示,系统在t=0s时刻开始输入阶跃信号,经过一段时间后达到稳态值。
相轨迹曲线如图6所示,系统在相平面上的运动轨迹呈现出稳定的闭环运动。
3. 典型环节频率响应的数字仿真(1)系统描述本次实验选取典型环节频率响应,为G(S) = 10/S(S+1),并对其进行频率响应仿真。
自抗扰控制器(ADRC)仿真软件第11卷第5期t999年10月{,文章编号:1004—731X【199****4834系统仿真JOURNAL0FSYSTEMSIMULA T10N自抗扰控制器(ADRC)仿真软件,f,(中国科学院系统科学研究所.北京100080)弋Vn【1lNo5Oclober,l999摘要:介绍新型非线性控制器白抗扰控制器(ADRC)的基本原理.其数字仿真软件总体设计及宴现方法谊仿真软件基于WIN95平台.具有友好的用户界面,可随时动态修改控制对象,控制器参数,并具有存储记录琦能.仿真结果静态和动态的囤开j方式显示.该软件有助于使用户了解,ad3RC的强土功能.并为控制器设计和验证提供定量他的依据关键词:白抗扰控制器(ADRC);数字仿真中围分类每_文献标识■软件平Auto-Disturbance-Rejection-ControIler(ADRC)SimulatorPIAOJun,HANJing-qing(InstituteofSyst~sScience,ChineseAcademyofSciences.Beijing10(1080.Chi~) Abstract:Thearticleintroducestheprincipleofane~,vtypenonlinearcontrolIe~-ADRC. itssimulator'sdesignandingr[ementati0n.ThesimulatorisbasedonWIN95andhastnendIyinterface.Theusercanmoditypl ant.parametersotcomroller dynamicallyTheexperimentcanbestoredforthetuturousing,andthemsuhcanbeexpressedb ygraphinstzticanddynamicwayBythea_ercfinrealizethepowerofADRC.designthecontrolleri n.ad3RCmethod.andveritycontrollerKeywords:ADRC;digita]simulation;sottware1引言实现,最后通过具体例子对该软件进行椅骑.自抗扰控制器(ADRC)是中国科学院系统科学研究所韩京清研究员经过1O多年努力发明的新一代非线性控制器,其基本思想和方法_l与传统控制器相比有很大突破,其特点是:1被控对象内涵广泛.卓商人一输出描述对象,形式没有特定要求.可以是非线性,也可包括随机涨落.2.利用跟踪微分器(TD)安排过渡过程.利用TD.对参考输入安排过菠过程并提取其微分信号.3利用扩张状态观测器对对象估计.不仅能得到各个状态变量的估计,还能得到对象方程右端估计.4控制量组合方式灵活:可以是线性.也可以是非线性.目前.随着ADRC在不同实际领域的应用,其影啊日益广泛,其教率逐渐得到各领域专家的认同ADRC仿真软件是ADRC的数字仿真工具.一方面使用户了解掌握,~J3RC功能.另一方面可为控制器设计提供定虽化依据和验证.文章首先介绍了ADRC原理,然后给出了总体设计及其收稿日期:1999—06.312ADRC基本原理尊图l二阶系统的ADRC框图2.1ADRC框图(以二阶系统为例,见图1)2.2ADRC各组成部分说明(以二阶系统为例2.2.1被控对象被控对象的疗程384?系统仿真1999年l0月^(.….,l(,?,扰动补偿;——误差增益;卢2——误差微分增益. '"3ADRC仿真软件总体设计式中,,bo——系统已知部分{^t-——系统未知部分;3. 1仿真软件实现的功能(t)——未知扰动.2.2.2跟踪微分器ITD}【]㈨跟踪输入信号并给出其微分信号的一输入两输出的离散动态环节:1ll(t+1)=£l1(t)+ht2(t)l£l2(t+1)=2l2()+h.t2(l】(t),£L2(t),(£),r,h)(2)式中,(t)——输入信号;2ll(£)——跟踪输入信号;z12 (t)一l(t)的微分信号,从而近似(£)的嗽分;^——积分步长;r——决定跟踪快慢的参数;r越大.l1()跟踪越好,从而()越近似(£)的微分;向2——离散系统时间晟优控制综合函数.2.2.3扩张状态观谰器IESO以对象的输出Y(2)和输入"(£)作为其输入,估计出对象的状态变量及对象不确定部分=2l(f)+h(22一¨1fal(,LL,8))=22(f)+h(23一02fal(P,2,8)(3)+(2l(t),22(£))+自0"())=2(£)一^3fal(,3,占)式中,21(t)——》l(t);22(f)——》2(t);"(£)——》n()=未知扰动:fal(,——输出误差校正律;l,卢t——输出误差校正增益;h一积分步长.2.2.4控制量…£l=l】一2【——误差信号;E2=【2一22——误差嗽分信号;"(t):fa1(£1.口.)+2f(E2.口0.)一(23十,0(£2l,22))/b0;fal——误差反馈律;——(23+,0(2【,22))/6¨——系统总固仿真软件是基于WIN95的MD[程序用delphi40开发,实现的功能如F1可设置任意形式的对象.可舍有噪苫:2可设置,修改控制器参数.3可保存当前参数设置,也可通过参数文件设置当前参数.4仿真结果以图形方式直接给出:5可控制仿真进程,中进修改参数,动态显示仿真过程.6提供帮助系统,随时得到系统帮助:7.提供安垒机制,可"修改密码.8.不仅有完整的控制器仿真,也有控制器各部分仿真.9.提供解常微分方程,差分方程仿真.3.2仿真软件的总体构成仿真软件的总体框图见图2.本仿真软件包括不同阶数的对象模块.在各个对象模块中,可以定义各种对象,数字仿真结果立即以图形方式给出,对于感兴趣的对象可以存储起来,便于将来的研究利用.由于函数的性质对于对象的性质有直接的影响.因此也提供了函数性质模块,可以直观地把握函数的性质.为了分析TD安排过渡过程的效率,本软件包括阶,二阶TD模块.通过TD模块,可"研究TD参数r对效率的影啊.ESO是ADRC的重要组成部分.它使ADRC具有智能特点,是ADRC具有优越控制功能的基础:通过ESO模块, 可以研究ES0的估计效率与对象的变化规律闻的关系,提高调参技能.为了说明非线性控制器的控制效率,也是为了与ADRC相比较.仿真软件也包括NLPID模块NLP1D也是韩京清研究员发明的一种非线性控制器,利用两个TD作为安排过渡过程和提取被控对象的输出的微分信号,利用非线性PID 反馈作为控制量.其控制品质虽不如ADRC似比传统PID控制器优越.图2仿真软件蓉框架+"+6)+订)(U第11卷5期朴军,韩京清:自抗扰控制器(ADRC)仿真软件f}『于微分方程,差分方程是设计控制器的数学基础仿真鞋件也包括微分,差分方程模块.利用该模块,可以自由定阶,解任意阶的微分,差分方程,其结果以图形方式结出,对于方程的定性研究有很大帮助.仿真软件的恢心模块是ADRc模块,包括一阶,二阶,三阶.通过ADRc模块,可以认识.M)RC的控制品质.可以对系统响应的慢,是否超调,对控制器的鲁棒性,适应性作出评判.ADRC模块是综台模块,把被控对象,控制目标,安排过渡过程,系统辨识,控制反馈融为一体.作为完整的软件产品,本仿真软件也包括标准WIN95帮助,以及规范的密码授令模块.4ADRc仿真软件子模块设计4.1函数识别与计算函数的识别与计算是ADRC仿真软件的基本功能模块,对象的描述方程的计算都是基于该模块.要求对输入的函数表选式字符串,该模块能够输出基本函数复台形式的字符串.并能够把基本函数复合形式的字符串转化成适当的函数指针形式以便计算.函数表述式字符串由基本函数(sin, cos,powor,log等),基本算符(+,,*,/,一),常数表达式,变量表达式,括号构成,其表达方式与人们的书写习暾相一致, 如(sin()*c∞()+2)/(tog(1一)+4)埘其复杂程度不做限制.完全取决于使用者.为了符合上述要求,把基本算符(+,一,*,/,')转化为(add,minus,mul6ply.divid,power)基本函数形式,利用了非线性数据结构一树,树的节点表示基本函数,树的端点表示常数和变量,整个树用递归生成.整个过程分以下阶段:a.把包古基本算符(+,一,*,/,一)和括号的函数表达式字符串转化为基本函数复合形式的字符串.b把基本函数复合形式的字符串套到树上,树的节点表示基本函数的指针,树的端点是指向常数和变量的指针.c从树根到树梢递归计算得到对某个变量的函数值.基本函数的识别是通过规定其标准形式而实现,标准形式为基本函数名(参数,参数,?).例如,对于表达式3*+6'2—1.a步后应生成add(multiply(3,),minus(power(6,2),1))b步后应生成如图3.树的节电都是指向函数的指针,树的末端是指向常数或变量的指针.田/l\l,圆圆\/\,r]r一\lx_Ipower]/\L———/\——62国3非线性数据结构树在c步,设取L,则相应地mul6ply一>3power> 36.minus>35,add一>38,最后输出38.4.2解常微分方程组解常微分方程组是ADRC仿真软件数字仿真的基本功能模块,所有的仿真模块都用到它.要求对输入的方程右端(任意的而非固定的)给出数值解.具体实现是通过把41和欧拉法结合起来,其过程如下:a利用41得到表示右端函数的树,方程的阶数与树的个数相等.b赋初值或把上一步结果结树梢中的变量.c利用递归得到右端函数的计算结果.d利用欧拉法得到下一步状态量值e循环到b步.直到规定的循环次数.4.3数字仿真图形表示图形功能是~nfl3RC仿真软件的基本功能,把数字仿真结果以曲线形式直观地表示出来.可以对其图形进行局部放大,拖动操作,这是del【Dhi40本身提供的图形工具的功能. 其实现过程如下:a生成Tserie~对象,个数与状态变量十数相等:b利用41或42得到状态变量值.c利用tser[esaddxy(,Y,labe1.color)为序列赋值.d循环到指定步数.e利用Tcharrrepaint显示生成的序列结果.4.4数字仿真图形的动态表示43的图形功能是静态的,使用者看到的是最终仿真结果,没有给出曲线的生成过程,而在实际应用中,使用者往往不仅要求了解曲线生成的结果,还要求知道过程,甚至要求在生成过程中暂停,修改参数,然后进行对比.数字仿真图形的动态表示模块满足了这种要求.实现是用了MULTI THREAD技术,生成更新状态曲线的后台线程不断地更新曲线,后台进程每算一步都从全局变量中得到参数值.其实现过程如下a主线程生成Tthread对象,运行Tthread.execute.b如果threadterminated=trlle则结束线程,否则执行c.c从全局变量中得到参数值.d利用敢拉法算下一步状态.eTserires.addxy(T.Y,label,color)为序列赋值.f子线程thread要求更新曲线.g进入b.直到循环结束.可以从主线程结束子线程,也可以从主线程暂停子线程,然后再恢复子线程的运行.4.5文件系统的实现对于仿真软件来说,文件系统是必须的.很多有典型意386系统仿真1999年10月义的对象需萼存储起来,以便将来研究,或者相互比较:同时凋出来的好的控制参数也需要存起束备将来的借鉴随着时问的推移,原米所存信包的价值也会发生改变,因此仿真软件的文件系统必须允许对其存储信息进行增加,删除,更改使用ADRC仿真软件实现上述要求的过程如下: 生成新信息:把生成信息的环境中的关键标识连同其值一同作为一条记录写入memo对象,不同的标识对应不同的字段使用历史情包:把选中的memo对象中的历史信息根据其标识对当前的仿真环境进行恢复,使其达到生成信息时的状况删除历史信息:把选中的历史信息删掉.让后一十记录上移修改历史信息:可以任意修改,不用特别处理.文件系统都是标准ASCII文奉文件,相关表(FORM)显示前把文本挚十一次性读人相应的对象中.相关表(FORM)关闭时把相应的对象中字符内眷写入文本由f仿真软件对文件系统要求不高.因此未使用delphi40所提供的interbase数据库系统,诚系境对计算机资源要求高.非常鹿大,实在没有必要用它.5数字仿真实验情况为了验证和了解:'aJ)RC的控制功效,我们举例说明:5.1对象及参数设置对象的厅程及ADRC各组成部分的参数如图4所示.O图4ADRC各组成部分的参数0123456789101112131415161718192O圈5阶跃响业这里要仿真的是用ADRC控制对象1—1012345678g101112131415161718192O图6系统扰动及其估计ljt2=,J+bJ"+0+60"【:使其单位阶跃响应快速,无超调,无静差.其中f.=va'0(t) (函数形状见图6),bL=0.fo=0,b0=1.仿真初始时刻为0,步长为0.01秒,仿真2000步.对设定值1安排过渡过程,这里TD的参数r=0.5,相当于安排近3秒而无超调的过渡过程,ESO的参数=1.(2=05,3=025),a一00001,.so】=100,2=65.卢¨3=85;误差反馈律:=0+75(0=05).l=100,p2=10.5.2数字仿真结果图5显示的是设定值,安排的过渡过程和实际响应.后两者几乎看不出差异.只在11秒多一的时刻和接近14秒时由于系统有较大的跳跃(见图6)而呈现一点差别.图6显示的是系统扰动v.r0()和ESO对它的估计£23 (),几乎重台从以上实验可以看出,ADRC控制效果是很好的.仿真软件也方便,直观地体现了ADRC.6结束语ADRC控制器,作为新型的非线性控制器,其理论也币断发腱,H趋成熟.相应的应用领域不断扩展.基于ADRC思想的新方法不断涌现.ADRC仿真软件,理应随着ADRC的发展而发展仿真软件现在仅包括基本的要素,其版率现在是10,相信在ADRC研究者的共同努力下,功能更强,使用更方便的新一代的ADRC仿真软件在不久的将来到ADRC使用者手中.参考文献:_】]韩京清控制系统鲁棒性与GODE[不完备性定理【A]中国控制会议论文集[C]l995248—255[2]韩球清王伟非线性跟踪微分器!J]系统科学与教学.1994.14(2)[3】韩清,袁露林跟踪微分器的离散形式[A]96控制采境仿真与CAD会议戈集.C]1~6[4]韩京清一娄不确定对象的扩张状志观测器[J]控制与决策.1995.10(1)[5]韩京清白抗扰控耩器及其应用[J]控制决策,1998,13(1)第11卷5期朴军,韩京清:自抗扰控制器(ADRc)仿真软件?387? 朴军1968年12月生,1991年毕业于七海复旦大学应用数学专业.1997年起在中科院系统所开始硕士阶段学习,师从韩京清教授学习非线性控制:韩京清1937年11月生,1958年毕业于吉林大学数学系,1966年于苏联莫斯科大学数学力学系研究生毕业.现为中科院数学与系统科学研究院研究员,博导主要研究方向为控制理论及应用,控制系统非线性设计,控制系统CAD设计,人口系统理论.(上接第360页)6算法实例上述算法已在微机上实现,井把它纳入了东风汽车公司总装广的计算机辅助装配工艺设计系统中,应用结果表明算法具有高的稳定性和准确性.以下是该算法应用的一个实Station1Statien2Station3(450)(450)(45O)例.图2是该AIB实倒问题应满足的紧前关系网络图,图中给出了工位编排的结果.该实倒由16个作业单元构成, 总工时为25.5,以节拍4.5为优化目标,最小工位数的下界LB(1)=int(255/45)=6;LB(2)=3,算法优化结果为6个工位,与LB(1)相等,编成效率为25.5/(6×4.5)=944%. Station4Station5Station6(380)(400f420)2.o15i1.0104.2.n!/\\f1.5@.@0-P是自由节点一tx:作业单元号CycleTime=450(x)t:怍业时同图2紧前关系约束图7结语AIB问题在求解还需考虑更多的实际约束,因此必须对同题的数学模型作进一步的修正,以期优化结果能更好地指导流水线作业设计另外ALB问题属于复杂网络最优化问题,也是一个NP难题,要获得该问题解决的最好方法,还需进一步探讨,除了用启发式算法外,有必要尝试譬如分枝定界,枚举寻优等其它的求解方法.参考文献:[1]RobertKlein.ArnlinSchollM~imizithgtheproductionratein simplea~mblelinebal~cing—Abranchandhoundprocedure[.]1 EuropeanJournalofOperationa]Research,1996.91:3673852.Joh—RVOpti~lBalancingLfgesmb】eLinesWith'Fa—hie'【J]ManasementScience.1988,34r,2)3Ba),ba~IASu~'eyofExactAlgorithmsfortheS~mpleAssembly[4.[5]LineBalancingProblem,Managea'aeatScience,1986,32(8) HaekmanSTFast.EffeetiveAlgorithlTIsformpleAssembly LineBalancingProblems[J]OperationResearch,1989,37(6) JohnmnRV.ABranehandBoundAlgorithn~forA~mblyLine BalancingProblemsw【thFormulationI丌曙arities[J].Manage—II1Efl3tSdenee.1983.29(11).互吴君华男,1971年l2月9日生.华中理工大学博士研究生.主要研究方向:流水线产品总装工艺规划(IE),CAPP的应用与实践.夏巨谌,男57岁.华中理工大学材料学院院长主要研究方向:精密塑性成型,模具及工艺CAD.。