纳米多晶体的热力学函数及其在相变热力学中的应用

热力学理论在材料科学中的应用热力学是研究物质热运动状态与热现象的学科，广泛应用于物理学、化学、工程学等领域。

在材料科学中，热力学理论也发挥着重要作用。

本文将从材料物性、热力学基础、热力学中的热力学函数、相变等方面探讨热力学理论在材料科学中的应用。

一、材料物性材料的物理性质是十分重要的，通常包括密度、熔点、导热系数、热容等等。

这些性质通常可以通过热力学理论来计算和预测，这种方法被称为热力学计算方法。

热力学计算方法需使用基本的热力学函数，如热力学势、自由能和焓等等，这些函数包含了材料的物理性质。

二、热力学基础热力学基础是理解热力学计算方法的重要前提。

物质的热运动状态，如温度、压力和密度等，与其热力学参数有着密切的关系。

例如，材料的温度与热容、热膨胀系数等相关，材料的压力与压缩系数相关。

这些参数可以通过热力学基本方程来计算，进而预测材料的物理性质。

三、热力学中的热力学函数在热力学中，热力学函数是描述材料热学性质的基本量。

热力学函数有很多种，如熵、内能、焓、自由能等等。

这些函数通常描述了热力学系统的能量和热学性质，可以用来计算和预测材料的物理性质。

例如，内能是系统的能量总和，可以帮助计算材料的热容；自由能可以帮助计算材料的相变过程。

四、相变热力学理论在材料相变的研究中也有广泛的应用。

相变是指材料在温度、压力等条件变化下从一种热力学相平衡态到另一种热力学相平衡态的过程。

相变涉及到热能、热动力学、统计物理等方面的知识，热力学理论提供了很好的研究方法。

热力学理论中的相图可以帮助预测材料的相变点和相变类型，同时也可以预测材料的构造和性能变化。

热力学理论还可以帮助研究材料的晶体结构和非晶态结构，这对于设计合金、氧化物陶瓷、玻璃等新材料具有重要意义。

总之，热力学理论在材料科学中有着广泛的应用。

通过对材料的物性、热力学基础、热力学函数、相变等方面的研究，可以更好地预测和设计材料的性质和应用。

在未来的研究中，热力学理论将继续发挥着重要作用。

纳米材料的热学性质纳米材料是一种既不同于晶态，又不同于非晶态的第三类固体材料，通常指三维空间尺寸至少有一维处于纳米量级 ( 1 n m～1 0 0 n m)的固体材料。

由于纳米材料粒径小，比表面积大，处于粒子表面无序排列的原子百分比高达 l 5 ～5 0 ％。

纳米粒子的这种特殊结构导致其具有不同于传统材料的物理化学特性。

纳米材料的高浓度界面及原子能级的特殊结构使其具有不同于常规块体材料和单个分子的性质，纳米材料具有表面效应，体积效应，量子尺寸效应宏观量子隧道效应等，从而使得纳米材料热力学性质具有特殊性，纳米材料的各种热力学性质如晶格参数，结合能，熔点，熔解焓，熔解熵，热容等均显示出尺寸效应和形状效应。

可见，纳米材料热力学性质在各方面均显现出与块体材料的差异性，研究纳米材料的热力学性质具有极其重要的科学意义和应用价值。

一热容1996年，在低温下测定了纳米铁随粒度变化的比热，发现与正常的多晶铁相比，纳米铁出现了反常的比热行为，低温下的电子比热系数减50 %。

1998年，通过研究了粒度和温度对纳米粒子热容的影响，建立了一个预测热容的理论模型，结果表明:过剩的热容并不正比于纳米粒子的比表面，当比表面远小于其物质的特征表面积时，过剩的热容可以认为与粒度无关。

2002年，又把多相纳米体系的热容定义为体相和表面相的热容之和，因为表面热容为负值，所以随着粒径的减小和界面面积的扩大，将导致多相纳米体系总的热容的减小，二.晶格参数，结合能，内聚能纳米微粒的晶格畸变具有尺寸效应，利用惰性气体蒸发的方法在高分子基体上制备了1. 45nm 的pd纳米微粒，通过电子微衍射方法测试了其晶格参数，发现 Pd 纳米微粒的晶格参数随着微粒尺寸的减小而降低。

结合能的确比相应块体材料的结合能要低。

通过分子动力学方法，模拟 Pd 纳米微粒在热力学平衡时的稳定结构，并计算微粒尺寸和形状对晶格参数和结合能的影响，定量给出形状对晶格参数和结合能变化量的贡献研究表明:在一定的形状下，纳米微粒的晶格参数和结合能随着微粒尺寸的减小而降低，在一定尺寸时，球形纳米微粒的晶格参数和结合能要高于立方体形纳米微粒的相应量。

工程热力学（2015 秋）课程论文姓名：班级：学号：日期：纳米晶材料的热力学函数研究一、摘要 (1)二、纳米晶材料的几何假设 (1)三、界面热力学函数分析 (2)四、内部热力学函数分析 (6)五、整体热力学函数分析 (6)六、总结 (6)七、纳米晶材料热力学应用展望 (6)一、摘要纳米晶材料（nanophase material )是具有纳米级超细晶组织的材料。

由于超细晶粒(小于100nm)、高的界面体积分数(高达50%)和界面区的原子间距分布较宽，其性能特别是和近邻原子相关联的性能，如力学性能、热学性能、磁学性能，与一般多晶材料或同成分的非晶态材料有很大的差别[1]。

本文应用界面膨胀模型[2]并以普适状态[3]为基础对纳米材料的整体的热力学函数计算模型进行了阐述分析，进而对其应用进行了展望。

二、纳米晶材料的几何假设纳米晶材料中的原子可分为两部分，一部分是位于晶粒内部点阵位置上有序排列的原子，另一部分是位于晶界面上无序或部分有序的原子。

假设纳米晶粒子为球形，直径为d ，界面厚度为δ，如图1所示。

原子在晶界面区域和晶粒内部的排布密度（原子的空间占据百分数）分别为b ρ和i ρ。

位于晶界面上和晶粒内部的原子个数b N 和i N 可由下式计算：bb b V d δρδπ2)2(4-=N (1) 03)22(34V d ii ρδπ-=N (2) 其中：V b 为纳米晶体界面上一个原子所占的体积， V 0为平衡状态的原子体积。

所以，晶体面处的原子分数x b 为bi b bi b ib bb r r d d V V d d N N N x ρρδδδρρδδδ3023023)()(6)2(11)(6)2(11--+=--+=+=(3)其中，r b 和r 0分别为纳米晶界面处原子的半径和平衡状态时原子的半径。

图1 球形纳米晶粒及表征几何尺寸示意图[4]为方便表达，设定纯物质纳米晶体的热力学函数为以纳米晶界面处和晶粒内部两部分热力学函数的求和。

热力学知识：热力学相转化和热力学状态函数热力学是探讨热力现象及其发生规律的学科，有着广泛的应用基础。

本文将主要讨论热力学相转化和热力学状态函数两个方面。

热力学相转化相转化是物质从一个相到另一个相的过程，如气体转化成液体、液体转化成固体等。

热力学相转化是指物质在相变过程中吸收或放出的热量，并且在一定条件下发生的状态改变。

相转化是一种热力学过程，因为在相变中物质的温度不改变，只有物质内部的分子结构或排布发生改变。

在一个相转化过程中，热量的转移是一个非常重要的因素。

以融化过程为例，当我们给固体物质添加热量时，固体的温度不变，而是直到它融化为止。

在相变开始后，物质消耗了除了潜热以外的热量来完成相变，这是因为在相变时，物质转化为新的相，维持原来相的结构将消耗热量。

同样地，当物质从液态转变为气态时，这个过程也需要吸收热量。

需要注意的是，物质在相变时需要吸收或放出的热量与是否是样品同质性的影响有关系。

如果物质发生相变是由于样品同质性的改变，需要吸收或放出的热量就很小，相变温度也很容易察觉。

而如果相变是由于Physico-chemical factors的影响导致的，则需要吸收或放出大量的热量，相变温度就很容易被忽略。

热力学状态函数热力学状态函数是指在热力学系统中，只与它的初始和最终状态有关的量。

这些函数包括内能、熵、焓、自由能和吉布斯。

内能是指热力学系统中分子带有的总能量，其中注意只有温度相同的系统之间才能比较它们的内能。

熵是指系统的随机性和不可逆过程的度量。

随着时间的推移，熵会增加。

当一个物体热量释放时，总的熵始终增加，因为热量在自由流动时必然增加系统的随机性。

当系统从更高熵的状态向更低熵的状态转化时，它就会吸收能量，而当它向更高熵的状态转化时就会释放能量。

焓是指系统的热量和体积的和。

在一个恒容系统中发生的相变所需要的焓是0，以固态至液态为例，固态相的体积小于液态相，相变时体积会发生改变，因此如果我们保持温度不变，我们需要完全把焓送入固态相内来完成相变。

纳米材料与团簇物理结课论文纳米材料的热学性质纳米材料是一种既不同于晶态，又不同于非晶态的第三类固体材料，通常指三维空间尺寸至少有一维处于纳米量级( 1 n m～1 0 0 n m)的固体材料。

由于纳米材料粒径小，比表面积大，处于粒子表面无序排列的原子百分比高达l5～5 0％。

纳米粒子的这种特殊结构导致其具有不同于传统材料的物理化学特性。

纳米材料的高浓度界面及原子能级的特殊结构使其具有不同于常规块体材料和单个分子的性质，纳米材料具有表面效应，体积效应，量子尺寸效应宏观量子隧道效应等，从而使得纳米材料热力学性质具有特殊性，纳米材料的各种热力学性质如晶格参数，结合能，熔点，熔解焓，熔解熵，热容等均显示出尺寸效应和形状效应。

可见，纳米材料热力学性质在各方面均显现出与块体材料的差异性，研究纳米材料的热力学性质具有极其重要的科学意义和应用价值。

纳米材料的热学性质概述一、纳米材料的熔点及内能材料热性能与材料中分子、原子运动行为有着不可分割的联系。

当热载子(电子、声子及光子)的各种特征尺寸与材料的特征尺寸(晶粒尺寸、颗粒尺寸或薄膜厚度)相当时，反应物质热性能的物性参数如熔化温度、热容等会体现出鲜明的尺寸依赖性。

特别是，低温下热载子的平均自由程将变长，使材料热学性质的尺寸效应更为明显。

图1 几种纳米金属粒子的熔点降低现象上图（图1）为几种纳米金属粒子的熔点降低现象。

随粒子尺寸的减小，熔点降低。

当金属粒子尺寸小于10nm后熔点急剧下降，其中3nm左右的金微粒子的熔点只有其块体材料熔点的一半，用高倍率电子显微镜观察尺寸2nm的纳米金粒子结构可以发现，纳米金颗粒形态可以在单晶、多晶与孪晶间连续转变。

这种行为与传统材料在固定熔点熔化的行为完全不同，伴随着纳米材料的熔点降低，单位质量粒子熔化时的潜热吸收(焓变)也随尺寸的减小而减少。

人们在具有自由表面的共价半导体的纳米晶体、惰性气体和分子晶体也发现了熔化的尺寸效应现象。

根据固体物理的基本原理，可以说明材料热学性质出现尺寸效应的根本原因，一般情况下，晶体材料的内能U可依据其晶格振动的波特性在德拜假设下估计出，即：(1) 式中，Θ为德拜温度；k为波矢；T为热力学温度；h为普朗克常数；k B为玻尔兹曼常数。

热力学中的热力学函数热力学函数是热力学研究中的核心概念之一，用于描述系统在不同状态下的性质和行为。

它们通过数学函数的形式，将系统的热力学性质与物质的物理性质联系起来，使得我们可以通过研究这些函数来了解系统的特性。

本文将介绍几种常见的热力学函数及其在研究中的应用。

一、内能（U）内能是热力学中最基本、最常用的热力学函数之一，它表示系统所含能量的总和。

内能的变化可以用来分析系统的能量转移和能量转化过程。

当系统中没有发生化学反应和质量转移时，内能变化可以用下式表示：ΔU = Q + W其中，ΔU表示内能变化，Q表示系统吸收或释放的热量，W表示系统对外界做功。

当系统对外界做功时（W>0），内能会减少；而当外界对系统做功时（W<0），内能会增加。

二、焓（H）焓是描述恒压热力学过程中能量变化的重要函数。

在恒压条件下，焓的变化等于系统吸收或释放的热量。

即：ΔH = Qp其中，ΔH表示焓变化，Qp表示系统在恒压过程中吸收或释放的热量。

由于焓变化只与物质的初末状态有关，因此焓是一种状态函数。

三、自由能（G）自由能是一种描述系统在恒温、恒压条件下的能量变化的函数，它可以用来预测物质反应的方向和可逆性。

自由能由内能和系统对外界做功的能力两部分组成，可以用下式表示：G = U + pV - TS其中，G表示自由能，U表示内能，p表示压强，V表示体积，T表示温度，S表示熵。

自由能的变化量ΔG与反应的可逆性有关，当ΔG<0时，反应是可逆的；当ΔG>0时，反应是不可逆的。

四、熵（S）熵是描述系统有序程度的函数，也是描述系统混乱度或无序程度的度量。

熵的增加可以用来判断反应的可逆性，熵的减少则表示反应的趋于有序。

熵是与统计力学深度相关的一个量，它可以通过统计力学的方法来计算。

总结：热力学函数是热力学研究中不可或缺的工具，它们通过数学函数的形式，将热力学性质与物质的物理性质联系起来，为研究热力学系统提供了便利。

晶体生长中的热力学分析晶体生长是一个具有很高科学研究价值和实际应用前景的研究领域。

在过去的几十年中，科学家和研究人员对晶体生长进行了大量的研究，建立了一套完整的理论和实验技术体系。

其中，热力学是晶体生长中不可或缺的一部分，既可以用来解释晶体生长中的各种现象，也可以指导晶体生长的实验过程。

晶体生长中的热力学分析主要涉及晶体生长物质的化学势、热力学参数和晶体生长过程中的热力学平衡等方面。

下面我们将从这三个方面入手进行讲述。

一、晶体生长物质的化学势晶体生长物质的化学势是指晶体生长中各组分在溶液中的活度和相平衡条件下的摩尔自由能。

在晶体生长过程中，物质的化学势决定了晶体生长的驱动力和动力学控制因素。

因此，对于晶体生长的研究和控制来说，深入了解和正确预测晶体生长物质的化学势是非常重要的。

晶体生长物质的化学势主要受到晶体生长条件、物质组成、物质状态和溶液中其他离子的影响。

在晶体生长过程中，物质从溶液中向晶体表面扩散，使晶体表面饱和度降低，从而导致晶体生长。

因此，晶体生长物质的化学势直接影响晶体生长速率和形态。

在晶体生长实验中，通过调整晶体生长条件、控制物质组成和物质状态，可以有效地改善晶体生长物质的化学势，提高晶体生长的质量和效率。

二、热力学参数热力学参数是指晶体生长物质在热力学平衡状态下的参数，包括物质的热力学势、热力学活度、热力学平衡常数、反应热等。

在晶体生长中，这些热力学参数对晶体生长的控制和调节起到了至关重要的作用。

晶体生长物质的热力学势是晶体生长过程中的驱动力和动力学控制因素。

在晶体生长过程中，必须满足晶体生长物质的化学势大于等于晶体表面的化学势，并且晶体生长过程中的热力学参数必须满足平衡条件。

只有在这种情况下，晶体生长才能持续进行，形成高质量的晶体。

晶体生长物质的热力学平衡常数是另一个重要的热力学参数。

在晶体生长过程中，晶体表面和溶液中的化学势之间需要满足一定的平衡条件。

晶体生长物质的热力学平衡常数可以用来描述溶质在晶体和溶液之间的平衡状态，有效地预测晶体生长过程中的平衡状态和反应动力学。

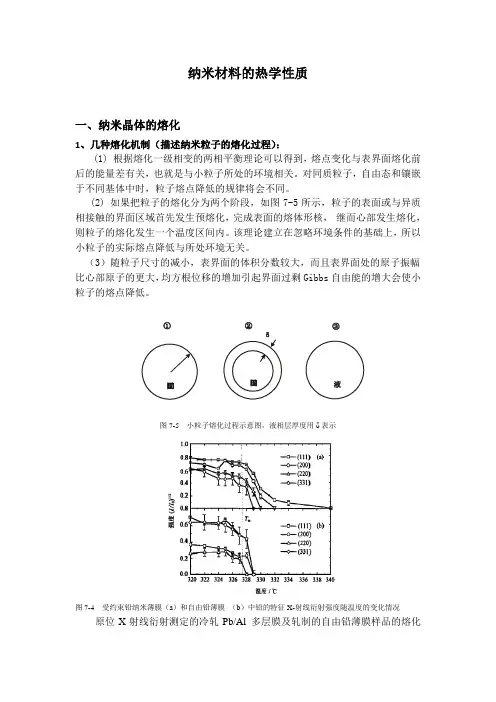
纳米材料的热学性质一、纳米晶体的熔化1、几种熔化机制（描述纳米粒子的熔化过程）：(1) 根据熔化一级相变的两相平衡理论可以得到，熔点变化与表界面熔化前后的能量差有关，也就是与小粒子所处的环境相关。

对同质粒子，自由态和镶嵌于不同基体中时，粒子熔点降低的规律将会不同。

(2) 如果把粒子的熔化分为两个阶段，如图7-5所示，粒子的表面或与异质相接触的界面区域首先发生预熔化，完成表面的熔体形核，继而心部发生熔化，则粒子的熔化发生一个温度区间内。

该理论建立在忽略环境条件的基础上，所以小粒子的实际熔点降低与所处环境无关。

（3）随粒子尺寸的减小，表界面的体积分数较大，而且表界面处的原子振幅比心部原子的更大，均方根位移的增加引起界面过剩Gibbs自由能的增大会使小粒子的熔点降低。

图7-5 小粒子熔化过程示意图，液相层厚度用δ表示图7-4 受约束铅纳米薄膜（a）和自由铅薄膜（b）中铅的特征X-射线衍射强度随温度的变化情况原位X射线衍射测定的冷轧Pb/Al 多层膜及轧制的自由铅薄膜样品的熔化行为，图中虚线为块体Pb平衡熔点。

X射线衍射分析是测定晶体结构的重要手段, 由于原子周期排列的晶体结构对X 射线的散射会产生反映晶体结构的特征衍射,而熔化后的液态金属原子排列无序,对X 射线不会产生特征衍射. 因此,熔化过程中X 射线特征衍射只能由剩余的晶体部分产生,特征衍射强度将因晶体的熔化而显著降低.图7-4为可以看出，自由铅薄膜的四个特征衍射的强度到大约326℃开始急剧降低，并在329℃之前均下降为零。

Pb/Al多层膜样品中铅膜的四个特征衍射的强度在326～329℃也会降低，但并未降到零，而是在高于329℃不同的温度降低到零，其中的（111）衍射直到340℃才完全消失。

这说明，Pb/Al多层膜样品中部分铅膜在达到334℃时依然存在，其熔化温度超过了自由铅薄膜的熔化温度，夹在铝中的部分铅薄膜出现了过热现象。

纳米晶体的熔化2、纳米材料的过热意义：纳米材料熔点降低在很多情况下限制了其应用领域，人们经常希望提高纳米材料热稳定性。

纳米材料的热力学性质及其应用纳米材料是一种颇为热门的材料，在物理、化学、生物、医药等领域中都有广泛的应用。

其所具有的独特性质和应用价值也受到了广泛的关注。

其中，纳米材料的热力学性质是其应用的基础而且也是极其重要的一部分。

纳米材料的热力学性质纳米材料具有高比表面积、量子尺寸效应和表面效应等特点。

这些独特的性质决定了纳米材料的热力学性质也与传统材料有很大的不同。

首先是纳米材料的比热。

由于纳米材料具有更多的表面原子和少量的体积原子，因此其比表面积将会比普通材料大得多。

这样就会产生更多的表面能和重要的贡献。

由于纳米材料的比表面积巨大，因此纳米材料的比热也会相应地增大，这将会增大材料的热容量。

其次是纳米材料的比熵。

纳米材料比熵增大的直接后果便是纳米材料的比熵增大。

当纳米材料的尺寸小得足够小时，纳米材料的比熵将达到最大值。

而当纳米材料的尺寸继续减小时，比熵将会降低。

同时，不同的纳米材料在它们的比熵变化方面也有区别。

例如，金属结构具有强的增量性，而陶瓷则具有减量性。

第三是纳米材料的比能。

纳米材料比能的变化主要是受到表面效应、量子限制和应变等因素的影响。

受到这些因素的共同作用，一些纳米材料的比能甚至超过了它们的布里渊能，因此纳米材料的比能大大增加。

纳米材料的应用纳米材料的热力学性质不用于直接的应用，但却与其许多应用息息相关。

其应用分散在物理、化学、生物和医药等多个领域中，下面对一些典型的应用进行简单的介绍。

首先是在生物、医药领域中的应用。

纳米材料由于具有超静电场和表面效应等特殊性质，因此可以用于制备肿瘤治疗和生物成像等。

例如，纳米材料可以用作分子靶向药物的载体，能够选择性地将药物送到癌细胞内，从而减少对人体正常细胞的损伤。

此外，纳米材料还可以通过修饰表面来增加生物相容性和疏水性，从而在生物体内获得更长的循环时间。

其次是在催化领域的应用。

纳米材料表面的高反应活性、化学惰性和结构特征等独特性质，使得其在催化反应中有广泛的应用。

纳米材料的热力学性质分析纳米材料是一种具有特殊结构和性质的材料，其尺寸范围在纳米级别。

由于纳米材料的尺寸效应和表面效应的存在，其热力学性质与宏观材料有很大差异。

本文将从纳米材料的熵、内能和自由能三个方面来分析其热力学性质。

首先，我们来看纳米材料的熵。

在宏观物体中，熵是描述系统无序程度的变量。

然而，在纳米尺度下，纳米材料的表面积增大，原子之间的相对位置变得更加复杂，系统的无序性增加。

因此，纳米材料的熵相对于宏观材料来说更大。

这也意味着纳米材料更容易发生相变和热力学过程，其对外界环境的敏感性也大大增强。

其次，我们研究纳米材料的内能。

内能是一个系统所包含的全部能量，包括系统的热能和势能。

由于纳米材料的尺寸效应，其内能与宏观材料相比也有所不同。

尺寸效应是指由于纳米材料的尺寸特征不同，其内部原子排列的方式和势场能量的分布也会发生变化。

举个例子，纳米金颗粒的表面原子会形成一层类似于固体的自由电子层，与周围原子产生强烈的相互作用。

这种电子层的存在对纳米材料的热力学性质产生了显著的影响，使其内能变化与宏观材料不同。

最后，我们关注纳米材料的自由能。

自由能是在恒温恒压条件下描述系统稳定性的指标。

与宏观材料不同，纳米材料的自由能受到尺寸效应和表面效应的影响。

由于纳米材料的比表面积大，表面原子和周围原子之间会产生较大的相互作用，导致纳米材料的自由能增大。

这种增大的自由能会导致纳米材料的稳定性降低，从而使其更容易发生相变和热力学过程。

总之，纳米材料的热力学性质与宏观材料存在很大差异。

纳米材料的熵相对较大，内能与宏观材料不同，并且自由能受到尺寸效应和表面效应的影响。

这些特性使得纳米材料对环境和外界条件更加敏感，容易发生相变和热力学过程。

研究纳米材料的热力学性质有助于深入理解纳米世界的奥秘，对于纳米材料的制备和应用具有重要意义。