八年级数学下册微专题勾股定理在古代问题中的应用核心素养课件新版沪科版20191212215

1.求下列图中表示边的未知数x、y、z的值. 144 81 144 ① 169 ②
z
625
576
③
2.求下列直角三角形中未知边的长:
比 一 比 看 看 谁 算 得 快 ！
5 8 17
x
20
16
x
12
x
方法小结: 可用勾股定理建立方程.
小结
数学知识：


勾股定理
勾股定理的简单计算及运用
观 经历过程： 察
B
C
A
勾 股 定 理
一、情景引入
如图，一根电线杆在离地面5米处断裂，电 线杆顶部落在离电线杆底部12米处，电线 杆折断之前有多高？
B
C
12米
A
电线杆折断之前的高度=BC+AB=5米+AB的长
SA+SB=SC C
B 图甲 图甲 图乙 4 A的面积 4 B的面积 C的面积 8 1.观察图甲，小方格 的边长为1. ⑴正方形A、B、C的 ⑵正方形 面积各为多少？ 面积有什么关系？
a 勾
股 b 弦 c
a b c
2
2
2
即直角三角形两直角边的平方和等于 斜边的平方.
勾 股 世 界
两千多年前，古希腊有个哥拉 两千多年前，古希腊有个毕达哥拉斯 斯学派，他们首先发现了勾股定理，因此 学派，他们首先发现了勾股定理，因此在 在国外人们通常称勾股定理为毕达哥拉斯 国外人们通常称勾股定理为毕达哥拉斯定 定理。为了纪念毕达哥拉斯学派， 1955 理。为了纪念毕达哥拉斯学派， 1955年 年希腊曾经发行了一枚纪念票。 希腊曾经发行了一枚纪念邮票。
2.观察图乙，小方格 的边长为1. ⑵正方形A、B、C的 面积有什么关系？

美国总统证法
那个小男孩头也不抬地说：“请问先生， 如果直角三角形的两条直角边分别为3 和4，那么斜边长为多少呢？”加菲尔 德答道：“是5呀。”小男孩又问道： “如果两条直角边分别为5和7，那么这 个直角三角形的斜边长又是多少？”加 菲尔德不加思索地回答到：“那斜边的 平方一定等于5的平方加上7的平方．” 小男孩说：“先生，你能说出其中的道 理吗？”加菲尔德一时语塞，无法解释 了，心里很不是滋味。加菲尔德不再散 步，立即回家，潜心探讨小男孩给他出 的难题。他经过反复思考与演算，终于 弄清了其中的道理，并给出了简洁的证 明方法。
A
13
?
C
12
B
试一试:
３、一个直角三角形的三边长为三个连续 偶数,则它的三边长分别为 ( B )
A 2、4、6 Ｃ 4、 6、 8
Ｂ 6、8、10
Ｄ 8、10、12
试一试:
４、已知：Rt△ＡBC中，AB＝４，AC＝３,则 BC的长为 B 4 C 4
5或
7
.
B
3
A
A
3
C
2.求下列直角三角形中未知边的长:
a c b
2
C
c2－b2
2
2
=c2-a2 b= c2-a2
2
a
B
c a b
勾股小常识：勾股数
1.基本勾股数如：大家一定要熟记
3、、 45
1、 1、 2
5、 12、 13
7、 24、 25
1、3、 2
2.如果a,b,c是一组勾股数，则ka、kb、kc（k为正整 数）也是一组勾股数， 如： 6、8、10 ； 9、12、15； 15、36、39……
方法 小结
(4) 已知: a:b=3:4, c=15,求a、b.

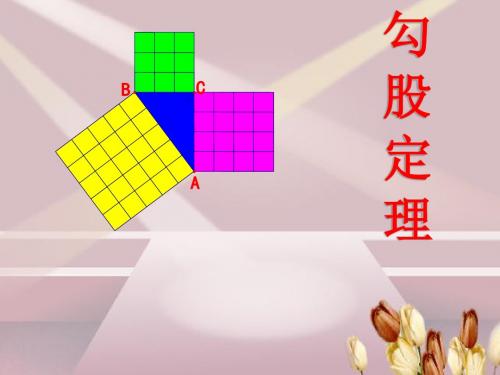
系，用它们的边长表示，是： a2+b2=c2 ．
新知导入
勾股定理
由上面的例子，我们猜想： 定理：直角三角形两直角边的平方和，等于斜边的平方.
如果直角三角形的两条直角边长分别为a,b，斜边长为c,那 么a2+b2=c2.
a
c
b
结论：直角三角形两条直角边的平方和等于斜
边的平方.
说一说：我国古代把直角三角形 中较短的直角边称为勾，较长的 直角边称为股，斜边称为弦，因 此，我们称上述定理为勾股定理
a
b
c
证明：
S梯形
1 (a 2
b)(a
b),
c a
S梯形
1 ab 2
1 ab 2
1 c2, 2
∴a2 + b2 = c2.
b
归纳总结
勾股定理
ac
如果直角三角形的两直角边长分 别为a,b,斜边长为c,那么a2+b2=c2.
b 在我国又称商高定理，在外国则叫毕达哥拉斯定理， 或百牛定理.
公式变形： a c2 - b2 ,
第18章 勾股定理
18.1 勾股定理
第1课时 勾股定理
史话·勾股定理
勾股定理是一个基本的几何定理，它在许多 领域都有着广泛的应用，国内外都有很多科学 家、知名人士对此都有过研究，至今已有500 多种证明方法。
国内：公元十一世纪周朝数学家就提出“勾三 股四弦五”，在《周髀算经》中有所记载。
公元3世纪三国时代的赵爽对《周髀算经》 内的勾股定理作出了详细注释，创制了一幅 “勾股圆方图”，把勾股定理叙述成：勾股各 自乘，并之为弦实，开方除之即弦。
方法2：分割法(把以斜边为边长的正方形分割成易 求出面积的三角形和四边形）：

.
解：由图可知大正方形的边长为：a+b则面 积为(a+b)2，图中把大正方形的面积分成了四部 分，分别是：边长为a的正方形，边长为b的正 方形，还有两个长为b，宽为a的长方形.
根据同一个图形面积相等，由左图可得
(a+b)2=a2+b2+4×1 ab，
由右图可得(a+b)22=c2+4×1 ab.
所以a2+b2=c2.
把它们拼成如图（2）所示的边长为 a+b 的正方形
EFGH.
H
b D1 a G
a
c
A1
cb （2）
bc
c
C1 a
E a B1 b F
从图中可见，
H
b D1 a G
a
A1B1=B1C1=C1D1=A1D1=c. 因为∠B1A1E+∠A1B1E=90°，
A1
c
cb
而∠A1B1E=∠D1A1H，
bc
因此∠B1A1E+∠D1A1H=90°，
赵爽弦图
你是如何理解的？你会证明吗？
世界上几个文明古国相继发现和研究过勾股 定理，据说其证明方法多达 400 多种，有兴趣的 同学可以继续研究.
E
1874年美国总统 A
Garfield证明
b
C
c
ca
a B bD
练习
作8个全等的直角三角形(2条直角边长分别 为a、b斜边长为 c)再作3个边长分别为 a、b、c 的正方形把它们拼成两个正方形(如图)你能利用 这两个图形验证勾股定理吗？写出你的验证过程
课堂小结
定理 直角三角形两条直角边的平方和，等 于斜边的平方.
a2+b2=c2

a
Bb c C
SA+SB=SC
2.观察图乙，小方格 的边长为1. ⑵正方形A、B、C的
面积有什么关系？
SA+SB=SC
C Aa c
b
图乙 a
bc C
图甲 B
SA+SB=SC
3.猜想a、b、c 之间的关系？ a2 +b2 =c2
3.猜想a、b、c 之间的关系？ a2 +b2 =c2
用 拼 图 法 证 明
试一试
在Rt△ABC中， 若a=5，b=12， 则c =___________.
当c是斜边时， c2= a2+b2 当b是斜边时， b2= a2+c2
课堂小结
这一节课我们一起学习了哪些 知识和思想方法？
作业
必做题：课本56页第1、2题 选做题：
探索
做一个长，宽，高分别为50厘米，40 厘米，30厘米的木箱，一根长为70厘米 的木棒能否放入，为什么？试用今天学 过的知识说明。
图甲 图乙 A的面积 4 9 B的面积 4 16 C的面积 8 25
B C
SA+SB=SC
2.观察图乙，小方格 的边长为1. ⑴ ⑵正方形A、B、C的 的面积有什么关系？
面积各为多少？
SA+SB=SC
C Aa c
b B 图甲
图甲 图乙 A的面积 4 9 B的面积 4 16 C的面积 8 25
图乙
A
勾股定理
弦图
它标志着我国 古代数学的伟
大成就！
这个图形里蕴 涵着怎样博大 精深的知识呢 ？
SA+SB=SC
C A
B 图甲
A的面积 B的面积 C的面积
图甲 图乙 4 4 8

定 理
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明， 就把这一证法称为“总统”证法。
应用知识回归生活
1、如图，受台风麦莎影响，一棵树在离地面4米处断裂 ，树的顶部落在离树跟底部3米处，这棵树折断前有多高 ？
4米
3米
应用知y识=回0 归生活
cb
a
勾
股
在中国古代，人们把弯曲成直角的手臂的上半部分称为 "勾"，下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”，较长的直角边称为“股”， 斜边称为“Байду номын сангаас”.
千古第一定理
勾 股
是第一个不定方程
毕 达
（ 数与形的第一定理 哥
商
拉
高 ） 定 理
导致第一次数学危机 斯
数学由计算转变为证明
9 个单位面积。 正方形C的面积是
25 个单位面积。
（图中每个小方格代表一个单位面积）
你是怎样得到正方形c 的面积。
C A
（2）在图1-2中，正方 形A，B，C中各含有多 少个小方格？它们的面 积各是多少？
B
图1-1
C A
B
（3）你能发现图1-1中 三个正方形A，B，C的 面积之间有什么关系吗？ 图1-2中呢？
图1-2
即：两条直角边上的正方形面积之和等S于A+斜S边B上=的S正C
方形的面积
C A
B
C
图1-1 A
（1）你能用三角 形的边长表示正方 形的面积吗？
（2）你能发现直 角三角形三边长度 之间存在什么关系 吗？与同伴进行交 流。