九年级数学下学期课时随堂测试12

26.1 反比例函数（满分100分；时间：90分钟）一、选择题（本题共计10 小题，每题3 分，共计30分，）1. 已知反比例函数y=kx ，当x=2时，y=−12，那么k等于（）A.1B.−lC.−4D.−142. 已知反比例函数y=kx的图象经过P(−2, 6)，则这个函数的图象位于()A.第二、三象限B.第一、三象限C.第三、四象限D.第二、四象限3. 已知反比例函数y=kx(k≠0)的图象经过点M(−2, 2)，则k的值是()A.−4B.−1C.1D.44. 已知反比例函数y=2k−1x，当x<0时，y随x的增大而减小，则k的范围（）A.k>12B.k<12C.k=12D.k≠125. 如图，在同一平面直角坐标系中，反比例函数y=−kx与一次函数y=kx−3(k为常数，且k≠0)的图象可能是()A. B.C. D.相交于A、B两点，点A坐标为(−1, 2)，则点B坐标6. 如图，直线y=−2x与双曲线y=kx为（）A.(1, −2)B.(2, −1)C.(−2, 1)D.(−1, −2)在各自象限内，y随x的增大而减小，那么m的取值范围是7. 如果反比例函数y=m+1x()A.m<0B.m>0C.m<−1D.m>−1(k≠0)的图象上，过点P作PM⊥x轴于点M，PN⊥8. 如图，若点P在反比例函数y=kxy轴于点N，若矩形PMON的面积为6，则k的值是（）A.−3B.3C.−6D.6(m>0)图象上，则y1，9. 已知点A(2, y1)，B(4, y2)，C(−2, y3)都在反比例函数y=mxy2，y3的大小关系（）A.y2>y1>y3B.y1>y2>y3C.y3>y2>y1D.y1>y3>y210. 如图，在直角坐标系中，正方形的中心在原点O，且正方形的一组对边与x轴平行，(k>0)的图象上与正方形的一个交点，若图中阴影部分的点P(4a, a)是反比例函数y=kx面积等于16，则k的值为（）A.16B.1C.4D.−16二、填空题（本题共计10 小题，每题3 分，共计30分，），当x=2时，y=−3，则k=________．11. 已知反比例函数y=kx的图象经过点(−2, −3)，则k=________．12. 已知反比例函数y=kx的图象不经过第二象限，则k的取值范围是________．13. 若反比例函数y=kx14. 反比例函数的表达式为y=(m−1)x m2−2，则m=________．15. 写出一个图象位于二、四象限的反比例函数的表达式，y=________．16. 在平面直角坐标系xOy中，A(1, 1)，B(3, 1)，双曲线y=k与线段AB有公共点，则kx的取值范围是________.17. 点P(2m−3, 1)在反比例函数y=1的图象上，则m=________．x18. 若函数y=y1−y2，其中y1与x+1成正比例，y2与x成反比例，且当x=1和x=−1时，y的值都是−2，则当y=−5时，x的值为________．19. 已知反比例函数y=2，则当x>0时，函数值y随x增大而________（填“增大”或“减x小”）．(x>0)的图象20. 如图，矩形ABCD中，E是AC的中点，点A，B在x轴上，若函数y=6x过D，E两点，则矩形ABCD的面积为________.三、解答题（本题共计6 小题，共计60分，）图象上的两点，已知点B的坐标为(3, 2)，△AOB 21. 如图，点A、B是反比例函数y=kx的面积为2.5，求该反比例函数的解析式和点A的坐标．22. 在平面直角坐标系xOy中，已知：直线y=−x反比例函数y=k的图象的一个交点为xA(a, 3)．（1）试确定反比例函数的解析式；（2）写出该反比例函数与已知直线l的另一个交点坐标．的图象上，且点A，B的横坐标分别为a，23. 如图，点A，B在反比例函数y=−4x2a(a<0)，若点C在x轴上，点D在y轴上，且四边形ABCD为正方形，求a的值．(k≠0)的图象上．24. 已知点P(1, 2)在反比例函数y=kx（1）当x=−2时，求y的值；（2）当1<x<4时，求y的取值范围．25. 在平面直角坐标系中，过一点分別作坐标轴的垂线，若与坐标轴围成矩形的周长的数值与面积的数值相等，则这个点叫做和谐点．例如．图中过点P分別作x轴，y轴的垂线．与坐标轴围成矩形OAPB的周长的数值与面积的数值相等，则点P是和谐点．（1）判断点M(3, 6)是否为和谐点，并说明理由；（k为常数）上，求a，k的值．（2）若和谐点P(a, 3)(a>0)在双曲线y=kx26. 如图，在平面直角坐标系中，矩形ABCD的顶点B，C在x轴的正半轴上，AB＝8，BC(x>0)的图象经过点E，分别与AB，＝6．对角线AC，BD相交于点E，反比例函数y=kxCD交于点F，G．（1）若OC＝8，求k的值；（2）连接EG，若BF−BE＝2，求△CEG的面积．参考答案一、选择题（本题共计10 小题，每题 3 分，共计30分）1.【答案】B【解答】解：∵ 当x=2时，y=−12，∵ −12=k2，解得，k=−1．故选：B．2.【答案】D【解答】解：∵ 反比例函数y=kx的图象经过点(−2, 6)，∵ k=−12，∵ k<0，∵ 反比例函数的图象在第二、四象限，故选D．3.【答案】A【解答】解：把点M(−2, 2)代入反比例函数y=kx(k≠0)中，得2=k−2，∵ k=−4.故选A.4.【答案】A【解答】解：∵ 反比例函数y=2k−1x，当x<0时，y随x的增大而减小，∵ 2k−1>0，．解得，k>12故选A．5.【答案】A【解答】解：由一次函数图象知k>0，∵ 一次函数的图象经过第一、三、四象限，故选项C，D 错误；此时反比例函数图象分别在第二、四象限，故A选项正确，B选项错误.故选A.6.【答案】A【解答】解：由于点A和点B关于原点对称，点A坐标为(−1, 2)，则点B坐标为(1, −2)．故选A．7.【答案】D【解答】的图象在所在象限内，y的值随x值的增大而减小，解：∵ 反比例函数y=m+1x∵ m+1>0，解得m>−1．故选D．8.【答案】C【解答】解：设PN=a，PM=b，则ab=6，∵ P点在第二象限，∵ P(−a, b)，代入y=k中，得xk=−ab=−6，故选C．9.【答案】B【解答】(m>0)，∵ 反比例函数y=mx∵ 函数图象的两个分式分别位于一、三象限，且在每一象限内y随x的增大而减小．∵ −2<2<4，∵ 点C(−2, y3)位于第三象限，∵ y3<0，∵ A(2, y1)和B(4, y2)位于第一象限，∵ y1>0，y2>0，∵ 2<4，∵ y1>y2，∵ y1>y2>y3．10.【答案】C【解答】解：∵ 图中阴影部分的面积等于16，∵ 正方形OABC的面积=16，∵ P点坐标为(4a, a)，∵ 4a×4a=16，∵ a=1（a=−1舍去），∵ P点坐标为(4, 1)，把P(4, 1)代入y=k，得xk=4×1=4．故选：C．二、填空题（本题共计10 小题，每题 3 分，共计30分）11.【答案】−6【解答】解：把x=2，y=−3代入y=kx 得：k2=−3，解得：k=−6．故答案是：−6．12.【答案】6【解答】解：由y=kx，得k=xy，∵ 反比例函数y=kx的图象经过点(−2, −3)，∵ k=(−2)×(−3)=6．故答案是：6．13.【答案】k>0【解答】反比例函数y=kx的图象不经过第二象限，则经过一三象限，∵ k>0．14.【答案】−1【解答】解：依题意有m2−2=−1且(m−1)≠0，所以m=−1．故答案为：−1．15.【答案】答案不唯一，如y=−1x等【解答】解：根据反比例函数的性质，其图象位于第二、四象限，则其系数k<0；故只要给出k 小于0的反比例函数即可；答案不唯一，如y =−1x 等．16.【答案】1≤k ≤3【解答】解：当(1, 1)在y =k x 上时，k =1， 当(3, 1)在y =k x 的图象上时，k =3．若双曲线y =k x 与线段AB 有公共点，则k 的取值范围是1≤k ≤3． 故答案为：1≤k ≤3.17.【答案】2【解答】解：∵ 点P(2m −3, 1)在反比例函数y =1x 的图象上，∵ (2m −3)×1=1，解得m =2． 故答案为：2．18.【答案】−12或2【解答】解：∵ y 1与x +1成正比例，∵ y =k 1(x +1)．∵ y 2与x 成反比例，∵ y 2=k 2x ．y =k 1(x +1)−k 2x ．当x =±1时，y =−2；∵ {2k 1−k 2=−2k 2=−2解得：{k 1=−2k 2=−2，∵ y=−2(x+1)+2．x当x=−5时，−5=−2(x+1)+2，x解得x=−1或x=22或2．故答案为−1219.【答案】减小【解答】解：∵ k=2>0，∵ 图象在第一、三象限，且在每一个象限y随x的增大而减小．故答案为：减小．20.【答案】12【解答】解：过E作EF⊥AB于F，如图，∵ 点E是矩形ABCD对角线的交点，∵ AE=CE，∵ EF是△ABC的中位线，∵ AD=2EF.(x>0)上，设点D的横坐标为m，且点D在反比例函数y=6x)，∵ D点坐标为(m, 6m，∵ AD=6m∵ EF=3，m∵ E(2m, 3m)，∵ AF=m，∵ AB=2m，∵ 矩形ABCD的面积=2m⋅6m=12.故答案为：12.三、解答题（本题共计6 小题，每题10 分，共计60分）21.【答案】解：把点B的坐标(3, 2)代入y=kx，得k=xy=3×2=6，则该反比例函数为解析式为：y=6x．如图，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D．设A(a, 6a)．∵ 点A、B是反比例函数y=kx图象上的两点，∵ S△AOC=S△BOD，∵ S△AOB=S△AOC+S梯形ACDB−S△BOD=S梯形ACDB，则2.5=2+6a2×(3−a)，整理，得(a−2)(a+9)=0，解得a1=2，a2=−9（舍去）．则A(2, 3)．综上所述，该反比例函数的解析式是y=6x，点A的坐标是(2, 3)．【解答】解：把点B的坐标(3, 2)代入y=kx，得k=xy=3×2=6，则该反比例函数为解析式为：y=6x．如图，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D．设A(a, 6a)．∵ 点A、B是反比例函数y=kx图象上的两点，∵ S△AOC=S△BOD，∵ S△AOB=S△AOC+S梯形ACDB−S△BOD=S梯形ACDB，则2.5=2+6a2×(3−a)，整理，得(a−2)(a+9)=0，解得a1=2，a2=−9（舍去）．则A(2, 3)．综上所述，该反比例函数的解析式是y=6x，点A的坐标是(2, 3)．22.【答案】解：（1）因为A(a, 3)在直线y=−x上，则a=−3，即A(−3, 3)，的图象上，又因为A(−3, 3)在y=kx可求得k=−9，；所以反比例函数的解析式为y=−9x（2）另一个交点坐标是(3, −3)．【解答】解：（1）因为A(a, 3)在直线y=−x上，则a=−3，即A(−3, 3)，又因为A(−3, 3)在y=k的图象上，x可求得k=−9，所以反比例函数的解析式为y=−9；x（2）另一个交点坐标是(3, −3)．23.【答案】解：作BE⊥x轴于E，AF⊥y轴于F，∵ 四边形ABCD是正方形，∵ AB=BC=CD=DA，∠A=∠B=∠C=∠D=90∘，∵ ∠BCE=∠CDO=∠DAF，在△BEC和△COD和△DFA中，{∠BCE=∠CDO=∠DAF ∠BEC=∠COD=∠DFABC=CD=DA，∵ △BEC≅△COD≅△DFA，∵ BE=CO=DF，EC=OD=AF，∵ 点A，B的横坐标分别为a，2a(a<0)，∵ EC=OD=AF=−a，EC+OC=−2a，∵ BE=CO=DF=−a，∵ B(2a, −a)，∵ 点B在反比例函数y=−4x的图象上，∵ −a=−42a，解得，a=−√2．【解答】解：作BE⊥x轴于E，AF⊥y轴于F，∵ 四边形ABCD是正方形，∵ AB=BC=CD=DA，∠A=∠B=∠C=∠D=90∘，∵ ∠BCE=∠CDO=∠DAF，在△BEC和△COD和△DFA中，{∠BCE=∠CDO=∠DAF ∠BEC=∠COD=∠DFABC=CD=DA，∵ △BEC≅△COD≅△DFA，∵ BE=CO=DF，EC=OD=AF，∵ 点A，B的横坐标分别为a，2a(a<0)，∵ EC=OD=AF=−a，EC+OC=−2a，∵ BE=CO=DF=−a，∵ B(2a, −a)，∵ 点B在反比例函数y=−4x的图象上，∵ −a=−4，解得，a=−√2．2a24.【答案】解：（1）∵ 点P(1, 2)在反比例函数y=k的图象上，x，∵ 2=k1∵ k=2，，∵ y=2x=−1；当x=−2时，y=2−2；（2）∵ 当x=1时，y=2；当x=4时，y=12在x>0时，y值随x的增大而减小，又∵ 反比例函数y=2x<y<2．∵ 当1<x<4时，y的取值范围为12【解答】的图象上，解：（1）∵ 点P(1, 2)在反比例函数y=kx∵ 2=k，1∵ k=2，，∵ y=2x=−1；当x=−2时，y=2−2（2）∵ 当x=1时，y=2；当x=4时，y=1；2又∵ 反比例函数y=2在x>0时，y值随x的增大而减小，x<y<2．∵ 当1<x<4时，y的取值范围为1225.【答案】解：（1）∵ 点M(3, 6)，∵ 矩形OAPB的周长=2(3+6)=18，面积=3×6=18，∵ 18=18，∵ 则点P是和谐点；（2）∵ 点P(a, 3)，∵ 矩形OAPB的周长=2(a+3)，面积=3a，∵ 点P是和谐点．∵ 2(a+3)=3a，解得a=6，所以，点P(6, 3)，∵ 点P在双曲线y=k上，x=3，∵ k6解得k=18．【解答】解：（1）∵ 点M(3, 6)，∵ 矩形OAPB的周长=2(3+6)=18，面积=3×6=18，∵ 18=18，∵ 则点P是和谐点；（2）∵ 点P(a, 3)，∵ 矩形OAPB的周长=2(a+3)，面积=3a，∵ 点P是和谐点．∵ 2(a+3)=3a，解得a=6，所以，点P(6, 3)，∵ 点P在双曲线y=kx上，∵ k6=3，解得k=18．26.【答案】∵ 在矩形ABCD的顶点B，AB＝8，BC＝6，而OC＝8，∵ B(2, 0)，A(2, 8)，C(8, 0)，∵ 对角线AC，BD相交于点E，∵ 点E为AC的中点，∵ E(5, 4)，把E(5, 4)代入y=kx得k＝5×4＝20；∵ AC=√62+82=10，∵ BE＝EC＝5，∵ BF−BE＝2，∵ BF＝7，设OB＝t，则F(t, 7)，E(t+3, 4)，∵ 反比例函数y=kx(x>0)的图象经过点E、F，∵ 7t＝4(t+3)，解得t＝4，∵ k＝7t＝28，∵ 反比例函数解析式为y=28x，当x＝10时，y=2810=145，∵ G(10, 145)，∵ △CEG的面积=12×3×145=215．【解答】∵ 在矩形ABCD的顶点B，AB＝8，BC＝6，而OC＝8，∵ B(2, 0)，A(2, 8)，C(8, 0)，∵ 对角线AC，BD相交于点E，∵ 点E为AC的中点，∵ E(5, 4)，把E(5, 4)代入y =k x 得k ＝5×4＝20； ∵ AC =√62+82=10，∵ BE ＝EC ＝5，∵ BF −BE ＝2，∵ BF ＝7，设OB ＝t ，则F(t, 7)，E(t +3, 4)，∵ 反比例函数y =k x (x >0)的图象经过点E 、F ，∵ 7t ＝4(t +3)，解得t ＝4，∵ k ＝7t ＝28，∵ 反比例函数解析式为y =28x ， 当x ＝10时，y =2810=145， ∵ G(10, 145)，∵ △CEG 的面积=12×3×145=215．26.1.2 反比例函数的图象和性质的应用一、选择题（共10小题，3*10=30）1．如图所示，点P 是反比例函数y ＝k x 的图象上一点，过点P 分别作x 轴、y 轴的垂线，如果构成的矩形的面积是4，那么反比例函数的解析式是( )A.y ＝－2xB.y ＝2xC.y ＝－4xD.y ＝4x2．点(－1，4)在反比例函数y ＝k x的图象上，则下列各点在此函数图象上的是( ) A ．(4，－1) B ．(－14 ，1) C ．(－4，－1) D ．(14 ，2)3．如图，双曲线y ＝k x 与直线y ＝－12x 交于A ，B 两点，且A(－2，m)，则点B 的坐标是( )A.(2，－1)B.(1，－2)C.(12，－1)D.(－1，12)4．已知A(x 1，y 1)，B(x 2，y 2)都在y ＝6x 的图象上，若x 1·x 2＝－3，则y 1·y 2的值为( )A.－6B.6C.－12D.125．如图，在平面直角坐标系内，点A 是反比例函数y ＝2x (x ＞0)图象上的一点，过点A 作x 轴的垂线，垂足为点B ，则△AOB 的面积为( )A ．12B ．1C ．2D ．46. 反比例函数y ＝－2x 的图象上有两点P 1(x 1，y 1)，P 2(x 2，y 2)，若x 1＜0＜x 2，则下列结论正确的是( )A ．y 1＜y 2＜0B ．y 1＜0＜y 2C ．y 1＞y 2＞0D ．y 1＞0＞y 27．如图，点A 是反比例函数y ＝kx (x ＞0)图象上的一点，AB 垂直于x 轴，垂足为点B ，△OAB 的面积为6.若点P(a ，7)也在此函数的图象上，则a 的值是( )A.－127B. 127C.－67D. 678．如图，在平面直角坐标系xOy 中，函数y ＝kx ＋b(k≠0)与y ＝mx (m≠0)的图象相交于点A(2，3)，B(－6，－1)，则不等式kx ＋b>mx的解集为( )A.x<－6B.－6<x<0或x>2C.x>2D.x<－6或0<x<29．若点A(a －1，y 1)，B(a ＋1，y 2)在反比例函数y ＝kx (k ＜0)的图象上，且y 1＞y 2，则a 的取值范围是( )A ．a ＜－1B ．－1＜a ＜1C ．a ＞1D ．a ＜－1或a ＞110．如图，平行于y 轴的直线分别交y ＝k 1x 与y ＝k 2x 的图象(部分)于点A ，B ，点C 是y轴上的动点，则△ABC 的面积为( )A ．k 1－k 2B ．12 (k 1－k 2)C ．k 2－k 1D ．12 (k 2－k 1)二．填空题（共8小题，3*8=24）11．已知一个反比例函数的图象经过点(3，1)，若该反比例函数的图象也经过点(－1，m)，则 m ＝_____________．12. 如图，点A 在双曲线y ＝kx 上，AB ⊥x 轴于点B ，且△AOB 的面积是2，则k 的值是________.13．如图，Rt△ABC的两个锐角顶点A，B在函数y＝kx(x＞0)的图象上，AC∥x轴，AC＝2，若点A的坐标为(2，2)，则点B的坐标为.14．如图，O是坐标原点，菱形OABC的顶点A的坐标为(－3，4)，顶点C在x轴的负半轴上，函数y＝kx(x<0)的图象经过顶点B，则k的值为__________.15．如图，直线y＝3x－6分别交x轴，y轴于点A，B，点M是反比例函数y＝kx(x>0)的图象上位于直线上方的一点，MC∥x轴交AB于点C，MD⊥MC交AB于点D，AC·BD ＝4 3，则k的值为__________.16．如图，在平面直角坐标系中，过点M(－3，2)分别作x轴、y轴的垂线，与反比例函数y＝4x的图象交于A，B两点，则四边形MAOB的面积为_______.17．点A(a，b)，B(a－1，c)在反比例函数y＝1x的图象上，且a＞1，则b与c的大小关系为_________.18．如图，是反比例函数y＝k－2x的图象的一个分支，对于给出的下列说法：①常数k的取值范围是k>2；②另一个分支在第三象限；③在函数图象上取点A(a1，b1)和B(a2，b2)，当a1>a2时，b1<b2；④在函数图象的某一个分支上取点A(a1，b1)和B(a2，b2)，当a1>a2时，b1<b2.其中正确的是____________．(填出所有正确说法的序号)三．解答题（共7小题，46分）19．(6分) 已知点A(3，－2)在反比例函数y＝kx的图象上，若点B也在此反比例函数的图象上，过点B作BC⊥x轴于点C，连接OB，求△OBC的面积.20．(6分) A(4，m)，AB⊥x轴，且△AOB的面积为4.(1)求k和m的值；(2)若点C(x，y)也在反比例函数y＝kx的图象上，当y≤2(y≠0)时，求自变量x的取值范围．21．(6分) 如图，一次函数y ＝kx ＋b 与反比例函数y ＝mx 的图象交于A(1，4)，B(4，n)两点.(1)求反比例函数的解析式； (2)求一次函数的解析式.22．(6分) 如图，一次函数y ＝2x －4的图象与反比例函数y ＝kx 的图象交于A ，B 两点，且点A 的横坐标为3. (1)求反比例函数的解析式； (2)求点B 的坐标.23．(6分) 如图，一次函数y ＝kx ＋b 的图象与坐标轴分别交于A ，B 两点，与反比例函数y ＝nx 的图象在第一象限的交点为C ，CD ⊥x 轴，垂足为点D.若OB ＝3，OD ＝6，△AOB 的面积为3.(1)求一次函数与反比例函数的解析式； (2)直接写出当x ＞0时，kx ＋b －nx＜0的解集.24．(8分) 设函数y 1＝k x ，y 2＝－kx(k ＞0).(1)当2≤x≤3时，函数y 1的最大值是a ，函数y 2的最小值是a －4，求a 和k 的值； (2)设m≠0，且m≠－1，当x ＝m 时，y 1＝p ；当x ＝m ＋1时，y 1＝q.圆圆说：“p 一定大于q”．你认为圆圆的说法正确吗？为什么？25．(8分) 如图，在平面直角坐标系中，一次函数y＝kx＋b的图象经过点A(0，－4)，B(2，0)，交反比例函数y＝mx(x＞0)的图象于点C(3，a)，点P在反比例函数的图象上，横坐标为n(0＜n＜3)，PQ∥y轴交直线AB于点Q，D是y轴上任意一点，连接PD，QD.(1)求一次函数和反比例函数的表达式；(2)求△DPQ面积的最大值．参考答案1-5 CAACB 6-10DBBBB11. －312. －413. (4，1) 14.－32 15.－3 16. 10 17. b ＜c 18. ①②④19. 解：∵点A(3，－2)在反比例函数y ＝kx 的图象上，∴－2＝k 3，解得k ＝－6.∴△OBC 的面积＝12|k|＝12×6＝3.20. 解：(1)∵△AOB 的面积为4，A(4，m)，∴12 ×4×m ＝4，解得m ＝2，∴A(4，2)，∴k＝2×4＝8.(2)当y≤2(y≠0)时，x ＜0或x≥4.21. 解：(1)把A(1，4)代入y ＝m x 中，得m ＝4，∴反比例函数的解析式为y ＝4x .(2)把B(4，n)代入y ＝4x 中，得n ＝1，∴B(4，1).把A(1，4)，B(4，1)代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧4＝k ＋b ，1＝4k ＋b ，解得⎩⎪⎨⎪⎧k ＝－1，b ＝5.∴一次函数的解析式为y ＝－x ＋5. 22. 解：(1)把x ＝3代入y ＝2x －4，得y ＝6－4＝2，则点A 的坐标是(3，2). 把(3，2)代入y ＝k x ，得k ＝6，则反比例函数的解析式是y ＝6x .(2)根据题意，得⎩⎪⎨⎪⎧y ＝2x －4，y ＝6x .解方程组，得⎩⎪⎨⎪⎧x ＝3，y ＝2和⎩⎪⎨⎪⎧x ＝－1，y ＝－6，∴点B 的坐标是(－1，－6).23. 解：(1)∵OB ＝3，△AOB 的面积为3，∴B(3，0)，OA ＝2，即A(0，－2).∴⎩⎪⎨⎪⎧b ＝－2，3k ＋b ＝0.∴⎩⎪⎨⎪⎧k ＝23，b ＝－2.∴一次函数的解析式为y ＝23x －2.易知D(6，0)，将x ＝6代入y ＝23x －2，得y ＝2.∴C(6，2).由y ＝n x 过点C 可知n ＝12，∴反比例函数的解析式为y ＝12x .(2)当x ＞0时，kx ＋b －nx＜0的解集是0＜x ＜6.24. 解：(1)∵k ＞0，2≤x≤3，∴y 1随x 的增大而减小，y 2随x 的增大而增大，∴当x ＝2时，y 1取得最大值，为k 2 ＝a ①，y 2取得最小值，为－k2 ＝a －4②.联立①，②，得a ＝2，k ＝4.(2)圆圆的说法不正确，理由：设m ＝m 0，且－1＜m 0＜0，则m 0＜0，m 0＋1＞0，∴当x ＝m 0时，p ＝y 1＝k m 0 <0，当x ＝m 0＋1时，q ＝y 1＝km 0＋1＞0，∴p ＜0＜q ，∴圆圆的说法不正确．25. 解：(1)把A(0，－4)，B(2，0)代入一次函数y ＝kx ＋b ，得⎩⎪⎨⎪⎧b ＝－4，2k ＋b ＝0， 解得⎩⎪⎨⎪⎧k ＝2，b ＝－4， ∴一次函数的表达式为y ＝2x －4，当x ＝3时，y ＝2×3－4＝2，∴点C 的坐标为(3，2)，∵点C 在反比例函数y ＝mx (x ＞0)的图象上，∴m ＝3×2＝6，∴反比例函数的表达式为y＝6x. (2)∵点P 在反比例函数的图象上，横坐标为n ，点Q 在一次函数的图象上，PQ ∥y 轴，∴点P 的坐标为(n ，6n )，点Q 的坐标为(n ，2n －4)，又0＜n ＜3，∴PQ ＝6n －(2n －4)，∴S △PDQ ＝12 n[6n －(2n －4)]＝－n 2＋2n ＋3＝－(n －1)2＋4，∵－1＜0，∴当n ＝1时，S 最大＝4.。

一、选择题（每题5分，共25分）1. 下列各数中，绝对值最小的是（）A. -3B. 0C. 2D. -52. 已知a > 0，且a² + 2a + 1 = 0，则a的值为（）A. 1B. -1C. 2D. -23. 若a、b是方程x² - 3x + 2 = 0的两个实数根，则a + b的值为（）A. 2B. 3C. 4D. 54. 在直角坐标系中，点A（2，3）关于x轴的对称点是（）A. （2，-3）B. （-2，3）C. （2，-3）D. （-2，-3）5. 若sin A = 1/2，且A为锐角，则cos A的值为（）A. √3/2B. 1/2C. √3/4D. 1/4二、填空题（每题5分，共25分）6. 已知x² - 4x + 4 = 0，则x的值为______。

7. 若a、b是方程2x² - 5x + 2 = 0的两个实数根，则a + b的值为______。

8. 在直角坐标系中，点B（-3，4）关于y轴的对称点是______。

9. 若sin A = √3/2，且A为第二象限角，则cos A的值为______。

10. 若a、b、c是方程x³ - 6x² + 11x - 6 = 0的三个实数根，则a² + b² + c²的值为______。

三、解答题（共50分）11. （10分）解下列方程：(1) 2x² - 5x + 3 = 0(2) x² - 4x + 4 = 012. （15分）已知在直角坐标系中，点P（2，3）和点Q（-1，-2），求：(1) 点P关于x轴的对称点P'的坐标；(2) 直线PQ的方程。

13. （15分）已知sin A = 3/5，cos B = 4/5，且A、B均为锐角，求：(1) sin A + cos B的值；(2) sin (A + B)的值。

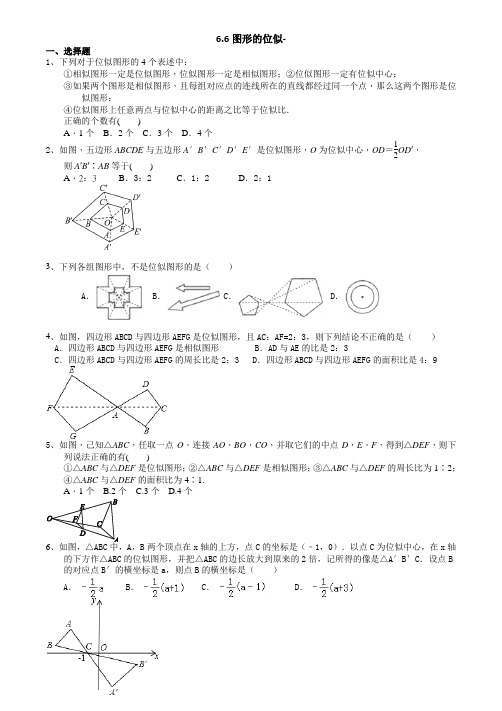
6.6图形的位似-一、选择题1、下列对于位似图形的4个表述中：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比． 正确的个数有( )A ．1个B ．2个C ．3个D ．4个2、如图，五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形，O 为位似中心，OD ＝12OD ′，则A ′B ′∶AB 等于( )A ．2：3B ．3：2C ．1：2D ．2：13、下列各组图形中，不是位似图形的是（ ）A ．B ．C ．D ．4、如图，四边形ABCD 与四边形AEFG 是位似图形，且AC ：AF=2：3，则下列结论不正确的是（ ） A ．四边形ABCD 与四边形AEFG 是相似图形 B ．AD 与AE 的比是2：3C ．四边形ABCD 与四边形AEFG 的周长比是2：3 D ．四边形ABCD 与四边形AEFG 的面积比是4：95、如图，己知△ABC ，任取一点O ，连接AO ，BO ，CO ，并取它们的中点D ，E ，F ，得到△DEF ，则下列说法正确的有( )①△ABC 与△DEF 是位似图形；②△ABC 与△DEF 是相似图形；③△ABC 与△DEF 的周长比为1∶2；④△ABC 与△DEF 的面积比为4∶1. A ．1个 B .2个 C .3个 D .4个A ，B 两个顶点在x 轴的上方，点C 的坐标是（﹣1，0）．以点C 为位似中心，在x 轴的下方作△ABC 的位似图形，并把△ABC 的边长放大到原来的2倍，记所得的像是△A ′B ′C ．设点B 的对应点B ′的横坐标是a ，则点B 的横坐标是（ ）A ．B ．C ．D ．7、如图，已知点E （﹣4，2)，点F （﹣1，﹣1），以O 为位似中心，把△EFO 放大为原来的2倍，则E 点的对应点坐标为（ ） A ．（2,﹣1）或（﹣2，1） B ．（8，-4）或（﹣8，4） C ．（2，﹣1） D ．（8，﹣4）8、如图所示，正方形OEFG 和正方形ABCD 是位似图形，点F 的坐标为(－1，1)，点C 的坐标为(－4，2)，则这两个正方形位似中心的坐标是________．A.(2，0)B.(－43，23)C.(2,2)D.(2，0)或(－43，23)二、填空题9、如图，△ABO 三个顶点的坐标分别为A (2，4)，B (6，0)，O (0，0)．以原点O 为位似中心，把这个三角形缩小为原来的12，可以得到△A ′B ′O ，已知点B ′的坐标是(3，0)，则点A ′的坐标是________．10、如图所示，△ABC 与△A ′B ′C ′是位似图形，且位似比是1∶2.若AB ＝2 cm ，则A ′B ′＝_______cm ，在图中画出位似中心O .11111是以点O 为位似中心的位似三角形，若C 1为OC 的中点，AB ＝4，1B 1的长为________.12ABCDE 放大后得到五边形A ′B ′C ′D ′E ′，已知OA=10cm ，OA ′=20cm ，则五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是______．13、如图，A′B′∥AB ，B′C′∥BC ，且OA′∶A′A ＝4∶3，则△ABC 与___________是位似图形，相似比是_________．14、如图，△ABC与△DEF位似，位似中心为点O，且BC：EF＝3：2，则S△ABC：S△DEF＝．15、如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD＝90°，CO＝CD，若B（1，0），则点C的坐标为．16、如图，O点是△ABC与△D1E1F1的位似中心，△ABC的周长为1.若D1、E1、F1分别是线段OA、OB、OC的中点，则△D1E1F1的周长为12；若OD2＝13OA、OE2＝13OB、OF2＝13OC，则△D2E2F2的周长为13；…若ODn＝13OA、OEn＝13OB、OFn＝13OC，则△DnEnFn的周长为_____．(用正整数n表示)三、解答题17、如图，在网格图中，每格是边长为1的正方形，四边形ABCD的顶点均为格点．（1）请以点O为位似中心，在网格中作出四边形A'B'C'D'，使四边形A'B'C'D'与四边形ABCD位似，且＝2；（2）线段C'D'的长为；（3）求出△A'B'O的面积．18、如图，在矩形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BC于E点，连接DE交OC于F点，作FG⊥BC于G点，则△ABC与△FGC是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，请说明理由．19、如图，△ABC 三个顶点的坐标分别为A (－1，3)，B (－1，1)，C (－3，2)．(1)请画出△ABC 关于y 轴对称的△A 1B 1C 1； (2)以原点O 为位似中心，将△A 1B 1C 1放大为原来的2倍，得到△A 2B 2C 2，请在第三象限内画出△A 2B 2C 2，并求出S △A △A 2B 2C 2的值．20、如图，方格纸中每个小正方形的边长为1，ABC 和DEF 的顶点都在方格纸的格点上．（1）判断ABC 和DEF 是否相似，并说明理由；（2）以点E 为中心，在位似中心的同侧画出EDF 的一个位似11ED F ，使得它与EDF 的相似比为2:1； （3）求ABC 与11ED F 的面积比．6.6图形的位似-苏科版九年级数学下册 巩固训练（答案）一、选择题1、下列对于位似图形的4个表述中：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比． 正确的个数有( )A ．1个B ．2个C ．3个D ．4个[解析] 相似图形不一定是位似图形，位似图形一定是相似图形，①错误；位似图形一定有位似中心，②正确；如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形，③正确；位似图形上对应两点与位似中心的距离之比等于位似比，④错误．故选B .2、如图，五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形，O 为位似中心，OD ＝12OD ′，则A ′B ′∶AB 等于( )A ．2：3B ．3：2C ．1：2D ．2：1[解析] 因为OD ＝12OD′，所以OD OD′＝12，所以五边形ABCDE 与五边形A′B′C′D′E′的位似比为12，所以AB A′B′＝12，所以A′B′∶AB ＝2∶1.故选 D3、下列各组图形中，不是位似图形的是（ B ）A ．B ．C ．D ．4、如图，四边形ABCD 与四边形AEFG 是位似图形，且AC ：AF=2：3，则下列结论不正确的是（ B ） A ．四边形ABCD 与四边形AEFG 是相似图形B ．AD 与AE 的比是2：3C ．四边形ABCD 与四边形AEFG 的周长比是2：3 D ．四边形ABCD 与四边形AEFG 的面积比是4：95、如图，己知△ABC ，任取一点O ，连接AO ，BO ，CO ，并取它们的中点D ，E ，F ，得到△DEF ，则下列说法正确的有( )①△ABC 与△DEF 是位似图形；②△ABC 与△DEF 是相似图形；③△ABC 与△DEF 的周长比为1∶2；④△ABC 与△DEF 的面积比为4∶1. A ．1个 B .2个 C .3个 D .4个ABC 与△DEF 是位似图形，故①正确； △ABC 与△DEF 是相似图形，故②正确；∵将△ABC 的三边缩小为原来的一半得到△DEF ，∴△ABC 与△DEF 的周长比为2∶1，故③错误；根据面积比等于相似比的平方，得△ABC 与△DEF 的面积比为4∶1，故④正确．故选C.6、如图，△ABC 中，A ，B 两个顶点在x 轴的上方，点C 的坐标是（﹣1，0）．以点C 为位似中心，在x 轴的下方作△ABC 的位似图形，并把△ABC 的边长放大到原来的2倍，记所得的像是△A ′B ′C ．设点B 的对应点B ′的横坐标是a ，则点B 的横坐标是（ D ）A ．B ．C ．D ．7、如图，已知点E （﹣4，2)，点F （﹣1，﹣1），以O 为位似中心，把△EFO 放大为原来的2倍，则E 点的对应点坐标为（ B ） A ．（2,﹣1）或（﹣2，1） B ．（8，-4）或（﹣8，4） C ．（2，﹣1） D ．（8，﹣4）8、如图所示，正方形OEFG 和正方形ABCD 是位似图形，点F 的坐标为(－1，1)，点C 的坐标为(－4，2)，则这两个正方形位似中心的坐标是________．A.(2，0)B.(－43，23)C.(2,2)D.(2，0)或(－43，23)[①当两个位似图形在位似中心O ′同旁时，位似中心就是直线CF 与x 轴的交点．设直线CF 的函数表达式为y ＝kx ＋b (k ≠0)，将C (－4，2)，F (－1，1)的坐标代入，得⎩⎨⎧－4k ＋b ＝2，－k ＋b ＝1，解得⎩⎨⎧k ＝－13，b ＝23，即y ＝－13x ＋23.令y ＝0，得x ＝2，∴点O ′的坐标是(2，0)． ②当位似中心O ′在两个正方形之间时，可求直线OC 的函数表达式为y ＝－12x ，直线DE 的函数表达式为y ＝14x ＋1，由⎩⎨⎧y ＝－12x ，y ＝14x ＋1， 解得⎩⎨⎧x ＝－43，y ＝23，即O ′(－43，23)．故答案为(2，0)或(－43，23)．二、填空题9、如图，△ABO 三个顶点的坐标分别为A (2，4)，B (6，0)，O (0，0)．以原点O 为位似中心，把这个三角形缩小为原来的12，可以得到△A ′B ′O ，已知点B ′的坐标是(3，0)，则点A ′的坐标是________．[解析] ∵点A 的坐标为(2，4)，以原点O 为位似中心，把这个三角形缩小为原来的12，∴点A ′的坐标是(2×12，4×12)，即(1，2)．故答案为(1，2)．10、如图所示，△ABC 与△A ′B ′C ′是位似图形，且位似比是1∶2.若AB ＝2 cm ，则A ′B ′＝__4______cm ，在图中画出位似中心O .A 1B 1C 1是以点O 为位似中心的位似三角形，若C 1为OC 的中点，AB ＝4，则A 1B 1的长为________.[解析] ∵△ABC 和△A 1B 1C 1是以点O 为位似中心的位似三角形，C 1为OC 的中点，AB ＝4，∴A 1B 1＝12AB ＝2.12、如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形A ′B ′C ′D ′E ′，已知OA=10cm ，OA ′=20cm ，则五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是__1：2____．13、如图，A′B′∥AB ，B′C′∥BC ，且OA′∶A′A ＝4∶3，则△ABC 与___________是位似图形，相似比是_________．答案:△A′B′C′；7∶414、如图，△ABC 与△DEF 位似，位似中心为点O ，且BC ：EF ＝3：2，则S △ABC ：S △DEF ＝ ．解：∵△ABC 与△DEF 位似，∴△ABC ∽△DEF ， ∵BC ：EF ＝3：2，∴＝（）2＝，故答案为：9：4．15、如图，△OAB 与△OCD 是以点O 为位似中心的位似图形，相似比为1：2，∠OCD ＝90°，CO ＝CD ，若B （1，0），则点C 的坐标为 ．解：∵∠OAB ＝∠OCD ＝90°，AO ＝AB ，CO ＝CD ，等腰Rt △OAB 与等腰Rt △OCD 是位似图形，点B 的坐标为（1，0），∴BO ＝1，则AO ＝AB ＝， ∴A （，），∵等腰Rt △OAB 与等腰Rt △OCD 是位似图形，O 为位似中心，相似比为1：2， ∴点C 的坐标为：（1，1）． 故答案为：（1，1）．16、如图，O 点是△ABC 与△D 1E 1F 1的位似中心，△ABC 的周长为1.若D 1、E 1、F 1分别是线段OA 、OB 、OC 的中点，则△D 1E 1F 1的周长为12；若OD 2＝13OA 、OE 2＝13OB 、OF 2＝13OC ，则△D 2E 2F 2的周长为13；…若ODn ＝13OA 、OEn ＝13OB 、OFn ＝13OC ，则△DnEnFn 的周长为___1n __．(用正整数n 表示)三、解答题17、如图，在网格图中，每格是边长为1的正方形，四边形ABCD的顶点均为格点．（1）请以点O为位似中心，在网格中作出四边形A'B'C'D'，使四边形A'B'C'D'与四边形ABCD位似，且＝2；（2）线段C'D'的长为；（3）求出△A'B'O的面积．解：（1）如图所示，四边形A'B'C'D'即为所求；（2）线段C'D'的长为＝，故答案为：；（3）△A'B'O的面积为×4×2+×4×2＝4+4＝8．18、如图，在矩形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BC于E点，连接DE交OC于F点，作FG⊥BC于G点，则△ABC与△FGC是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，请说明理由．解:△ABC与△FGC是位似图形，位似中心是点C.因为在矩形ABCD中，AD∥B C，所以∠FAD＝∠FCE，∠FDA＝∠FEC，所以△AFD∽△CFE，所以CF CE AF AD=因为AD＝BC，所以CF CE AF CB=因为∠ABC＝90°，OE⊥BC，所以OE∥AB.因为OA＝OC，所以CE＝12BC，所以CFAF＝12,所以CFAC＝13.即△ABC与△FGC的相似比为3∶1.19、如图，△ABC三个顶点的坐标分别为A(－1，3)，B(－1，1)，C(－3，2)．(1)请画出△ABC关于y轴对称的△A1B1C1；(2)以原点O为位似中心，将△A1B1C1放大为原来的2倍，得到△A2B2C2，请在第三象限内画出△A2B2C2，并求出S△A1B1C1S△A2B2C2的值．解：(1)如图所示，△A1B1C1即为所求．(2)如图所示，△A2B2C2即为所求．∵将△A1B1C1放大为原来的2倍得到△A2B2C2，∴△A1B1C1∽△A2B2C2，且位似比为12，∴S△A1B1C1∶S△A2B2C2＝(12)2＝14.20、如图，方格纸中每个小正方形的边长为1，ABC和DEF的顶点都在方格纸的格点上．（1）判断ABC和DEF是否相似，并说明理由；（2）以点E为中心，在位似中心的同侧画出EDF的一个位似11ED F，使得它与EDF的相似比为2:1；（3）求ABC与11ED F的面积比．解:()1AB25AC5BC5EF10FD2ED22，，，，，======，∴BC10AC510AB2510EF FD ED10222======，，，∴BC AC ABEF FD ED==，∴ABC DEF∽；（2）延长ED到点1D，使12ED ED=，延长EF到点1F，使12EF EF=，连结11D F，则11ED F 为所求，如图；()113ABC DEF DEF D EF∽，∽，∴11ABC D EF∽，∴11ABC ED F与的面积比2211AC55()(D F822===．6.7 《用相似三角形解决问题》（满分120分；时间：120分钟）真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！题号一二三总分得分一、选择题（本题共计9小题，每题3 分，共计27分，）1. 如图，在中，．C.①②③D.①②③④ A.①② B.③④2 某同学想利用影长测量学校旗杆的高度，如图，他在某一时刻立米长的标杆测得其影厂为米，同时旗杆的投影一部分在地面上，另一部分在某一建筑的墙上，分别测得其长度为米和米，则学校旗杆的高度为（）米．A. B. C. D.3 如图，在中，＝，＝，点是的中点，连接，过点作，分别交，于点，，与过点且垂直于的直线相交于点，连接，给出以下五个结论：①；②＝；③点是的中点；④；⑤＝，其中正确结论有（）个．A. B. C. D.4. 如图，是一个照相机成像的示意图，如果底片宽，焦距是，所拍摄的外的景物的宽为( )A. B. C. D.5. 如图，在矩形中，点是的中点，的平分线交于点，将沿折叠，点恰好落在上点处，延长，交于点．有下列四个结论：①垂直平分；②平分；③；④．其中，将正确结论的序号全部选对的是（）A.①②③B.①②④C.②③④D.①②③④6. 如图，在正方形中，为正方形内一点，且，，将绕点逆时针旋转得到，连接、、，为的中点，连接．有下列结论：①为等腰直角三角形；②；③；④．其中正确结论的个数是（）A. B. C. D.7. 如图所示：两根竖直的电线杆长为，长为，交于于点点，则到地面的距离的长是（）A. B. C. D.8. 如图，为等边三角形，，，连接，为的中点，连接并倍长，连接、、．下列结论：①；②若，则；③在②的条件下，若，则．其中正确的有（）A.①②③都正确B.只有①②正确C.只有②③正确D.只有①③正确9 四边形为直角梯形，，为边上的中点，连接交于点，过点作于，的延长线交于点，则：①；②为的中点；③，则正确的结论有（）A.只有①②B.只有①③C.只有②③D.①②③二、填空题（本题共计7 小题，每题3 分，共计21分，）10. 有一支夹子如图所示，，，在夹子前面有一个长方体硬物，厚为，如果想用夹子的尖端、两点夹住、两点，那么手握的地方至少要张开________ ．11. 王宏身高米，为了测出路灯的高度，他从路灯出发沿平直道路以米/秒的速度向东匀速走开，某时他的影子长米，再过秒，他的影子长为米，则路灯高度为________米．12. 如图，测量小玻璃管管径的量具，的长为，被分为等份．如果玻璃管的管径正好对着量具上等份处，那么小玻璃管的管径________．13. 如图，在离某建筑物米处有一棵树，在某时刻，将长的竹竿竖直立在地面上，影长为，此时，树的影子照射到地面，还有一部分影子投影在建筑物的墙上，墙上的影子长为，那么这棵树高约为________米．14. 在同一时刻，米高的竹竿影长为米，那么影长为米的楼的高度为________米．15 如图，在等边中，于，点在的延长线上，点在上，，的延长线交的延长线于．若，，则________．三、解答题（本题共计7 小题，共计75分，）16 有一块三角形纸板（如图），，，小华想用它剪一个正方形，使正方形的每个顶点都在三角形的边上，请你帮她计算剪下的正方形的边长．17. 两棵树的高度分别是米，米，两棵树的根部之间的距离米．小强沿着正对这两棵树的方向从右向左前进，如果小强的眼睛与地面的距离为米，当小强与树的距离等于多少时，小强的眼睛与树、的顶部、恰好在同一条直线上，请说明理由．18. 如图，在梯形中，，，，，动点从点出发沿方向以的速度向点运动，动点同时以相同速度从点出发沿方向向终点运动，其中一个动点到达端点时，另一个动点也随之停止运动．（1）求的长：（2）当的面积为时，求运动时间；（3）当运动时间为何值时，的面积达到最大，并求出的最大值．19. 如图，小明和大伟想利用所学的几何知识测量学校操场上旗杆的高度，他们的测量方案如下：他们两次利用镜子，第一次他把镜子放在点，人在点正好在镜子中看见旗杆顶端：第二次把镜子放在点，人在点正好在镜子中看到旗杆顶端；已知图中的所有点均在同一平面内，，，，小明的眼晴距离地面的距离＝＝米，量得＝米，＝米，＝米，请你利用这些数据求出旗杆的高度．20. 如图，在中，，，，动点从点开始沿边向点以每秒个单位长度的速度运动，动点从点沿边向点以每秒个单位长度的速度运动，过点作，交于点，连接．点，分别从、同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为秒．（1）当为何值时，的面积为？（2）当为何值时，以点、、为顶点的三角形与相似？（3）是否存在这样的，使为等腰三角形？若存在，求出的值；若不存在，请说明理由．21. 如图，在中，，．（1）求的度数；（2）如图，延长到，使，延长到，使，、交于点．求证：；（3）如图，点、分别是、上的动点，且，作，，分别交于点、，线段、、能否始终组成直角三角形？给出你的结论，并说明理由．22. 如图，四边形是矩形，点是对角线上一动点（不与、重合），连接，过点作，交射线于点，已知，．设的长为．（1）________；当时，________；（2）①试探究：否是定值？若是，请求出这个值；若不是，请说明理由；②连接，设的面积为，求的最小值．（3）当是等腰三角形时．请求出的值；。

2021—2022学年度下学期九年级随堂练习数 学 试 卷人教版一、选择题(每小题3 分，共30 分) 1.下列方程是一元二次方程的是 （）A.3x-2=0B.x 2-3=5C.x+y 2=4D.211x x+= 2.抛物线y=-3x 2 的顶点坐标为（ ） A.（0，0） B.（0，-3） C.（-3,0）D.（-3，-3）3.在下图右侧的四个三角形中，不能由图示△ABC 经过旋转或平移得到的是（）4.如图，⊙O 的半径为4，点A 为⊙O 上一点，OA 的垂直平分线分别交⊙O 于点B ，C ，则BC 的长为（ ）A. 3B. 4C. 23D. 435. “比赛中，郭艾伦罚篮命中”，这一事件是（）A.必然事件B. 不可能事件C.随机事件D.确定事件6. 如图，点C 在反比例函数y =kx(x ＞0)的图像上，过点C 的直线与x轴,y 轴分别交于点A ，B ，且AB=AC ，△ABO 的面积为1，则k 的值为（ ）A.4B. 340 6C. 2D. 17.如图，三个边长相等的正方形如图摆放，则∠1+∠2+∠3的值为（）A.60°B.75°C.90°D.105°8.如图，点A ，B ，C 在正方形网格的格点上，则sin ∠ABC= （）A.26 B.2626 26139.图2是图1 中的长方体的三视图，若用S 表示面积，且S 主=x 2+2x ，S 左=x 2+x ，则S 俯=（A. x 2+2B. 2x 2+3xC. x 2+3x+2D. x 2+2x+1第9 题图10.如图，正方形ABCD 的边长为2，在正方形ABCD 的右侧以边CD 为底边作等腰△CDE ，连接AE ，AC ，AE 交CD 于点F ；则下列说法:①S △ADE =1，②当△CDE 为直角三角形时，S △ACE =2③当△CDE 为直角三角形时，sin ∠CAE=55，④当△CDE 为等边三角形时，S △CEF =33 （）A.①②B.②③C.①③④D.①②③④二、填空题（每小题3 分，共24 分）11.一元二次方程2x2-6=0的解为▲ ．12.从长度分别为2cm，3cm，5cm，6cm的四根木棍中随机取三根，能构成三角形的概率是▲ .13.如图，AB为⊙0的直径，点C，点D是⊙0上的两点，连接CB，CD，BD，若∠BDC=120°，则∠ABC的度数为是▲ .14.如图，点D是矩形ABCO的对称中心，点A（6,0），C（0,4），经过点D的反比例函数的图像交AB于点P，则点P的坐标为▲ ．第14题图第15题图第16题图15.二次函数y=mx2+2mx-(3-m)的图像如图所示，则m的取值范围是▲ ．16.如图，将矩形ABCD绕点A逆时针旋转α（0°＜α＜90°），连接EC，ED,当α为▲ °时EC=ED．17.如图，将边长为4的等边△ABC沿射线BC平移得到△DEF，点G，H分别为AC，DF的中点，连接GH，点P 为GH 的中点，连接AP，CP.当△APC为直角三角形时，BE= ▲ 第17题图第18题图18.如图，△ABC和△DEF均为等腰三角形，∠ACB=∠DFE=90°，点D 为AB的中点，△DEF绕点D旋转，旋转过程中，线段DF与线段AC相交于点G，线段DE与BC的延长线相交于点H，若AB=,AG=2，则CH的长为▲ .三、解答题（19 题10 分，20题12分，共22 分）19.4张相同的卡片上分别写有数字-1，1，2，3，从中任意抽取两张卡片，卡片上的数字恰好都是一元二次方程x2-2x-3=0的解的概率为多少？请用画树状图或列表的方法说明理由.20.某批发商以每件50 元的价格购进800件卫衣，第一个月以单价80元销售，售出了200 件，第二个月如果单价不变，预计仍可售出200 件，批发商为增加销售量，决定降价销售.根据市场调查，单价每降低1 元，可多售出10 件，但最低单价应高于购进的价格；第二个月结束后，批发商将剩余的卫衣一次性清仓销售，清仓时单价为40 元，设第二个月单价降低x 元.（1）填表（需化简）（2单价应是多少元？四、（每小题12分，共24分）21. 如图，直线y=-x+1 与反比例函数y kx的图像相交，其中一个交点的横坐标是-2.（1）求反比例函数的表达式；（2）将直线y=-x+1向下平移2个单位，求平移后的直线与反比例函数y= kx的图像的交点坐标；（3）直接写出一个一次函数，使其过点（0，-3），且与反比例函数y=k x的图像没有公共点.22.如图，在Rt△ABC中，∠ACB=90°，⊙O与AC，BC分别相切于点D，E，AO平分∠BAC，连接BO.（1）求证：AB是⊙O的切线；（2）若AD=BC=3，⊙O 的半径为1，求阴影部分的面积.五、（本题12 分）23.如图，在矩形ABCD中，点E为边AB上的一动点（点E不与点A，B重合），连接DE，过点C作CF⊥DE，垂足为F.（1）求证：△ADE∽△FCD；（2）若AD=6，tan∠DCF=13，求AE的长.六、（本题12 分）24．风力发电是指把风的动能转为电能.风能是一种清洁无公害的可再生能源，利用风力发电非常环保，且风能蕴量巨大，因此风力发电日益受到我们国家的重视.某校学生开展综合实践活动，测量风力发电扇叶轴心的高度.如图，已知侧倾器的高度为1.6m，在测点A处安置侧倾器，测得扇叶轴心点M的仰角∠MCE=33°，再与点A相距3.5m的测点B处安置侧倾器，测得点M 的仰角∠MDE=45°（点A，B与N在一条直线上），求扇叶轴心离地面的高度MN的长.（结果精确到1m；参考数据：sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）七、（本题12 分）25.如图，边长为2的正方形ABCD中，点E为边CD上一动点（不与点C，D重合），连接BE，过点A，C分别作AF⊥BE，CG⊥BE，垂足分别为F，G，点O为正方形ABCD的中心，连接OF，OG.（1）求证：BF=CG；（2）请判定△OFG的形状，并说明理由；（3）当△OFG的面积为15时，请直接写出CE的长.八、（本题14 分）26.如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（1,0）和点B，与y轴交于点C（0,4），对称轴为直线x=5 2 .（1）求抛物线的解析式；（2）如图1，连接BC，若点M是线段BC上一动点（不与B，C重合），过点M作MN∥y轴，交抛物线于点N，连接ON，当MN的长度最大时，判断四边形OCMN的形状并说明理由；（3）如图2，在（2）的条件下，D是OC的中点，过点N的直线与抛物线交于点E，且∠DNE=2∠ODN.在y轴上是否存在点F，使得△BEF为等腰三角形？若存在，请直接写出点F的坐标，无需说明理由；若不存在，请说明理由.。

28.1锐角三角函数一．选择题1．计算sin230°+cos260°的结果为（）A．B．C．1D．2．在Rt△ABC中，∠C＝90°，cos A＝，则sin A＝（）A．B．C．D．3．在Rt△ABC中，锐角A的对边和斜边同时扩大100倍，sin A的值（）A．扩大100倍B．缩小C．不变D．不能确定4．如图，在Rt△ABC中，∠C＝90°，AB＝4，AC＝3，则cos B＝＝（）A．B．C．D．5．下列式子正确的是（）A．cos60°＝B．cos60°+tan45°＝1C．tan60°﹣＝0D．sin230°+cos230°＝6．规定：sin（﹣x）＝﹣sin x，cos（﹣x）＝cos x，cos（x+y）＝cos x cos y﹣sin x sin y，给出以下四个结论：（1）sin（﹣30°）＝﹣；（2）cos2x＝cos2x﹣sin2x；（3）cos（x﹣y）＝cos x cos y+sin x sin y；（4）cos15°＝．其中正确的结论的个数为（）A．1个B．2个C．3个D．4个7．如图，在6×6的正方形网格中，△ABC的顶点都在小正方形的顶点上，则tan∠BAC的值是（）A．B．C．D．8．若角α，β都是锐角，以下结论：①若α＜β，则sinα＜sinβ；②若α＜β，则cosα＜cosβ；③若α＜β，则tanα＜tanβ；④若α+β＝90°，则sinα＝cosβ．其中正确的是（）A．①②B．①②③C．①③④D．①②③④9．在△ABC中，∠A，∠B都是锐角，tan A＝1，sin B＝，你认为△ABC最确切的判断是（）A．等腰三角形B．等腰直角三角形C．直角三角形D．锐角三角形10．因为cos60°＝，cos240°＝﹣，所以cos240°＝cos（180°+60°）＝﹣cos60°；由此猜想、推理知：当α为锐角时有cos（180°+α）＝﹣cosα，由此可知：cos210°＝（）A．﹣B．﹣C．﹣D．﹣二．填空题11．已知α是锐角，且sin（α+15°）＝，那么tanα＝．12．如图，已知Rt△ABC中，斜边AB的长为m，∠B＝40°，则直角边AC的长是．13．如图，边长为1的小正方形网格中，点A，B，C，D，E均在格点上，半径为2的⊙A 与BC交于点F，则tan∠DEF＝．14．在Rt△ABC中，∠C＝90°，cos A＝，则BC：AC：AB＝．15．如图，AD是正五边形ABCDE的一条对角线，则∠BAD＝．三．解答题16．计算：3tan30°+cos230°﹣2sin60°17．如图，在Rt△ABC中，∠C＝90°，tan A＝，BC＝2，求AB的长．18．（1）在△ABC中，∠B＝45°，cos A＝．求∠C的度数．（2）在直角三角形ABC中，已知sin A＝，求tan A的值．参考答案一．选择题1．解：sin230°+cos260°＝（）2+（）2＝+＝．故选：A．2．解：∵sin2A+cos2A＝1，即sin2A+（）2＝1，∴sin2A＝，∴sin A＝或﹣（舍去），∴sin A＝．故选：C．3．解：锐角A的三角函数值随着∠A角度的变化而变化，而角的大小与边的长短没有关系，因此sin A的值不会随着边长的扩大而变化，故选：C．4．解：∵在Rt△ABC中，∠C＝90°，AB＝4，AC＝3，∴BC＝＝，∴cos B＝＝．故选：C．5．解：A．cos60°＝，故本选项不符合题意；B．cos60°+tan45°＝+1＝1，故本选项不符合题意；C．tan60°﹣＝﹣＝﹣＝0，故本选项符合题意；D．sin230°+cos230°＝1，故本选项不符合题意；故选：C．6．解：（1），故此结论正确；（2）cos2x＝cos（x+x）＝cos x cos x﹣sin x sin x＝cos2x﹣sin2x，故此结论正确；（3）cos（x﹣y）＝cos[x+（﹣y）]＝cos x cos（﹣y）﹣sin x sin（﹣y）＝cos x cos y+sin x sin y，故此结论正确；（4）cos15°＝cos（45°﹣30°）＝cos45°cos30°+sin45°sin30°＝＝＝，故此结论错误．所以正确的结论有3个，故选：C．7．解：如图，过点B作BD⊥AC，交AC延长线于点D，则tan∠BAC＝＝，故选：C．8．解：①∵sinα随α的增大而增大，∴若α＜β，则sinα＜sinβ，此结论正确；②∵cosα随α的增大而减小，∴若α＜β，则cosα＞cosβ，此结论错误；③∵tanα随α的增大而增大，∴若α＜β，则tanα＜tanβ，此结论正确；④若α+β＝90°，则sinα＝cosβ，此结论正确；综上，正确的结论为①③④，故选：C．9．解：由题意，得∠A＝45°，∠B＝45°．∠C＝180°﹣∠A﹣∠B＝90°，故选：B．10．解：∵cos（180°+α）＝﹣cosα，∴cos210°＝cos（180°+30°）＝﹣cos30°＝﹣．故选：C．二．填空题11．解：∵sin60°＝，∴α+15°＝60°，解得，α＝45°，∴tanα＝tan45°＝1，故答案为：1．12．解：在Rt△ABC中，sin B＝，∴AC＝AB•sin B＝m sin40°，故答案为：m sin40°．13．解：由题意可得：∠DBC＝∠DEF，则tan∠DEF＝tan∠DBC＝＝．故答案为：．14．解：在Rt△ABC中，∠C＝90°，∵cos A＝＝，设AC＝2x，则AB＝3x，∴BC＝＝x，∴BC：AC：AB＝：2：3．15．解：∵正五边形ABCDE的内角和为（5﹣2）×180°＝540°，∴∠E＝×540°＝108°，∠BAE＝108°又∵EA＝ED，∴∠EAD＝×（180°﹣108°）＝36°，∴∠BAD＝∠BAE﹣∠EAD＝72°，故答案为：72°．三．解答题16．解：原式＝＝＝．17．解：∵在Rt△ABC中，∠C＝90°，∴tan A＝＝．∵BC＝2，∴＝，AC＝6．∵AB2＝AC2+BC2＝40，∴AB＝．18．解：（1）∵在△ABC中，cos A＝，∴∠A＝60°，∵∠B＝45°，∴∠C＝180°﹣∠B﹣∠A＝75°；（2）∵sin A＝＝，设BC＝4x，AB＝5x，∴AC＝3x，∴tan A＝＝＝．28.2 解直角三角形及其应用（满分120分；时间：120分钟）一、选择题（本题共计10 小题，每题3 分，共计30分，）1. 在中，，，，则的长度为（）A. B. C. D.2. 在高为米的楼顶测得地面上某目标的俯角为，那么楼底到该目标的水平距离是（）A. B. C. D.3. 如图，利用标杆测量建筑物的高度，如果标杆长为米，若，米，则楼高是（）A.米B.米C.米D.米4. 如图，一艘海轮位于灯塔的北偏东方向，距离灯塔海里的处，它沿正南方向航行一段时间后，到达位于灯塔的南偏东方向上的处，这时，海轮所在的处与灯塔的距离为（）A.海里B.海里C.海里D.海里5. 在直角中，＝，＝，，下列判断正确的是（）A.＝B.C.＝D.＝6. 如图，，，于点，则的长为（）A. B. C. D.7. 如图，为了测量小河的宽度，小明从河边的点处出发沿着斜坡行走米至坡顶处，斜坡的坡度为＝，在点处测得小河对岸建筑物顶端点的俯角＝，已知建筑物的高度为米，则小河的宽度约为（精确到米，参考数据：＝，＝，＝）（）A.米B.米C.米D.米8. 如图，等腰的底角为，底边上的高，则腰、的值为（）A. B. C. D.9. 在中，是斜边上的高，如果，，那么等于（）A. B. C. D.10. 如图，小明同学在东西方向的环海路处，测得海中灯塔在北偏东方向上，在处东米的处，测得海中灯塔在北偏东方向上，则灯塔到环海路的距离米．A. B. C. D.二、填空题（本题共计10 小题，每题3 分，共计30分，）11. 小明同学从地出发沿北偏东的方向到地，再由地沿南偏西的方向到地，则________．12. 在中，，，，则的值是________．13. 在中，，若，，则________．14. 一次综合实践活动中，小明同学拿到一只含角的三角板和一只含角的三角板，如图放置恰好有一边重合，则的值为________．15. 如图，已知是等腰底边上的高，且．上有一点，满足．那么的值是________．16. 某市为了美化环境，计划在如图所示的三角形空地上种植草皮，已知这种草皮每平方米售价为元，则购买这种草皮至少需要________元．17. 如图，水平面上有一个坡度的斜坡，矩形货柜放置在斜坡上，己知．，，则点离地面的高为________．（结果保留根号）18. 如图，测量河宽（河的两岸平行），在点测得，，则河宽约为________．（用科学计算器计算，结果精确到）19. 如图，设，，为射线上一点，于，于，则等于________ （用、的三角函数表示）20. 如图，某飞机于空中处探测得地面目标，此时飞行高度米，从飞机上看地面控制点的俯角为，那么飞机到控制点的距离是________米．三、解答题（本题共计6 小题，共计60分，）21. 如图，在中，，是高，，求证：．22. 一艘轮船由西向东航行，在处测得小岛的方位角是北偏东，又航行海里后，在处测得小岛的方位角是北偏东，若小岛周围海里内有暗礁，则该船一直向东航行有无触礁的危险？23. 某航班在某日凌晨从甲地（记为）起飞，沿北偏东方向出发，以的速度直线飞往乙地，但飞机在当日凌晨左右在处突然改变航向，沿北偏西方向飞到处消失，如果此航班在处发出求救信号，又测得在的北偏西方向，求与求救点的距离（结果保留整数，参考数据：，）．24. 如图，某中心广场灯柱被钢缆固定，已知米，且．（1）求钢缆的长度；（2）若米，灯的顶端距离处米，且，则灯的顶端距离地面多少米？25. 已知：在四边形中，，，，，（1）求的值；（2）求的长．26. 某校兴趣小组想测量一座大楼的高度．如图，大楼前有一段斜坡，已知的长为米，它的坡度＝，在离点米的处，用测角仪测得大楼顶端的仰角为，测角仪的高为米，求大楼的高度约为多少米？（结果精确到米）（参考数据：，，，．）参考答案一、选择题（本题共计10 小题，每题 3 分，共计30分）1.【答案】B【解答】解：在中，，、∵，∴．故选．2.【答案】B【解答】∵＝，＝，∴＝＝．3.【答案】B【解答】解：如图，∵在中，，米，，∴（米）．又∵米，∴米．又∵在直角中，，，∴（米）故选：．4.【答案】A【解答】解：过点作于点，由题意可得出：，，(海里)，故（海里），则（海里）．故选5.【答案】D【解答】∵在直角中，＝，＝，，，∴，∴，∵，，∴，6.【答案】C【解答】解：∵，∴，∴，∵，∴．故选．7.【答案】B【解答】作交的延长线于，作于，则四边形为矩形，∴＝，＝＝，设＝米，∵斜坡的坡度为＝，∴＝米，由勾股定理得，＝，解得，＝，∴＝米，＝米，∴＝＝＝，在中，，则，∴＝＝（米），8.【答案】C【解答】解：∵等腰的底角为，底边上的高，∴．故选．9.【答案】C【解答】解：．故选．10.【答案】C【解答】解：∵，．又∵，∴．∴．在直角中，．故选．二、填空题（本题共计10 小题，每题 3 分，共计30分）11.【答案】【解答】解：如图：由题意知，，，∴.故答案为： .12.【答案】【解答】解：作于，如图，∵，∴，在中，，∵，∴，∵，∴，∴，在中，，∴．故答案为．13.【答案】【解答】解：在中，∵，∴为斜边．∴．14.【答案】【解答】解：作于，如图，设，在中，∵，∴，在中，∵，∴，∴，在中，，在中，，∴••，•，∴．故答案为．15.【答案】【解答】解：作于，如图，∵为等腰三角形，为高，∴，∴设，，而，∴，∵，∴，∴，即，∴，，∴，在中，∴．故答案为．16.【答案】【解答】解：如图，作边的高，设与的延长线交于点，∵，∴，∴，∵，∴，∵每平方米售价元，∴购买这种草皮的价格为元．故答案为：．17.【答案】【解答】解：作，垂足为，且与相交于．∵，，∴，∴，∵，∴，∴，，设，则，∴，∴，∴．故答案是：．18.【答案】【解答】解：在中，∵，，∴故答案为．19.【答案】【解答】解：∵于，于，∴，∴，，∴．故答案为：．20.【答案】【解答】解：在直角中，，，∴．三、解答题（本题共计6 小题，每题10 分，共计60分）21.【答案】证明：∵，，∴，∴，∵，，∴，∴，∵，∴．【解答】证明：∵，，∴，∴，∵，，∴，∴，∵，∴．22.【答案】解：如图所示：由题意可得：，，则，，故，则（海里），可得：海里海里．则该船一直向东航行有触礁的危险．【解答】解：如图所示：由题意可得：，，则，，故，则（海里），可得：海里海里．则该船一直向东航行有触礁的危险．23.【答案】解：过点作于点，由题意可得：，，则，，∵，∴，∵，∴∴，则．．【解答】解：过点作于点，由题意可得：，，则，，∵，∴，∵，∴∴，则．．24.【答案】解：（1）在中，，∴设，，∴，解得，∴米，米．（2）如图，过点作于点．∵，∴，∴（米），∴（米）．∴灯的顶端距离地面米．【解答】解：（1）在中，，∴设，，∴，解得，∴米，米．（2）如图，过点作于点．∵，∴，∴（米），∴（米）．∴灯的顶端距离地面米．25.【答案】解：（1）如图，作于点．∵在中，，，∴，，∵，∴．∴∵，∴．∵，，∴．∴．（2）如图，作于点．在中，，，∴．∵在中，，∴．∴．∴在中，由勾股定理得：．【解答】解：（1）如图，作于点．∵在中，，，∴，，∵，∴．∴∵，∴．∵，，∴．∴．（2）如图，作于点．在中，，，∴．∵在中，，∴．∴．∴在中，由勾股定理得：．26.【答案】大楼的高度约为米．【解答】延长交直线于点，过点作，垂足为点．∵在中，＝，∴设＝，则，＝．又∵＝，∴＝，∴＝，＝．∵＝，∴＝．∵在中，，∴＝（米），∵＝，∴＝＝．∵＝，∴＝＝．。