2012年中考数学计算题专项训练

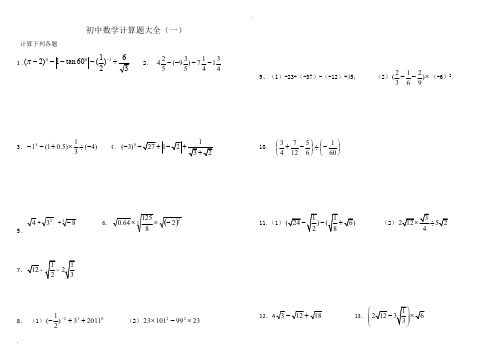
2012中考专项训练——计算题集训一（计算）1. 计算：（1）3082145+-Sin （2）错误！未找到引用源。

（3）2×(－5)＋23－3÷12． （4）22＋(－1)4＋(5－2)0－|－3|； （6）︒+-+-30sin 2)2(20． （8）()()022161-+-- （9）( 3 )0 - ( 12 )-2 +tan45° （10）()()0332011422---+÷- 1.计算：345tan 32312110-︒-⨯⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-- 。

【原式32+=】 2.计算：()()()︒⨯-+-+-+⎪⎭⎫ ⎝⎛-30tan 331212012201031100102。

【原式= 8】 3.计算：()()0112230sin 4260cos 18-+︒-÷︒---。

【原式32-=】（6）120100(60)(1)|2(301)cos tan -÷-+-集训二（分式化简）注意：此类要求的题目，如果没有化简，直接代入求值一分不得！考点：①分式的加减乘除运算 ②因式分解 ③二次根式的简单计算1. ．2. 21422---x x x 3.（a+b ）2+b （a ﹣b ）． 4. 11()a a a a --÷ 5.2111x x x -⎛⎫+÷ ⎪⎝⎭ 4.化简求值（1）⎝⎛⎭⎫1＋ 1 x －2÷ x 2－2x ＋1 x 2－4，其中x ＝－5．（2）（a ﹣1+错误！未找到引用源。

）÷（a 2+1），其中a=错误！未找到引用源。

﹣1．（3）2121(1)1a a a a++-⋅+，其中a （4）)252(423--+÷--a a a a ， 1-=a5. (1))12(1aa a a a --÷-，并任选一个你喜欢的数a 代入求值. (2)22121111x x x x x -⎛⎫+÷ ⎪+--⎝⎭然后选取一个使原式有意义的x 的值代入求值(3)6.已知实数a 、b 满足ab ＝1，a ＋b ＝2，求代数式a 2b ＋ab 2的值．10.化简2111x x x -⎛⎫+÷ ⎪⎝⎭1、化简，求值： 111(11222+---÷-+-m m m m m m ）, 其中m =3． 2、先化简，再求代数式2221111x x x x -+---的值，其中x=tan600-tan450 3、化简：xx x x x x x x x 416)44122(2222+-÷+----+, 其中22+=x化简并求值：221122a b a b a a b a -⎛⎫--+ ⎪-⎝⎭，其中33a b =-=． 4、计算：332141222+-+÷⎪⎭⎫ ⎝⎛---+a a a a a a a ． 7、先化简，再求值：13x -·32269122x x x x x x x-+----，其中x ＝－6． 8、先化简：再求值：⎝⎛⎭⎫1－1a －1÷a 2－4a ＋4a 2－a ，其中a ＝2＋ 2 .10、先化简，再求值：a －1a ＋2·a 2＋2a a 2－2a ＋1÷1a 2－1，其中a 为整数且－3＜a ＜2. 11、先化简，再求值：222211y xy x x y x y x ++÷⎪⎪⎭⎫ ⎝⎛++-，其中1=x ，2-=y ． 12、先化简，再求值：2222(2)42x x x x x x -÷++-+，其中12x =. 13、先化简，再求值：222112()2442x x x x x x-÷--+-，其中2x =（tan45°-cos30°） 14、22221(1)121a a a a a a +-÷+---+．15、先化简再求值：1112421222-÷+--∙+-a a a a a a ，其中a 满足20a a -=． 16、先化简：144)113(2++-÷+-+a a a a a ，并从0，1-，2中选一个合适的数作为a 的值代入求值。

2012年中考数学练习题4 初三（ ）班 学号_______ 姓名_______________一、选择题（本试卷每小题6分，共30分。

原试卷每小题3分，共15分）1、 －4的倒数的相反数是（ ）A ．－4B ．4C ．－41D ．412、计算32)(a 的结果是（ ）A . 23aB . 32aC . 5aD . 6a3、科学记数法51056.4⨯的原数是（ ）（A ）45 600 000 （B ）4 560 000 （C ）456 000 （D ）0.000004564、在平面直角坐标系中，点A （2,3）与点B 关于x 轴对称，则点B 的坐标为A.（3,2）B.（－2，－3）C.（－2,3）D.(2,－3)5、下列各点中，在函数6y x =-图象上的是（ ） A. A ．（－2，－4）B ．（2，3）C ．（－1，6）D ．1(,3)2- 已知样本数据l ，0，6，l ，2，下列说法不正确．．．的是（ ） A ．中位数是6 B ．平均数是2 C ．众数是l D ．极差是6二、填空题（本试卷每小题8分，共40分。

原试卷每小题4分，共20分）1、.数据“0.0000963”用科学记数法可表示为______．2、分解因式:225x -= .3、若二次根式1-x 有意义，则x 的取值范围是4、5、三、解答题（一）（本试卷每小题12分，共60分。

原试卷每小题6分，共30分）1、计算：0022sin 304(2)π--++-2、方程组237,38.x y x y +=⎧⎨-=⎩3、如图，正比例函数12y x =的图象与反比例函数k y x=(0)k ≠在第一象限的图象交于A 点，过A 点作x 轴的垂线，垂足为M ，已知OAM ∆的面积为1.（1）求反比例函数的解析式；（2）如果B 为反比例函数在第一象限图象上的点（点B 与点A 不重合），且B 点的横坐标为1，在x 轴上求一点P ，使PA PB +最小.4、5、卫生部修订的《公共场所卫生管理条例实施细则》从今年5月1日开始正式实施，这意味着“室内公共场所禁止吸烟”新规正式生效.为配合该项新规的落实，某校组织了部分同学在“城阳社区”开展了“你最支持哪种戒烟方式”的问卷调查，并将调查结果整理后分别制成了如图所示的扇形统计图和条形统计图，但均不完整．O M xyA(第20题)请你根据统计图解答下列问题：（1）这次调查中同学们一共调查了多少人？（2）请你把两种统计图补充完整；(3)求以上五种戒烟方式人数的众数．。

二元一次方程组（历年中考题）一、解方程1. （2012年广东）解方程组： {x −y =43x +y =16解：{x −y =4 ⋯⋯①3x +y =16⋯⋯② ① + ②，得：4x = 20，∴ x = 5，把x = 5代入①，得：5—y = 4，∴ y = 1，∴ 原方程组的解是{x =5y =1。

2. （2013年广东）解方程组： {x =y +12x +y =8解：{x =y +1 ⋯⋯①2x +y =8 ⋯⋯②把x =y +1 代入②，得：2y+2+y = 8，3y=6∴ y = 2，把y = 2代入①，得：x = 3，∴ 原方程组的解是{x =3y =2。

3．（2021年广东）解方程组 {y =x −4x +y =6． 解：{y =x −4⋯⋯①x +y =6⋯⋯②把y=x-4代入②，得：x +x −4=6,2x=10,x=5,把x=5代入①得：y=1,∴ 原方程组的解是{x =5y =1。

4．（2018年福建）解方程组：{x +y =14x +y =10． 解：{x +y =1 ⋯⋯①4x +y =10⋯⋯②， ②﹣①得：3x=9，解得：x=3，把x=3代入①得：y=﹣2，则方程组的解为{x =3y =−2． 5．（2013年四川）解方程组{x +y =1 2x −y =5解：{x +y =1 ⋯⋯①2x −y =5⋯⋯②， ①+②得：3x=6，解得：x=2，把x=2代入①得：y=﹣1，则方程组的解为{x =2y =−1． 二、列方程解应用题1.（2017年广东）学校团委组织志愿者到图书馆整理一批新进的图书。

若干男生每人整理30本，女生每人整理20本，共能整理680本；若男生每人整理50本，女生每人整理40本，共能整理1240本，求男生 、女生志愿者各有多少人？解：设男生x 人，女生y 人，则有{30x +20y =680 ⋯⋯①50x +40y =1240 ⋯⋯②2×① - ②得：10x=120,x=12把x=4代入①得，30×12+20y=680,20y=320,y=16∴ 原方程组的解是{x =12y =16。

2012中考数学试题及答案2012年中考数学试题是每年中学生们备战中考的重要资源之一。

在本篇文章中，我们将为您提供2012年中考数学试题及答案，帮助您更好地了解试题的类型和解题方法。

1. 选择题：A. 单项选择题：1. 若一个扇形的半径为8 cm，弧长为12 cm，则该扇形的圆心角为：A) 45° B) 60° C) 90° D) 120°解析：我们知道，扇形的圆心角等于扇形所对的圆心弧的度数，而弧长占的圆周长的比值就是扇形的圆心角占的整圆的比值。

因此，设该扇形的圆心角为x，则12cm/2πr = x/360°。

代入r=8 cm，解得x = 90°。

所以答案选C。

2. 若x+2 = 5，则x的值为：A) 5 B) 3 C) 4 D) 7解析：将x+2=5两边同时减去2，得x=3。

所以答案选B。

B. 完形填空：下面是一道完形填空题，请根据上下文和所给选项，选择最佳答案。

Jonas felt nervous as he 1 to the front of the classroom. His legs feltweak and shaky. He could hear his classmates 2 softly to each other, but the teacher's 3 was low and pleasant. He looked out at the rows of faces, all ofthem 4 at him. His heart was pounding, and he felt as if he could hardly breathe. But he liked that 5 . It made him feel alive.1. A) went B) go C) was going D) is going2. A) talk B) talked C) were talking D) talking3. A) voice B) noise C) sound D) words4. A) lay B) sat C) stood D) walking5. A) situation B) idea C) feeling D) chance解析：根据上下文，我们可以知道Jonas走到了教室前面，所以选项A) went符合语境。

2012年中考数学练习题2 初三（ ）班 学号_______ 姓名_______________一、选择题（中考原试卷每小题3分，共15分）1、－32的倒数是 A ．32 B ．23 C ．32- D ．23-2、数56 070 000用科学记数法表示是（ ）（A ）610607.5⨯ （B ）710607.5⨯ （C ）61007.56⨯ （D ）810607.5⨯3、计算x 2·4x 3的结果是（ ）A ．4x 3B ．4x 4C ．4x 5D ．4x6 4、8的立方根是（ ） A ．2 B ．-2 C ．3 D ．45、在平面直角坐标中，点M (－2，3)在（▲）A ．第一象限B ．第二象限C ．第三象限D ．第四象限某车间5名工人日加工零件数分别为6，10，4，5，4，则这组数据的中位数是（ ）.A.4B.5C.6D.10二、填空题（本试卷每小题8分，共40分。

原试卷每小题4分，共20分）6、0.0000016秒请你用科学记数法表示_________________________秒.7、若622=-n m ，且2m n -=，则=+n m ．8、9、10、如图，直线1l x ⊥轴于点(1,0)，直线2l x ⊥轴于点(2,0)，直线3l x ⊥轴于点(3,0)，…直线n l x ⊥轴于点(,0)n .函数y x =的图象与直线1l ，2l ，3l ，…n l 分别交于点1A ，2A ，3A ，…n A ；函数2y x =的图象与直线1l ，2l ，3l ，…n l 分别交于点1B ，2B ，3B ，…n B .如果11OA B ∆的面积记作1S ,四边形1221A A B B 的面积记作2S ,四边形2332A A B B 的面积记作3S ,…四边形11n n n n A A B B --的面积记作n S ,那么2011S = .三、解答题（一）（本试卷每小题12分，共60分。

1 .23621601214314175395243 40431511454233862328125647--8123220113212399101232210601651274311121241318123214 1531246612131321620212529363181712312712661833218243352741581920112|4120131124212223231|1|3333325=14-9=5387431511441312318118741-44011536414233832527------813229200121012-992(101-99)21220091-3;210121-23+-37--12+45410-30=-45-606512743606560127604335+50=-3011121212121312131431323157.21113262969276161212233633231212122312231712233411851451424334155275424335274155424335274158019-2.+2-=-2.1. 2.201212352122232------------------------------------------------------------------63253--------71　220130　3|1|012013567　8　10　111213+|3|+1　151612120130+||222+412　17112013|7|+0121819122012302452211|3|+162320130222122312+124122512+12612272829201322012420113011一．解答题（共3011211+12121211101220130+1+13|1|01201312+1111212451141144362744421811139210+31111111212原式第一项利用立方根的定义化简，第二项利用负数的绝对值等于它的相反数计算法则计算，第四项利用负指数幂法则计算，第五项利用1181311321132132214 3.140+|3|+120131415221612120130+||222+412121122424242+4　17112013|7|+01211211115218原式第一项利用立方根的定义化简，第二项利用二次根式的化简公式化简，第三项利用零指数幂法则计算，1451912121114+1+|12|142121112012302452121222311416314211|3|+16232013021）原式第一项利用负数的绝对值等于它的相反数计算，第二项先计算乘方运算，再计算除法运算，第2131234622212121121313122312+11）原式第一项利用负数的绝对值等于它的相反数计算，第二项利用特殊角的三212172+1+324121）原式第一项利用绝对值的代数意义化简，第二项利用零指数幂法则计算，第三项利用负指数幂法则21+13+3213212512+112112+126121）原式第一项利用特殊角的三角函数值化简，第二项利用零指数幂法则计算，212211118272282129201322012420112011201122420112242011+522420110301819126-6 3020151351251513 223113415322 2215113656 709422023432852213222330 920121451012456011 ---3622337956347181213343144201232221113．解方程（本小题共61 2532436431.60.20.5140||6015 233218342101216241940 17582818 192221121276521223201120+|4|×0.5+21 21 49322922121212423424 25 0116033230148 31|4|201634232212117538131383171. 2. 3. 4. 5.62-36:-363-17.=-1+1-9-8=-174172312x-2=3x+5 2x-3x=2+5x=-7262(2x+1)-(5x-1)=6x=-354113【解析】先把第二个方程去分母得3x-4y=-2,4113622114211222212221117363236322182323931410123211212111-192-111=-9÷9-18=-1-18=-192753796418=-28+30-27+14=-111221311326313 1532436112171217129128122121543326452431.60.20.529362762732661361263616220561235414试题分析：原式第一项利用零指数幂法则计算，第二项利用绝对值的代数意义化简，第三项利用特殊角的三角函数值计算，最后一项利用立方根定义化简计算即可得到2. 3.153222123x-3+6≥2x332181-3x+3-8+x 0-23223421012122221161747 189190 2021-40--19-24=-40+19-24=-45 2-5-8--28 3-1256712=6+10-74-22--22-23-12011=-4-4+85-32+|-4|×0.52+2-12942912=-4+1+521 312124234 712166 102244124322421 1212423412166224001160341313200116034131322425 =2-1+230-76=-48+8-36=-76316412 95。

2012年各地中考数学汇编 --- 一元二次方程１、（山西）山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：（1）每千克核桃应降价多少元？（2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？２、（济宁））一学校为了绿化校园环境，向某园林公司购买力一批树苗，园林公司规定：如果购买树苗不超过60棵，每棵售价120元；如果购买树苗超过60棵，每增加1棵，所出售的这批树苗每棵售价均降低0.5元，但每棵树苗最低售价不得少于100元，该校最终向园林公司支付树苗款8800元，请问该校共购买了多少棵树苗？3、（乐山）菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售，由于部分菜农盲目扩大种植，造成该蔬菜滞销．李伟为了加快销售，减少损失，对价格经过两次下调后，以每千克3.2元的单价对外批发销售．（1）求平均每次下调的百分率；（2）小华准备到李伟处购买5吨该蔬菜，因数量多，李伟决定再给予两种优惠方案以供选择：方案一：打九折销售；方案二：不打折，每吨优惠现金200元．试问小华选择哪种方案更优惠，请说明理由．4、（南充）关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2．（1）求m的取值范围．（2）若2（x1+x2）+ x1x2+10=0．求m的值.5、（成都）一件商品的原价是100元，经过两次提价后的价格为121元，如果每次提价的百分率都是x，根据题意，下面列出的方程正确的是（）A．100(1)121x+= B．100(1)121x-=C．2100(1)121x+= D．2100(1)121x-=6、（资阳）关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根，则k的取值范围是．7、.(黄石）解方程：2214yyx-=⎨-=⎪⎩8、.(湘潭）如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用25m），现在已备足可以砌50m长的墙的材料，试设计一种砌法，使矩形花园的面积为300m2．。

湖北省黄石市2012年初中毕业生学业考试数学试题卷姓名：准考证号：注意事项：1.本试卷分为试题卷和答题卷两部分，考试时间120分钟，满分120分。

2.考生在答题前请阅读答题卷中的“注意事项”，然后按要求答题。

3.所有答案均须做在答题卷相应区域，做在其它区域内无效。

一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每个小题给出的四个选项中，只有一个是正确的，请把正确的选项所对应的字母在答题卷中相应的格子涂黑，注意可用多种不同的方法来选取正确答案。

1.13-的倒数是（C）A.13B. 3C. －3D.13-【考点】倒数．【分析】一个数的倒数就是把这个数的分子、分母颠倒位置即可得到．【解答】解：13-的倒数是331-=-．故选C．【点评】此题考查倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．2.某星球的体积约为66354213km，用科学计数法（保留三个有效数字）表示为6.6410n⨯3km，则n=（C）A. 4B. 5C. 6D. 7【考点】科学记数法与有效数字．【分析】科学记数法的形式为 a×10n，其中1≤|a|＜10，n是整数．此时的有效数字是指a中的有效数字．【解答】×106≈×106．故选C．【点评】此题考查科学记数法的表示方法，以及用科学记数法表示的数的有效数字的确定方法．有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字．用科学记数法表示的数的有效数字只与前面的a有关，与10的多少次方无关．3.已知反比例函数byx=（b为常数），当0x>时，y随x的增大而增大，则一次函数y x b=+的图像不经过第几象限（ B）A.一B.二C. 三D.四【考点】一次函数图象与系数的关系；反比例函数的性质．【专题】探究型．【分析】先根据反比例函数的增减性判断出b的符号，再根据一次函数的图象与系数的关系判断出次函数y=x+b 的图象经过的象限即可．【解答】解：∵反比例函数b y x =（b 为常数），当x ＞0时，y 随x 的增大而增大， ∴b ＜0，∵一次函数y=x+b 中k=1＞0，b ＜0，∴此函数的图象经过一、三、四限，∴此函数的图象不经过第二象限．故选B ．【点评】本题考查的是一次函数的图象与系数的关系及反比例函数的性质，熟知一次函数y=kx+b （k ≠0）中，当k ＞0，b ＜0时函数的图象在一、三、四象限是解答此题的关键．4. 2012年5月某日我国部分城市的最高气温统计如下表所示：城 市 武汉 成都 北京 上海 海南 南京 拉萨 深圳 气温（℃） 27 27 24 25 28 28 23 26 请问这组数据的平均数是（ C ）【考点】算术平均数．【分析】求这组数据的算术平均数，用8个城市的温度和÷8即为所求．【解答】解：（27+27+24+25+28+28+23+26）÷8=208÷8=26（℃）．故选C ．【点评】考查了算术平均数，只要运用求平均数公式：121()n x x x x n =++⋅⋅⋅+. 即可求出，为简单题．5.如图（1）所示，该几何体的主视图应为（ C ）【考点】简单组合体的三视图．【分析】几何体的主视图就是从正面看所得到的图形，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看可得到一个大矩形左上边去掉一个小矩形的图形．故选C ．【点评】本题主要考查了三视图的知识，主视图是从物体的正面看得到的视图，关键是掌握主视图所看的位置．6.如图（2）所示，扇形AOB 的圆心角为120°，半径为2，则图中阴影部分的面积为（ A ） A. 433π- B. 4233π- C. 4332π- D. 43π 【考点】扇形面积的计算．【专题】探究型．【分析】过点O 作OD ⊥AB ，先根据等腰三角形的性质得出∠OAD的度数，由直角三角形的性质得出OD 的长，再根据S 阴影=S 扇形OAB -S △AOB 进行计算即可．【解答】解：过点O 作OD ⊥AB ，图（1） A B C D OAB 图（2）∵∠AOB=120°，OA=2，∴∠OAD=90°-∠AOB/2 =180°-120°/2 =30°，∴OD=12 OA=12×2=1，∴2AB AD ==，∴S 阴影=S 扇形OAB -S △AOB =120π×22/360 -1/2×1=43π 故选A ．【点评】本题考查的是扇形面积的计算及三角形的面积，根据题意得出S 阴影=S 扇形OAB -S△AOB 是解答此题的关键．7.有一根长40mm 的金属棒，欲将其截成x 根7mm 长的小段和y 根9mm 长的小段，剩余部分作废料处理，若使废料最少，则正整数x ，y 应分别为（ B ）A. 1x =，3y =B. 3x =，2y =C. 4x =，1y =D. 2x =，3y =【考点】一次函数的应用．【分析】根据金属棒的长度是40mm ，则可以得到7x+9y ≤40，再 根据x ，y 都是正整数，即可求得所有可能的结果，分别计算出省料的长度即可确定．【解答】解：根据题意得：7x+9y ≤40，则x ≤40-9y 7 ，∵40-9y ≥0且y 是非负整数，∴y 的值可以是：0或1或2或3或4．当x 的值最大时，废料最少，因而当y=0时，x ≤40 7 ，则x=5，此时，所剩的废料是：40-5×7=5mm ；当y=1时，x ≤31 7 ，则x=4，此时，所剩的废料是：40-1×9-4×7=3mm ；当y=2时，x ≤22 7 ，则x=3，此时，所剩的废料是：40-2×9-3×7=1mm ；当y=3时，x ≤13 7 ，则x=1，此时，所剩的废料是：40-3×9-7=6mm ；当y=4时，x ≤4 7 ，则x=0，此时，所剩的废料是：40-4×9=4mm ．则最小的是：x=3，y=2．故选B ．【点评】本题考查了不等式的应用，正确确定x ，y 的所有取值情况是关键．8.如图（3）所示，矩形纸片ABCD 中，6AB cm =，8BC cm =，现将其沿EF 对折，使得点C 与点A 重合，则AF 长为（ B ）A. 258cmB. 254cmC. 252cm D. 8cm 【考点】翻折变换（折叠问题）．【分析】设AF=xcm ，则DF=（8-x ）cm ，利用矩形纸片ABCD 中，现将其沿EF 对折，使得点C 与点A 重合，由勾股定理求AF 即可． D (C) AB CE F D 图（3）【解答】解：设AF=xcm ，则DF=（8-x ）cm ，∵矩形纸片ABCD 中，AB=6cm ，BC=8cm ，现将其沿EF 对折，使得点C 与点A重合，∴DF=D ′F ，在Rt △AD ′F 中，∵AF 2=AD ′2+D ′F 2，∴x 2=62+（8-x ）2，解得：x=25/4 （cm ）．故选：B ．【点评】本题考查了图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变是解题关键．9.如图（4）所示，直线CD 与线段AB 为直径的圆相切于点D ，并交BA 的延长线于点C ，且2AB =，1AD =，P 点在切线CD 上移动.当APB ∠的度数最大时，则ABP ∠的度数为（ B ）A. 15°B. 30°C. 60°D. 90° 【考点】切线的性质；三角形的外角性质；圆周角定理．【分析】连接BD ，有题意可知当P 和D 重合时，∠APB 的度数最大，利用圆周角定理和直角三角形的性质即可求出∠ABP 的度数．【解答】解：连接BD ，∵直线CD 与以线段AB 为直径的圆相切于点D ，∴∠ADB=90°，当∠APB 的度数最大时，则P 和D 重合，∴∠APB=90°，∵AB=2，AD=1，∴sin ∠DBP=AD/AB =1/2 ，∴∠ABP=30°，∴当∠APB 的度数最大时，∠ABP 的度数为30°．故选B ．【点评】本题考查了切线的性质，圆周角定理以及解直角三角形的有关知识，解题的关键是有题意可知当P 和D 重合时，∠APB 的度数最大为90°．(圆内角＞圆周角＞圆外角)10.如图（5）所示，已知11(,)2A y ，2(2,)B y 为反比例函数1y x =图像上的两点，动点(,0)P x 在x 正半轴上运动，当线段AP 与线段BP 之差达到最大时，点P 的坐标是（ D ） A. 1(,0)2B. (1,0) P 图（4） · O A C D B yx O ABP图（5）C. 3(,0)2D. 5(,0)2【考点】反比例函数综合题；待定系数法求一次函数解析式；三角形三边关系．【专题】计算题．【分析】求出AB 的坐标，设直线AB 的解析式是y=kx+b ，把A 、B 的坐标代入求出直线AB 的解析式，根据三角形的三边关系定理得出在△ABP 中，|AP-BP|＜AB ，延长AB 交x 轴于P ′，当P 在P ′点时，PA-PB=AB ，此时线段AP 与线段BP 之差达到最大，求出直线AB 于x 轴的交点坐标即可．【解答】解：∵把A （1/2 ，y 1），B （2，y 2）代入反比例函数y=1/ x 得：y 1=2，y 2=1/2 ，∴A （1/2 ，2），B （2，1/2 ），∵在△ABP 中，由三角形的三边关系定理得：|AP-BP|＜AB ，∴延长AB 交x 轴于P ′，当P 在P ′点时，PA-PB=AB ，即此时线段AP 与线段BP 之差达到最大，设直线AB 的解析式是y=kx+b ，把A 、B 的坐标代入得： 2=1/2k+b ,1/2 =2k+b ，解得：k=-1，b=5/2 ，∴直线AB 的解析式是y=-x+5/2 ，当y=0时，x=5/2 ，即P （5/2 ，0），故选D ．【点评】本题考查了三角形的三边关系定理和用待定系数法求一次函数的解析式的应用，解此题的关键是确定P 点的位置，题目比较好，但有一定的难度．二、认真填一填（本题有6个小题，每小题3分，共18分）11.分解因式：22x x +-＝(2)(1)x x +-.【考点】因式分解-十字相乘法等．【专题】探究型．【分析】因为（-1）×2=-2，2-1=1，所以利用十字相乘法分解因式即可．【解答】解：∵（-1）×2=-2，2-1=1，∴x 2+x-2=（x-1）（x+2）．故答案为：（x-1）（x+2）．【点评】本题考查的是十字相乘法分解因式，运用十字相乘法分解因式时，要注意观察，尝试，并体会它实质是二项式乘法的逆过程．12.若关于x 的不等式组{23335x x x a >-->有实数解，则a 的取值范围是4a <. 【考点】解一元一次不等式组．【专题】计算题．【分析】分别求出各不等式的解集，再根据不等式组有实数解即可得到关于a 的不等式，求出a 的取值范围即可．【解答】解： 2x ＞3x-3①, 3x-a ＞5② ，由①得，x ＜3，由②得，x ＞5+a 3 ，∵此不等式组有实数解，∴5+a/3 ＜3，解得a ＜4．故答案为：a ＜4．【点评】本题考查的是解一元一次不等式组，根据不等式组有实数解得出关于a 的不等式是解答此题的关键．13.某校从参加计算机测试的学生中抽取了60名学生的成绩（40～100分）进行分析，并将其分成了六段后绘制成如图（6）所示的频数分布直方图（其中70～80段因故看不清），若60分以上（含60分）为及格，试根据图中信息来估计这次测试的及格率约为0075. 【考点】频数（率）分布直方图；用样本估计 总体． 【专题】计算题．【分析】先根据频率分布直方图，利用频数=频数组距 ×组距，求出每一阶段内的频数，然后让60减去已求的每一阶段内的人数，易求70≤x ＜80阶段内的频数，再把所有大于等于60分的频数相加，然后除以60易求及格率．【解答】解：∵频数=频数 组距 ×组距，∴当40≤×10=6，同理可得：50≤x ＜60，频数=9，60≤x ＜70，频数=9，80≤x ＜90，频数=15，90≤x ＜100，频数=3，∴70≤x ＜80，频数=60-6-9-9-15-3=18，∴这次测试的及格率=9+18+15+3 60 ×100%=75%，故答案是75%．【点评】本题考查了频率分布直方图，解题的关键是利用公式频数=频数 组距 ×组距，求出每一阶段内的频数．14.将下列正确的命题的序号填在横线上② .①若n 大于2的正整数，则n 边形的所有外角之和为0(2)180n -.②三角形三条中线的交点就是三角形的重心.③证明两三角形全等的方法有：SSS ,SAS ,ASA ,SSA 及HL 等.【考点】三角形的重心；全等三角形的判定；多边形内角与外角；命题与定理．【专题】探究型．【分析】分别根据多边形内角和定理、三角形的重心及全等三角形的判定定理得出结论．【解答】解：①若n 为大于2的正整数，则n 边形的所有内角之和为（n-2）•180°，故本小题错误；②三角形三条中线的交点就是三角形的重心，符合重心的定义，故本小题正确；③SSA 不能证明两三角形全等，故本小题错误．故答案为：②．【点评】本题考查的是多边形内角和定理、三角形的重心及全等三角形的判定定理，熟知以上知识是解答此题的关键．15.“数学王子”高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出12398991005050+++⋅⋅⋅⋅⋅⋅+++=，今天我们可以将高斯的做法归纳如下：令1239899100S =+++⋅⋅⋅⋅⋅⋅+++ ①1009998321S =+++⋅⋅⋅⋅⋅⋅+++ ②分数 图（6）①＋②：有2(1100)100S =+⨯ 解得：5050S =请类比以上做法，回答下列问题：若n 为正整数，357(21)168n +++⋅⋅⋅⋅⋅⋅++=，则n =12. 【考点】有理数的混合运算．【专题】规律型．【分析】根据题目提供的信息，列出方程，然后求解即可．【解答】解：设S=3+5+7+…+（2n+1）=168①，则S=（2n+1）+…+7+5+3=168②，①+②得，2S=n （2n+1+3）=2×168，整理得，n 2+2n-168=0，解得n 1=12，n 2=-14（舍去）．故答案为：12．【点评】本题考查了有理数的混合运算，读懂题目提供的信息，表示出这列数据的和并列出方程是解题的关键．16.如图（7）所示，已知A 点从点（１，０）出发，以每秒１个单位长的速度沿着x 轴的正方向运动，经过t 秒后，以O 、A 为顶点作菱形OABC ，使B 、C 点都在第一象限内，且060AOC ∠=，又以P（０，４）为圆心，PC 为半径的圆恰好与OA 所在直线相切，则t =431-. 【考点】切线的性质；坐标与图形性质；菱形的性 质；解直角三角形．【专题】动点型．【分析】先根据已知条件，求出经过t 秒后，OC 的长，当⊙P 与OA ，即与x 轴相切时，如图所示，则切点为O ，此时PC=OP ，过P 作PE ⊥OC ，利用垂径定理和解直角三角形的有关知识即可求出t 的值．【解答】解：∵已知A 点从（1，0）点出发，以每秒1个单位长的速度沿着x 轴的正方向运动，∴经过t 秒后，∴OA=1+t ，∵四边形OABC 是菱形，∴OC=1+t ，当⊙P 与OA ，即与x 轴相切时，如图所示，则切点为O ，此时PC=OP ，过P 作PE ⊥OC ，∴OE=CE=1/2 OC ，∴OE=1+t/2 ，在Rt △OPE 中，OE=OP •cos30°=23，O 1 A B CP · yx图（7）∴112t +=∴1t =故答案为：1．【点评】本题综合性的考查了菱形的性质、坐标与图形性质、切线的性质、垂径定理的运用以及解直角三角形的有关知识，属于中档题目．三、全面答一答（本题有9个小题，共72分）解答应写出文字说明，证明过程或推演步骤，如果觉得有的题目有点困难，那么把自己能写出的解答尽量写出来。

2012年江西省南昌市中考数学试卷一．选择题（共12小题）1．（2012江西）﹣1的绝对值是（）A． 1 B． 0 C．﹣1 D．±1考点：绝对值。

分析：根据绝对值的性质进行解答即可．解答：解：∵﹣1＜0，∴|﹣1|=1．故选A．点评：本题考查的是绝对值的性质，即一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是零．2．（2012南昌）在下列表述中，不能表示代数式“4a”的意义的是（）A． 4的a倍B． a的4倍C． 4个a相加D． 4个a相乘考点：代数式。

分析：说出代数式的意义，实际上就是把代数式用语言叙述出来．叙述时，要求既要表明运算的顺序，又要说出运算的最终结果．解答：解：A．4的a倍用代数式表示4a，故本选项正确；B．a的4倍用代数式表示4a，故本选项正确；C．4个a相加用代数式表示a+a+a+a=4a，故本选项正确；D．4个a相乘用代数式表示a•a•a•a=a4，故本选项错误；故选D．点评：本题考查了用语言表达代数式的意义，一定要理清代数式中含有的各种运算及其顺序．具体说法没有统一规定，以简明而不引起误会为出发点．3．（2012江西）等腰三角形的顶角为80°，则它的底角是（）A． 20°B． 50°C． 60°D． 80°考点：等腰三角形的性质。

分析：根据三角形内角和定理和等腰三角形的性质，可以求得其底角的度数．解答：解：∵等腰三角形的一个顶角为80°∴底角=（180°﹣80°）÷2=50°．故选B．点评：考查三角形内角和定理和等腰三角形的性质的运用，比较简单．4．（2012江西）下列运算正确的是（）A． a3+a3=2a6B． a6÷a﹣3=a3C． a3a3=2a3D．（﹣2a2）3=﹣8a6考点：同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方。

2012年中考数学试题一、选择题：1．若x 5＝，则x 的值是【 】A ．5B ．－5C ．5±D ．51 2．下列运算正确的是【 】A ．5510a a a +=B ．339a a a ⋅=C ．()3393a 9a = D ．1239a a a ÷=3．函数y x 2=-中自变量x 的取值范围是【 】A ．x 2>B ．x 2≥C ．x 2≤D ．x 2<4．某种微粒子，测得它的质量为0.00006746克，这个质量用科学记数法表示（保留三个有效数字应为【 】 A ．56.7510⨯- 克 B ．56.7410-⨯ 克 C ．66.7410-⨯ 克 D ． 66.7510-⨯克 5．若关于x 的一元二次方程2x 2x m 0-+=有两个不相等的实数根，则m 的取值范围是【 】 A ．m 1< B ．m 1<- C ．m 1> D ． m 1>- 6．下列命题中，真命题是【 】A ．有两条对角线相等的四边形是等腰梯形B ．两条对角线互相垂直且平分的四边形是正方形C ．等边三角形既是轴对称图形又是中心对称图形D ．有一个角是60°的等腰三角形是等边三角形7．如图，在△ABC 中，∠ACB ＝90°，∠A ＝20°，若将△ABC 沿CD 折叠，使B 点落在AC 边上的E 处，则∠ADE 的度数是【 】A ．30°B ．40°C ．50°D ．55°8．一组数据为2、3、5、7、3、4，对于这组数据，下列说法错误的是【 】A ．平均数是4B ．极差是5C ．众数是3D ． 中位数是6 9．若m 、n 是一元二次方程2x 5x 20--=的两个实数根，则m n mn +-的值是【 】 A ．－7 B ．7 C ．3 D ． －310．圆锥底面圆的半径为1㎝，母线长为6㎝，则圆锥侧面展开图的圆心角是【 】 A ．30° B ．60° C ．90° D ． 120°第Ⅱ卷（非选择题）二、填空题：11．因式分解：2ax 2ax a -+= ▲ ．12．如图，□ABCD 中，AB ＝5，AD ＝3，AE 平分∠DAB 交BC 的延长线于F 点，则CF ＝ ▲ ．13．已知：P A 、PB 与⊙O 相切于A 点、B 点，OA ＝1，P A ＝3，则图中阴影部分的面积是 ▲ （结果保留π）．14．某学校有80名学生，参加音乐、美术、体育三个课外小组（每人只参加一项），这80人中若有40%的人参加优育小组，35%的人参加美术小组，则参加音乐小组的有 ▲ 人． 15．直线y (3a)x b 2=-+-在直角坐标系中的图象如图所示， 化简：2b a a 6a 92b ---+--= ▲ ．16．在△ABC 中，AB ＝5，AC ＝3，AD 是BC 边上的中线，则AD 的取值范围是 ▲ ．第14题 第15题 第17题 三、计算题：本大题共2个小题，每小题6分，共12分．17．计算：)2014cos301212-⎛⎫+-⎪⎝⎭18．解方程：11x 3x 22x -+=-- 解不等式组()2x 13x 22x 4⎧--⎪⎨-⎪⎩≥＜19．如图，图中的小方格都是边长为1的正方形，△ABC的顶点坐标分别为A（－3 ，0），B（－1 ，－2），C（－2 ，2）．（1）请在图中画出△ABC绕B点顺时针旋转90°后的图形；（2）请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标．20．如图，在与河对岸平行的南岸边有A、B、D三点，A、B、D三点在同一直线上，在A点处测得河对岸C点在北偏东60°方向；从A点沿河边前进200米到达B点，这时测得C点在北偏东30°方向，求河宽CD．21．有质地均匀的A．B．C．D四张卡片，上面对应的图形分别是圆、正方形、正三角形、平行四边形，将这四张卡片放入不透明的盒子中摇匀，从中随机抽出一张（不放回），再随机抽出第二张．（1）如果要求抽出的两张卡片上的图形，既有圆又有三角形，请你用列表或画树状图的方法，求出出现这种情况的概率；（2）因为四张卡片上有两张上的图形，既是中心对称图形，又是轴对称图形，所以小明和小东约定做一个游戏，规则是：如果抽出的两个图形，既是中心对称图形又是轴对称图形，则小明赢；否则，小东赢。