当前位置：文档之家 › 窄带系统和窄带随机过程

窄带系统和窄带随机过程

  • 格式：ppt
  • 大小：1014.00 KB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

4.3 窄带随机过程的基本特点

4.3 窄带随机过程的基本特点

S AC (ω ) = S AS (ω ) = FT [ R X (τ ) cos(ω0τ ) + RX (τ ) sin(ω0τ )]
1 j = [ S X (ω + ω0 ) + S X (ω ω0 )] + [ S X (ω + ω0 ) S X (ω ω0 )] 2 2
S X (ω ) = j sgn( ω ) S X (ω )
AC (t)与AS (t)的互相关函数是奇函数
当τ = 0时, 有 : RAC AS (0) = 0
在同一时刻 AC (t)与AS (t)之间是正交的 , .
16
RAC AS (τ ) = RAS AC (τ ) SAC AS (ω) = SAS AC (ω) = FT[RAC AS (τ )]
RAC AS (τ ) = RX (τ ) sin( ω0τ ) + RX (τ ) cos(ω0τ )
1 SAC (ω) = SAS (ω) = {SX (ω +ω0 )[1+ sgn( ω +ω0 )] 2 + SX (ω ω0 )[1sgn( ω ω0 )]}
10
ω
SX (ω ω0 ) + SX (ω +ω0 )
1 ω 2
偶函数
11
ω SX (ω +ω0 ) + SX (ω ω0 ) ω < SAC (ω) = SAS (ω) = 2 0 其它
8
E[ AC (t)] = E[ AS (t)] = 0
AC (t)和AS (t)都是平稳过程
RAC (τ ) = RAS (τ ) = RX (τ ) cos(ω0τ ) + RX (τ ) sin( ω0τ )
窄带随机过程

窄带随机过程

窄带随机过程通信系统都有发送机和接收机，为了提高系统的可靠性，通常在接收机的输入端接有一个带通滤波器，信道内的噪声构成了一个随机过程，经过该带通滤波器之后，则变成了窄带随机过程，因此，讨论窄带随机过程的规律是重要的。

一、窄带随机过程的定义窄带随机过程的定义借助于它的功率谱密度的图形来说明。

图3.5.1（a）中，波形的中心频率为，带宽为，当满足时，就可认为满足窄带条件。

若随机过程的功率谱满足该条件则称为窄带随机过程。

若带通滤波器的传输函数满足该条件则称为窄带滤波器。

随机过程通过窄带滤波器之后变成窄带随机过程。

图3.5.1窄带波形的频谱及示意波形&nbsp;二、窄带随机过程的表示方式如果在示波器上观察这个过程中一个样本函数的波形，则会发现它像一个包络和相位缓慢变化的正弦波，如图3.5.1（b）所示。

因此窄带随机过程可用下式表示成：式中，是窄带随机过程包络；是窄带随机过程的随机相位。

窄带随机过程也可用下式表示其中: 这里的和分别被称作的同相分量和正交分量。

可见，的统计特性可以由、或、的统计特性来确定。

反之，若已知的统计特性，怎样来求、或、的特性呢？三、同相分量与正交分量的统计特性设窄带随机过程是均值为零平稳的窄带高斯过程。

可以证明，它的同相分量和正交分量也是均值为零的平稳高斯过程，而且与具有相同的方差。

1.数学期望已设是平稳的，且均值为零，即对于任意时刻，有，所以，可得即 2.自相关函数我们知道一些统计特性可以从自相关函数中得到，所以，按定义的自相关函数为将上式展开，并取数学期望为其中因为是平稳的，可以令，得（1）同理，令，得（2）如果是平稳的，则、也是平稳的。

由于式（1）和式（2）相等，则应有可见，的同相分量和正交分量具有相同的自相关函数，而且根据互相关函数的性质，有可见，有上式表示，为的奇函数，所以同理可以证明得到即这表明，和具有相同的方差。

3.概率密度函数因为和统计独立，则和的二维概率密度函数为利用式（3.5.16），上式改写为以上讨论的是由的统计特性推导出同相分量和正交分量的统计特性。

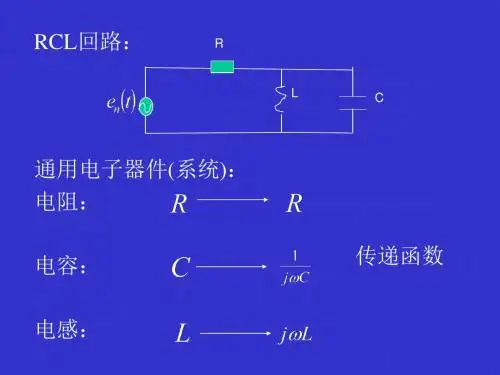
第五章 窄带系统和窄带随机过程

第五章 窄带系统和窄带随机过程


图5-2 窄带系统包络线
§5.1.1 窄带－对称网络的包络线定理 线性系统的冲激响应函数 变化域 时间域: (1) 单个元器件的传递函数 函数 ; (2) 拉普拉斯反变换
R
L
系统的传递
C
窄带系统冲激响应
窄带-对称系统的包络定理
窄带-对称系统的包络定理: 1) 求解出系统传递函数 的零-极点形式;
包络检波器
宽带随 机信号
高频窄带 系统
理想带通限幅器
低通网络
接收机
§5.3窄带随机过程的包络和相位分 布
准正弦振荡表示：
包络服从 瑞丽分布
相位服从等 概率分布
同一时刻，包络和 相位是相互独立
§5.4 窄代随机信号包络线的自相关特 性
R L
拖尾
C
具有相关性：
1.衰减因子 越长; ，衰减越快， 的拖尾(尾迹)
传递函数雷达系统发送机接收机hpflpf第五章窄带系统和窄带随机过程窄带系统窄带随机过程的一般概念窄带随机过程包络和相位分布窄带随机过程包络线的自相关特性正弦信号叠加窄带高斯噪声的合成振幅分布51窄带系统511窄带系统及其包络线特性一窄带系统只允许靠近中心频率附近很窄范围的频率成分通过的系统称为窄带系统
C
解 (1) 电路的传输函数
电路的品质因数>>1
2)画出
的“极点分布图”,得到
极点分布图；
3)对 其中
取拉氏反变换,得到
4）由
恢复
§5.2 窄带随机过程的一般概念
§5.2.1 定义 平稳随机过程
，若其功率谱密度函数
为
则称此随机过程为平稳随机过程。
窄带高通滤波器
§5.2.2 窄带随机过程表示为准正弦振荡
第6章 窄带随机过程

第6章 窄带随机过程


Z (t ) B(t ) cos[ (t )], 其中 B( t ) 0, ( t ) t ( t ) 。 0
上 海 大 学 通 信 学 院
表达式1： Z ( t ) B( t ) cos[ 0 t ( t )],
B( t ) 0, ( t ) 0 t ( t ) 表达式2： Z ( t ) X ( t ) cos 0 t Y ( t ) sin 0 t
上 海 大 学 通 信 学 院
二、解析信号与希尔伯特变换*
1． 解析信号的引入
S ( f ) s(t )e j 2 f t dt R( f ) jI ( f ) 时域实信号S(t)

S ( f )满足共轭对称性，即，
R( f ) R( f ), 偶函数 S ( f ) S ( f ) I ( f ) I ( f )， 奇函数

上 海 大 学 通 信 学 院
2．解析信号的构造
对给定的时域实信号s(t)，设构造的时域复信号为
ˆ(t ) z( t ) s( t ) js
ˆ(t ) 为一由s(t)构造的信号，其构造方法可为， 其中，s
s( t )
即，
h( t )
ˆ s( t )
z( t ) s( t ) js( t ) h( t )
ˆ ( t ) 的互相关函数满足： X

T
T
R X ( t , t )dt
性质5. 平稳随机过程X(t)和其对应的Hilbert变换
ˆ ( ) ˆ RX X ( ) R ( ), R ( ) R ˆ ˆ X X XX
上 海 大 学 通 信 学 院
随机信号分析_第五章_窄带随机过程

随机信号分析_第五章_窄带随机过程


定义复指数函数： ~s (t) ae j (t) ae j e j0t a~e j0t 式中 a~ ae j ，称为复包络。 可以看出s(t)是~s (t) 的实部，即：
s(t) Re[~s (t)]
某些情况下，用复指数形式来分析 问题更加简便，可以简化信号和滤波器 的分析。
复信号~s (t) 的频谱为：
1. s(t) Re[~s (t)]
2.
X~ (
)
2 0
X
(
)
0 0
式中X~ ( )为~s (t)的频谱。
可以证明：满足上面要求的 ~s (t) 是 存在的，称为解析信号。把它用解析表 达式表示为：~s (t) s(t) jsˆ(t)
可以推导出： sˆ(t)
1
s( ) d
t
上式称为希尔伯特(Hilbert)变换，记做
0
ω ω0-ωc ω0 ω0+ωc
|X~H(ω)|
0
ω0-ωc ω0 ω0+ωc
ω
2. 复指数表示
设s(t)为窄带信号，其频谱为X(ω) 。 定义窄带信号s(t)的复指数函数 ~se (t) 为：
~se (t) A(t)e j[0t (t)] A~(t)e j0t 其中A~(t)＝A(t)e j (t) sc (t) jss (t)
用复数表示为：
s(t)=acosφ(t)=a[ejφ(t)+ e-jφ(t)]/2
因为 e j0t ( 0 )
所以s(t)的频谱为：
X(ω)= a[ejθδ(ω-ω0)+e-jθδ(ω+ω0)]/2 |X(ω)|= a[δ(ω-ω0)+δ(ω+ω0)]/2 说明正弦型信号包含正负两种频率成分， 其频谱为对称的两根单一谱线。
《随机信号分析》第五章-窄带随机过程

《随机信号分析》第五章-窄带随机过程

高斯 同一时刻不相关
独立
2020/10/24
06-9-27 28
5.3.2 结论1
对于均值为零的窄带平稳高斯过程
其同相分量和正交分量同样是平稳高斯过程， 而且均值都为零，方差也相同；
在同一时刻上的同相分量与正交分量是不相 关的或统计独立的。
2020/10/24
29
5.3.2
Rc Rs R cos 2 fc Rˆ sin 2 fc
15
2.随机信号的复信号表示
X (t) X (t) jXˆ (t)
R X
(
)
E
X
(t
)
X
*
(t)
E{[ X (t ) jXˆ (t )][ X (t) jXˆ (t)]}
RX ( ) RXˆ ( ) j[RXˆX ( ) RXXˆ ( )]
RX ( ) RXˆ ( ) RXˆX ( ) Rˆ X ( ) RXXˆ ( )
2020/10/24
2
希尔伯特变换 (Hilbert Transform)
1.定义
正变换定义：
H[x(t)] xˆ(t) 1 x( ) d
t
xˆ(t) x(t) 1
t
反变换：
H 1[xˆ(t)] x(t) 1 xˆ( ) d
t
H 1[xˆ(t)] xˆ(t) 1
第5章 窄带随机过程
Narrow-band Random Process
希尔伯特变换 信号的复信号表示 窄带随机过程的统计特性 窄带正态随机过程包络和相位的分布
2020/10/24
1
希尔伯特，D.(Hilbert,David，1862～ 1943)德国著名数学家。
希尔伯特领导的数学学派是19世纪末20 世纪初数学界的一面旗帜，希尔伯特被称 为“数学界的无冕之王”。
13第八章窄带随机过程

13第八章窄带随机过程


步骤1 求a(t)和b(t)的联合分布
ˆ (t)= X(t)cosw 0t X(t)sinw 0t ˆ b (t)= -X(t)sinw 0t X(t)cosw 0t
所以： (at , bt ) 的二维概率密度函数为：
f ab (at , bt ) f a (at ) fb (bt ) at2 bt2 = exp{ } 2 2 2 2 At2 1 exp{ 2 } 2 2 2 1

1




X (t )


d X (t )] ˆ ( ) d R X



E[ X (t ) X (t )] 1 d




R ( )

ˆ R XX ˆ ( ) E[ X (t ) X (t )] E[ X (t )( 1
(t)，b(t )为另外两个随机过程。
ˆ )sinw t (t)= X(t)cosw 0t X(t 0 ˆ b(t)= -X(t)sinw 0t X(t)cosw 0t 证明：
证明： 若X(t)为实随机过程，则其解析过程为： ˆ X(t)=X(t) jX(t) 用乘e jw0t 上式两端得： ˆ (t)][cos w t j sin w t ] X(t)e jw0t [X(t) jX 0 0 ˆ sin w t ] j[ X(t)sin w t X(t) ˆ [X(t)cos w t X(t) cos w t ]
证明:
例题：求S (t ) sin w0t , w0 >0的希尔伯特变换。 解：
H [sin w0t ] 1

1

窄带随机过程

窄带随机过程


正
交
滤
相频特性为：
()
/ 2
/
2
0 0
波 器
二、希尔伯特变换的性质
（1） H[xˆ(t)] x(t)
（2） H[cos(0t )] sin(0t )
H[sin(0t )] cos(0t )
（3） 如果a(t)是低频信号
H[a(t) cos0t] a(t)sin 0t H[a(t)sin 0t] a(t) cos0t
低频信号
是窄带确知信号，其解析信号为
x%(t) A(t)cos0t+(t) jA(t)sin0t+(t)
A(t)e j0t+ (t) A%(t)e j0t
其中 A%(t) A(t)e j (t) ，称为复包络。
一、确知信号的复信号表示
对解析信号取傅里叶变换，得
X%() X () jX ()
第五章 窄带随机过程
窄带随机过程
5.1 窄带随机过程 5.2 信号的复信号表示 5.3 窄带随机过程的统计特性 5.4 窄带正态随机过程包络和相位的分布
5.1 窄带随机过程
一、希尔伯特变换的定义
假定一实函数x(t)，其希尔伯特变换为：
H[x(t)] xˆ(t) 1 x( ) d
t
其反变换为：
4、同相分量和正交分量的统计特性
RY ( ) cos0t cos0 (t ) RYˆY ( ) sin 0t cos0 (t )
RYYˆ ( ) cos0t sin 0 (t ) RYˆ ( ) sin 0t sin 0 (t ) 利用如下关系 RY ( ) RYˆ ( ) RYYˆ ( ) RˆY ( ) RYˆY ( )
具有系统函数为 jsgn 的网络是一个使相位滞 π 后 2 弧度的宽带相移全通网络。
窄带随机过程

窄带随机过程

0
0 为高频载波。
窄带随机过程----- 若一个随机过程的功率谱密度，只分布在高频载波
ω0 附近的一个较窄的频率范围∆ω内，且满足ω0>>∆ω 时，则称该过程为窄带随机过程。记为：Z( t ) 。
例：图6.1为以窄带随机过程的功率谱密度函数
GZ(ω)
0
0
0
0
问题: 对应于功率谱密度GZ (ω)的窄带随机过程Z(t)的表达 式为何？即如何 Gz ( ) Z(t ) 。
t t
称为Hilbert变换。
Hilbert 变换与反变换:
sˆ(t) H[s(t)] 1 s( ) d
t
s(t) H 1[sˆ(t)] 1 sˆ( ) d sˆ(t) * 1
t
1
全通滤
| H( )|
波器
H ( )
0
90
1
0
f
0
f
0
90
表达式(二)： Z(t) X (t)cos 0t Y (t)sin0t
其中：
X (t ) B(t )cos (t ) Y (t ) B(t )sin(t )
B(t ) X 2 (t ) Y 2 (t ), tan (t) Y (t) / X (t)
由于 cos 0t 与sin0t 正交，故称 X( t )-----Z( t )的同相分量， Y( t )-----Z( t )的正交分量。
窄带随机过程的定义 解析信号与希尔伯特变换 窄带随机过程的性质 窄带高斯随机过程Z(t)的高斯分布 余弦波加窄带高斯过程
§6.1 窄带随机过程的定义
窄带系统---------很多无线电系统的通频带 是比较窄的，
它们远小于其中心频率 ，0 这种系统只允许输入信号靠近
Matlab仿真窄带随机过程

Matlab仿真窄带随机过程

随机过程数学建模分析任何通信系统都有发送机和接收机，为了提高系统的可靠性，即输出信噪比，通常在接收机的输入端接有一个带通滤波器，信道内的噪声构成了一个随机过程，经过该带通滤波器之后，则变成了窄带随机过程，因此，讨论窄带随机过程的规律是重要的。

一、窄带随机过程。

一个实平稳随机过程X(t)，若它的功率谱密度具有下述性质：中心频率为ωc，带宽为△ω=2ω0，当△ω<<ωc时，就可认为满足窄带条件。

若随机过程的功率谱满足该条件则称为窄带随机过程。

若带通滤波器的传输函数满足该条件则称为窄带滤波器。

随机过程通过窄带滤波器传输之后变成窄带随机过程。

图1 为典型窄带随机过程的功率谱密度图。

若用一示波器来观测次波形，则可看到，它接近于一个正弦波，但此正弦波的幅度和相位都在缓慢地随机变化，图2所示为窄带随机过程的一个样本函数。

图1 典型窄带随机过程的功率谱密度图图2 窄带随机过程的一个样本函数二、窄带随机过程的数学表示1、用包络和相位的变化表示由窄带条件可知,窄带过程是功率谱限制在ωc附近的很窄范围内的一个随机过程,从示波器观察(或由理论上可以推知):这个过程中的一个样本函数(一个实现)的波形是一个频率为ƒc且幅度和相位都做缓慢变化的余弦波。

写成包络函数和随机相位函数的形式：X(t)=A(t)*cos[ωc t+ Φ(t)]其中:A(t)称作X(t)的包络函数; Φ(t)称作X(t)的随机相位函数。

包络随时间做缓慢变化，看起来比较直观，相位的变化，则看不出来。

2、莱斯（Rice）表示式任何一个实平稳随机过程X(t)都可以表示为：X(t)=A c(t) cosωc t-A S(t) sinωc t其中同相分量：A c(t)= X(t) cosφt= X(t) cosωc t＋sinωc t=LP[X(t) *2cosωc t]正交分量：A S(t) = X(t)sinφt=cosωc t— X(t) sinωc t= LP[-X(t) *2sinωc t]（LP[A]表示取A的低频部分）。

第6章 窄带随机信号

第6章 窄带随机信号


,
r2
=
a2 2σ 2
1
fAt (a t ) ≈
1 2πσ
exp
而所有样本函数的总体---窄带随机信号 X (t) ，则可写成：
6-1
《随机信号分析基础》第六章：窄带随机信号分析
第2页 共9页
X (t ) = A(t ) cos ⎡⎣ω0t + Φ (t )⎤⎦ 上式就是窄带随机信号常用的数学模型。由于 ak (t ) ，ϕk ( t ) 相对 cosω0t 来说是慢变化的时
上式中， cosω0t ， sinω0t 都是确定函数。其中
Ac(t) = A(t) cos Φ(t) 同相分量(In-phase Component)
As(t) = A(t) sin Φ(t) 正交分量(Quadrature Component,书上称为几何“垂直”分量)
A(t ) = Ac2 (t ) + As2 (t )
G
X
(ω) Δω
x k (t)
a k (t)
−ω 0 0
0 ω0 ω
t cos[ω 0t + ϕk (t)]
(a)窄带随机信号的功率谱密度
(b)窄带随机信号的样本函数波形
图 6.1 窄带随机信号
6.1.2 窄带随机信号的数学模型与表示
1.窄带随机信号的数学模型
随机信号 X(t) 的样本函数可写成：
xk (t ) = ak (t ) cos ⎡⎣ω0t + ϕk ( t )⎤⎦ ξk ∈ Ω (k = 1, 2, )
说明 X (t)与同相分量 Ac(t) 、正交分量 As (t) 具有相同的方差，即平均功率相等。
⑸ Ac (t) 、 As (t) 的概率分布

窄带随机过程知识点总结

窄带随机过程知识点总结一、基本概念1. 随机过程随机过程是指一组随机变量的集合，这些随机变量依赖于一个或多个自变量。

在时间变量上，我们称之为时间随机过程。

时间随机过程又可以分为宽带随机过程和窄带随机过程，前者指随机过程在整个频谱上都有一定的随机分布，后者指随机过程在频谱上只占有有限的频带。

2. 窄带随机过程窄带随机过程在频谱中仅占有有限频带，其特性是信号的频率成分远小于信号的中心频率。

在实际应用中，窄带随机过程通常指的是在主载波频率附近的一小段频带范围内的随机过程。

3. 时域和频域描述窄带随机过程可以通过时域和频域来进行描述。

在时域上，窄带随机过程可以用随机函数的均值、自相关函数和功率谱密度来描述；在频域上，窄带随机过程可以用频谱函数和功率谱密度来描述。

二、数学描述1. 自相关函数窄带随机过程的自相关函数是该随机过程的期望值，它表示了信号在不同时刻的取值之间的相关性。

自相关函数通常用时间差来表示，可以通过对随机过程的样本进行计算来得到近似值。

2. 功率谱密度窄带随机过程的功率谱密度是其频谱的表示，它表示了信号在不同频率上的功率分布。

功率谱密度可以通过对随机过程的频率分量进行计算来得到。

3. 高斯窄带随机过程如果一个窄带随机过程在任意时刻的取值都服从高斯分布，则称之为高斯窄带随机过程。

高斯窄带随机过程具有许多重要的性质，包括线性性、平稳性和正态性等。

三、性质1. 平稳性平稳窄带随机过程是指在不同时间段上统计性质相同的随机过程，在实际应用中往往对平稳性的要求比较高。

2. 正态性正态窄带随机过程是指在不同时间点上的取值服从正态分布的随机过程，这种类型的随机过程在许多实际问题中都有重要应用。

3. 独立性在许多实际问题中，我们通常要求随机过程的不同时刻的取值是相互独立的，这样便于进行概率分析和数学建模。

四、应用1. 通信系统在通信系统中，窄带随机过程的功率谱密度是研究通信链路性能的重要工具，通过对其进行频谱分析可以得到信号的频谱特性和频谱利用率等信息。

第五章 窄带随机信号

X
c) R ( ) RX ( )
X
7
d) S
XX XX


( ) j sgn( ) S X ( ) S ( ) j sgn( ) S X ( ) S
XX XX

XX

( )
e) R ( ) R f )R
XX
( )
ˆ ( ) ( ) h( ) * RX ( ) R X
x( ) (1)实值函数x(t ), ( x ), x(t ) H [ x(t )] d t ^ 1 x(t ) 1 x(t ) x(t ) d d
^
1


Βιβλιοθήκη (2)相当于一个正交滤波器 1 x(t ) x(t ) * t
2 t 2
19
20
0 0
ˆ (t ) cos t b(t ) X (t ) sin 0t X 0 2. a(t )与b(t )在同一时刻是正交的,不相关，独立， 高斯RVS 3.若S X ( )是关于0 对称，则a(t ), b(t )是相互正交， 不相关及独立
14
二
f ab (at , bt )
^
x(t )
1 h(t ) t
x(t )
^
j 0 (3) H ( ) j 0
4
(4)希尔伯特变换是一90 全通相移网络 (5)希尔伯特逆变换 x(t ) H [ x(t )]
^ 1 ^

1

x(t )
^
^

d

11
Sa ( ) Sb ( ) LP[ S X ( 0 ) S X ( 0 )]

概率论第六章 窄带随机过程


pB (
ut )
1
2
2
exp(
ut
2
2
)
ut 0
可见，窄带高斯过程包络平方的一维概率密度函数 为指数分布。一个重要的特例是σ2=1的情况，此时有
pu (ut )
1 exp( ut ),
2
2
ut
0
其均值为E[ut]=2,方差为D[ut]=4.
§6.5余弦信号与窄带高斯过程之 和的概率分布
一、余弦信号加窄带高斯过程的包络和相位概率分布
类似地，如果一个随机过程的功率谱密度，只分 布在高频载波ω0附近的一个窄频率范围Δω内，在 此范围之外全为零，且满足ω0>>Δω时，则称之为 窄带过程。
一、窄带过程的物理模型和数学模型
一个典型的确定性窄带信号可表示为
x(t) a(t) cos[0t (t)]
其中，a(t)为幅度调制或包络调制信号，Ф(t)为 相位调制信号，它们相对于载频ω0而言都是慢变化的。
根据希尔伯特变换的性质： RXˆ ( ) RX ( )
RXˆX ( ) RXXˆ ( ) RˆX ( )
整理，得 RX ( ) RZ ( )cos0 RˆZ ( )sin0
同理可以证明 RY ( ) RZ ( )cos0 RˆZ ( )sin0
RX ( ) RY ( )
窄带过程性质的证明
第六章 窄带随机过程
6.1 窄带随机过程的一般概念 6.2希尔伯特变换 6.3 窄带随机过程的性质 6.4窄带高斯随机过程的包络和相位的概率分布 6.5余弦信号与窄带高斯过程之和的概率分布
§ 6.1 窄带随机过程的一般概念
窄带信号的频率或窄带系统的频率响应被限制在 中心频率ω0附近一个比较窄的范围内，而中心频率ω0 又离开零频足够远。

第5章 _窄带随机过程


综合： 零均值窄带平稳高斯过程 X (t ) 的同相分量 Ac (t ) 和正交分量 As (t ) 也是具有相同方差的零 均值平稳高斯过程。 5.1.2 包络和相位的概率密度 反过来， X (t ) 可用两个分量来描述： 幅度
A(t ) = Ac2 (t ) + As2 (t ) ，相位
Φ(t ) = arctan
n(t ) 是均值为零、方差为 σ 2 的高斯随机信号，得 n(t ) 的概率密度函数： f n (t ) = 1 2πσ e
− n2 2σ 2
5‐ 5 / 7
又 n(t ) = X (t ) − a cos ωt ，带入上式即可得到 X (t ) 的概率密度函数：
f X (t ) =
1 2πσ
S m (t ) 的功率谱密度 Ps ( f ) 与其自相关函数 Rs m (τ ) 是一对傅立叶变换对。则有：
5‐ 6 / 7
1 Ps (ω) = FT [Rs m (τ )] = FT [ Rm (τ )cos(ω cτ )] 2 1 = [Pm (ω) ∗ Pc (ω)] 2
其中 Pm ( f ) 是 m(t ) 的功率谱密度， Pc (ω) 是 cos(ω cτ ) 的频谱， 又因为 Pc (ω) = π[δ(ω − ω c ) + δ(ω + ω c )] 所以 1 1 Ps (ω) = i Pm (ω) * π[δ(ω − ω c ) + δ(ω + ω c )] 2 2π 1 = [Pm (ω − ω c ) + Pm δ(ω + ω c ] 4 1 1 功率 P = Rs m (0) = Rm (0)cos 0 = 2 2 1 ∞ 1 ∞ 1 或则 P = Ps (ω)d ω = dω = [Pm (ω − ω c ) + Pm (ω + ω c )] ∫ ∫ 2π −∞ 2π −∞ 2 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

第5章-窄带随机过程


RXXˆ () RXXˆ ()
RXXˆ (0) 0
互相关函数是奇函数
ˆ (t )正交 意味着 X (t )与 X
17
（9）偶函数的希尔伯特变换为奇函数，奇函数的希 尔伯特变换为偶函数 2015/6/2
Hilbert变换

常用变换
xt
cos 2 f0 t sin 2 f0 t
X () X () j ( j sgn()) X () (1 sgn()) X () =2 X ( w)U ( w) 2 X ( w), W 0 W 0 0, 即，解析信号的频谱在负频率部分为0，在正频率部分是 是信号的两倍。
2015/6/2 22
解析信号的特点2：解析信号频谱与复包络频谱
2015/6/2
6
希尔伯特变换 (Hilbert Transform)
1. 定义 ：
正变换定义：
ˆ (t ) H [ x(t )] x
反变换：
ˆ ( ) x ˆ (t )] x(t ) H [x d t 1 1 ˆ (t )] x ˆ (t ) H [x t
2015/6/2 20

解析信号的性质(2)
4) 解析信号 x(t ) 的能量为其实信号 x (t)能量的2倍
x1 t x 2 t 0 5) 提示：利用性质2）和3） x t x2 t 0 1 6) 已知实函数 x t , 求其解析信号的方法
x( t ) A( t )cos 2 f 0 t x( t ) A t e j 2 f0t
2015/6/2
注：A t 为低通信号，其带宽W f 0 .

随机信号处理教程 第5章 窄带系统和窄带随机信号

随机信号处理教程
——献给进入信息领域学习的你！
随机信号处理教程
第1章 概率论基础 第2章 随机过程 第3章 随机过程的功率谱密度 第4章 随机信号通过线性系统 第5章 窄带系统和窄带随机信号 第6章 随机信号通过非线性系统 第7章 马尔可夫过程
第5章 窄带系统和窄带随机信号
1 2
窄带系统及其特点 窄带随机信号的基本概念 窄带高斯随机信号分析 窄带随机信号包络的自相关特性 正弦信号叠加窄带高斯噪声的包络和相位的分布
k E k 0 k 0 0
R(t )
(t )
X (t )
x
图5.12 随机衰减矢量叠加示意 图
5.2 窄带随机信号的基本概念
1) X (t ) 和 Y (t ) 分别是宽平稳随机过程，且 X (t ) 和 Y (t )是联合 宽平稳的 2) X (t ) 和 Y (t )的均值都为0，即 X (t ) Y (t ) 0 n0 (t) 3) X (t ) 和 Y (t )的自相关函数相等，即 BX ( ) BY ( ) 4) X (t ) 和 Y (t )的功率谱密度相等，即 S X ( ) SY ( ) 5) X (t ) 和 Y (t )的平均功率相等，它们也等于窄带随机信号 n0 (t ) 的平均功率，即 6) BXY ( ) BYX ( ) 7) BXY (0) BYX (0) 0 8) S XY ( ) SYX ( )
E
0
E
E
X
hE
E
0
hE
E

hE

E
E
5.4 窄带随机信号包络的自相关特性
结论：白色过程通过窄带线性系统后，输出准正弦过程包 络的自相关函数等于该过程的自相关函数的包络。即 cos 0 B0 ( ) BE ( ) 2 (5.4.9)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3
j 0
p*
1
p*
p 3
2
j0
RCL串联回路
SX
0
0
R
L
ni t
C not
高斯白噪声由大量独立的面积随机变化的 型随机脉冲迭加。
N
ni takt tk k1
线性电路性质： n otn it*h t
N
notakht tk k1
h t0 e 1 tsi0 t n t h t t k 0 e 1 t t k s 0 i t t n k t t k
y
hEtL1HEs2KA
其中
A 1 Lc
n 1 K2j012j0
hE
t
L 1 H
E
s 2 A
K
e 1t 2 1 t
LC 2 0
1 LC 0
e 1t
e 1t
0
4）由hEt 恢复 ht
K 20
K
K
2
ht
hE t
hthEtcos0tKt
e1t
0
cos0t2t
§5.2 窄带随机过程的一般概念
j
j 0
j0
(b)极点分布
图5-1 窄带系统特性与极点分布
无源窄带系统特点： 1、传输函数的极点只能出现在左半平面或
虚轴上； 2、如果是低耗系统，则极点一定远离原点
且靠近虚轴； 3、极点簇对其中心线jj0对称； 4、冲击响应函数可写成 h t h E tc o 0 t s，其
中 hEt——变化缓慢，cos0t——变化快。
N
not
a e1ttk k0
s
in0
t
tk
ttk
k1
N
a e1ttk k0
s
in0t
0tk
t
tk
k1
输出信号由大量幅度为ak0，以e1ttk衰减的， 相位随机 0tk 的谐振振荡为 0 的信号组成。
输出信号的振幅 Rt 就是大量幅度为ak0 ，以 e1ttk 衰减的，相位随机 0tk 的信号矢量rk t迭加而成。
Hj
HEj
0 c 0 c 0 c 0 c
c
c
ht
hE t
窄带-对称系统的包络定理
窄带-对称系统的包络定理: 1) 求解出系统传递函数Hs 的零-极点形式;
H sA s s p z1 1s s z p 2 2 s s zp m n
H s A s p 1 s p 2 s s p z 1 3 s s z p 2 1 * s p 2 *s p 3 *
R 2L
j
1 Lc
cR 2 1
4L
1
R 2L
R j 2L
1 Lc
1
1 4Q0 2
Q0
LR C
电路的品质因数>>1
1 j0
0
1 1 1 LC 4Q02
1 LC
2)画出Hs的“极点分布图”,得H到Es 极点分布图；
j p1
j
HE
s
s
1 p1
p 1
p1 p1j01
1
1
p
1
3)对HEs取拉氏反变换,得到 hEt
4)对 HEs取拉氏反变换,得到 hEt
hEtL1HEs2KA
其中, , Kj20n n是 Hs 在第二象限极点个数.
2A、K 是Hs在幅度和相位上对hEt幅度补偿。
j
p1
p 2
j 0
p3
p*
1
p
*
p
3
2
j0
n3
j
p 1
p
2
p 3
5) 由 hEt恢复 ht
h t h E tco 0 t s K t
窄带系统和窄带随机 过程
第五章 窄带系统和窄带随机过程
➢窄带系统 ➢窄带随机过程的一般概念 ➢窄带随机过程包络和相位分布√ ➢窄带随机过程包络线的自相关特性√ ➢正弦信号叠加窄带高斯噪声的合成振幅分布
§5.1 窄带系统
§5.1.1 窄带系统及其包络线特性 一、窄带系统
只允许靠近中心频率 0 附近很窄范围( 0) 的频率成分通过的系统称为窄带系统。
其中，K K， t 单位阶跃的函数。
例 5.1 用包络线定理求RCL电路的单位冲
击响应 ht R R L sL
1
sc
en t
C uc t
解 (1) 电路的传输函数
1
Hs sc
R sL
1
1
1
Lc s2 R s
1
sc
L Lc
1 Lc
s
p1
1
s
p1
s2 Rs 1 0 L Lc
p1 ,
p1
SX
X t
Rt
t
0
0
X t R tco 0 t s t 准正弦振荡
式中 Rt是随机过程的慢变幅度，称为窄带随 机过程的包络； t是慢变相位，称为窄带随机 过程的随机相位。
窄带随机过程准正弦振荡表示物理解释
Sn 窄带高通滤波器 SX
Hj
SXSnH j2
白高斯 噪声
Sn
H j j
p1
p2
p
Y s s z 1 s z 2 s z m
X s s z 1 s z 2 s z n
A
Xs和 Ys是实系数的有理函数，则系统的零
点和极点或者位于 s平面的实轴上，或者成
对地位于与实轴对称的位置上。
Hj
0 c 0 c 0 c 0 c
(a)频率特性
2) 画出 Hs 的“极点分布图”；
j
p1
p 2
j 0
p3
p*
1
p
*
p
3
2
j0
3)去除第三象限的极点，并将二象限的极点沿 虚轴平移，使其中心与实轴重合；
j
p1
p 2
j 0
p3
p*
1
p
*
pห้องสมุดไป่ตู้
3
2
j0
j
p 1
p
2
p 3
(a) Hs极点分布 HEssp1 s 1p2 sp3
(b) HEs极点分布
p1 p1j0 p2 p2j0 p3 p3j0
ht
hE t
图5-2 窄带系统包络线
§5.1.1 窄带－对称网络的包络线定理
线性系统的冲激响应函数 ht
变化域
时间域:
(1) 单个元器件的传递函数His 函数 Hs ;
系统的传递
(2) 拉普拉斯反变换 Hs
ht
R
L
en t
C uc t
1
H s
sc R sL
1
sc
Hs
ht
窄带系统冲激响应 h t h E tc o 0 t s
Hj
0 c 0 c 0 c 0 c
H j H j 0 c0c
0
others
二、信号与系统复频域分析
xt
yt
ht
Xj
Hj
Yj
Xs
Hs
Y s
sj
Hs
Ys Xs
传输函数零极点表示
H s Y X s s A s s p z 1 1 s s z p 2 2 s s z p m n m n 其中
§5.2.1 定义
平稳随机过程 Xt ，若其功率谱密度函数SX为
SX SX 0 2 0 2 0
0
others
则称此随机过程为平稳随机过程。
SX
0
0
Sn 窄带高通滤波器 SX
Hj
SXSnH j2
H j j
p1
p2
p
3
j 0
p*
1
p*
p 3
2
j0
Sn
SX
0
0
§5.2.2 窄带随机过程表示为准正弦振荡