波动光学课后习题

第十八章 波动光学18-1 由光源S 发出的λ=600nm 的单色光，自空气射入折射率n =1.23的一层透明物质，再射入空气(如图18-1)，若透明物质的厚度为d =1.00cm,入射角θ=ο30，且S A=BC =5.00cm.求:（1）1θ为多大?（2）此单色光在这层透明物质里的频率、速度和波长各是多少？(3)S 到C 的几何路程为多少？光程为多少？分析 光在不同介质中传播的频率相同，但波长和波速不相同．而要把光在不同介质中所走的路程都折算为光在真空中的路程，以便比较光在不同介质中所走的路程——这就引入了光程．介质中某一几何路程的光程，相当于光在走这段路程的时间内在真空中走过的路程．解 （1）由折射定律θθsin sin 1=n n 空 得 46.212123.11sin sin 1=⨯==θθn n 空 οθ24=1(2)分别以 v 1 、1ν、1λ表示光在透明物质中传播的速度、频率和波长，则8811044.2m/s 23.1103⨯=⨯==n c v m/s 又光在不同介质中传播的频率相同，即1410_81105Hz 106000103⨯=⨯⨯===λννcHz 7_148111088.4m 1051044.2⨯=⨯⨯==νλv m (3)从S 到C 的几何路程为1.11cm 5cm 24cos 1cm 5cos 1=++=++οθBC d SA cm S 到C 的光程3.11cm 51cm 24cos 1123.1cm 51cos S 1=⨯+⨯⨯+⨯=++οθBC n d n A n 空空cm 18-2 在杨氏双缝干涉实验中，双缝间距d =0.500mm,缝与屏相距D =50.0cm,若以白光入射，(1)分别求出白光中4001=λnm 和6002=λnm 的两种光干涉条纹的间距；（2）这两种波长的干涉明纹是否会发生重叠？如果可能，问第一次重叠的是第几级明纹？重叠处距中央明纹多远？分析 本题的难点在于如何理解“重叠”——若屏上某一位置同时满足两种波长明纹出现条件，则发生明纹重叠.解 （1）据（18-3）式，1λ 和2λ 所产生的干涉明纹的间距各为4.0mm 5.010400500Δ611=⨯⨯==-λd D x mm 6.0mm 5.010600500Δ622=⨯⨯==-λd D x mm(2) 据（18-1）式，杨氏双缝实验中，明纹到屏中心的距离为 λdDkx ±= () 2,1,,0=k 在x 处两种波长的明纹重叠，即 2211λλk dDk d D x ==1221λλ=k k 由已知2340060012==λλ 故2321=k k 所以在n k n k 2,321== () ,2,1=n 处都可能发生重叠.当1=n ，即2,321==k k 时发生第一次重叠，重叠处距中央明纹的距离为2.1mm 5.010********11=⨯⨯⨯==-λk d D x mm18-3 在劳埃德镜中，光源缝S 0 和它的虚象S 1 位于镜左后方20.0cm 的平面内(如图18-3)，镜长30.0cm,并在它的右边缘放一毛玻璃屏幕.如果从S 0 到镜的垂直距离为2.0mm, nm 720=λ ,试计算从右边缘到第一最亮纹的距离. 分析 讨论劳埃德镜还有一个重要意义，就是验证光从光密介质表面反射时有半波损失.劳埃德镜实验中，相邻明纹的间距也为λdDx =∆ ，平面镜右边缘与毛玻璃屏接触处为暗纹.解 据（18-3）式，劳埃德镜实验中相邻明纹或相邻暗纹的间距为λdD . 据题意，平面镜右边缘与毛玻璃屏接触处为暗纹，其到第一级明纹中心的距离为315105.4cm 104102.7502121Δ---⨯=⨯⨯⨯⨯==λd D x cm 18-4 在菲涅耳双镜中，若光源离两镜交线的距离是1.00m, 屏距交线2.00m,所用光波的波长为500 nm ，所得干涉条纹的间距为1.00mm, 试计算两反射镜的夹角ε.解 εεs i n ≈ 1c o s ≈ε ∴ r L D r d +==ε2由(18-4)式,干涉条纹间距 λελr rL d D x 2+==∆ 故 910500001.012122-⨯⨯⨯⨯+=⋅⋅+=λ∆εx r r L rad rad 105.74-⨯= 18-5 如图18-5(a)所示的杨氏双缝实验中,P 点为接收屏上的第2级亮斑所在.假设将玻璃片（n =1.51）插入从1S 发出的光束途中，P 点变为中央亮斑，求射率乘以光在该介质中的几何路程.光连续通过几种介质时的光程，等于在各种介质中光程之和.讨论在S 1P 中加入玻片条纹上移还是下移时可以这样分析：以中央明纹为研究对象，不加玻片时，中央明纹出现在P 点，有P P 21S S =，加了玻片中央明纹出现在P '点，也应有1S 到P '的光程等于2S 到P '的光程.加玻片后，欲维持P '→1S 与P '→2S 的光程相等，只有缩短P '→1S 的几何路程.所以中央明纹上移，从而推出整个条纹上移.解 据题意，整个装置放在空气中.设未加玻璃片时1S 、2S 到 P 点几何路程分别为1r 、2r ，如图(b)所示，据相干条件,第2级亮纹出现的条件是λδ212=-=r r (1) 如图(c),加上厚度为l 的玻璃片时，1S 到P 点的光程差为 nl l r r nl r +-=''++'1112S 到 P 点光程仍为r 2. 二者的光程差()()()l n r r nl l r r 112122---=+--=δ据题意，加上玻璃片后P 点变为中央亮斑，根据相干条件即()()01122=---=l n r r δ (2)由(1)式-(2)式得()λ21=-l n∴玻片厚度 m 1048.2m 151.11063221269--⨯=-⨯⨯=-=n l λ 且条纹上移.18-6 观察肥皂膜的反射光时，皂膜表面呈绿色.若膜的法线与视线间夹角约为ο30，试估算膜的最小厚度.设肥皂水的折射率为1.33，绿光波长为500nm.分析反射产生的双光束实现干涉. 膜上下两表面反射后干涉加强. 需考虑反射光是否有半波损.n =1.33,周围介质为空气n '=1, 皂膜上表面反射的反射光有半波损. 膜的法线与视线间间有夹角 30=i ，即入射光以 30=i 入射到薄膜上，因而需利用（18-8）式.解 如图18-6,从膜上表面反射的反射光有半波损失，现 nm 500 ,30 ,1' ,33.1====λ i n n据（18-8）式反射加强条件为λλk i n n d =+-2sin '2222 （k =1，2，…）d 为最小值时k =1，得18-7 在空气中有一厚度为500nm 的薄油膜（n=1.46）,并用白光垂直照射到此膜上，试问在300nm 到700nm 的范围内，哪些波长的光反射最强？分析 此题与上题类似，只是考虑的波长范围更宽些，且为垂直入射︒=90i ，因而反射光干涉加强的条件为 λλk nd =+22 （k =1，2，…）.解 在油膜上表面反射的光有半波损，垂直入射︒=90i ,据(18-8)式,反射光m 1001.1m 4133.121025030sin 2272922min--︒⨯=-⨯=-=n d λ加强的条件为λλk nd =+22 （k =1，2，…）∴入射光波长为12102920121050046.1412499-⨯=-⨯⨯⨯=-=--k k k nd λ 当k =3时，5843=λnm, k =4时4174=λnm, k =5时3245=λnm ，k =6时2666=λnm,所以在300-700nm 范围内波长为584nm ，417nm ，324nm 的光反射最强.18-8 白光透射到肥皂水薄膜(n =1.33)的背面呈黄绿色(λ=590nm),若这时薄膜法线与视线间的角度为 30=i ,问薄膜的最小厚度是多少?分析射，透射光的强度相应减弱.亦然.皂膜置于空气中，要使590nm 光的透射最大，其等价的讨论是光反射最小的条件.出的光无半波损失, λ=590nm 减弱对应的膜厚；二是直接求透射光加强对应的膜厚.解 如图18-8, 直接从下表面透射出的光无半波损失, 经下、上表面两次反射后又从下表面透射出的光也无半波损失.透射光的相干条件为λk i n n d =-222s i n'2 (k =1,2…) 加强2)12(sin '2222λ+=-k i n n d (k =0,1,2…) 减弱透射光加强k =1时,d 有最小值,为18-9 激光器的谐振腔主要由两块反射镜组成，射出激光的一端为部分反射镜，另一端为全反射镜.为提高其反射能力，常在全反射镜的玻璃面上镀一层膜，问为了加强反射，氦氖激光器全反射镜上镀膜层的厚度应满足什么条件？膜的最小厚度为多少？（设激光器发射的激光波长 λ=632.8nm ，玻璃的折射率n 1 =1.50，膜的折射率为n 2 =1.65）分析 如图18-9, n 2 =1.65材料组成薄膜,薄膜上方为空气n =1，薄膜下方为玻璃n 1 =1.50.需仔细分析从膜的上下表面反射的反射光半波损失情况.解 如图18-9,n <2n >∴1n 只有在空气与膜的分界面反射的反射光有半波损失.设膜厚为d ，在膜上下表面反射的双光束反射加强的条件是λλk d n =+222 (k =1,2,…)解出()9.95)12(65.148.632)12(4122⨯-=⨯⨯-=-=k k n k d λk =1时膜最薄，最小膜厚为m1039.2m 4133.121059030sin 272922min --︒⨯=-⨯=-=n d λ9.95min =d nm18-10 可见光谱中心可视为波长为550nm 黄绿光.若想提高照相机镜头对该波段的透射率，可在镜头表面镀氟化镁薄膜.已知氟化镁折射率为1.38,玻璃折射率1.50,镀膜的最小厚度需为多少？分析 与18-8题类似.注意薄膜由氟化镁构成，从薄膜上、下表面反射的两束光都有半波损失.解 在膜的上下表面反射的光均有半波损失，所以两反射光的光程差为nd 2.使反射最小即透射最强的条件为2)12(2λ+=k nd （k =0,1,2…）令k =05m i n 1096.922/-⨯==nd λmm18-11 ，利用劈尖空气气隙造成的等厚干涉条纹，可以测量精密加工工件表面的极小纹路的深度.测量方法是：把待测工件放在测微显微镜的工作台上（使待测表面向上），在工件上面放一平玻璃（光学平面向下），以单色光垂直照射到玻璃片上，在显微镜中可以看到等厚干涉条纹.由于工件表面不平，在某次测量时，观察到干涉条纹弯曲如图18-11（a ）所示.试根据弯曲的方向，说明工件表面上的纹路是凹还是凸，并证明纹路深度H 可用下式表示:2λ⋅'=b b H分析 从条纹局部的弯曲方向判断工件表面缺陷，要抓住等厚条纹是劈尖等厚点的轨迹.条纹局部弯向棱边，表明条纹弯的部分和直的部分对应同一膜厚，所以工件表面有缺陷的地方膜厚度增加,故工件的缺陷为凹痕.图18-11解 相邻两明纹(暗纹)对应的空气劈尖厚度差为2λ∆=d由图18-11（b ）知b H b d'=∆∴ 纹路深度为 2λ∆H ⋅'='=b b d b b条纹局部弯向棱边，故工件的缺陷为凹痕.18-12 在两叠合的玻璃片的一端塞入可被加热膨胀的金属丝D 使两玻璃片成一小角度，用波长为589nm 的钠光照射，从图18-12（a ）所示之劈尖正上方的中点处（即L /2处），观察到干涉条纹向左移动了10条，求金属丝直径膨胀了多少？若在金属丝D 的上方观察又可看到几条条纹移动？分析 金属丝直径膨胀时迫使空气劈形膜厚度增加，干涉条纹向左移动,这样原来出现在膜较厚处的条纹自然要向棱边移动（左移）.图18-12解 如图18-12（b ），设在L /2处，膨胀前膜厚为d ,膨胀后膜厚为d '. 210'λ⋅=-d d又因三角形相似2''L Ld d l l =-- ∴ 金属丝直径的膨胀为58902102)(2'=⨯⨯=-'=-λd d l l nm=31089.5-⨯mm D 处劈尖厚度每增加2λ（即直径每膨胀2λ），条纹移过一条, 金属丝直径膨胀了31089.5-⨯mm ，所以在D 上方看到的条纹移动为20条.18-13 块规是一种长度标准器，为一钢质长方体，两端面经过磨平抛光精确地相互平行.图18-13（a ）中A 是一块合格块规，两端面间距离为标准长度.B 是与A 同一规号的待校准块规.校验时将A 、B 置于平台上，用一平玻璃盖住，平玻璃与块规端面间形成空气劈尖.（1）设入射光的波长为589.3nm,两组干涉条纹的间距都是L =0.55mm,A 、B 间距d =5.00cm,试求两块规的高度差；（2）如何判断B 比A 长还是短？（3）现观察到平玻璃与A 、B 形成的干涉条纹间距分别为L =0.55nm 和L =0.30nm,这表明B 的加工有什么缺陷？如B 加工合格应观察到什么现象？尖干涉作一总结.图18-13解 （1）如图18-13（b ），因两组条纹间距相等为mm 55.0=L∴ dh L ∆=2λm 1068.2m 1055.0105103.589Δ5329----⨯=⨯⨯⨯⨯=h (2)如图18-13(b)，两块规有可能与平玻璃接触的位置分别标以a 、b 、c 、d ．轻压平玻璃,如b 、d 两处暗纹位置不变,则B 比A 短;如a 、c 两处暗纹位置不变，则B 比A 长.(3)如图18-13（c ），据题意有2sin sin 2211λθθ==L L∵ 21L L > ∴ 12θθ>表明B 与平玻璃间的间隙较大，B 的上端面有向左下斜的缺陷，如图18-13（c ）. B 加工合格，在平玻璃上方将看不干涉条纹.18-14 当牛顿环装置的透镜与平面玻璃间充以某种折射率小于玻璃的液体时，某一级暗环的直径由1.40cm 变为1.27cm,求液体的折射率.分析 牛顿环也是等厚干涉，与劈尖比较，形成牛顿环的薄膜等厚点的轨迹是以接触点为圆心的同心圆.故干涉条纹为同心圆环.（18-12）、（18-14）式给出充以空气时环的直径和半径. 若充以某种流体，可推出第k 级暗环半径nkr ∝ (n 为所充流体的折射率).解 当透镜与平面玻璃间介质的折射率为n （小于玻璃的折射率）时，从介质上下表面反射的光的光程差为22λδ+=nd ，据（18-9）式出现第k 级暗环条件为2)12(22λλ+=+k nd将（18-13）式 Rr d 22= 代入上式，得第k 级暗环半径为nkR r λ=设空气折射率为1n ,第k 级暗环直径为1D ，充以折射率为2n 的液体，第k 级暗环直径为2D ，则122221n n D D =∴ 22.1127.140.1212212=⨯⎪⎭⎫ ⎝⎛=⋅⎪⎪⎭⎫ ⎝⎛=n DD n 18-15 如图18-15（a ），平玻璃与柱面凹透镜组成空气隙.若用波长为λ的平面单色光垂直照射，在空气隙上下表面反射的反射光形成等厚干涉条纹，设隙间最大高度为47λ（1）试画出干涉暗纹的形状、疏密情况，并标明级次；（2）若把柱面凹透镜换为球面凹镜，气隙高度仍为47λ又如何？图18-15分析 圆柱面透镜沿母线切开，取其凸面为柱面凸透镜，取其凹面为柱面凹透镜，也可两柱面都是圆柱形. 解本题要抓住以下几点：(1)干涉条纹的形状：平玻璃与柱面凹透镜组成空气隙，空气隙等厚点的轨迹是与柱面凹透镜母线平行的直线，所以干涉条纹也是与母线平行的直线.把柱面凹透镜换成球面镜，显然条纹应为同心圆；(2)考虑从空气隙上下表面反射的两束光是否有半波损；(3)判明膜厚d =0处为明纹还是暗纹. 现只有一束反射光有半波损失，所以d =0处（左右棱边）为暗纹.这三条对解劈尖干涉题同样重要.解 （1）截面图如图18-15(b). 从空气隙上表面反射的光无半波损，从空气隙下表面反射的光有半波损失，所以在气隙厚度为d 处反射的双光束的光程差为22λδ+=nd相干条件为)( ,2,122=±=+k k nd λλ明纹())( ,2,1,021222=+±=+k k nd λλ暗纹∴左右棱边0=d 处为暗纹. λ47=d 处对应的级次为 λλλλ4282472==+⨯n 的明纹为4±=k .可见，k 的取值由两棱边向中央气隙厚度最大处递增.与牛顿环的讨论相仿，知干涉条纹到气隙最厚处的距离r 与气隙厚度d 的d 成正比，即r 的增加速率小于气隙厚度的增加速率,因此条纹内疏外密.干涉条纹是平行棱边的直线,条纹示意图如图18-15(c).(2)换成球面镜时，球面镜与平玻璃所成空气隙等厚点的轨迹是同心圆，所以干涉条纹是以λ47为中心的同心圆，其余讨论与柱透镜同. 18-16在牛顿环实验中，两平凸透镜按图18-16（a ）配置，上面一块是标准件，曲率半径为R 1 =550.0cm,下面一块是待测样品.入射光是波长为632.8nm 的氦氖激光，测得第40级暗环的半径为1.0cm,求待测样品的曲率半径.分析 实为两个曲率半径不等的凸透镜叠合.空气隙的厚度为两个平凸透镜分别与平玻璃组成的气隙厚度之和.解 牛顿环第k 级暗环出现的条件为 ()21222λλ+=+k d即 λk d =2（1）如图18-16（b ），从（18-13）式得膜厚1212r r d k=2222r rd k=⎪⎪⎭⎫ ⎝⎛+=+=21221112R R r d d d k∴ ⎪⎪⎭⎫ ⎝⎛+=212112R R r d k （2）（2）式代入（1）式得λk R R r k =⎪⎪⎭⎫⎝⎛+⋅21211 待测样品的曲率半径为()m838.5 m 105501101108.632401112229122=⨯-⨯⨯⨯=-=---R r k R k λ 18-17 如果迈克耳孙干涉仪中2M 反射镜移动距离0.233mm, 则数得的条纹移动数为792，求所用的光波的波长. 分析 迈克耳孙干涉仪是利用分振幅法产生双光束以实现干涉.在书p.120图18-17中，2M 垂直1M 可演示等倾干涉，2M 与1M 不严格垂直可演示等厚干涉.因而前面关于等倾干涉、等厚干涉的讨论对迈克耳孙干涉仪都适用.解 2M 每移动2λ ,条纹平移过一条. ∴ 2M 移过的距离 2λ⋅=n d 所用的光波的波长为588.4nmmm 10884.5mm 792233.0224=⨯=⨯==-n d λ 18-18 迈克耳孙干涉仪的两臂中，分别放入长0.200m 的玻璃管，一个抽成真空，另一个充以1atm 的氩气.今用汞绿线λ=546nm 照明，在将氩气徐徐抽出最终也达到真空的过程中，发现有205个条纹移过视场，问分析 参阅18-5题，再考虑到光是来回两次通过臂，所以从充氩气到抽完氩气过程中，光程的改变为l n )1(2-.解 设玻璃管长为l ,并忽略两端管壁的厚度.由迈克耳孙干涉仪原理知，抽气前后光程的改变为l n )1(2-，据题意有λN l n =-)1(2，氩气在1atm 时的折射率为12.0210546205129+⨯⨯⨯=+=-l N n λ =1.002818-19 波长为700nm 的红光正入射到一单缝上，缝后置一透镜，焦距为0.700mm.在透镜焦距处放一屏，若屏上呈现的中央明条纹的宽度为2.00mm,问该缝的宽度是多少？假定用另一种光照射后，测得中央明条纹的宽度为1.50 mm,求该光的波长.分析 正入射是指光源在透镜的焦平面上，线光源平行于缝长方向，且经过透镜的主焦点.参阅书p.127图18-26,用菲涅耳半波带法处理单缝衍射时，经过宽为b 的单缝上下边缘两束光的光程差为AC = ϕsin b (ϕ 为衍射角).要体会用半波长分割AC 后，过分点作平行BC 的平面，单缝上的波阵面便被分为等数的面积相等的波带称为半波带.半波带上各点为新的子波源，相邻半波带上对应点发出的相干光到达屏时相位差为π.书p.129图18-28又提示，中央明纹的宽度为正负一级暗纹间距离，第一级明纹宽度为第一级暗纹与第二级暗纹间距离，以此类推.解 中央明纹的宽度为0l ,为正负一级暗纹之间的距离.又因级次低，ϕ很小,有fl 2tan sin 0=≈ϕϕ对第一级暗纹λϕ=s i nb 代入上式m 109.41027.010700224390---⨯=⨯⨯⨯⨯==l f b λ =0.49 mm 对应另一种光, 中央明纹宽度为5.1'0=l mm 时4301025.5107.025.149.02'-⨯=⨯⨯⨯=='f al λ mm =525nm18-20 一单缝用波长为1λ 和2λ 的光照明，若1λ的第一级衍射极小与2λ的第二级衍射极小重合.问：（1）这两种波长的关系；（2）所形成的衍射图样中，还有哪些极小重合？分析 题目练习两条：(1)不同波长、不同级次的衍射条纹,在它们的衍射角相同时重合；(2)单缝衍射出现极大值、极小值的条件. 解 （1）单缝衍射产生极小值的条件是λϕk b ±=s i n(k =1,2,…) 设重合时衍射角为ϕ，则212s i n s i n λϕλϕ==b b(1)式(2)式联立,解出212λλ=（2）设衍射角为'ϕ时，1λ的1k 级衍射极小与2λ的2k 级衍射极小重合，则2211sin sin λϕλϕk b k b ='='由第一问得出212λλ=，代入得22212λλk k =∴ 212k k = 即当212k k =时两种光的衍射极小重合.18-21在单缝衍射实验装置中，用细丝代替单缝成为衍射细丝测径仪.已知光波波长为630nm ，透镜焦距为50.0cm.今测得中央明纹的宽度为1.00 cm ，试求细丝的直径.分析 衍射是波前进过程中,遇现象.单缝衍射的障碍物是缝屏,的细丝也是障碍物. 与光波波长可以比较，宽.解 如图18-21，于单缝宽b .设x 1心点P 0的距离,中央明纹宽度为110t a n22ϕf x l == 对低级次1ϕ很小，有11tan sin ϕϕ≈∴ b f f l λϕ⋅=≈2s i n210细丝直径为 063.0mm 01.0106305.02290=⨯⨯⨯==-l f b λmm 18-22 波长为500nm 的单色光，以30º 入射角入射到光栅上，发现正入射时的中央明纹位置现变为第二级光谱的位置.若光栅刻痕间距3100.1-⨯=d mm.（1）求光栅每毫米有多少条刻痕？（2）最多可能看到几级光谱？（3）由于缺级，实际又看到哪几条光谱线？分析 斜入射是指光源在透镜的焦平面上，线光源平行缝长方向，但光源不经过透镜的主焦点. 这样光栅相邻两缝对应光线到达屏的光程差还应包含入射光的那部分.本题涉及衍射光栅几个基本问题：光栅方程；当衍射角ϕ=ο90时，对应最高级次max k ；光栅衍射图样的缺级现象.解 （1）由例题18-6，入射角为 30 时光栅相邻两缝对应光线到达屏的光程差为ϕs i n )(30sin )(b b b b '++'+ 对于第二级光谱λϕ2s i n )(30sin )(='++'+b b b b 因该光谱位置为原正入射时中央明纹位置，则 0=ϕ∴ 30sin 2λ='+b b光栅刻痕数为500/m m 10525.0230sin 14=⨯⨯=='+=条λ b b N 条/mm 又最高级次对应衍射角 90=ϕ.设最高级次为k max ，即λmax 90sin )(30sin )(k b b b b ='++'+()()λλN b b k90sin 30sin 90sin 30sin max+=+'+=610550015.04=⨯⨯+=- 最多可能看到6级光谱.（3）光栅常数 63102m 500101--⨯=⨯='+b b m k 满足下式为缺级(),2,1'±±=''+=k k bb b k而210110266=⨯⨯='+--b b b 即 k k '=2∴为缺6,4,2±±±= k 级 故实际可以看到光谱线是5,3,1,0±±± 共7条 .18-23一平面单色光投射于衍射光栅，其方向与光栅的法线成θ 角.法线两侧与法线分别成ο11和ο53角的方向上出现第一级光谱线.（1）求θ角；（2）用衍射角表示中央明纹出现的位置；（3）计算斜入射时在光栅法线两侧有可能看到的最高级次.分析 本题也是斜入射问题.题目没有给出两衍射光与入射光在光栅平面法线的异侧还是同侧，可分别假设一种配置，判断所得θ角是否合理,从而决定取舍. 第三问的计算表明与入射光同侧的光谱项有可能获得更高级次. 在实际工作中，通过加大入射角以期获得光栅较高的分辨率.解 （1）先设衍射角为 11和 53的衍射光位置如图18-23，此时 11的衍射光与入射光在光栅平面法线的同侧， 11衍射角为正； 53衍射角的衍射光与入射光在光栅平面法线的两侧， 53衍射角为负（参考书p.139例题18-6关于正负号的说明）.又入射角为θ，据已知光栅方程写为()()()())2(11sin sin ')1(53sin sin 'λθλθ=++-=-+b b b b(1)式(2)式联立,解出()3039.011sin 53sin 21sin ≈-= θ7.17=θ再设衍射角为 53的衍射光与入射光在法线同侧，从相应光栅方程解出()53sin 11sin 21sin -=θ，这样θ<0,不合题意舍去.所以合理的配置是ο11角的衍射光与入射光在法线同侧,入射角 7.17=θ.（2）中央明纹对应的衍射角为 ϕ，有()7.170sin sin 00-=-==+θϕϕθ即入射光与中央明纹分列在法线两侧.（3）当衍射角为 90时，对应最高级次.如图18-23，与入射光同侧的光谱项的最高级次k 满足下式()()()()λθλ=++=++11sin sin '90sin 7.17sin 'b b k b b 解出 264.211sin 7.17sin 90sin 7.17sin ≈=++≤k 与入射光异侧的光谱项的最高级次k '满足下式()()()()λθλ-=-+'-=-+53sin sin '90sin 7.17sin 'b b k b b解出 141.153sin 7.17sin 90sin 7.17sin '≈=--≤k ∴ 在入射光同侧有可能获得更高级次光谱项.18-24 一束光线正入射到衍射光栅上，当分光计转过角ϕ时，在视场中可看到第三级光谱内nm 440=λ的条纹.问在同一角ϕ上可看见波长在可见光范围内的其他条纹吗？（可见光的波长范围为400nm-760nm ）分析 题目“在视场中可看到第三级光谱内λ=400nm 的条纹”一句给出()ϕsin 'b b +值，现寻求在400nm-760nm 范围内满足光栅方程的k 和λ值.解 据光栅方程 ()λϕk b b =+s i n' 得 ()nm 13204403sin '=⨯=+ϕb b若2=k ,则 nm 660213202=÷=λ 若 1=k ,则 nm 700nm 1320113201>=÷=λ∴可见到第二级nm 660=λ的条纹.18-25 宇航员瞳孔直径取为5.0mm ，光波波长λ=550nm.若他恰能分辨距其160km 地面上的两个点光源.只计衍射效应，求这两点光源间的距离.分析 根据瑞利准则，当两个物点刚能被分辨时，这两物点的艾里斑中心对透镜光心的角距0θ恰好等于艾里斑的角半径.人的瞳孔如同一透镜.解 恰能分辩时，两点光源对瞳孔的张角0θ为 dλθ22.10= ∴地面两点光源的距离m 4.21m 10510550106.122.122.13930=⨯⨯⨯⨯⨯==≈--df f l λθ∆ 18-26 如图18-26（a ）所示，在透镜L 前50m 处有两个相距6.0mm 的中心的距离为艾里斑半径.本题给出物距和焦距，必然用到成像公式fu 111=+v . 解 如图18-26（b ）， 在恰能分辨时，两个艾里斑中心的距离等于各个艾里斑半径.设衍射光斑直径为d ，艾里斑半径为2'ds =根据薄透镜成像公式fu 111=+v 50=u m 2.0=f m us ≈θ ∴2.0=≈f v m ∴ v θ≈'s衍射光斑直径为m 108.4m 502.0100.6222253--⨯=⨯⨯⨯==='u sf s v θ18-27 以波长为0.11nm 的X 射线照射岩盐晶面，实验测得在X 射线与晶面的夹角（掠射角）为0311'ο 时获得第一级极大的反射光，问：（1）岩盐晶体原子平面之间的间距d 为多大？（2）如以另一束待测的X 射线照射岩盐晶面，测得X 射线与晶面的夹角为0317'ο时获得第一级极大反射光，则待测的X 射线的波长为多少？分析 晶体构成光栅常数很小的空间衍射光栅.X 射线通过晶体时，将部分地被晶体中的原子散射.强度最大的散射光线的相互干涉，服从布拉格公式.本题第（1）问是在做X 射线结构分析实验.解 据布拉格公式λϕk d =s i n2 () 2,1=k (1) 当'3011 =ϕ 1=k 时 岩盐晶体原子平面之间的间距为cm 10759.2cm '3011sin 2101.1sin 288--⨯=⨯⨯== ϕλk d (2)当'3017' =ϕ 1'=k 时，待测的X 射线的波长为nm 1659.0nm '3017sin 10759.22'sin 28=⨯⨯⨯=='-ϕλd18-28 对于同一晶体，分别以两种X 射线实验，发现已知波长1λ=0.097nm 的 X 射线在与晶体面成ο30 的掠射角处给出第一级极大，而另一未知波长的X 射线在与晶体面成ο60 的掠射角处给出第三级反射极大.试求此未知X 射线的波长为多少？分析 同18-27题分析. 解 据布拉格公式λϕk d =s i n2 () 2,1=k 当11=k 301=ϕ 得nm 097.030sin 2097.0sin 2111=⨯==ϕλk d 又由32=k 602=ϕ 得nm 056.0360sin 097.02sin 2222=⨯⨯==k d ϕλ18-29 两偏振片A 和B 如图18-29放置，两者的偏振化方向成 45角，设入射光线是线偏振光，它的振动方向与A 的偏振化方向相同，试求：同一强度入射光分别从装置的左边及右边入射时，透射光的强度之比.分析 显然本题要用到马吕斯定律. 马吕斯定律给出入射到偏振片的偏振光与出射的偏振光强度间的关系.解 设入射偏振光的强度为0I .从左边入射时，通过A 和B 透射光的强度分别为0200cos I I I A ==022145cos I I I A B == 从右边入射时，通过B 和A 透射光的强度分别为0202145cos 'I I I B == 024145cos 'I I I BA ='= 两种情况下透射光强度之比为24121'00==I I I I A B 18-30 使自然光通过两个偏振化方向成 60夹角的偏振片，透射光强为1I .今在这两个偏振片之间再插另一偏振片，它的偏振化方向与前两个偏振片均成30 角，则透射光强为多少？分析 本题也要用马吕斯定律，但注意入射光是自然光.强度为0I 的自然光通过起偏器成为偏振光，强度变为 I 21.这是因为自然光的光矢量可以用两个振幅相等振动方向互相垂直的分振动表示，经过偏振片时只有与偏振片振动方向平行的分振动可以通过.解 如图18-30(a)，自然光通过一个偏振片后，其光强减为原来的21, 即0021I I ='据马吕斯定律，当两偏振化方向相 交 60 时,有2160cos I I ='=104I I =' 如图18-30(b),当中间又插入一偏振片时02014330cos I I I '='='101212491694330cos I I I I I ='='='=' 所以此时透射光光强为149I .18-31 一束平行的自然光，以ο58 角入射到一平面玻璃的表面上，反射光是全偏振光.问：（1）折射光的折射角是多少？（2）玻璃的折射率是多少？分析 反射光是全偏振光时，入射角为布儒斯特角，且折射光与反射光垂直.解 （1）因入射角是布儒斯特角，入射角与折射角互为余角折射角325890=-=（2）据布儒斯特定律60.158tan == 玻n18-32 一束光以起偏角0i 入射到平板玻璃的上表面，试证明玻璃下表面的反射光亦为偏振光.分析 本题论证了用玻璃片堆在折射光方向获得光的原理.可参阅第三册p.152.证 在上表面应用折射定律得1200sin sin n n r i =∴0210s i n s i n i n n r =上式两边同除以0cos r ,得2100cos sin cos sin r i n n r r = 又因i 0是起偏角，入射角与折射互为余角，即0cos sin 0r i =∴ 21002100s i n s i nc o s s i n n n i i n n r r ==210t a n n n r =表明折射光以 210arctan n n r =的角入射在下表面上.对玻璃与空气分界面,r 0是起偏角,因而反射光亦为偏振光.18-33 布儒斯特定律提供了一种测定透明电介质折射率的方法.今测得一电介质的布儒斯特角为5159'ο，试求该电介质的折射率.解 据布儒斯特定律 空介n n i = t a n∴ 681.1'1559tan tan 0=== i n n 空介18-34 如图18-34，自然光入射到水面上入射角为1i 时，反射光是全偏振光.今有一块玻璃浸入水中，且从玻璃面反射的光也是全偏振光，求水与玻璃面间的夹角α.（玻璃折射率3n =1.517,水的折射率2n =1.333）分析 注意题目点出自然光入射到水面上时，在空气与水的分界面上，反射光是全偏振光，说明入射角1i 是起偏角.又指出从玻璃面反射的光也是全偏振光，说明光入射到水与玻璃分界面上，入射角也是起偏角.剩下的问题就是搞清角之间的关系.解 由布儒斯特定律333.1tan 121==n ni∴12.531=i设光射到玻璃上的入射角为2i 333.1517.1tan 232==n n i∴69.482=i据折射定律 r n i n s i n s i n211=6001.0s i n s i n 21==n i r。

r1．如图，S1、S2 是两个相干光源，它们到P 点的距离分别为r1 和r2．路径S1P 垂直穿过一块厚度为t1，折射率为n1 的介质板，路径S2P 垂直穿过厚度为t2，折射率为S1t1 r1Pt21 2(A) (r2 + n2t2 ) − (r1 + n1t1 )(B) [r2 + (n2 − 1)t2 ] −[r1 + (n1 − 1)t2 ](C) (r2 − n2t2 ) − (r1 − n1t1 )S2 n2(D) n2t2 − n1t12. 如图所示，波长为λ的平行单色光垂直入射在折射率为n2 的薄膜上，经上下两个表面n1 λ反射的两束光发生干涉．若薄膜厚度为e，而且n1＞n2＞n3，则两束反射光在相遇点的相(B) 2πn2 e / λ．(A) λD / (nd) (B) nλD/d．(C) λd / (nD)．(A) 使屏靠近双缝．(B) 使两缝的间距变小．(C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源．5．在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光(A) r k = kλR ．(B) r k = kλR / n ．(C) r k = knλR ．(D) r k = kλ /(nR)二．填空题：1．在双缝干涉实验中，两缝分别被折射率为n1 和n2 的透明薄膜遮盖，二者的厚度均为e．波长为λ的平行单色光垂直照射到双缝上，在屏中央处，两束相干光的相位差∆φ＝．2. 在双缝干涉实验中，双缝间距为d，双缝到屏的距离为D (D>>d)，测得中央零级明纹与第五级明之间的距离为x，则入射光的波长为．3．在双缝干涉实验中，若使两缝之间的距离增大，则屏幕上干涉条纹间距；若使单色光波长减小，则干涉条纹间距．4. 在双缝干涉实验中，所用光波波长λ＝5.461×10–4 mm，双缝与屏间的距离D＝300 mm，双缝间距为d＝0.134 mm，则中央明条纹两侧的两个第三级明条纹之间的距离为．n2en3n一．选择题：n2的另一介质板，其余部分可看作真空，这两条路径的光程差等于( )位差为( )(A) 4πn2e/λ．(C) (4πn2e/λ)+π．(D) (2πn2e/λ)−π．3．把双缝干涉实验装置放在折射率为n的水中，两缝间距离为d，双缝到屏的距离为D(D>>d)，所用单色光在真空中的波长为λ，则屏上干涉条纹中相邻的明纹之间的距离是( )(D)λD/(2nd)．4.在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是( )程大2.5λ，则屏上原来的明纹处( )(A)仍为明条纹；(B)变为暗条纹；(C)既非明纹也非暗纹；(D)无法确定是明纹，还是暗纹6.在牛顿环实验装置中，曲率半径为R的平凸透镜与平玻璃扳在中心恰好接触，它们之间充满折射率为n的透明介质，垂直入射到牛顿环装置上的平行单色光在真空中的波长为λ，则反射光形成的干涉条纹中暗环半径r k的表达式为( )．一.光的干涉5. 图 a 为一块光学平板玻璃与一个加工过的平面一端接触，构成的空气劈尖，用波 长为λ的单色光垂直照射．看到反射光干涉条纹(实线为暗条纹)如图 b 所示．则干涉 图 a 条纹上 A 点处所对应的空气薄膜厚度为 e ＝ ．图 b6. 用波长为λ的单色光垂直照射到空气劈形膜上，从反射光中观察干涉条纹， 距顶点为 L 处是暗条纹．使劈尖角θ 连续变大，直到该点处再次出现暗条纹为止．劈尖角 的改变量∆θ是．7. 波长为λ的平行单色光垂直照射到劈形膜上，若劈尖角为θ (以弧度计)，劈形膜的折射率为 n ，则反射光形成的干 涉条纹中，相邻明条纹的间距为 ．8. 波长为λ的平行单色光垂直地照射到劈形膜上，劈形膜的折射率为 n ，第二条明纹与第五条明纹所对应的薄膜厚 度之差是 ．9. 已知在迈克耳孙干涉仪中使用波长为λ的单色光．在干涉仪的可动反射镜移动距离 d 的过程中，干涉条纹将移动 条．10. 在迈克耳孙干涉仪的一条光路中，插入一块折射率为 n ，厚度为 d 的透明薄片．插入这块薄片使这条光路的光 程改变了 ．11. 以一束待测伦琴射线射到晶面间距为 0.282 nm (1 nm = 10-9 m)的晶面族上，测得与第一级主极大的反射光相应 的掠射角为 17°30′，则待测伦琴射线的波长为 ．三．计算题：屏AθL1．在双缝干涉实验中，单色光源S 0到两缝S 1和S 2的距离分别为l 1和l 2，并且l 1－l 2＝3λ，λ为入射光的波长，双缝之间的距离为d ，双缝到屏幕的距离为D (D >>d )，如图．求：(1)零级明纹到屏幕中央O 点的距离．(2)相邻明条纹间的距离．2．在杨氏双缝实验中，设两缝之间的距离为 0.2 mm ．在距双缝 1 m 远的屏上观察干涉条纹，若入射光是波长为 400 nm 至 760 nm 的白光，问屏上离零级明纹 20 mm 处，哪些波长的光最大限度地加强？(1 nm ＝10-9 m)3．图示一牛顿环装置，设平凸透镜中心恰好和平玻璃接触，透镜凸表面的曲率半径是 R ＝400 cm ．用某单色平行光垂直入射，观察反射光形成的牛顿环，测得第 5 个明环的半径是 0.30 cm ．(1) 求入射光的波长． (2) 设图中 OA ＝1.00 cm ，求在半径为 OA 的范围内可观察到的明环数目．4．在 Si 的平表面上氧化了一层厚度均匀的 SiO 2 薄膜．为了测量薄膜厚度，将它的一部分磨成劈形(示意图中的 AB段)．现用波长为 600 nm 的平行光垂直照射，观察反射光形成的等厚干涉条纹．在图中 AB 段共有 8 条暗纹，且 B处恰好是一条暗纹，求薄膜的厚度．(Si 折射率为 3.42，SiO 2 折射率为1.50)5．在折射率为1.58 的玻璃表面镀一层MgF2（n = 1.38）透明薄膜作为增透膜．欲使它对波长为λ = 632.8 nm 的单色光在正入射时尽量少反射，则薄膜的厚度最小应是多少？一．选择题：二．光的衍射1 (A) a=2b．(B) a=b．(C) a=2b．(D) a=3 b．1．在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹( )(A)对应的衍射角变小．(B)对应的衍射角变大．(C)对应的衍射角也不变．(D)光强也不变．2．一单色平行光束垂直照射在宽度为1.0m m的单缝上，在缝后放一焦距为2.0m的会聚透镜．已知位于透镜焦平面处的屏幕上的中央明条纹宽度为2.0 mm，则入射光波长约为( )(1nm=10−9m)(A) 100n m(B) 400n m(C) 500n m(D) 600n m3．在单缝夫琅禾费衍射实验中波长为λ的单色光垂直入射到单缝上．对应于衍射角为30°的方向上，若单缝处波面可分成3个半波带，则缝宽度a等于( )(A)λ．(B) 1.5λ．(C) 2λ．(D) 3λ．4．在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹( )(A)对应的衍射角变小．(B)对应的衍射角变大．(C)对应的衍射角也不变．(D)光强也不变．5．测量单色光的波长时，下列方法中哪一种方法最为准确？( )(A)双缝干涉．(B)牛顿环．(C)单缝衍射．(D)光栅衍射．6．在光栅光谱中，假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上，因而实际上不出现，那么此光栅每个透光缝宽度a和相邻两缝间不透光部分宽度b的关系为( )二．填空题：1．将波长为λ的平行单色光垂直投射于一狭缝上，若对应于衍射图样的第一级暗纹位置的衍射角的绝对值为θ，则缝的宽度等于．2．在单缝夫琅禾费衍射实验中，如果缝宽等于单色入射光波长的 2 倍，则中央明条纹边缘对应的衍射角ϕ= ．3．波长为λ的单色光垂直投射于缝宽为a，总缝数为N，光栅常数为d 的光栅上，光栅方程(表示出现主极大的衍射角ϕ应满足的条件)为．4．若波长为625 nm(1nm=10−9m)的单色光垂直入射到一个每毫米有800 条刻线的光栅上时，则第一级谱线的衍射角为5．衍射光栅主极大公式(a＋b) sinϕ＝±kλ，k＝0,1,2……．在k＝2 的方向上第一条缝与第六条缝对应点发出的两条衍射光的光程差δ＝6．设天空中两颗星对于一望远镜的张角为4.84×10−6 rad，它们都发出波长为550 nm 的光，为了分辨出这两颗星，望远镜物镜的口径至少要等于cm．(1 nm = 10-9 m)三．计算题：1．在用钠光(λ=589.3 nm)做光源进行的单缝夫琅禾费衍射实验中，单缝宽度a=0.5 mm，透镜焦距f=700 mm．求透镜焦平面上中央明条纹的宽度．(1nm=10−9m)2．某种单色平行光垂直入射在单缝上，单缝宽a = 0.15 mm．缝后放一个焦距f = 400 mm 的凸透镜，在透镜的焦平面上，测得中央明条纹两侧的两个第三级暗条纹之间的距离为8.0 mm，求入射光的波长．3．用每毫米300 条刻痕的衍射光栅来检验仅含有属于红和蓝的两种单色成分的光谱．已知红谱线波长λR 在0.63─0.76µm 范围内，蓝谱线波长λB 在0.43─0.49 µm 范围内．当光垂直入射到光栅时，发现在衍射角为24.46°处，红蓝两谱线同时出现．(1) 在什么角度下红蓝两谱线还会同时出现？(2) 在什么角度下只有红谱线出现？4．一平面衍射光栅宽2 cm，共有8000 条缝，用钠黄光(589.3 nm)垂直入射，试求出可能出现的各个主极大对应的衍射角．(1nm=10­9m)5．某种单色光垂直入射到每厘米有8000 条刻线的光栅上，如果第一级谱线的衍射角为30°那么入射光的波长是多少？能不能观察到第二级谱线？6．用钠光(λ=589.3 nm)垂直照射到某光栅上，测得第三级光谱的衍射角为60°．(1) 若换用另一光源测得其第二级光谱的衍射角为30°，求后一光源发光的波长．(2) 若以白光(400 nm－760 nm) 照射在该光栅上，求其第二级光谱的张角．(1 nm= 10-9 m)三．光的偏振一．空题：1．马吕斯定律的数学表达式为I = I0 cos2 α．式中I 为通过检偏器的透射光的强度；I0 为入射的强度；α为入射光方向和检偏器方向之间的夹角．2．两个偏振片叠放在一起，强度为I0 的自然光垂直入射其上，若通过两个偏振片后的光强为I0 / 8 ，则此两偏振片的偏振化方向间的夹角(取锐角)是，若在两片之间再插入一片偏振片，其偏振化方向与前后两片的偏振化方向的夹角（取锐角）相等．则通过三个偏振片后的透射光强度为．3．要使一束线偏振光通过偏振片之后振动方向转过90°，至少需要让这束光通过块理想偏振片．在此情况下，透射光强最大是原来光强的倍．4．自然光以入射角57°由空气投射于一块平板玻璃面上，反射光为完全线偏振光，则折射角为．5．一束自然光以布儒斯特角入射到平板玻璃片上，就偏振状态来说则反射光为，反射光E 矢量的振动方向，透射光为．6．在双折射晶体内部，有某种特定方向称为晶体的光轴．光在晶体内沿光轴传播时，光和光的传播速度相等．二．计算题：1．将两个偏振片叠放在一起，此两偏振片的偏振化方向之间的夹角为60o ，一束光强为I0 的线偏振光垂直入射到偏振片上，该光束的光矢量振动方向与二偏振片的偏振化方向皆成30°角．(1) 求透过每个偏振片后的光束强度；(2) 若将原入射光束换为强度相同的自然光，求透过每个偏振片后的光束强度．2．两个偏振片叠在一起，在它们的偏振化方向成α1＝30°时，观测一束单色自然光．又在α2＝45°时，观测另一束单色自然光．若两次所测得的透射光强度相等，求两次入射自然光的强度之比．3．将三个偏振片叠放在一起，第二个与第三个的偏振化方向分别与第一个的偏振化方向成45°和90°角．(1) 强度为I0 的自然光垂直入射到这一堆偏振片上，试求经每一偏振片后的光强和偏振状态．(2) 如果将第二个偏振片抽走，情况又如何？波动光学解答一．光的干涉一． 选择题：1 2 3 4 5 6B A A B B B 二． 填空题：1．2π(n1 – n2) e / λ2．xd / (5D)3．变小变小4．7.32 mm35．λ26．λ / (2L)7． λ/(2nθ)8．3λ / (2n)9．2d/λ10．2( n – 1) d11．0.170 nm三．计算题：121．解：(1) 如图，设P 0为零级明纹中心 则 D O P d r r /012≈-(l 2 +r 2) - (l 1 +r 1) = 0 ∴ r 2 – r 1 = l 1 – l 2 = 3λ ∴()dD d r r D O P /3/120λ=-=(2) 在屏上距O 点为x 处, 光程差λδ3)/(-≈D dx明纹条件 λδk ±= (k ＝1，2，....)()d D k x k /3λλ+±= 在此处令k ＝0，即为(1)的结果．相邻明条纹间距d D x x x k k /1λ=-=+∆2．解：已知：d ＝0.2 mm ，D ＝1 m ，l ＝20 mm 依公式： λk l DdS ==∴ Ddl k =λ＝4×10-3 mm ＝4000 nm故当 k ＝10 λ1＝ 400 nm k ＝9 λ2＝444.4 nm k ＝8 λ3＝ 500 nm k ＝7 λ4＝571.4 nm k ＝6 λ5＝666.7 nm这五种波长的光在所给观察点最大限度地加强．3．解：(1) 明环半径 ()2/12λ⋅-=R k r()Rk r 1222-=λ＝5×10-5 cm (或500 nm)(2) (2k －1)＝2 r 2 / (R λ)对于r ＝1.00 cm ， k ＝r 2 / (R λ)＋0.5＝50.5故在OA 范围内可观察到的明环数目为50个．4．解：上下表面反射都有相位突变π，计算光程差时不必考虑附加的半波长. 设膜厚为e , B 处为暗纹，2ne ＝21( 2k ＋1 )λ， (k ＝0，1，2，…) A 处为明纹，B 处第8个暗纹对应上式k ＝7()nk e 412λ+=＝1.5×10-3 mm5．解：尽量少反射的条件为2/)12(2λ+=k ne ( k = 0, 1, 2, …)令 k = 0 得 d min = λ / 4n= 114.6 nm二．光的衍射一． 选择题： 1 2 3 4 5 6 B C D B D B一． 填空题：1．λ / sin θ2．±30° (答30° 也可以)3．d sin ϕ =k λ ( k =0，±1，±2,···)4．30 °5．10λ6．13.9三．计算题：1．解： a sin ϕ = λ a f f f x /sin tg 1λφφ=≈== 0.825 mm ∆x =2x 1=1.65 mm2．解：设第三级暗纹在ϕ3方向上，则有 a sin ϕ3 = 3λ此暗纹到中心的距离为x 3 = f tg ϕ3因为ϕ3很小，可认为tg ϕ3≈sin ϕ3，所以x 3≈3f λ / a ．两侧第三级暗纹的距离是 2 x 3 = 6f λ / a = 8.0mm∴ λ = (2x 3) a / 6f = 500 nm3．解： ∵ a +b = (1 / 300) mm = 3.33 μm(1) (a + b ) sin ψ =k λ∴ k λ= (a + b ) sin24.46°= 1.38 μm∵ λR =0.63─0.76 μm ；λB ＝0.43─0.49 μm对于红光，取k =2 , 则λR =0.69 μm对于蓝光，取k =3, 则 λB =0.46 μm红光最大级次 k max = (a + b ) / λR =4.8,取k max =4则红光的第4级与蓝光的第6级还会重合．设重合处的衍射角为ψ' , 则()828.0/4sin =+='b a R λψ∴ ψ'=55.9°(2) 红光的第二、四级与蓝光重合，且最多只能看到四级，所以纯红光谱的第一、三级将出现．()207.0/sin 1=+=b a R λψ ψ1 = 11.9° ()621.0/3sin 3=+=b a R λψ ψ3 = 38.4°4．解：由光栅公式 (a ＋b )sin ϕ = k λ sin ϕ = k λ/(a ＋b ) =0.2357kk =0 ϕ =0k =±1 ϕ1 =±sin -10.2357=±13.6°k =±2 ϕ2 =±sin -10.4714=±28.1°k =±3 ϕ3 =±sin -10.7071=±45.0°k =±4 ϕ4 =±sin -10.9428=±70.5°5．解：由光栅公式(a ＋b )sin ϕ =k λk =1， φ =30°，sin ϕ1=1 / 2∴ λ=(a ＋b )sin ϕ1/ k =625 nm 若k =2, 则 sin ϕ2=2λ / (a + b ) = 1, ϕ2=90° 实际观察不到第二级谱线6．解：(1) (a + b ) sin ϕ = 3λa +b =3λ / sin ϕ ， ϕ=60°a +b =2λ'/sin ϕ' ϕ'=30° 3λ / sin ϕ =2λ'/sin ϕ' λ'=510.3 nm (2) (a + b ) =3λ / sin ϕ =2041.4 nm2ϕ'=sin -1(2×400 / 2041.4) (λ=400nm)2ϕ''=sin -1(2×760 / 2041.4) (λ=760nm) 白光第二级光谱的张角 ∆ϕ = 22ϕϕ'-''= 25°三．光的偏振一．填空题：1．线偏振光(或完全偏振光，或平面偏振光) 光(矢量)振动 偏振化(或透光轴)2．60°(或π / 3)9I 0 / 32 3．2 1/44．33°5．完全（线）偏振光 垂直于入射面 部分偏振光6．寻常非常 或：非常寻常二．计算题：1．解：(1) 透过第一个偏振片的光强I 1I 1＝I 0 cos 230°＝3 I 0 / 4 透过第二个偏振片后的光强I 2， I 2＝I 1cos 260°＝3I 0 / 16(2) 原入射光束换为自然光，则I 1＝I 0 / 2 I 2＝I 1cos 260°＝I 0 / 82．解：令I 1和I 2分别为两入射光束的光强．透过起偏器后，光的强度分别为I 1 / 2和I 2 / 2马吕斯定律，透过检偏器的光强分别为1211cos 21αI I =', 2222cos 21αI I ='按题意，21I I '='，于是 222121cos 21cos 21ααI I = 得 3/2cos /cos /221221==ααI I3．解：(1) 自然光通过第一偏振片后，其强度 I 1 = I 0 / 2通过第2偏振片后，I 2＝I 1cos 245︒＝I 1/ 4通过第3偏振片后，I 3＝I 2cos 245︒＝I 0/ 8通过每一偏振片后的光皆为线偏振光，其光振动方向与刚通过的偏振片的偏振化方向平行． (2) 若抽去第2片，因为第3片与第1片的偏振化方向相互垂直，所以此时I 3 =0. I 1仍不变．4．解：由题可知i 1和i 2应为相应的布儒斯特角，由布儒斯特定律知 tg i 1= n 1＝1.33； tg i 2＝n 2 / n 1＝1.57 / 1.333，由此得 i 1＝53.12°，i 2＝48.69°．由△ABC 可得 θ＋(π / 2＋r )＋(π / 2－i 2)＝π整理得 θ＝i 2－r由布儒斯特定律可知， r ＝π / 2－i 1 将r 代入上式得θ＝i 1＋i 2－π / 2＝53.12°＋48.69°－90°＝11.8°5．解：设I 为自然光强；I 1、I 2分别表示转动前后透射光强．由马吕斯定律得8/330cos 2121I I I =︒=8/60cos 2122I I I =︒=故 3)8//()8/3(/21==I I I I。

第11章 波动光学一. 基本要求1. 解获得相干光的方法。

掌握光程的概念以及光程差与相位差的关系。

2. 能分析、确定杨氏双缝干涉条纹及等厚、等倾干涉条纹的特点（干涉加强、干涉减弱的条件及明、暗条纹的分布规律；了解迈克耳逊干涉仪的原理。

3. 了解惠更斯——菲涅耳原理；掌握分析单缝夫琅禾费衍射暗纹分布规律的方法。

4. 理解光栅衍射公式，会确定光栅衍射谱线的位置，会分析光栅常数及波长对光栅衍射谱线分布的影响。

5. 理解自然光和偏振光及偏振光的获得方法和检验方法。

6. 理解马吕斯定律和布儒斯特定律。

二. 内容提要1. 相干光及其获得方法 能产生干涉的光称为相干光。

产生光干涉的必要条件是：频率相同；振动方向相同；有恒定的相位差。

获得相干光的基本方法有两种：一种是分波阵面法（如杨氏双缝干涉、洛埃镜干涉、菲涅耳双面镜和菲涅耳双棱镜等）；另一种是分振幅法（如平行波膜干涉、劈尖干涉、牛顿环和迈克耳逊干涉仪等）。

2. 光程、光程差与相位差的关系 光波在某一介质中所经历的几何路程l 与介质对该光波的折射率n 的乘积n l 称为光波的光学路程，简称光程。

若光波先后通过几种介质，其总光程为各分段光程之和。

若在界面反射时有半波损失，则反射光的光程应加上或减去2λ。

来自同一点光源的两束相干光，经历不同的光程在某一点相遇，其相位差Δφ与光程差δ的关系为δλπϕ2=∆ 其中λ为光在真空中的波长。

3. 杨氏双缝干涉 经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况：一种是相位差为零或2π的整数倍，合成振幅最大—干涉加强；另一种是相位差为π的奇数倍，合成振动最弱或振幅为零——称干涉减弱或相消。

其对应的光程差为⎪⎩⎪⎨⎧=-±=±= 21k 212 210 干涉减弱），，（）（干涉加强），，（ΛΛλλδk k k 杨氏双缝干涉的光程差还可写成Dx d=δ ，式中d 为两缝间距离，x 为观察屏上纵轴坐标，D 为缝屏间距。

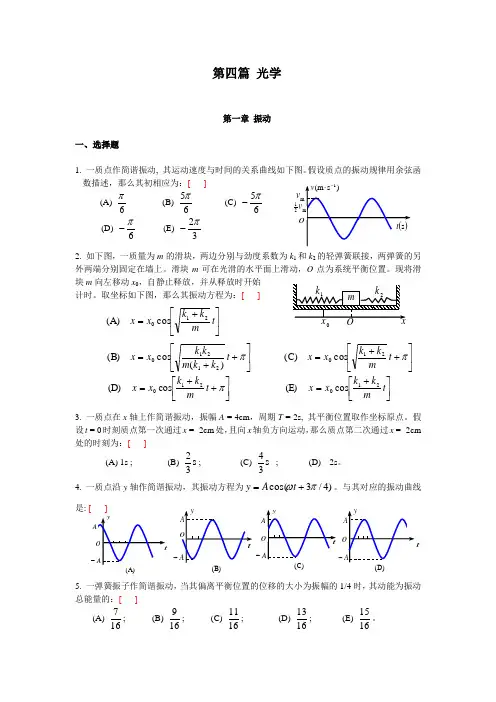
第四篇 光学第一章 振动一、选择题1. 一质点作简谐振动, 其运动速度与时间的关系曲线如下图。

假设质点的振动规律用余弦函数描述，那么其初相应为：[ ] (A)6π (B) 65π (C) 65π- (D) 6π- (E) 32π-2. 如下图，一质量为m 的滑块，两边分别与劲度系数为k 1和k 2的轻弹簧联接，两弹簧的另外两端分别固定在墙上。

滑块m 可在光滑的水平面上滑动，O 点为系统平衡位置。

现将滑块m 向左移动x0，自静止释放，并从释放时开始计时。

取坐标如下图，那么其振动方程为：[ ] ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos(A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D) ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (E)3. 一质点在x 轴上作简谐振动，振幅A = 4cm ，周期T = 2s, 其平衡位置取作坐标原点。

假设t = 0时刻质点第一次通过x = -2cm 处，且向x 轴负方向运动，那么质点第二次通过x = -2cm 处的时刻为：[ ](A) 1s ; (B)s 32; (C) s 34; (D) 2s 。

4. 一质点沿y 轴作简谐振动，其振动方程为)4/3cos(πω+=t A y 。

与其对应的振动曲线是: [ ]5. 一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的：[ ](A)167; (B) 169; (C) 1611; (D) 1613; (E) 1615。

(A)-(B)(C)(D)-06. 图中所画的是两个简谐振动的振动曲线，假设 这两个简谐振动可叠加，那么合成的余弦振动 的初相为： [ ] π21(A) π(B) π23(C) 0(D)二、填空题1. 一简谐振动的表达式为)3cos(ϕ+=t A x ，0=t 时的初位移为0.04m, s -1，那么振幅A = ，初相位 =2. 两个弹簧振子的的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动，经过0.5s 后，第二个振子才从正方向的端点开始运动，那么这两振动的相位差为 。

第十四章波动光学一、基本要求1. 掌握光程的概念以及光程差和相位差的关系。

2. 理解获得相干光的方法，能分析确定杨氏双缝干涉条纹及薄膜等厚干涉条纹的位置，了解迈克尔逊干涉仪的工作原理。

3. 了解惠更斯-菲涅耳原理; 掌握用半波带法分析单缝夫琅和费衍射条纹的产生及其明暗纹位置的计算，会分析缝宽及波长对衍射条纹分布的影响。

4. 掌握光栅衍射公式。

会确定光栅衍射谱线的位置。

会分析光栅常数及波长对光栅衍射谱线分布的影响。

5. 了解自然光和线偏振光。

理解布儒斯特定律和马吕斯定律。

理解线偏振光的获得方法和检验方法。

6. 了解双折射现象。

二、基本内容1. 相干光及其获得方法只有两列光波的振动频率相同、振动方向相同、振动相位差恒定时才会发生干涉加强或减弱的现象，满足上述三个条件的两束光称为相干光。

相应的光源称为相干光源。

获得相干光的基本方法有两种：（1）分波振面法（如杨氏双缝干涉、洛埃镜、菲涅耳双面镜和菲涅耳双棱镜等）；（2）分振幅法（如薄膜干涉、劈尖干涉、牛顿环干涉和迈克耳逊干涉仪等）。

2. 光程和光程差（1）光程把光在折射率为n的媒质中通过的几何路程r折合成光在真空x中传播的几何路程x，称x为光程。

nr（2）光程差在处处采用了光程概念以后就可以把由相位差决定的干涉加强，减弱等情况用光程差来表示，为计算带来方便。

即当两光源的振动相位相同时，两列光波在相遇点引起的振动的位相差πλδϕ2⨯=∆ （其中λ为真空中波长，δ为两列光波光程差） 3. 半波损失光由光疏媒质（即折射率相对小的媒质）射到光密媒质发生反射时，反射光的相位较之入射光的相位发生了π的突变，这一变化导致了反射光的光程在反射过程中附加了半个波长，通常称为“半波损失”。

4. 杨氏双缝干涉经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况：（1）位相差为0或2π的整数倍，合成振动最强；（2）位相差π的奇数倍，合成振动最弱或为0。

其对应的光程差()⎪⎩⎪⎨⎧-±±=212λλδk k ()()最弱最强 ,2,1,2,1,0==k k 杨氏的双缝干涉明、暗条纹中心位置：dD k x λ±= ),2,1,0( =k 亮条纹 d D k x 2)12(λ-±= ),2,1( =k 暗条纹 相邻明纹或相邻暗纹间距:λd D x =∆ （D 是双缝到屏的距离，d 为双缝间距） 5. 薄膜干涉以21n n <为例，此时反射光要计“半波损失”， 透射光不计“半波损失”。

一 计算题9-1-1 在双缝干涉实验中，用波长.1nm 546=λ的单色光照射，双缝与屏的距离mm 300='d 。

测得中央明纹两侧的两个第五级明条纹的间距为12.2mm ，求双缝间的距离。

9-1-2 √将一折射率58.1=n 的云母片覆盖于杨氏双缝中上面的一条缝上，使得屏上原中级极大的所在点O 改变为第五级明纹。

假定nm 550=λ，求：(1)条纹如何移动？(2)云母片厚度t 。

λk r r =-12λ`)1(12k n d r r =-+-=k5`=knm n k d 38.4741158.155051`=-⨯=-=λ9-1-3 使一束水平的氦氖激光器发出的激光(.8nm 632=λ)直照射一双缝。

在缝后.0m 2处的墙上观察到中央明纹和第一级明纹的间隔为4cm 1。

求：(1)两缝的间距；(2)在中央条纹以上还能看到几级明纹？9-1-4 用很薄的玻璃片盖在双缝干涉装置的一条缝上，这时屏上零级条纹移到原来第7级明纹的位置上。

如果入射光的波长nm 550=λ，玻璃片的折射率58.1=n ，求：此玻璃片的厚度。

9-1-5 劳埃德镜干涉装置如图所示，光源波长m 102.77-⨯=λ，求：镜的右边缘到第一条明纹的距离。

9-1-6白光垂直照射到空气中一厚度为nm 380的肥皂膜上，设肥皂的折射率32.1=n。

求：该膜习题9-1-5图的正面呈现的颜色。

9-1-7 √折射率60.1=n 的两块标准平面玻璃板直径形成一个劈形膜(劈尖角θ很小)。

用波长nm 600=λ的单色光垂直照射，产生等厚干涉条纹。

假如在劈形膜内充满40.1=n 的液体时，相邻明条纹间距比劈形膜内是空气时的间距缩小mm 5.0=∆l ，那么劈尖角θ应是多少？2/tan l λθθ=≈ln2/t a n λθθ=≈θλ20=lθλn l 2=)11(20nl l l -=-=∆θλr a d n l 4471071.1)4.111(1052106)11(2---⨯=-⨯⨯⨯=-∆=λθ9-1-8一薄玻璃片，厚度为m .40μ，折射率为1.50，用白光垂直照射，求：在可见光范围内，哪些波长的光在反射中加强？哪些波长的光在透射中加强？9-1-9 √一片玻璃(5.1=n )表面有一层油膜(32.1=n )，今用一波长连续可调的单色光垂直照射油面。

第11章 波动光学一. 基本要求1. 解获得相干光的方法。

掌握光程的概念以及光程差与相位差的关系。

2. 能分析、确定杨氏双缝干涉条纹及等厚、等倾干涉条纹的特点（干涉加强、干涉减弱的条件及明、暗条纹的分布规律；了解迈克耳逊干涉仪的原理。

3. 了解惠更斯——菲涅耳原理；掌握分析单缝夫琅禾费衍射暗纹分布规律的方法。

4. 理解光栅衍射公式，会确定光栅衍射谱线的位置，会分析光栅常数及波长对光栅衍射谱线分布的影响。

5. 理解自然光和偏振光及偏振光的获得方法和检验方法。

6. 理解马吕斯定律和布儒斯特定律。

二. 内容提要1. 相干光及其获得方法 能产生干涉的光称为相干光。

产生光干涉的必要条件是：频率相同；振动方向相同；有恒定的相位差。

获得相干光的基本方法有两种：一种是分波阵面法（如杨氏双缝干涉、洛埃镜干涉、菲涅耳双面镜和菲涅耳双棱镜等）；另一种是分振幅法（如平行波膜干涉、劈尖干涉、牛顿环和迈克耳逊干涉仪等）。

2. 光程、光程差与相位差的关系 光波在某一介质中所经历的几何路程l 与介质对该光波的折射率n 的乘积n l 称为光波的光学路程，简称光程。

若光波先后通过几种介质，其总光程为各分段光程之和。

若在界面反射时有半波损失，则反射光的光程应加上或减去2λ。

来自同一点光源的两束相干光，经历不同的光程在某一点相遇，其相位差Δφ与光程差δ的关系为δλπϕ2=∆ 其中λ为光在真空中的波长。

3. 杨氏双缝干涉 经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况：一种是相位差为零或2π的整数倍，合成振幅最大—干涉加强；另一种是相位差为π的奇数倍，合成振动最弱或振幅为零——称干涉减弱或相消。

其对应的光程差为⎪⎩⎪⎨⎧=-±=±= 21k 212 210 干涉减弱），，（）（干涉加强），，（ΛΛλλδk k k 杨氏双缝干涉的光程差还可写成Dx d=δ ，式中d 为两缝间距离，x 为观察屏上纵轴坐标，D 为缝屏间距。

学习资料收集于网络，仅供参考学习资料收集于网络，仅供参考学习资料学习资料 第七章 波动光学习题答案1．从一光源发出的光线，从一光源发出的光线，通过两平行的狭缝而射在距双缝通过两平行的狭缝而射在距双缝100 cm 的屏上，如两狭缝中心的距离为0.2 mm ，屏上相邻两条暗条纹之间的距离为3 mm ，求光的波长(Å为单位)。

已知已知 D=100cm a=0.2mm D=100cm a=0.2mm d x=3mm求l [解] l =a d x/D=3x/D=3××10-3×0.20.2××10-3/100/100××10-2=0.6=0.6××10-6m=6000 Å2．用波长为7000 Å的红光照射在双缝上，距缝1 m 处置一光屏，如果21个明条纹(谱线以中央亮条为中心而对称分布)共宽2.3 cm ，求两缝间距离。

，求两缝间距离。

[解] 明条纹间距明条纹间距 cm a=6.084．用波长为4800 Å的蓝光照射在缝距为0.1 mm 的双缝上，求在离双缝50 cm 处光屏上干涉条纹间距的大小。

涉条纹间距的大小。

[解]=2.4mm 5．什么是光程?在不同的均匀媒质中，在不同的均匀媒质中，单色光通过相等光程时，单色光通过相等光程时，单色光通过相等光程时，其几何路程是否相同其几何路程是否相同? 需要时间是否相同?[解]光程=nx 。

在不同的均匀媒质中，单色光通过相等光程时，其几何路程是不同。

需要时间相同相同6．在两相干光的一条光路上，在两相干光的一条光路上，放入一块玻璃片，其折射率为放入一块玻璃片，其折射率为1.6，结果中央明条纹移到原是第六级明条纹处，设光线垂直射入玻璃片，入射光波长为6.6×103 Å。

求玻璃片厚度。

求玻璃片厚度。

已知已知 n=1.6 n=1.6 l =6.6=6.6××103Å 求 d[解]光程差MP-d+nd-NP=0 ∵ NP-MP=6l∴ （n-1n-1））d=6ld=6l /(n-1)=6.6/(n-1)=6.6××10-6m7．在双缝干涉实验中，用钠光灯作光源(l =5893 Å)，屏幕离双缝距离D=500mm ，双缝间距a=1.2mm ，并将干涉实验装置整个地浸在折射率1.33的水中，相邻干涉条纹间的距离为多大?若把实验装置放在空气中，干涉条纹变密还是变疏?(通过计算回答)已知n 水=1.33 l =5893Å D=500 mm a=1.2mm 比较d x 水和d x 空气 [解] d x 水=D l /na=500/na=500××5893×10-10×10-3/(1.2×10-3×1.33)=1.85×10-4m d x 空气=D l /a=500×5893×10-10×10-3/(1.2×10-3)=2.46×10-4m∴ 干涉条纹变疏干涉条纹变疏8．用白光垂直照射到厚度为4×10-5 cm 的薄膜上，薄膜的折射率为1.5。

（答案1）波动光学习题波动光学习题光程、光程差1.在真空中波长为λ的单⾊光，在折射率为n 的透明介质中从A 沿某路径传播到B ，若A 、B两点相位差为3π，则此路径AB 的光程为(A) 1.5 λ． (B) 1.5 λ/ n ．(C) 1.5 n λ． (D) 3 λ．［ A ］2.在相同的时间内，⼀束波长为λ的单⾊光在空⽓中和在玻璃中(A) 传播的路程相等，⾛过的光程相等．(B) 传播的路程相等，⾛过的光程不相等．(C) 传播的路程不相等，⾛过的光程相等．(D) 传播的路程不相等，⾛过的光程不相等．［ C ］3.如图，S 1、S 2是两个相⼲光源，它们到P 点的距离分别为r 1和r 2．路径S 1P 垂直穿过⼀块厚度为t 1，折射率为n 1的介质板，路径S 2P 垂直穿过厚度为t 2，折射率为n 2的另⼀介质板，其余部分可看作真空，这两条路径的光程差等于 (A) )() (111222t n r t n r +-+(B) ])1([])1([211222t n r t n r -+--+(C) )()(111222t n r t n r ---(D) 1122t n t n - ［ B ］4.如图所⽰，平⾏单⾊光垂直照射到薄膜上，经上下两表⾯反射的两束光发⽣⼲涉，若薄膜的厚度为e ，并且n 1＜n 2＞n 3，λ1为⼊射光在折射率为n 1的媒质中的波长，则两束反射光在相遇点的相位差为 (A) 2πn 2e / ( n 1 λ1)． (B)[4πn 1e / ( n 2 λ1)] + π． (C) [4πn 2e / ( n 1 λ1) ]+ π．(D) 4πn 2e / ( n 1 λ1)．［ C ］5.真空中波长为λ的单⾊光，在折射率为n 的均匀透明媒质中，从A 点沿某⼀路径传播到B点，路径的长度为l ．A 、B 两点光振动相位差记为?φ，则(A) l ＝3 λ / 2，?φ＝3π． (B) l ＝3 λ / (2n )，?φ＝3n π．(C) l ＝3 λ / (2n )，?φ＝3π． (D) l ＝3n λ / 2，?φ＝3n π．［］6.如图所⽰，波长为λ的平⾏单⾊光垂直⼊射在折射率为n 2的薄膜上，经上下两个表⾯反射的两束光发⽣⼲涉．若薄膜厚度为e ，⽽且n 1＞n 2＞n 3，则两束反射光在相遇点的相位差为 (A) 4πn 2 e / λ． (B) 2πn 2 e / λ．(C) (4πn 2 e / λ) +π． (D) (2πn 2 e / λ) -π．［ A ］ P S 1S2 r 1 n 1 n 2 t 2 r 2 t 1n 13λ1 n 1 3λ7.如图所⽰，折射率为n 2、厚度为e 的透明介质薄膜的上⽅和下⽅的透明介质的折射率分别为n 1和n 3，已知n 1＜n 2＜n 3．若⽤波长为λ的单⾊平⾏光垂直⼊射到该薄膜上，则从薄膜上、下两表⾯反射的光束①与②的光程差是［ A ］ (A) 2n 2 e ． (B) 2n 2 e －λ / 2 . (C) 2n 2 e －λ． (D) 2n 2 e －λ / (2n 2)．8.若⼀双缝装置的两个缝分别被折射率为n 1和n 2的两块厚度均为e 的透明介质所遮盖，此时由双缝分别到屏上原中央极⼤所在处的两束光的光程差δ＝_____(n 1-n 2)e 或(n 2-n 1)e 均可__．9.如图所⽰，假设有两个同相的相⼲点光源S 1和S 2，发出波长为λ的光．A 是它们连线的中垂线上的⼀点．若在S 1与A 之间插⼊厚度为e 、折射率为n 的薄玻璃⽚，则两光源发出的光在A 点的相位差?φ＝___2π (n -1) e / λ_____．若已知λ＝500nm ，n ＝1.5，A 点恰为第四级明纹中⼼，则e ＝_ 4×103__nm ．10.如图，在双缝⼲涉实验中，若把⼀厚度为e 、折射率为n 的薄云母⽚覆盖在S 1缝上，中央明条纹将向___上__移动；覆盖云母⽚后，两束相⼲光⾄原中央明纹O 处的光程差为___(n -1)e _．11.波长为λ的单⾊光垂直照射如图所⽰的透明薄膜．膜厚度为e ，两束反射光的光程差δ＝___2.60 e _．12.⽤波长为λ的单⾊光垂直照射置于空⽓中的厚度为e 折射率为1.5的透明薄膜，两束反射光的光程差δ＝__ 3e +2/λ或 3e -2/λ _．双缝⼲涉1.⽤⽩光光源进⾏双缝实验，若⽤⼀个纯红⾊的滤光⽚遮盖⼀条缝，⽤⼀个纯蓝⾊的滤光⽚遮盖另⼀条缝，则(A) ⼲涉条纹的宽度将发⽣改变．(B) 产⽣红光和蓝光的两套彩⾊⼲涉条纹．(C) ⼲涉条纹的亮度将发⽣改变．(D) 不产⽣⼲涉条纹．［ D ］2. 在双缝⼲涉实验中，两条缝的宽度原来是相等的．若其中⼀缝的宽度略变窄(缝中⼼位置不变)，则(A) ⼲涉条纹的间距变宽．(B) ⼲涉条纹的间距变窄．(C) ⼲涉条纹的间距不变，但原极⼩处的强度不再为零．(D) 不再发⽣⼲涉现象．［ C ］3.在双缝⼲涉实验中，为使屏上的⼲涉条纹间距变⼤，可以采取的办法是(A) 使屏靠近双缝． (B) 使两缝的间距变⼩．(C) 把两个缝的宽度稍微调窄．(D) 改⽤波长较⼩的单⾊光源．［ B ］n 3 S4.在双缝⼲涉实验中，屏幕E 上的P 点处是明条纹．若将缝S 2盖住，并在S 1 S 2连线的垂直平分⾯处放⼀⾼折射率介质反射⾯M ，如图所⽰，则此时 (A) P 点处仍为明条纹． (B) P 点处为暗条纹．(C) 不能确定P 点处是明条纹还是暗条纹．(D) ⽆⼲涉条纹．［ B ］5.在双缝⼲涉实验中，光的波长为600 nm (1 nm ＝10－9 m )，双缝间距为2 mm ，双缝与屏的间距为300 cm ．在屏上形成的⼲涉图样的明条纹间距为(A) 0.45 mm ． (B) 0.9 mm ．(C) 1.2 mm (D) 3.1 mm ．［ B ］6.在双缝⼲涉实验中，⼊射光的波长为λ，⽤玻璃纸遮住双缝中的⼀个缝，若玻璃纸中光程⽐相同厚度的空⽓的光程⼤2.5 λ，则屏上原来的明纹处(A) 仍为明条纹； (B) 变为暗条纹；(C) 既⾮明纹也⾮暗纹； (D) ⽆法确定是明纹，还是暗纹．［ B ］7.在双缝⼲涉实验中，若单⾊光源S 到两缝S 1、S 2距离相等，则观察屏上中央明条纹位于图中O 处．现将光源S 向下移动到⽰意图中的S '位置，则 (A) 中央明条纹也向下移动，且条纹间距不变． (B) 中央明条纹向上移动，且条纹间距不变． (C) 中央明条纹向下移动，且条纹间距增⼤． (D)中央明条纹向上移动，且条纹间距增⼤。

波动光学篇习题十二·光的干涉12-1 某单色光从空气射入水中，其频率、波速、波长是否变化?怎样变化?12-2 在杨氏双缝实验中，作如下调节时，屏幕上的干涉条纹将如何变化?试说明理由． (1)使两缝之间的距离变小；(2)保持双缝间距不变，使双缝与屏幕间的距离变小； (3)整个装置的结构不变，全部浸入水中； (4)光源作平行于1S ，2S 联线方向上下微小移动；(5)用一块透明的薄云母片盖住下面的一条缝．12-3 什么是光程? 在不同的均匀媒质中，若单色光通过的光程相等时，其几何路程是否相同?其所需时间是否相同?在光程差与位相差的关系式∆λπϕ∆2=中,光波的波长要用真空中波长,为什么?12-4 如题12-4图所示，A ，B 两块平板玻璃构成空气劈尖，分析在下列情况中劈尖干涉条纹将如何变化?(1) A 沿垂直于B 的方向向上平移［见图(a)］； (2) A 绕棱边逆时针转动［见图(b)］．题12-4图12-5 用劈尖干涉来检测工件表面的平整度，当波长为λ的单色光垂直入射时,观察到的干涉条纹如题12-5图所示，每一条纹的弯曲部分的顶点恰与左邻的直线部分的连线相切．试说明工件缺陷是凸还是凹?并估算该缺陷的程度．题12-5图题12-6图12-6 如题12-6图，牛顿环的平凸透镜可以上下移动，若以单色光垂直照射，看见条纹向中心收缩，问透镜是向上还是向下移动?12-7 在杨氏双缝实验中，双缝间距d=0.20mm，缝屏间距D＝1.0m，试求：(1)若第二级明条纹离屏中心的距离为6.0mm，计算此单色光的波长；(2)相邻两明条纹间的距离．12-8 在双缝装置中，用一很薄的云母片(n=1.58)覆盖其中的一条缝，结果使屏幕上的第七级明条纹恰好移到屏幕中央原零级明纹的位置．若入射光的波长为5500oA，求此云母片的厚度．12-9 洛埃镜干涉装置如题12-9图所示，镜长30cm，狭缝光源S在离镜左边20cm的平面内，与镜面的垂直距离为2.0mm，光源波长=λ7.2×10-7m，试求位于镜右边缘的屏幕上第一条明条纹到镜边缘的距离．题12-9图12-10 一平面单色光波垂直照射在厚度均匀的薄油膜上，油膜覆盖在玻璃板上．油的折射率为1.30，玻璃的折射率为1.50，若单色光的波长可由光源连续可调，可观察到5000 o A 与7000 oA 这两个波长的单色光在反射中消失．试求油膜层的厚度．12-11 白光垂直照射到空气中一厚度为3800 oA 的肥皂膜上，设肥皂膜的折射率为1.33，试问该膜的正面呈现什么颜色?背面呈现什么颜色?12-12 在折射率1n =1.52的镜头表面涂有一层折射率2n =1.38的Mg 2F 增透膜，如果此膜适用于波长λ=5500 oA 的光，问膜的厚度应取何值?12-13 如题12-13图，波长为6800oA 的平行光垂直照射到L ＝0.12m 长的两块玻璃片上，两玻璃片一边相互接触，另一边被直径d =0.048mm 的细钢丝隔开．求： (1)两玻璃片间的夹角=θ?(2)相邻两明条纹间空气膜的厚度差是多少? (3)相邻两暗条纹的间距是多少? (4)在这0.12 m 内呈现多少条明条纹?题12-13图12-14 用=λ5000oA 的平行光垂直入射劈形薄膜的上表面，从反射光中观察，劈尖的棱边是暗纹．若劈尖上面媒质的折射率1n 大于薄膜的折射率n (n =1.5)．求： (1)膜下面媒质的折射率2n 与n 的大小关系； (2)第10条暗纹处薄膜的厚度；(3)使膜的下表面向下平移一微小距离e ∆，干涉条纹有什么变化?若e ∆=2.0 μm ，原来的第10条暗纹处将被哪级暗纹占据?12-15 (1)若用波长不同的光观察牛顿环，1λ＝6000oA ，2λ＝4500oA ，观察到用1λ时的第k 个暗环与用2λ时的第k+1个暗环重合，已知透镜的曲率半径是190cm ．求用1λ时第k 个暗环的半径．(2)又如在牛顿环中用波长为5000oA 的第5个明环与用波长为2λ的第6个明环重合，求未知波长2λ．12-16 当牛顿环装置中的透镜与玻璃之间的空间充以液体时，第十个亮环的直径由1d ＝1.40×10-2m 变为2d ＝1.27×10-2m ，求液体的折射率．12-17 利用迈克耳逊干涉仪可测量单色光的波长．当1M 移动距离为0.322mm 时，观察到干涉条纹移动数为1024条，求所用单色光的波长．12-18 把折射率为n =1.632的玻璃片放入迈克耳逊干涉仪的一条光路中，观察到有150条干涉条纹向一方移过．若所用单色光的波长为λ=5000oA ，求此玻璃片的厚度．习题十三·光的衍射13-1 衍射的本质是什么?衍射和干涉有什么联系和区别?13-2 在夫琅禾费单缝衍射实验中，如果把单缝沿透镜光轴方向平移时，衍射图样是否会 跟着移动?若把单缝沿垂直于光轴方向平移时，衍射图样是否会跟着移动?13-3 什么叫半波带?单缝衍射中怎样划分半波带?对应于单缝衍射第3级明条纹和第4级暗 条纹，单缝处波面各可分成几个半波带?13-4 在单缝衍射中，为什么衍射角ϕ愈大（级数愈大）的那些明条纹的亮度愈小?13-5 若把单缝衍射实验装置全部浸入水中时，衍射图样将发生怎样的变化?如果此时用公式),2,1(2)12(sin =+±=k k a λϕ来测定光的波长，问测出的波长是光在空气中的还是在水中的波长?13-6 在单缝夫琅禾费衍射中，改变下列条件，衍射条纹有何变化?(1)缝宽变窄；(2)入 射光波长变长；(3)入射平行光由正入射变为斜入射．13-7 单缝衍射暗条纹条件与双缝干涉明条纹的条件在形式上类似，两者是否矛盾?怎样 说明?13-8 光栅衍射与单缝衍射有何区别?为何光栅衍射的明条纹特别明亮而暗区很宽?13-9 试指出当衍射光栅的光栅常数为下述三种情况时，哪些级次的衍射明条纹缺级?(1) a+b=2a;(2)a+b=3a;(3)a+b=4a.13-10 若以白光垂直入射光栅，不同波长的光将会有不同的衍射角．问(1)零级明条纹能 否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大?不同波长的光分开程度与什 么因素有关?13-11 一单色平行光垂直照射一单缝，若其第三级明条纹位置正好与6000οA 的单色平行光的第二级明条纹位置重合，求前一种单色光的波长．13-12 单缝宽0.10mm ，透镜焦距为50cm ，用5000=λoA 的绿光垂直照射单缝．求：(1)位于透镜焦平面处的屏幕上中央明条纹的宽度和半角宽度各为多少?(2)若把此装置浸入水中(n=1.33)，中央明条纹的半角宽度又为多少?13-13 用橙黄色的平行光垂直照射一宽为a=0.60mm 的单缝，缝后凸透镜的焦距f=40.0cm ，观察屏幕上形成的衍射条纹．若屏上离中央明条纹中心1.40mm 处的P 点为一明条纹；求：(1)入射光的波长；(2)P 点处条纹的级数；(3)从P 点看，对该光波而言，狭缝处的波面可分成几个半波带?13-14 用5900=λoA 的钠黄光垂直入射到每毫米有500条刻痕的光栅上，问最多能看到第几级明条纹?13-15 波长为5000o A 的平行单色光垂直照射到每毫米有200条刻痕的光栅上，光栅后的透镜焦距为60cm ．求：(1)屏幕上中央明条纹与第一级明条纹的间距；(2)当光线与光栅法线成 30°斜入射时，中央明条纹的位移为多少?13-16 波长6000=λo A 的单色光垂直入射到一光栅上，第二、第三级明条纹分别出现在20.0sin =ϕ与30.0sin =ϕ处，第四级缺级．求：(1)光栅常数；(2)光栅上狭缝的宽度；(3)在90°＞ϕ＞-90°范围内，实际呈现的全部级数．13-17 一双缝，两缝间距为0.1mm ，每缝宽为0.02mm ，用波长为4800oA 的平行单色光垂直入射双缝，双缝后放一焦距为50cm 的透镜．试求：(1)透镜焦平面上单缝衍射中央明条纹的宽度；(2)单缝衍射的中央明条纹包迹内有多少条双缝衍射明条纹?13-18 在夫琅禾费圆孔衍射中，设圆孔半径为0.10mm ，透镜焦距为50cm ，所用单色光波长为5000oA ，求在透镜焦平面处屏幕上呈现的爱里斑半径．13-20 已知入射的X 射线束含有从0.95～1.30oA 范围内的各种波长，晶体的晶格常数为2.75oA ，当X 射线以45°角入射到晶体时，问对哪些波长的X 射线能产生强反射?习题十四·光的偏振14-1 自然光是否一定不是单色光?线偏振光是否一定是单色光?14-2 用哪些方法可以获得线偏振光?怎样用实验来检验线偏振光、部分偏振光和自然光?14-3 一束光入射到两种透明介质的分界面上时，发现只有透射光而无反射光，试说明这束光是怎样入射的?其偏振状态如何?14-4 什么是光轴、主截面和主平面?什么是寻常光线和非常光线?它们的振动方向和各自的主平面有何关系?14-5 在单轴晶体中，e 光是否总是以e n c /的速率传播?哪个方向以0/n c 的速率传播?14-6是否只有自然光入射晶体时才能产生O 光和e 光?14-7投射到起偏器的自然光强度为0I ，开始时，起偏器和检偏器的透光轴方向平行．然后使检偏器绕入射光的传播方向转过130°，45°，60°，试分别求出在上述三种情况下，透过检偏器后光的强度是0I 的几倍?14-8 使自然光通过两个偏振化方向夹角为60°的偏振片时，透射光强为1I ，今在这两个偏振片之间再插入一偏振片，它的偏振化方向与前两个偏振片均成30°，问此时透射光I 与1I 之比为多少?14-9 自然光入射到两个重叠的偏振片上．如果透射光强为，(1)透射光最大强度的三分之一，(2)入射光强的三分之一，则这两个偏振片透光轴方向间的夹角为多少?14-10 一束自然光从空气入射到折射率为1.40的液体表面上，其反射光是完全偏振光．试求：(1)入射角等于多少?(2)折射角为多少?14-11 利用布儒斯特定律怎样测定不透明介质的折射率?若测得釉质在空气中的起偏振角为58°，求釉质的折射率．14-12 光由空气射入折射率为n 的玻璃．在题14-12图所示的各种情况中，用黑点和短线把反射光和折射光的振动方向表示出来，并标明是线偏振光还是部分偏振光．图中.arctan ,00n i i i =≠题图14-12*14-13如果一个二分之一波片或四分之一波片的光轴与起偏器的偏振化方向成30°角，试问从二分之一波片还是从四分之一波片透射出来的光将是：(1)线偏振光?(2)圆偏振光?(3)椭圆偏振光?为什么?题14-13图*14-14 将厚度为1mm且垂直于光轴切出的石英晶片，放在两平行的偏振片之间，对某一波长的光波，经过晶片后振动面旋转了20°．问石英晶片的厚度变为多少时，该波长的光将完全不能通过?。